Abstract
Recombination has essential roles in increasing genetic variability within a population and in ensuring successful meiotic events. The objective of this study is to (i) infer the population-scaled recombination rate (ρ), and (ii) identify and characterize regions of increased recombination rate for the domestic cat, Felis silvestris catus. SNPs (n = 701) were genotyped in twenty-two East Asian feral cats (random bred). The SNPs covered ten different chromosomal regions (A1, A2, B3, C2, D1, D2, D4, E2, F2, X) with an average region size of 850 Kb and an average SNP density of 70 SNPs/region. The Bayesian method in the program inferRho was used to infer regional population recombination rates and hotspots localities. The regions exhibited variable population recombination rates and four decisive recombination hotspots were identified on cat chromosome A2, D1, and E2 regions. As a description of the identified hotspots, no correlation was detected between the GC content and the locality of recombination spots, and the hotspots enclosed L2 LINE elements and MIR and tRNA-Lys SINE elements.
Introduction
Recombination is a major source of genetic variation within sexually reproducing organisms, and is necessary for the proper alignment and segregation of homologous chromosomes during meiosis. New combinations of parental alleles across loci are generated via recombination and transmitted to succeeding generations. Lack of recombination may cause failure of meiotic division, or formation of gametes with chromosome number abnormalities (aneuploidy), which are often detrimental.
Localized chromosomal regions with high recombination rates relative to surrounding areas are referred to as recombination “hotspots” [1]. Known hotspots in mice and human are generally 1–2 kb regions of high recombination rates surrounded by regions of low recombination [2]. In humans, recombination hotspots are distributed about every 200 Kb [3] and over 25 000 hotspots have been identified [4]. The first human recombination hotspot was identified using restriction site polymorphisms in β-globin gene cluster [5]. A higher resolution human hotspot was localized using sperm typing via PCR in a region that harbors GC-rich mini-satellite (MS32) as a molecular signature [6].
Several genomic features exhibit correlations with recombination hotspots. The GC content has been found to be positively correlated with recombination hotspots in humans [4], dog [7], pig [8], and chicken [9] but not in mice [10]. Long terminal repeats (LTR), long interspersed elements (LINE), and short interspersed elements (SINE) were also observed to be positively correlated with the locality of recombination hot spots in human [4,11], mice [10] and pigs [8]. DNA motifs (cis) have been identified to be associated with recombination hot spots both in humans [4,12,13] and in other organisms [14]. In addition to the cis elements presented by the motifs, a trans element, PRDM9, was found to be a major determinant of recombination hotspots in human and mice [15,16] but not in dog and related wild relatives [7,17,18]. PRDM9 is thought to bind to a DNA motif via a zinc finger domain, altering the chromatin structure through methylation, and recruiting recombination molecular machinery [19,20].
Coarse-scale recombination in cats has previously been investigated through linkage map analyses using sparsely distributed microsatellite markers [21,22]. The objective of this study is to investigate fine-scale recombination rates, and recombination hotspots, in the domestic cat using population-level data for dense SNPs in ten selected genomic regions on ten different chromosomes.
Materials and Methods
Samples and genotypes
SNP genotype data of twenty-two feral cats from China were obtained as previously described in [23]. The data were generated using a custom Illumina GoldenGate array that represent ten different cat chromosomal regions (A1, A2, B3, C2, D1, D2, D4, E2, F2, X) and were composed of 1536 markers nearly equally distributed across the ten regions. Markers’ positions were updated to their location in the 6.2 cat genome assembly (http://genome.ucsc.edu/). To ensure successful inference, three criteria were used to filter the SNPs: (i) SNPs mapped to a single chromosomal location on the most recent genome assembly of cat with 100% sequence match, (ii) SNPs exhibiting a genotype call success rate of ≥ 80%, and (iii) SNPs possessing a minor allele frequency of ≥ 0.1. The final dataset, included in this study, is composed of 701 markers distributed over the ten regions (S1 Table). The genomic locations of the regions and related summaries are shown in Table 1 (see also Fig 1 and S2 Fig).
Table 1. Summary of the chromosomal regions analyzed for recombination in cats.
| Chr. | No. SNPs | Position (bp) 1 | Region size (bp) | Mean inter-SNP distance | Mean Rho (ρ/Mb) | Number bins with BF 2 | |||
|---|---|---|---|---|---|---|---|---|---|
| Start | End | < 100 | ≥ 100 | Total | |||||
| A1 | 53 | 187 299 691 | 188 082 901 | 783 210 | 15 061 | 127.68 | 3915 | 0 | 3915 |
| A2 | 73 | 98 172 535 | 98 956 464 | 783 929 | 10 890 | 186.51 | 3904 | 15 | 3919 |
| B3 | 88 | 126 081 886 | 126 859 181 | 777 295 | 8 934 | 202.67 | 3886 | 0 | 3886 |
| C2 | 53 | 4 360 303 | 5 085 917 | 725 614 | 13 950 | 291.85 | 3628 | 0 | 3628 |
| D1 | 70 | 50 348 845 | 51 177 183 | 828 338 | 12 000 | 176.72 | 4131 | 10 | 4141 |
| D2 | 86 | 59 655 061 | 60 470 312 | 815 251 | 9 591 | 192.93 | 4074 | 0 | 4074 |
| D4 | 73 | 45 514 026 | 46 304 562 | 790 536 | 10 980 | 259.47 | 3951 | 0 | 3951 |
| E2 | 90 | 42 987 235 | 43 794 319 | 807 084 | 9 068 | 309.48 | 4002 | 32 | 4034 |
| F2 | 78 | 10 965 562 | 12 451 350 | 1 485 788 | 19 300 | 185.95 | 7427 | 0 | 7427 |
| X | 37 | 100 018 322 | 100 740 914 | 722 592 | 20 070 | 77.45 | 3613 | 0 | 3613 |
| Mean | 70 | - | - | 851 964 | 12 984 | 201 | 4253 | 6 | 4259 |
| Total | 701 | - | - | 8 519 637 | - | - | 42531 | 57 | 42588 |
1 Start and end positions are based on the 2011 cat genome assembly (ICGSC Felis_catus 6.2)
2 BF: Bayes factor.
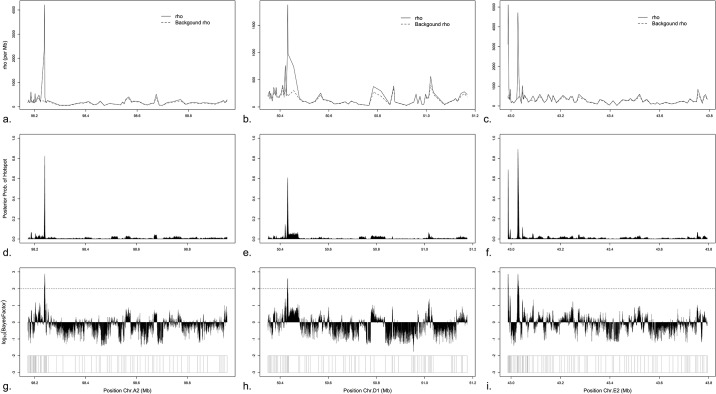
Fig 1. Recombination overview of chromosomes A2, D1, and E2 regions.
(a-c) Posterior recombination rates (population size scaled) across chromosomes A2, D1, and E2 regions, respectively. Solid line shows the whole recombination rates, while the dashed line shows the background recombination rates. (d-f) Posterior probability of hotspots along chromosomes A2, D1, and E2 regions, respectively. (g-i) Bayes factor of hotspots for chromosomes A2, D1, and E2 regions, respectively. Horizontal dotted line corresponds to Bayes factor of 100 in a log10 scale. Position and distribution of SNPs included in the recombination analysis are at the bottom.
Three SNPs residing in a recombination hotspot on chromosome E2 region (see results) were chosen for genotype validation via sequencing. Primers were designed to flank the SNPs (S2 Table) and PCR was performed using DNA Engine Gradient Cycler (MJ Research, GMI, Ramsey, MN) using the following conditions. For each reaction, 2μl of DNA was used in a 1.5mM magnesium concentration with 1μM primers in a total reaction volume of 20μl. The annealing temperature of all primers was 62°C. The PCR protocol was as follows: initial denaturation at 94°C for 5 min followed by 40 cycles of 94°Cx45 sec, 62°Cx20 sec, 72°Cx30 sec, and a final extension at 72°C for 20 min. The PCR products were purified with ExoSap (USB, Cleveland, OH) per the manufacture’s recommendations and directly sequenced using the BigDye terminator Sequencing Kit v3.1 (Applied Biosystems, Foster City, CA) as previously implemented [24]. Sequences were verified and aligned using the software sequencer version 4.10 (Gene Codes Corp., Ann Arbor, MI).
Recombination inference
The program inferRho uses the coalescent with recombination model [25–27] in a full Bayesian framework to infer recombination rates and hot spots along the chromosome regions [28,29]. The evolutionary relationship of the SNPs is represented by the ancestral recombination graph (ARG), which is an unobserved random variable that is integrated over using Markov Chain Monte Carlo (MCMC). In the variable recombination rate model, the population-scaled recombination rate is ρi = 4Neci, where Ne is the effective population size, ci is the recombination rate per generation in cM/Mb between marker i and i +1 (i = 1,…, k − 1, and k is the total number of SNPs). The total recombination rate (ci) consists of the background crossing-over rate and recombination hotspots (arising according to a Markov process) [28,29]. As genetic data (SNPs) from a population sample of unrelated individuals only provide information about evolutionary distance, the parameters in coalescent estimators are typically scaled by the effective population size (i.e. θ = 4Neμ, where μ is the substitution rate per site per generation; and ρ = 4Nec). To convert ρ into standard unit (cM/Mb), we need to divide it by the ploidy factor and effective population size (4Ne for the nuclear genome of cats), which typically comes from other sources of information.
To make the data analysis computationally tractable, each chromosomal region was divided into blocks, with 20 SNPs per block (e.g., chromosome A1 region with 53 SNPs was divided into 3 blocks, 20 SNPs in the first and second block and 13 SNPs in the third block). Blocks from each chromosomal region are assumed to share the same population size parameter (θ) but have an independent ARG for each block. Preliminary runs were executed to determine the appropriate length and thinning interval of the MCMC chain for each chromosomal dataset. The last half of the MCMC samples (1000 samples) was used to estimate the recombination rates (ρi) and to plot them with respect to the SNP marker positions. The mean population-scaled recombination rate per site for each chromosomal region was calculated using the following equation:
in which di is the distance between marker i and i+1, and k is the total number of markers in the region. The numerator is total population-scaled recombination rate of the region, while the denominator is the length of this region in Mb.
Designation of recombination hot spots
We calculated the Bayes factors [30] to locate the positions of hotspots and represent relative odds of a hotspot being present. Each chromosomal region was divided into bins (200 bp per bin) for analysis of posterior samples, which contain the start and end positions of the hotspots, to estimate the probability of having hotspot (pj) for each bin. The corresponding probability of hotspot for each bin (qj) from the prior was obtained by running the program without data (e.g., constant likelihood) but maintaining the same sample size and marker positions. The Bayes factor (BF) is defined as the ratio of the posterior and prior odds:
The odds ratio measures the proportional change in odds favoring a hotspot in the region (versus the prior odds) that results from including the data (SNPs). The total number of bins depends on the length of the region; thus the range of j is variable among the ten chromosome regions. Recombination hotspots are defined to have at least two consecutive bins with BF ≥ 100 whereas regions of BF < 100 are denoted as “neutral” bins awaiting further investigation (cf. section 3.2 in [30]).
GC content and genomic elements analyses
The GC content was calculated for the sequences of each bin using the function CG.content of package APE in R [31].
Variation and repeat elements within each of the ten chromosomal regions were downloaded from UCSC genome browser using RepeatMasker for the v6.2 cat genome assembly. Elements were analyzed separately for bins with BF < 100 and BF ≥ 100 (hotspot bins). The elements within neutral bins (BF < 100) were to provide the general overview of the elements within each chromosomal region.
Results
Samples and genotypes
The dataset is composed of 701 SNPs on ten different cat chromosomal regions with an average of 70 SNPs/region. The chromosome E2 region harbors the highest number of SNPs (n = 90) while chromosome X region has the lowest (n = 37). SNPs are distributed across the regions with an average distance between SNPs of 12 Kb and a range of 145 bp– 651 Kb (Table 1). Four SNPs were selected for genotype verification using direct sequencing. The sequencing results were concordant to the genotypes obtained previously using the genotyping platform.
Recombination rates and hotspots
The ten regions on chromosomes: A1, A2, B3, C2, D1, D2, D4, E2, F2, and X, were analyzed using inferRho. The lengths of the MCMC chains were determined by the trace plot and effective sample size (ESS) of the parameters as: 600 000 iterations for A1, C2; 800 000 iterations for A2, D1, D4, F2; 1 000 000 iterations for B3, D2, E2; and 500 000 iterations for X. Two thousand posterior samples for each chromosomal dataset were obtained after thinning, while the first half was discarded as burn-in. Using a parallel computing approach, each run could be accomplished within one to two weeks on a cluster with 2 Opteron 270 (2.0 GHz) processors per node.
Population recombination rate (ρ) is plotted for each region (Fig 1a–1c and S1a Fig). The mean recombination rate (ρ) across all regions is 200 per Mb. The E2 region exhibits the highest mean rate (309 /Mb) whereas X region has the lowest (77 /Mb) (Table 1). The difference between the background recombination rate and whole recombination rate is indicative of recombination spots. This difference is most noticeable in regions of chromosomes A2, D1, and E2 (Fig 1a–1c).
The posterior probability of hotspot was calculated for bins of size 200 bp in each region (Fig 1d–1f and S1b Fig). Chromosomes A2, D1, and E2 show distinctly high posterior probabilities (> 0.6) in four localized areas (Fig 1d–1f). The posterior probabilities for the other seven chromosome regions (A1, B3, C2, D2, D4, F2, and X) are less than 0.2, indicating little support for elevation of recombination rate in these areas.
The Bayes factors (Fig 1g–1i and S1c Fig) are consistent in pattern with the posterior probabilities (Fig 1d–1f and S1b Fig) and recombination rates (Fig 1a–1c and S1a Fig). Approximately 99% (n = 42,531) of bins were classified as “neutral” (BF < 100) across all regions examined. The hot spots were found in only three chromosomal regions (A2, D1, and E2) and represented ~ 0.13% (n = 57) of all bins studied. Summaries of the numbers and distribution of bins within each chromosomal region are provided in Table 1. The hotspots had size of 3 Kb in A2, 1.8 Kb in D1, and 1.8 Kb for the first and 4.6 Kb for the second in E2. The distance between the two hotspots on E2 was ~37.4 Kb (Table 2).
Table 2. Summary of recombination “hotspots” in cats selected regions.
| Chr. | Position (bp) | Size (Kb) | # bins | Mean | Elements | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Start | End | PP | BF | GC | LINE | SINE | LC | LTR | SR | DNA | |||
| A2 | 98 237 700 | 98 240 700 | 3 | 15 | 0.54 | 339.85 | 0.35 | L1MEg | SINEC-Fc2 MIR MIRb | AT-rich | - | - | MER46C |
| D1 | 50 430 400 | 50 432 200 | 1.8 | 9 | 0.56 | 271.90 | 0.38 | L2a | SINEC-Fc2 MIRb (2) | - | MLT1J | (TA)n | - |
| E2 | 42 987 500 | 42 989 300 | 1.8 | 9 | 0.54 | 418.27 | 0.40 | L2a | MIR3 | - | - | - | - |
| E2 | 43 026 700 | 43 031 300 | 4.6 | 23 | 0.65 | 293.30 | 0.42 | L2b (2) L2a | SINEC-Fc2 MIR | - | - | (GA)n (TG)n | MER20 |
| Mean | 2.80 | 14 | 0.57 | 330.83 | 0.39 | ||||||||
PP: mean posterior probability of hotspot,
BF: mean Bayes factor,
GC: mean GC content within interval,
Elements: variation and repeat elements within interval (start and end positions)
(LINE: long interspersed element,
SINE: short interspersed element,
LC: low complexity,
LTR: long terminal repeat,
SR: simple repeat,
DNA: MER—Medium reiterated repeats).
GC content analysis
The log10 of the Bayes factor was plotted as a function of the GC content in S2 Fig. Pearson’s correlation test revealed a positive correlation between GC and log10(Bayes factor) (cor = 0.077, p < 0.0001) but was not suggestive of strong correlation. Moreover, no significant differences in the mean GC content of each class of bins were observed (t-test, p = 0.05) (S2 Fig). The mean GC contents of the hotspots are shown in Table 2.
Repeat elements analysis
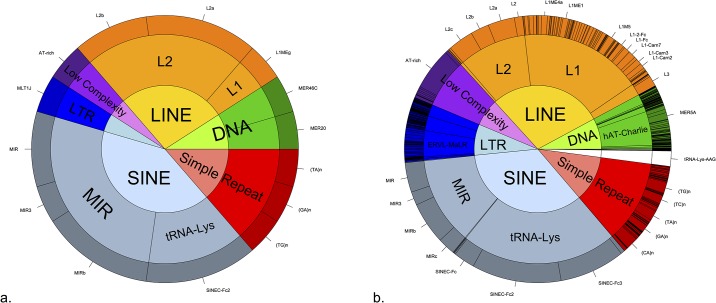
The four hotspot regions contained 22 repeat and variation elements (Table 2, Fig 2a). SINE elements constitute the highest proportion (40%) of the elements present in the hotspots followed by LINE elements (27%). Within LINE elements, L2 elements were present in three of the four hotspot regions. MIR family elements were present in all hotspot regions and tRNA-Lys family elements are present in three of the four elements. Low complexity, long terminal repeats, simple repeats, and DNA elements were inconsistently present across the hotspot regions.
Fig 2. A qualitative overview of variation and repeat elements in the cat chromosomal regions studied.
a) Variation and repeat element (n = 22) within four hotspots. All elements within the hotspots are shown at the tips of the outer circle. b) Variation and repeat element (n = 16,798) within “neutral” bins. Elements present more than a hundred times within the “neutral” bins are shown at the tips of the outer circle. The inner circle represents the elements’ classes, middle circle represents elements’ families, and outer circle represent the individual elements. Note: the Fig is intended a general description rather than a quantitative comparison.
Variation and repeat elements within neutral regions where investigated to get a picture of the general distribution of repeat elements (Fig 2b). In neutral regions, the SINE elements represent the highest proportion of elements, 34%. The tRNA-Lys SINE elements constitute 22% and MIR SINE elements represent 12%. The second highest repeat elements was the LINE elements, 29%, where L1 elements represent ~17% and L2 elements represent 9.5% of all elements in the neutral regions.
Discussion
Advances in population genetic theory and technology supports the estimation of recombination rates directly from genotype data on population samples, overcoming the limitations of sperm typing or using large extended families [32]. The strategy of the population genetics based approach is to use information on the number of recombination events that have occurred in the history of the population, which can be detected by modeling the patterns of genetic variation expected to be present in randomly selected individuals.
The model accounts for coalescent and recombination events in an Ancestral Recombination Graph (ARG). Markers will have coalescent trees that are likely to vary across the genome. In theory, all markers in a chromosome are correlated by an ARG. However, the size of the ARG may grow much faster than linear with the increasing number of SNPs, making it computational intractable to simultaneously analyze all markers in an analysis. In practice, the data are usually partitioned into blocks. Blocks from the same chromosomal region are assumed to share the same population size parameter (θ) but have an independent ARG for each block. For fast computation, some methods use an approximate likelihood instead of the full likelihood calculation, for example, the composite-likelihood method implemented in LDhat [33] and PAC-likelihood method implemented in PHASE [34]. Approximate-likelihood methods may be feasible to apply to large genomic regions, but may lack power to detect a moderate or low rate of recombination. Full-likelihood methods, such as implemented in inferRho, use all the information in the data and should therefore provide more accurate estimates [28,29].
The analysis of recombination hotspots in cats, presented here, constitutes the first application of the program inferRho to non-human data and the first analysis of fine-scale recombination rates in cats. The population recombination rate was found to be variable between the regions analyzed and, as expected, the mean recombination rate of X chromosome regions was lower than that of any autosomal regions. This variation in recombination rates and the notable reduced rate outside of the pseudoautosomal region of the X chromosome are in agreement with observations of recombination in human [4] and dog [7]. The latter result is expected due to that fact that recombination outside of the pseudoautosomal region occurs only in females.
Four decisive hot spots were identified on three chromosomes: A2, D1 and E2. The localities of the hotspots are in agreement with the localities of increased posterior probabilities and the general topography of recombination rates as expected. Acknowledging the limitation posed by the total size of the regions analyzed (total ~ 8.5 Mb) compared to the size of the genome and the lack of power to perform correlation and element enrichment analyses, the following observations have been made: (i) the cat hotspots, identified in this study, show no distinct positive correlation with GC content. (ii) The four hotspots contain at least one L2 LINE element and MIR and tRNA-Lys SINE elements. (iii) The similarity of the repeat elements in cat hotspots compared to other mammals might suggest similar recombination mechanisms.
This study represents a glimpse of recombination hotspots in cats and only an initial step toward understanding recombination in cats. The markers are sparsely sampled in some of the genomic regions, which may reduce power for inferRho to detect a large number of hotspots. As cat resources develop, genome-wide analyses could be performed allowing more definitive conclusions to be reached. Nonetheless, our preliminary description of the recombination landscape, and our finding that hotspots are present, helps shed light on the mechanism of recombination in cats compared to other species, furthering our understanding of the patterns of variation generated by recombination in cats, and potentially leading to better implementation of efficient disease mapping strategies in cats.
Supporting Information
(a) Estimated recombination rates (population size scaled crossing-over rate) along each region. Solid line shows the estimated recombination rates between markers, while the dashed line shows the background recombination rates. (b) Posterior probability of hotspots across each region. (c) Bayes factor of hotspots along each region. Horizontal dashed line corresponds to Bayes factor of 10 in a log10 scale.
(JPG)
(a) The GC contents (x-axis, 200 bp each bin) against the log10 of Bayes factors (y-axis). Gray circles represent neutral bins with BF < 100, and black circles represent hotspot bins with BF ≥ 100. (b) Boxplot of the GC content in the two classes of bins listed in (a).
(JPG)
(XLSX)
(DOC)
Acknowledgments
We would like to thank Drs. Jeffery Ross-Ibarra, Robert A. Grahn, and Barbara Gandolfi for their comments and suggestions.
Data Availability
All relevant data are within the paper and its supplementary files.
Funding Statement
LAL funding from National Center for Research Resources R24 RR016094 and is currently supported by the Office of Research Infrastructure Programs OD R24OD010928, the Winn Feline Foundation (W10-014, W11-041), the George and Phyllis Miller Feline Health Fund, and the Center for Companion Animal Health, School of Veterinary Medicine, University of California, Davis. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Steinmetz M, Minard K, Horvath S, McNicholas J, Srelinger J, Wake C, et al. (1982) A molecular map of the immune response region from the major histocompatibility complex of the mouse. Nature 300: 35–42. [DOI] [PubMed] [Google Scholar]
- 2.Paigen K, Petkov P (2010) Mammalian recombination hot spots: properties, control and evolution. Nat Rev Genet 11: 221–233. 10.1038/nrg2712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McVean GA, Myers SR, Hunt S, Deloukas P, Bentley DR, Donnelly P (2004) The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584. [DOI] [PubMed] [Google Scholar]
- 4.Myers S, Bottolo L, Freeman C, McVean G, Donnelly P (2005) A fine-scale map of recombination rates and hotspots across the human genome. Science 310: 321–324. [DOI] [PubMed] [Google Scholar]
- 5.Chakravarti A, Buetow KH, Antonarakis SE, Waber PG, Boehm CD, Kazazian HH (1984) Nonuniform recombination within the human beta-globin gene cluster. Am J Hum Genet 36: 1239–1258. [PMC free article] [PubMed] [Google Scholar]
- 6.Jeffreys AJ, Murray J, Neumann R (1998) High-resolution mapping of crossovers in human sperm defines a minisatellite-associated recombination hotspot. Mol Cell 2: 267–273. [DOI] [PubMed] [Google Scholar]
- 7.Axelsson E, Webster MT, Ratnakumar A, Ponting CP, Lindblad-Toh K (2012) Death of PRDM9 coincides with stabilization of the recombination landscape in the dog genome. Genome Res 22: 51–63. 10.1101/gr.124123.111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tortereau F, Servin B, Frantz L, Megens HJ, Milan D, Rohrer G, et al. (2012) A high density recombination map of the pig reveals a correlation between sex-specific recombination and GC content. BMC Genomics 13: 586 10.1186/1471-2164-13-586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Groenen MA, Wahlberg P, Foglio M, Cheng HH, Megens HJ, Crooijmans RP, et al. (2009) A high-density SNP-based linkage map of the chicken genome reveals sequence features correlated with recombination rate. Genome Res 19: 510–519. 10.1101/gr.086538.108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wu ZK, Getun IV, Bois PR (2010) Anatomy of mouse recombination hot spots. Nucleic Acids Res 38: 2346–2354. 10.1093/nar/gkp1251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee YS, Chao A, Chen CH, Chou T, Wang SY, Wang TH (2011) Analysis of human meiotic recombination events with a parent-sibling tracing approach. BMC Genomics 12: 434 10.1186/1471-2164-12-434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Myers S, Freeman C, Auton A, Donnelly P, McVean G (2008) A common sequence motif associated with recombination hot spots and genome instability in humans. Nat Genet 40: 1124–1129. 10.1038/ng.213 [DOI] [PubMed] [Google Scholar]
- 13.Zheng J, Khil PP, Camerini-Otero RD, Przytycka TM (2010) Detecting sequence polymorphisms associated with meiotic recombination hotspots in the human genome. Genome Biol 11: R103 10.1186/gb-2010-11-10-r103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Comeron JM, Ratnappan R, Bailin S (2012) The many landscapes of recombination in Drosophila melanogaster. PLoS Genet 8: e1002905 10.1371/journal.pgen.1002905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Baudat F, Buard J, Grey C, Fledel-Alon A, Ober C, Przeworski M, et al. (2010) PRDM9 is a major determinant of meiotic recombination hotspots in humans and mice. Science 327: 836–840. 10.1126/science.1183439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Parvanov ED, Petkov PM, Paigen K (2010) Prdm9 controls activation of mammalian recombination hotspots. Science 327: 835 10.1126/science.1181495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Munoz-Fuentes V, Di Rienzo A, Vila C (2011) Prdm9, a major determinant of meiotic recombination hotspots, is not functional in dogs and their wild relatives, wolves and coyotes. Plos One 6: e25498 10.1371/journal.pone.0025498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Auton A, Rui Li Y, Kidd J, Oliveira K, Nadel J, Holloway JK, et al. (2013) Genetic recombination is targeted towards gene promoter regions in dogs. PLoS Genet 9: e1003984 10.1371/journal.pgen.1003984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Grey C, Barthes P, Chauveau-Le Friec G, Langa F, Baudat F, de Massy B (2011) Mouse PRDM9 DNA-binding specificity determines sites of histone H3 lysine 4 trimethylation for initiation of meiotic recombination. PLoS Biol 9: e1001176 10.1371/journal.pbio.1001176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baker CL, Walker M, Kajita S, Petkov PM, Paigen K (2014) PRDM9 binding organizes hotspot nucleosomes and limits Holliday junction migration. Genome Res 24: 724–732. 10.1101/gr.170167.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Menotti-Raymond M, David VA, Lyons LA, Schaffer AA, Tomlin JF, Hutton MK, et al. (1999) A genetic linkage map of microsatellites in the domestic cat (Felis catus). Genomics 57: 9–23. [DOI] [PubMed] [Google Scholar]
- 22.Menotti-Raymond M, David VA, Schaffer AA, Tomlin JF, Eizirik E, Phillip C, et al. (2009) An autosomal genetic linkage map of the domestic cat, Felis silvestris catus. Genomics 93: 305–313. 10.1016/j.ygeno.2008.11.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Alhaddad H, Khan R, Grahn RA, Gandolfi B, Mullikin JC, Cole SA, et al. (2013) Extent of linkage disequilibrium in the domestic cat, Felis silvestris catus, and its breeds. Plos One 8: e53537 10.1371/journal.pone.0053537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bighignoli B, Niini T, Grahn RA, Pedersen NC, Millon LV, Polli M, et al. (2007) Cytidine monophospho-N-acetylneuraminic acid hydroxylase (CMAH) mutations associated with the domestic cat AB blood group. BMC Genet 8: 27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hudson RR (1991) Gene genealogies and the coalescent process. Oxford Survey in Evolutionary Biology 7: 1–44. [Google Scholar]
- 26.Kingman JFC (1982) On the Genealogy of Large Populations. Journal of Applied Probability 19: 27–43. [Google Scholar]
- 27.Kingman JFC (1982) The coalescent. Stochastic Processes and their Applications 13: 235–248. [Google Scholar]
- 28.Wang Y, Rannala B (2008) Bayesian inference of fine-scale recombination rates using population genomic data. Philos Trans R Soc Lond B Biol Sci 363: 3921–3930. 10.1098/rstb.2008.0172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang Y, Rannala B (2009) Population genomic inference of recombination rates and hotspots. Proc Natl Acad Sci U S A 106: 6215–6219. 10.1073/pnas.0900418106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kass RE, Raftery AE (1995) Bayes Factors. Journal of the American Statistical Association 90: 773–795. [Google Scholar]
- 31.Paradis E, Claude J, Strimmer K (2004) APE: Analyses of Phylogenetics and Evolution in R language. Bioinformatics 20: 289–290. [DOI] [PubMed] [Google Scholar]
- 32.Hellenthal G, Stephens M (2006) Insights into recombination from population genetic variation. Curr Opin Genet Dev 16: 565–572. [DOI] [PubMed] [Google Scholar]
- 33.McVean G, Awadalla P, Fearnhead P (2002) A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics 160: 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stephens M, Donnelly P (2003) A comparison of bayesian methods for haplotype reconstruction from population genotype data. Am J Hum Genet 73: 1162–1169. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(a) Estimated recombination rates (population size scaled crossing-over rate) along each region. Solid line shows the estimated recombination rates between markers, while the dashed line shows the background recombination rates. (b) Posterior probability of hotspots across each region. (c) Bayes factor of hotspots along each region. Horizontal dashed line corresponds to Bayes factor of 10 in a log10 scale.
(JPG)
(a) The GC contents (x-axis, 200 bp each bin) against the log10 of Bayes factors (y-axis). Gray circles represent neutral bins with BF < 100, and black circles represent hotspot bins with BF ≥ 100. (b) Boxplot of the GC content in the two classes of bins listed in (a).
(JPG)
(XLSX)
(DOC)
Data Availability Statement
All relevant data are within the paper and its supplementary files.