Biphasic Analysis of Cartilage Stresses in the Patellofemoral Joint

Abstract

The objective of this study was to examine the state of stress within the solid matrix of articular cartilage in the patellofemoral joint, using anatomically faithful biphasic models of the articular layers, with the joint subjected to physiological muscle force magnitudes. Finite element models of five joints were created from human cadaver knees. Biphasic sliding contact analyses were performed using FEBio software to analyze the response of the joint from 30 to 60 degrees of knee flexion. Results demonstrated that the collagen matrix always sustains tensile stresses, despite the fact that the articular layers are loaded in compression. The principal direction of maximum solid stresses was consistent with the known orientation of collagen fibrils in cartilage. The magnitudes of these tensile stresses under muscle forces representative of activities of daily living were well below tensile failure stresses reported in the prior literature. Results also hinted that solid matrix stresses were higher in the patellar versus femoral superficial zone. These anatomically correct finite element models predicted outcomes consistent with our understanding of structure-function relationships in articular cartilage, while also producing solid matrix stress estimates not observable from experiments alone, yet highly relevant to our understanding of tissue degeneration.

Introduction

The patellofemoral joint (PFJ) is a frequent site of cartilage degeneration, often initiated by injuries, soft tissue imbalances, or congenital conditions such as patella alta or trochlear dysplasia ¹. It is generally believed that these various conditions result in excessive stresses within the cartilage layers, which initiate a damage process that may not be sufficiently compensated by the tissue’s limited repair ability ². A considerable body of work has thus focused on the examination of PFJ contact mechanics, most notably using experimental measurements of articular contact stresses ^3–6. Computational models of this joint have also been developed to complement and extend these experimental measurements by performing parametric analyses to assess the influence of various factors on the contact stresses ⁷. Thus, computational models have investigated the role of Q-angle and patella alta ^8,9, or muscle force imbalances ^10,11 on contact forces and stresses. Other models have examined the potential outcome of various tuberosity transfer surgeries on PFJ contact forces and stresses ^12–14, or differences in the mechanics of open and closed kinetic chain exercises ¹⁵.

The sophistication of these models has increased considerably with advances in computational methods and analyses. Many models use realistic geometries of the bones and articular layers of the PFJ ^11,16. Some of these prior computational models have employed finite element analyses of the PFJ, where the stress-strain response of the articular layers is described using elastic materials under infinitesimal or finite strains ^10,17–19. However, despite the ability of these models to provide the state of stress within the articular layers, these analyses often focus on reporting contact stresses and kinematics, since these parameters may also be measured experimentally, or stress within the bone.

Because of the tensorial nature of the stress, the complete state of stress may not be measured directly in any material. Only traction components (such as the contact stress) may be measured at boundary surfaces. Therefore, investigating the hypothesis that excessive stresses might cause cartilage damage may only be performed thoroughly by evaluating stresses from theoretical or computational models. The accuracy of these predictions is thus critically dependent on the modeling assumptions, and may only be validated indirectly (since direct measurements of the complete state of stress is impossible).

Accordingly, it is now well recognized that articular cartilage may be modeled more accurately as a porous deformable biphasic material ²⁰ than an elastic material, since a biphasic model can describe the tissue’s experimentally observed creep and stress-relaxation responses under various loading configurations ^21–23, its time-dependent interstitial fluid pressure ^24,25 and frictional ²⁶ responses. Moreover, theoretical biphasic contact analyses indicate that the contact stress between articular surfaces results primarily from the pressurization of its interstitial fluid ^27,28, implying that experimental contact stress measurements do not necessarily provide direct measures of the state of stress within the collagen-proteoglycan solid matrix.

Therefore, the objective of this study was to examine the state of stress within the solid matrix of articular cartilage in the PFJ, using anatomically faithful biphasic models of the articular layers, with the joint subjected to physiological muscle force magnitudes. The solid phase of articular cartilage includes a fibrous matrix to describe collagen, and a ground matrix to describe proteoglycans, and its material properties vary from the surface to the deep zone, to properly reflect the known depth-dependent inhomogeneity of this tissue ^29,30.

Methods

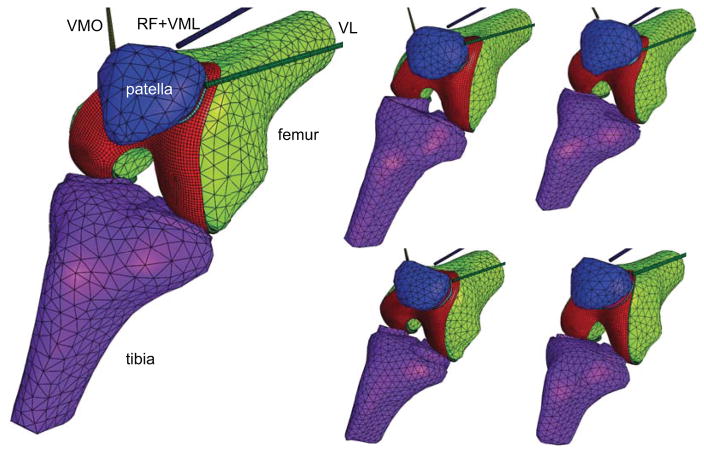
Finite element models of five patellofemoral joints were created from measurements acquired previously from human cadaver knees (age range 49–89 years, three male, two female), using stereophotogrammetry for the topography of the articular layers and a coordinate measuring machine for the topography of the bones and the insertion points of quadriceps muscle and patella tendon ³¹. Point cloud data were imported into the commercial Solidworks computer-aided design software (Dassault Systemes, version 2014), fitted with smooth splines surfaces to generate solid geometries of the articular layers and bones, then transferred to the Cubit meshing software (cubit.sandia.gov, version 13.2). Articular layers were meshed using 8-node hexahedral elements; bone surfaces were meshed using 4-node tetrahedral elements. Based on a previous mesh convergence study ³², five elements were used through the thickness of the articular layer, using a mesh bias that produced finer elements near the articular surface and the subchondral bone. Meshes were imported into the FEBio finite element software suite (www.febio.org) ³³ to prescribe material models and boundary conditions (Figure 1).

Figure 1.

Finite element models of five human patellofemoral joints were created for this study. The bones were modeled as rigid bodies whereas the articular layers of the patella and femur were modeled using biphasic (porous-deformable) materials. The patella tendon was modeled using two linear springs (not shown). VL: vastus lateralis; VMO: vastus medialis obliquus; RF: rectus femoris; VML: vastus medialis longus.

Articular layers were modeled as biphasic materials, with a solid matrix consisting of a mixture of a neo-Hookean elastic solid (Young’s modulus E and Poisson’s ratio ν, FEBio User Manual 2.3, section 4.1.3.15), representing the proteoglycan ground matrix, and a continuous spherical (random) fiber distribution (fiber modulus ξ and power-law exponent β, sections 4.2.1, 4.2.3.1 and 4.2.4.1), representing the collagen; interstitial fluid transport was modeled using a constant, isotropic hydraulic permeability (k, section 4.6.2.1).

Depth-dependent material properties of human PFJ cartilage were obtained from unconfined compression stress-relaxation experiments reported previously ³⁰, from measurements on six human cadaver knees (ages 45.5±12 years, four males, two females). Measurements from that earlier study were refitted to the biphasic tissue model employed here. Material properties for each of four layers through the depth of each of the femur and patella articular cartilage were averaged over all tested cadaver specimens (Table 1). These depth-dependent properties were then respectively assigned to the femur and patella cartilage meshes, using polynomial interpolations to match experimental depth-varying measurements to the biased mesh through the thickness.

Table 1.

Depth-dependent material properties of human patellar and distal femoral articular cartilage. Properties ξ (fiber modulus), E (ground matrix modulus) and k (hydraulic permeability) were obtained by refitting experimental data from unconfined compression stress-relaxation tests reported previously ³⁰ and averaged over six specimens; the power-law exponent for the fiber response was set to β=2.15 and Poisson’s ratio for the ground matrix was set to ν=0. Mean and standard deviations are reported at normalized depths z/h through the articular layer of the patella and distal femur (z/h=0 at subchondral bone and 1 at articular surface). The full thickness of the articular layers at the test sites was h=2.55±0.39 mm for the patella and h=2.41±0.22 mm for the femur.

	layer	z/h	ξ (MPa)	E (MPa)	k (×10−3 mm4/N·s)
patella	4	0.82±0.03	24.6±25.1	0.20±0.12	1.11±0.88
	3	0.54±0.06	13.2±5.3	0.38±0.14	1.05±0.51
	2	0.33±0.04	10.2±6.4	0.67±0.19	1.17±0.64
	1	0.11±0.01	11.9±5.4	0.83±0.30	0.95±0.65
femur	4	0.76±0.04	17.7±5.8	0.25±0.10	1.14±0.29
	3	0.43±0.06	21.1±4.2	0.76±0.27	0.55±0.23
	2	0.25±0.03	12.4±0.7	0.54±0.17	0.96±0.55
	1	0.08±0.00	17.9±0.3	1.06±0.21	0.53±0.05

The patella tendon was modeled using two linear springs, each with a stiffness of 100 N/mm, which was shown in our previous study to produce excellent agreement between measured and modeled PFJ kinematics ³⁴. The quadriceps muscle was divided into the vastus lateralis (VL), vastus medialis obliquus (VMO), and a combination of the rectus femoris and vastus medialis longus (RF+VML). Muscle force magnitudes (VL=178 N, VMO=89 N, RF+VML=267 N) and insertion points replicated those of our previous experiments on those same cadaver knees; unless noted, force magnitudes remained constant throughout the modeled range of knee flexion, for consistency with the prior experimental study that informed our finite element models ³¹.

The patella, femur and tibia bones were modeled as rigid bodies. The femur was fixed throughout the analyses. The tibia motion was prescribed to interpolate experimental measurements of tibia kinematics in the range of knee flexion from 60 to 30 degrees, and back to 60 degrees, at a rate of 15 degrees per second. The frictionless biphasic contact algorithm implemented in FEBio was used for the patellofemoral contact interface; this algorithm automatically enforces continuity of fluid pressure and normal fluid flux inside the contact regions, while assigning free-draining conditions outside of those regions ³⁵.

Two finite element analyses were performed on each of five knees: The baseline model, described above, examined cartilage stresses in naturally inhomogeneous cartilage layers, over a range of knee flexion. In the second analysis, the baseline model was kept at 60 degrees of knee flexion, and muscle forces were increased proportionally by a factor of three (from a net force of 534 N to 1600 N), to examine whether cartilage stresses vary linearly or nonlinearly with muscle force magnitude. All finite element computations were performed using FEBio 2.3, with custom modifications to account for finite rotations in prescribed tibia kinematics. Analyses were executed on a high-performance computing cluster (Yeti, hpc.cc.columbia.edu) using one node with 12 cores per analysis.

Results

In the baseline analysis, the contact pressure distribution over the patellar and femoral surfaces was consistent across all PFJ models and similar to previously reported experimental results ^3,4,36 (Figure 2): The contact area migrated from the distal end of the patella articular surface at 30 degrees of flexion, toward the mid-horizontal section at 60 degrees, with a broad distribution along the medial-lateral direction and a narrow distribution along the proximal-distal direction. On the femoral trochlea, the contact area migrated from the anterior-most edge at 30 degrees of flexion, toward the trochlear notch at 60 degrees. In three of the PFJ models, the peak contact stress occurred on the medial side, whereas the remaining two models exhibited peak contact stress on the lateral side. Biphasic analyses account for loss of interstitial fluid pressurization over time; an analysis of the response at the start and end of the cycle of loading (60 degrees of knee flexion) showed a small decrease (<9%) in the fluid pressure and stresses over the 4 s cycle duration; therefore, results are reported for the last two seconds of the cycle (the return motion from 30 to 60 degrees of knee flexion).

Figure 2.

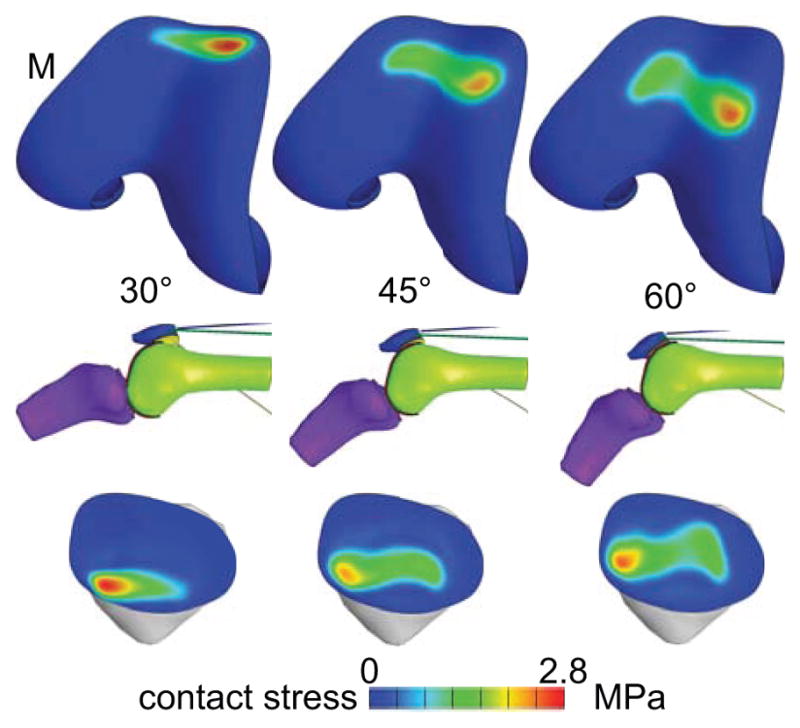
Contact stress distribution on one representative knee model, at three knee flexion angles. The contact stress must be the same on the patella and femur. M: medial side.

In a biphasic material, the mixture stress tensor is given by T = −pI + T^e, where p is the fluid pressure, I is the identity tensor, and T^e is the elastic stress in the solid matrix, arising from solid matrix strains. The contact stress |t_n| is the absolute value of the normal component of T at the articular surface (i.e., t_n = n·T·n where n is the unit outward normal to the articular surface). For all models, the peak and average articular contact stresses are reported in Table 2 at 30, 45 and 60 degrees of flexion. In all cases, the interstitial fluid pressure at the cartilage surface was nearly identical in magnitude and spatial distribution to the contact stress distribution (Figure 3).

Table 2.

Average and standard deviations of the peak and average contact stress $\left|t_n^e\right|$, and the peak maximum principal solid stress $T_{max}^e$ at the surface and deep zones of the patella and femur, at three flexion angles.

flexion (deg)	peak |tn| (MPa)	average |tn| (MPa)	zone	peak Temax patella (MPa)	peak Temax femur (MPa)
30	3.6±0.9	1.7±0.6	surface	3.2±0.6	3.2±1.1
			deep	2.8±0.7	3.9±1.8
45	2.6±0.6	1.4±0.3	surface	2.3±0.4	1.5±0.4
			deep	2.0±0.3	2.1±0.6
60	2.7±0.6	1.3±0.4	surface	2.3±0.6	1.2±0.4
			deep	2.1±0.5	1.9±0.4

Figure 3.

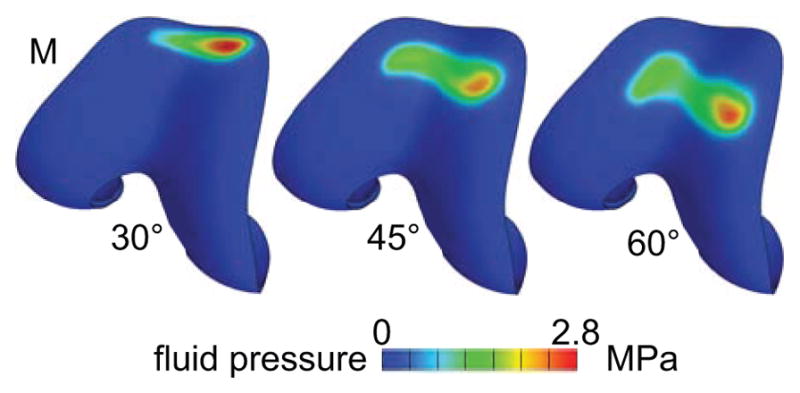
Interstitial fluid pressure on the femoral articular layer of one representative knee model (same as in Figure 2). The fluid pressure is almost equal to the contact stress. M: medial side.

An examination of the three principal normal components (eigenvalues) of the mixture stress T showed that the minimum normal stresses T_min were always compressive throughout the entire articular layer (from the articular surface to the subchondral bone, and across the entire joint surface) at all flexion angles, with a magnitude comparable to that of p (recalling that T_min = t_n at the articular surface in the case of frictionless contact). The maximum normal mixture stresses T_max were mostly compressive as well, though they occasionally straddled into the tensile range. In contrast, all three principal normal components of the solid stress T^e exhibited tensile values throughout the articular layer, with $T_{max}^e$ exhibiting the largest magnitude. Representative distributions of $T_{max}^e$ are presented in Figure 4: For both patellar and femoral layers, the distribution pattern for $T_{max}^e$ at the articular surface was similar to that of the contact stress, being greatest at the same location as the peak contact stress t_n, though its magnitude was generally lower (Figure 2). With increasing depth from the articular surface however, the peak value of $T_{max}^e$ shifted progressively away from the peak contact stress footprint, achieving its greatest magnitude at the subchondral bone interface under the footprint of the peak gradient in contact stress. This characteristic response was evident in the appearance of a ring-like distribution of peak $T_{max}^e$ values at the subchondral bone interface (Figure 4).

Figure 4.

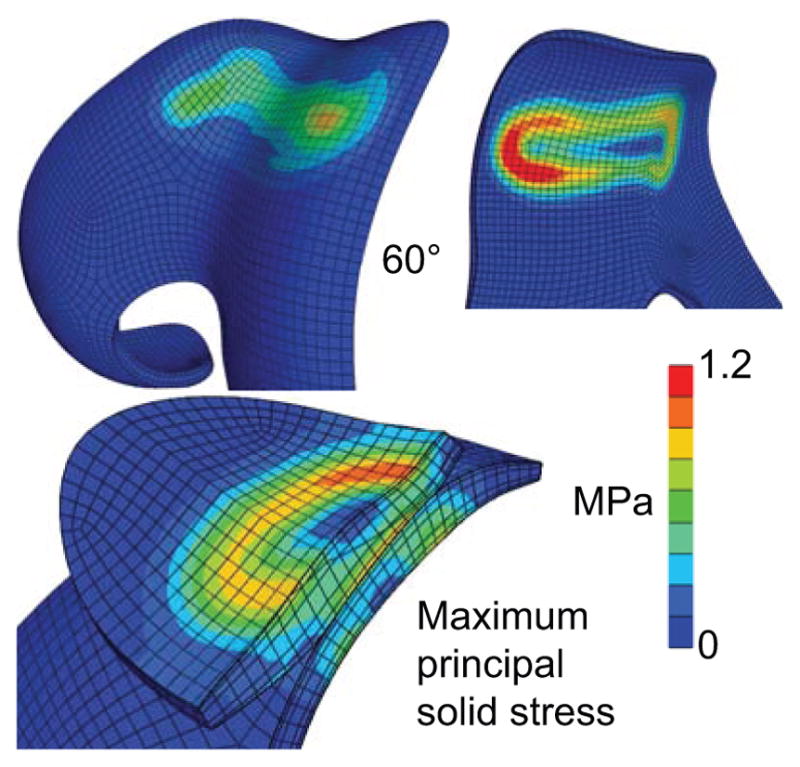
Maximum principal solid stress $T_{max}^e$ on a representative patellofemoral joint at 60 degrees of knee flexion. The distribution of $T_{max}^e$ at the articular surface (top left) has a similar pattern to (but smaller magnitude than) the contact stress (Figure 2). At the subchondral bone surface (top right), $T_{max}^e$ shows a ring-like pattern coinciding with the footprint of the peak contact stress gradient. The transition in the distribution of this solid stress from the articular surface to the subchondral bone is visible on the cross-section of the PFJ (bottom left).

Peak values of $T_{max}^e$ at the articular surface and deep zone of the patellar and femoral cartilage layers are summarized in Table 2, at 30, 45 and 60 degrees of knee flexion. In all PFJ models, the contact area extended to the edge of either the patellar or femoral articular layer, usually when the knee was at 30 degrees of flexion. These cases produced higher peak values of $T_{max}^e$ than the rest. In contrast to the contact stress t_n, which must be the same on the patellar and femoral surfaces (according to Newton’s law of action and reaction), the values of $T_{max}^e$ need not be the same. Using results from the five knee models at these three selected flexion angles (Table 2), statistical comparisons (ANOVA for the factors of articular layer and depth) at each flexion angle showed that $T_{max}^e$ was significantly higher in the patella than the femur, at the articular surface, at 60 degrees of flexion (p<0.01); no differences were observed in the deep zone or at 45 and 30 degrees of flexion (p>0.05).

At the articular surface, the principal direction of maximum normal solid stress (i.e., the eigenvector corresponding to the eigenvalue $T_{max}^e$) was tangential to the surface, as expected theoretically when the contact interface is idealized as frictionless (Figure 5); it was generally oriented along the direction of the gradient of t_n, which coincided with the direction of relative sliding. At the subchondral bone surface, the principal direction was consistently oriented at approximately ±45 degrees from the normal to that surface, at locations of peak $T_{max}^e$ values (Figure 5). As the knee flexed and extended, the principal direction at each location on the subchondral bone surface could thus shift from +45 to −45 degrees, depending on the direction of the gradient of t_n at the articular surface.

Figure 5.

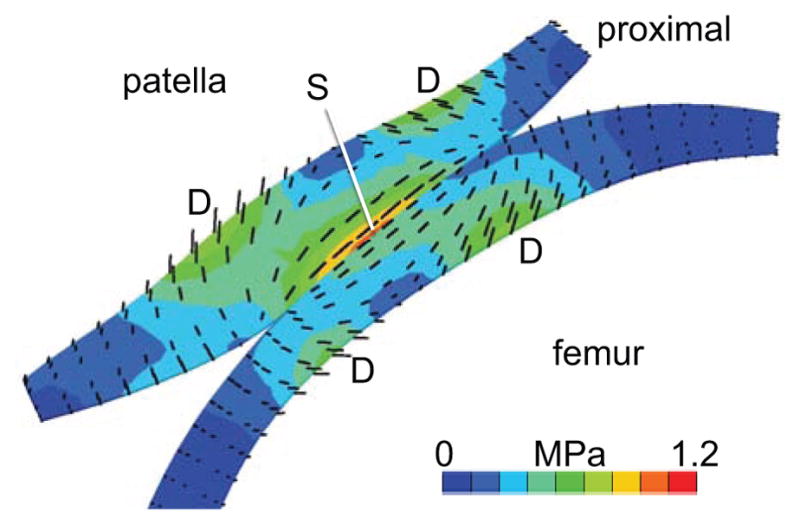
Mid-sagittal cross-section of a PFJ model at 60 degrees of flexion, showing principal directions of the maximum solid stress (black lines, scaled to the magnitude of $T_{max}^e$). Principal directions in the superficial zones of the patella and femur (S) are parallel to the articular surface and aligned with the direction of relative motion. In the deep zone, principal directions at the site of local peak stress magnitudes (D) make an angle of ±45 degrees with the normal direction to the subchondral bone surface.

The second analysis (increasing muscle forces while keeping the knee at 60 degrees of flexion) showed that peak and average contact stresses increased nearly linearly with the net muscle force. The same trend was also observed in the peak value of the maximum principal solid stress, $T_{max}^e$, in the femur and patella (Figure 6).

Figure 6.

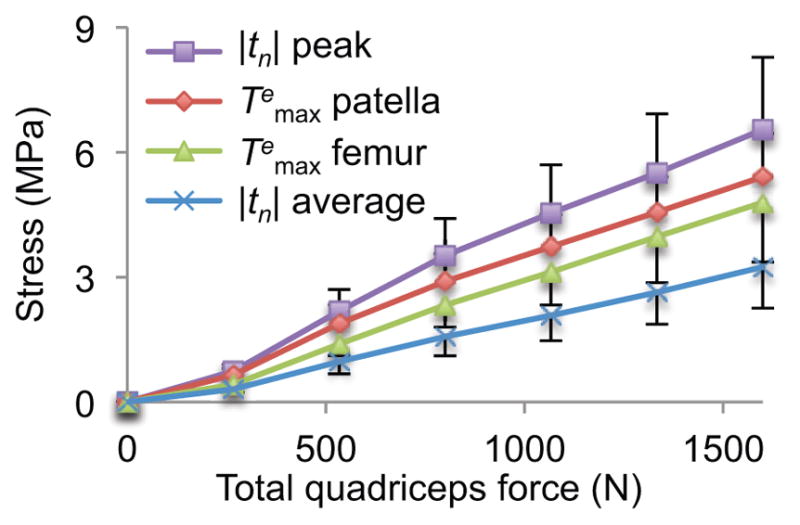
Effect of increasing total quadriceps force on contact stress |t_n| (peak and average), and maximum principal solid stress $T_{max}^e$ (peak value throughout entire articular layer) on the patella and femur, at 60 degrees of knee flexion. Symbols provide mean values over five knee models and error bars represent standard deviations.

Discussion

To the best of our knowledge, this study represents the first investigation of cartilage stresses in the patellofemoral joint using a biphasic analysis, which accounts for the experimentally attested interstitial fluid pressurization within articular cartilage ^24,25,37. This analysis was able to explicitly differentiate between interstitial fluid pressure and solid matrix stresses, providing an opportunity to investigate the functional response of the collagen-proteoglycan matrix of articular cartilage in anatomically faithful finite element models that account for the depth-dependent properties of the articular layers. The availability of five distinct models also provided representative results for the general population, reducing the chance of reporting results from an outlier.

As reported in our earlier theoretical study of biphasic contact ²⁷, the contact stress |t_n| at the articular surfaces is mostly representative of the interstitial fluid pressure magnitude (Figure 2 & Figure 3); therefore this measure, which is observable experimentally, does not provide direct evidence of the magnitude of stresses in the collagen matrix. Instead, the maximum principal solid stress $T_{max}^e$ indicates that the solid matrix of cartilage is always subjected to tensile stresses, consistent with the fibrillar structure of this tissue. Thus, a biphasic analysis provides further evidence of the structure-function relationships in articular cartilage: Despite the fact that contact stresses are always compressive, the collagen matrix is always in tension under contact loading. This seemingly counter-intuitive finding is even more remarkable considering that the biphasic cartilage constitutive model employed here did not explicitly account for the swelling caused by the charged proteoglycans ^38,39.

Furthermore, the principal direction of maximum solid stress is oriented tangential to the articular surface in the superficial zone and directed predominantly along the relative motion of the articular layers, consistent with the fibrillar organization and split line directions in that zone ^40,41. In the deep zone, the maximum principal solid stress direction alternates between plus and minus 45 degrees relative to the normal to the subchondral bone surface, as the contact area migrates back and forth on the articular surface; collagen fibrils in that zone are predominantly oriented along the normal direction ⁴¹, thus providing equal support for alternating stress directions.

Though the magnitude of the maximum principal solid stress $T_{max}^e$ was often smaller than that of the contact pressure |t_n|, this trend was not always consistent, especially when the contact area reached the edges of the articular layers. Consequently, the contact stress may not be used directly as a proxy for the magnitude of tensile stresses in the solid matrix. It is likely that edge contact produced higher-than-realistic stress magnitudes, since articular layer edges are buttressed by soft tissues (e.g., supratrochlear and infrapatellar fat pads) not modeled in this analysis. Nevertheless, since contact stresses predicted in this study were consistent with experimental measurements reported previously ^3,4 at comparable muscle forces and flexion angles, the predicted values of $T_{max}^e$ reported here may be used to estimate the physiological range of collagen stresses in the articular layers of the PFJ. Thus, these predicted values could be used to better understand conditions that can cause cartilage tissue fibrillation or delamination. In particular, at 60 degrees of flexion where edge contact was minimal, solid matrix stresses were found to be higher in the patellar versus femoral surface zone, despite the fact that contact stresses must be the same. This finding may be related to the oft-reported condition of chondromalacia patella ^42,43.

The quadriceps muscle force of 534 N employed in the baseline analysis was based on prior experimental studies ^3,31; this force magnitude is equivalent to the quadriceps force produced in a closed kinetic chain exercise at 30 degrees of knee flexion, or open kinetic chain exercise from 20 to 90 degrees of flexion with a 25 N load at the ankle ¹⁵. The 1600 N quadriceps muscle force used in the second analysis was representative of muscle forces for a closed kinetic chain exercise up to 60 degrees of knee flexion ¹⁵. The fact that these forces produced a slight medial pull on three models and a slight lateral pull on the remaining two suggests that the chosen distribution of quadriceps muscles forces was reasonably balanced on average, but that contact stresses in individual joints are sensitive to the precise muscle force distribution.

In all these cases, the peak contact stresses reached 6.5±1.7 MPa over the five PFJ models, whereas the corresponding peak value of the maximum principal solid stress was 4.8±1.4 MPa in the femur and 5.4±1.0 MPa in the patella (Figure 6). These peak contact stress values are well within the contact stresses reported to produce fracture of the patella or femur under impact loading (~25 MPa ^6,44). The peak maximum principal solid stresses are similarly below the values of tensile fracture stresses reported by Kempson et al. ⁴⁵ for human femoral condyle cartilage, which ranged from ~40 MPa at age 30 down to ~10 MPa over the age of 70. Prior to these biphasic finite element investigations, a direct comparison of experimental cartilage tensile failure properties and contact analyses were not possible.

A limitation of this modeling study was the assumption that collagen fibers are oriented randomly through the articular layer thickness. This assumption was adopted because a thorough quantitative characterization of the fiber orientation through the thickness of the human patellar and femoral articular layers has not yet been reported in the literature, though an early study by Aspden and Hukins ⁴¹ provides some data and a promising methodology that may be applied in future investigations. Another limitation is that the true distribution of muscle forces among the various components of the quadriceps is not known and was based on assumptions adopted in prior experimental studies ^3,31. These assumed values may explain the shift in peak contact stresses between medial and lateral sides in the various models analyzed here, as a result of a slight imbalance of the assumed muscle force components with respect to the specific anatomy of each joint.

In summary, the finite element analyses of the PFJ performed here reproduced the kinematics and contact stresses reported in previous experimental studies and provided new insights into the state of stress within the PFJ articular layers. Employing biphasic models for cartilage made it possible to separate the contributions from interstitial fluid pressure and solid matrix stresses. These results demonstrated that the collagen matrix always sustains tensile stresses, despite the fact that the articular layers are loaded in compression. Though the cartilage model assumed that fibers were randomly oriented throughout the thickness of the articular layer, model predictions demonstrated that the principal direction of maximum solid stresses was consistent with the known orientation of collagen fibrils in PFJ cartilage. The magnitudes of these tensile stresses under muscle forces representative of activities of daily living were well below tensile failure stresses reported in the prior literature. Results also hinted that solid matrix stresses were higher in the patellar versus femoral superficial zone. Overall, these results show that anatomically correct finite element models that employ depth-dependent material properties can predict outcomes consistent with our understanding of structure-function relationships in articular cartilage, while also producing solid matrix stress estimates not observable from experiments alone, yet highly relevant to our understanding of tissue degeneration. Therefore, these models may be further extended to investigate cartilage damage resulting from various conditions hypothesized as initiating factors in the pathogenesis of PFJ osteoarthritis and other disorders.