Brain responses in humans reveal ideal observer-like sensitivity to complex acoustic patterns

Significance

We reveal the temporal dynamics and underlying neural sources of the process by which the brain discovers complex temporal patterns in rapidly unfolding sound sequences. We demonstrate that the auditory system, supported by a network of auditory cortical, hippocampal, and frontal sources, continually scans the environment, efficiently represents complex stimulus statistics, and rapidly (close to the bounds implied by an ideal observer model) responds to emergence of regular patterns, even when these are not behaviorally relevant. Neuronal activity correlated with the predictability of ongoing auditory input, both in terms of deterministic structure and the entropy of random sequences, providing clear neurophysiological evidence of the brain's capacity to automatically encode high-order statistics in sensory input.

Abstract

We use behavioral methods, magnetoencephalography, and functional MRI to investigate how human listeners discover temporal patterns and statistical regularities in complex sound sequences. Sensitivity to patterns is fundamental to sensory processing, in particular in the auditory system, because most auditory signals only have meaning as successions over time. Previous evidence suggests that the brain is tuned to the statistics of sensory stimulation. However, the process through which this arises has been elusive. We demonstrate that listeners are remarkably sensitive to the emergence of complex patterns within rapidly evolving sound sequences, performing on par with an ideal observer model. Brain responses reveal online processes of evidence accumulation—dynamic changes in tonic activity precisely correlate with the expected precision or predictability of ongoing auditory input—both in terms of deterministic (first-order) structure and the entropy of random sequences. Source analysis demonstrates an interaction between primary auditory cortex, hippocampus, and inferior frontal gyrus in the process of discovering the regularity within the ongoing sound sequence. The results are consistent with precision based predictive coding accounts of perceptual inference and provide compelling neurophysiological evidence of the brain's capacity to encode high-order temporal structure in sensory signals.

Accumulating work suggests that the brain is sensitive to statistical regularities in sensory input, at multiple time scales (1–9). The auditory system has been a useful testbed to investigate these processes (2, 3, 9–13), largely due to the vantage point provided by the mismatch negativity (MMN) paradigm (12, 13). The MMN is an auditory-evoked response generated by sounds violating some regular aspect of the prior sequence and is hypothesized to reflect a discrepancy between the memory trace, or expectations, generated by the standard stimulus, and the deviant information (12,13). A large body of MMN work has demonstrated that listeners are sensitive to the violation of a variety of acoustic sequences, including very complex regularities (14, 15), and interpreted as indirect evidence for exquisite sensitivity to patterns in sound.

Due to the physical constraints that characterize animate objects in the environment, sounds emanating from those sources are usually statistically regular and often repetitive (e.g., flapping wings and locomotion sounds). The ability to discover regularities within the sensory input is therefore a critical aspect of scene analysis: providing the anchor that enables an observer to identify and track a behaviorally relevant signal from within the brouhaha of a busy scene. Detecting temporally recurrent auditory features enables listeners to recognize auditory objects (because most auditory signals only have meaning as patterns over time), but also to form rules, or models, that characterize the past and expected behavior of objects within the environment (4, 16). Indeed, experimental work demonstrates that regularities within an ongoing stimulus are exploited to tune the system to the statistics of the current sensory input by optimizing behavior (17), facilitating source segregation (10), and enabling rapid detection of changes in one’s surroundings (18).

However, a crucial link (19), missing in much of the sensory processing and statistical learning literature, is an understanding of the processes through which patterns within ongoing sensory input are recognized or instantiated in the first instance. Here, we use a paradigm based on measuring brain responses to rapid tone-pip sequences governed by specific statistical rules. This method enables us to directly tap the brain processes subserving the online accumulation of stimulus statistics and recognition of complex recurrent patterns within the unfolding sensory input. The temporal properties of listeners’ behavioral and brain responses are then compared with the probabilistic predictions of a variable-order Markov model. The model acts as an ideal listener free from constraints on memory and attention and allows us to establish (upper) bounds on efficient recognition. Our results demonstrate that the brains of (distracted) human listeners act as Bayes optimal inference machines, supported by a network of sources in primary sensory areas, the hippocampus, and inferior frontal gyrus (IFG).

Results

Listeners are sensitive to repeating sound patterns, even when they are embedded in rapid sequences (20–24). Here we describe a series of behavioral and brain imaging experiments in which we sought to understand the processes through which such regularities are detected by the brain. The first experiment measured behavioral responses to transitions between regular and random acoustic patterns. The remaining experiments used magnetoencephalography (MEG) and functional MRI (fMRI) to examine brain responses to implicit (bottom-up driven) pattern detection, whereas distracted listeners performed an incidental (n-back) visual task.

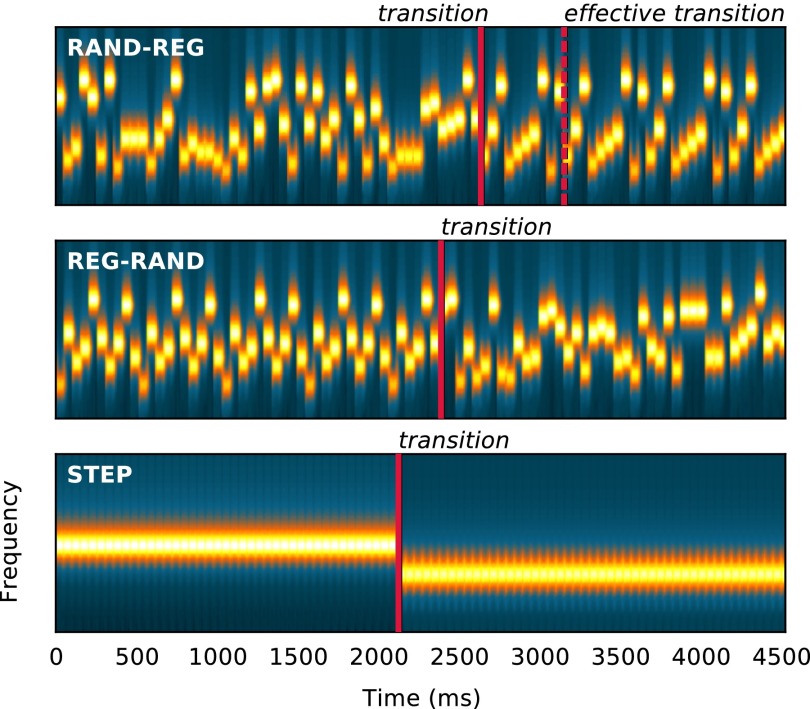
The basic stimuli are illustrated in Fig. 1 (Audio Files S1–S8). Signals consisted of sequences of abutting 50-ms tone-pips arranged according to four frequency patterns: REG sequences were generated by randomly selecting (with replacement) a number (R_cyc; alphabet size) of frequencies from the pool and then iterating that sequence to create a regularly repeating pattern (new patterns were generated for each trial; Materials and Methods). RAND sequences consisted of tones of random frequencies. REG-RAND and RAND-REG sequences contained a transition between a regular and a random pattern. In addition, STEP stimuli, consisting of a simple step change in frequency between two series of repeating tones, were used to estimate basic response times (RTs). Transition times varied across trials.

Fig. 1.

Spectrograms of the stimuli used in the experiment (Top: RAND-REG; Middle: REG-RAND; Bottom: STEP). Transitions are marked with a solid line in each exemplar. The transition in RAND-REG is not detectable until one regularity cycle has elapsed (i.e., until the pattern starts repeating). This time point is labeled effective transition in the figure. REG (and RAND) patterns were generated anew for each trial.

Experiment 1: Psychophysics.

Subjects listened to RAND-REG stimuli, and two types of controls (REG-RAND and STEP; Fig. 1) presented in random order. They were instructed to detect the changes within the stimuli (transitions from RAND to REG or vice versa) and respond as quickly as possible by pressing a keyboard button. RTs were measured by calculating the latency between the nominal transition and the subject’s key press. For each subject and condition, RTs that deviated by more than 2 SDs from the mean were discarded from analysis. RAND-REG responses that occurred before the start of the second cycle (i.e., at a time when the transition is physically undetectable) were counted as false positives. The number of false positives was small (Table S1), confirming that subjects responded when they were reasonably sure of the occurrence of the transition.

Table S1.

Behavioral detection results from experiment 1

	Rcyc = 10				Rcyc = 20
	RAND-REG		REG-RAND		RAND-REG		REG-RAND
	FA	Hit	FA	Hit	FA	Hit	FA	Hit
Mean (%)	3.8	95.5	2	97.1	3.6	94.5	5.1	96.7
SD	4.2	3.7	1.9	2.3	2.9	4.4	4.5	3

RT to transitions in the STEP stimuli served to estimate the response time to a simple (computationally nondemanding) stimulus change. In addition to any effects of hardware latency, this includes the time taken for the change to reach awareness and to program and/or generate the motor response and the subject’s general state of vigilance. RTs in RAND-REG and REG-RAND were then baselined by subtracting the STEP RT. This procedure estimates a lower-bound measure of the raw computation time required to detect the emergence, or violation, of a regular pattern.

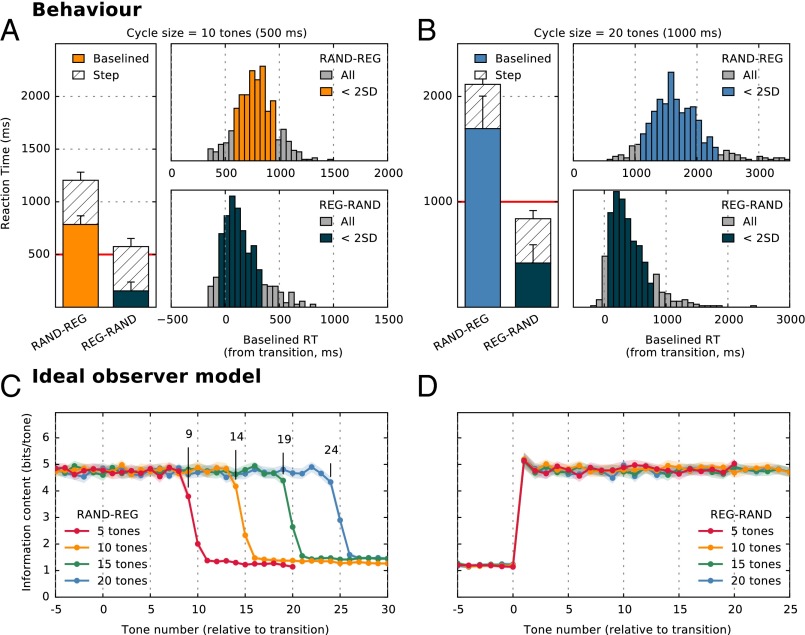
Theoretically, the transition in the REG-RAND sequence is detectable immediately at the nominal transition time: the first tone-pip in the RAND sequence suffices to signal that the regular pattern has been violated. To detect the opposite transition—from random to regular (RAND-REG)—an observer must wait until the pattern begins to repeat (i.e., after the first cycle; effective transition; Fig. 1). The number of further tones required to determine that a regular pattern has emerged depends on the statistical properties of the ongoing sequence and on the observer’s decision settings (how much evidence is sufficient to conclude that the pattern is repeating). We used an ideal observer model (Materials and Methods) to determine the theoretical minimum number of tones required to detect the transition. The model results (Fig. 2 C and D) confirm that REG-RAND transitions are statistically resolvable after the first RAND tone (Fig. 2D). For RAND-REG (Fig. 2C), model results suggest that an observer with perfect memory requires about four tones after the effective transition (i.e., 1 cycle + 4 tones) to detect the regular pattern, irrespective of the size of the regularity cycle. This result is in line with the fact that the ability to detect the regularity should largely depend on the statistics (transition probabilities) within the RAND sequence.

Fig. 2.

Behavioral results (experiment 1). (A) Detection times for RAND-REG and REG-RAND transitions where REG patterns consisted of 10 tones (R_cyc = 10). Bar plots show the mean RT as measured relative to the nominal transition time. The total height of the bars corresponds to the raw RTs from which the RT to the STEP condition (hatched bars) was subtracted to obtain baselined RT (solid bars). Error bars indicate 1 SD. Also plotted are RT histograms for RAND-REG (Upper) and REG-RAND (Lower). The histograms were computed over all trials and all subjects. Raw RT in each trial was corrected by that subject’s mean STEP RT (thus resulting in instances of negative RT, or responses occurring before the nominal transition in RAND-REG). Orange or dark-blue colored bars indicate responses which fell within 2 SDs from the mean. The results demonstrate that, on average, subjects require about 1.5 cycles to detect the emergence of regularity (with >80% of the responses occurring before the pattern has repeated). The average time required to detect the violation of a REG pattern is three tones. (B) Detection times for RAND-REG and REG-RAND transitions where REG patterns consisted of 20 tones (R_cyc = 20). (C) Ideal observer model responses to RAND-REG signals showing the average information content of each tone-pip (from five tones before the transition). The model required a cycle + four tones to detect the emergence of regularity. Shading indicates 2 SEM. (D) Ideal observer model responses to REG-RAND signals showing the average information content of each tone-pip (from five tones before the transition). Transitions are detected immediately following the first RAND tone.

Participant detection results are summarized in Fig. 2 A and B (see Table S1 for information on hits/false alarms and Fig. S1 and Table S2 for information on RT variability). For R_cyc = 10, listeners required, on average, 773 ms (15.5 tones) to detect the emergence of a regular pattern in RAND-REG sequences (Fig. 2A, orange). As the pattern is not detectable before the first cycle has elapsed, the RT data suggest that listeners required only an additional half cycle to detect the transition, performing on par with the estimate provided by the ideal observer model. RT distributions were computed by collapsing data from all subjects and all trials. In the vast majority of the trials (88.5%) subjects required fewer than two cycles to detect the regularity.

Fig. S1.

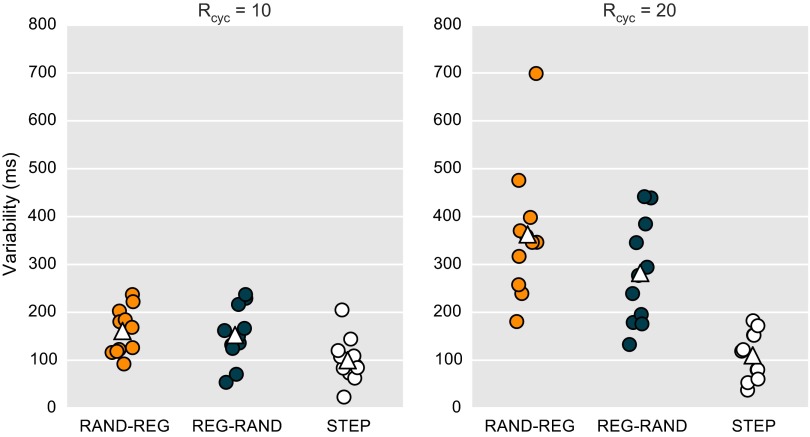
Subject RT variability for the behavioral experiment (experiment 1). Each dot represents the SD of the RT over trials for one subject on a given condition (RAND-REG, REG-RAND, STEP), for R_cyc = 10 (Left) and R_cyc = 20 (Right). White triangles indicate mean SD for each condition.

Table S2.

Summary of reaction times from experiment 1

	Rcyc = 10			Rcyc = 20
	RAND-REG	REG-RAND	STEP	RAND-REG	REG-RAND	STEP
Mean (ms)	1,210	592	437	2,129	863	447	As measured
SD	91	119	80	314	207	86
Mean (ms)	773	155		1,682	415		Baselined
SD	92	88		292	160

When the regularity cycle is increased to 20 tones (R_cyc = 20), listeners exhibit a significant lag relative to the ideal observer, on average responding 9 tones later than the lower bound implied by the model. Listeners required an average of 1,682 ms (33.6 tones) to detect the regularity, with 80.4% of the responses occurring before they heard two full repetitions of the pattern. The sequences are too rapid for a conscious search of pattern emergence. Instead, the regularity appears to automatically “pop out” of the ongoing sound stream. To detect the emergence of regularity, the auditory system must presumably maintain and update a statistical model of the auditory input, registering tone repetitions, and decide at which point there is sufficient evidence to indicate a regular pattern. The results suggest that the ability to do this efficiently deteriorates after R_cyc= 10, likely due to insufficient memory capacity.

Interestingly, despite behaving essentially like ideal observers in the RAND-REG R_cyc = 10 condition, performance in the matching REG-RAND condition (Fig. 2 A and B, blue bars) is significantly more sluggish than that implied by an ideal observer: listeners required an average of 155 ms (3.1 tones) to detect the violation of the REG pattern. This discrepancy is mirrored in the MEG data below.

Experiment 2: MEG Responses to the Emergence of Regular Patterns.

MEG responses to RAND-REG and REG-RAND signals (with R_cyc = 10) were measured in experiment 2. Listeners were naïve to the auditory stimuli and attended to an incidental visual task; the observed brain responses can therefore be taken as reflecting largely automatic processes. Group RMS data for the two stimulus conditions, together with their respective no-change controls, are presented in Fig. 3A. Evoked responses consist of an onset peak (M100) at ∼100-ms poststimulus onset and a subsequent rise to a sustained response. Generally, brain activity evoked by both transitions is characterized by large-scale DC shifts, on which responses to individual tones are superimposed. To disambiguate slow (steady-state) and fast (phasic stimulus-bound) responses, the data were also high pass filtered (at 2 Hz), and those waveforms are presented in the insets.

Fig. 3.

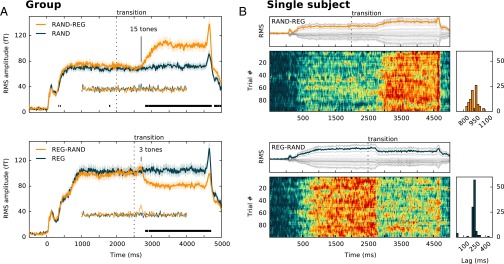
MEG responses to the emergence and violation of a regular pattern. (A) Group-RMS (RMS of individual RMSs; 13 subjects) of brain responses to RAND-REG (Upper) and REG-RAND (Lower) conditions, along with their respective no-change controls. The figures show the entire stimulus epoch, from stimulus onset (t = 0) to offset (t = 4,500 ms). Shaded areas around the curves represent twice the SEM, computed with bootstrap resampling (60; 1,000 iterations; with replacement). Respective transition times are marked by a dotted black line. Intervals where a repeated measures bootstrap procedure indicated significant differences between conditions are marked with a black line, underneath the brain response. The high pass-filtered responses are also plotted underneath the main curve. (B) Single trial data from a representative subject for RAND-REG (Upper) and REG-RAND (Lower). In each panel, the top plot displays the RMS response (in orange or blue, respectively) computed across averaged data from the 40 selected channels for that subject (in gray). Raster plots (Lower) show the single trial data for each condition. Data for each trial were temporally smoothed using a moving average over 10 adjacent samples (16.6 ms) and normalized between 0 and 1 to facilitate visualization. To quantify the temporal jitter in transition responses, the transition time within each trial is estimated by cross-correlating the single trial RMS time course with an ascending (for RAND-REG) or descending (REG-RAND) Heaviside-step function. The lags that gave the maximum correlation value for each trial are plotted in the histograms.

The response to the RAND-REG transition is manifested as a gradual increase in amplitude (over 250 ms; five tones) and a subsequent plateau. The first difference between the mean RAND-REG and RAND responses (determined with bootstrap resampling; Materials and Methods) emerges at 775-ms after transition in the left hemisphere (LH) and 790 ms in the right hemisphere (RH), i.e., just under 16 tones. This estimate is essentially identical to that derived behaviorally in experiment 1 (and to the ideal observer model), indicating that regularity detection processes operate efficiently even in naïve listeners, when the stimulus is not behaviorally relevant. There were no differences between the high pass filtered responses for this condition, suggesting that the detection of regularity is a contextual effect that is expressed in changes in the amplitude of slow (steady-state) activity.

The mean response to the transition in the REG-RAND signals (cessation of a regular pattern) is characterized by a small power increase at about 150 ms after transition (this is more prominent in the high pass-filtered data), followed by a sharp decrease and a plateau. The first significant difference between the mean REG-RAND and REG responses occurs during the downward slope, at 223 ms after transition in the LH and 281 ms afrer transition in the RH. High pass filtering the data reveals an earlier difference between REG and REG-RAND at 173–190 ms in the RH (not significant in the LH), consistent with latencies commonly associated with the MMN response. Overall, the data suggest that, on average, the brain requires about three tones to detect the violation of the regular pattern, consistent with the behavioral estimates in experiment 1. Brain responses to the violation of regularity are characterized by an MMN-like response and a sharp decrease in DC power that occurs immediately after the MMN.

Single trial data, from a representative subject, are shown in Fig. 3B. The mean (across trials) REG-RAND response (Upper) first emerges at 775 ms after transition (14.6 tones); however, this latency is variable across trials as seen from the raster plot and summary latency distribution. In contrast, REG-RAND response latencies are consistent across trials, resulting in a sharp mean transition response at 216 ms after transition (five tones). The delay (relative to an ideal observer) in this condition therefore appears to be a constant, presumably imposed, interval.

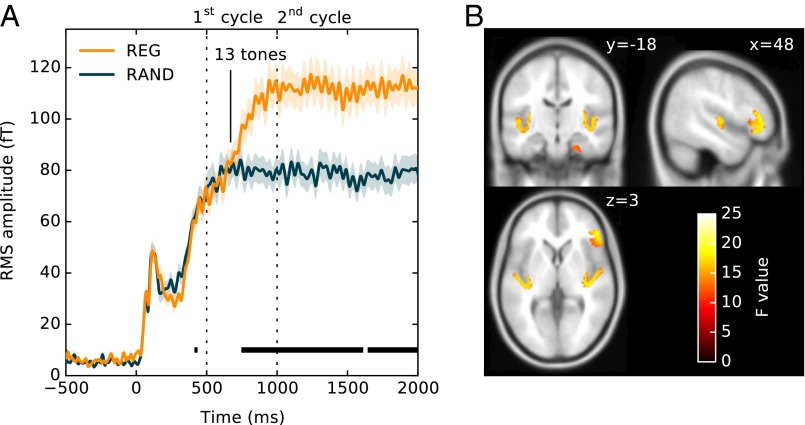
Rather than focusing on transitions between REG and RAND, sensitivity to regularity can also be investigated by comparing brain responses to the onset of REG and RAND sequences. During the initial portion of the sequence (first cycle), responses to the two types of sequences should be identical, with differences emerging as soon as the auditory system discovers that the pattern is repeating. Fig. 4 focuses on the initial responses to REG and RAND signals, irrespective of whether they contain a later transition. The difference between the two responses emerges around 650 ms after onset (roughly 13 tones or 1.3 cycles). A repeated measures bootstrap analysis, thresholded at P < 0.01, comparing REG and RAND responses (Materials and Methods), indicated that a significant difference between conditions emerges at 743 ms in the LH and 746 ms in the RH (i.e., just under 15 tones). At that time point, the response to RAND plateaus while that to REG continues to rise, plateauing at 1,000 ms (2 cycles) after onset. Further to this, there is no evidence, at least in the time-locked signal analyzed here, for additional accumulation of evidence concerning the regular pattern. Notably, similarly to the transition responses (Fig. 3), the difference between REG and RAND is manifest as a marked increase in the DC amplitude (increase in power).

Fig. 4.

Buildup of regularity (experiment 2). (A) Responses to the onset of REG and RAND signals. The responses, including an M100 onset response, and a rise to a sustained response, are identical up to about 650 ms. Subsequently, activity in REG continues to build up until about 1,000 ms (two cycles) where it plateaus. Shading around the lines represents 2 SEM, computed with bootstrap resampling (60; 1,000 iterations; with replacement). Intervals where a repeated measures bootstrap procedure indicated significant differences between conditions are marked with a black line, underneath the brain response. (B) MEG source localization results. Shown is a group SPM t map for the REG > RAND contrast in the 650- to 950-ms interval, thresholded at P = 0.005 (uncorrected). These are superimposed on the MNI152 T1 template with the coronal and axial sections at x = 48, y = −18, and z = 3 mm, respectively.

Source localization (Fig. 4B and Materials and Methods), applied to the interval 650–950 ms (containing the period over which REG and RAND diverge), showed increased activity in auditory cortex (bilaterally), hippocampus (bilaterally), and IFG (RH only). Table S3 provides coordinate information.

Table S3.

Summary of MEG source localization results, experiment 2

Location	Side	MNI coordinates			Peak
		x	y	z	F	P (uncorrected)
HC	Right	26	2	−34	19.007	0.001
		30	−2	−28	18.907	0.001
AC	Right	54	−4	6	17.038	0.001
		38	−20	2	13.414	0.003
IFG	Right	44	32	−12	16.868	0.001
		44	34	4	14.160	0.003
AC	Left	−54	−6	6	16.445	0.002
		−42	−20	−6	13.563	0.003
HC	Left	−36	−22	2	13.240	0.003
		−26	−2	−32	13.961	0.003

HC, hippocampus.

Experiment 3: fMRI.

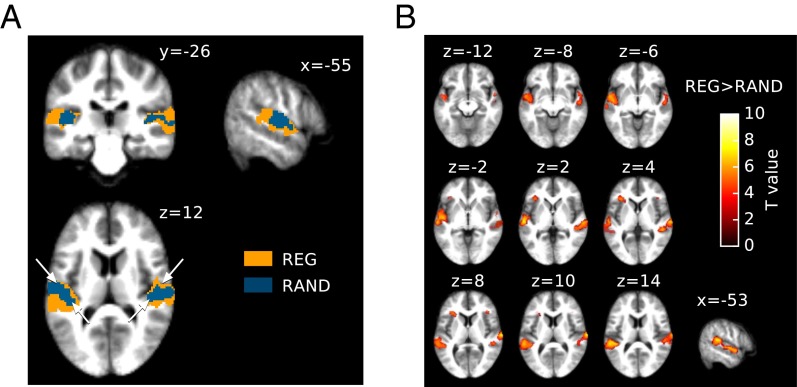
fMRI BOLD activation was measured in response to a continuous sequence randomly alternating between REG (R_cyc = 10), RAND, and silent intervals. The duration of each interval was randomized between 4 and 10 s. Due to the temporal constraints associated with the fMRI technique, it is likely that this manipulation predominantly captures the brain systems associated with the sustained portion of REG- and RAND-related processing. Fig. 5A presents the activation elicited by the REG and RAND conditions, overlaid on the subjects’ average anatomy. Both signals produced very similar patterns of activation along heschl’s gyrus (HG) and planum temporale (PT) bilaterally (the approximate position of HG is indicated by two arrowheads on the axial section in Fig. 5A). For REG, the activation cluster was larger, extending into more posterior regions of the superior temporal plane as well as the superior temporal gyrus (STG). In contrast, group activation for RAND was mostly centered on HG and extended less into PT, in line with the MEG results, above, which consistently demonstrate increased activation for REG relative to RAND sequences.

Fig. 5.

fMRI results. (A) fMRI group activation for REG and RAND conditions, superimposed onto coronal (y = −26), sagittal (x = −55), and axial (z = 12) sections of the average structural image. The height threshold for activation was P < 0.001 (uncorrected) at the peak level, P < 0.05 (FWEc.) at the cluster level. Blue, activation for RAND; orange, activation for REG. The white arrowheads on the axial section indicate the midline of Heschl’s gyrus in each hemisphere. (B) Regions showing increased hemodynamic responses to REG sequences compared with RAND, thresholded at P < 0.001 (uncorrected, but see familywise error corrected coordinate information in Table S5). Results are shown for different axial sections on the subjects’ average structural anatomy. The color map indicates peak level significance. The contrast revealed increased hemodynamic responses to REG bilaterally in PT, STG, and planum polare (PP). Additional activation in the left inferior frontal gyrus (IFG; right IFG was also present but does not survive correction for multiple comparisons; Table S5).

A “REG vs. RAND” contrast was examined to isolate regions associated with the processing of regularity (Fig. 5B; see Table S4 for coordinate information). This contrast revealed increased hemodynamic responses to REG in the left hemisphere in the lateral part of HG, bilaterally in PT, all along the upper bank of the STG, extending to planum polare (PP). Additionally, IFG activation was found in the left hemisphere (right IFG was also present but did not survive the P < 0.05 familywise error cluster correction). The RAND vs. REG contrast was also inverted to isolate potential regions specific to RAND sequences (RAND > REG), but no candidates were found; all of the regions activated by random sequences were activated to at least the same degree by regular sequences.

Table S4.

Areas of significant fMRI activation for the REG > RAND contrast in experiment 3

Location	Side	MNI localization			Cluster		Peak
		x	y	z	P (FWEc)	kE	P (uncorrected)	T value
PT	Right	71	−17	11	0.000	2007	0.000	7.49
		51	−35	3			0.000	6.22
		62	−21	0			0.000	5.89
PT/PP	Left	−51	−33	13	0.000	3506	0.000	7.12
		−59	−18	1			0.000	6.98
		−51	−9	−5			0.000	6.85
IFG	Left	−32	27	6	0.031	316	0.000	5.70
PP	Right	56	−12	−8	0.018	355	0.000	5.50
		54	6	−9			0.000	4.63

Results are thresholded at P < 0.001 (uncorrected) at the peak level, and P < 0.05 [familywise error-corrected (FWEc)] at the cluster level. P value of 0.000 means P < 0.001.

Experiment 4: MEG Responses to Regular and Random Patterns of Varying Alphabet Size.

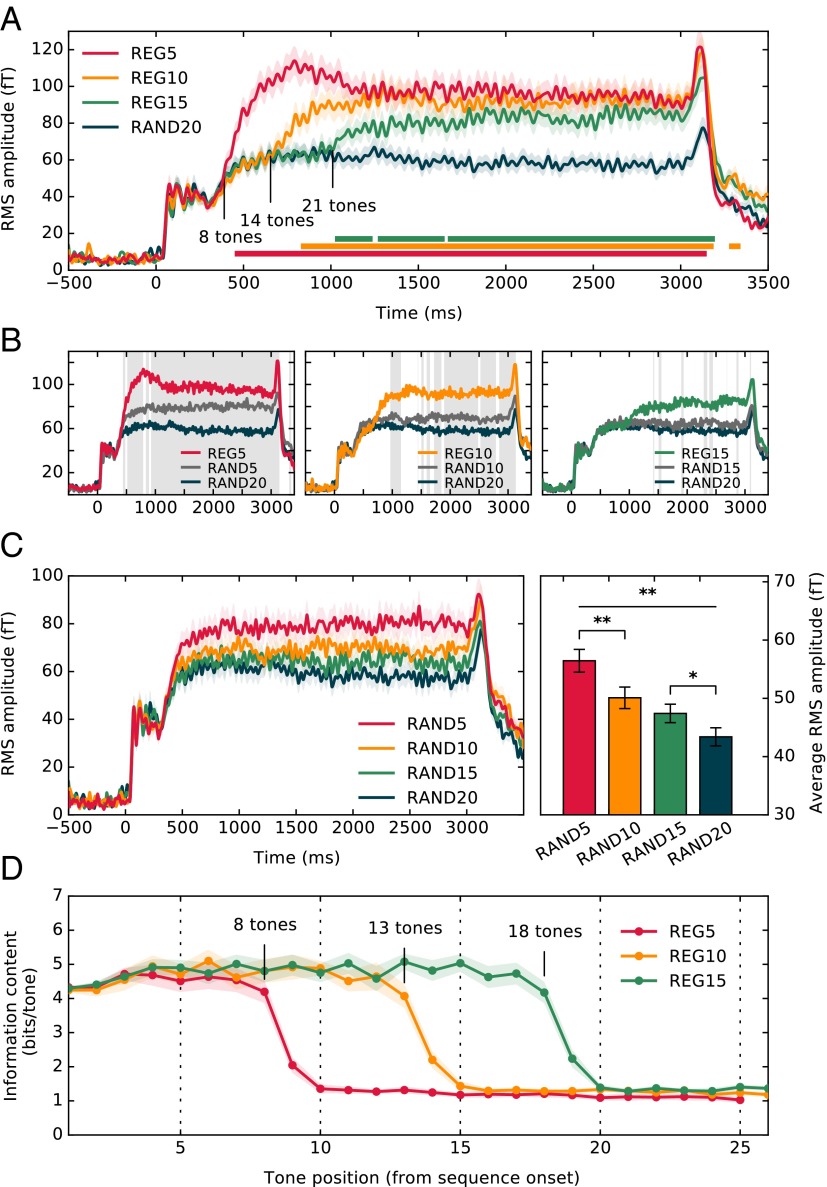
Experiments 2 and 3 focused on regular patterns with a fixed cycle length (10 tones; 500 ms). In experiment 4, three different regularity cycle lengths (R_cyc = 5, 10, and 15) were presented in random order. RAND signals with matched alphabet sizes were also included in the data set (e.g., RAND5 is a random sequence consisting of only five frequencies). Overall, on any given trial the presence of regularity or its cycle length were unpredictable. Fig. 6A (Upper) shows the group RMS response at stimulus onset to the REG5/10/15 and RAND20 conditions. The results demonstrate rapid detection of regularity even when the duration of the regularity is a priori unknown. Mean response latencies for the different regularities (relative to RAND20) scaled with cycle duration. A comparison of each regularity condition with its matched RAND signal is plotted in Fig. 6B. The latencies at which responses to relevant condition pairs first diverge are summarized in Table S5.

Fig. 6.

MEG responses to sequences of varying alphabet size (experiment 4). (A) Group RMS of brain responses to REG5, REG10, and REG15 conditions, along with RAND20. Plotted is the entire stimulus epoch, from stimulus onset (t = 0) to offset (t = 3,500 ms). Intervals where a repeated measures bootstrap procedure indicated significant differences between each REG condition and RAND20 are marked with a line, underneath the brain responses. (B) Responses to REG5, REG10, and REG15 (identical to A) with those to their respective random controls (RAND5, RAND10, RAND15), and RAND20. Gray shading indicates temporal intervals where a significant difference (repeated measures bootstrap analysis; Materials and Methods) was found between responses to RAND5/10/15, respectively, and RAND20. (C) (Left) Responses to the different RAND stimuli (identical to B). (Right) Average RMS amplitude over the entire stimulus duration. Error bars indicate 1 SEM. (D) Model output showing trial-averaged information content for each tone pip from sequence onset for REG5, REG10, and REG15. Shading indicates 2 SEM.

Table S5.

Experiment 4: Latency of divergence between conditions, calculated with repeated measures bootstrap resampling (Materials and Methods)

Cond1 vs. Cond2		Latency (ms)
Cond1	Cond2	Left hemisphere sensors	Right hemisphere sensors
REG5	RAND20	485 (±1)	396 (±2)
REG10	RAND20	691 (±45)	745 (±28)
REG15	RAND20	1,001 (±28)	1,020 (±19)
REG5	RAND5	450 (±1)	476 (±3)
REG10	RAND10	732 (±3)	862 (±15)
REG15	RAND15	1,044 (±19)	1,192 (±54)
RAND5	RAND20	598 (±23)	400 (±2)
RAND10	RAND20	1,621 (±13)	518 (±8)
RAND15	RAND20	1,018 (±22)	1,016 (±85)

Because the bootstrap is a stochastic process, slightly different values were obtained for each application of the test. Therefore, for each condition pair, the test was run 1,000 times, and we report the average obtained latency. Numbers in parentheses indicate the SD across the 1,000 runs. We note that the RH latency for RAND10 vs. RAND20 is lower than what might be expected. This effect corresponds to a brief significant interval (not visible in Fig. 6B due to its short duration) that likely stems from noise in the data.

Sustained response patterns are identical to those observed in experiment 2 above, with the three regularity conditions tending to the same amplitude level. RAND sequences of different alphabet sizes also exhibit sustained amplitude differences, with the most predictable (RAND5) presenting the highest amplitude (Fig. 6B). This pattern of results is consistent with a hypothesis that the observed brain responses are modulated by the predictability (rather than complexity) of the pattern. For example, in the leftmost panel in Fig. 6B, the deterministic regularity (REG5) shows the highest amplitude, followed by RAND5 (where, if the rule is learnt, an observer can expect one of five frequencies). RAND20 (where the prediction precision is lowest) is associated with the lowest DC amplitude.

To facilitate comparison, responses to RAND signals of increasing alphabet size are replotted in Fig. 6C. The mean RMS amplitude (over the entire epoch duration) was computed for each subject in each condition (Fig. 6C, Right). A repeated-measures ANOVA (Greenhouse–Geisser corrected) demonstrated a main effect of alphabet size [F(1.3, 15.4) = 9.70, P < 0.005]. Post hoc comparisons (least significant difference) indicated significant reduction in activity between RAND5 and RAND10 (P < 0.005), as well as between RAND15 and RAND20 (P < 0.05), indicating sensitivity to nondeterministic regularities.

Model results for the same stimuli are plotted in Fig. 6D. Independent of the regularity cycle, the ideal observer model required a cycle plus three tones to detect the emergence of regularity. A comparison with the MEG data suggests that brain responses from distracted humans exhibit ideal observer behavior for REG5 and REG10, with growing sluggishness emerging for larger cycle sizes. It is noteworthy that this pattern correlated with the observed DC amplitude effects: REG5 and REG10, for which performance is ideal observer like, also exhibit the same amplitude, whereas the sustained amplitude of REG15 is just below this level.

Discussion

The aim of this series of experiments was to understand whether, and how, the brains of naïve listeners detect the emergence of complex patterns within rapidly evolving sound sequences. Our results suggest that the auditory system continually scans the environment and efficiently represents complex stimulus statistics, even when they are not behaviorally relevant.

Sensitivity to Acoustic Patterns.

Listeners demonstrate remarkable sensitivity to the emergence of patterns within rapidly unfolding random tone-pip sequences. On most trials, listeners required less than one full repetition of a pattern to detect the regularity. This performance held for all cycle durations tested (up to R_cyc = 20) (25, 26) and appears to take place automatically: estimates based on brain response latencies from naïve, passively listening participants (experiments 2 and 4) were essentially identical to those obtained behaviorally (experiment 1). For cycles of up to 10 tones, detection time was similar to that estimated from an ideal observer model with perfect memory. Longer cycles were associated with increasing sluggishness suggestive of growing strain on some form of memory store (see below).

Experiment 4 (Fig. 6) examined responses to deterministic regularities with varying complexity (repeating patterns of increasing length) and nondeterministic, increasingly complex, regularities (random tone sequences varying in alphabet size). The pattern of MEG responses demonstrates that the brain is sensitive to both the alphabet size of a pattern (e.g., responses differentiate RAND5 from RAND20), as well as the specific sequence structure (e.g., responses differentiate REG5 and RAND5).

The ideal observer model, used to benchmark performance, was based on storing ongoing sequence statistics in terms of the transition probabilities with which tones in the alphabet have appeared following each sequential context (i.e., tallying all tones, pairs, and triplets). Examining model output revealed that it was sufficient to store contexts of three tones (four in the case of RAND-REG transitions) to detect transitions within the sequences used here. That human performance could be reproduced by the ideal observer model suggests that listeners may be storing similar statistics.

In addition to memory processes associated with storing transition probabilities, while scanning the unfolding sequence, listeners must maintain a certain portion of the sequence in short-term memory for comparison with the stored transition probabilities. Both memory processes could impose constraints on performance. Our results do not speak directly to how sequential information is encoded; however, subjectively (Audio Files S1–S8), it seems that once the RAND-REG transition has been detected, one becomes aware of the preceding pattern. In other words, the brain appears to call on mnemonic representations to reverse scan the stored representation of the pattern and infer when the regularity began (27, 28). In experiments using stimuli similar to those used here (RAND-REG transitions with R_cyc = 6), Jaunmahomed and Chait (27) investigated the nature of this retrospective assignment. Participants were asked to indicate whether a light flash occurred before or after the onset of the regular pattern. The point of subjective simultaneity did not occur at the point of detection, but preceded it by about a cycle. This effect was reduced by half when the tone duration decreased (from 100 to 50 ms), suggesting that the memory representation of the ongoing sequence, used to infer regularity onset, is not limited by a fixed duration but rather by information (number of events).

Having established regularity detection formally, in terms of ideal Bayesian assumptions—and having identified robust neurophysiological correlates—means that we are now in a position to further explore the underlying memory mechanisms by systematically manipulating various properties of the regularities and how they are violated and by examining whether these processes might be affected by effort or attentional set.

Substrates.

Two complementary approaches were used to identify the neural substrates underlying the processing of REG vs. RAND patterns: MEG source analysis, focused specifically on the interval where responses to REG and RAND first diverged, suggested that the process of regularity detection is subserved by a network comprised of early—auditory cortical (AC)—sources along with sources in frontal cortex (right IFG). This finding is a first demonstration of the involvement of these networks in implicit learning of rapidly evolving statistical structure but is generally consistent with previous reports implicating these structures in auditory sequence learning. Activations in IFG and AC are commonly reported in the context of the MMN oddball paradigm (27, 28) and interpreted (29) as suggesting that the MMN arises from an interaction between bottom-up and reentrant effects (9, 11, 30). Similarly, violations of artificial grammars consisting of complex, nonadjacent, or hierarchical relationships between elements in sound sequences have been shown to activate IFG during both explicit decision making and implicit tasks (31–33). IFG has also been consistently implicated during encoding and retention periods in working memory experiments (34–36), including in working memory paradigms for pitch (37).

Our MEG results suggest that the hippocampus also contributes to the process of refining the generative model and discovering the regularity within the ongoing sound sequence. Although it is not often observed in auditory experiments, MEG has been previously reported to be sensitive to hippocampal sources (38, 39). The present findings are consistent with recent suggestions that the hippocampus might be involved in the integration of complex temporal patterns in audition (40). Importantly, these data provide support for the emerging literature on hippocampal involvement in high resolution pattern perception (41–43), and statistical learning (44–46), adding converging evidence for the role of the medial temporal lobe in the rapid detection of regularities within continuously presented sensory signals.

fMRI analysis was focused on identifying BOLD response differences between REG and RAND. Due to the limits on temporal resolution, it is likely that this is mostly driven by the sustained response portion of the signals rather than the (brief) period of evidence accumulation. This analysis revealed a largely similar network, comprised of auditory cortical and frontal sources, but notably differing in the lateralization of IFG activation and lacking hippocampus activity. Within the auditory cortex, RAND activity was mostly centered on HG and extended less into PT, indicating that the processing of random sequences is associated with more local computations than REG sequences. This pattern of activation is also consistent with the large sustained response difference between REG and RAND observed in the time domain data (see more discussion below).

The absence of hippocampal activity in the fMRI data are difficult to interpret due to the various differences in sensitivity between the MEG and fMRI methods (47). One possibility is that hippocampal activity is too slow to be accompanied by BOLD increases, which are conventionally considered to occur for oscillatory local field potentials above beta range (48). Another is that the contribution of the hippocampus to regularity detection is time delimited and restricted to the early stages of pattern detection. However, further work is required to understand the nature of this involvement.

Sustained-Response Amplitude Reflects Sequence Predictability.

The emerging divergence between REG and RAND, when transitioning between the two sequences (Fig. 3) and at onset (Figs. 4 and 6), is manifest as an increase in the sustained amplitude of the evoked response. This result cannot be attributed to low-level effects such as refractoriness or neural adaptation. Adaptation effects, measured with MEG or EEG, are commonly revealed as a decrease in response amplitude over time (49). The present data are characterized by the opposite effects. For instance, REG10 (a repeated sequence of 10 tones) is associated with higher sustained amplitude than RAND20 (a random pattern of 20 tones; Figs. 4 and 6). The data are also not consistent with explanations in terms of attention effects. Although gain increases are often observed in the context of attentional manipulations (selective attention often enhances sensory-evoked responses), and it is theoretically possible that regularly repeating signals might attract attention even in naïve distracted subjects (5) leading to a gain increase, rapid gain decreases are difficult to account for within this framework.

Instead, the observed sustained amplitude modulations appear to be contingent on the predictability of the sequence such that

• i)The sustained amplitude correlates with the alphabet size of the sequence: RAND5 > RAND10 > RAND15 > RAND20 (Fig. 6).
• ii)For a given alphabet size, the sustained amplitude is higher when the sequence is deterministic (REG5 > RAND5, REG10 > RAND10, etc.).
• iii)The DC amplitude appears to not depend on the complexity of the regular pattern per se, but rather on the degree to which the pattern has been learned: REG5 and REG10, for which performance (quantified as the latency at which the response diverges from that to RAND) is ideal observer like, are also associated with similar DC amplitudes. However, the sustained amplitude of REG15—for which detection is slower than that of an ideal observer—is just below this level.
• iv)The transition from REG to RAND, when the sequence becomes unpredictable, is associated with an immediate drop in the sustained response.

In the predictive coding framework, evoked responses have usually been interpreted as reflecting prediction error (7, 11, 50, 51). In this context, increasing stimulus predictability and the concomitant suppression of prediction error are associated with a decrease in the sensory evoked response: an effect which is indeed commonly observed for the relatively simple stimulus sequences previously used to investigate predictive coding (2, 3, 7, 9, 51, 52). In contrast, increasing predictability in the present dataset is associated with an amplitude increase. These effects have not been observed previously, possibly due to the significantly simpler signals used in those studies, where predictability is often confounded with low-level neural adaptation. The complex, wide-band tone patterns used here are largely free of this constraint, enabling a new view of brain mechanisms that underlie bottom-up driven statistical learning.

The observed effects are compatible with an interpretation of the responses as reflecting precision-weighted sensory signals. Precision (the inverse variance of a variable) is a key element of predictive coding, enabling the system to operate optimally under different degrees of uncertainty by reweighting signals according to their inferred reliability (53, 54). Reliable inputs—associated with low uncertainty (high precision)—indicate salient sensory evidence and give rise to heightened sensitivity (increased gain), such that subsequent prediction errors, suggestive of a genuine change in the environment, are up-weighted in the process of model updating. Conversely, unreliable (low precision) inputs, indicative of a weak model or a high degree of uncertainty, are down-weighted. The present data are consistent with such effects: rapid, bottom-up driven response modulation concomitant with adaptive predictive precision. However, the shape of the response does not resemble a classic gain effect, and it is unclear whether the signals reflect a single process (gain modulation of sensory units) or a superposition of independent processes (a sustained current + a sensory evoked response). Additionally, because it is impossible to disambiguate excitatory and inhibitory processes with MEG, it is possible that the DC modulation reflects a sustained inhibitory current.

MMN.

Most previous work on sensitivity to acoustic patterning has been conducted in the context of the MMN paradigm where the occurrence of a mismatch response to a signal that violates a previously established regularity is taken as a (indirect) measure of the extent to which this regularity has been acquired (10, 11, 16, 30).

An MMN-like response is observed here, evoked by the transition from a regular to random pattern in the REG-RAND signals. This response is immediately followed by a sharp amplitude decrease, consistent with a process by which the MMN, reflecting precision-weighted prediction error (9), signals the incompatibility of sensory input with the existing internal model, which then leads to an immediate down-regulation of gain on the relevant sensory units.

It is noteworthy that the drop in amplitude occurs some five tones after the transition to RAND, in contrast to an almost immediate (relative to an ideal observer) rise in amplitude following the emergence of regularity. This result reveals an apparent asymmetry: the brain immediately detects the rising predictability associated with the transition to a REG signal but is delayed at updating its estimate of precision following the violation of a REG signal. The intrinsic delay associated with reacting to violation of regularity suggests that the auditory system is programmed to hold on to regularities for slightly longer than is objectively warranted, perhaps because of operational time-constants associated with the mechanisms giving rise to regulation of gain. In other words, there appears to be a bias in the precision-weighted modulation (observable also in behavior) toward discovering patterns and against losing patterns that have been discovered.

Materials and Methods

Experiment 1.

Stimuli.

Stimuli were sequences of 50-ms tone-pips (gated on and off with 5-ms raised cosine ramps) with frequencies drawn from a pool of 20 values equally spaced on a logarithmic scale between 222 and 2,000 Hz (12% steps). RAND-REG stimuli (Fig. 1) consisted of an initial sequence of random tones that after a certain duration, changed into a REG pattern. REG sequences were generated by randomly selecting (with replacement) a number (R_cyc) of frequencies from the pool and then iterating that sequence to create a regularly repeating pattern. In this manner, novel regular patterns were created on each trial. The complexity of the pattern depends on the length of the regularity cycle (R_cyc). R_cyc was set to 10 or 20 in this experiment.

Two control transitions were included in the stimulus set: (i) REG-RAND stimuli contained a transition between a regular and a random pattern. (ii) STEP stimuli consisted of a step change in frequency between two sequences of repeated tones. A series of no-change sequences (either REG, RAND, or a sequence of fixed frequency tones) were also included. All signals comprised between 7*R_cyc and 9*R_cyc tones. The time of change varied randomly across trials, with the transition occurring between the 4*R_cyc-th and 5*R_cyc-th tones.

The tone durations used are well below the range of durations of notes in melodies (55) and below the reported thresholds for order discrimination within tone sequences (22, 56–58). The sequences are therefore much too rapid to enable any form of explicit reasoning regarding pattern emergence. Rather, the emergence of regularity appears to perceptually pop out from the ongoing sequence irrespective of subjective effort. The present experiments aim to characterize this apparent pop-out process.

Procedure.

Two consecutive blocks of 130 stimuli (50 REG-RAND, 50 RAND-REG, 50 RAND, 50 REG, 15 STEP, and 15 constant frequency tone) were presented for R_cyc = 10, followed by two blocks of 130 stimuli with R_cyc = 20. Subjects also completed a short practice session (40 trials) for each R_cyc. Stimulus presentation was controlled with the Cogent software (www.vislab.ucl.ac.uk/cogent.php). Subjects were tested in a darkened, acoustically shielded room (IAC triple-walled sound attenuating booth). They were instructed to fixate a white cross in the center of the computer screen while listening to the stimuli and respond, by pressing a keyboard button, as soon as they detected the stimulus transitions in REG-RAND, RAND-REG, or STEP stimuli, presented in random order within the block.

Stimuli were rendered offline and stored as 16-bit .wav files at 44.1 kHz, delivered to the subjects’ ears with Sennheiser HD555 headphones (Sennheiser) and presented at a comfortable listening level (self-adjusted by each listener). The interstimulus interval (ISI) was 2,000 ms. The stimulus set was generated anew for each participant.

Participants.

Thirteen paid subjects (nine female; average age, 24 ± 8 y) participated in the experiment. All reported no history of hearing or neurological disorders. Two subjects were excluded from analysis due to inability to perform the task (no response for >50% of the trials). All experimental procedures reported in this manuscript were approved by the research ethics committee of University College London, and written informed consent was obtained from each participant.

Experiment 2 (MEG).

Stimuli.

The stimulus set included the RAND-REG and REG-RAND signals as described above, as well as their no-change controls (REG and RAND). The cycle length within the regular patterns was fixed at R_cyc = 10. Stimulus duration was 4.5 s, and the transition time was fixed at 2.5 s after onset for REG-RAND and 2 s after onset for RAND-REG. One hundred four signals were generated for each of the stimulus conditions. In this way, the probability of change was maintained at 0.5, and the occurrence of a transition within any specific stimulus was unpredictable. The stimuli were presented to the listeners in a random order with an ISI that varied between 700 and 2,000 ms.

Subjects were naïve to the auditory stimuli and engaged in an incidental (N-back) visual task. The task consisted of a sequence of landscape images, grouped in series of three (duration of each image was 5 s, with a 2-s between series interval during which the screen was blank). Subjects were instructed to fixate at a cross, drawn in the middle of the display, and press a button whenever the third image in a series was a repetition of the first or second one. Such repetitions occurred in 10% of the trials. The visual task served as a decoy task: a means to maintain attentional set and to divert attention away from the auditory stimuli. The instructions encouraged speed and accuracy, and feedback (number of hits, misses, and false positives) was provided at the end of each block. Visual and auditory stimuli were presented simultaneously from different computers to preclude correlation between audio and visual stimulus timing.

Procedure.

The experimental session always began with a preliminary “functional localizer” block, followed by the main experiment. In the functional localizer recording, subjects listened to about 200 repetitions of a 50-ms pure tone at 1 KHz, with an ISI randomized between 750 and 1,550 ms. The corresponding brain responses were used to ensure that recorded signals had a reasonable signal-to-noise ratio (SNR) and to determine which MEG channels were most sensitive to evoked activity within the auditory system. In the main experiment, which lasted about 40 min (excluding breaks), subjects listened to stimuli while performing the visual task as described above. All listeners were naïve as to the different stimulus conditions and informed that they were participating in a visual processing study. The presentation was divided into four runs of about 10 min. Between runs, subjects were permitted a short rest but were required to remain still.

Recording and data analysis.

Magnetic signals were recorded using a CTF-275 MEG system (axial gradiometers, 274 channels; 30 reference channels; VSM MedTech). Acquisition was continuous, with a sampling rate of 600 Hz and a 100-Hz hardware low-pass filter. Offline low-pass filtering was applied at 30 Hz for all time domain analyses (two-pass, fifth-order Butterworth), but there was no offline filtering for source-space analysis.

Functional localizer data were divided into 700-ms epochs, including 200 ms before onset, and baseline corrected to the preonset interval. The M100 component of the onset response (59) was identified for each subject as a source/sink pair located over the temporal region of each hemisphere on the subjects’ scalp maps. The M100 current source is generally robustly localized to posterior superior temporal plane in both hemispheres (59). For each subject, the 40 most strongly activated channels at the peak of the M100 (20 in each hemisphere) were considered to best reflect activity in the auditory cortex and thus selected for subsequent analyses. This procedure serves the dual purpose of enhancing the auditory response components over other response components and compensating for any channel misalignment between subjects.

For the data from the main experiment, 5,500-ms epochs (from 500 ms before stimulus onset to 500 ms after stimulus offset) were created for each of the stimulus conditions, averaged, and baseline corrected to the silent prestimulus interval. Trials with power that deviated from the mean by more than twice the SD (typically less than 7%) were flagged as outliers and discarded automatically from further analyses. Denoising source separation (DSS) analysis was applied to maximize reproducibility across trials (60, 61). For each subject, the first two DSS components (i.e., the two most reproducible components) were then selected and projected back into sensor space. Electromagnetic responses showed profound fluctuations in steady-state levels between the stimulus conditions and at the transitions. To identify additional (fast) activity, potentially masked by the slow DC changes, the same analysis was also performed on 2-Hz high-pass filtered data (Fig. 3).

In each hemisphere, the RMS of the field strength across the 20 channels, selected in the functional source localizer run, was calculated for each sample point. The time course of the RMS, reflecting the instantaneous amplitude of neural responses, was used as a measure of neuronal responses evoked in the auditory system. For purposes of illustration, group RMS (RMS of individual subject RMSs) is shown, but statistical analysis was always performed across subjects. The figures (except for the representative subject data in Fig. 3B) plot group RMS in the RH. The LH activation was always qualitatively identical.

To statistically evaluate the latency of the transition response (the time point at which RAND-REG or REG-RAND first show a statistical difference from their respective controls) the (squared) difference between the RMSs was calculated for each participant and subjected to bootstrap resampling (1,000 iterations, balanced) (62). The difference was deemed significant if the proportion of bootstrap iterations that fell above/below zero was more than 99% (i.e., P < 0.01) for 12 or more adjacent samples (20 ms). The bootstrap analysis was run over the entire epoch duration; all significant intervals identified in this way are indicated in the relevant figures.

Source localization.

To identify the brain areas subserving the process of regularity detection, we focused on comparing responses to the onset of REG and RAND signals. This approach allowed us to pool over the transition and control (no transition) conditions, substantially increasing the SNR. Focusing on the onset (Fig. 4), rather than transitions (Fig. 3), was also useful for specifically isolating the process of regularity extraction from those related to signaling a change in the sequences.

Source localization (based on data from all 274 sensors) was performed on the nonfiltered, time-averaged data using a minimum norm prior model (61). Before inversion, DSS component analysis (60, 61) was applied to each subject’s sensor data to maximize the difference between RAND and REG responses from 500 ms before stimulus onset to 1,500 ms after stimulus onset. The first two DSS components (those that maximized the difference between REG and RAND) were projected back into sensor space and used for the localization analysis. After inversion, source estimates were averaged over the interval of 650–950 ms, corresponding to the period over which the difference between REG and RAND builds up, projected to a 3D source space, and smoothed [8-mm full width at half maximum (FWHM) Gaussian smoothing kernel] to create Neuroimaging Informatics Technology Initiative (NIfTI) images of source activity for each subject. Source reconstructed responses were then used for the second level analysis using standard (statistical parametric mapping) procedures in SPM8 (www.fil.ion.ucl.ac.uk/spm/). Fig. 4B shows the activation map (F contrast) thresholded at P < 0.005 (uncorrected).

Participants.

Thirteen paid subjects (eight female; mean age = 27.6 y) participated in the experiment. All but one were right handed (63).

Experiment 3 (fMRI).

Stimuli.

The stimulus set included the REG (fixed at R_cyc = 10) and RAND signals as described above, as well as silent (scanner noise only) periods, which were treated as a stimulus condition in this experiment. The durations of each sequence type were randomized between 4 and 10 s using a truncated Poisson distribution with a parameter of 6 s. The minimum of 4 s was used to ensure that there was ample time to detect the regular patterns. One hundred fifty signals were generated for each of the stimulus conditions (REG, RAND, and Silence). A single, long sequence was built by presenting abutting REG, RAND, and Silence periods in a randomized fashion, such that the nature and the timing of the transitions were completely unpredictable. See SI Materials and Methods for details regarding image acquisition and analysis.

Procedure.

In the main experiment, which lasted about 60 min, participants passively listened to the auditory stimuli while performing the same visual task as in the MEG experiments above. Sounds were delivered dichotically with tube-phones (EARTONE 3A 10 Ω; Etymotic Research) inserted into the ear canal. All participants were naïve to the different stimulus conditions and informed that they were taking part in a visual processing study. The presentation was divided into five runs of about 12 min each. Between runs, participants were permitted a short rest but were required to remain in the scanner. Performance feedback on the visual task was provided at the end of every block.

Participants.

Sixteen paid subjects (six female; mean age = 27.6 ± 3 y) took part in the fMRI experiment. All but one were right handed (61).

Experiment 4 (MEG).

Stimuli.

The stimulus set included REG sequences with R_cyc = 5, 10, and 15 (henceforth referred to as REG5, REG10, and REG15, respectively). Each REG signal was matched with a RAND signal, comprising the same subset of frequencies (the same alphabet) but presented in a random order (henceforth referred to as RAND5, RAND10, and RAND15). Also included were RAND20 sequences (identical to RAND sequences in experiments 1, 2, and 3), sampling the entire frequency pool (alphabet size of 20). One hundred four sequences were generated for each of the stimulus conditions. Stimuli were presented in random order such that on each trial the type of stimulus (REG or RAND) and cycle duration (or alphabet size) were unpredictable. The stimuli were generated anew for each subject. The ISI was randomized between 700 and 2,000 ms. Subjects were naïve to the auditory stimuli and engaged by an incidental visual task, as described in experiment 2.

Procedure.

The procedure was the same as in experiment 2.

Participants.

Thirteen paid subjects (seven female; average age, 28 ± 8 y) participated in the experiment. All but one were right handed (63).

Statistical Model.

A model of auditory expectation, based on a variable-order Markov model, was used to quantify the predictability of each tone-pip within the experimental sequences (64). This model has previously been used successfully to predict listeners’ pitch expectations in musical melody assessed both behaviorally and using EEG (65, 66). Here, we use the responses of the model as an ideal observer to compare with those of the participants.

Information Dynamics of Music (IDyOM) uses unsupervised statistical learning to acquire transitional dependencies through exposure to sequences of auditory events. Here, the model is configured to learn online throughout an experimental session, starting with a null model, given the same experience as a typical participant in the study. The model’s output at each tone-pip position within a sequence is a conditional (or posterior) probability distribution governing the frequency of the next tone-pip, given the preceding context. This distribution accumulates the model’s experience during the experimental session. Using the posterior distribution, the model estimates the predictability of each possible continuation tone-pip, including the tone-pip that actually follows. The model’s output is formalized using the information-theoretic concept of information content (IC). IC is the negative log probability ($-\log P$) of a tone pip and is used as a measure of the unexpectedness of each tone-pip in the sequence, given the preceding context. The model is predominantly used to provide a benchmark for the earliest time at which RAND-REG (and REG-RAND) transitions can be detected. This time point is quantified by identifying the tone-pip position for which the IC begins to deviate (fall or rise). Because the model is based on storing high-order transition probabilities, it is particularly tuned to detect the emergence of deterministic regular patterns. In this research, an initially empty model is trained incrementally on a stimulus set identical to those presented to participants. Because it learns dynamically from the entire stimulus set of short tone sequences, the model is not sensitive to alphabet size within individual stimuli.

The modeling data presented here are computed by running the model on the full stimulus set for one participant, in the same order as would be presented to a participant in the study. The model output is summarized by averaging IC for each tone position in each condition over trials in the same way that participant responses are averaged across trials.

SI Materials and Methods

fMRI Methods.

Image acquisition.

Gradient weighted echo planar images were acquired on a 3-T Siemens Allegra MRI scanner using a continuous imaging paradigm with the following parameters: 42 contiguous slices per volume; time to repeat (TR) = 2,940 ms; time to echo (TE) = 30 ms; matrix size: 64 × 74; phase oversampling = 13%; slice thickness: 2 mm with 1-mm gap between slices; echo spacing = 500e−3 ms; ascending slice acquisition order. Subjects completed five scanning sessions, and a total of about 1,000 volumes were acquired. Field maps were acquired for each subject with a double-echo gradient echo field map sequence (short TE = 10.00 ms and long TE = 12.46 ms) to correct for geometric distortions in the functional images due to magnetic field variations (67). At the end of the functional scan (at the beginning for two subjects, due to technical reasons), a structural T1-weighted scan was also acquired.

Image analysis.

Functional data were analyzed using SPM12b (www.fil.ion.ucl.ac.uk/spm/). The first two volumes were rejected to control for saturation effects, and the remaining volumes were realigned to the first volume and unwarped using fieldmaps. The realigned images were spatially normalized to stereotactic space (68) and smoothed by an isotropic Gaussian kernel of 8-mm FWHM. Statistical analysis was conducted using a general linear model (69). A high-pass filter with a cutoff frequency of 1/128 Hz was applied to remove low-frequency signal fluctuations. A whole-brain random-effects model (70) was used to account for within-subject variance. Each subject’s first-level contrast images were entered into second-level t tests for the primary contrast of interest (REG vs. Silence, RAND vs. Silence, REG vs. RAND). Statistical maps were initially thresholded at P < 0.001 (uncorrected), and only clusters significant at P < 0.05 (familywise error-corrected for multiple comparisons) are reported. Functional results are overlaid onto the average T1-weighted structural scan based on the subjects’ individual structural scan.