Significance
Plants thrive in natural sunlight in part because photosystem II (PSII) flexibly captures sunlight. PSII is composed of pigment–protein complexes that densely pack the thylakoid membrane in chloroplasts. We explain the mechanisms underlying the high quantum efficiency of PSII light harvesting in ideal conditions using a quantum mechanical model of excitation energy transport in the membrane. We show that the diffusion length of excitation energy determines the way in which modifications to the membrane affect PSII’s, and ultimately a plant’s, photosynthetic efficiency. The model could be useful for developing artificial light-harvesting materials that are robust to the fluctuations inherent in natural sunlight and rationally engineered crops that achieve higher yields in adverse environments.
Keywords: excitation energy transfer, quantum coherence, structure−function relationships, photosynthesis, fluorescence lifetime
Abstract
The first step of photosynthesis in plants is the absorption of sunlight by pigments in the antenna complexes of photosystem II (PSII), followed by transfer of the nascent excitation energy to the reaction centers, where long-term storage as chemical energy is initiated. Quantum mechanical mechanisms must be invoked to explain the transport of excitation within individual antenna. However, it is unclear how these mechanisms influence transfer across assemblies of antenna and thus the photochemical yield at reaction centers in the functional thylakoid membrane. Here, we model light harvesting at the several-hundred-nanometer scale of the PSII membrane, while preserving the dominant quantum effects previously observed in individual complexes. We show that excitation moves diffusively through the antenna with a diffusion length of 50 nm until it reaches a reaction center, where charge separation serves as an energetic trap. The diffusion length is a single parameter that incorporates the enhancing effect of excited state delocalization on individual rates of energy transfer as well as the complex kinetics that arise due to energy transfer and loss by decay to the ground state. The diffusion length determines PSII’s high quantum efficiency in ideal conditions, as well as how it is altered by the membrane morphology and the closure of reaction centers. We anticipate that the model will be useful in resolving the nonphotochemical quenching mechanisms that PSII employs in conditions of high light stress.
The first step of photosynthesis is light harvesting, the absorption and conversion of sunlight into chemical energy. In photosynthetic organisms, the functional units of light harvesting are self-assembled arrays of pigment–protein complexes called photosystems. Antenna complexes absorb and transfer the nascent excitation energy to reaction centers, where long-term storage as chemical energy is initiated (1). In plants, photosystem II (PSII) flexibly responds to changes in sunlight intensity on a seconds to minutes time scale. In dim light, under ideal conditions, PSII harvests light with a >80% quantum efficiency (2), whereas, in intense sunlight PSII dissipates excess absorbed light safely as heat via nonphotochemical quenching pathways (3). The ability of PSII to switch between efficient and dissipative states is important for optimal plant fitness in natural sunlight conditions (4). Understanding how PSII’s function arises from the structure of its constituent pigment−protein complexes is a prerequisite for systematically engineering the light-harvesting apparatus in crops (5–7) and could be useful for designing artificial materials with the same flexible properties (8, 9).
Recent advances have established structure−function relationships within individual pigment−protein complexes, but not how these relationships affect the functioning of the dynamic PSII (grana) membrane (10). Electron microscopy and fitting of atomic resolution structures (11) place the pigment−protein complexes in the grana membrane in close proximity, enabling long-range transport. Indeed, connectivity of excitation between different PSII reaction centers has been discussed since 1964 (12), suggesting that the functional unit for PSII must involve a large area of the membrane. Two limiting cases have been used to model PSII light harvesting: The lake model assumes perfect connectivity between reaction centers across the membrane; alternatively, the membrane can be described as a collection of disconnected “puddles” of pigments that each contain one reaction center (1, 13). At present, however, resolving the spatiotemporal dynamics within the grana membrane on the relevant length (tens to hundreds of nanometers) and time (1 ps to 1 ns) scales experimentally is not possible. Structure-based modeling of the grana membrane, however, can access this wide range of length and time scales.
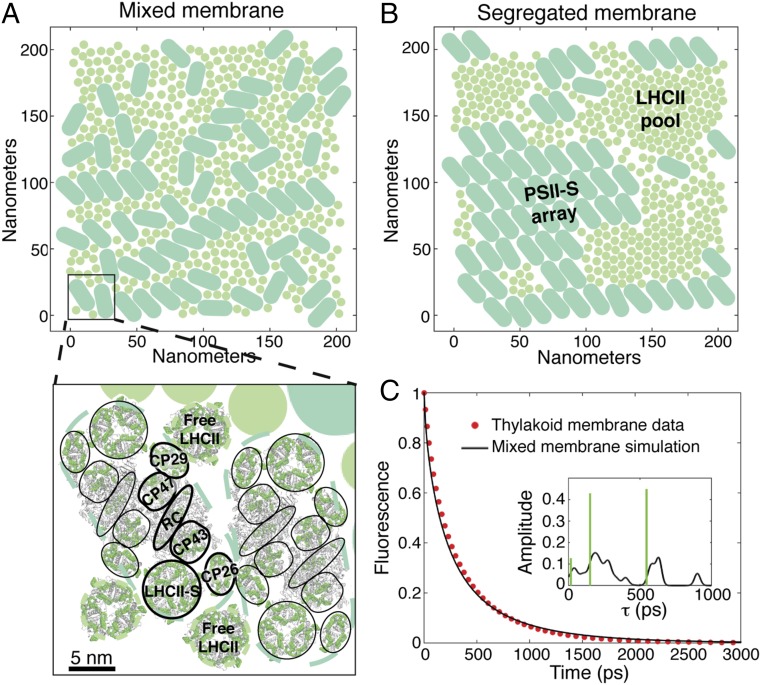
The dense packing of the major light-harvesting antenna (LHCII, discs), which is a trimeric complex, and PSII supercomplexes (PSII-S, pills) in the grana membrane is shown in Fig. 1 A and B. PSII-S is a multiprotein complex (14) that contains the PSII core reaction center dimer, along with several minor light-harvesting complexes and LHCII (Fig. 1A, Inset). Electronic excited states in LHCII and PSII-S are delocalized over several pigments (15–17), making conventional Förster theory inadequate to describe the excitation dynamics. On the protein length scale, generalized Förster (18, 19) calculations between domains of tightly coupled chlorophylls agree very well with more exact methods [e.g., the zeroth-order functional expansion of the quantum-state diffusion model (ZOFE) approximation to non-Markovian quantum state diffusion (20)] for simulating the excitation population dynamics (21, 22). This agreement suggests that the primary quantum phenomenon involved in PSII energy transfer is the site basis coherence that arises from excited states delocalized across a few (approximately three to four) pigments.
Fig. 1.
Accurate simulation of chlorophyll fluorescence dynamics from thylakoid membranes using structure-based modeling of energy transfer in PSII. (A and B) The representative mixed (A) and segregated (B) membrane morphologies generated using Monte Carlo simulations and used throughout this work. PSII-S are indicated by the light teal pills, and LHCII, which are trimeric complexes, are indicated by the light grey-green circles. The segregated membrane forms PSII-S arrays and LHCII pools. As shown schematically in A (Bottom) existing crystal structures of PSII-S (14) and LHCII (24) were overlaid on these membrane patches to establish the locations of all chlorophyll pigments. The light teal and light grey-green dashed lines outline the excluded area associated with PSII-S and LHCII trimers respectively, in the Monte Carlo simulations. The chlorophyll pigments are indicated in green, and the protein is depicted by the grey cartoon ribbon. PSII-S is a twofold symmetric dimer of pigment−protein complexes that are outlined by black lines. LHCII-S (strongly bound LHCII), CP26, CP29, CP43, and CP47 are antenna proteins, and RC indicates the reaction center. The inhomogeneously averaged rates of energy transfer between strongly coupled clusters of pigments were calculated using generalized Förster theory. (C) Simulated fluorescence decay of the mixed membrane (solid black line) and the PSII component of experimental fluorescence decay data from thylakoid membranes from ref. 26 (red, dotted line). Inset shows the lifetime components and amplitudes of the simulated decay as calculated using our model with a Gaussian convolution (σ = 20 ps) (black line) or by fitting to three exponential decays (green bars).
Here, we construct a generalized Förster model for the ∼104 pigments covering the few-hundred-nanometer length scale of the grana membrane that correctly incorporates the dynamics occurring within and between complexes on the picosecond time scale. We show how delocalized excited states, or excitons, in individual complexes affect light harvesting on the membrane length scale. The formation of excitons is sufficient to explain the high quantum efficiency of PSII in dim light. The model, by being an accurate representation of the complex kinetic network that underlies PSII light harvesting, provides mechanistic explanations for long-observed biological phenomena and sets the stage for developing a better understanding of PSII light harvesting in high light conditions.
Results and Discussion
Simulation of Fluorescence Data from Thylakoid Membranes.
To generate examples of the mixed (Fig. 1A) and segregated (Fig. 1B) organizations previously observed (11), we performed Monte Carlo simulations of 200 nm × 200 nm patches of the grana containing coarse-grained PSII-S and LHCII particles (23). In the segregated membrane, PSII-S and LHCII separate into PSII-S arrays and LHCII pools. Modern, minimally invasive imaging methods such as atomic force microscopy can resolve the location of the PSII-S, not the LHCII. On the other hand, the Monte Carlo model contains a small number of energetic interactions based on in vivo phenomenology and generates physically reasonable positions for both the PSII-S and LHCII. We superimposed the crystal structures of the chlorophyll pigments in PSII-S (14) and LHCII (24) on these simulations (Fig. S1) to establish the locations of all of the chlorophylls in a grana patch (Fig. 1A, Bottom). We assume that the energy transfer kinetics within LHCII and PSII-S are the same as that calculated previously on isolated complexes (17). Inhomogeneously averaged rates of energy transfer between domains on different complexes were calculated using generalized Förster theory. The inhomogeneously averaged rate matrix gives the correct overall dynamics and is representative of the energetics of PSII (Fig. S2), while decreasing the computational cost by several orders of magnitude. We modeled photochemistry in the reaction centers with two phenomenological “radical pair” (RP) states. The rate constants between the RP states are those established in previous work on the PSII-S (17). The many parameters of the model have been set in a self-consistent fashion, such that they simultaneously reproduce the time-resolved fluorescence of each type of isolated PSII-S (17) and the picosecond dynamics of LHCII (16) and the core complex (15).
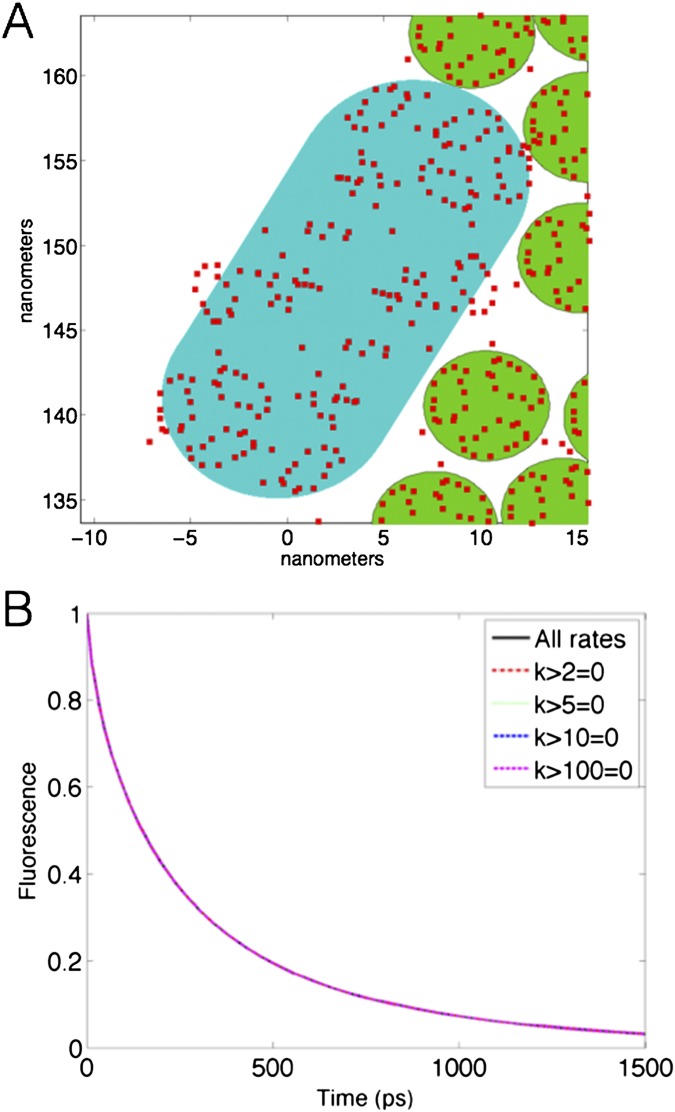
Fig. S1.
Overlay of pigment locations on the shapes used for the Monte Carlo simulations. (A) The chlorophyll pigments of LHCII (green circles) and PSII (teal discorectangle) are indicated by the red squares in this zoom in of a section of a simulated thylakoid membrane. (B) Fluorescence decays of the mixed membrane with energy transfer rates greater than 2 ps−1, 5 ps−1, 10 ps−1, or 100 ps−1 set equal to zero. Also indicated is the fluorescence decay of the mixed membrane with all rates included in the rate matrix.
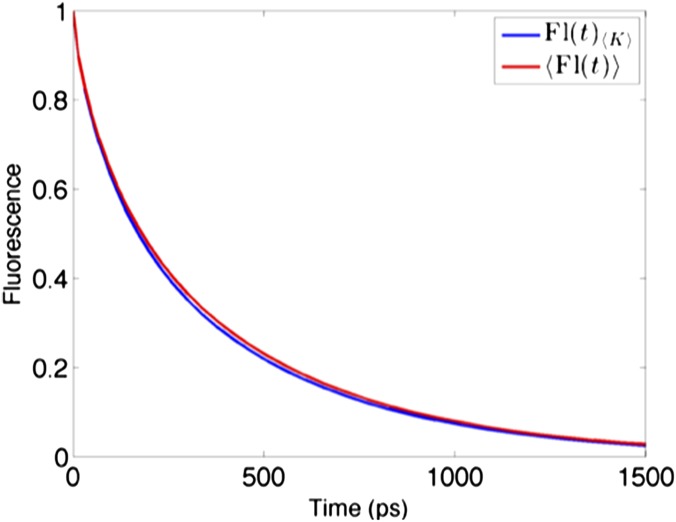
Fig. S2.
Effects of averaging energy transfer rates over inhomogeneous realizations on fluorescence decay of a PSII-S (C2S2 supercomplex). Comparison between the fluorescence decay of the rate matrix averaged over inhomogeneous realizations, (blue), and the average of the fluorescence decays of many inhomogeneous realizations of K, (red), for the C2S2 supercomplex.
The simulation of the chlorophyll fluorescence decay of the mixed membrane (black solid line), which is the predominantly observed morphology (25), shows excellent agreement with the experimental data (red dotted line) from dark-adapted thylakoids in ref. 26 (Fig. 1C). Unlike all previous models of PSII light harvesting (27–29), our model contains no free parameters, and thus the agreement achieved here was not guaranteed a priori. The simulation predicts a photochemical yield of 0.82, which is also in excellent agreement with the estimated value of 0.83 derived from chlorophyll fluorescence yield measurements (2). The agreement with membrane data suggests that the speedup of excitation transfer due to delocalized excited states (see, e.g., ref. 30) is sufficient to explain the high quantum yield of PSII in ideal, dim light conditions.
Our model demonstrates that extracting the amplitude and lifetime components by fitting the fluorescence decay curve does not correctly describe the underlying kinetics of PSII light harvesting. The simulated decay can be fit well to a sum of a few exponentials (Fig. 1C, Inset, green bars), as is frequently done to extract the amplitude and lifetime components (31). However, the fit does not capture the complex distribution calculated from the rate matrix (Fig. 1C, Inset, black solid line). In particular, the computed fluorescence lifetime contributions reveal more than three clusters including a long lifetime (>700 ps) contribution that is unresolved by fitting the fluorescence decay to three exponentials. Simulating the excitation dynamics underlying the fluorescence decay indicates that the longer lifetime components are due to excitation initiated farther away from reaction centers (Movies S1 and S2).
Excitation Dynamics in the Grana Membrane.
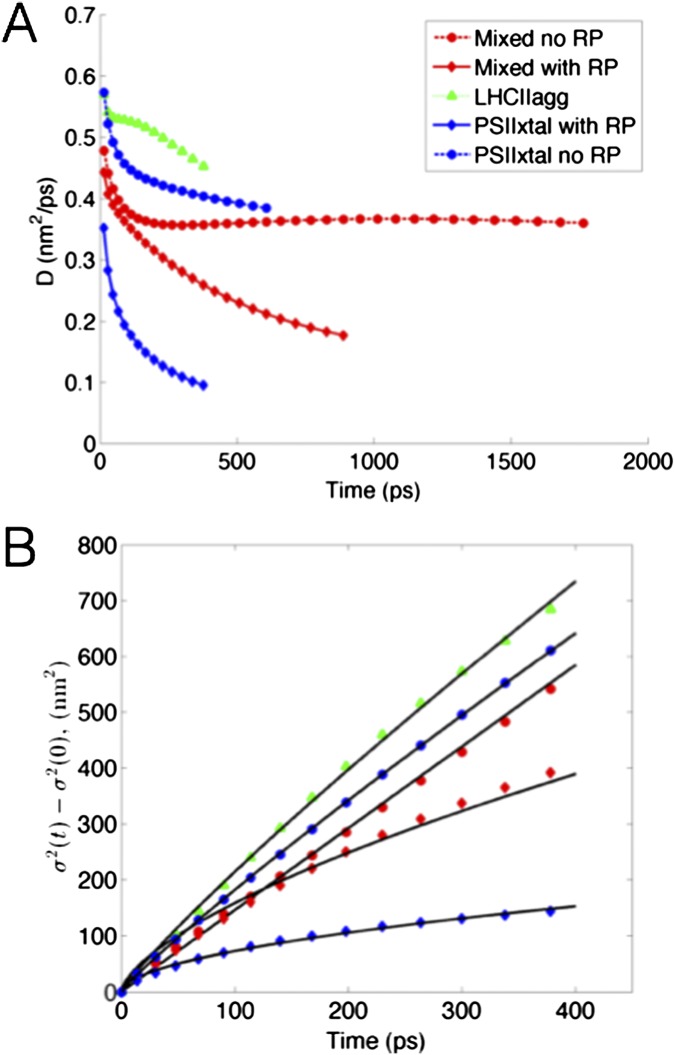
To understand the excitation dynamics in the membrane, we simulated excitation energy flow from single pigment−protein complexes in LHCII pools, PSII-S arrays, and mixed membranes (Movies S3–S7). To determine the effect of charge separation on excitation movement, we simulated the PSII-S arrays and mixed membranes both with and without the RP states in the reaction centers. We quantified excitation transport in these simulations by calculating the time dependence of the variance of the excitation probability distribution (Fig. 2A). Transport across the grana was well described by fitting the equation
| [1] |
where is the variance at time t, is the variance of the initial distribution of excitation, and A and α are fit parameters. For , transport is diffusive, whereas subdiffusive transport results if α is significantly less than 1. For the LHCII pool (Fig. 2A, green triangles), and for both the mixed membrane and PSII-S array without RP states (Fig. 2A, red and blue dashed lines, respectively), , and thus transport within the antenna can be considered diffusive. However, transport for both the mixed and PSII-S array cases with RP states (Fig. 2A, red and blue solid lines, respectively) was subdiffusive (). Subdiffusivity can occur when the energetic differences between sites is on the order of or greater than . We calculated the for the RC RP1 (radical pair 1) step to be −5.5 on the basis of our previously published rates (17). Thus, RP1 serves as an energetic trap that causes subdiffusive transport. The energy transfer rates in our model are averaged over inhomogeneous realizations, which could mitigate the slowdown of diffusion that occurs when the width of the inhomogeneous distribution is greater than (24). The largest standard deviation of exciton energies across an inhomogeneous distribution in our model is 107 cm−1 (17), which is significantly less than at room temperature (210 cm−1).
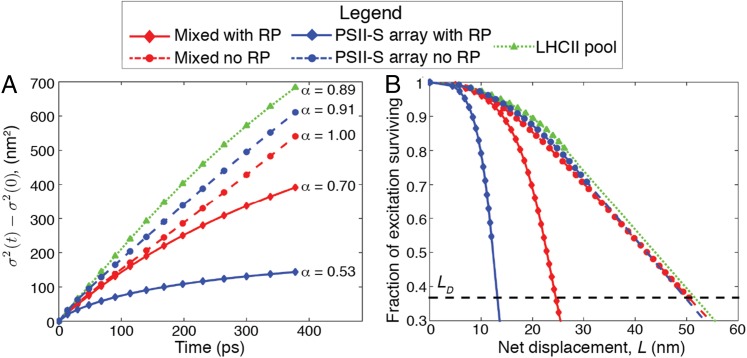
Fig. 2.
Excitation transport in grana membranes. Simulation of excitation movement in the five grana membrane configurations shown in the legend: mixed membrane with and without the RP states in the reaction center, PSII-S array with and without the RP states, and LHCII pool. In each case, excitation was initiated on a single pigment−protein complex. (A) The change in the spread of excitation over time. The diffusion exponent (Eq. 1) is shown on the right of the plot. (B) Fraction of surviving excitation as a function of net displacement L from the initial starting point. The dashed line, where the fraction of surviving excitation is , demarcates the excitation diffusion length (). The dimensions of some of the configurations were too small to calculate an , so linear extrapolation was used to approximate it (line segments that do not include markers). Using the same extrapolation, the fraction of surviving excitation goes to 0 when L is ∼70 nm for the LHCII pool.
Delocalization-enhanced transfer between domains of tightly coupled chlorophylls enables fast, diffusive energy transport on the grana membrane length scale. We calculated the diffusion constant D and net displacement L as a function of time to reduce the complex multiscale excitation dynamics to single parameters.
| [2] |
In our simulations, the excitation diffusion coefficient ranges from 1 to 5 × 10−3 cm2/s (Fig. S3), which is in good agreement with singlet−singlet annihilation measurements that suggested a lower limit of 1 × 10−3 cm2/s (32). Diffusive transport is consistent with predictions from PSII-S (17, 21) and suggests that, in the grana, excitation energy flows neither “directionally” nor energetically downhill on “preferred pathways” (10). The diffusion length , which is defined as the minimum net displacement in one dimension achieved by 37% of the excitation population, was 50 nm in the PSII antenna (Fig. 2B). This value compares favorably with measurements from other heterogeneous molecular light-harvesting materials, such as quantum dot arrays [30 nm (33)], crystalline thin films [20 nm (34)], and conjugated polymer aggregates [60 nm in exceptional cases (35)].
Fig. S3.
Additional plots of simulated diffusion of excitation. (A) Diffusivity D plotted against time for the five types of regions in the membrane (Eq. 1). (B) Plots of the fits of the equation , in which A and α were fit parameters, to diffusion dynamics in each of the five membrane regions.
The Role of Diffusion Length in the Functional Behavior of PSII.
The diffusion length in the antenna and the spatial distribution of open reaction centers determine the photochemical yield of PSII. Excitation moves through the antenna on a relatively flat energy landscape until it experiences a rapid downhill transition to the charge-separated state in the reaction centers, which serves as an effective trap. Therefore, the in the antenna sets the length scale over which an excitation can efficiently reach an RC. We sought to use this principle to explain two longstanding observations observed in the intact membrane. First, we explored the effect of the formation of PSII-S arrays, which have been observed since the 1970s (e.g., ref. 36), on PSII quantum yield. Second, we simulated the effect of reaction center closure to understand the nonlinear (“hyperbolic”) dependence of the rate of oxygen evolution (photochemical yield) with the fraction of open reaction centers, which was first observed in the 1960s (12). In natural conditions, RCs close in response to stresses that result in the rate of light absorption exceeding downstream electron transfer or photodamage of the reaction center.
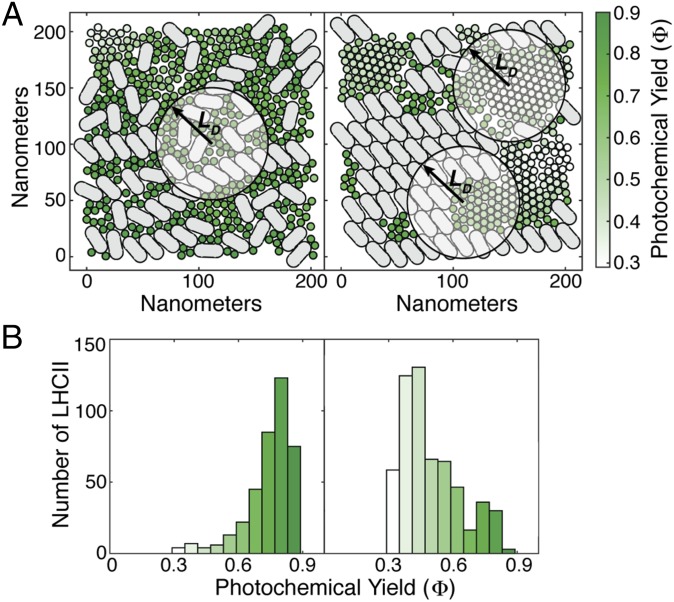
We mapped the photochemical yield upon excitation of each LHCII and PSII-S in both the mixed and segregated membranes. The average yield when excitation is initiated on a PSII-S is 0.9 in both membranes. However, the mean yield of the LHCIIs in the mixed membrane, 0.75, was significantly higher than that in the segregated membrane, 0.49 (Fig. 3B). Most of the LHCIIs in the mixed membrane are surrounded by PSII-S within a radius of , which led to the 82% maximum quantum efficiency of the membrane upon uniform chlorophyll a (ChlA) excitation (Fig. 3A, Left). The segregated membrane had a 70% maximum quantum efficiency, because it contains LHCIIs that are surrounded by few reaction centers within (Fig. 3A, Right). In line with this reasoning, energetically disconnecting an LHCII from reaction centers, as has been proposed (26), requires an LHCII to be in the middle of a pool with a radius of ∼70 nm at protein densities and LHCII:PSII ratios typically observed in plants (Fig. 2B).
Fig. 3.
The diffusion length in the antenna determines the effect of grana membrane morphology on photochemical yield. (A) Excitation was initiated at each LHCII in both the mixed (Left) and segregated (Right) morphologies. The color of the LHCII indicates the fraction of excitation that results in productive photochemistry (Φ; see colorbar on far right) as simulated with our model. The circles with radius indicate the area of the membrane accessible to excitation initiated at the center of the circle. (B) Histograms representing the distribution of Φ for the mixed (Left) and segregated (Right) membranes using the coloration from A.
Joliot and Joliot (12) attributed the hyperbolic dependence of photochemical yield with fraction of open reaction centers to “excitonic connectivity,” or the transfer of excitation from a closed reaction center to another reaction center in the membrane. The lack of a physically sound model has prevented the determination of the connectivity and also opened the door to other suggestions for the cause of the hyperbolic dependence (37). We first closed different fractions of reaction centers in the both the mixed and segregated membranes (Fig. 4). For each fraction of closed reaction centers simulated, we calculated 20 independent realizations of reaction center closures and plotted the mean value. Both simulations reproduce the curvature seen in the data originally taken by Joliot and Joliot (12) on the green alga Chlorella, as reproduced in ref. 37 (Fig. 4, Inset, compares the mixed membrane simulation with the data). The data have been normalized to have the same quantum yield with all reaction centers open and all reaction centers closed as the mixed membrane. We assumed that the fraction of open reaction centers in the data from ref. 37 varies between 0 and 1. For all fractions of closed reaction centers, we see that the mixed membrane achieves a higher quantum yield than the segregated membrane. To understand the origin of the observed nonlinear shapes, we directly simulated the connectivity for a reaction center in the mixed membrane by closing (Fig. S4; Electron Transfer Model) one or both of the two reaction centers in a PSII-S and calculated the probability that excitation started on the closed reaction center reached any other reaction center in the membrane. Closing a single reaction center in a PSII-S resulted in an average connectivity of 83%, whereas closing both of the reaction centers reduced the average connectivity to 75%. These values suggest that light harvesting in the grana membrane resembles the lake model (connectivity ≈ 100%) more than the puddle model (connectivity = 0). The dimerization of the PSII-S offers only a small benefit over a monomer, at the PSII:LHCII ratios and protein densities typically observed, in contrast to previous predictions (38). Ninety-eight percent of the connectivity was due to reaction centers within an of the closed reaction center. The hyperbolic dependence of photochemical yield with the fraction of open reaction centers is the result of the relatively large number of PSII-S within any given membrane patch of radius and the relatively weak trapping behavior associated with closed RCs (SI Results and Discussion).
Fig. 4.
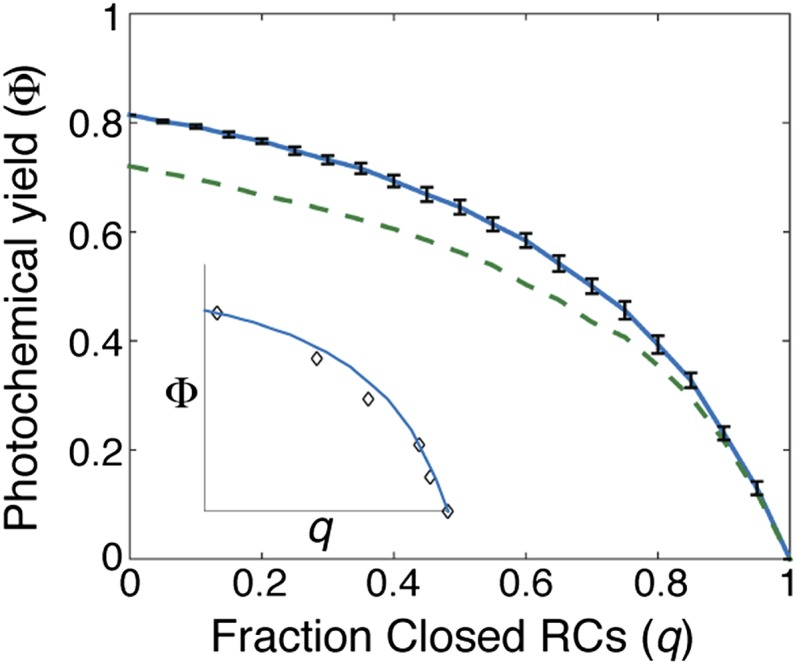
Simulation of the effect of closing reaction centers on photochemical yield. The solid blue line indicates the mixed membrane and the dashed green line the segregated membrane. Each calculated photochemical yield (Φ) along the membrane curve represents an average over different configurations of closed RCs. The standard deviation of each distribution along the mixed membrane is represented by black bars. (Inset) Comparison of the mixed membrane simulation with data (open black diamonds) from ref. 12, as reproduced in ref. 37.
Fig. S4.
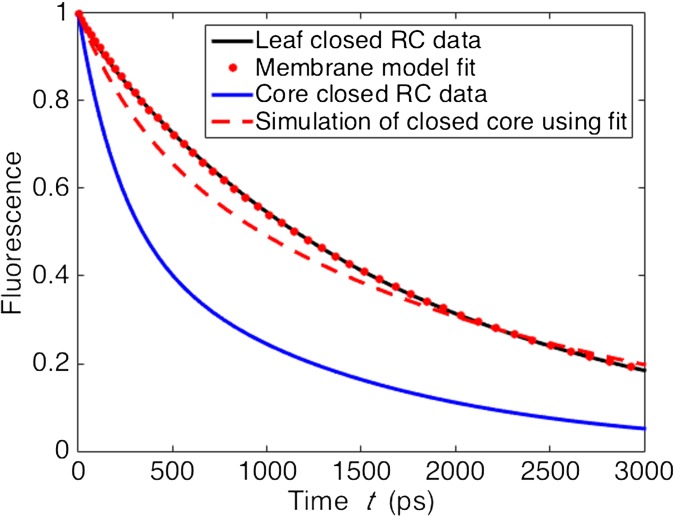
Fit of closed RC model to closed RC fluorescence lifetime data from leaves, with closed RC core data and simulation using fit. The blue line indicates the PSII contribution to the fluorescence decay measured on dark-adapted wild-type leaves of Arabidopsis thaliana with closed reaction centers (42). The dotted red line indicates the fit of the closed RC model using either the mixed or segregated membrane. See Electron transfer model for details of procedure. The blue line indicates fluorescence decay data from PSII cores with closed reaction centers (46). The dashed red line is the simulation of closed PSII core fluorescence with the electron transfer parameters from the membrane fit. See SI Results and Discussion for a brief discussion of all four curves.
Concluding Remarks
Our model of PSII light harvesting uses insights from structural biology, advanced spectroscopy, and theory to reproduce observed phenomena spanning 5 nm to hundreds of nanometers and 1 ps to 1 ns. The excitation diffusion length, given a spatial distribution of open reaction centers, is a single parameter that accurately determines PSII function. The diffusion length effectively integrates the complex dynamics occurring on shorter time and length scales, and might be used to develop accurate coarse-grained models. Our model does not incorporate nonphotochemical quenching, as the mechanisms of this process are still under debate. However, our model will serve as a useful framework for determining how proposed mechanisms play out in the functional membrane. Our model can be extended to address the dynamics occurring on longer length and time scales by, for example, incorporating the unappressed regions of the thylakoid that contain Photosystem I (11) to address spillover excitation from PSII, and ultimately can be integrated into systems models of the biochemistry in the thylakoid (39) to fully describe the light reactions of photosynthesis.
On the pigment length scale, our work indicates that the dominant quantum effect involved in PSII energy transfer in physiological conditions is the formation of delocalized states, or excitons. Further development of models that are consistent from low-temperature transient absorption to room temperature fluorescence lifetime measurements will complete our understanding of how function arises from structure in PSII. As these more exact models (e.g., refs. 20, 22, and 40) become capable of handling systems of the size considered here (∼104−105 Chl), we expect that our coarse-grained simulations will be refined, but that the basic picture described here will remain valid.
Materials and Methods
Structures of Grana Membrane.
The positions and orientations of PSII-S and LHCII in the mixed and segregated membranes shown in Fig. 1 were determined using Monte Carlo simulations, as previously described in ref. 23 and in SI Materials and Methods. Representative configurations from the stroma-side-up layers of the Monte Carlo simulations were selected for analysis. For each configuration, chlorophyll coordinates were assigned for each pigment−protein particle by aligning the center and axis of rotation of the chlorophyll coordinates from refs. 14 and 24 to the center and axis of rotation of the simulated particle (Fig. 1A, Inset). As discussed and motivated in ref. 17, we have substituted the structure of an LHCII monomer in the place of the minor light-harvesting complexes in PSII-S. Because simulated LHCII particles were radially symmetric, an axis of rotation was randomly selected for each LHCII particle. For additional discussion of the chlorophyll configurations, see SI Materials and Methods.
Excitation Energy Transfer Theory.
We followed the approach of Novoderezhkin and Renger for treating excitation transport through LHCII (16, 41) and PSII core complexes (15), as we described in our previous work on PSII supercomplexes (17). In this model, chlorophylls are grouped into well-defined domains of tightly coupled chlorophyll. Within a domain, we assume infinitely fast thermalization, and, between domains, we assume a generalized Förster hopping model. Domains, on average, extend over two to four pigments, and the hopping transport assumes that excitons are always localized within one domain. We have shown previously that this approach can reproduce the time-resolved fluorescence curves measured for isolated PSII supercomplexes (17). Separately, we have shown that this description of excitation transport for PSII supercomplexes also reproduces the transport time scales observed using a non-Markovian treatment using ZOFE (21). ZOFE has been shown to reproduce results using the hierarchical equations of motion method on the Fenna−Matthews−Olson complex (20).
Rate Matrix for PSII Light Harvesting.
To efficiently simulate excitation transport across the membrane, we propagate the probability of finding an excitation in a domain of a pigment−protein complex or an electron transport compartment in the reaction centers at time t after initial excitation. The master equation formalism was used to calculate the population dynamics,
| [3] |
where K is a rate matrix containing the first-order thermally averaged rate constants of excitation transfer between all compartments in the network, and is the vector of compartment populations.
K is composed of all energy transfer and loss pathways in the grana membrane. The energy transfer rates between domains of tightly coupled chlorophylls were calculated using generalized Förster theory and averaged over inhomogeneous realizations. For a full discussion of this approach, see SI Materials and Methods. Electron transfer in open reaction centers was treated using a simple kinetic model using two kinetic compartments denoted as RP states RP1 and RP2 that is described in ref. 17 and in more detail in SI Materials and Methods. Electron transfer in closed reaction centers was modeled by making the irreversible step in our model () equal to 0 and fitting the remaining rates ( and ) to fluorescence lifetime data taken on intact leaves (42) (SI Materials and Methods). The nonradiative decay constant from each domain was (2 ns)−1 (17). The fluorescence rate constant for each exciton was scaled by its transition dipole moment squared with the average fluorescence rate constant across all excitons set to (16 ns)−1 (17).
Simulations of Excitation Dynamics and Yield.
Solving Eq. 3 for gives
| [4] |
where C is a matrix which contains the eigenvectors of K, is a diagonal matrix containing the eigenvalues of K, and is the initial vector of populations. Calculating the eigenvalues and eigenvectors needed for Eq. 4 required the use of supercomputers with ∼30 GB of memory.
Except for the connectivity calculations, was for uniform ChlA excitation either across the membrane or on a single LHCII or PSII-S. The photochemical yield was calculated by summing over the populations in all RP2 states at t = 1 s. To calculate the excitonic connectivity, all excitation was started on the reaction center domain of a PSII monomer or dimer that cannot perform productive photochemistry. The remaining reaction centers in the membrane were given very high rates of irreversible trapping from the reaction center domain. The connectivity was calculated by summing up the population of trapped excitation at s. Fluorescence decays were calculated using the equations described in ref. 17.
Fig. 4 required the calculation of the photochemical yield for several hundred membrane configurations because of the need for repeated sampling (Nsample = 50 for the mixed membrane and 25 for the segregated membrane) of the spatial distribution for a given number of open reaction centers. Thus, for these calculations, we used a trajectory-based approach that efficiently reproduced calculation of the yields using Eq. 4 at two to three orders of magnitude smaller computational cost. We describe this approach in SI Materials and Methods.
SI Materials and Methods
Monte Carlo Simulations of Paired Grana Membranes.
Grana-scale pigment−protein complex configurations were generated via computer simulations of an extension of the model presented in ref. 23. Briefly, disk-shaped particles L representing LHCII complexes and rod-shaped particles P representing so-called C2S2 PSII-S in 2D layers α and β interacted via hard-core repulsive interactions, plus the attractive energetic potentials
| [S1] |
| [S2] |
| [S3] |
with , , , and all other parameters as in ref. 23.
The potentials in Eqs. S1 and S2 are motivated in ref. 23. The square-well attraction in Eq. S3 acts as a phenomenological, nonspecific energetic driving force for pooling of LHCII. In the mixed condition, , whereas, in the segregated condition, .
Canonical ensemble Metropolis Monte Carlo simulations of this model were performed as in ref. 23. A ratio of free LHCII to PSII-S particles of 6 was chosen to match the conditions of ref. 20, and a particle packing fraction of 0.75 was chosen to match typical grana conditions. Thus, 64 PSII-S particles and 384 free LHCII particles were initialized in each of two square boxes of side length 200 nm. Simulations were equilibrated with periodic boundary conditions for at least 15 million Monte Carlo sweep steps.
Chlorophyll Configurations.
In a small number of cases across the membrane, pigments belonging to one complex enter into the excluded area of a different complex. This overlap originates from a mismatch between the idealized geometries used for the Monte Carlo simulations and the real pigment structure as shown in Fig. S1A. As a result of protein overlap, there exist a small number of anomalously high transfer rates within the membrane rate matrix. To understand the influence of such rates on the overall description of transport in the membrane, we have removed transfer rates exceeding certain thresholds from the rate matrix and recalculated the resulting fluorescence decay. As can be seen in Fig. S1B, this does not alter the fluorescence decay dynamics, though it can alter the distribution of yields between reaction centers.
Excitation Energy Transfer Rates.
The rate of energy transfer from a donor domain d to an acceptor domain a, (Eq. S4), is typically calculated for each inhomogeneous realization of a pigment−protein complex using generalized Förster theory (15–17). Here, is the Boltzman-weighted (Eq. S5) sum of the rates from the excitons in d () to the excitons in a (). The rates between excitons are calculated using the generalized Förster equation (Eqs. S4 and S5), where is the overlap integral, is the electronic coupling between the two excitons, and is the coefficient of the Mth exciton on the site μ. Calculation of some observable of the system, such as the fluorescence lifetime, is usually done for each realization and then averaged. However, the thylakoid membrane contains >10,000 chlorophylls. Generating hundreds of realizations of the population coefficients and the overlap integrals for the membrane is not only computationally intensive, but is not necessary to accurately describe the dynamics of the system at the protein length scale (Fig. S2).
| [S4] |
| [S5] |
| [S6] |
| [S7] |
Directly calculating the inhomogeneous average transfer rates between domains substantially reduces the computational burden, because a single PSII-S contains all of the different domains that occur throughout the grana membrane. The most computationally demanding components for determining the rate matrix for a given inhomogeneous realization are the overlap integral in Eq. S6 and the matrix to transform from the site to the exciton basis in Eq. S7. We have assumed that domain definitions, overlap integrals, and the transformation matrices for PSII-S and LHCII are the same at the membrane level as they are in isolated complexes. As a result, these terms have been computed previously for several hundred realizations of inhomogeneous broadening for the four different types of transfers (from LHCII to LHCII, PSII to PSII, LHCII to PSII, and PSII to LHCII) in the membrane (17). We tabulated these values and combined them with a calculation of the electrostatic coupling between sites (the only term that must be calculated for each domain-to-domain rate in the membrane). By using our tabulated values for the population matrices and overlap integrals, we have reduced the computational time by three to four orders of magnitude, turning an otherwise burdensome calculation into one that can be performed in less than 1 d on a single CPU. We note that this simplification works only because we calculate the inhomogeneously averaged rate between each domain. This allows for a much smaller sampling of the possible combinations of site energies than would be required for even a single inhomogeneous realization of the entire thylakoid membrane.
Our algorithm for calculating for each domain pair in the membrane was as follows. We first checked if the two domains were within 60 Å of each other. If yes, we proceeded to calculate the average rate; if no, the rate was set equal to 0. We used 60 Å as a cutoff based on the distance dependence of rates in the PSII supercomplex. If the two domains were from the same complex, we used the inhomogeneously averaged rate of transfer from already performed generalized Förster/modified Redfield calculations (17). If not, we noted which type of complex the donor domain and the acceptor domain were in, either LHCII or PSII-S. We calculated using Eqs. S4−S7 with pretabulated values of the overlap integral, the population matrices, and the energies of the excitons for a few hundred inhomogeneous realizations. The electronic coupling was uniquely calculated for that pair of domains using the ideal dipole approximation. We then averaged over these tabulated inhomogeneous realizations to get .
Electron Transfer Model.
Both the identity of the primary donor and the kinetics and mechanism of charge separation in the PSII reaction center remain controversial (43). The lack of agreement between various experimental results and theory has resulted in a variety of phenomenological and conceptual models being used to interpret experimental data (27, 29). In previous work on PSII supercomplexes, we used the simplest kinetic model that describes the processes known to occur in the PSII reaction center (17),
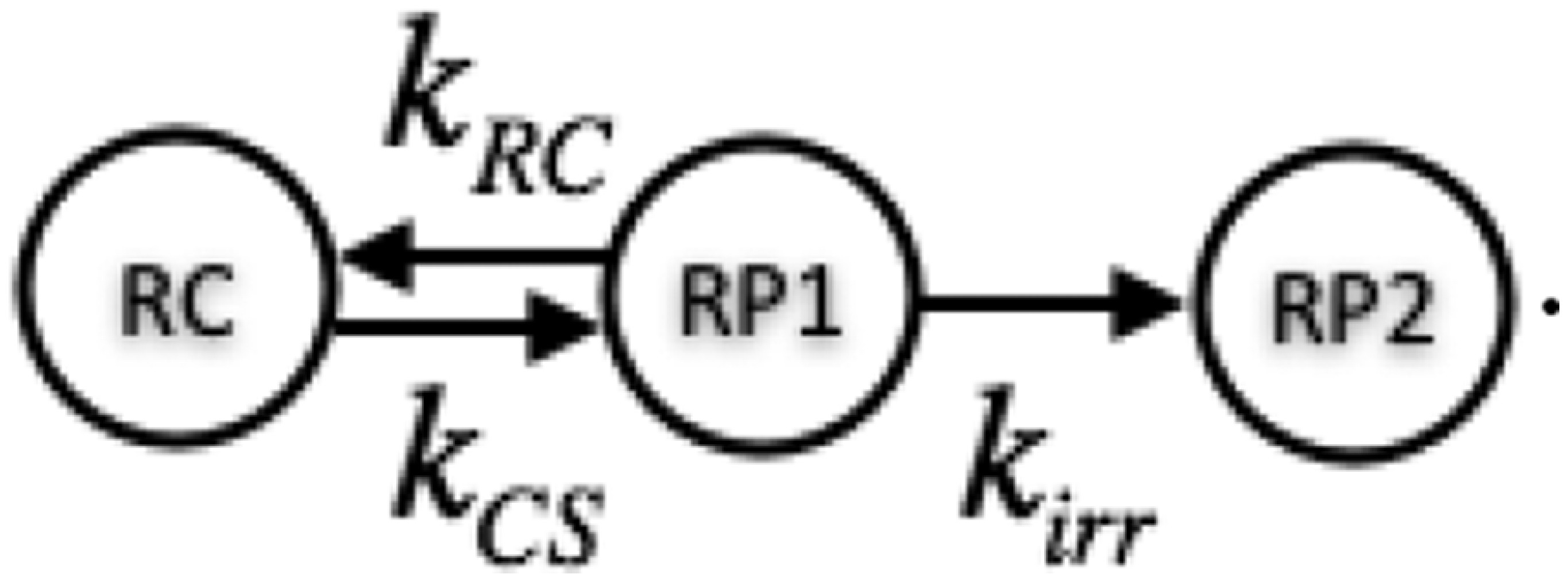 |
[S8] |
Here, RC is the reaction center domain composed of the six pigments of the reaction center. The RP states RP1 and RP2 and the rate constants , , and are used to model the electron transfer steps in the reaction center. RP1 and RP2 are nonemissive states that do not have a direct physical analog with charge-separated states in the reaction center. Rather, this approach allows us to describe the overall process of a reversible charge separation step followed by an irreversible step and establish the approximate time scales of these events relative to energy transfer in the light-harvesting antenna. The rates were previously parameterized using fluorescence decays of PSII supercomplexes of different sizes (38), with ps, ps, and ps () (17).
The reaction centers close when they cannot convert excitation to chemical energy, which occurs during high light and other stresses (1). We modeled closed reaction centers by setting . Determining and required a fit to fluorescence decay data from leaves with closed reaction centers (42) (Fig. S4). The data had three lifetime components: 70 ps, 0.93 ns, and 2.3 ns. We performed a least-squares fit of , , and the amplitude of the 70-ps component to simultaneously fit the charge separation parameters and remove the contributions of photosystem I to the 70-ps component (26, 44). The best fit values were ps and ps and a small amplitude (0.01) for the 70-ps component.
Rate Matrix Structure.
Taken together, we can write K as follows:
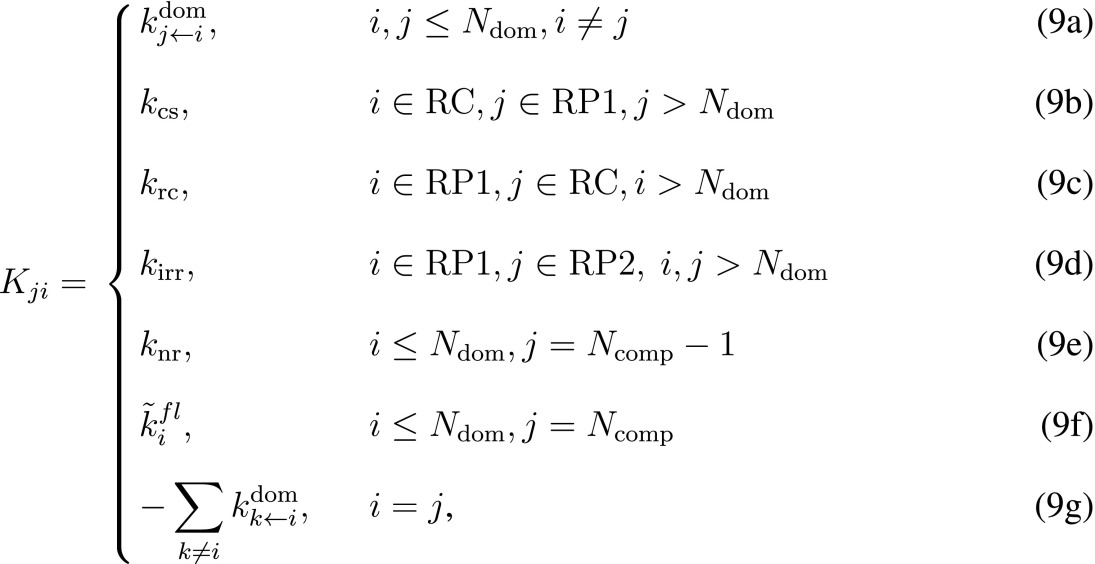 |
[S9] |
where is a matrix element of row i and column j, is the total number of domains, RC is the reaction center domain, and is the total number of compartments. The size of K for the membranes was on the order of 10,000 × 10,000.
Kinetic Monte Carlo.
Sampling trajectories.
Although excitation dynamics are efficiently calculated using Eq. 4, it is possible to dramatically reduce computational cost for calculating just the distribution of final yields (i.e., productive photochemistry, nonradiative decay, and fluorescence). Given a rate matrix K and an initial population distribution , we use a kinetic Monte Carlo method to sample an ensemble of trajectories in the absence of any irreversible loss pathways or RP states (i.e., trajectories do not sample transitions associated with fluorescence, nonradiative decay, and RP states). The initial domain of each trajectory is selected using the distribution. At each step along the trajectory, there is a double indexing scheme where n is the step number and j is the domain index associated with the rate matrix. The probability of a trajectory sampling an irreversible loss at domain j is given by , which we will describe in detail in Irreversible pathways. The next step in the trajectory is determined by randomly sampling the transition probability distribution as calculated in
| [S10] |
The probability a trajectory will survive to the Nth step is determined by the cumulative probability of loss as shown in Eq. S11. When sampling trajectories, we assume all reaction centers are closed and the trajectory is terminated when the probability of loss to either fluorescence or nonradiative decay is greater than 99.9% [i.e., ].
| [S11] |
Irreversible pathways: Probability of loss.
For domains within the PSII membrane that are not reaction centers, the probability that excitation is lost due to fluorescence or intersystem crossing can be calculated using Eq. S14.
| [S12] |
| [S13] |
| [S14] |
Because the trajectories we have constructed do not sample the RP states, we must construct an effective set of probabilities associated with loss to fluorescence, nonradiative decay, and photochemistry that implicitly account for the RP structure of the reaction center. For each reaction center, we can calculate the fraction of excitation that is lost to each irreversible process by explicitly solving for the long-time population distribution for a reduced rate matrix shown in Eq. S15. Those excitations that escape being irreversibly trapped while visiting a reaction center will have a transition probability given by Eq. S10 and are correctly sampled using the kinetic Monte Carlo scheme described above. The values of depend slightly on how each RC is situated in the membrane. In the description below, however, we will treat all reaction centers as having the same connectivity with other chlorophyll excitation domains. Correcting for the slight heterogeneity of connectivities for reaction centers is a simple generalization of this approach. The remainder of the variable terms, , , and , depend only on whether the RC is open or closed, as described previously. Solving for the long-time population distribution gives four important values each for open and closed reaction centers: (i) , the probability that excitation initially reaching the reaction center is lost as fluorescence; (ii) , the probability that excitation initially reaching the reaction center is lost due to intersystem crossing; (iii) , the probability that excitation initially reaching the reaction center performs productive photochemistry; and (iv) , the probability that excitation initially reaching the reaction center is irreversibly quenched.
| [S15] |
Calculating yields.
For each trajectory, we calculate the probability distribution of final product states by treating a hypothetical set of trajectories that follow the same steps along the chlorophyll domains but sample the irreversible loss states. The total probability of fluorescence along the trajectory is determined by the sum over all steps of the probability that excitation reaches the nth step multiplied by the probability of fluorescence at the nth step, as shown in Eq. S16. The total probability for nonradiative decay or photochemistry can be solved in an analogous fashion. We note here that productive photochemistry, unlike fluorescence and intersystem crossing, can only occur at open reaction centers. As a result, is zero for most of a trajectory while excitation samples domains outside of any reaction center. It is also possible to extend this framework to track the photochemical yield of each RC individually.
| [S16] |
Coarse-grained trajectories.
Because trajectories do not sample the RP states of the reaction center, they are invariant to the distribution of open and closed reaction centers. This provides an opportunity for efficient calculation of reaction center yields for different combinations of open and closed reaction centers without recalculating the trajectories. The computational cost can be further reduced by recognizing that only the loss occurring during a visit to a reaction center domain changes with the distribution of open and closed reaction centers. As a result, trajectories can be described by a sequence of reaction center visits with an effective , , and describing the intervening dynamics outside of a reaction center. From this perspective, the first step in performing our coarse-graining is to determine all step indices that correspond to visits to a reaction center domain. The effective loss that occurs between the and steps along the trajectory can be calculated similarly to the treatment in Eq. S16.
| [S17] |
The overall yield for the different pathways is determined by the relative open/closed states of the different reaction centers. Therefore, the minimal information that is required to calculate the photochemical yield for a given trajectory is , , and for the visits to reaction centers recorded in the set . In both Eqs. S18 and S19, the initial product terms and describe the portion of excitation lost before the ith reaction center visit as a result of dynamics outside of reaction centers and loss within reaction centers, respectively. In Eq. S19, the last term is a sum of two different contributions: The first term, , describes the fluorescence arising during the ith reaction center visit, whereas the second term, , describes the fluorescence occurring during the excitation dynamics between the and ith reaction center visits. Again, a simple extension of these equations can be written to separate out yield for each reaction center.
| [S18] |
| [S19] |
Using this coarse-grained approach, the yields averaged over a small ensemble of trajectories (∼50,000) efficiently reproduce calculations using Eq. 4 at two to three orders of magnitude smaller computational cost. We use this capability to rapidly calculate yield distributions with different collections of open and closed reaction centers to simulate the behavior of the membrane as a variable number of reaction centers are closed.
Spatial Distribution of Closed Reaction Centers.
For a given number of closed reaction centers (), the resulting photochemical yield depends on the specific combination of reaction centers that are closed. In turn, the relative probability of each reaction center being closed depends on what other reaction centers are closed—a reaction center spatially adjacent to a closed reaction center has an increased probability of being closed as well. To correctly account for these correlations, we determine the spatial distribution of closed reaction centers using an iterative Monte Carlo simulation. Initially, reaction centers are selected, with all reaction centers have an equal probability of being closed. We subsequently perform 500 swap moves where one closed reaction center opens and an open reaction center is closed. For each swap, all closed reaction centers have an equal probability of opening. We calculate the probability for an open reaction center closing during a swap using its photochemical yield calculated in the presence of the closed reaction centers.
SI Results and Discussion
A variety of kinetic models (27, 29) have been used to describe charge separation in the PSII reaction center because it is not well understood (43). We used a two-compartment (RP) model (Eq. S8) because it was the simplest model that simultaneously fit open RC PSII supercomplex data (17). Within this model, a closed RC has no irreversible loss () but may have a different rate of charge separation and recombination compared with the open RC. We fit the and rates using our model of the intact PSII membrane and the fluorescence lifetime data from leaves with closed RCs (Fig. S4, red dotted line). The resulting fit (, ) describes an RP1 state that acts as a weak trap within the PSII membrane.
The electron transport model for an RC remains a phenomenological description that returns the overall dynamics of charge separation at the reaction center. In the current paper, we found that using the charge separation parameters fit to the supercomplex fluorescence decay curves returns an excellent description of the PSII membrane fluorescence (Fig. 1C). As noted in our previous work on supercomplexes (17), however, charge separation in a core dimer does not appear to have the same dynamics as the PSII supercomplexes, although determining the precise difference is complicated by the variation in open reaction center core data from different groups (38, 45). Interestingly, we similarly find that using the fit values for and above to simulate the fluorescence decay of closed PSII cores (Fig. S4, dashed red line) also does not agree with previous measurements (46) (Fig. S4, blue line). Future experiments are needed to determine the source of this variation between the core dimer samples and the remaining supercomplexes/PSII membrane to enable a consistent description of the electron transfer kinetics across different samples.
Supplementary Material
Acknowledgments
The authors thank R. van Grondelle, R. Blankenship, R. Cogdell, G. S. Schlau-Cohen, C. Chidley, and members of the O’Shea laboratory for helpful comments on the manuscript. This research used resources of the National Energy Research Scientific Computing Center, a Department of Energy (DOE) Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract DE-AC02-05CH11231. This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, of the US Department of Energy under Contract DE-AC02-05CH11231 and the Division of Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, through Grant DEAC03-76SF000098 (at Lawrence Berkeley National Labs and U.C. Berkeley).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1524999113/-/DCSupplemental.
References
- 1.Blankenship RE. Molecular Mechanisms of Photosynthesis. 2nd Ed Blackwell Sci; Malden, MA: 2014. [Google Scholar]
- 2.Baker NR. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu Rev Plant Biol. 2008;59:89–113. doi: 10.1146/annurev.arplant.59.032607.092759. [DOI] [PubMed] [Google Scholar]
- 3.Ruban AV, Johnson MP, Duffy CDP. The photoprotective molecular switch in the photosystem II antenna. Biochim Biophys Acta. 2012;1817(1):167–181. doi: 10.1016/j.bbabio.2011.04.007. [DOI] [PubMed] [Google Scholar]
- 4.Külheim C, Ågren J, Jansson S. Rapid regulation of light harvesting and plant fitness in the field. Science. 2002;297(5578):91–93. doi: 10.1126/science.1072359. [DOI] [PubMed] [Google Scholar]
- 5.Ort DR, et al. Redesigning photosynthesis to sustainably meet global food and bioenergy demand. Proc Natl Acad Sci USA. 2015;112(28):8529–8536. doi: 10.1073/pnas.1424031112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Long SP, Marshall-Colon A, Zhu X-G. Meeting the global food demand of the future by engineering crop photosynthesis and yield potential. Cell. 2015;161(1):56–66. doi: 10.1016/j.cell.2015.03.019. [DOI] [PubMed] [Google Scholar]
- 7.Murchie EH, Niyogi KK. Manipulation of photoprotection to improve plant photosynthesis. Plant Physiol. 2011;155(1):86–92. doi: 10.1104/pp.110.168831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Croce R, van Amerongen H. Natural strategies for photosynthetic light harvesting. Nat Chem Biol. 2014;10(7):492–501. doi: 10.1038/nchembio.1555. [DOI] [PubMed] [Google Scholar]
- 9.Fleming GR, Schlau-Cohen GS, Amarnath K, Zaks J. Design principles of photosynthetic light-harvesting. Faraday Discuss. 2012;155:27–41. doi: 10.1039/c1fd00078k. [DOI] [PubMed] [Google Scholar]
- 10.Croce R, van Amerongen H. Light-harvesting and structural organization of Photosystem II: From individual complexes to thylakoid membrane. J Photochem Photobiol B. 2011;104(1-2):142–153. doi: 10.1016/j.jphotobiol.2011.02.015. [DOI] [PubMed] [Google Scholar]
- 11.Dekker JP, Boekema EJ. Supramolecular organization of thylakoid membrane proteins in green plants. Biochim Biophys Acta. 2005;1706(1-2):12–39. doi: 10.1016/j.bbabio.2004.09.009. [DOI] [PubMed] [Google Scholar]
- 12.Joliot A, Joliot P. Kinetic study of the photochemical reaction liberating oxygen during photosynthesis. C R Hebd Seances Acad Sci. 1964;258:4622−4625. [PubMed] [Google Scholar]
- 13.Lazár D. Chlorophyll a fluorescence induction. Biochim Biophys Acta. 1999;1412(1):1–28. doi: 10.1016/s0005-2728(99)00047-x. [DOI] [PubMed] [Google Scholar]
- 14.Caffarri S, Kouřil R, Kereïche S, Boekema EJ, Croce R. Functional architecture of higher plant photosystem II supercomplexes. EMBO J. 2009;28(19):3052–3063. doi: 10.1038/emboj.2009.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Raszewski G, Renger T. Light harvesting in photosystem II core complexes is limited by the transfer to the trap: Can the core complex turn into a photoprotective mode? J Am Chem Soc. 2008;130(13):4431–4446. doi: 10.1021/ja7099826. [DOI] [PubMed] [Google Scholar]
- 16.Novoderezhkin V, Marin A, van Grondelle R. Intra- and inter-monomeric transfers in the light harvesting LHCII complex: The Redfield-Förster picture. Phys Chem Chem Phys. 2011;13(38):17093–17103. doi: 10.1039/c1cp21079c. [DOI] [PubMed] [Google Scholar]
- 17.Bennett DIG, Amarnath K, Fleming GR. A structure-based model of energy transfer reveals the principles of light harvesting in photosystem II supercomplexes. J Am Chem Soc. 2013;135(24):9164–9173. doi: 10.1021/ja403685a. [DOI] [PubMed] [Google Scholar]
- 18.Sumi H. Theory on rates of excitation-energy transfer between molecular aggregates through distributed transition dipoles with application to the antenna system in bacterial photosynthesis. J Phys Chem B. 1999;103(1):252–260. [Google Scholar]
- 19.Scholes GD, Fleming GR. On the mechanism of light harvesting in photosynthetic purple bacteria: B800 to B850 energy transfer. J Phys Chem B. 2000;104(8):1854–1868. [Google Scholar]
- 20.Ritschel G, Roden JJJ, Strunz WT, Eisfeld A. An efficient method to calculate excitation energy transfer in light-harvesting systems: Application to the Fenna−Matthews−Olson complex. New J Phys. 2011;13:113034. [Google Scholar]
- 21.Roden JJJ, Bennett DIG, Whaley KB. 2015. Long-range coherent energy transport in photosystem II. arXiv:1501.06674.
- 22.Kreisbeck C, Kramer T, Aspuru-Guzik A. Scalable high-performance algorithm for the simulation of exciton dynamics. Application to the light-harvesting complex II in the presence of resonant vibrational nodes. J Chem Theory Comput. 2014;10(9):4045–4054. doi: 10.1021/ct500629s. [DOI] [PubMed] [Google Scholar]
- 23.Schneider AR, Geissler PL. Coexistence of fluid and crystalline phases of proteins in photosynthetic membranes. Biophys J. 2013;105(5):1161–1170. doi: 10.1016/j.bpj.2013.06.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu Z, et al. Crystal structure of spinach major light-harvesting complex at 2.72 Å resolution. Nature. 2004;428(6980):287–292. doi: 10.1038/nature02373. [DOI] [PubMed] [Google Scholar]
- 25.Onoa B, et al. Atomic force microscopy of photosystem II and its unit cell clustering quantitatively delineate the mesoscale variability in Arabidopsis thylakoids. PLoS One. 2014;9(7):e101470. doi: 10.1371/journal.pone.0101470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van Oort B, et al. Effect of antenna-depletion in Photosystem II on excitation energy transfer in Arabidopsis thaliana. Biophys J. 2010;98(5):922–931. doi: 10.1016/j.bpj.2009.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Broess K, et al. Excitation energy transfer and charge separation in photosystem II membranes revisited. Biophys J. 2006;91(10):3776–3786. doi: 10.1529/biophysj.106.085068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holzwarth AR, Miloslavina Y, Nilkens M, Jahns P. Identification of two quenching sites active in the regulation of photosynthetic light-harvesting studied by time-resolved fluorescence. Chem Phys Lett. 2009;483(4-6):262–267. [Google Scholar]
- 29.Chmeliov J, Trinkunas G, van Amerongen H, Valkunas L. Excitation migration in fluctuating light-harvesting antenna systems. Photosynth Res. 2016;127(1):49–60. doi: 10.1007/s11120-015-0083-3. [DOI] [PubMed] [Google Scholar]
- 30.Kassal I, Yuen-Zhou J, Rahimi-Keshari S. Does coherence enhance transport in photosynthesis? J Phys Chem Lett. 2013;4(3):362–367. doi: 10.1021/jz301872b. [DOI] [PubMed] [Google Scholar]
- 31.Zaks J, Amarnath K, Sylak-Glassman EJ, Fleming GR. Models and measurements of energy-dependent quenching. Photosynth Res. 2013;116(2-3):389–409. doi: 10.1007/s11120-013-9857-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Swenberg CE, Geacintov NE, Breton J. Laser pulse excitation studies of the fluorescence of chloroplasts. Photochem Photobiol. 1978;28(6):999–1006. [Google Scholar]
- 33.Akselrod GM, et al. Subdiffusive exciton transport in quantum dot solids. Nano Lett. 2014;14(6):3556–3562. doi: 10.1021/nl501190s. [DOI] [PubMed] [Google Scholar]
- 34.Lunt RR, Giebink NC, Belak AA, Benziger JB, Forrest SR. Exciton diffusion lengths of organic semiconductor thin films measured by spectrally resolved photoluminescence quenching. J Appl Phys. 2009;105(5):053711. [Google Scholar]
- 35.Vogelsang J, Adachi T, Brazard J, Vanden Bout DA, Barbara PF. Self-assembly of highly ordered conjugated polymer aggregates with long-range energy transfer. Nat Mater. 2011;10(12):942–946. doi: 10.1038/nmat3127. [DOI] [PubMed] [Google Scholar]
- 36.Staehelin LA. Reversible particle movements associated with unstacking and restacking of chloroplast membranes in vitro. J Cell Biol. 1976;71(1):136–158. doi: 10.1083/jcb.71.1.136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stirbet A. Excitonic connectivity between photosystem II units: What is it, and how to measure it? Photosynth Res. 2013;116(2-3):189–214. doi: 10.1007/s11120-013-9863-9. [DOI] [PubMed] [Google Scholar]
- 38.Caffarri S, Broess K, Croce R, van Amerongen H. Excitation energy transfer and trapping in higher plant Photosystem II complexes with different antenna sizes. Biophys J. 2011;100(9):2094–2103. doi: 10.1016/j.bpj.2011.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zaks J, Amarnath K, Kramer DM, Niyogi KK, Fleming GR. A kinetic model of rapidly reversible nonphotochemical quenching. Proc Natl Acad Sci USA. 2012;109(39):15757–15762. doi: 10.1073/pnas.1211017109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Moix JM, Zhao Y, Cao J. Equilibrium-reduced density matrix formulation: Influence of noise, disorder, and temperature on localization in excitonic systems. Phys Rev B. 2012;85(11):115412. [Google Scholar]
- 41.Müh F, El-Amine Madjet M, Renger T. Structure-based identification of energy sinks in plant light-harvesting complex II. J Phys Chem B. 2010;114(42):13517–13535. doi: 10.1021/jp106323e. [DOI] [PubMed] [Google Scholar]
- 42.Sylak-Glassman EJ, Zaks J, Amarnath K, Leuenberger M, Fleming GR. Characterizing non-photochemical quenching in leaves through fluorescence lifetime snapshots. Photosynth Res. 2016;127(1):69–76. doi: 10.1007/s11120-015-0104-2. [DOI] [PubMed] [Google Scholar]
- 43.Renger T, Schlodder E. Primary photophysical processes in photosystem II: Bridging the gap between crystal structure and optical spectra. ChemPhysChem. 2010;11(6):1141–1153. doi: 10.1002/cphc.200900932. [DOI] [PubMed] [Google Scholar]
- 44.Ihalainen JA, et al. Kinetics of excitation trapping in intact photosystem I of Chlamydomonas reinhardtii and Arabidopsis thaliana. Biochim Biophys Acta. 2005;1706(3):267–275. doi: 10.1016/j.bbabio.2004.11.007. [DOI] [PubMed] [Google Scholar]
- 45.Miloslavina Y, et al. Charge separation kinetics in intact photosystem II core particles is trap-limited. A picosecond fluorescence study. Biochemistry. 2006;45(7):2436–2442. doi: 10.1021/bi052248c. [DOI] [PubMed] [Google Scholar]
- 46.Schatz GH, Brock H, Holzwarth AR. Picosecond kinetics of fluorescence and absorbance changes in photosystem II particles excited at low photon density. Proc Natl Acad Sci USA. 1987;84(23):8414–8418. doi: 10.1073/pnas.84.23.8414. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.