Subunit stoichiometry and arrangement in a heteromeric glutamate-gated chloride channel

Significance

Cys-loop receptors (CLRs) are transmembrane ion channels activated by neurotransmitters to mediate chemoelectric excitation or inhibition throughout the nervous system. Hence, CLRs play a key role in our day-to-day life, from coordination of motions to cognition. Impairment of CLRs’ activity leads to various pathophysiological conditions. The CLR studied here is a glutamate-gated chloride-selective receptor (GluClR). GluClRs are unique to invertebrates, yet they are pharmacologically important because they serve as targets for ivermectin, an anthelmintic drug used to treat humans suffering from filarial diseases. This study provides better understanding of the subunit arrangement and stoichiometry of Glu-binding sites in GluClRs.

Abstract

The invertebrate glutamate-gated chloride-selective receptors (GluClRs) are ion channels serving as targets for ivermectin (IVM), a broad-spectrum anthelmintic drug used to treat human parasitic diseases like river blindness and lymphatic filariasis. The native GluClR is a heteropentamer consisting of α and β subunit types, with yet unknown subunit stoichiometry and arrangement. Based on the recent crystal structure of a homomeric GluClαR, we introduced mutations at the intersubunit interfaces where Glu (the neurotransmitter) binds. By electrophysiological characterization of these mutants, we found heteromeric assemblies with two equivalent Glu-binding sites at β/α intersubunit interfaces, where the GluClβ and GluClα subunits, respectively, contribute the “principal” and “complementary” components of the putative Glu-binding pockets. We identified a mutation in the IVM-binding site (far away from the Glu-binding sites), which significantly increased the sensitivity of the heteromeric mutant receptor to both Glu and IVM, and improved the receptor subunits’ cooperativity. We further characterized this heteromeric GluClR mutant as a receptor having a third Glu-binding site at an α/α intersubunit interface. Altogether, our data unveil heteromeric GluClR assemblies having three α and two β subunits arranged in a counterclockwise β-α-β-α-α fashion, as viewed from the extracellular side, with either two or three Glu-binding site interfaces.

Glutamate-gated chloride-selective receptors (GluClRs) are pentameric glutamate-gated chloride channels unique to invertebrates. They belong to the Cys-loop receptor superfamily of transmembrane oligomers that open an intrinsic cationic or anionic channel pore upon binding of neurotransmitters, such as ACh, serotonin, GABA, Gly, histamine, or Glu (1–9). GluClRs are specific targets for ivermectin (IVM), a broad-spectrum anthelmintic drug used to treat filarial diseases like onchocerciasis (river blindness) and elephantiasis (lymphatic filariasis) that afflict hundreds of millions of people worldwide (10, 11). IVM is also broadly used in cattle, swine, and pets to kill gastrointestinal roundworms, lungworms, grubs, sucking lice, and mange mites (12). The high efficiency of IVM stems from its capacity to act as an agonist that keeps the receptor’s ion channel continuously open (13–18). Because the GluClR is chloride-selective, IVM causes sustained hyperpolarization across postsynaptic membranes in the parasitic nematodes. This long-term hyperpolarization leads to suppression of excitation in motor neurons and inhibition of locomotion (19); inhibition of the pharyngeal muscle activity, which interrupts with feeding behavior (20); and interruption of secretion processes that are crucial for evading the host immune system (21).

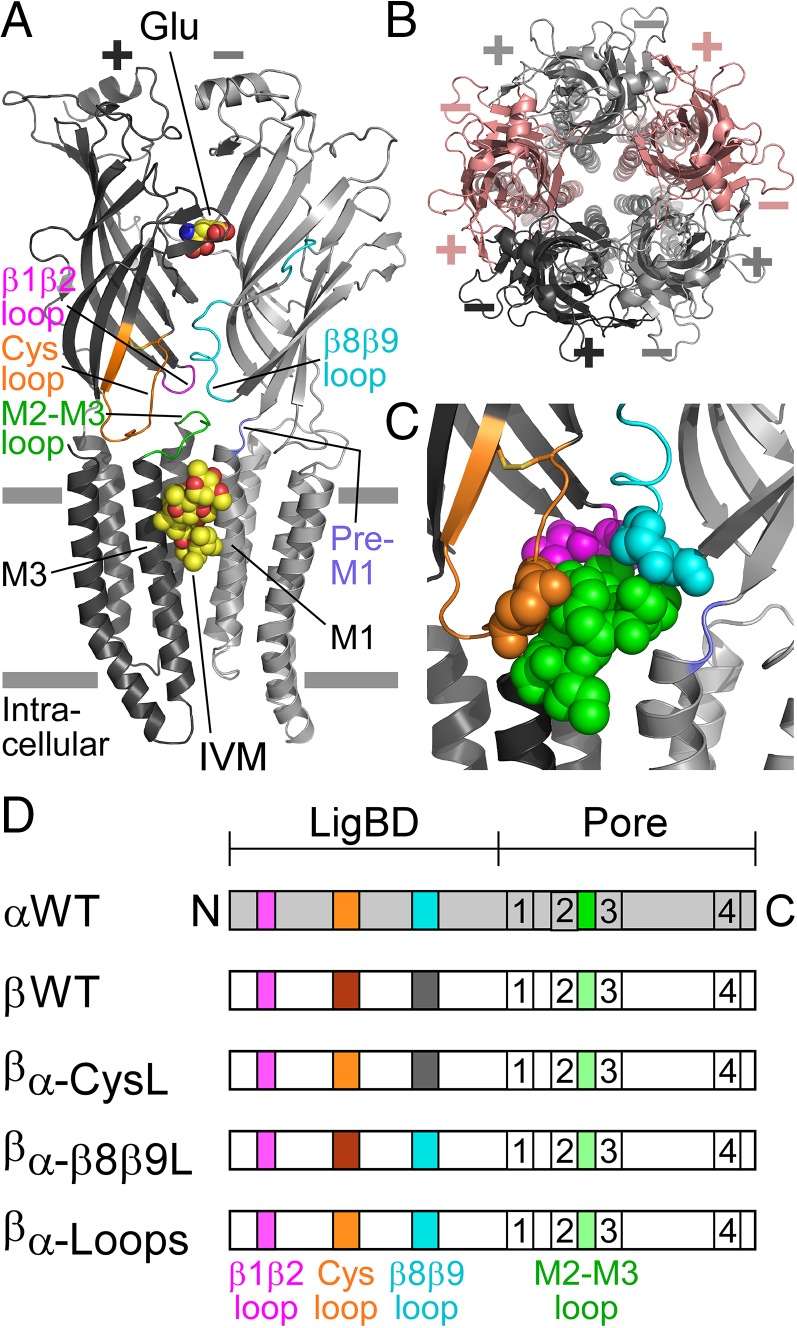
Genes encoding two GluClR homologous subunits, GluClα and GluClβ (glc-1 and glc-2, respectively), were first cloned from Caenorhabditis elegans (13). When expressed in Xenopus oocytes, homomeric GluClαRs respond to IVM but not to Glu and, in contrast, homomeric GluClβRs respond to Glu but not to IVM (13, 16, 17, 22). A recent 3D crystal structure of a truncated homomeric GluClαR (GluClα_crystR; Protein Data Bank ID code 3RIF) shows that when IVM is bound at the five α/α intersubunit interfaces in the ion-channel pore periphery, Glu is lodged at the five α/α intersubunit interfaces in the ligand-binding domain (LigBD) (23) (Fig. 1A). These Glu-binding sites are homologous to the neurotransmitter/agonist-binding sites of other Cys-loop receptors (1, 2, 24), bacterial homologs of Cys-loop receptors (25–30), and ACh-binding proteins (31–34).

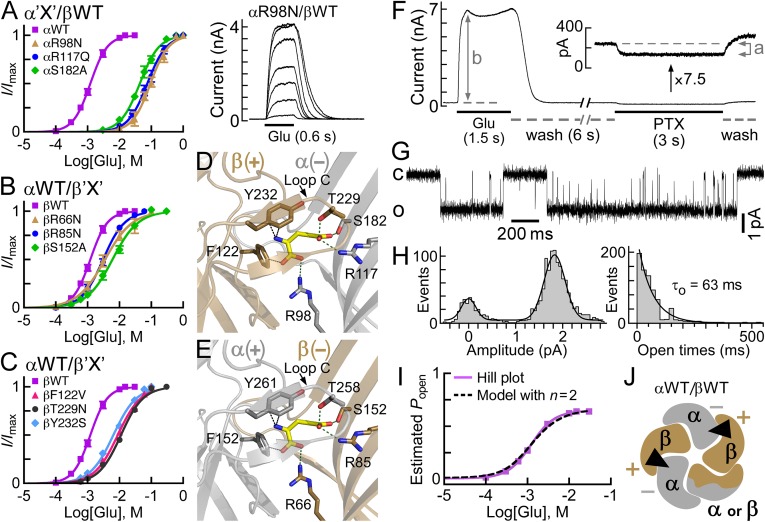
Fig. 1.

Structural characteristics of GluClRs. (A) Two neighboring subunits of the homopentameric GluClα_crystR [Protein Data Bank (PDB) ID code 3RIF] are shown from the side in light and dark gray colors. Wide gray horizontal lines mark the putative membrane borders. The four coupling loops are colored as shown in C and the upper row of D. Glu and IVM are shown as space-filling models with carbon, oxygen, and nitrogen atoms colored in yellow, red, and blue, respectively. They are bound at the α(+)/α(−) intersubunit interface far away from each other: Glu in the extracellular LigBD and IVM in the upper part of the pore-domain periphery, between M1 (of the light gray subunit) and M3 (of the dark gray subunit). Note that in Cys-loop receptors, the principal and complementary faces of a neurotransmitter-binding pocket are formed by the (+) and (−) sides of two adjacent subunits, respectively. (B) Top view of the GluClα_cryst pentamer showing five identical subunits, which are colored differently to highlight the intersubunit interfaces located between the (+) and (−) sides. (C) Space-filling models of residues belonging to the coupling loops, which create an extensive bond network at the interface between the LigBD and the ion-channel pore domain. (D) Schemes of GluClR subunits used in this study. The M1–M4 transmembrane segments are numbered 1–4. Different colors reflect differences in amino acid sequences (Fig. S1).

Importantly, the naturally occurring GluClR robustly responds to both Glu and IVM independently; therefore, it is considered to consist of both GluClα and GluClβ subunit types (13–18). However, little is known about the stoichiometry and molecular arrangement of the subunits in heteromeric GluClRs. Furthermore, the aforementioned crystallographic observations (23) are consistent with earlier studies showing that Glu elicits current responses in homomeric GluClαRs only when applied after activation by IVM (14), which gives rise to the following question: Could an α/α intersubunit interface be formed in a heteromeric assembly, bind Glu, and functionally participate in the activation process even without IVM preassociation? To resolve this question, we clarified here the stoichiometry and positions of the α and β subunits in GluClα/βR heteromeric assemblies that carry mutations in both the putative Glu- and IVM-binding pockets.

Results

Can the Coupling Loops of the GluClα Subunit Mediate Channel Opening upon Glu Binding?

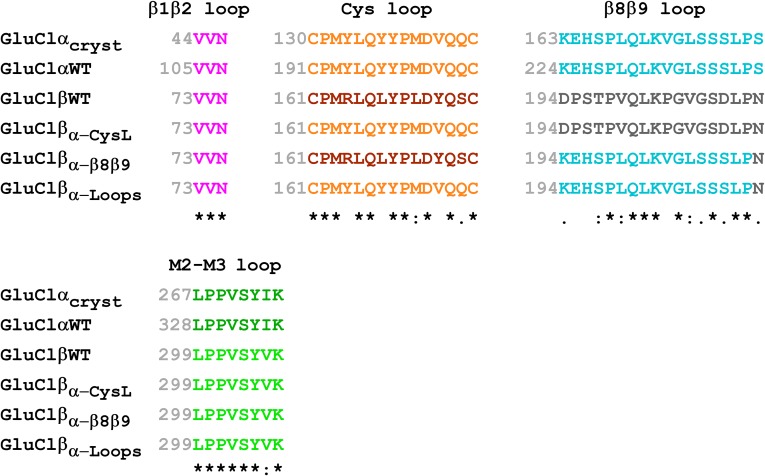
Based on the capability of the WT homomeric GluClα (GluClαWT) receptor to respond to Glu only following exposure to IVM, it was suggested that IVM binding induces a conformational change that enables coupling of Glu binding at α/α intersubunit interfaces to the opening of the ion-channel gate (14, 23). To explore this suggestion further, we used a strategy of microchimerism that is based on previous studies showing that in various Cys-loop receptors, the β1β2, Cys, and β8β9 loops of the LigBD interact with the M2–M3 loop of the pore domain to couple neurotransmitter binding to channel gating (23, 35–44) (e.g., Fig. 1 A and C). These four loops are termed the coupling loops. Fig. 1D shows schemes of the WT GluClα and GluClβ subunits, as well as three microchimeric GluClβ subunits where we replaced the Cys loop, β8β9 loop, or both loops with the homologous loops of the GluClα subunit. These microchimeric subunits are termed GluClβ_α-CysL, GluClβ_α-β8β9L, and GluClβ_α-Loops, respectively. Note that the C. elegans GluClα and GluClβ subunits share an identical β1β2 loop sequence, whereas their M2–M3 loop sequence is almost identical (Fig. S1).

Fig. S1.

Partial sequence alignment of the microchimeric GluClR subunits used in this study. An asterisk indicates identical amino acids. A colon indicates groups of strongly similar properties. A period indicates groups of weakly similar properties. Colors match the colors used in Fig. 1. GluClα_cryst is a truncated α subunit used by Hibbs and Gouaux (23) for structure determination by X-ray crystallography (PDB ID code 3RIF). GluClαWT is the WT α subunit of a GluClR from C. elegans (entry code G5EBR3 in the UniProtKB database). GluClβWT is the WT type β subunit of a GluClR from C. elegans (entry code Q17328 in the UniProtKB database). GluClβ_α-CysL, GluClβ_α-β8β9L, and GluClβ_α-Loops are three microchimeric β subunits where the Cys loop, β8β9 loop, or both loops were replaced by the homologous loops of the GluClα subunit, respectively.

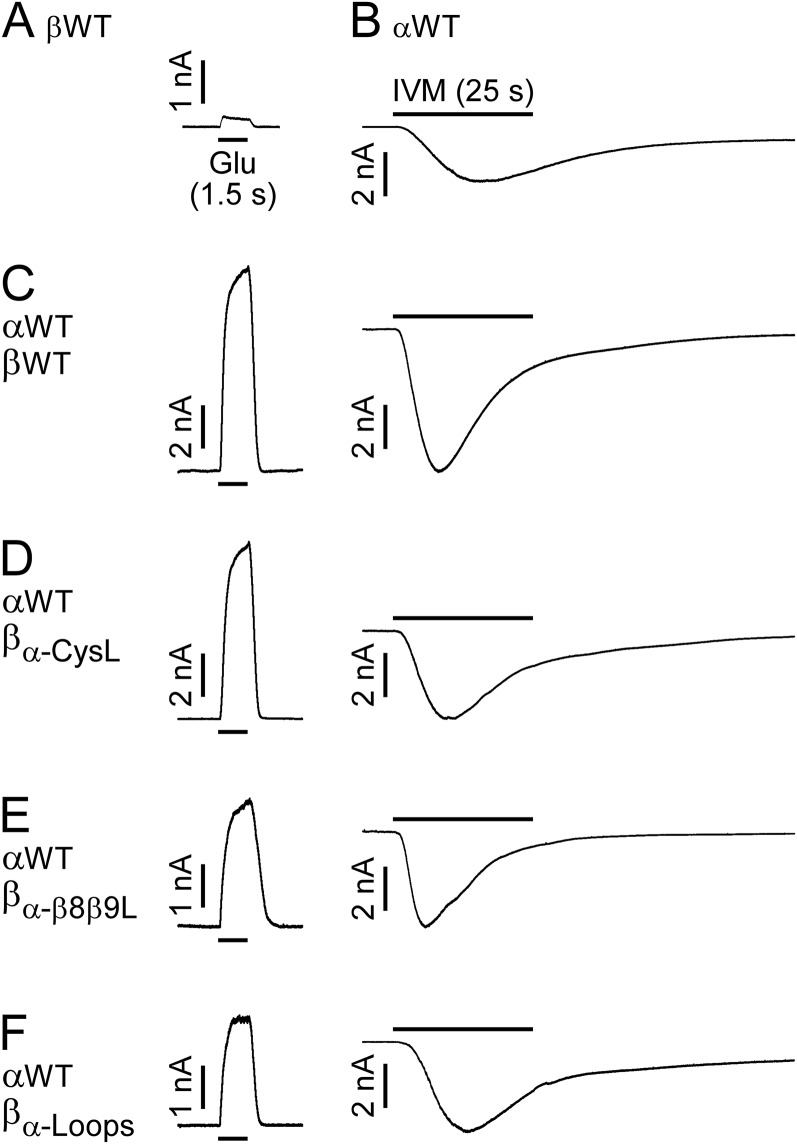
CHO cells transfected with the GluClαWT subunit alone showed very weak responses to 10 mM Glu (135 ± 27 pA in eight cells; mean ± SEM), but responded well to 500 nM IVM (Fig. S2B; 14 cells). This observation is in line with the findings of Frazier et al. (45), who reported that HEK cells expressing GluClα homomers are responsive to IVM but not to Glu. CHO cells transfected with the GluClβWT subunit alone showed very weak, rare responses to 10 mM Glu (less than 230 pA in eight cells; Fig. S2A), in line with results obtained in HEK cells (45). No responses to 500 nM IVM in CHO cells transfected with the GluClβWT subunit alone were observed (10 cells), in agreement with the same observations in HEK cells (18, 22). In contrast to these differential responses, cells cotransfected with both GluClαWT and GluClβWT subunits displayed robust responses to 1.5 mM Glu (EC₅₀ concentration) and 500 nM IVM (Fig. S2C). We therefore deduce that robust responses to Glu and IVM (independently) in a cell cotransfected with the GluClαWT and microchimeric GluClβ subunits (Fig. S2 D–F) reflect the function of heteromeric GluClα/βR complexes. This deduction also applies for the site-specific mutants discussed further below.

Fig. S2.

Sensitivity of WT and microchimeric GluClRs to Glu and IVM. (A–F) Representative current traces recorded from CHO cells transfected with the indicated subunits. Shown are responses obtained upon the application of 10 mM Glu (A), 500 nM IVM (B), and EC₅₀ concentrations of Glu (C–F, Left) (values in Table S1) followed, in the same cell, by 500 nM IVM (C–F, Right). The responses to Glu (A and C–F, Left) or IVM (B and C–F, Right) were measured at +60 mV or −60 mV, respectively. In all panels, Glu or IVM applications lasted 1.5 s or 25 s, respectively. The IVM/Glu amplitude ratios are 0.8 ± 0.18 for the GluClαWT/βWT receptor (nine cells), 0.7 ± 0.09 for the GluClαWT/β_α-CysL receptor (10 cells), 2.2 ± 0.35 for the GluClαWT/β_α-β8β9L receptor (11 cells), and 2.3 ± 0.29 for the GluClαWT/β_α-Loops receptor (nine cells). Data are mean ± SEM.

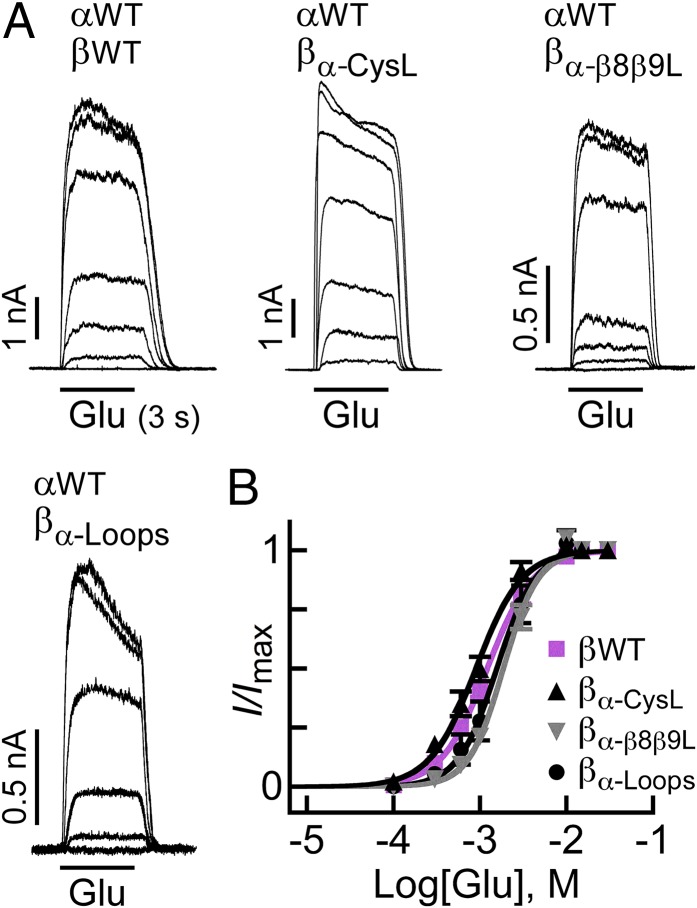
Fig. 2 shows representative current traces elicited by increasing Glu concentrations (Fig. 2A) and the corresponding dose–response curves (Fig. 2B) for the heteromeric WT and microchimeric GluClRs. The Glu-EC₅₀ values specified in Table S1 indicate that the apparent affinities of the GluClαWT/β_{microchimeric} receptors for Glu were very close to the apparent affinity of the GluClαWT/βWT receptor. The Hill coefficients of all four receptors (Table S1) were >1, indicating their activation with positive cooperativity. Note that the Glu-EC₅₀ and the Hill coefficient determined here for the GluClαWT/βWT receptor (Table S1) are very close to those values determined in Xenopus oocytes [Glu-EC₅₀ = 1.36 ± 0.05 mM and Hill coefficient (n_H) = 1.7 ± 0.1] (13). Remarkably, Glu readily activates the GluClαWT/β_α-Loops receptor, all of whose LigBD’s coupling loops are of the GluClα subunit (Fig. 2 and Table S1). We thus conclude that the β1β2, Cys, and β8β9 loops of the GluClα subunit are inherently capable of coupling Glu binding to pore gating, with no need for IVM prebinding.

Fig. 2.

Glu-activation properties of WT and microchimeric GluClRs. (A) Representative Glu-elicited currents measured in cells cotransfected with the indicated subunits. In all cases, Glu was applied for 3 s. Glu concentrations: 0.1 mM, 0.3 mM, 0.6 mM, 1 mM, 3 mM, 10 mM, and 30 mM in the upper row and 0.1 mM, 0.3 mM, 0.6 mM, 1 mM, 10 mM, and 30 mM in the lower row. Measurements were performed at +60 mV. (B) Dose–response curves plotted for responses measured in cells cotransfected with the GluClαWT subunit and the GluClβ subunits indicated in the figure. Curves were fitted to the averaged data points with a nonlinear regression using the Hill equation (Eq. 1) (r² > 0.99). Error bars correspond to SEM.

Table S1.

Basic properties of GluClRs activated by Glu

GluClR subunit combination	Mutation location	EC50 of Glu, mM	nH	ANOVA
				EC50	nH
αWT		ND	ND	ND	ND
βWT		ND	ND	ND	ND
αWT/βWT		1.5 ± 0.1 (27)	1.6 ± 0.1	—	—
αWT/βα-CysL	β(+)	1.1 ± 0.2 (13)	1.6 ± 0.1	ns	ns
αWT/βα-β8β9L	β(−)	2.1 ± 0.2 (11)	2.2 ± 0.2	ns	***
αWT/βα-Loops	β(+),β(−)	2.0 ± 0.3 (10)	2.1 ± 0.1	ns	**
αR98N/βWT	α(−)	111.0 ± 14 (14)	1.8 ± 0.1	***	ns
αR117N/βWT	α(−)	ND	ND	ND	ND
αR117Q/βWT	α(−)	81.2 ± 11 (9)	1.6 ± 0.1	***	ns
αR117S/βWT	α(−)	ND	ND	ND	ND
αS182A/βWT	α(−)	48.7 ± 6.2 (13)	1.5 ± 0.1	***	ns
αWT/βR66N	β(−)	4.4 ± 0.8 (14)	1.3 ± 0.1	ns	ns
αWT/βR85N	β(−)	3.2 ± 0.3 (12)	1.4 ± 0.1	ns	ns
αWT/βF122A	β(+)	6.5 ± 0.6 (11)	1.2 ± 0.1	*	***
αWT/βF122V	β(+)	9.1 ± 0.7 (11)	1.2 ± 0.1	***	**
αWT/βS152A	β(−)	6.9 ± 0.9 (13)	1.2 ± 0.1	*	**
αWT/βT229N	β(+)	11.8 ± 0.8 (22)	1.3 ± 0.1	***	**
αWT/βT229W	β(+)	12.1 ± 2.5 (10)	1.1 ± 0.1	***	***
αWT/βY232S	β(+)	7.2 ± 0.8 (17)	1.3 ± 0.1	**	**
αL279W/βWT	α(−)	0.06 ± 0.01 (15)	2.6 ± 0.1	***	***
αL279W/βT229N	α(−),β(+)	0.3 ± 0.1 (13)	1.5 ± 0.1	**	ns
α(L279W,T258N)/βWT	α(−),α(+)	3.4 ± 0.6 (19)	1.6 ± 0.1	ns	ns
α(L279W,T258N)/βT229N	α(−),α(+),β(+)	27.3 ± 2.5 (14)	1.8 ± 0.1	***	ns
αL279W alone	α(−)	ND†	ND†	ND	ND

EC₅₀, half-maximal effective concentration. n_H, Hill coefficient. One-way ANOVA with Dunnett’s correction was performed for the EC₅₀ values and n_H values. Data are mean ± SEM (number of cells is indicated in parentheses). Asterisks indicate a statistically significant difference in comparison with the GluClαWT/βWT receptor: ***P < 0.001; **0.001 < P < 0.01; *0.01 < P < 0.05. ND, not determined due to very small current traces; ns, does not differ significantly from the GluClαWT/βWT receptor (P > 0.05).

^†In cells expressing the homomeric GluClαL279W receptor, currents were readily measured at very high Glu concentrations (up to ∼600 pA; Fig. S7); however, because these currents did not reach saturation at 1 M Glu, the Glu-EC₅₀ and n_H for this mutant could not be determined.

Contribution of the GluClα Subunit (−) Side to Glu Accommodation in Heteromeric GluClR Mutants.

The aforementioned observations brought us to the recognition that a thorough study of how the GluClα subunit contributes to Glu binding in heteromeric GluClRs is necessary. Therefore, we first introduced mutations in the (−) side of the GluClα subunit based on the crystal structure of the homomeric GluClα_crystR (23) [the (−) and (+) subunit sides are defined in Fig. 1 A and B]. This structure indicates that the δ-guanidino groups of α(−)R98 and α(−)R117 are at an appropriate distance to form ion pairing with the α- and γ-carboxyl groups of Glu, respectively (Fig. 3D). A mutation that eliminated the charge and drastically reduced the side-chain size of α(−)R117, but kept hydrophilicity at this position (i.e., R→S), did not provide a functional GluClαR117S/βWT receptor. We therefore replaced the two Args (one at a time) with a more conservative and bulkier hydrophilic residue, Asn or Gln, which can function as hydrogen bond donor (or acceptor) with no capability to form salt bridges. A mutant having an αR98N substitution (GluClαR98N/βWT receptor) provided robust responses, but very high Glu concentrations were necessary to reach saturation [Fig. 3A, traces (Right) and brownish dose–response curve (Left)]. Note that to dissolve Glu, it was titrated with equimolar concentrations of NaOH; therefore, we did not change the Nernst potential for Cl⁻ during Glu application. However, the osmolarity and negative charge of the external solution drastically increased during the application of high Glu concentrations (for 0.6 s). Even so, we assume that these factors did not affect the responses, as discussed in SI Text, section 1, in conjunction with Fig. S3.

Fig. 3.

Sensitivity to Glu of heteromeric GluClRs carrying single-site mutations within the putative Glu-binding pockets. (A–C) Dose–response curves plotted for the activation of various heteromeric receptors by Glu. Curves were fitted as described in Fig. 2 (r² > 0.99). Error bars correspond to SEM. “X” corresponds to mutations that were introduced in the GluClα(−) (A), GluClβ(−) (B), and GluClβ(+) (C) subunit sides. (A, Right) Representative current traces evoked by increasing Glu concentrations of 10 mM, 30 mM, 60 mM, 100 mM, 250 mM, 600 mM, and 1,000 mM in cells coexpressing the indicated GluClR subunits. Currents were measured at +60 mV. (D and E) Three-dimensional homology models of potential β(+)/α(−) and α(+)/β(−) intersubunit interfaces. Glu is shown with yellow-colored carbon atoms, whereas the carbons of receptor residues are colored in gray or gold for the α or β subunit, respectively. Oxygen and nitrogen atoms are colored in red and blue, respectively. Hydrogen atoms are not shown. Dotted green lines correspond to potential ion pairing or hydrogen bonding, whereas dotted black lines indicate distances compatible with van der Waals or cation–pi interactions. Loop C caps the putative Glu-binding pocket. (F) Representative current trace elicited by 15 mM Glu (saturating concentration) in cells expressing the GluClαWT/βWT receptor, followed by inhibition of the leak current by 200 μM picrotoxin (PTX). (Inset) Magnification (7.5-fold) of the trace observed upon PTX application. Measurements were performed at +80 mV. (G) Representative single-channel current recorded from a cell-attached patch containing the GluClαWT/βWT receptor. The pipette solution included 15 mM Glu (saturating concentration). The voltage command was −90 mV. The closed and open state levels are indicated by c and o, respectively. The single-channel P_o-max is 0.64. (H, Left) Curve fitted to an event amplitude histogram by two Gaussian functions for the single-channel currents exemplified in G. The mean amplitude of the open state is 1.9 pA. (H, Right) Histogram of distribution of open times whose best-fit decay constant corresponds to the mean channel open time (τ₀). (I) Averaged dose–response data points of the GluClαWT/βWT receptor (purple squares) normalized to obtain the estimated P_open values that are plotted as a function of varying Glu concentrations. The purple line is the Hill curve. The dashed black line is the curve fitted based on an MWC allosteric model with two equivalent Glu-binding sites (n = 2) (Eq. 2). (J) Plausible subunit arrangement of a heteromeric GluClRαWT/βWT receptor with two equivalent Glu-binding sites (black triangles), as viewed from the extracellular side.

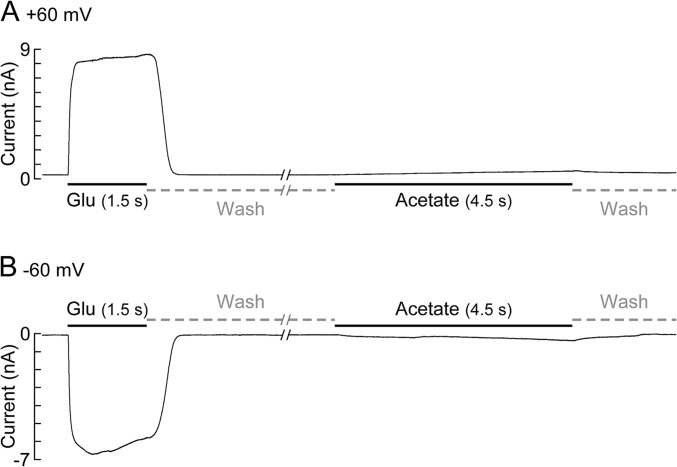
Fig. S3.

Control experiments examining the effect of external application of a nonspecific negatively charged small molecule on the activation of the GluClαWT/βWT receptor. Representative current traces were measured in a cell expressing the GluClαWT/βWT receptor. Shown are applications of Glu at saturating concentration (30 mM), followed by an 18.5-s-long wash and an application of 0.5 M acetate [in a solution containing 0.5 M Tris and NES (pH 7.35)]. Because a similar effect of acetate is observed at positive and negative membrane voltages (A and B, respectively), the possibility that the pore is blocked by acetate is excluded. The presented experiment was repeated in six cells, and the ratio between the response to acetate measured at 4.5 s and the peak responses for Glu was calculated. These ratios are 0.04 ± 0.02 and 0.03 ± 0.01 for the measurements at +60 mV and −60 mV, respectively. Data are mean ± SEM. Note that the response to acetate measured at 0.6 s (the time of Glu application in the dose–response experiments) is very weak compared with the Glu response, so the acetate/Glu response ratio is even much smaller.

In the case of the GluClαR117N/βWT receptor, the current responses did not allow us to analyze the dose–response relation reliably because they were very low (∼300 pA at 1 M Glu) and did not reach saturation, unlike in the case of the GluClαR98N/βWT receptor. In contrast, introducing Q at position α(−)117, which has a longer side chain than N, created a responsive GluClαR117Q/βWT receptor that enabled us to determine its Glu-EC₅₀ and Hill coefficient (Fig. 3A and Table S1).

The crystal structure also indicates that α(−)S182 forms a hydrogen bond with the γ-carboxyl group of Glu (23) (Fig. 3D). Preventing this hydrogen bonding in the heteromeric GluClαS182A/βWT receptor produced an effect similar to the effect observed with the α(−)R98N and α(−)R117Q substitutions (Fig. 3A and Table S1). The drastic effects exerted by mutations in the GluClα(−) side raised the question of whether mutations at the homologous positions in GluClβ would exert the same effects.

Contribution of the GluClβ Subunit to Glu Accommodation in Heteromeric GluClR Mutants.

Sequence alignments (17, 23) indicate that the GluClβ subunit has identical residues at positions homologous to GluCl α(−)R98, α(−)R117, and α(−)S182. These residues are β(−)R66, β(−)R85, and β(−)S152, respectively (Fig. 3E). A 3D homology model built here for the α(+)/β(−) intersubunit interface (SI Materials and Methods and Fig. S4) predicts that these three β-subunit residues are sufficiently close to interact with Glu (Fig. 3E). However, heteromeric mutant receptors assembled of the αWT subunit, together with β(−)R66N, β(−)R85N, or β(−)S152A, did not display the drastic increase in Glu-EC₅₀ typical of the homologous α-subunit mutants (Fig. 3B and Table S1). Most recently, Daeffler et al. (22) published a study where they investigated homomeric GluClβRs carrying a βT283S mutation in the pore-lining segments (see sequence with entry code Q17328 in the UniProtKB database). The latter mutation, per se, caused a dramatic improvement in the response to Glu (70-fold decrease in Glu-EC₅₀). Interestingly, when the βT283S mutation was combined with a β(−)S152A mutation (no. 126 in ref. 22), the Glu-EC₅₀ relatively increased by 590-fold (22). Clearly, if the β-subunit (−) side were to contribute the “complementary” Glu-binding components in our heteromeric GluClαWT/βS152A receptor, we would have observed a much larger rightward shift of the dose–response curve (complementary is defined in Fig. 1). Taken the results of the previous and current sections together, we infer that in the recombinant heteromeric receptors studied here, the GluClα(−) side, rather than the GluClβ(−) side, contributes the complementary components to Glu binding. Hence, we hypothesized that the GluClβ(+) side contributes the “principal” Glu-binding components in heteromeric GluClRs (principal is defined in Fig. 1).

Fig. S4.

Pairwise sequence alignment used for 3D homology modeling of the GluClβ subunit. Sequence alignment between a truncated GluClβ subunit lacking the M3–M4 connecting segment (GluCl-beta-tr.) and the truncated GluClα subunit used for expression, crystallization, and X-ray crystallography of the homomeric GluClα_crystR (PDB ID code 3RIF) (23). The α-helices and β-strands of the GluClβ subunit 3D homology model are indicated with the gray letters “h” and “s,” respectively. An asterisk indicates identical amino acids. A colon indicates groups of strongly similar properties. A period indicates groups of weakly similar properties.

To examine this hypothesis, we mutated residues β(+)F122, β(+)T229, and β(+)Y232 that might contact Glu, as predicted by sequence alignments (17, 23) and our 3D homology model (Fig. 3D). We then coexpressed the mutated β subunits (one at a time), together with the αWT subunit, and found that they shifted the dose–response curves rightward (Fig. 3C). Table S1 shows the extent of increase in the Glu-EC₅₀ values, with the most prominent shift in the GluClαWT/βT229N and GluClαWT/βT229W receptors (by approximately eightfold compared with the GluClαWT/βWT receptor). We infer that the GluClβ(+) side in the heteromeric assemblies generated here contributes the principal Glu-binding components. Daeffler et al. (22) added to the homomeric GluClβT283S receptor a β(+)T229A mutation (no. 203 in ref. 22), which increased the Glu-EC₅₀ to a much larger extent than observed here for the heteromeric GluClαWT/βT229N or GluClαWT/βT229W receptor. This difference can be attributed to the nature of the replacing amino acids. In the current study, we did not wish to change the chemical properties of the amino acids too much. This approach was adopted because the GluClαWT/βWT receptor inherently displays low affinity for Glu, which would probably make a dramatic increase in Glu-EC₅₀ difficult to probe. Hence, we kept the capability of the replacing residues at position β(+)T229 to act as hydrogen bond donors (Asn, Trp) or a hydrogen bond acceptor (Asn). We expected that the greater size of the replacing residues would interfere with, but not abolish, Glu accommodation. This expectation emerged because position β(+)229 is located on loop C, which caps the putative Glu-binding pocket but, on the other hand, is considered to be flexible and mobile (46) (Fig. 3 D and E). As to the β(+)Y232S substitution, we probably eliminated a cation–pi interaction that was recently suggested to be formed in a homomeric GluClβR, between the β(+)Y232 aromatic ring and the α-amino nitrogen of Glu (22). Still, one cannot exclude hydrogen bonding between the hydroxyl group of the Ser we introduced at this position [β(+)232] and the α-amino nitrogen of Glu, which could explain the moderate effect of the β(+)Y232S mutation.

Stoichiometry of the Glu-Binding Sites in a Heteromeric WT GluClα/βR.

The results presented in the previous sections suggest that a β(+)/α(−) intersubunit interface is involved in Glu accommodation; so, how many such functional interfaces exist per heteropentamer? The various single-site mutant receptors discussed so far share with the GluClαWT/βWT receptor Hill coefficients smaller than 2 but clearly larger than 1 (Table S1). This property suggests that there is more than one Glu-binding site per heteropentamer. To determine the number of functional sites and their microscopic equilibrium dissociation constants for Glu binding in the heteromeric GluClαWT/βWT receptor, we used an allosteric model based on the Monod–Wyman–Changeux (MWC) theory (47), as applied also by Karlin (48) to the nicotinic ACh receptor (nAChR) (reviewed in refs. 49 and 50). Because the GluClαWT/βWT receptor displays very slow and weak desensitization, we simplified the allosteric model by focusing on two major states as previously performed for weakly or nondesensitizing Cys-loop receptors such as: homomeric α7-nAChR mutants (51), homomeric α7-5HT_3AR chimeras (52), and heteromeric GABA receptors (53, 54). If the GluClαWT/βWT receptor has two equivalent (identical) Glu-binding sites, then Scheme I describes its MWC allosteric activation mechanism as follows:

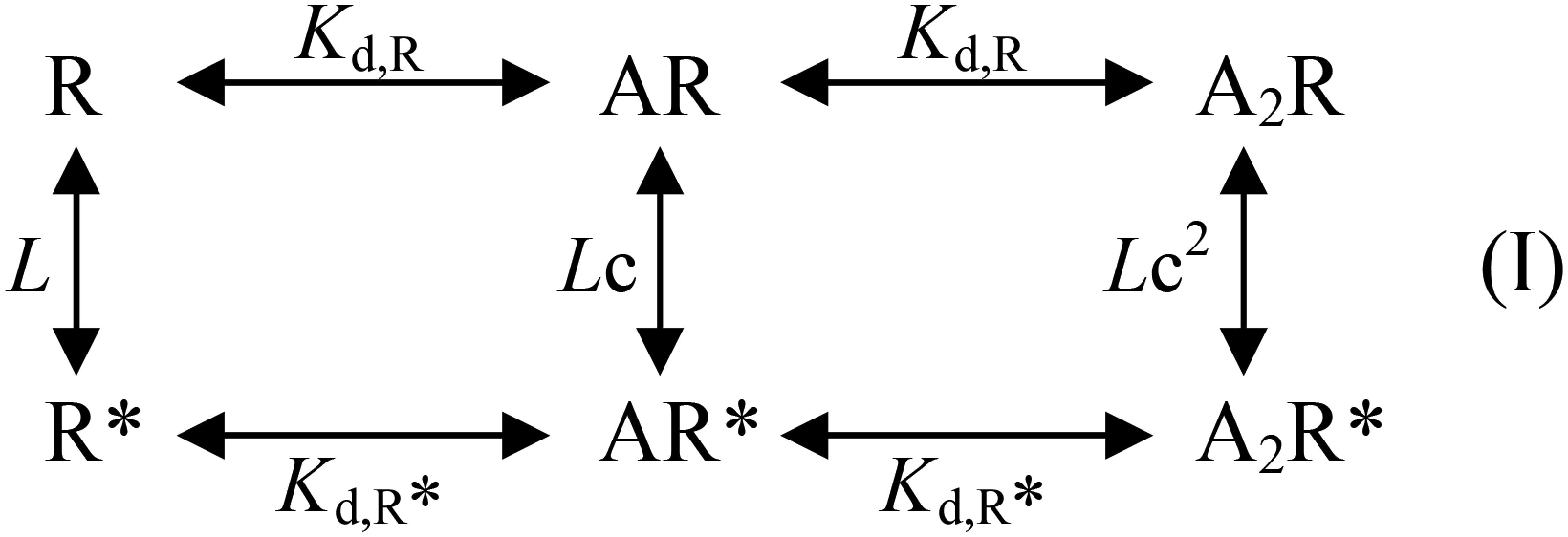
where R and R* are resting (closed) and active (open) receptor conformational states, respectively; A is an agonist molecule (Glu) that can complex with the receptor; K_d,R and K_d,R* are the microscopic equilibrium dissociation constants for agonist binding to the closed and open receptor states, respectively; and L is the equilibrium constant of the two receptor states (closed and open) in the absence of ligands. L is calculated by R/R* based on quantitative determinations, as follows.

Unoccupied R* corresponds to spontaneously open channels. Spontaneous activity (I_spont) was measured as the fraction of the leak current that could be blocked by picrotoxin, an ion-channel pore blocker of GluClRs (55) (e.g., Fig. 3F, indicated by “a”; elaborated in SI Text, section 2). Unoccupied R is estimated based on the current elicited by saturating Glu concentrations [maximal current response (I_max)]. That is, I_max represents the activatable receptor population, which is at rest in the absence of Glu (Fig. 3F, indicated by “b”). However, I_max might not represent all of the activatable channels because not all of them are necessarily open at saturating Glu concentrations. Therefore, we determined the maximum open probability (P_o-max) of the ion channel by single-channel recordings at a saturating Glu concentration (Fig. 3 G and H) and then calculated R by I_max/P_o-max. Thus, L = (I_max/P_o-max)⋅(1/I_spont). Experimental P_o-max and L values of three receptors are specified in Table S2 (footnotes).

Table S2.

Parameters of the MWC allosteric model applied for curve fitting with different number of Glu-binding sites

n or n, m	Kd,R, M	Kd,R*, M	K′d,R, M	K′d,R*, M	c	c′	Po-max*	∆AICc
GluClαWT/βWT receptor
1	5.68 × 10−3	2.72 × 10−5	—	—	0.48 × 10−2	—	0.71	451.2
2	1.32 × 10−3	1.04 × 10−4	—	—	7.88 × 10−2	—	0.65	0.0
3	1.12 × 10−3	1.98 × 10−4	—	—	17.7 × 10−2	—	0.68	110.7
4	9.08 × 10−4	2.49 × 10−4	—	—	27.4 ×10−2	—	0.68	86.4
5	8.01 × 10−4	2.84 × 10−4	—	—	35.5 × 10−2	—	0.68	44.4
GluClαL279W/βWT receptor
1, 0	8.22 × 10+10	1.01 × 10−6	—	—	1.23 × 10−17	—	1.00	432.0
2, 0	4.64 × 10−4	7.74 × 10−6	—	—	1.67 × 10−2	—	0.98	187.0
3, 0	1.75 × 10−4	1.40 × 10−5	—	—	8.00 × 10−2	—	0.96	163.4
4, 0	1.20 × 10−4	1.87 × 10−5	—	—	15.6 × 10−2	—	0.95	86.3
5, 0	9.70 × 10−5	2.23 × 10−5	—	—	23.0 × 10−2	—	0.95	77.6
2, 1	9.05 × 10−5	8.89 × 10−6	9.45 × 10−5	1.42 × 10−5	9.82 × 10−2	15.0 × 10−2	0.89	0.0
GluClα(L279W,T258N)/βWT receptor
1	9.87 × 10−3	2.85 × 10−5	—	—	0.29 × 10−2	—	0.63	490.0
2	2.93 × 10−3	1.67 × 10−4	—	—	5.70 × 10−2	—	0.60	0.0
3	2.22 × 10−3	3.23 × 10−4	—	—	14.5 × 10−2	—	0.62	83.1
4	1.79 × 10−3	4.23 × 10−4	—	—	23.6 × 10−2	—	0.61	59.6
5	1.57 × 10−3	4.95 × 10−4	—	—	31.5 × 10−2	—	0.61	34.6

n, number of sites displaying the specified microscopic equilibrium dissociation constants K_d,_R and K_d,_R* for Glu binding in the resting (closed) and active (open) states, respectively. c = K_d,_R*/K_d,_R. m, number of sites displaying the specified microscopic equilibrium dissociation constants K′_d,_R and K′_d,_R* for Glu binding in the closed and open states, respectively. c′ = K′_d,_R*/K′_d,_R. P_o-max*, theoretical maximum open probability. Values of the experimental P_o-max are 0.64 for the GluClαWT/βWT receptor, 0.86 for the GluClαL279W/βWT receptor, and 0.60 for the GluClα(L279W,T258N)/βWT receptor. Bold numbers correspond to the MWC allosteric model that is likely to be the most appropriate model for curve fitting, and for which ΔAICc = 0 (SI Materials and Methods, Evaluation of the Allosteric Model Using the AIC). Values (mean ± SEM) of L, which is the experimental equilibrium constant of the two receptor states (closed and open) in the absence of ligands, are 85 ± 5 for the GluClαWT/βWT receptor (11 cells), 81 ± 9 for the GluClαL279W/βWT receptor (11 cells), and 203 ± 17 for the GluClα(L279W,T258N)/βWT receptor (nine cells).

I_spont and P_o-max (0.64) were also used to normalize the dose–response data points of the GluClαWT/βWT receptor to estimate its open probability (P_open) at varying Glu concentrations by [(I + I_spont)/(I_max + I_spont)]⋅P_o-max (Fig. 3I). Then, to assess the applicability of Scheme I to the WT receptor activation mode, a curve was fitted to the normalized data points using an MWC allosteric model with two equivalent Glu-binding sites (n = 2) and the experimental mean L value (85) (Fig. 3I, dashed black curve and Eq. 2). Table S2 provides the resulting K_d values (in bold). At very high Glu concentrations, the theoretical maximum open probability P_o-max* = 1/(1 + cⁿL), where c = K_d,R*/K_d,R (54). So, when n = 2, the theoretical P_o-max* = 0.65 for the GluClαWT/βWT receptor, which closely predicts the experimental P_o-max (0.64). In contrast, fitting curves using an MWC model with other n values (one or equivalent three, four, or five Glu-binding sites; Eq. 2) resulted in a theoretical P_o-max* ≥ 0.68 (Table S2). Moreover, analysis of the second-order Akaike information criterion difference (∆AICc) (56) (SI Materials and Methods) selected the allosteric model with n = 2 as the most suitable MWC model for curve fitting in the GluClαWT/βWT receptor case (Table S2). Hence, we infer that the GluClαWT/βWT receptor has two functional equivalent Glu-binding sites. Taken together with the results shown in Fig. 3 A–C, we suggest that these two Glu-binding sites likely lie at two β(+)/α(−) intersubunit interfaces (Fig. 3J). Although one cannot absolutely exclude the possibility of a change in subunit stoichiometry due to mutations, we argue that such a change is unlikely to occur here (SI Text, section 3, Fig. S5, and Table S3).

Fig. S5.

Responses to Glu in cells cotransfected with the indicated subunits at an α/β cDNA ratio of 1:4. (A) Representative current traces evoked by Glu at concentrations as follows: 0.1 mM, 0.3 mM, 0.6 mM, 1 mM, 3 mM, 10 mM, and 30 mM for the αWT/βWT receptor; 0.01 mM, 0.02 mM, 0.03 mM, 0.06 mM, 0.1 mM, 0.2 mM, and 0.6 mM for the αL279W/βWT receptor; 0.1 mM, 0.3 mM, 1 mM, 3 mM, 10 mM, 30 mM, and 100 mM for the α(L279W,T258N)/βWT receptor; and 1 mM, 3 mM, 10 mM, 30 mM, 100 mM, 300 mM, and 1,000 mM for the α(L279W,T258N)/βT229N receptor. Currents were measured at +60 mV. (B) Glu dose–response curves plotted for the activation of the indicated heteromeric receptors as described in Fig. 2 (r² > 0.99). Error bars correspond to SEM.

Table S3.

Basic properties of GluClR activation by Glu as tested in cells transfected with α/β cDNA ratio of 1:4

GluClR subunit combination	Mutation location	EC50, mM	nH
αWT/βWT		1.0 ± 0.2 (11)	1.5 ± 0.1
αL279W/βWT	α(−)	0.05 ± 0.003 (10)	2.5 ± 0.2
α(L279W,T258N)/βWT	α(−),α(+)	1.5 ± 0.4 (8)	1.3 ± 0.1
α(L279W,T258N)/βT229N	α(−),α(+),β(+)	22.4 ± 4.2 (10)	1.9 ± 0.2

Data are mean ± SEM (number of cells is indicated in parentheses). One-way ANOVA with Tukey’s multiple comparison test was performed for the EC₅₀ and n_H values of receptors obtained by coexpressing the indicated subunits at α/β cDNA ratios of 1:1 (Table S1) and 1:4 (this table). For both the EC₅₀ and n_H values, the ANOVA showed no significant statistical difference between the values obtained by 1:1 and 1:4 transfection ratios in each receptor type (P > 0.05).

Mutation in the IVM-Binding Pocket Gives Rise to a Third Glu-Binding Site.

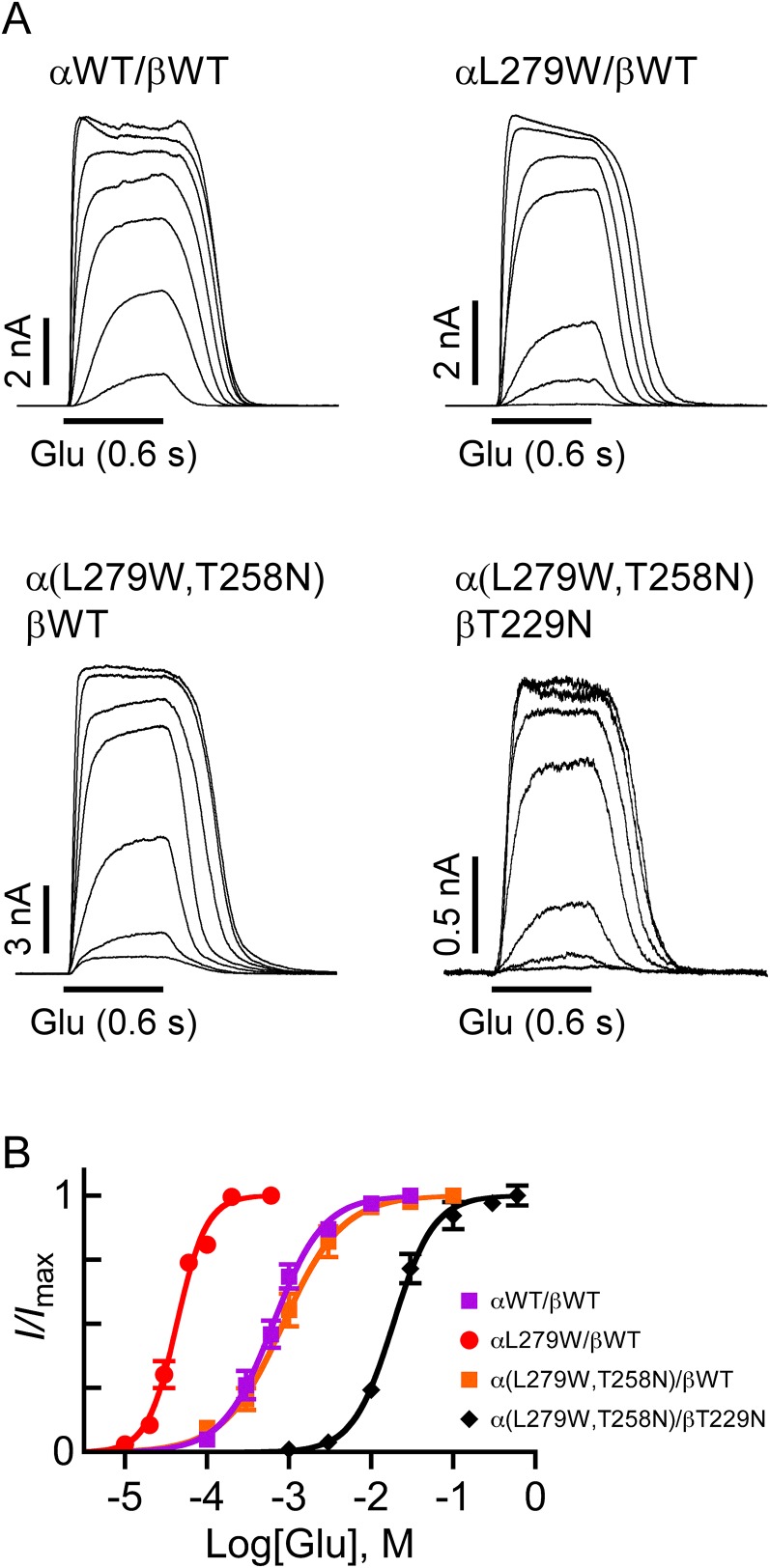
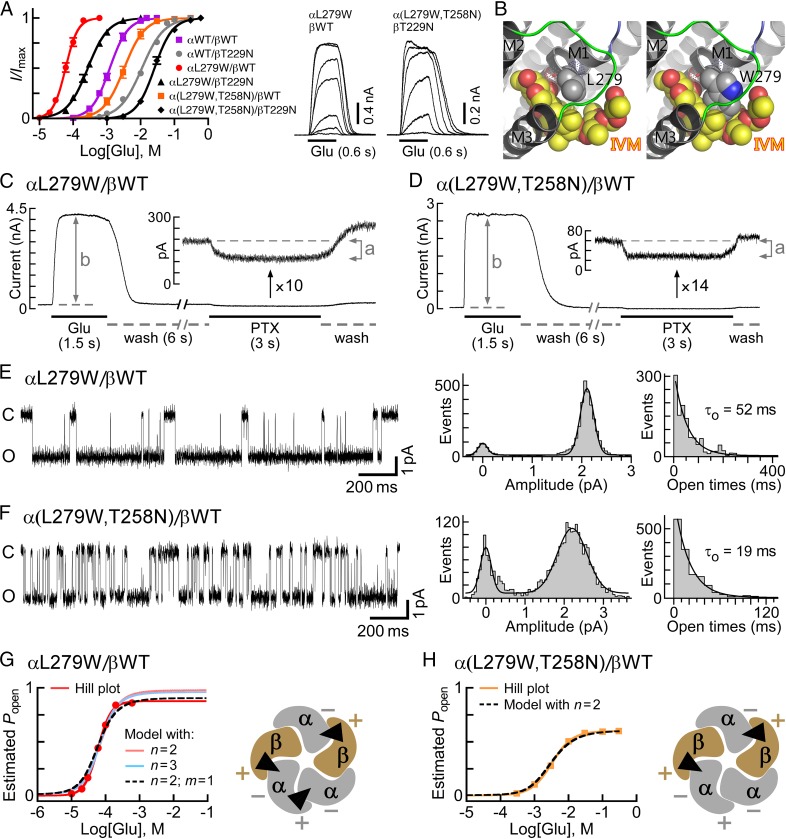
During our research, we identified a mutation in the putative IVM-binding site (αL279W; position α(−)L218 in GluClα_crystR) that decreased the Glu-EC₅₀ of the GluClαL279W/βWT receptor by ∼25-fold, compared with the GluClαWT/βWT receptor (Fig. 4A and Table S1). This mutation increased the Hill coefficient to 2.6, suggesting that the number of occupiable Glu-binding sites in the receptor mutant is probably not less than three. Intrigued by this possibility, we initially examined an MWC allosteric model with either two or three equivalent Glu-binding sites. To this end, we determined the values of I_spont, I_max, P_o-max, and L for the GluClαL279W/βWT receptor [Fig. 4 C and E and Table S2 (footnotes)] and estimated its P_open at varying Glu concentrations, all as described above for the GluClαWT/βWT receptor. Then, a curve was fitted to the normalized dose–response data points using an MWC allosteric model with n = 2 and the experimental mean L value (81) (Fig. 4G, salmon-colored curve and Eq. 2). The resulting K_d values (Table S2, same line of “2, 0”) were applied to calculate the theoretical P_o-max* by 1/(1 + c²L) = 0.98, which turned out to be much higher than the experimental P_o-max (0.86). Extrapolating the salmon-colored curve in Fig. 4G (model with n = 2) until the theoretical P_o-max* is reached indicates a strong deviation of this curve from the Hill plot at high Glu concentrations. Alternatively, a curve was fitted to the normalized dose–response data points using an MWC allosteric model with three equivalent Glu-binding sites (n = 3) and the same L value (81) (Fig. 4G, cyan-colored curve and Eq. 2). The resulting K_d values (Table S2, same line of “3, 0”) were used to calculate the theoretical P_o-max* by 1/(1 + c³L) = 0.96, which is also much higher than the experimental P_o-max (0.86). Extrapolation of the cyan-colored curve in Fig. 4G (model with n = 3) until the theoretical P_o-max* is reached indicates a strong deviation of this curve from the Hill plot at high Glu concentrations. Curve fitting with other values for n (one, or equivalent four or five Glu-binding sites) resulted in a theoretical P_o-max* ≥ 0.95 (Table S2). We therefore applied an MWC allosteric model with two equivalent and a third distinct Glu-binding sites (n = 2, m = 1), using the same L value (81) (Fig. 4G, dashed black curve and Eq. 3). In this case, K_d,R and K_d,R* characterize the two equivalent Glu-binding sites in the closed and open states, respectively; and K′_d,R and K′_d,R* characterize the third Glu-binding site in the closed and open states, respectively [Table S2 (in bold)]. Scheme II describes the MWC allosteric mechanism that corresponds to the GluClαL279W/βWT receptor:

Fig. 4.

Subunit stoichiometry and arrangement in heteromeric GluClα/βR mutants. (A, Left) Glu dose–response curves plotted for the activation of receptors consisting of the indicated subunits. Curves were fitted as described in Fig. 2B (r² > 0.99). Error bars correspond to SEM. (A, Right) Representative current traces evoked by applying increasing Glu concentrations on cells cotransfected with the indicated receptor subunits. Glu concentrations: 0.01 mM, 0.02 mM, 0.03 mM, 0.06 mM, 0.1 mM, 0.2 mM, and 0.3 mM (for the αL279W/βWT receptor) and 3 mM, 10 mM, 30 mM, 100 mM, 300 mM, and 600 mM [for the α(L279W,T258N)/βT229N receptor]. Currents were measured at +60 mV. (B) Three-dimensional models of the IVM-binding pocket at an α(+)/α(−) intersubunit interface. (Left) Side chain of the native αL279, which does not interact with IVM. (Right) Side chain of the substituting Trp, which potentially forms multiple van der Waals interactions with the lactone backbone of IVM. Side chains are shown as gray (carbon atoms) and blue (nitrogen) spheres. IVM is shown as yellow (carbon atoms) and red (oxygen atoms) spheres. Hydrogen atoms were removed for better viewing. The PDB 3RIF structure was used for generating the αL279W mutant and the pictures. (C and D) Representative current traces elicited by saturating concentrations of Glu in cells cotransfected with the indicated subunits (0.5 mM and 30 mM Glu in C and D, respectively). (Insets) Magnifications for the effect of picrotoxin (PTX; 200 μM) are shown. (E and F) Representative single-channel currents recorded in cell-attached patches from cells cotransfected with the indicated receptor subunits. The pipette solution included saturating Glu concentrations (0.5 mM and 30 mM Glu in E and F, respectively). The voltage command was −90 mV. The closed and open state levels are indicated by c and o, respectively. P_o-max values are 0.86 and 0.60 for the receptors indicated in E and F, respectively. On the right side of each current trace shown are curves fitted to event histograms plotted as described in Fig. 3H; they provide mean amplitudes of 2.1 pA and 2.2 pA for the open states of the receptors indicated in E and F, respectively. Mean channel open times (τ_o) are indicated inside the rightmost panels. (G and H) Estimated P_open plotted as a function of varying Glu concentrations. Red and orange lines correspond to the Hill curves. Other curves were plotted based on an MWC allosteric model using Eq. 2 for cases with either two (n = 2) or three (n = 3) equivalent Glu-binding sites or, alternatively, Eq. 3 for a case with two equivalent and a third distinct Glu-binding sites (n = 2, m = 1). (G and H, Right) Plausible subunit arrangements with intersubunit Glu-binding sites (black triangles), as viewed from the extracellular side.

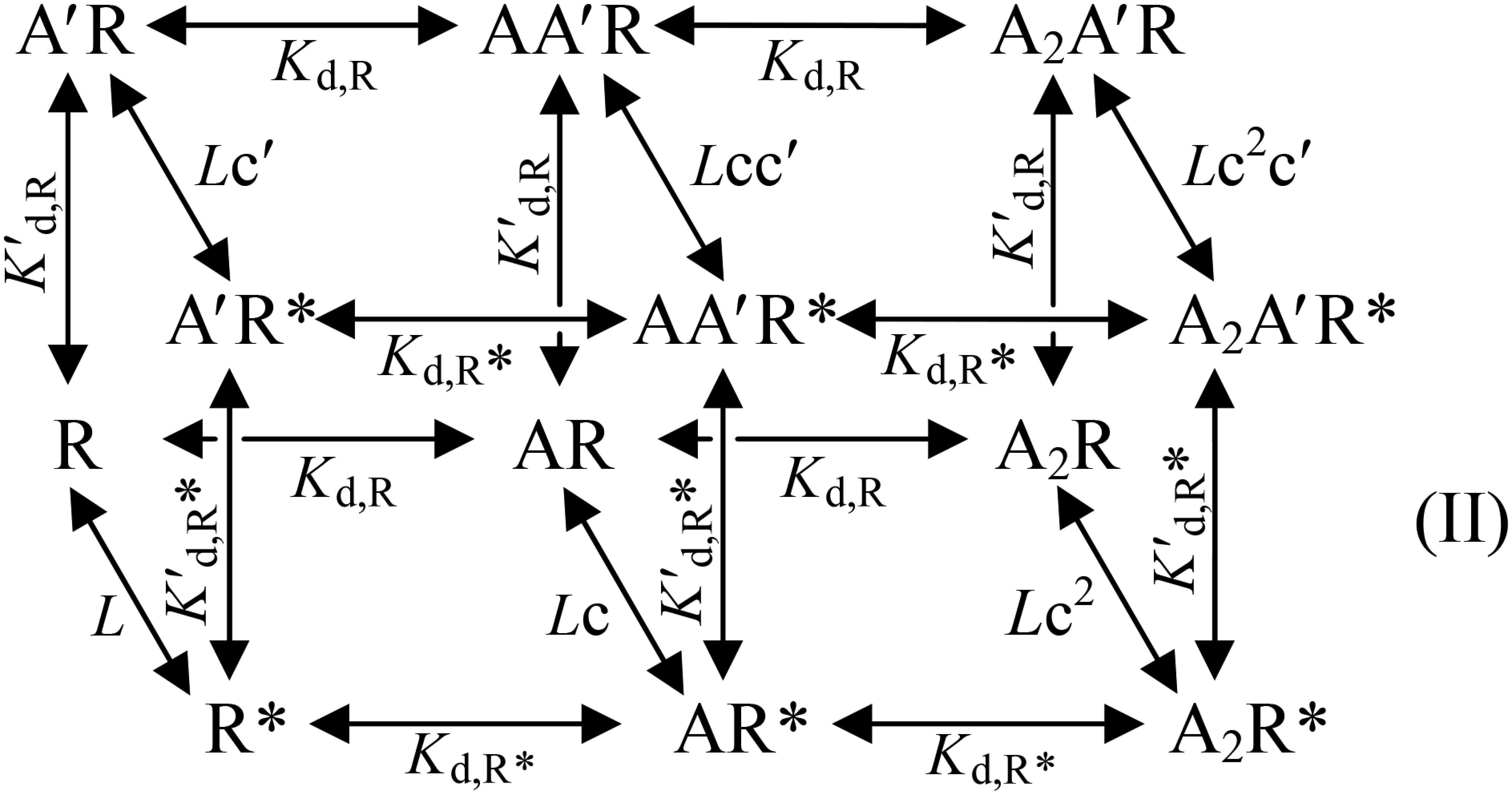
where c = K_d,R*/K_d,R and c′ = K′_d,R*/K′_d,R. In this case, the theoretical P_o-max* = 1/(1 + cⁿc′^mL) = 1/(1 + c²c′¹L) = 0.89, which is much closer to the experimental P_o-max (0.86) than in cases of curve fitting with other numbers of Glu-binding sites (Table S2). Analysis of the ∆AICc selected the allosteric model with two equivalent and a third distinct Glu-binding sites (n = 2, m = 1) as the most appropriate MWC model for curve fitting in the GluClαL279W/βWT receptor case (Table S2).

The allosteric mechanism suggested above does not provide details regarding the subunit types that form the third Glu-binding site interface in the GluClαL279W/βWT receptor, however. If the fifth subunit is GluClβ, then it will give rise to α(+)/β(−) and β(+)/β(−) intersubunit interfaces (envisioned in Fig. 3J); however, based on the aforementioned results, the GluClβ(−) side is less likely to contribute to Glu binding. If the fifth subunit is GluClα, then it will give rise to α(+)/α(−) and α(+)/β(−) intersubunit interfaces (envisioned in Fig. 4G, Right); so, the α(+)/α(−) intersubunit interface remains a reasonable candidate to form the third Glu-binding site. However, this working hypothesis required further experimental investigation. Because the GluClα(−) side was inferred to line the two Glu-binding pockets (Fig. 3 and main text), we introduced an α(+)T258N mutation (in loop C), in addition to the αL279W mutation. The homologous mutation [β(+)T229N] in the GluClαWT/βT229N receptor was shown to increase the Glu-EC₅₀ by approximately eightfold, compared with the GluClαWT/βWT receptor (Fig. 3C and Table S1; presented again in Fig. 4A in gray for convenience). Hence, an α(+)T258N mutation was anticipated to affect a potential α(+)/α(−) intersubunit Glu-binding site, without directly interfering with Glu binding at the two β(+)/α(−) sites. Fig. 4A shows that the dose–response curve of the GluClα(L279W,T258N)/βWT receptor is significantly shifted to the right relative to the curve of the GluClαL279W/βWT receptor, with an ∼57-fold increase in the Glu-EC₅₀ and a decrease of the Hill coefficient to n_H = 1.6 (Table S1). These macroscopic properties resemble the properties displayed by the GluClαWT/βWT receptor, which has two equivalent Glu-binding sites.

To quantify the effect of the α(+)T258N mutation further, we determined the values of I_spont, I_max, P_o-max, and L for the GluClα(L279W,T258N)/βWT receptor [Fig. 4 D and F and Table S2 (footnotes)] and estimated its P_open at varying Glu concentrations, all as described above for the GluClαWT/βWT receptor. Then, a curve was fitted to the normalized dose–response data points using an MWC allosteric model with two equivalent Glu-binding sites (n = 2) and the experimental mean L value (203) (Fig. 4H, dashed black curve and Eq. 2). The resulting K_d values are provided in Table S2 (in bold). The theoretical and experimental maximum open probabilities were found to be equal (0.60), whereas other values for n (one, or equivalent three, four, or five Glu-binding sites) resulted in higher theoretical P_o-max* values (Table S2). In addition, the analysis of the ∆AICc selected the allosteric model with n = 2 as the most suitable MWC model for curve fitting in the GluClα(L279W,T258N)/βWT receptor case (Table S2). Hence, the results imply that this double-mutant receptor lost the third Glu-binding site, and its remaining two equivalent Glu-binding sites display slightly lower affinity for Glu than the GluClαWT/βWT receptor [Table S2 (in bold)]. Provided that the mutations have not changed the subunit stoichiometry (as argued in SI Text, section 3), the two Glu-binding sites of the GluClα(L279W,T258N)/βWT receptor likely lie at β(+)/α(−) intersubunit interfaces (Fig. 4H, Right). As discussed above, the GluClβ(−) side is less likely to contribute to Glu binding, and so is an α(+)/β(−) intersubunit interface. We therefore infer that the α(+)T258N mutation is likely located at an α(+)/α(−) intersubunit interface. Taken together, our results suggest that in the GluClαL279W/βWT receptor, an α(+)/α(−) intersubunit interface likely forms a third Glu-binding site (Fig. 4G, Right), whereas Glu binding to this interface is impaired by adding the α(+)T258N mutation (Fig. 4H, Right).

β(+)T229N is the homologous mutation of α(+)T258N. Combining the αL279W mutation with the β(+)T229N mutation, to give a GluClαL279W/βT229N receptor, led to a fivefold rightward shift of the dose–response curve relative to the GluClαL279W/βWT receptor (Fig. 4A and Table S1). This shift is much smaller than the 57-fold rightward shift observed in the GluClα(L279W,T258N)/βWT receptor relative to the GluClαL279W/βWT receptor (Fig. 4A and Table S1). This difference is in line with the above conclusion that an α(+)/α(−) intersubunit interface forms the third Glu-binding site in the GluClαL279W/βWT receptor.

Interestingly, the α(+)T258N mutation in the GluClα(L279W,T258N)/βWT receptor has not only eliminated the third α(+)/α(−) intersubunit Glu-binding site but also considerably decreased the Glu-binding affinity of the two equivalent β(+)/α(−) interfaces relative to the GluClαL279W/βWT receptor [Table S2 (in bold)]. We suggest that the mutation in the (+) side of the plausible α(+)/α(−) Glu-binding site interface could allosterically affect the other Glu-binding site interfaces. Combining all three mutations to produce a GluClα(L279W,T258N)/βT229N receptor shifted the dose–response curve by 455-fold rightward relative to the GluClαL279W/βWT receptor (Fig. 4A and Table S1). This rightward shift is larger by ∼90-fold than the fivefold rightward shift observed for the GluClαL279W/βT229N receptor, which suggests that also in the triple mutant, the α(+)/α(−) intersubunit interface has a strong allosteric relationship with the β(+)/α(−) Glu-binding site interfaces. Notably, the Hill coefficient decreased from n_H = 2.6 in the GluClαL279W/βWT receptor to n_H = 1.5 in the GluClαL279W/βT229N receptor (Table S1), suggesting that the β(+)T229N mutation exerts a reciprocal allosteric effect on the third α(+)/α(−) intersubunit interface.

Effect of the αL279W Mutation on the Responsiveness of the Heteromeric GluClαL279W/βWT Receptor to IVM.

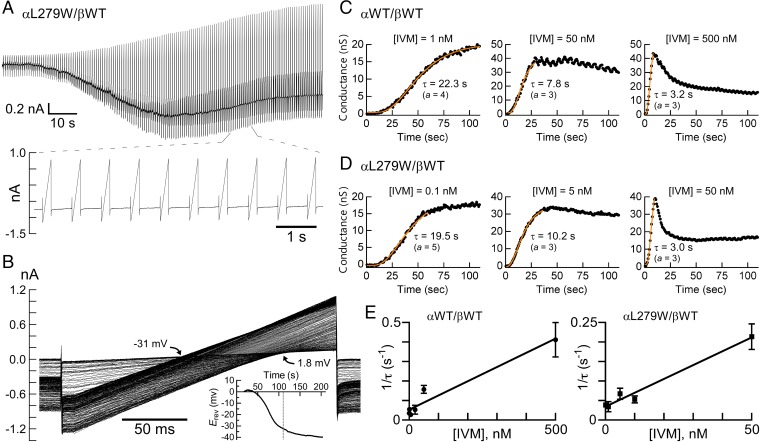
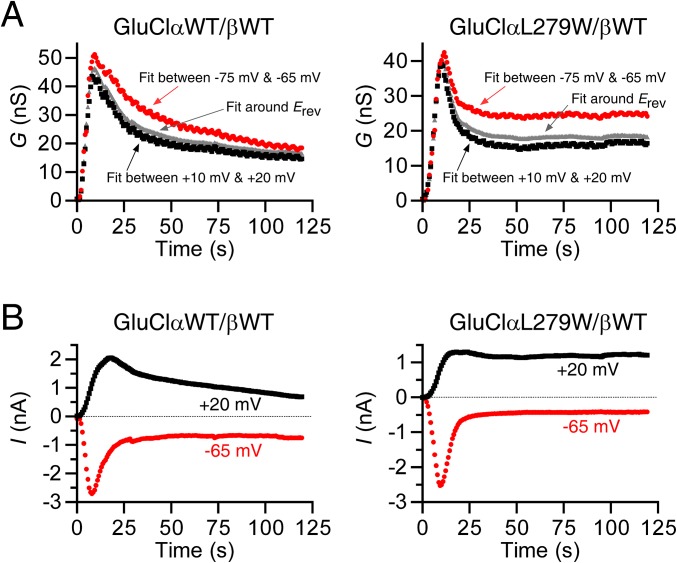
The crystal structure of the homomeric GluClα_crystR indicates that the backbone carbonyl oxygen of αL279 (L218 in GluClα_crystR) forms a hydrogen bond with hydroxyl O13-H of IVM, whereas the αL279 side chain does not interact with IVM (23) (Fig. 4B, Left). Three-dimensional homology modeling predicts that a Trp side chain introduced at position α279 might form multiple contacts with IVM (Fig. 4B, Right). If so, how might this mutation affect the responsiveness of the GluClαL279W/βWT receptor to IVM? To answer this question, we had to determine the IVM EC₅₀ for the WT and mutant receptors. However, unlike the fully reversible responses to Glu, after activation by IVM, the response could not be reproduced by reapplication of IVM even when the first IVM application was followed by a long-term wash (up to 30 min). Other groups also observed this phenomenon when the wash was applied for several minutes (13) or an hour (18). Hence, to quantify the effect of the mutation, we first used the methodology of Lester and coworkers (18) to determine the time constant of conductance development following IVM application. To this end, voltage ramps were carried out during the application of various IVM concentrations, with each application in a different cell. Fig. 5A shows an example of such an experiment. Superimposition of the output currents of the voltage ramps shows a sharp increase in slopes that reflects the robust IVM-induced conductance and a clear leftward shift (decrease) of the reversal potential that occurs mainly after the conductance reached its maximum (Fig. 5B). The shift of the reversal potential indicates a change in the Nernst potential for Cl⁻ and in the electrochemical driving force acting on Cl⁻ ions. The chloride conductance is defined by the slope of the current--voltage (I/V) relations extracted from the output currents of the voltage ramps, and could be determined at several membrane voltage spans. Fig. S6A shows the slope conductance determined between −75 mV and −65 mV, around the reversal potential, and between +10 mV and +20 mV, as a function of time. The rise time of the conductance increment was found to be similar for all of the three aforementioned voltage spans (Fig. S6A). Notably, during the applications of high IVM concentrations, the conductance rise was followed by a decrease in the conductance to a steady state in all voltage spans and in both the WT and indicated mutant receptors (Fig. S6A). Because the current decay under high IVM concentrations was faster at −65 mV than at +20 mV (Fig. S6B), and because the exponential fits of the conductance rise time were very similar at the different membrane voltage spans, we chose to analyze the conductance development further between +10 mV and +20 mV. Fig. 5 C and D shows the development of the conductance under the application of different IVM concentrations in different representative cells.

Fig. 5.

Affinity of WT and mutant heteromeric GluClRs for IVM. (A) Representative current trace elicited by 0.1 nM IVM in a cell coexpressing the indicated receptor subunits. IVM was applied throughout the entire time of the recording (210 s), which was made at −60 mV with intervening 200-ms-long voltage ramps from −80 mV to +20 mV as described in SI Materials and Methods. Note that only the output currents of the first 152 (of 290) voltage ramps are shown for clarity and the lower part shows a magnification of some output currents. (B) Superimposition of the output currents corresponding to the first 152 voltage ramps shown in A. Black arrows indicate the reversal potential (E_rev) span for the first 152 output currents of the voltage ramps. (Inset) Decrease in the E_rev throughout the entire recording time. The dotted line marks 110 s, which is the time recording of the output currents of the first 152 voltage ramps. (C and D) Chloride conductance as a function of time in different representative cells. The points corresponding to the conductance (in black) were determined based on the output currents of the voltage ramps (main text and SI Materials and Methods). To determine the time constants of conductance development (τ), exponential curves (orange) were fitted to the conductance points with a nonlinear regression using Eq. S2, with varying “a” values to account for the sigmoid time course. Note that the cell shown in the leftmost panel of D under 0.1 nM IVM, is the same cell shown in A and B. (E) Points corresponding to the averaged 1/τ plotted as a function of IVM concentrations. Curves were fitted to the data points by linear regression. The lowest IVM concentration was 0.1 nM for both the WT and mutant receptors. Forty-nine and 32 cells were analyzed as described throughout this figure to obtain the left (r² = 0.95) and right (r² = 0.98) graphs, respectively. Error bars correspond to SEM.

Fig. S6.

Conductance and current measured at different membrane voltages during application of saturating IVM concentrations. (A) Chloride conductance, G, measured during IVM application based on the slopes of the current–voltage (I/V) relations that were determined between −75 mV and −65 mV, around the reversal potential (E_rev), and between +10 mV and +20 mV (SI Materials and Methods, Whole-Cell Patch-Clamp Recordings). Concentrations of 500 nM and 50 nM IVM were applied to the cells expressing the indicated WT and mutant receptors, respectively. (B) Current amplitudes extracted at the indicated membrane voltages from the voltage ramps’ output currents obtained during IVM application. Concentrations of 500 nM and 50 nM IVM were applied to the cells expressing the indicated WT and mutant receptors, respectively. Presented, for example, are the same cells whose conductance is shown in the rightmost panels of Fig. 5 C and D.

The exponential fits of the conductance rise time (e.g., Fig. 5 C and D, orange curves) provide the time constant of conductance development (τ), whose reciprocal (1/τ) increased linearly with the increase in IVM concentration (Fig. 5E). Because IVM does not readily dissociate from the receptor (13, 18) and the number of possible intermediate IVM-bound closed states is not known, the simplest possible kinetic model that could describe the activation mechanism by IVM would be one in which the channel opens when IVM binds and closes after a very long time when IVM dissociates. Scheme III describes this kinetic model:

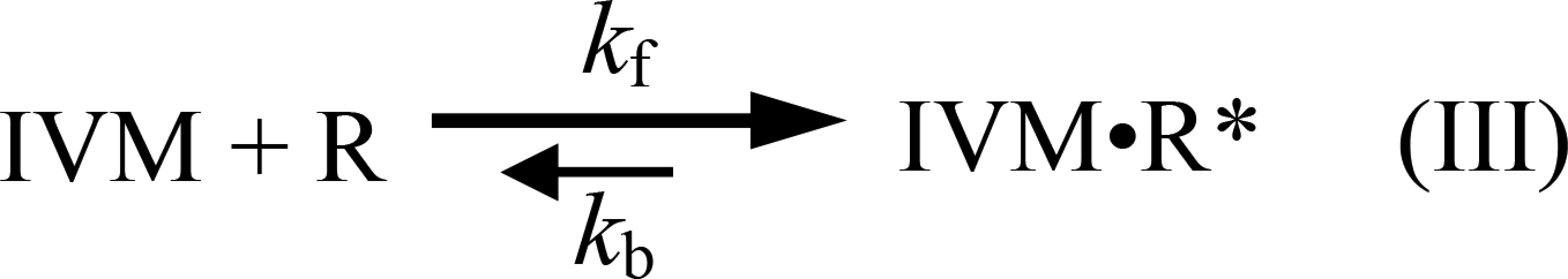
where R is the unoccupied closed receptor, IVM⋅R* is the IVM-bound open receptor, and 1/τ = k_f [IVM] + k_b. The slope of the curves in Fig. 5E corresponds to the IVM association rate constant (k forward, k_f). The IVM dissociation rate constant (k backward, k_b) is the extrapolated intercept of the linear curve with the y axis in Fig. 5E. The apparent K_d would be k_b/k_f, giving 73 × 10⁻⁹ M for IVM binding to the GluClαWT/βWT receptor (k_b = 5.3 × 10⁻² s⁻¹ and k_f = 7.3 × 10⁵ s⁻¹⋅M⁻¹). In contrast, the apparent K_d for IVM binding to the GluClαL279W/βWT receptor was 9.7 × 10⁻⁹ M (k_b = 3.4 × 10⁻² s⁻¹ and k_f = 3.5 × 10⁶ s⁻¹⋅M⁻¹), which indicates that the affinity of the mutant receptor for IVM is 7.5-fold higher than the affinity of the WT receptor for IVM. Note that because no experiments revealed that IVM could be washed out of the receptor (13, 18), the k_b values are expected to be on the order of <10⁻⁴ s⁻¹. However, the values here were found to be on the order of 10⁻² s⁻¹, implying that IVM should be removable. We therefore cannot exclude the possibility that after opening of the GluClR ion channel by IVM, a subsequent conformational change leads to trapping of IVM between the transmembrane helices irreversibly.

SI Text

Section 1. Receptor Responses Are Not Likely to be Affected by Short-Term Exposure to High Osmolarity or High External Negative Charge.

In a few mutant receptors, up to 1.0 M Glu concentrations were necessary to reach saturation [Fig. 3A, dose–response curves (Left) and, e.g., current traces (Right)]. Because the acidic pH of Glu was titrated with equimolar concentrations of NaOH, the expressing cells were exposed to high osmolarity for a short term (applications of 0.6 s). It seems, however, that the Glu-elicited responses were not affected by the drastic short-term increase in osmolarity. This assumption is supported by the macroscopic activation rates that became consistently faster with the increase in Glu concentrations, displaying activation rates similar to the activation rates of the GluClαWT/βWT receptor. For example, under saturating Glu concentrations, τ_activation was 49 ± 7.6 ms for the GluClαWT/βWT receptor (27 cells) and 65 ± 12 ms for the GluClαR98N/βWT receptor (14 cells) (analyzed by using Eq. S1). In addition, the dose–response curves of these mutant receptors exhibited a typical sigmoid shape (Fig. 3A, Left), with cooperativity similar to the cooperativity of the GluClαWT/βWT receptor (n_H values in Table S1). Still, we performed control experiments to ascertain that the observed currents reflect specific responses. First, CD8-transfected or nontransfected cells displayed very weak responses to 1.0 M Glu (124 ± 47 pA, six cells). Second, the responses of cells expressing the GluClαWT/βWT receptor to long-term application of 0.5 M acetate (buffered by an equimolar Tris concentration) were examined. Fig. S3 shows a typical cell that displayed a robust response to Glu, followed by a slow and very weak response to acetate, at both +60 and −60 mV. Notably, exposure of nontransfected cells to 1 M acetate for 0.6 s (the time of 1 M Glu applications) gave weak responses (169 ± 85 pA, five cells). These control experiments prove that despite the drastic increase in the osmolarity and the negative charge around the receptor, when high Glu concentrations are applied, the elicited currents are specific to the interaction of Glu with the receptor’s neurotransmitter-binding sites.

Section 2. Determination of a Spontaneously Open-Channel Population.

Picrotoxin (PTX) acts as a channel blocker of GluClRs (55) that binds deep in the pore (23) [Protein Data Bank (PDB) ID code 3RI5]. In Xenopus oocytes expressing heteromeric GluClαWT/βWT receptors, PTX blocks IVM- or Glu-elicited currents with IC₅₀ concentrations of 42 μM or 52 μM, respectively (55). Here, we used 200 μM PTX to ensure a total block of leak currents conducted via spontaneously open GluClRs (Figs. 3F and 4 C and D). Note that CHO cells do not inherently express PTX-blockable channels/currents (64) (verified here as well). Therefore, the reduction in the leak currents observed in the presence of PTX (and absence of Glu) could be attributed to a specific block of the heterologously expressed, spontaneously open GluClRs (indicated by “a” in Figs. 3F and 4 C and D).

Section 3. Mutations in This Study Are Not Likely to Change the Receptor Subunit Composition.

Although one cannot rule out with absolute certainty the possibility that a mutation might change the receptor subunit composition, we argue that it is not likely to be the case with the specific mutations introduced in the current study. It was recently demonstrated that an αL315F mutation in the second transmembrane helix (M2) of the GluClα subunit (entry code G5EBR3 in the UniProtKB database) facilitates the incorporation of the β subunit in the pentamer to form heteromeric GluClRs (45) (αL315 is position 9′ counted from the formerly considered beginning of M2). This GluClαL315F/βWT receptor displayed a biphasic dose–response relation with a component (61%) of high sensitivity to IVM (45) (note that both subunits also contained an insertion of dimerizable YFP in their M3–M4 loops). Interestingly, the biphasic dose–response relation was observed in cells expressing the GluClαL315F/βWT receptor when using α/β cDNA transfection ratios of 1:1, 4:1, and 1:4 (displayed 64%, 26%, and 58% IVM-sensitive components, respectively) (45) (in this case, both subunits contained a nondimerizable YFP). It was concluded that “incorporation of the β subunit confers increased receptor sensitivity to IVM, but transfection of equal amounts of α and β subunit DNA appears to be optimal” (45). It was also noted that variation in subunit stoichiometry might account for the biphasic IVM dose–response relations (45), in agreement with the view that multicomponent dose–response relations seen in various Cys-loop receptors might reflect several receptor populations with different subunit stoichiometries and distinct agonist sensitivities [e.g., ion channels activated by ACh (65–67)].

It should be noted that we did not use the mutational combinations used in the above-mentioned study (45). In all our experiments (except for the experiments in Fig. S5 and Table S3), we have consistently used an α/β cDNA ratio of 1:1. The resulting dose–response curves displayed monophasic behavior, as was previously observed for activation of the GluClαWT/βWT receptor by IVM when cotransfecting the cells with an α/β cDNA ratio of 1:1 (45). Therefore, our results indicate the existence of a single receptor population. In addition, the linear curves shown in Fig. 5E reflect one receptor population when activating the GluClαWT/βWT and GluClαL279W/βWT receptors with IVM. Taken together, we suggest that the receptor subunit stoichiometry likely remained unchanged throughout our study.

To challenge our suggestion regarding the unchanged stoichiometry further, we examined the macroscopic behavior of four receptors following cell transfection with an α/β cDNA ratio of 1:4. These four receptors include the three receptors used for the allosteric modeling [the αWT/βWT, αL279W/βWT, and α(L279W,T258N)/βWT receptors], as well as the α(L279W,T258N)/βT229N receptor whose β subunit was also mutated (in loop C; Fig. 3 D and E). As such, the triple-mutant receptor carries two mutations in side chains that face the putative Glu-binding pockets and are located on different subunits. Fig. S5A shows representative currents evoked by increasing Glu concentrations in cells transfected with various receptor subunits at an α/β cDNA ratio of 1:4. Fig. S5B shows the corresponding monophasic dose–response curves, indicating a single population for each receptor type. Table S3 provides the EC₅₀ values and Hill coefficients, which indicate that 1:4 and 1:1 α/β cDNA transfection ratios result in receptors sharing similar macroscopic features. These results indicate that the transfection of cells with equal amounts of α and β subunit DNA (as performed in all other experiments in this study) seems optimal in terms of the maximal number of β subunits that can be incorporated in the receptor complex. Furthermore, the monophasic Hill curves support our suggestion that the subunit stoichiometry was not changed in the mutant receptors.

The availability of a high-resolution 3D structure (GluClα_crystR; PDB ID code 3RIF) (23) allowed us to assess, from a structural viewpoint, the likelihood of changing the subunit stoichiometry by our specific mutations. The αL279W mutation studied here is located near the tip of M1. Three-dimensional homology modeling implies that a Trp side chain inserted at position α(−)279 (218 in GluClα_crystR) can adopt only two low-energy conformers that do not clash with proteinaceous moieties [validated using the deposited electron density maps and the crystallographic object-oriented toolkit (Coot)]. These conformers protrude into the intersubunit interface. The side chain of the first conformer is predicted to form multiple van der Waals interactions with the side chain of α(+)I334 of the adjacent subunit (I273 in the M2–M3 loop of the GluClα_crystR). Based on a previously published sequence alignment (23) (Fig. S4), β(+)V305 shares a homologous position with α(+)I334. Formation of multiple van der Waals interactions between a Trp substituted at position α(−)279 is also predicted with either α(+)V334 (I273V mutation introduced in silico in the GluClα_crystR) or β(+)V305 [in the β(+)/α(−) 3D homology model].

The side chain of the second potential low-energy α(−)W279 conformer is predicted to form multiple van der Waals interactions with the backbone of α(+)D338 and α(+)G342 (D277 and G281 in the GluClα_crystR), as well as a hydrogen bond with the side chain of α(+)D338. Based on a previously published sequence alignment (23) (Fig. S4), identical amino acids exist at homologous positions on the β subunit [β(+)D309 and β(+)G313]. Indeed, the 3D homology model suggests that these interactions are predicted to be formed also in the β(+)/α(−)W279 intersubunit interface. Taken together, the α(−)W279 would reasonably display the same preference to the α and β subunits, and therefore would likely not serve as a determinant of differential subunit assembly.

In various Cys-loop receptors, sequence determinants for subunit assembly were reported to be in the NH₂-terminal domain preceding the first transmembrane domain (e.g., 68–70). However, to the best of our knowledge, the specific positions mutated in our study have never been reported to play a role in receptor subunit assembly. Based on sequence alignments published previously (17, 23) (Fig. S4), all of the amino acids mutated here in the NH₂-terminal domain of one subunit share identity with the residues located at the homologous positions in the other subunit. Hence, these residues are a priori not expected to prefer one subunit type to another and to serve as determinants of subunit assembly; rather, they must be solvent-accessible to accommodate the neurotransmitter.

However, it was recently shown that a GluClR consisting of both mutations, the αL315F mutation together with a β(+)Y182F mutation in the putative Glu-binding pocket, lost the aforesaid biphasic dose–response relation and the high IVM sensitivity component (45). This GluClαL315F/β(+)Y182F receptor also contained a dimerizable YFP in the M3–M4 loop of both mutated subunits. Remarkably, it was necessary to replace the dimerizable YFP by one that cannot dimerize (monomeric YFP) to restore the biphasic behavior and the high-sensitivity component of activation by IVM. Hence, it was suggested that the β(+)Y182F mutation likely prevented efficient incorporation of the β subunit (45). Notably, in our study, the mutations introduced in the β(+) side did not include mutations at position Y182, and they did not exert dramatic effects that could be pinpointed on a different subunit stoichiometry than the subunit stoichiometry of the GluClαWT/βWT receptor.

Taking everything into account, we suggest that the mutations used in our study are not likely to affect the process of assembly and to change the subunit stoichiometry typical of the recombinant GluClαWT/βWT receptor expressed by us at an α/β cDNA transfection ratio of 1:1.

Section 4. Possible Structural Reasons for the Mutual Allosteric Influence Between the Glu-Binding Site Intersubunit Interfaces.

Inspection of the bond network at the α(+)/α(−) intersubunit interface in GluClα_crystR indicates that the side chain of α(+)T258 (T197 in GluClα_crystR) forms a hydrogen bond with α(+)Y261 (Y200 in GluClα_crystR) on the same subunit and two van der Waals interactions with α(−)R117 (R56 in GluClα_crystR) on the neighboring subunit. In contrast, an in silico α(+)T258N mutation (T197N in GluClα_crystR) implies that the introduced Asn (N) side chain would likely lose the hydrogen bond with α(+)Y261 and become sufficiently close to form two hydrogen bonds with α(−)R117 and a van der Waals interaction with α(−)L180 (L119 in GluCl_crystR). Such a change in the bond network of α(+)T258 upon its replacement by N has the potential to initiate a conformational change that might propagate from the α(+)/α(−) intersubunit interface to the β(+)/α(−) intersubunit interfaces. Similar potential changes in the bond network were also seen in silico in the β(+)/α(−) intersubunit interface of the 3D homology model, which could suggest that conformational changes in the β(+)/α(−) interfaces might propagate to the α(+)/α(−) intersubunit interface. The propagation trajectories of such potential conformational changes could be a subject for future studies.

SI Materials and Methods

Generation of cDNA Constructs.

The cDNA encoding the GluClα subunit was a kind gift from Henry A. Lester, Caltech, Pasadena, CA (optGluClα EYFP; plasmid 15104, Addgene), and was used to prepare the C. elegans GluClαWT subunit. The cDNA encoding the C. elegans GluClβ subunit was prepared by RT of total C. elegans RNA and PCR amplification of the relevant ORF, which was subsequently cloned into a pcDNA3.1 vector. Swapping of the Cys and β8β9 loops was performed at the level of the cDNA by PCR amplification of the entire plasmid as performed previously (71). To this end, we used primers that contained the bases corresponding to the replacing sequence with flanks that hybridize to 17–23 ORFs’ bases on each side of the sequence to be replaced. Site-specific mutations were introduced by using the QuikChange Site-Directed Mutagenesis Kit (Stratagene). The entire ORFs of all microchimeras and site-specific mutants were sequenced and subcloned into an original pcDNA3.1 vector.

Preparation of Cells for Electrophysiological Experiments.

CHO cells were cultured as performed previously (71) in DMEM containing 10% (vol/vol) FCS, 2 mM Glutamax (Gibco), 100 units/mL penicillin G, and 100 μg/mL streptomycin, and were grown in 5% CO₂ at 37 °C under 90–95% humidity. CHO cells were seeded on glass coverslips (13-mm diameter) placed in a 24-multiwell plate. PTX (5 μM) was added to the cells immediately before transfection to prevent chloride fluxes through the expressed GluCl channels, owing to the presence of Glu in the FCS. For the expression of GluClRs, cells were transiently cotransfected with pcDNA3.1 plasmids containing the ORFs of interest using transit-LT1 transfection reagent (Mirus) according to the manufacturer’s protocol. For the expression of heteromeric receptors, GluClα and GluClβ cDNAs (200–600 ng per well) were used at a 1:1 ratio, and pIRES-CD8 plasmid (200 ng per well) was added to enable visualization of the expressing cells by beads coated with anti-CD8 Abs (Invitrogen). The same protocol was used for expression at an α/β cDNA ratio of 1:4 (Fig. S5 and Table S3), but with adjusted cDNA quantities accordingly. The same protocol was also used for the expression of homomeric GluClRs, but only with one GluCl subunit type of interest. Recordings were performed 72–96 h following the transfection.

Whole-Cell Patch-Clamp Recordings.

Recordings were performed as described previously (71) in CHO cells that were prepared as described above. For whole-cell patch-clamp experiments, the normal external solution (NES) contained 140 mM NaCl, 2.8 mM KCl, 2 mM CaCl₂, 2 mM MgCl₂, 10 mM glucose, and 10 mM Hepes, adjusted to pH 7.35 with NaOH (310 mOsm/L). The pipette solution contained 130 mM KCl, 4 mM MgCl₂, 4 mM Na₂ATP, 1 mm EGTA, and 10 mM Hepes, adjusted to pH 7.35 with KOH (290 mOsm/L). The osmolarity of these solutions was maintained by adding sucrose. The electrode resistance was 6–10 MΩ when filled with the pipette solution. External solutions were applied onto the cell by using the VC-77SP Fast-Step System (Warner Instruments) combined with an N₂ pressure of 3–4 psi to produce laminar flow of the external solution onto the patched cell. All measurements were performed at room temperature. The currents were measured with an Axopatch 200B patch-clamp amplifier (Molecular Devices) and a Digidata 1440A interface (Molecular Devices). Acquisition of recording data was performed at 2.5 kHz, and recordings were low-pass-filtered at 1 kHz through a four-pole Bessel filter. The pClamp 10 software (Molecular Devices) was used for data acquisition.

To determine the time constant of the macroscopic current rise, the current rise was best fitted with a single exponential time course using the Clampfit 10 program (implemented in pClamp 10) and Eq. S1:

$$Y=A\cdot e^{-t/\tau }+C,$$ [S1]

where A is the current amplitude, t is the time, τ is the time constant, and C is the constant y-offset. Note that the Chebyshev method was used for fitting between the deflection of the rising current (close to the baseline) and the beginning of the steady-state current, which corresponds to most of the Glu-elicited rising phase.

To determine the chloride conductance and the reversal potential during IVM application, currents were elicited by application of IVM (at different concentrations) at a holding potential of −60 mV. A step to −80 mV was applied for 10 ms, and 200-ms-long voltage ramps from −80 mV to +20 mV were then applied every 723.2 ms. Leak currents, which were obtained by the same protocol but in the absence of IVM, were subtracted from the IVM-elicited currents. Then, a current–voltage (I/V) relationship was plotted for each voltage ramp, and the slope conductance was obtained from a linear fit of the 10- to 20-mV portion of the graph. Slope conductance was also measured in the −75- to −65-mV portion of the I/V graph and around the reversal potential for each cell. The relationship between conductance values and time was plotted for each cell, and the time constant of conductance development was determined as by Adams and Gage (72), by fitting an exponential curve to the data points using Eq. S2 (e.g., Fig. 5 C and D), as follows:

$$G_{Cl}\left(t\right)=G_{Cl}\left(\text{max}\right){(1-e^{-t/\tau })}^a,$$ [S2]

where G_Cl(t) is the chloride conductance at a given time, G_Cl(max) is the maximal chloride conductance, t is the time, τ is the time constant of the conductance rise to its maximum, and a is a parameter describing the sigmoid time course. Values of 2, 3, 4, 5, or 6 were assigned to parameter a to obtain the best fit, as assessed by the correlation coefficient (r, ranged from 0.95 to 0.98).

Single-Channel Recordings.

For measurements of single-channel currents from cell-attached membrane patches, electrodes were coated with Sylgard 184 (Dow Corning Corporation) to reduce pipette capacitance. The resistance of the recording electrodes was set on 10–15 MΩ when filled with the pipette solution. Both the bath and pipette contained NES, and the pipette contained saturating concentrations of Glu as well. Acquisition of recorded data was performed at 10 kHz, and recordings were low-pass-filtered at 1 kHz. Single-channel events were detected by the half-amplitude threshold criterion using the Clampfit 10 program. The mean value of the unitary current amplitude was obtained by curve fitting to the single-channel event amplitude histogram using Gaussian function (Eq. S3):

$$f\left(X\right)={\displaystyle \sum }_{i=1}^q{A}_i\frac{e^{-{(x-{\mu }_i)}^2/2{\text{σ}}_i^2}}{{\text{σ}}_i\sqrt{2\text{π}}}+C,$$ [S3]

where A is the amplitude; µ is the Gaussian mean; σ is the Gaussian SD; C is the constant y-offset for each component i; and q = 2 components, i₁ and i₂, that correspond to the closed and open channel states, respectively.

The distributions of open times were fitted with a single exponential function, yielding the time constant that corresponds to the mean channel open time. In cases of patches containing two or three channels, the mean channel open time (${\overline{t}}_o$) was estimated by using Eq. S4 as originally described by Fenwick et al. (73), which has also been used for muscarinic K⁺ channels and the cystic fibrosis transmembrane conductance regulator (CFTR) (74, 75):

$${\overline{t}}_o=\frac{{{\displaystyle \sum }}^{\text{}}j{t}_j}{N},$$ [S4]

where j indicates the current level, t_j is the time interval spent in each current level, and N is a count of all channel openings (transitions from a given level j to a subsequent level j + 1).

Single-channel P_o-max was obtained by using Eq. S5 (76):

$$N{P}_{o-\text{max}}={\displaystyle \sum }_{S=1}^N\left(t_{s}S\right)/T,$$ [S5]

where N is the number of channels in a patch (one, two, or three here), P_o-max is the maximum open probability of a single channel obtained by measurements performed under saturating Glu concentrations, t_s is the total time spent at each current opening level, S is the current opening level, and T is the total time of recording.

Evaluation of the Allosteric Model Using the AIC.

To compare between goodness-of-fit of curves plotted based on an MWC allosteric model with various numbers of Glu-binding sites, we used the AIC (56). This criterion allowed us to select the allosteric model that is more likely to describe the behavior of a given receptor; that is, the model having the lowest AICc value. We calculated the AICc by using Eq. S6 (56):

$$\text{AICc}=\text{N}\times \text{ln}\left\{\frac{\text{RSS}}{\text{N}}\right\}+2\text{K}+\frac{2\text{K}\left(\text{K}+1\right)}{\text{N}-\text{K}-1},$$ [S6]

where N is the number of points, K is the number of free parameters plus 1, and RSS is the residual sum of squares (i.e., the sum of the squares of the vertical distances between the points comprising the fitted Hill curve and the points comprising a curve fitted based on the MWC allosteric model). The RSS was calculated by using Eq. S7:

$$\text{RSS}={{\displaystyle \sum }}^{\text{}}{(y-\widehat{y})}^2,$$ [S7]

where y is a point (of a set of points) on the Hill curve and $\widehat{y}$ is the corresponding point on the curve fitted based on the MWC allosteric model. Note that our calculation of the AICc takes into account the theoretical P_o-max*. For example, in the GluClαL279W/βWT receptor case, when comparing an MWC allosteric model having three equivalent Glu-binding sites (n = 3) with an MWC allosteric model having two equivalent and a third distinct Glu-binding sites (n = 2, m = 1), the Hill curve and the two MWC-based curves were extrapolated to the value of the higher theoretical P_o-max* (i.e., to 0.96, which is the theoretical P_o-max* of the allosteric model with n = 3). Then, the extrapolated curves were used to calculate the AICc values of the two MWC-based curves.

The ∆AICc was calculated by subtracting the lowest AICc value (AICc_min) from the AICc values obtained for curves fitted using allosteric models with different numbers of Glu-binding sites (AICc_i); so, ΔAICc = AICc_i − AICc_min. ΔAICc = 0 is obtained for the case of an AICc_i value, which is the AICc_min. An MWC allosteric model whose curve provides a ΔAICc value of 0 is likely to be the most suitable model for curve fitting. For less appropriate cases, ∆AICc > 0.

Homology Modeling.

The sequence alignment shown in Fig. S4 was submitted for automated comparative (homology) protein modeling via the SWISS-MODEL alignment interface (77), using the atomic structure of the GluClα_crystR (PDB ID code 3RIF) as a template for building a 3D homology model of the GluClβ subunit. The rmsd between 336 Cα atoms of the 3D homology model and the template was 0.16 Å. Note that the GluClβ 3D homology model and the A chain of the 3RIF template consist of 345 and 340 amino acids, respectively. To create 3D homology models of the α(+)/β(−) and β(+)/α(−) intersubunit interfaces, the 3D homology model was superimposed in three dimensions onto the B chain and then the A chain of 3RIF, respectively. The 3D homology models were subjected to validation in the Research Collaboratory for Structural Bioinformatics (RCSB) PDB Validation Server under the Auto Dep Input Tool (ADIT) deposition tool (deposit.rcsb.org/adit/) to run geometric checks outside of the deposition pipeline and to find violations in terms of close contacts, bond deviations, and covalent bond distances and angles. Subsequently, clashes have been eliminated by choosing low-energy side-chain conformations using Coot, whereas other violations have been minimized by using Coot in combination with segmental in vacuo energy minimization with GROMOS96. As a final step, the 3D homology models were subjected to geometry validation by SFCHECK at the RCSB PDB Validation Server (validate.rcsb.org/). No issues have been found in terms of atomic clashes, peptide linkage, covalent geometry, chirality errors, and Phi/Psi torsion angles.

Discussion

To determine unequivocally the subunit stoichiometry and arrangement in native GluClα/βRs, high-resolution X-ray crystallography of heteropentameric receptors purified from the organisms that naturally express them is necessary. To the best of our knowledge, such a determination is yet out of reach. Hence, an alternative methodology must be considered. In Cys-loop receptors, the neurotransmitter-binding pockets lie at the interface between adjacent subunits (1–9). One could therefore use site-specific mutagenesis and biophysical characterization of activation mechanisms in recombinant receptors to find the types of subunits that line the agonist-binding pockets. By working with recombinant receptors, however, one cannot exclude the possibility that the ratio of subunit cDNA transfected, the type of the expressing cell, or a mutation might influence the receptor’s subunit composition (e.g., 45, 57, 58). We nevertheless argue that the specific mutations we introduced are less likely to change the subunit stoichiometry of the recombinant receptors studied here (SI Text, section 3).

In various Cys-loop receptors, the β1β2, Cys, and β8β9 loops were shown to play a key role in transducing the agonist-binding energy into ion-channel gating force (35–44). Here, we first demonstrated that although the homomeric GluClαR is not responsive to Glu, the β1β2, Cys, and β8β9 loops of the GluClα subunit are fully capable of coupling Glu binding to channel gating in a heteromeric GluClα/β microchimera that has the sequences of the α-subunit loops. Subsequently, we undertook to identify the intersubunit interfaces involved in Glu accommodation by heteromeric GluClα/βRs. Taking advantage of the crystal structure of a truncated homomeric GluClα_crystR as a template, we built a 3D homology model for the GluClβ subunit. Then, based on the two structures, we introduced single-site mutations in the (−) side of either the GluClα subunit or the GluClβ subunit at positions carrying residues that putatively interact with Glu. Characterization of the effects of these mutations on the receptor function allowed us to suggest that in the heteromeric GluClα/βRs studied here, the (−) side of the α subunit, rather than the (−) side of the β subunit, contributes complementary components to Glu binding. Single-site mutations and functional analysis of heteromeric GluClα/βRs carrying mutations in the (+) side of the β subunit imply that this side contributes principal components to Glu binding.

When considering the GluClαWT/βWT receptor in terms of the MWC allosteric mechanism, we infer that a maximum of two equivalent binding sites can be occupied by Glu [Fig. 3I, Scheme I, and Table S2 (in bold)]. Provided that the aforementioned single-site mutations introduced at the intersubunit interfaces have not changed the subunit stoichiometry (as argued in SI Text, section 3), Glu binding likely takes place at two β(+)/α(−) intersubunit interfaces. Hence, one can envision a subunit arrangement as illustrated in Fig. 3J for a recombinant GluClαWT/βWT receptor expressed in CHO cells, with no information regarding the type of the fifth subunit.

When considering the GluClαL279W/βWT receptor in terms of the MWC allosteric mechanism, we infer that Glu can occupy three sites (Fig. 4G and Scheme II). These sites are (i) two equivalent Glu-binding sites that are likely located at β(+)/α(−) intersubunit interfaces and display considerably higher affinity for Glu than their homologous binding sites in the GluClαWT/βWT receptor and (ii) a third distinct site with slightly lower Glu-binding affinity, in both the resting (closed) and active (open) receptor states [Table S2 (in bold)]. We argue that the third Glu-binding site is formed between two adjacent α subunits; the arguments for that conclusion are as follows:

• i)In CHO cells, a WT GluClβ subunit does not assemble into a homopentamer capable of responding to Glu or IVM, which indicates that the β subunit has difficulties in creating Glu-binding β(+)/β(−) intersubunit interfaces (Fig. S2A and Table S1).
• ii)In the heteromeric GluClα/βRs studied here, three single-site mutations in the β(−) side did not lead to drastic effects on the receptor activation by Glu, unlike the case of the same mutations introduced at the homologous positions in the α(−) side.
• iii)The homomeric GluClαL279W receptor responds to very high Glu concentrations (Fig. S7), indicating the capability of an α(+)/α(−) intersubunit interface to accommodate Glu (with no need for IVM prebinding).
• iv)Adding a mutation in loop C (+ side) of the αL279W subunit gave rise to an α(L279W,T258N)/βWT receptor that lost the third Glu-binding site (Fig. 4H), whereas the remaining two equivalent Glu-binding sites display microscopic equilibrium dissociation constants slightly higher than the microscopic equilibrium dissociation constants of the GluClαWT/βWT receptor [Table S2 (in bold)].

Fig. S7.

Homomeric GluClαL279W receptor responds to very high Glu concentrations. Representative current traces evoked by increasing Glu concentrations of 100 mM, 300 mM, 600 mM, and 1,000 mM in cells expressing the homomeric GluClαL279W receptor. Currents were measured at +60 mV, and did not reach saturation (five cells).

A third Glu-binding site located at an α(+)/α(−) intersubunit interface requires that the fifth subunit would be a GluClα subunit. We therefore suggest that the subunits of the recombinant heteromeric GluClα/βRs studied here assemble in an anticlockwise β-α-β-α-α fashion, as viewed from the extracellular side (Fig. 4 G and H, Right). Notably, previous studies show that expressing the heteromeric α4β2 nAChR under conditions that favor an (α4β2)₂α4 stoichiometry (three α4 and two β2 subunits) results in a receptor having two α4(+)/β2(−) interfaces with high agonist sensitivity and a third binding site at the α4(+)/α4(−) interface that displays low agonist sensitivity (59–61).

As discussed in Results, the function of heteromeric receptors containing the αL279W mutation, together with a Thr→Asn substitution in loop C of the α subunit, β subunit, or both subunits, suggests that the two intersubunit interface types, α(+)/α(−) and β(+)/α(−), likely affect each other allosterically. Possible structural reasons for this mutual allosteric influence are provided in SI Text, section 4. Interestingly, an allosteric relationship between different extracellular intersubunit interfaces was proposed for the heteromeric α1β2γ2 GABA_A receptor (62). In the latter case, conformational movements induced by benzodiazepine binding at the α/γ extracellular interface were suggested to propagate across the α1 subunit to the β/α GABA-binding site interface (62).

In the GluClα_crystR, L218 (αL279 in the full-length subunit used here) is part of the IVM-binding pocket located between M1 and M3 of adjacent subunits (23) (Fig. 4B, Left). The clear increase in the affinity of the GluClαL279W/βWT receptor for IVM (Fig. 5E; 7.5-fold) implies that the IVM-binding pockets of the heteromeric receptor are homologous to the IVM-binding pockets of the homomeric GluClα_crystR. The structural mechanism underlying the effect of the αL279W mutation in the IVM-binding site is not clear. However, the microscopic equilibrium dissociation constants for Glu binding determined here imply that the conformational change induced by this mutation in the IVM-binding pocket propagates to the Glu-binding pockets and affects their affinity for Glu. It is not known whether Glu and IVM induce the same conformational change in the coupling loops. In the heteromeric α1β2γ2 GABA_A receptor, for example, it was demonstrated that positive benzodiazepine modulators induce movements in loop F (β8β9 loop) of the γ2 subunit near the transmembrane channel domain (63). Such movements were not triggered by the binding of GABA, the allosteric modulator pentobarbital, or the inverse agonist methyl-6,7-dimethoxy-4-ethyl-β-carboline-3-carboxylate (63).

In conclusion, our study provides evidence that the C. elegans heteromeric GluClR contains three α subunits and two β subunits arranged in an anticlockwise β-α-β-α-α fashion, as viewed from the extracellular side, with two Glu-binding sites located at the β(+)/α(−) intersubunit interfaces. The α(+)/α(−) intersubunit interface creates a third “dormant” Glu-binding site that becomes functional upon a conformational change induced by a mutation in the IVM-binding pocket.

Materials and Methods

Additional experimental procedures and data analyses are described in SI Materials and Methods.

Data analysis and mathematical modeling were performed using the Clampfit 10 program implemented in pClamp 10, and GraphPad Prism software.

Dose–response curves were fitted to the data points by a nonlinear regression using the Hill equation (Eq. 1):

$$\frac{I}{I_{\text{max}}}=\frac{1}{1+{10}^{\left({\text{logEC}}_{50}-\log \left[\text{Glu}\right]\right)n_{\text{H}}}},$$ [1]

where I is the current response, I_max is the maximal current response, EC₅₀ is the agonist effective concentration that elicits 50% of the maximal current response, [Glu] is the concentration of Glu, and n_H is the Hill coefficient.

For the allosteric modeling, Eq. 2 was used:

$$P_{\text{open}}=\frac{1}{1+L{\left\{\frac{1+\left[\text{Glu}\right]/K_{\text{d},\text{R}}}{1+\left[\text{Glu}\right]/K_{\text{d},\text{R}*}}\right\}}^n},$$ [2]

where P_open is the open probability estimated at varying Glu concentrations (54) (main text). [Glu] is the concentration of the agonist (Glu) for which there are n equivalent binding sites, each with a microscopic equilibrium dissociation constant of K_d,R in the resting (closed) state and K_d,R* in the active (open) state. L is the equilibrium constant of the two states in the absence of ligands. The L values were determined by functional experiments, as described in the main text.

For a receptor phenotype that does not behave as a receptor having only n equivalent Glu-binding sites, Eq. 3 [cf. Karlin (48)] was used:

$$P_{\text{open}}=\frac{1}{1+L{\left\{\frac{1+\left[\text{Glu}\right]/K_{\text{d},\text{R}}}{1+\left[\text{Glu}\right]/K_{\text{d},\text{R}*}}\right\}}^n{\left\{\frac{1+\left[\text{Glu}\right]/{K\prime }_{\text{d},\text{R}}}{1+\left[\text{Glu}\right]/{K\prime }_{\text{d},\text{R}*}}\right\}}^m},$$ [3]

where m is the number of sites that Glu binds with microscopic equilibrium dissociation constants, K′_d,R in the closed state and K′_d,R* in the open state.