Abstract
Fusing information from different imaging modalities is crucial for more accurate identification of the brain state because imaging data of different modalities can provide complementary perspectives on the complex nature of brain disorders. However, most existing fusion methods often extract features independently from each modality, and then simply concatenate them into a long vector for classification, without appropriate consideration of the correlation among modalities. In this paper, we propose a novel method to transform the original features from different modalities to a common space, where the transformed features become comparable and easy to find their relation, by canonical correlation analysis. We then perform the sparse multi-task learning for discriminative feature selection by using the canonical features as regressors and penalizing a loss function with a canonical regularizer. In our experiments on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, we use Magnetic Resonance Imaging (MRI) and Positron Emission Tomography (PET) images to jointly predict clinical scores of Alzheimer’s Disease Assessment Scale-Cognitive subscale (ADAS-Cog) and Mini-Mental State Examination (MMSE) and also identify multi-class disease status for Alzheimer’s disease diagnosis. The experimental results showed that the proposed canonical feature selection method helped enhance the performance of both clinical score prediction and disease status identification, outperforming the state-of-the-art methods.
Keywords: Alzheimer’s disease, Feature selection, Canonical correlation analysis, Multi-class classification, Mild cognitive impairment conversion
Introduction
The world is now facing the explosion of Alzheimer’s Disease (AD) prevalence in accordance with the population aging. It is expected that about 1 out of 85 people will be affected by AD by 2050 (Brookmeyer et al. 2007; Wee et al. 2012). In this regard, it has been of great interest to investigate the pathological changes and to find biomarkers for diagnosis of AD and its prodromal stage, Mild Cognitive Impairment (MCI). For the last decade, neuroimaging has been successfully used to observe AD-related pathologies in the spectrum between cognitive normal and AD (Tang et al. 2009; Wu et al. 2006; Zhu et al. 2014b), and machine learning techniques have played core roles to analyze the complex patterns in medical image data (Li et al. 2012; Liu et al. 2012; Suk et al. 2014a, 2015b, c).
The study of computer-aided AD diagnosis via machine learning techniques often encounters the problem of so-called ‘High Dimension, Low Sample Size’ (HDLSS) (Fan et al. 2007), that is, the number of features is much larger than the number of observations. In a neuroimaging study, selecting informative features (or equivalently discarding uninformative features) has become a prevalent step before building a regression model for predicting clinical scores or a classification model for identifying the disease status (Salas-Gonzalez et al. 2010; Stonnington et al. 2010; Zhang et al. 2011; Zhang and Shen 2012). For example, (Salas-Gonzalez et al. 2010) used a t-test to select voxels of interest for binary classification, while (Stonnington et al. 2010) integrated relevance vector regression into the feature selection model for the prediction of clinical scores, such as the Alzheimer’s Disease Assessment Scale-Cognitive subscale (ADAS-Cog) and Mini-Mental State Examination (MMSE) using MR images.
Among various methods in the literature, the sparse least square regression model has shown its effectiveness for solving the HDLSS problem in many applications (Cho et al. 2012; Cuingnet et al. 2011; Hall et al. 2005; Zhang and Shen 2012; Zhu et al. 2014c; Suk et al. 2014b, 2015a). For example, (Liu et al. 2009) proposed an ℓ2,1-norm regularized regression model to select features that could be jointly used to represent multiple response variables and (Zhang and Shen 2012) applied the method for the tasks of clinical status identification and clinical scores prediction in AD diagnosis. Since the ℓ2,1-norm penalization couples the multiple response variables in finding the optimal coefficients, the sparse regression with an ℓ2,1-norm regularizer is regarded as a sparse Multi-Task Learning (MTL) method. Mathematically, the sparse MTL model is formulated as follows:
| (1) |
where Y, X, and W denote, respectively, a response matrix, a regressor matrix, and a weight coefficient matrix, and ν is a sparsity control parameter. The ℓ2,1-norm ||W||2,1 drives some rows in W to be zeros, based on which we can discard the corresponding features whose weight coefficients are zero or very small (Zhu et al. 2013b, 2014b).
Recently, the studies of neuroimaging-based AD diagnosis showed that different modalities provide different pieces of information, such as structural brain atrophy by Magnetic Resonance Imaging (MRI) (De Leon et al. 2007; Fjell et al. 2010) and metabolic alterations in the brain by Positron Emission Tomography (PET) (Morris et al. 2001; Santi et al. 2001). Moreover, it has also been shown that AD significantly affects both structures and functions of the brain (Greicius et al. 2004; Guo et al. 2010) and the utilization of data from multiple modalities can complement each other in AD diagnosis (Wang et al. 2011; Zhang and Shen 2012). In this regard, the sparse MTL method has been used for multimodality data (such as MRI and PET) to improve the performance of AD diagnosis in the literature (Cho et al. 2012; Cuingnet et al. 2011). Furthermore, recent studies on joint disease status identification and clinical scores prediction successfully used the sparse MTL in a unified framework by taking account of the clinical scores in classification and also the clinical label information in regression (Wang et al. 2011; Zhang and Shen 2012). However, it is limited for the conventional sparse MTL (Perrin et al. 2009; Westman et al. 2012) to apply for a multi-modality fusion, e.g., MRI and PET, because it does not efficiently utilize the feature correlation across modalities, which could be a good indicator for AD diagnosis.
In the spectrum between normal aging and AD, the clinical scores such as ADAS-Cog and MMSE are often used as indicators of symptom severity. However, these clinical scores are highly variable between evaluations mostly due to various psychophysical factors, thus it is very challenging to estimate them precisely. To tackle this problem, in this work, we leverage the intrinsic relation between diagnostic status and clinical scores, which measure an individual’s neurological pathology from different aspects, by means of joint estimation of all these quantities. Concretely, it is believed that the structural and functional information of a brain useful to identify disease status is also informative to predict clinical scores. Unlike existing methods in the literature that typically treat disease status classification and clinical score prediction as independent problems, we estimate them jointly, thus allowing their common information to boost each other for robust estimation. Specifically, in this paper, we propose a novel canonical feature selection method1 that efficiently integrates the relational information between modalities into a sparse MTL along with a new regularizer. Specifically, we first employ Canonical Correlation Analysis (CCA) to project the multi-modality data into a common canonical space, in which the features of different modalities become comparable to each other and thus the modality-fusion becomes more straightforward. Note that in the original feature space, the features of different modalities are inhomogeneous and it is, thus, difficult to find their relations, which may be helpful to improve classification and regression performances. We call the features projected to the common canonical space as canonical representations. We then perform a sparse MTL for feature selection2 by using the canonical representations as regressors. To further utilize their relational characteristics, we also define a new canonical regularizer that penalizes the pair of less correlated features more. With the use of the canonical representations and also a canonical regularizer, the proposed method selects canonical-cross-modality features that are useful for the tasks of clinical scores regression and clinical status identification. We validate the effectiveness of the proposed method by applying it to the tasks of regressing clinical scores of ADAS-Cog and MMSE, and identifying a multi-stage clinical status on the ADNI dataset. It is noteworthy that, unlike the previous work (Wang et al. 2011; Zhang and Shen 2012) that mostly considered binary classes such as AD vs. Normal Control (NC) or MCI vs. NC, we focus on multi-class scenarios of (1) AD vs. MCI vs. NC and (2) AD vs. MCI converter vs. MCI non-converter vs. NC for more practical applications.
Materials and image preprocessing
In this work, we use the publicly available dataset–ADNI3 for performance evaluation. The ADNI was launched in 2003 by several organizations, including the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies, and non-profit organizations. The initial goal of ADNI was to test if serial MRI, PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. To this end, over 800 adults (aged 55 to 90) participated in the ADNI research. The research protocol was approved by each local institutional review board and written informed consent was obtained from each participant.
Subjects
The general inclusion/exclusion criteria of the subjects are briefly described as follows:
The MMSE score of each NC subject is between 24 and 30, with Clinical Dementia Rating (CDR) of 0. Moreover, the NC subject is non-depressed, non MCI, and non-demented.
The MMSE score of each MCI subject is between 24 and 30, with CDR of 0.5. Moreover, each MCI subject is an absence of significant level of impairment in other cognitive domains, essentially preserved activities of daily living, and an absence of dementia.
The MMSE score of each Mild AD subject is between 20 and 26, with the CDR of 0.5 or 1.0.
We used the baseline MRI and PET data obtained from 202 subjects including 51 AD subjects, 52 NC subjects, and 99 MCI subjects.4 The detailed demographic information is summarized in Table 1.
Table 1.
Demographic information of the subjects
| AD (51) | NC (52) | MCI-C (43) | MCI-NC (56) | |
|---|---|---|---|---|
| Female/male | 18/33 | 18/34 | 15/28 | 17/39 |
| Age | 75.2 ± 7.4 | 75.3 ± 5.2 | 75.8 ± 6.8 | 74.8 ± 7.1 |
| Education | 14.7 ± 3.6 | 15.8 ± 3.2 | 16.1 ± 2.6 | 15.8 ± 3.2 |
| MMSE (baseline) | 23.8 ± 2.0 | 29.0 ± 1.2 | 26.6 ± 1.7 | 28.4± 1.7 |
| ADAS-Cog (baseline) | 18.3 ± 6.0 | 7.3 ± 3.2 | 12.9 ± 3.9 | 10.2± 4.3 |
The numbers in parentheses denote the number of subjects in each clinical category. (MCI-C: MCI Converters; MCI-NC: MCI Non-Converters)
MRI and PET
MRI
We downloaded raw Digital Imaging and COmmunications in Medicine (DICOM) MRI scans from the public ADNI website.5 The MRI scans have been reviewed for quality, and automatically corrected for spatial distortion caused by gradient nonlinearity and B1 field inhomogeneity.
PET
We downloaded the baseline PET data from the ADNI web site.6 The PET images were acquired 30–60 minutes post-injection. They were then averaged, spatially aligned, interpolated to a standard voxel size, intensity normalized, and smoothed to a common resolution of 8 mm full width at half maximum.
Image analysis
We conducted the image processing of all MR and PET images by following the same procedures in (Zhang and Shen 2012). First, we used MIPAV software7 on all images to perform anterior commissure-posterior commissure correction, and then utilized the N3 algorithm (Sled et al. 1998) to correct the intensity inhomogeneity. Second, we extracted the brains on all structural MR images using a robust skull-stripping method, by which we then conducted manual edition and intensity inhomogeneity correction (if needed). Third, we removed cerebellum based on registration and intensity inhomogeneity correction by repeating N3 algorithm three times, and then used FAST algorithm (Zhang et al. 2001) to segment the structural MR images into three different tissues: Gray Matter (GM), White Matter (WM), and CerebroSpinal Fluid (CSF). Next, we used HAMMER software (Shen and Davatzikos 2002) to conduct registration and obtained the Region-Of-Interest (ROI)-labeled image based on the Jacob template, which dissects a brain into 93 ROIs (Kabani 1998). For each of all 93 ROI regions in the labeled image of one subject, we computed the GM tissue volumes in the ROI region by integrating the GM segmentation result of this subject. And, for each subject, we first aligned the PET image to its respective MR T1 image using affine registration and then computed the average intensity of each ROI in the PET image.
Finally, for each subject, we obtained a total of 93 features from MRI and 93 features from PET.
Method
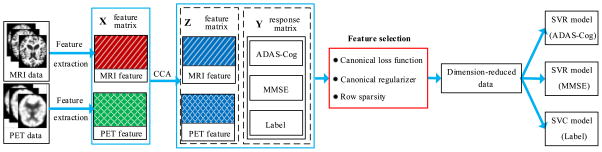
In this section, we describe the proposed canonical feature selection method that effectively integrates the ideas of CCA and sparse MTL into a unified framework. Figure 1 presents a schematic diagram of our framework for clinical scores prediction and a class label identification. Given the MRI and PET data, we first extract modality-specific features separately, preceded by the image preprocessing as described in section “Image analysis”. We then transform the features into a common space via CCA and find their canonical representations. By taking the canonical representations along with their respective clinical scores and the class labels as observations, we perform feature selection with the proposed method that integrates the newly designed canonical regularizer and an ℓ2,1-norm regularizer in sparse least square regression. We finally build clinical score regression models with Support Vector Regression (SVR) and a clinical label identification model with Support Vector Classification (SVC), respectively.
Fig. 1.
The framework of AD/MCI diagnosis with the proposed feature selection method
Notations
We denote matrices as boldface uppercase letters, vectors as boldface lowercase letters, and scalars as normal italic letters, respectively. For a matrix X = [xij], its i-th row and j-th column are denoted as xi and xj, respectively. The Frobenius norm and an ℓ2,1-norm of a matrix X are denoted as and , respectively. We denote the transpose operator, the trace operator, and the inverse of a matrix X as XT, tr(X), and X−1, respectively.
Canonical correlation analysis (CCA)
Since imaging data of different modalities can provide complementary perspectives on the complex nature of brain disorders, it is crucial to fuse information from different imaging modalities for more accurate diagnosis of the neurodegenerative disease. However, most existing fusion methods often extract features independently from each modality, and then simply concatenate them into a long vector, with no consideration of the heterogeneity in the spaces and their distributions. To cater the heterogeneous and complex feature distributions from different modalities, we seek a set of linear transforms that project the features of different modalities to a common space so that they can be comparable.
Assume that we have a number n of d-dimensional samples from two different modalities: X(1) ∈ ℝd×n and X(2) ∈ ℝd×n. Let X = [X(1), X(2)] ∈ ℝd×2n and denote a multi-modal feature matrix and its covariance matrix, respectively, where Σkl = X(k) (X(l))T and k, l = {1, 2}. To find a common space, in which we can effectively compare the features of different modalities and thus find complementary information, we exploit a CCA method (Duda et al. 2012). Specifically, it seeks two sets of basis matrices B(1) and B(2) such that the correlations between the projections of X(1) and X(2) onto the new common space spanned by these basis matrices are mutually maximized (Hardoon et al. 2004; Zhu et al. 2012):
| (2) |
where I ∈ ℝd×d is an identity matrix, l ≠ k, and i ≠ j. We can effectively solve this problem by means of a generalized eigen-decomposition (Duda et al. 2012; Zhu et al. 2012), obtaining the optimal solution (B̂(1), B̂(2)) and the corresponding correlation coefficients {λj}j=1:d, without loss of generality 1 ≥λ1 ≥λ2 ≥ … ≥λd ≥0. Although, in general, B(m) ∈ ℝd×d′, m ∈ {1, 2}, d′ = min {rank(X(1)), rank(X(2))}, we set d = d′ for simplicity in this paper. In our practical implementation of CCA, we applied a shrinkage technique for Σ11 and Σ22 to avoid a possible singularity problem.
The projections of the original features onto their respective canonical bases can be considered as new representations:
| (3) |
where , and m ∈ {1, 2}. We call these projected vectors as ‘canonical representations’. It is noteworthy that the canonical representations in the common space satisfy the following properties:
Orthogonality:
Correlation:
where 𝔼[a] denotes an expectation of a random variable a and δ(·, ·) is a Kronecker delta function.8 That is, canonical features of a modality are orthogonal to each other and the canonical features of different modalities are mutually correlated as the amount of λj in an element-wise manner.
Canonical feature selection
According to Kakade and Foster’s work (Kakade and Foster 2007), it was shown that a model can precisely fit data with the guidance of the canonical information between modalities. In this regard, we propose a new feature selection method by exploring the correlations of features of different modalities in a canonical space and also defining a new canonical regularizer. Let Y ∈ ℝc×n denote a response matrix with the number c of the response variables.9 We first formulate a sparse multi-class linear regression model in an MTL framework by using our canonical representations Z = [Z(1); Z(2)] ∈ ℝ2d×n as regressors:
| (4) |
where W ∈ ℝ2d×c is a regression coefficient matrix and β is a tuning parameter controlling the row-wise sparsity of W. It should be emphasized that, due to the ℓ21-norm regularizer in Eq. 4, we simultaneously consider both the relationships among response variables and the inter-modality relations via the canonical representations Z.
Based on the sparse MTL regression model, we further penalize the loss function with a canonical norm of the regression coefficients, by which it is encouraged to encompass multi-modal features of high correlation. A canonical norm over a vector p = [pj] ∈ ℝd is defined (Kakade and Foster 2007) as follows:
| (5) |
where {λj}j=1:d is a set of canonical correlation coefficients. The canonical norm in Eq. 5 becomes small for a vector with high correlation coefficients while it becomes large for a vector with low correlation coefficients. We utilize this characteristic in feature selection. That is, in Eq. 4, we concatenate both Z(1) and Z(2) to obtain the canonical representations Z, in which the correlated features (e.g., and ) share the correlation coefficient λj, j = 1, …, d. Note that while we use canonical representations, Eq. 4 doesn’t guarantee the correlated features to be selected jointly. To better utilize the inherent correlational information between modalities, we use the canonical norm in Eq. 5 and extend to a matrix as follows:
| (6) |
Note that two rows in W, i.e., wi and wi+d, each of which corresponds to different modalities, share the same coefficient λi.
In the canonical regularizer of Eq. 6, the correlation coefficients play a role of controlling the penalty level of the corresponding features. A small correlation coefficient penalizes less on weights and thus helps induce the corresponding features to be selected. Concretely, the proposed canonical regularizer enforces the highly correlated canonical representations of modalities, i.e., large canonical correlation coefficients, to be selected; while the merely or uncorrelated canonical representations between modalities, i.e., small canonical correlation coefficients, to be unselected. Equipped with our canonical regularizer, we define a novel canonical feature selection model as follows:
| (7) |
where β and γ are the tuning parameters. To find the optimal solution of Eq. 7, which is convex but non-smooth, we use the accelerated proximal gradient method (Zhu et al. 2013b, 2015). We summarize the implementation details of the proposed method in Algorithm 1. Please refer to Appendix A for the proof of the convergence.
Algorithm 1.
Pseudo code of the proposed method
| Input: X(1) ∈ ℝd×n, X(2) ∈ ℝd×n, Y ∈ ℝc×n, β, γ |
| Output: W |
| 1 Conduct CCA to obtain (B̂(1), B̂(2)) and λ1, …, λd |
| 2 Generate canonical representations by Eq. 3: Z = [Z(1); Z(2)] ∈ ℝ2d×n |
| 3 Define the canonical regularizer according to Eq. 6 |
| 4 Optimize Eq. 7 via Algorithm 2 in A |
Unlike the sparse MTL-based feature selection methods (Zhang and Shen 2012) that employed the least square loss function by using the original features as regressors in an ambient space, the proposed feature selection model is defined in a canonical space, in which we can naturally handle the problem of heterogeneity between different modalities. First, the canonical regularizer in Eq. 7 ensures that the larger the correlation between two features of different modalities, the smaller the penalty on the corresponding weight coefficient vector. As a result, the canonical regularizer helps keep the canonical-cross-modality features, which contain much information and benefit for improving the learning ability. Second, the canonical loss function (i.e., the first term in Eq. 7) has been discovered to better fit data achieving smaller estimation errors (Kakade and Foster 2007), than the conventional sparse MTL framework. Furthermore, the CCA converts the original features X into the canonical representations Z in a common space B, in which the concatenation of the representations in Z are more comparable than those in X, which are often heterogeneous in real applications. Therefore, the proposed model in Eq. 7 should be more predictive than the previous sparse MTL framework (Kakade and Foster 2007; McWilliams et al. 2013; Zhu et al. 2013a). Last but not least, regarding both MRI and PET data, either the conventional MTL framework or our proposed method has the same number of samples. However, the conventional MTL framework using the original multi-modality features (i.e., simply concatenating both MRI and PET into a long vector) has almost double number of features, while our proposed method aligning both MRI and PET features to the CCA space significantly reduces the number of features and more importantly the complexity of distribution of features. In this way, the conventional MTL framework makes the HDLSS issue more serious, while our proposed CCA based method helps significantly improve the performance.
Experimental results
To validate the effectiveness of the proposed method, we considered the Joint clinical scores Regression and Multi-class AD status Identification (JRMI) problem on a subset of the ADNI dataset (‘http://www.adni-info.org’), where we consider two modalities of MRI and PET. Specifically, we conducted two sets of experiments: (a) AD vs. MCI vs. NC (3-JRMI), where we regarded both MCI-C and MCI-NC as MCI, and (b) AD vs. MCI-C vs. MCI-NC vs. NC (4-JRMI). For each JRMI problem, we followed the same steps: (1) feature reduction by the competing methods; (2) learning SVR models for ADAS-Cog and MMSE, respectively, and a SVC model for disease status identification using the LIB-SVM toolbox10; (3) evaluating the performances with the metrics of Correlation Coefficient (CC) and Root Mean Squared Error (RMSE) in regression and the classification ACCuracy (ACC) in classification.
Experimental setting
We compared the proposed method with different types of conventional dimensionality reduction methods, namely, Fisher Score (FS) (Duda et al. 2012), Principal Component Analysis (PCA) (Jolliffe 2005), and CCA (Hardoon et al. 2004).
Fisher Score (FS): This method searches for a subset of features, by which the similarity between any pair of data points in different classes is large, while the similarity between any pair of data points in the same class is small.
Principal Component Analysis (PCA): This method seeks the bases such that the derived features keep maximal variance.
Canonical Correlation Analysis (CCA): This method transforms two feature matrices/variables to a common space, where they are maximally correlated.
For these three methods, we used a generalized eigen-decomposition method and determined dimensions based on the eigenvalues. For both FS and PCA, we fused the modalities of MRI and PET by concatenating their features into a single long vector before the dimensionality reduction. As for CCA, we regarded each modality of MRI and PET as separate view, and then extracted the canonical representations by maximizing the correlation of MRI and PET (Hardoon et al. 2004).
In our experiments, we also compared with the following state-of-the-art feature selection methods:
Multi-Modal Multi-Task (M3T) (Zhang and Shen 2012): This method selects a set of features that are jointly used to represent the multiple target response variables by solving Eq. 1 but using the original features as regressors.
Sparse Joint Classification and Regression (SJCR) (Wang et al. 2011): This method simultaneously uses the logistic loss function and the least square loss function along with an ℓ2,1-norm for multi-task feature selection.
For M3T and SJCR, we followed the corresponding literatures to build their feature selection models in the sparse based multi-task learning framework by using clinical scores (i.e., ADAS-Cog and MMSE) and class labels as response variables. Note that, unlike these competing methods, our method operated with canonical representations rather than the original feature vectors.
After dimension reduction or feature selection, we built one multi-class classifier and two regression models via the LIBSVM toolbox. There are two approaches for multi-class classification (Suk and Lee 2013; Zhang and Shen 2012), such as one-against-rest and one-against-one. The ‘one-against-rest’ method builds c binary classifiers (here c is the number of classes) and each binary classifier fi (i = 1, …, c) is built between the i-th class and the other (c − 1) classes, while the ‘one-against-one’ method builds binary classifiers and each binary classifier fi,j (i, j = 1, …, c) is built between the i-th class and the j-th class (i ≠ j ). With the consideration of both the computational efficiency and the training cost, in this work, we used ‘one-against-one’ approach, which classifies a test sample xte according to the following rule:
| (8) |
We applied a 10-fold cross-validation technique to compensate for the small sample size in our dataset and conducted 5-fold inner cross-validation for model selection. We repeated the process 10 times to avoid the possible bias occurring in data partitioning for cross-validation. The final performances were reported by averaging the repeated cross-validation results. We conducted a line search for model selection with β ∈ {10−5, …, 105} and γ ∈ {10−3, …, 108} in Eq. 7, and C ∈ {2−5, …, 25} for the SVR/SVC models. The parameters that resulted the best performance in the inner cross-validation were finally used in testing.
Results
Classification
Table 2 shows the classification performance for the competing methods as well as our method. The proposed method achieved the best classification performance in both 3-JRMI and 4-JRMI problems. Concisely, in the 3-JRMI problem, the proposed method improved 5.3 %, compared to SJCR that achieved the best performance among the competing methods. For the 4-JRMI problem, the classification performance improvements by the proposed method were 10.2 %, compared to FS that achieved the worst, and 6.0 %, compared to SJCR that achieved the best among the competing methods. These experimental results demonstrate that the use of canonical information, i.e., canonical representations and the canonical regularizer, in the proposed method helps improve the performances in the JRMI problems.
Table 2.
Comparison of the classification ACCuracy (ACC) of all methods with bi-modality data on 3-JRMI (the second column) and 4-JRMI (the last column), respectively
| Method | ACC (3-JRMI) | ACC (4-JRMI) |
|---|---|---|
| FS | 0.628 ± 1.30 | 0.517 ± 1.54 |
| PCA | 0.646 ± 1.59 | 0.525 ± 2.21 |
| CCA | 0.648 ± 1.81 | 0.536 ± 1.29 |
| SJCR | 0.676 ± 1.68 | 0.559 ± 1.64 |
| M3T | 0.679 ± 1.67 | 0.545 ± 1.61 |
| Proposed | 0.729 ± 1.38 | 0.619 ± 1.54 |
The boldface denotes the best performance of each column
Regression
Tables 3 and 4 show the regression performance of all the methods on the 3-JRMI and 4-JRMI, respectively. In Table 3, we can see that our method consistently achieved the best performance on both CC and RMSE in the prediction of ADAS-Cog and MMSE scores, compared to the other competing methods. For example, the proposed method obtained the CCs of 0.740 and 0.675, respectively, and the RMSEs of 3.727 and 1.800, respectively, for the prediction of ADAS-Cog and MMSE scores, respectively. The best performance among the competing methods was 0.716 (ADAS-Cog) and 0.655 (MMSE) in CC, and 4.391 (ADAS-Cog) and 2.116 (MMSE) in RMSE, respectively, while the best performance among all competing methods was 0.716 and 0.655 (CCs), and 4.336 and 2.107 (RMSEs), respectively.
Table 3.
Comparison of the regression performance of all methods with bi-modality data on 3-JRMI, i.e., AD/MCI/NC
| Methods | ADAS-Cog
|
MMSE
|
||
|---|---|---|---|---|
| CC | RMSE | CC | RMSE | |
| FS | 0.695 ± 0.16 | 5.193 ± 1.15 | 0.594 ± 0.14 | 2.290 ± 0.35 |
| PCA | 0.698 ± 0.12 | 4.988 ± 1.06 | 0.599 ± 0.13 | 2.159 ± 0.32 |
| CCA | 0.702 ± 0.22 | 44.760 ± 0.90 | 0.602 ± 0.19 | 2.107 ± 0.32 |
| SJCR | 0.716 ± 0.38 | 4.391 ± 0.86 | 0.655 ± 0.37 | 2.116 ± 0.35 |
| M3T | 0.709 ± 0.92 | 4.336 ± 0.86 | 0.647 ± 0.28 | 2.118 ± 0.34 |
| Proposed | 0.740 ± 0.18 | 3.727 ± 0.170 | 0.675 ± 0.23 | 1.800 ± 0.13 |
The boldface denotes the best performance of each column. (CC: Correlation Coefficient; RMSE: Root Mean Squared Error) Brain Imaging and Behavior
Table 4.
Comparison of the regression performance of all methods with bi-modality data on 4-JRMI, i.e., AD/MCI-C/MCI-NC/NC
| Methods | ADAS-Cog
|
MMSE
|
||
|---|---|---|---|---|
| CC | RMSE | CC | RMSE | |
| FS | 0.491 ± 0.34 | 5.759 ± 1.05 | 0.440 ± 0.16 | 2.366 ± 0.38 |
| PCA | 0.510 ± 0.56 | 5.647 ± 0.97 | 0.453 ± 0.47 | 2.390 ± 0.27 |
| CCA | 0.522 ± 0.25 | 5.531 ± 0.91 | 0.462 ± 0.53 | 2.334 ± 0.31 |
| SJCR | 0.538 ± 0.85 | 5.639 ± 0.97 | 0.493 ± 0.33 | 2.389 ± 0.30 |
| M3T | 0.521 ± 0.71 | 5.452 ± 1.01 | 0.528 ± 0.32 | 2.321 ± 0.27 |
| Proposed | 0.553 ± 0.34 | 3.926 ± 0.19 | 0.567 ± 0.23 | 1.929 ± 0.13 |
The boldface denotes the best performance of each column. (CC: Correlation Coefficient; RMSE: Root Mean Squared Error)
For the 4-JRMI problem in Table 4, compared to FS that achieved the worst, the proposed method improved by 0.062 and 1.833, respectively, in CC, and 0.127 and 0.437, respectively in RMSE, for ADAS-Cog and MMSE. Compared to M3T that achieved the best among the competing methods, the proposed method improved by 0.032 and 0.03, respectively, in CC, and 1.526 and 0.392, respectively, in RMSE, for ADAS-Cog and MMSE.
Discussion
In this section, we justify the rationale of using both the canonical loss function and the canonical regularizer. To do this, we further consider the Canonical Spare Regression (CSR for short) in Eq. 4 and summarize its performance on both 3-JRMI and 4-JRMI in Table 5. Note that CSR uses the canonical representation Z to replace the original representation X in M3T and does not have the canonical regularizer compared to our method.
Table 5.
The performance of CSR on 3-JRMI and 4-JRMI, respectively
| Tasks | ACC | CC-A | RMSE-A | CC-M | RMSE-M |
|---|---|---|---|---|---|
| 3-JRMI | 0.686 ± 1.30 | 0.719 ± 0.81 | 4.201 ± 0.82 | 0.655 ± 0.31 | 2.110 ± 0.41 |
| 4-JRMI | 0.562 ± 1.82 | 0.528 ± 0.46 | 5.007 ± 0.49 | 0.533 ± 0.48 | 2.241 ± 0.20 |
(ACC: classification ACCuracy; CC-A: Correlation Coefficient for ADAS Cog; RMSE-A: Root Mean Squared Error for ADAS Cog; CC-M: Correlation Coefficient for MMSE; RMSE-M: Root Mean Squared Error for MMSE)
From Tables 2, 3, 4 and 5, we can see that in comparison with M3T, CSR, on average, improved by about 1.2 % in classification accuracy, 0.009 and 0.007 in CC for the prediction of ADAS-Cog and MMSE, respectively, and 0.320 and 0.044 in RMSE for the prediction of ADAS-Cog and MMSE scores, respectively. This indicates that the canonical loss function outperforms the least square loss function, due to the use of the canonical representations of modalities. On the other hand, CSR is inferior to our method, by having a lower classification error of 5.0 %, lower CCs of 0.023 and 0.027 for the prediction of ADAS-Cog and MMSE, respectively, and higher RMSEs of 0.778 and 0.311 for the prediction of ADAS-Cog and MMSE scores, respectively. This supports the benefit of adding canonical information of the data into the sparse canonical feature selection framework. Specifically, the canonical information, as the penalty of variables, pushes the the regression towards to selecting useful features across the modalities.
Algorithm 2.
Pseudo code to find the solution of Eq. (7).
In this regard, we argue that the selected features by the proposed method are more powerful in predicting the target response variables than either CSR and the conventional sparse MTL-based feature selection method, i.e., M3T.
Conclusion
In this work, we focused on multi-modality feature selection for a joint regression and multi-class classification problem and proposed a canonical feature selection method by explicitly using the correlation between modalities. Specifically, we discovered canonical representations of the original inputs by projecting them into a common space spanned by the canonical bases obtained by CCA. In a sparse MTL framework, we set the regressors with our canonical representations and further penalized it with a newly defined canonical regularizer. In our experiments on the ADNI dataset, we achieved the best performances for the joint clinical scores regression and multi-class clinical status identification. Although it is not performed in this work, we would like to emphasize that the proposed method can be easily extended to more than two modalities via multi-view CCA (Hardoon et al. 2004).
Acknowledgments
This work was supported in part by NIH grants (EB006733, EB008374, EB009634, MH100217, AG041721, AG042599). Xiaofeng Zhu was supported in part by the National Natural Science Foundation of China under grant 61263035. Heung-Il Suk was supported in part by ICT R&D program of MSIP/IITP [B0101-15-0307, Basic Software Research in Human-level Lifelong Machine Learning (Machine Learning Center)]. Seong-Whan Lee was support by the National Research Foundation of Korea (NRF) grant funded by the Korea government (NRF-2015R1A2A1A05001867).
Appendix A: Convergence
In this work, we solve Eq. 7, which is a convex but non-smooth function, by designing a new accelerated proximal gradient method (Nesterov 2004). We first conduct the proximal gradient method on Eq. 7 by letting
| (9) |
| (10) |
where Q ∈ ℝ2d×2d is a diagonal matrix with the j-th diagonal element set to , j = 1, …, d. Note that f (W) is convex and differentiable, while β||W||2,1 is convex but non-smooth (Nesterov 2004). To optimize W with the proximal gradient method, we iteratively update it by means of the following optimization rule:
| (11) |
where , ∇f (W(t)) = (ZZT + γQ)W(t) − ZYT, and η(t) and W(t) are, respectively, a parameter and the value of W obtained at t-iteration.
By ignoring the terms independent of W in Eq. 11, we can rewrite it as
| (12) |
where and πη(t)(W(t)) is the Euclidean projection of W(t) onto the convex set η(t), is the stepsize and η(t) is determined by the line search (with detail given in the literature (Liu et al. 2009)). Thanks to the separability of W(t + 1) on each row, i.e., wi (t + 1), we can update the weights for each row individually:
| (13) |
where and wi (t) are the i-th row of U(t) and W(t), respectively. According to Eq. 13, wi (t + 1) takes a closed form solution (Liu et al. 2009) as follows:
| (14) |
Meanwhile, in order to accelerate the proximal gradient method in Eq. 11, we further introduce an auxiliary variable V(t + 1) as:
| (15) |
where the coefficient α(t + 1) is usually set as (Nesterov 2004). Finally, we list the pseudo of our proposed optimization method in Algorithm 2 and its convergence in Theorem 1.
Theorem 1
(Nesterov 2004) Let {W(t)} be the sequence generated by Algorithm 2, then for ∀ t ≥ 1, the following holds
where μ is a positive predefined constant, L is the Lipschitz constant of the gradient of f (W) in Eq. 10, and .
Theorem 1 shows that the convergence rate of the proposed accelerated proximal gradient method is , where t is the count number of iterations in Algorithm 2 (Nesterov 2004).
Footnotes
Compared to the preliminary version of this work that appeared in (Zhu et al. 2014a), we carried out more extensive analysis of the results on the ADNI dataset, and thus provided better insights into the proposed method.
Note that it is difficult to interpret the features selected and used for classification with the proposed ‘subspace learning’ method.
Including 43 MCI converters and 56 MCI non-converters.
In our work, the response variables correspond to ADAS-Cog, MMSE, and a multi-class label coding vector. For the multi-class label representation, we here use a 0/1 encoding scheme.
Available at ‘http://www.csie.ntu.edu.tw/~cjlin/libsvm/’
Conflict of interests Xiaofeng Zhu, Heung-Il Suk and Dinggang Shen declare that they have no conflict of interests.
Compliance with Ethical Standards
Ethical approval: We confirm that this article does not contain any studies with either human participants or animals performed by any of the authors.
Informed consent: We confirm that informed consent was obtained from all individual participants included in the study.
Contributor Information
Xiaofeng Zhu, Email: xiaofeng@med.unc.edu.
Heung-Il Suk, Email: hisuk@korea.ac.kr.
Seong-Whan Lee, Email: swlee@image.korea.ac.kr.
Dinggang Shen, Email: dgshen@med.unc.edu.
References
- Brookmeyer R, Johnson E, Ziegler-Graham K, Arrighi MH. Forecasting the global burden of Alzheimer’s disease. Alzheimer’s & Dementia : the Journal of the Alzheimer’s Association. 2007;3(3):186–191. doi: 10.1016/j.jalz.2007.04.381. [DOI] [PubMed] [Google Scholar]
- Cho Y, Seong JK, Jeong Y, Shin SY. Individual subject classification for Alzheimer’s disease based on incremental learning using a spatial frequency representation of cortical thickness data. NeuroImage. 2012;59(3):2217–2230. doi: 10.1016/j.neuroimage.2011.09.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuingnet R, Gerardin E, Tessieras J, Auzias G, Lehéricy S, Habert MO, Chupin M, Benali H, Colliot O. Automatic classification of patients with Alzheimer’s disease from structural MRI: a comparison of ten methods using the ADNI database. NeuroImage. 2011;56(2):766–781. doi: 10.1016/j.neuroimage.2010.06.013. [DOI] [PubMed] [Google Scholar]
- De Leon MJ, Mosconi L, Li J, De Santi S, Yao Y, Tsui WH, Pirraglia E, Rich K, Javier E, Brys M, Glodzik L, Switalski R, Saint Louis LA, Pratico D. Longitudinal CSF isoprostane and MRI atrophy in the progression to AD. Journal of Neurology. 2007;254(12):1666–1675. doi: 10.1007/s00415-007-0610-z. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern classification. New York: Wiley; 2012. [Google Scholar]
- Fan Y, Rao H, Hurt H, Giannetta J, Korczykowski M, Shera D, Avants BB, Gee JC, Wang J, Shen D. Multivariate examination of brain abnormality using both structural and functional MRI. NeuroImage. 2007;36(4):1189–1199. doi: 10.1016/j.neuroimage.2007.04.009. [DOI] [PubMed] [Google Scholar]
- Fjell AM, Walhovd KB, Fennema-Notestine C, McEvoy LK, Hagler DJ, Holland D, Brewer JB, Dale AM. the Alzheimer’s Disease Neuroimaging Initiative CSF biomarkers in prediction of cerebral and clinical change in mild cognitive impairment and Alzheimer’s disease. The Journal of Neuroscience. 2010;30(6):2088–2101. doi: 10.1523/JNEUROSCI.3785-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V. Default-mode network activity distinguishes Alzheimer’s disease from healthy aging: evidence from functional MRI. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(13):4637–4642. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, Wang Z, Li K, Li Z, Qi Z, Jin Z, Yao L, Chen K. Voxel-based assessment of gray and white matter volumes in Alzheimer’s disease. Neuroscience Letters. 2010;468(2):146–150. doi: 10.1016/j.neulet.2009.10.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall P, Marron J, Neeman A. Geometric representation of high dimension, low sample size data. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2005;67(3):427–444. [Google Scholar]
- Hardoon DR, Szedmak S, Shawe-Taylor J. Canonical correlation analysis: An overview with application to learning methods. Neural Computation. 2004;16(12):2639–2664. doi: 10.1162/0899766042321814. [DOI] [PubMed] [Google Scholar]
- Jolliffe I. Principal component analysis. New York: Wiley; 2005. [Google Scholar]
- Kabani NJ. 3D anatomical atlas of the human brain. NeuroImage. 1998;7:0700–0717. [Google Scholar]
- Kakade SM, Foster DP. Multi-view regression via canonical correlation analysis. Learning theory. 2007:82–96. [Google Scholar]
- Li Y, Wang Y, Wu G, Shi F, Zhou L, Lin W, Shen D. Discriminant analysis of longitudinal cortical thickness changes in Alzheimer’s disease using dynamic and network features. Neurobiology of aging. 2012;33(2):427–15. doi: 10.1016/j.neurobiolaging.2010.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Ji S, Ye J. Multi-task feature learning via efficient ℓ2,1-Norm minimization. UAI. 2009:339–348. [Google Scholar]
- Liu M, Zhang D, Shen D. Ensemble sparse classification of Alzheimer’s disease. NeuroImage. 2012;60(2):1106–1116. doi: 10.1016/j.neuroimage.2012.01.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McWilliams B, Balduzzi D, Buhmann JM. Correlated random features for fast semi-supervised learning. NIPS. 2013:440–448. [Google Scholar]
- Morris J, Storandt M, Miller J, et al. Mild cognitive impairment represents early-stage Alzheimer disease. Archives of Neurology. 2001;58(3):397–405. doi: 10.1001/archneur.58.3.397. [DOI] [PubMed] [Google Scholar]
- Nesterov Y. Introductory lectures on convex optimization: A basic course. Applied optimization. Boston: Kluwer Academic Publishers; 2004. [Google Scholar]
- Perrin RJ, Fagan AM, Holtzman DM. Multimodal techniques for diagnosis and prognosis of Alzheimer’s disease. Nature. 2009;461:916–922. doi: 10.1038/nature08538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salas-Gonzalez D, Garriz JM, Ramarez J, Illan IA, Lapez M, Segovia F, Chaves R, Padilla P, Puntonet CG. ADNI, Feature selection using factor analysis for Azheimer’s diagnosis using F18-FDG PET images. Medical Physics. 2010;37(11):6084–6095. doi: 10.1118/1.3488894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santi SD, de Leon MJ, Rusinek H, Convit A, Tarshish CY, Roche A, Tsui WH, Kandil E, Boppana M, Daisley K, Wang GJ, Schlyer D, Fowler J. Hippocampal formation glucose metabolism and volume losses in MCI and AD. Neurobiology of Aging. 2001;22(4):529–539. doi: 10.1016/s0197-4580(01)00230-5. [DOI] [PubMed] [Google Scholar]
- Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21(11):1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Transactions on Medical Imaging. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Stonnington CM, Chu C, Klöppel S, Jack CR, Jr, Ashburner J, Frackowiak RS. Predicting clinical scores from magnetic resonance scans in Alzheimer’s disease. NeuroImage. 2010;51(4):1405–1413. doi: 10.1016/j.neuroimage.2010.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk HI, Lee SW. A novel Bayesian framework for discriminative feature extraction in brain-computer interfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(2):286–299. doi: 10.1109/TPAMI.2012.69. [DOI] [PubMed] [Google Scholar]
- Suk HI, Lee SW, Shen D. Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage. 2014a;101(0):569–582. doi: 10.1016/j.neuroimage.2014.06.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk H-I, Lee S-W, Shen D. Subclass-based multitask learning for Alzheimer’s disease diagnosis. Frontiers in Aging Neuroscience. 2014b;6(168) doi: 10.3389/fnagi.2014.00168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk H-I, Lee S-W, Shen D. Deep sparse multitask learning for feature selection in Alzheimer’s disease diagnosis. Brain Structure and Function. 2015a:1–19. doi: 10.1007/s00429-015-1059-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk HI, Lee SW, Shen D. Latent feature representation with stacked auto-encoder for AD/MCI diagnosis. Brain Structure and Function. 2015b;220(2):841–859. doi: 10.1007/s00429-013-0687-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk HI, Wee CY, Lee SW, Shen D. Supervised discriminative group sparse representation for mild cognitive impairment diagnosis. Neuroinformatics. 2015c;13(3):277–295. doi: 10.1007/s12021-014-9241-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang S, Fan Y, Wu G, Kim M, Shen D. RABBIT: rapid alignment of brains by building intermediate templates. NeuroImage. 2009;47(4):1277–1287. doi: 10.1016/j.neuroimage.2009.02.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Nie F, Huang H, Risacher S, Saykin AJ, Shen L. Identifying AD-sensitive and cognition-relevant imaging biomarkers via joint classification and regression. MICCAI. 2011:115–123. doi: 10.1007/978-3-642-23626-6_15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Zhang D, Denny K, Browndyke JN, Potter GG, Welsh-Bohmer KA, Wang L, Shen D. Identification of MCI individuals using structural and functional connectivity networks. Neuroimage. 2012;59(3):2045–2056. doi: 10.1016/j.neuroimage.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westman E, Muehlboeck JS, Simmons A. Combining MRI and CSF measures for classification of Alzheimer’s disease and prediction of mild cognitive impairment conversion. NeuroImage. 2012;62(1):229–238. doi: 10.1016/j.neuroimage.2012.04.056. [DOI] [PubMed] [Google Scholar]
- Wu G, Qi F, Shen D. Learning-based deformable registration of MR brain images. IEEE Transactions on Medical Imaging. 2006;25(9):1145–1157. doi: 10.1109/tmi.2006.879320. [DOI] [PubMed] [Google Scholar]
- Zhang D, Shen D. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer’s disease. NeuroImage. 2012;59(2):895–907. doi: 10.1016/j.neuroimage.2011.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Wang Y, Zhou L, Yuan H, Shen D. Multimodal classification of Alzheimer’s disease and mild cognitive impairment. NeuroImage. 2011;55(3):856–867. doi: 10.1016/j.neuroimage.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging. 2001;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zhu X, Li X, Zhang S. Block-row sparse multiview multilabel learning for image classification. IEEE Transactions Cybernetics. 2015 doi: 10.1109/TCYB.2015.2403356. [DOI] [PubMed] [Google Scholar]
- Zhu X, Suk H-I, Shen D. Multi-modality canonical feature selection for Alzheimer’s disease Diagnosis. MICCAI. 2014a:162–169. doi: 10.1007/978-3-319-10470-6_21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Suk H, Shen D. A novel matrix-similarity based loss function for joint regression and classification in AD diagnosis. NeuroImage. 2014b;100:91–105. doi: 10.1016/j.neuroimage.2014.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Zhang L, Huang Z. A sparse embedding and least variance encoding approach to hashing. IEEE Transactions on Image Processing. 2014c;23(9):3737–3750. doi: 10.1109/TIP.2014.2332764. [DOI] [PubMed] [Google Scholar]
- Zhu X, Huang Z, Shen HT, Cheng J, Xu C. Dimensionality reduction by mixed kernel canonical correlation analysis. Pattern Recognition. 2012;45(8):3003–3016. [Google Scholar]
- Zhu X, Huang Z, Yang Y, Shen HT, Xu C, Luo J. Self-taught dimensionality reduction on the high-dimensional small-sized data. Pattern Recognition. 2013a;46(1):215–229. [Google Scholar]
- Zhu X, Huang Z, Cheng H, Cui J, Shen HT. Sparse hashing for fast multimedia search. ACM Transactions on Information Systems. 2013b;31(2):1–9. [Google Scholar]