Renal nerves dynamically regulate renal blood flow in conscious, healthy rabbits

Abstract

Despite significant clinical interest in renal denervation as a therapy, the role of the renal nerves in the physiological regulation of renal blood flow (RBF) remains debated. We hypothesized that the renal nerves physiologically regulate beat-to-beat RBF variability (RBFV). This was tested in chronically instrumented, healthy rabbits that underwent either bilateral surgical renal denervation (DDNx) or a sham denervation procedure (INV). Artifact-free segments of RBF and arterial pressure (AP) from calmly resting, conscious rabbits were used to extract RBFV and AP variability for time-domain, frequency-domain, and nonlinear analysis. Whereas steady-state measures of RBF, AP, and heart rate did not statistically differ between groups, DDNx rabbits had greater RBFV than INV rabbits. AP-RBF transfer function analysis showed greater admittance gain in DDNx rabbits than in INV rabbits, particularly in the low-frequency (LF) range where systemic sympathetic vasomotion gives rise to AP oscillations. In the LF range, INV rabbits exhibited a negative AP-RBF phase shift and low coherence, consistent with the presence of an active control system. Neither of these features were present in the LF range of DDNx rabbits, which showed no phase shift and high coherence, consistent with a passive, Ohm's law pressure-flow relationship. Renal denervation did not significantly affect nonlinear RBFV measures of chaos, self-affinity, or complexity, nor did it significantly affect glomerular filtration rate or extracellular fluid volume. Cumulatively, these data suggest that the renal nerves mediate LF renal sympathetic vasomotion, which buffers RBF from LF AP oscillations in conscious, healthy rabbits.

renal blood flow (RBF) is tightly regulated by multiple mechanisms to maintain proper kidney function. While the tubuloglomerular feedback mechanism (TGF) and myogenic response (MR) of autoregulation are widely appreciated, the importance of renal sympathetic nerve activity (RSNA) in the physiological regulation of RBF is still debated.

One side of this debate maintains that the renal nerves do not play a physiological role in RBF control based primarily on two sets of findings. The first set of findings derives from studies in which the renal nerve was electrically stimulated at varying frequencies. Substantial decreases in RBF were observed at much greater frequencies than those that caused renin release and sodium reabsorption (20, 34, 47). Such high stimulation frequencies are considered to be in the pathophysiological range of RSNA (17).

The second set of findings that opposes the importance of the renal nerves in the physiological regulation of RBF comes from a plethora of studies in which renal denervation did not affect baseline RBF (12, 30, 42). While this has been cast as a universal finding (17, 33), the literature is in fact quite mixed, with many studies finding no difference and many finding increases in RBF after renal denervation (8, 29, 39).

Both of these arguments have serious flaws. Electrical stimulation is a nonphysiological stimulus that is inherently unable to delineate between effects of physiological, pathophysiological, and supraphysiological magnitude. Moreover, studies in both physiology and anatomy argue for the exquisite selectivity and specificity of the neural control of renal function (3–5, 36). In contrast to an electrical field's indiscriminate activation of all nearby axons, reflex control of RSNA recruits specific renal postganglionic fibers in response to specific stimuli with differential effects (21). These postganglionic fibers themselves are often highly specific; individual axons may selectively innervate the tubules, vessels, or juxtaglomerular cells (4). Even the axons that innervate the juxtaglomerular arterioles can be differentiated from those that innervate the rest of the renal vasculature (36). Finally, to affect steady-state RBF, the changes in RSNA that are induced either by stimulation or denervation need to overcome powerful autoregulatory mechanisms, making such measures misleadingly insensitive.

Several convincing recent studies have challenged the dogma that RSNA does not play a role in the physiological regulation of RBF (37). In particular, chronically instrumented rats performing normal activities, such as grooming or sleeping, exhibit increases in RSNA and concomitant decreases in RBF (55). Similarly, chronic, home-cage recordings of unilaterally denervated rabbits instrumented with bilateral renal flow probes also showed significant differences in the RBF of the innervated and denervated kidney during brief elevations of heart rate (HR) and RSNA (29). These studies clearly show that changes in RSNA within the physiological range influence RBF and warrant further investigation into the role of the renal nerves in the dynamic regulation of resting RBF.

Beat-to-beat measures of cardiovascular variability (CVV) are under autonomic control and may be more sensitive to autonomic influences than mean hemodynamic measures. While mounting clinical interest in therapeutic renal denervation has precipitated numerous studies examining the effects of renal denervation on HR variability (HRV) and arterial pressure variability (APV) (44, 50), a comprehensive time-domain, frequency-domain, and nonlinear characterization of the effect of renal denervation on beat-to-beat renal blood flow variability (RBFV) has never been performed. We hypothesized that renal denervation would significantly affect RBFV. Moreover, as RBF control mechanisms can be identified by AP-RBF transfer function analysis, we hypothesized that the effect of renal denervation would impact the AP-RBF transfer function. We also tested the effect of renal denervation on glomerular filtration rate (GFR) and extracellular fluid volume (ECFV) to assess the necessity of the renal nerves in volume homeostasis in healthy rabbits.

METHODS AND MATERIALS

Animals.

Experiments were carried out on 12 male New Zealand White rabbits ranging in weight from 3.7 to 3.9 kg (Charles River Laboratories, Wilmington, MA). All experiments were reviewed and approved by the University of Nebraska Medical Center Institutional Animal Care and Use Committee.

Each rabbit underwent two separate surgeries. Under isoflurane anesthesia and positive pressure ventilation, a radiotelemetry device was implanted in the left femoral artery record AP. This was done by performing a femoral cutdown and threading a catheter attached to a radiotelemetry transducer (PA-C40, Data Sciences International, St. Paul, MN) into the abdominal aorta. The incision was closed in layers, and the rabbit was allowed to recover for at least 14 days. Rabbits were randomized to either the innervated (INV) group or the bilateral renal denervated (DDNx) group at the time of the second surgery. During the second surgery, bilateral flank incisions were made and the renal arteries and veins were carefully dissected using glass rods. In rabbits randomized to the DDNx group, the renal arteries were stripped of all visible neural tissue. In all rabbits, a 2-mm renal flow probe (2P2P, Transonics Systems, Ithaca, NY) was secured around the left renal artery using a piece of Silastic sheeting and 4-0 silk suture. The probe cable was tunneled beneath the skin and exited in the midscapular region of the rabbit. After each surgery, rabbits received a 5-day course of antibiotics (Baytril, 22.7 mg/day subcutaneously, Bayer Health Care, Shawnee Mission, KS) and 3 days of pain control via a transdermal patch (fentanyl, 25 μg/h, Mylan Pharmaceuticals, Morgantown, WV). Before any experiments, rabbits were allowed to recover for at least 14 days. At the conclusion of the experiments, denervation was validated by the absence of a renal vasoconstrictor response to the nasopharyngeal reflex as previously used by our laboratory (13, 50).

Baseline hemodynamic recordings.

Before any data was collected, rabbits were acclimated to the procedure room and a Plexiglas experiment box. The rabbits were handled almost daily until any signs of stress or excitement were absent from the animals while sitting in the box for at least 30 min. After this acclimation period, pulsatile RBF and AP were digitized at 1 kHz via a 16-channel PowerLab system (AD Instruments, Colorado Springs, CO) for at least 20 min. Artifact-free, 10-min segments from these recordings were used to perform all subsequent analysis. All sections of data were relatively stationary with regard to AP, RBF, and HR.

Beat-to-beat data extraction.

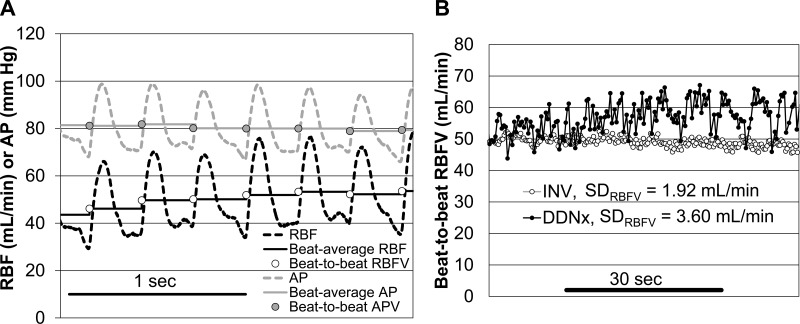
To eliminate time delays, the pulsatile AP and RBF signals were synchronized using the maximum of the cross-correlation. Pulse onsets were detected using the maximum of the second derivative of the RBF signal and were manually screened for artifacts. The pulsatile RBF and AP were averaged over each pulse, yielding beat-to-beat data used to determine RBFV and APV (Fig. 1). Pulse intervals were used for HRV analysis (45).

Fig. 1.

Beat-to-beat data extraction. A: representative tracing demonstrating the method used to extract beat-to-beat data from the time-locked renal blood flow (RBF) and arterial pressure (AP) signals. B: representative short section of beat-to-beat RBF variability (RBFV) for a sham denervated (INV) and bilateral surgical renal denervated (DDNx) rabbit showing greater RBFV in the DDNx rabbit.

Time- and frequency-domain analysis of cardiovascular variability.

Linear measures of RBFV, APV, and HRV were calculated using MATLAB (MathWorks, Natick, MA). The mean and standard deviation of the beat-to-beat data for each measure of CVV were computed. To look for differences in modality or symmetry of the beat-to-beat data, histograms of both the mean-subtracted CVV beat series and the normalized (mean 0, standard deviation 1) beat series were constructed.

For spectral analysis, the beat-to-beat data were linearly interpolated at 5.12 Hz, 50%-overlapped 256-point windows of the mean-subtracted interpolated time series were transformed into the frequency domain by Fast Fourier Transform (14), and the resulting power spectra were averaged per Welch's periodogram method (54). Based on previously published studies of RBFV and dynamic autoregulation in rabbits (28, 39), TGF operates between 0.02 and 0.08 Hz, MR operates between 0.08 and 0.20 Hz, the low-frequency (LF) band where sympathetic vasomotion gives rise to the so-called Mayer waves ranges from 0.20 to 0.46 Hz, and the high-frequency (HF) band encompassing the respiratory frequency ranges from 0.76 to 1.5 Hz. Normalized spectra were obtained by expressing power as a percentage of the total power.

Transfer function analysis.

Before transfer function analysis, APV and RBFV were high-passed filtered using a rectangular filter with 0.01 Hz corner frequency. With the use of Welch's cross-spectrogram method with the same parameters as above, transfer function gain, phase, and coherence were then estimated for RBF as a function of AP. Admittance gain was calculated by normalizing the transfer function gain by RVC.

Nonlinear analysis of RBFV.

Univariate nonlinear analysis was conducted using code publically available as part of PhysioNet (22, 48) and TISEAN (26). RBF was characterized as a strange attractor by estimating the largest Lyapunov exponent (49) and correlation dimension. The embedding space was constructed using the first minimum of the time-lagged mutual information for the time delay, and the embedding dimension was varied from 3 to 9. Analysis of the space-time separation plots showed 150 beats to be a conservative estimate of the Theiler window. Detrended fluctuation analysis was performed to characterize the self-affinity of RBF (46). Data were integrated and linearly detrended, and the root-mean-square fluctuation was calculated for boxes of lengths from 4 to 181 beats. Log-log plots of the root-mean-square fluctuation as a function of box length showed robust, steep linear behavior from 4 to 16 beats, which transitioned to a flatter, less linear region. We have denoted the slope of the log-log plot for each rabbit from 4 to 16 beats as α1, the slope from 32 to 78 beats as α2, and the box length at which the root-mean-square fluctuation crosses over from this fast (α1) to slow (α2) behavior. To estimate complexity, multiscale (MSE) entropy was computed for all scales from 1 to 39 for epoch lengths from 1 to 9 with tolerance of 0.15 (15).

Assessment of volume homeostasis and GFR.

Volume homeostasis and GFR were assessed in conscious rabbits using fluorescein-isothiocyanate (FITC)-sinistrin plasma clearance. FITC-sinistrin was purchased in a powder form (Fresenius Kabi, Linz, Austria) and diluted to 50 mg/ml aliquots in PBS and stored at −20°C. The marginal ear vein and central ear artery of the conscious rabbit were catheterized after local lidocaine infiltration. A baseline arterial blood sample (∼1.5 ml) was taken. Between 15 and 25 mg of FITC-sinistrin were given inravenously and quickly flushed with 3 ml of saline. Blood samples from the arterial catheter were collected at 3, 7, 10, 15, 45, 75, and 105 min after the FITC-sinistrin bolus. Blood samples were collected in heparinized blood tubes (Ref. 367960, Beckton-Dickinson, Franklin Lakes, NJ), stored on ice in a foam cooler, and protected from light until the end of the experiment. At the completion of the experiment, the blood samples were subjected to centrifugation at 1,000 g for 15 min. The plasma was then collected and stored at −20°C until the FITC fluorescence of the plasma samples was measured. Stored plasma samples were diluted 1:10 in PBS, and 100 μl of each diluted sample was loaded into a 96-well plate. A standard curve was generated using 0.25 mg/ml of FITC-sinistrin serially diluted 16 times. Fluorescence was measured using a TECAN Infinite M200 fluorescent plate reader using 485-nm excitation and 520 emission-nm wavelengths (51).

The fluorescence of the FITC-sinistrin standard was then used to convert the fluorescence readings of the plasma samples to FITC-sinistrin concentration. The FITC-sinistrin concentration was fitted to a two-exponential decay equation with each sample weighted by the inverse of the magnitude of the concentration. The physiological parameters of the fitted open two-compartment pharmacokinetic model (43) were derived. Specifically, GFR, the volumes of the high- and low-perfusion compartments (V_{high-perfusion} and V_{low-perfusion}, respectively), and the first-order kinetic constants between the compartments k_high→low and k_low→high and out of the system k_elim (i.e., GFR/V_{high-perfusion}) are reported. The sum of the high- and low-perfusion compartments equals the ECFV.

Study design and statistical analysis.

The study was powered to detect the effect of renal denervation on SD_RBFV observed in an independent pilot study with >95% statistical power for two-sided α = 0.05. All group data are expressed as means ± SE. Single measures were tested by Student's two-tailed, unpaired t-test, with P < 0.05 considered statistically significant. Repeated-measure indexes were tested by repeated measure analysis of variance (RM-ANOVA) with Greenhouse-Geisser corrections for sphericity. Only group differences and interactions between group and repeated measures are reported.

RESULTS

Baseline hemodynamics.

Resting baseline hemodynamics of INV and DDNx rabbits are shown in Table 1. None of the mean hemodynamic parameters differed statistically between the groups, but, of note, renal vascular conductance tended to be greater in DDNx rabbits (P = 0.10). Consistent with our paradigm, HR for both groups was around 200 beats/min, indicating calm, unstressed rabbits.

Table 1.

Baseline hemodynamics in INV and DDNx rabbits

	INV	DDNx	P
RBF, ml/min	44.1 ± 2.1	49.8 ± 3.7	0.22
MAP, mmHg	74.8 ± 3.1	70.4 ± 1.4	0.26
PI, ms	288.9 ± 6.4	290.5 ± 13.7	0.92
HR, beats/min	208.2 ± 4.8	208.5 ± 8.4	0.97
RVC, ml·min−1·mmHg−1	0.59 ± 0.02	0.70 ± 0.06	0.10

Data are presented as means ± SE, n = 6. Baseline mean hemodynamic measurements do not differ between innervated (INV) and renal denervated (DDNx) rabbits used in this study.

RBF, renal blood flow; AP, arterial pressure; PI, pulse interval of heart rate; HR, heart rate; RVC, renal vascular conductance.

Time-domain CVV results.

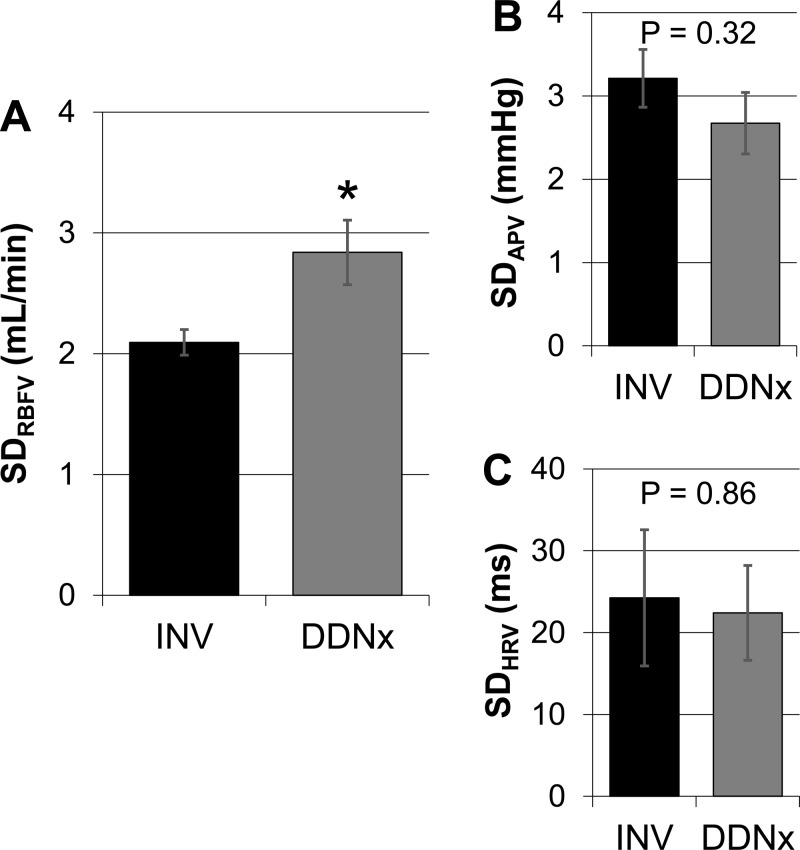
The effects of renal denervation on the standard deviation (SD) of beat-to-beat CVV are depicted in Fig. 2. Although SD_APV and SD_HRV (i.e., SD_NN) were not significantly affected by renal denervation, SD_RBFV was significantly higher in DDNx rabbits compared with INV rabbits. This suggests that physiological levels of renal nerve activity limit RBFV.

Fig. 2.

Time-domain cardiovascular variability (CVV). Chronic denervation increased standard denervation (SD) of RBFV (SD_RBFV) (A) but did not affect SD of arterial pressure variability (SD_APV) (B) or SD of HR variability (SD_HRV) (C). Values are expressed as means ± SE. *P < 0.05 vs. INV, n = 6/group.

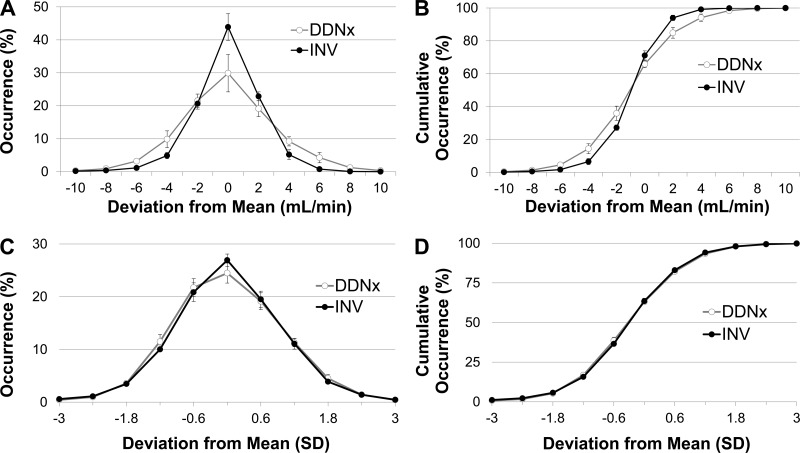
To further assess the role of the renal nerves in RBFV regulation, probability and normalized probability histograms of RBFV were constructed (Fig. 3). Denervation flattens the probability histogram and decreases the slope of the cumulative probability histogram, consistent with the finding of increased SD_RBFV in the DDNx group, but does not affect other aspects of the RBFV distribution, like skew or modality. This is emphasized by the normalized probability histograms, which show that displaying the deviations from the mean as SD instead of milliliters per minute eliminates between-group differences.

Fig. 3.

Probability and cumulative probability histograms of RBFV. INV rabbits have tighter regulation of beat-to-beat RBFV than DDNx rabbits (A and B), but normalization of the histograms by SD_RBFV shows that DDNx does not affect other aspects of the RBFV distribution, like skewness or modality (C and D).

Frequency-domain CVV results.

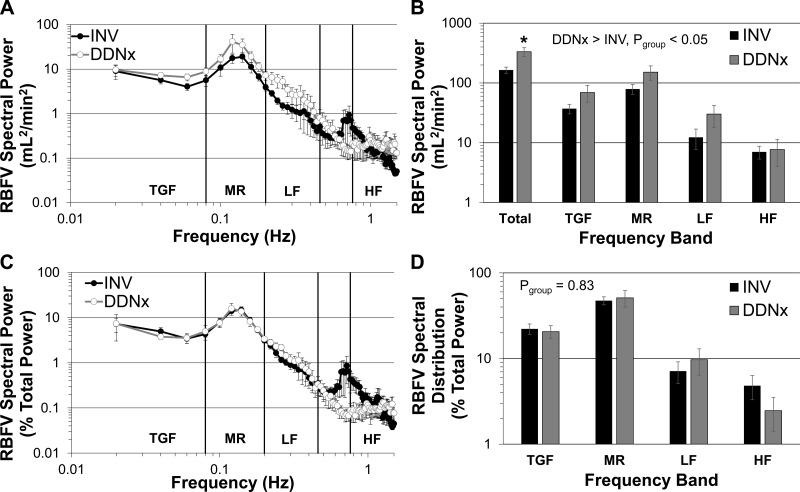
The autonomic nervous system is known to contribute to oscillations in CVV in specific frequency bands (2, 7, 52). Frequency-domain analysis of RBFV was performed to assess the contribution of the renal nerves to the RBFV spectrum (Fig. 4). DDNx rabbits had significantly increased RBFV spectral power over all frequencies with no statistical interaction between group and frequency (Fig. 4A), indicating that the spectral power, while greater after renal denervation, was not distributed differently between groups. Statistical testing of the defined frequency bands showed that renal denervation increased power over all frequency bands, but only total power was significantly higher by post hoc testing (Fig. 4B). Importantly, by Parseval's Theorem, total power is theoretically equal to the variance (i.e., SD²), and thus these observations follow logically from the increased SD_RBFV in DDNx rabbits. To specifically assess spectral distribution independent of differences in time-domain variability, spectra were normalized to total power. After normalization, no between-group differences were observed in the whole spectra or the defined frequency bands (Fig. 4, C and D). This indicates that, although the renal nerves limit the total power of RBFV, they do not selectively affect a particular frequency range. Neither raw nor normalized spectral measures of APV or HRV differed statistically between INV and DDNx rabbits (data not shown).

Fig. 4.

Power spectra of RBFV. DDNx rabbits have greater RBFV total power (A and B), but normalization to total power shows that the spectral distribution is not significantly different between INV and DDNx rabbits (C and D). *P < 0.05 vs. INV.

Transfer function results.

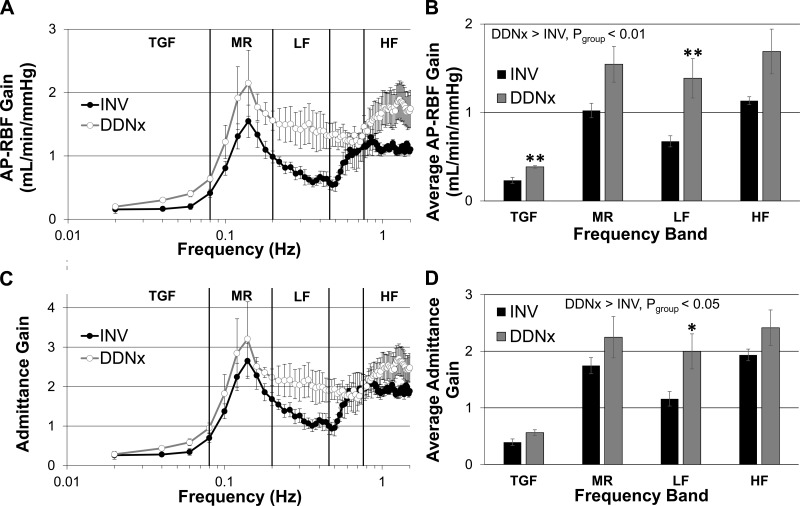
Transfer function analysis of AP-RBF is widely used to probe autoregulatory function as different physiological control mechanisms exhibit distinct transfer function signatures. We performed transfer function analysis to assess whether the observed increases in RBFV in DDNx rabbits could be explained by greater contributions of AP oscillations to RBFV. Consistent with this hypothesis, AP-RBF transfer function gain was increased in DDNx rabbits compared with INV rabbits (Fig. 5, A and B). Post hoc testing showed statistically significant increases both at the frequency range where TGF operates and in the LF range where sympathetic vasomotion is prominent.

Fig. 5.

AP-RBF gain and admittance gain. DDNx rabbits have greater AP-RBF transfer function gain, particularly in the tubuloglomerular feedback mechanism (TGF) and low-frequency (LF) bands (A and B). Similarly, admittance gain is higher for DDNx than INV rabbits with only the LF band reaching statistical significance (C and D).

It is customary to normalize the AP-RBF transfer function gain by the renal vascular conductance, yielding admittance gain, to control for static pressure-flow differences between individuals. As with AP-RBF gain, admittance gain was higher in DDNx rabbits than INV rabbits (Fig. 5, C and D). The strength of autoregulatory mechanisms is frequently estimated by the slope or the magnitude of the increase in admittance gain in the frequency range where that mechanism operates (11, 16). Neither the slope nor the magnitude of the change in admittance gain differed for TGF or MR between DDNx and INV rabbits (data not shown, P > 0.40 for all). Post hoc testing of average admittance gain showed statistical differences between INV and DDNx rabbits only in the LF region, although the TGF frequency band was close to statistical significance (P = 0.051). This indicates that the renal nerves attenuate the effect of AP oscillations on RBF, particularly in the LF range.

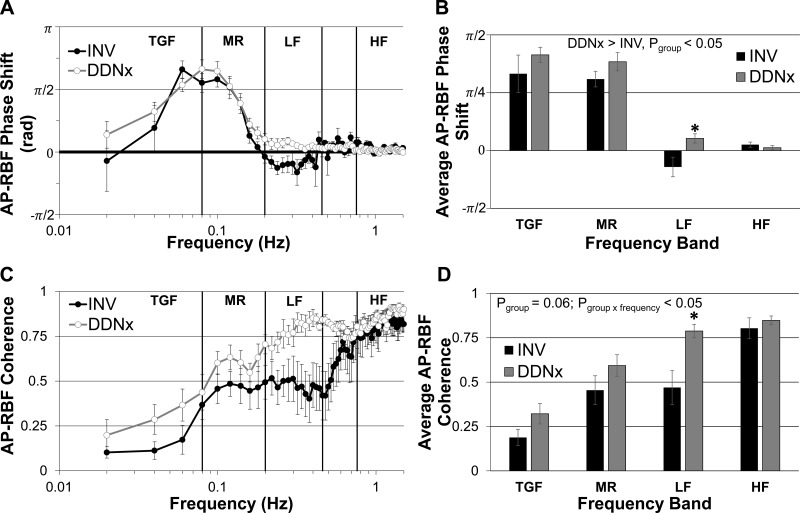
Transfer function phase shift also gives important insight into the nature of physiological control systems. A positive AP-RBF phase shift indicates an active control system that modulates renal vascular conductance in response to changes in RBF (e.g., TGF, MR). A negative AP-RBF phase shift could indicate either an active control system that responds to changes in AP (e.g., the baroreflex) or an active system that lags behind AP oscillations (e.g., if the renal vasculature responds more slowly than other vascular beds to synchronized sympathetic nerve activity). A phase shift of zero is characteristic of a passive system (i.e., Ohm's law). The TGF and MR phase peaks, indexes of the strength of these autoregulatory mechanisms, did not differ statistically between INV and DDNx rabbits. Interestingly, in the LF band, INV rabbits showed a negative phase peak and a significantly lower phase shift than DDNx rabbits while no other band showed a statistically significant phase difference (Fig. 6, A and B). This LF phase shift in INV rabbits corresponds to a time lag of ∼200 ms. This negative phase signature was absent in the DDNx rabbits, whose phase shifts simply decayed to zero after the positive MR phase peak. This indicates that, in healthy, conscious rabbits, the renal nerves exert an influence on renal vascular conductance in the LF region which lags behind LF oscillations in AP.

Fig. 6.

AP-RBF phase shift and coherence. INV rabbits show a negative phase shift in the LF band, which is absent in DDNx rabbits (A). The average LF phase shift is significantly different between INV and DDNx rabbits (B). INV and DDNx rabbits have very different coherence plots with DDNx rabbits showing greater coherence in the LF range (C and D).

Coherence, the frequency-domain analog of correlation, measures the strength of the linear, time-invariant relationship between AP and RBF. AP-RBF coherence showed a statistically significant group × frequency band interaction, with DDNx rabbits exhibiting greater coherence in the LF band than INV rabbits (Fig. 6, C and D). This indicates that the renal nerves decrease the strength of the linear, time-invariant relationship between AP and RBF in the LF band, highlighting the importance of renal sympathetic vasomotion on the AP-RBF transfer function in this frequency range.

Nonlinear results.

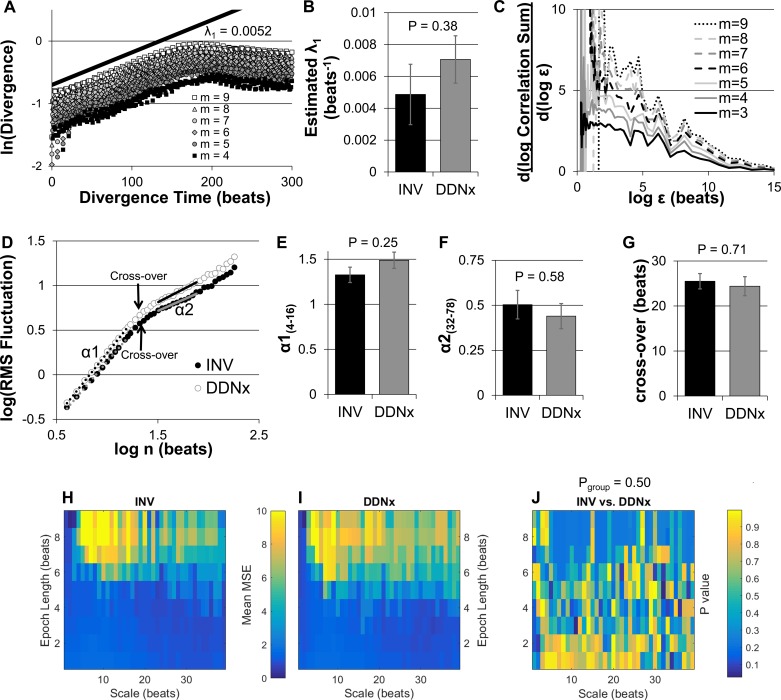
Others have characterized RBF as a strange, chaotic attractor (53). We performed a similar characterization of RBF in INV and DDNx rabbits by calculating the largest Lyapunov exponent, a measure of chaotic behavior, and the correlation dimension, a fractal dimension of the attractor. As shown in Fig. 7A, semilog plots of the divergence of nearest neighbors in the embedding space as a function of time showed robust, positive linear behavior that was stable as embedding dimension was varied, which is consistent with chaos. Fitting the slope of this exponential divergence yields an estimate of the largest Lyapunov exponent, which did not differ significantly between INV and DDNx rabbits (Fig. 7B). Correlation dimension is estimated by identifying a plateau in the slope of the log-log plot of the correlation sum as a function of neighborhood size that is stable across multiple embedding dimensions, but no such plateau existed for any of the rabbits (Fig. 7C).

Fig. 7.

Nonlinear analysis of RBFV. A representative semilog plot shows robust exponential divergence of nearest neighbors in an RBFV embedding space, which is consistent for multiple embedding dimensions (A). Linear fitting such plots shows no differences in the estimated λ₁ between INV and DDNx rabbits (B). Attempts to characterize the correlation dimension of RBFV failed to show a consistent plateau with increasing embedding dimensions (C). Log-log plots of the root-mean-square (RMS) fluctuation for INV and DDNx rabbits show linear behavior for both short (α1, 4 to 16 beats) and long box lengths (α2, 32–78 beats), indicative of self-affinity. The slopes of the log-log plot for short box lengths (E), long box lengths (F), and the scale at which the crossover from α1 to α2 behavior occurred (G) were not statistically different between INV and DDNx rabbits. Multiscale sample entropy (MSE) for scales from 1 to 39 beats and epoch lengths from 1 to 9 beats for INV (H) and DDNx (I) rabbits was not statistically different (J). λ₁, largest Lyapunov exponent; m, embedding dimension; ε, neighborhood size; n, box length; RMS, root-mean-square.

The absence of saturation of the estimated correlation dimension as embedding dimension is increased and the power-law behavior of the RBFV power spectrum are highly suggestive of a self-affine fractal. Characterization of the self-affinity using detrended fluctuation analysis showed linear relationships on the log-log plot of the root-mean-square fluctuation as a function of box length. For box lengths of 4 to 16 beats, which correspond to frequencies faster than the autoregulatory range, the log-log plot for both INV and DDNx rabbits were robustly linear (R > 0.99) with a slope (α1) of around 1.5, indicative of Brownian noise (Fig. 7, D and E). At longer box lengths, the log-log plot crossed over to a less linear (0.90 < R < 0.99) and less steep region. For box lengths of 32 to 78 beats, this slope (α2) for both INV and DDNx rabbits was ∼0.5, consistent with white noise and the flat RBFV power spectra in the autoregulatory range (Fig. 7F). The log-log slopes for short box lengths, long box lengths, and the box length at which the transition between the two behaviors occurred did not significantly differ between INV and DDNx rabbits (Fig. 7, E–G).

Finally, we calculated multiscale entropy of RBFV for varying epoch lengths to characterize the contribution of the renal nerves to the complexity of RBFV. As shown in Fig. 7, H and I, the mean multiscale entropy for INV and DDNx rabbits shows very similar patterns, and Fig. 7J shows that that there is no clustering or robust patterns in the statistical difference between groups at various scales or epochs. In fact, of the 351 scale-epoch combinations, only two reached P < 0.05, neither of which was statistically significant after liberally correcting for multiple comparisons by the Benjamini-Hochberg false discovery rate procedure. In summary, the renal nerves do not appear to significantly affect the exponential divergence, self-affinity, or complexity of RBFV.

Volume homeostasis and glomerular filtration rate.

The classical rationale for the tight regulation of RBF by multiple mechanisms is that RBF must be kept constant to maintain GFR and volume homeostasis. We assessed the effect of renal denervation on GFR and ECFV. The results for all of the physiological descriptors of the fitted two-compartment model are displayed in Table 2. There were no statistically significantly differences between the DDNx and INV groups for GFR, ECFV, the compartment volumes, or the kinetic constants. This suggests that the renal nerves are not necessary for the physiological maintenance of GFR and ECFV in unstressed, healthy rabbits, paralleling the lack of statistically significant effects on steady-state parameters such as mean RBF.

Table 2.

Parameters from two-compartment FITC-sinistrin pharmacokinetics

	INV	DDNx	P
GFR, ml/min	11.2 ± 0.5	10.6 ± 2.0	0.78
ECFV, ml	604.3 ± 28.8	549.7 ± 59.8	0.44
Vhigh-perfusion, ml	242.7 ± 11.6	261.1 ± 32.8	0.62
Vlow-perfusion, ml	361.7 ± 20.8	288.6 ± 37.8	0.31
kelim, min−1	0.047 ± 0.004	0.04 ± 0.002	0.13
khigh→low, min−1	0.083 ± 0.007	0.073 ± 0.010	0.41
klow→high, min−1	0.057 ± 0.005	0.068 ± 0.012	0.43

Data are presented as means ± SE, n = 6. V_{high-perfusion} and V_{low-perfusion}, volumes of high- and low-perfusion compartments, respectively; k, first-order kinetic constant. Renal denervation did not significantly affect any physiological parameters derived from two-compartment modeling of the fluorescein isothiocyanate (FITC)-sinistrin plasma decay, including glomerular filtration rate (GFR) and extracellular fluid volume (ECFV).

DISCUSSION

The aim of this study was to characterize the physiological role of the renal nerves on RBFV. We acquired resting baseline recordings of well-acclimatized, conscious rabbits after bilateral chronic renal denervation or sham procedure to eliminate spurious influences of surgical stress, short-term excitations, or anesthesia. We found that the renal nerves decrease RBFV and significantly affect the gain, phase, and coherence of the LF region of the AP-RBF transfer function. Steady-state measures of hemodynamics and volume homeostasis were not statistically affected by renal denervation.

To the best of our knowledge, this is the first report of the effects of renal denervation on time- and frequency-domain measures of calibrated beat-to-beat RBF. A previous study in anesthetized rats showed that acute renal denervation tended to flatten the RBF probability distribution for both Wistar-Kyoto and Sprague-Dawley rats, although this study used linearly downsampled instead of beat-to-beat RBF data and did not compare any parameters of RBFV (such as SD) before and after renal denervation (18). In another study in rabbits, mean RBF was increased but the coefficient of variation (i.e., SD/mean) of beat-to-beat RBF did not differ after renal denervation, possibly indicating an increase in the SD in this study (29). The same study also found a slight difference in the normalized RBF spectra after chronic renal denervation, but both of these findings are complicated by the inability of the Doppler flow probes used at the time to be calibrated to raw RBF (i.e., all flows are measured in kHz instead of ml/min). A subsequent study from the same group using superior transit-time flow probes also computed normalized RBF spectra and, similar to our study, found that renal denervation did not affect RBF spectral distribution; however, this study did not report raw RBF power (39). These results are consistent with our observations that the renal nerves of normal animals decrease time-domain RBFV without significantly affecting the RBFV spectral distribution.

Taken together, our findings concerning the influence of the renal nerves on the AP-RBF transfer function indicate that, in conscious rabbits, the renal nerves mediate LF renal sympathetic vasomotion which buffers RBF from LF AP oscillations. This observation could be explained under the two theories concerning the origin of sympathetic LF AP oscillations (i.e., the so-called Mayer waves) (31, 38). The first theory holds that these LF AP oscillations are a manifestation of resonance arising from time delays in the sympathetic baroreflex arc. The second theory holds that LF AP oscillations occur due to a central oscillator that creates LF sympathetic nerve activity rhythms that, in turn, produce LF oscillations in total peripheral resistance and thus pressure. Regardless of which theory is correct, removal of this sympathetic vasomotion from a single vascular bed would increase LF admittance gain via a vascular steal phenomenon. Indeed, we observed higher admittance gain in the LF range of DDNx rabbits. Similarly, removal of this sympathetic vasomotion would result in passive (i.e., Ohm's law) behavior of the AP-RBF transfer function with a phase shift of zero and high coherence which, again, corresponds to the near-zero LF AP-RBF phase shift and elevated LF coherence observed in DDNx rabbits. The negative LF AP-RBF phase shift in INV rabbits could be characteristic of a baroreflex, as hypothesized for the mesenteric circulation (1), or it could be due to the fact that the renal circulation responds more slowly to synchronized sympathetic outflow than the vascular beds which have a larger influence on total peripheral resistance (23).

The effect of renal denervation on the AP-RBF relationship has been assessed in three other studies (1, 18, 39). One study in anesthetized rats showed that acute renal denervation of either Wistar-Kyoto or spontaneously hypertensive (SH) rats increased the AP-RBF admittance gain in frequencies above the autoregulatory range (1). Coherence was not reported, but the authors found that acute renal denervation did not affect the AP-RBF phase shift. Similarly, a study in conscious rabbits showed that chronic denervation increased AP-RBF gain and coherence without affecting phase shift (39). Both of these studies corroborate our finding that the renal nerves attenuate the effects of AP oscillations on RBF but differ in their findings on phase shift. The latter study also supports our finding that the renal nerves decrease the strength of the linear relationship between AP and RBF. The third study, performed on four different groups of anesthetized rats, failed to show statistical differences in AP-RBF gain or coherence after acute renal denervation of Wistar-Kyoto, Sprague-Dawley, or chronic heart failure rats. SH rats showed a contradictory attenuation of AP-RBF gain and a concordant increase in AP-RBF coherence after acute renal denervation(18). This study also found differences in AP-RBF phase shift in Sprague-Dawley and SH rats, but not Wistar-Kyoto or chronic heart failure rats after renal denervation.

One novel finding of our study is the negative phase shift in the LF range of the AP-RBF transfer function of INV, but not DDNx, rabbits. In mice, the LF range of the AP-RBF transfer function shows a negative phase shift that can be abolished by systemic administration of the calcium channel blocker amlodipine (27). The origin of this control mechanism has interested others but remains unknown (16); we propose that it is mediated by the renal nerves. In some conscious and anesthetized rats, a negative LF AP-RBF phase shift has been reported (1, 35). By contrast, the mesenteric circulation, a classic resistance bed, shows a negative phase shift in all rats which, consistent with our data, is abolished by denervation (1). Denervation of the mesenteric circulation in rats also increases admittance gain in the LF range, again consistent with our observation in the renal circulation. While autoregulatory mechanisms operate at the same frequencies in all species, the period of the Mayer waves varies with the cardiac cycle frequency. In dogs and humans, the LF band (0.04–0.15 Hz) overlaps completely with autoregulatory mechanisms, which may overshadow the influence of the renal nerves on RBF.

Our study differs from previous rabbit studies in two ways that may have helped us to expose a negative LF AP-RBF phase signature in INV rabbits. First, we were very stringent about our animal acclimation and data selection process to avoid the influence of excitations. Excitations may result in renal sympathetic vasomotion that is pressure-independent, driving the LF AP-RBF phase shift to zero. Indeed, it appears that the role of the renal nerves in regulating RBF in the resting state is very different from that during episodic excitations, which were the focus of a previous well-conducted study (6). Second, our signal processing parameters were different from previous studies and were chosen to maximize the signal-to-noise ratio in the LF range.

Two other relevant studies have examined the effect of systemic sympatholysis on the AP-RBF transfer function in conscious animals. One study used hexamethonium in dogs (32) while the other used rilmenidine in rabbits (28). Neither study found a significant change in the AP-RBF transfer function after systemic sympatholysis, but this finding is confounded by the fact that both drugs eliminate not only renal sympathetic vasomotion but also sympathetic LF AP oscillations. As our data indicate that the main effect of the renal nerves on the AP-RBF relationship stems from their interaction with these sympathetic LF AP oscillations, we would not expect global sympatholysis to strongly affect the renal pressure-flow relationship.

One might hypothesize that the removal of one RBF control mechanism would increase the strength of others. Despite this, we did not find an increase in indexes of the strength of TGF or MR (i.e., slope of increase in admittance gain, total change in admittance gain, phase peak) between INV and DDNx rabbits. We observed a strong trend for higher average admittance gain over the TGF range of DDNx rabbits, which may indicate an effect of the renal nerves on TGF. But, beyond the lack of a statistical basis to make any strong conclusions on this matter, TGF is also notoriously difficult to assess by dynamic autoregulation (16). While further studies using proximal tubular perfusion to assess TGF in INV and DDNx animals would be interesting, it is also very possible that the classic autoregulatory mechanisms become more active but not stronger to maintain steady-state RBF after renal denervation. In addition, renin-angiotensin system blockade by angiotensin-converting enzyme inhibition increases admittance gain in the TGF band in both anesthetized rats (25) and conscious rabbits (28), and the removal of sympathetically mediated renin release is a possible explanation for this similar trend in our study.

Our nonlinear characterization of RBFV did not reveal differences between INV and DDNx rabbits based on measures of chaos, self-affinity, or complexity. A previous study indicated that RBF behaves as a chaotic strange attractor (53), but we were not able to identify a stable estimate of correlation dimension indicative of a strange attractor. We did, however, find that RBFV demonstrated consistent exponential divergence, but in the absence of a valid estimate of correlation dimension, this likely is not to be due to traditional, low-dimensional deterministic chaos. The presence or absence of the renal nerves did not significantly affect this exponential divergence. Similarly, the renal nerves did not significantly affect the self-affinity of renal blood flow variability at the scales we measured. Some investigators have shown self-affinity at much longer scales (41), which we were not able to resolve with our short-term recordings, and we are not able to make any conclusions about the role of the renal nerves in long-term self-affinity. Finally, nonlinear complexity of RBFV as quantified by sample entropy over multiple scales and epoch lengths did not differ significantly between INV and DDNx rabbits.

Recent results from clinical trials and classic studies in conscious dogs have shown that chronic removal of the renal nerves does not affect estimates of GFR (8, 9), indicating that the renal nerves are not necessary for long-term regulation of GFR. Our studies would agree with this observation as DDNx rabbits did not appear to have alterations in GFR. We also did not find a statistically significant effect of renal denervation on ECFV, indicating the renal nerves may not necessary for long-term fluid volume regulation in healthy rabbits with free access to food and water. This is an interesting finding, given that the renal nerves are thought to increase sodium reabsorption at relatively low levels of activation (20). This could corroborate the idea that compensatory mechanisms mask the physiological role of the renal nerves on steady-state parameters, but we hesitate to make strong conclusions about these unpowered observations.

Along these lines, we wanted to make an important point about the power of our study. As presented in the introduction, the literature is mixed regarding the effect of renal denervation on mean RBF. Our study is not powered to test the hypothesis that the renal nerves have a physiological effect on mean RBF. Based on the variability of mean RBF observed in our study, renal denervation would need to affect mean RBF by at least 13.2 ml/min (26.5%) for a study of this size to have an 80% chance of detecting the effect. Thus our study is not sensitive to moderate physiological effect sizes on RBF. This problem is widespread in the literature, and we are not aware of any study that performed a prospectively powered test of the hypothesis that the renal nerves have a physiological effect on mean RBF in healthy animals. While our underpowered hypothesis testing cannot tell us whether or not renal denervation itself affects RBF, our data indicate that any effect of renal denervation on mean RBF is much smaller than its effects on dynamic measures of RBF.

The present study has several limitations. First, RSNA was not recorded in INV rabbits, and the addition of this parameter would certainly have added valuable insight to this study. Several studies have examined the RSNA-RBF transfer function by different methods (19, 24, 29). Second, biological input-output relationships are never completely linear and time invariant as assumed by the Welch method for transfer function estimation. Since such analysis is a mainstay in studies focusing on the particularly nonlinear frequency ranges involved in autoregulation (10), the assumption of linearity appears acceptable for our study of short-term variability. More sophisticated nonlinear analysis of renal autoregulation has been championed by some in the field (40), but the techniques used for such studies (i.e., pseudorandom forcing of AP) are problematic as they are generally performed only after renal denervation to obviate the confounding reflex vasoactive effects of the renal nerves. Additionally, more sophisticated, dynamic measures of sodium excretion and urine flow may have better demonstrated the role of the renal nerves in the regulation of volume homeostasis and GFR where our steady-state measures did not.

Perspectives and Significance

Many studies have failed to show an effect of renal denervation on steady-state RBF, leading to the belief that the renal nerves do not regulate RBF in resting, healthy animals. Using dynamic analysis of RBF, however, we show that renal denervation increases beat-to-beat variability of RBF in resting, healthy rabbits.

Using transfer function analysis, we show that renal denervation results in the loss of an active control mechanism in the LF range where sympathetic vasomotion is prominent. This LF renal sympathetic vasomotion buffers RBF from LF AP oscillations.

Despite notable differences in dynamic measures, renal denervation did not statistically affect steady-state measures such as RBF, GFR, and volume status.

Our study indicates that the renal nerves regulate RBF on a beat-to-beat basis and cautions against using steady-state measures to draw conclusions about physiological parameters which are dynamically regulated by multiple control mechanisms.

GRANTS

This work was supported by a National Institutes of Health National Heart, Lung, and Blood Institute (NIH NHLBI) Grant P01 HL62222. A. M. Schiller was partially supported by an American Heart Association predoctoral fellowship, and P. R. Pellegrino was partially supported by a NIH NHLBI F30 predoctoral fellowship.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.M.S. and P.R.P. performed experiments; A.M.S. and P.R.P. analyzed data; A.M.S. and P.R.P. interpreted results of experiments; A.M.S. and P.R.P. prepared figures; A.M.S. and P.R.P. drafted manuscript; A.M.S., P.R.P., and I.H.Z. edited and revised manuscript; A.M.S., P.R.P., and I.H.Z. approved final version of manuscript; P.R.P. and I.H.Z. conception and design of research.