Exciton diamagnetic shifts and valley Zeeman effects in monolayer WS₂ and MoS₂ to 65 Tesla

Abstract

In bulk and quantum-confined semiconductors, magneto-optical studies have historically played an essential role in determining the fundamental parameters of excitons (size, binding energy, spin, dimensionality and so on). Here we report low-temperature polarized reflection spectroscopy of atomically thin WS₂ and MoS₂ in high magnetic fields to 65 T. Both the A and B excitons exhibit similar Zeeman splittings of approximately −230 μeV T⁻¹ (g-factor ≃−4), thereby quantifying the valley Zeeman effect in monolayer transition-metal disulphides. Crucially, these large fields also allow observation of the small quadratic diamagnetic shifts of both A and B excitons in monolayer WS₂, from which radii of ∼1.53 and ∼1.16 nm are calculated. Further, when analysed within a model of non-local dielectric screening, these diamagnetic shifts also constrain estimates of the A and B exciton binding energies (410 and 470 meV, respectively, using a reduced A exciton mass of 0.16 times the free electron mass). These results highlight the utility of high magnetic fields for understanding new two-dimensional materials.

The spin and valley degrees of freedom are coupled in two-dimensional transition-metal dichalcogenides. Here, the authors use high magnetic fields to optically measure the valley Zeeman effect and diamagnetic exciton shift in tungsten disulphide and molybdenum disulphide, and determine the exciton binding energies.

Atomically thin crystals of the transition-metal disulphides (MoS₂ and WS₂) and diselenides (MoSe₂ and WSe₂) constitute a novel class of monolayer semiconductors that possess direct optical bandgaps located at the degenerate K and K′ valleys of their hexagonal Brillouin zones¹,². The considerable recent interest in these two-dimensional (2D) transition-metal dichalcogenides (TMDs) derives from their strong spin–orbit coupling and lack of structural inversion symmetry, which, together with time-reversal symmetry, couples spin and valley degrees of freedom and leads to valley-specific optical selection rules³,⁴,⁵,⁶,⁷,⁸: light of σ⁺ circular polarization couples to inter-band exciton transitions in the K valley, while the opposite (σ⁻) circular polarization couples to transitions in the K′ valley. The ability to populate and/or probe electrons and holes in specific valleys using polarized light has renewed long-standing interests⁸,⁹,¹⁰,¹¹ in understanding and exploiting such ‘valley pseudospin' degrees of freedom for both fundamental physics and far-reaching applications in, for example, quantum information processing.

The bands and optical transitions at the K and K′ valleys are nominally degenerate in energy and related by time-reversal symmetry. However, in analogy with conventional spin degrees of freedom, this K/K′ valley degeneracy can be lifted by external magnetic fields B, which break time-reversal symmetry. Recent photoluminescence studies of the monolayer diselenides MoSe₂ and WSe₂ in modest fields have indeed demonstrated this ‘valley Zeeman effect', and revealed an energy splitting between σ⁺ and σ⁻ polarized photoluminescence from the lowest-energy ‘A' exciton transition¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷. In most cases, valley splittings in these monolayer diselenides were found to increase linearly with field at a rate of approximately −4μ_B (≡−232 μeV T⁻¹), where μ_B=57.9 μeV T⁻¹ is the Bohr magneton. While this value agrees surprisingly well with simple expectations from a two-band tight-binding model (namely, that electron and hole masses are equal, and that the exciton Zeeman shifts derive solely from the hybridized 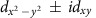atomic orbitals with magnetic moment ±2μB that comprise the K/K′ valence bands¹²,¹³,¹⁴,¹⁵), it is also widely appreciated that a more complete treatment based on established k·p theory should, with proper inclusion of strong excitonic effects, also provide an accurate description. However, initial k·p models have so far had limited success accounting for the measured valley Zeeman effect in monolayer TMDs¹²,¹⁶,¹⁸,¹⁹.

Regardless of circumstances, magneto-optical studies of these new monolayer semiconductors are still at a relatively early stage, and several outstanding questions remain. In particular, measurements of valley Zeeman effects in the monolayer disulphides WS₂ and MoS₂ have not been reported to date, which would provide a natural complement to the existing data on monolayer WSe₂ and MoSe₂. In addition, the valley Zeeman splitting of the higher-energy ‘B' exciton has not yet been reported in any of these 2D materials. Both of these studies would provide a more complete experimental basis against which to benchmark new theoretical approaches. And finally, the diamagnetic energy shift of these excitons, which is anticipated to increase quadratically with field and from which the spatial extent of the fundamental (1s) exciton wavefunctions can be directly inferred²⁰,²¹,²², has not yet been observed in any of the monolayer TMDs. Likely, this is because the diamagnetic shift, ΔE_dia=e²〈r²〉_1sB²/8m_r, is expected to be very small and difficult to spectrally resolve in these materials owing to the small root mean squared (r.m.s.) radius of the 1s exciton 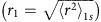, and large reduced mass 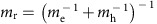. For example, if r₁≈1.5 nm and m_e=m_h≈m₀/2 (where m₀ is the bare electron mass and m_e/h is the effective electron/hole mass), then ΔE_dia is only ∼20 μeV at B=10 T, clearly motivating the need for large magnetic fields. Crucially, knowledge of ΔE_dia can also constrain estimates of the exciton binding energy—a subject of considerable recent interest in the monolayer TMDs²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³²,³³,³⁴,³⁵, wherein the effects of non-local dielectric screening and Berry curvature can generate a markedly non-hydrogenic Rydberg series of exciton states and associated binding energies³⁶,³⁷,³⁸,³⁹,⁴⁰.

In the following, we address these questions with a systematic study of circularly polarized magneto-reflection from large-area films of monolayer WS₂ and MoS₂ at low temperatures (4 K) and in very high pulsed magnetic fields up to 65 T. Clear valley splittings of about −230 μeV T⁻¹ are observed for both the A and B excitons, providing measurements of the valley Zeeman effect and associated g-factors in monolayer transition-metal disulphides. Moreover, due to the very large magnetic fields used in these studies, we are also able to resolve the small quadratic diamagnetic shifts of both A and B excitons in monolayer WS₂ (0.32±0.02 and 0.11±0.02 μeV T⁻², respectively), permitting estimates of the r.m.s. exciton radius r₁. These results are compared with similar measurements of bulk WS₂ crystals, and are quantitatively modelled within the context of the non-hydrogenic binding potential²³,³⁶,³⁷ that is believed to exist in 2D semiconductors due to non-local dielectric screening. Within this framework, we estimate A and B exciton binding energies of ∼410 and ∼470 meV, respectively, and we show how these values scale with reduced mass m_r.

Results

Samples and experimental set-up

Large-area samples of monolayer WS₂ and MoS₂ were grown by chemical vapour deposition on SiO₂/Si substrates⁴¹,⁴². MoO₃ and pure sulphur powder were used as precursor and reactant materials, respectively, and the growth was performed at a reactant temperature of 625 °C. In addition, perylene-3,4,9,10-tetracarboxylic acid tetrapotassium salt was loaded on the SiO₂/Si substrate, which acted as a seeding promoter to achieve uniform large-area monolayer crystals⁴³. The monolayer nature and high quality of these samples were confirmed by photoluminescence and Raman studies⁴² (Supplementary Figs 1–5 and Supplementary Notes 1–5). In addition, a freshly exfoliated surface of a bulk WS₂ crystal was also prepared.

Magneto-reflectance studies were performed at cryogenic temperatures (down to 4 K) in a capacitor-driven 65 T pulsed magnet at the National High Magnetic Field Laboratory in Los Alamos. Broadband white light from a xenon lamp was coupled to the samples using a 100 μm diameter multimode optical fibre. The light was focused onto the sample at near-normal incidence using a single aspheric lens, and the reflected light was refocused by the lens into a 600 μm diameter collection fibre. A thin-film circular polarizer mounted over the delivery or collection fibre provided σ⁺ or σ⁻ circular polarization sensitivity. The collected light was dispersed in a 300 mm spectrometer and detected with a charge-coupled device detector. Spectra were acquired continuously at a rate of 500 Hz throughout the ∼50 ms long magnet pulse.

Exciton transitions and Zeeman effects in monolayer TMDs

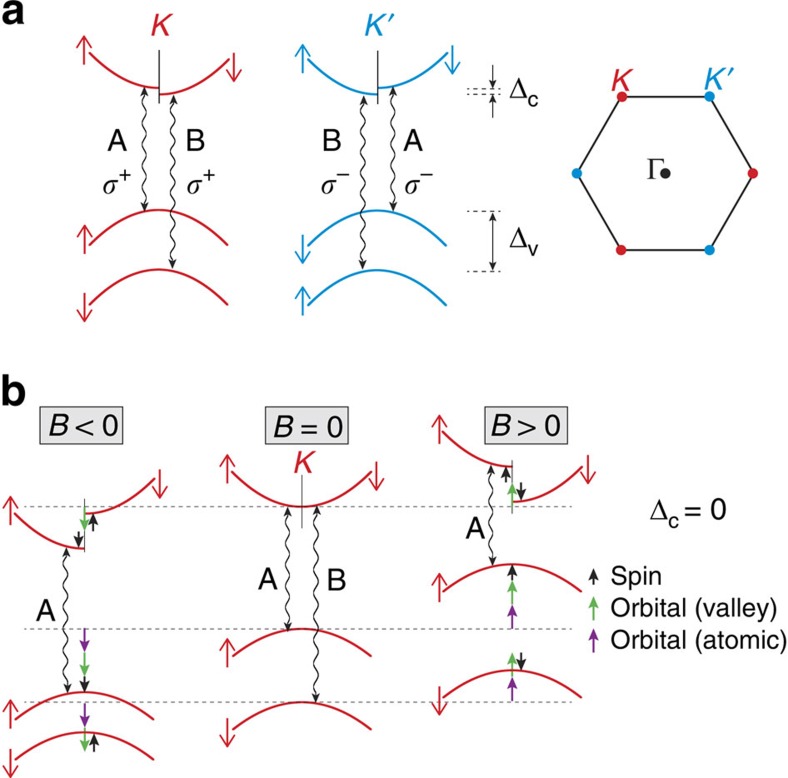
Figure 1a depicts a single-particle energy diagram of the conduction and valence bands in monolayer TMDs at the K and K′ points of the hexagonal Brillouin zone, along with the A and B exciton transitions (wavy lines) and valley-specific optical selection rules. Strong spin–orbit coupling of the valence band splits the spin-up and spin-down components (by Δ_v ∼400 and 150 meV in WS₂ and MoS₂, respectively), giving rise to the well-separated A and B exciton transitions that are observed in optical absorption or reflection spectra. As depicted, σ⁺ circularly polarized light couples to both the A and B exciton transitions in the K valley, while light of the opposite σ⁻ circular polarization couples to the exciton transitions in the K′ valley.

Figure 1. Excitonic transitions and Zeeman shifts in monolayer TMDs.

(a) Diagrams of the conduction and valence bands at the K and K′ valleys of the monolayer transition-metal dichalcogenides, showing the A and B exciton transitions (wavy lines) and the associated valley-specific optical selection rules for σ⁺ and σ⁻ light. For clarity, the spin-up and spin-down conduction bands are separately drawn on the left and right sides within each valley, respectively. A small spin–orbit splitting in the conduction band, Δ_c, is also depicted for completeness (theory predicts Δ_c∼+30 and −5 meV for WS₂ and MoS₂, respectively⁴⁵). (b) Diagrams depict the relative shifts of the conduction and valence bands in the K valley (that is, σ⁺ transitions) due to applied magnetic fields 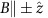. For clarity, Δ_c=0 here. The contributions to each band's Zeeman shift from spin, atomic orbital and valley orbital (Berry curvature) magnetic moment are depicted separately by black, purple and green arrows. The σ⁺ polarized A and B exciton transition energies decrease (increase) in positive (negative) field. By time-reversal symmetry, the shifts depicted here for B<0 in the K valley are equivalent to those in the K′ valley (σ⁻ transitions) when B>0.

At zero magnetic field, time-reversed pairs of states in the K and K′ valleys—for example, spin-up conduction (valence) bands in K and spin-down conduction (valence) bands in K′—necessarily have the same energy and have equal-but-opposite total magnetic moment 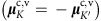. Therefore, an applied magnetic field, which breaks time-reversal symmetry, will lift the K/K′ valley degeneracy by shifting time-reversed pairs of states in opposite directions in accord with the Zeeman energy −μ·B. This will Zeeman shift the measured exciton energy if the relevant conduction and valence band moments are unequal; viz, ΔE_Z=−(μ^c−μ^v)·B. In the following, we consider strictly out-of-plane fields, .

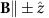Figure 1b depicts the field-dependent energy shifts of the conduction and valence bands in the K valley (σ⁺ polarized light), for both positive and negative fields. The various contributions to the total Zeeman shift in the monolayer TMDs have been discussed in several recent reports³,¹²,¹³,¹⁴,¹⁵,⁴⁴, which we summarize as follows. In general, the total magnetic moment μ of any given conduction or valence band in the K or K′ valley contains contributions from three sources: spin (μ_s); atomic orbital (μ_l); and the valley orbital magnetic moment that is associated with the Berry curvature (μ_k). Note that the latter two have been referred to as ‘intracellular' and ‘intercellular' contributions to the orbital magnetic moment, respectively¹²,¹³. The spin contribution to the exciton Zeeman shift ΔE_Z is expected to be zero, since the optically allowed transitions couple conduction and valence bands having the same spin 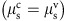. In contrast, the conduction and valence bands are comprised of entirely different atomic orbitals: the 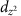orbitals of the conduction bands have azimuthal orbital angular momentum l_z=0 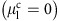, while the hybridized 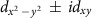orbitals that comprise the valence bands have l_z=±2ħ 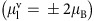in the K and K′ valleys, respectively. This contribution is expected to generate a Zeeman shift of the K and K′ exciton of 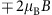, respectively, and therefore, a total exciton splitting of −4μ_BB. 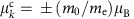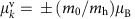Finally, the valley orbital (Berry curvature) contributions to the conduction and valence band moments are and in the K and K′ valleys, respectively. In a simple two-band tight-binding model where m_e=m_h, then 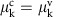and shifts due to the valley orbital magnetic moment do not appear in ΔE_Z. In more general models⁴⁵ where m_e≠m_h, these Berry curvature contributions may play a role and cause a deviation of the exciton Zeeman splitting away from −4μ_B.

To selectively probe the K and K′ transitions in our magneto-reflectivity experiments, we typically fixed the handedness of the circular polarizer to σ⁺, and pulsed the magnet in the positive (+65 T) and then the negative (−65 T) field direction. The latter case is exactly equivalent (by time-reversal symmetry) to measuring the σ⁻ optical transitions in positive field (we also explicitly verified this by changing the circular polarizer). Sign conventions were confirmed via magneto-reflectance from a diluted magnetic semiconductor (Zn_0.92Mn_0.08Se)⁴⁶.

Valley Zeeman effect in monolayer WS₂

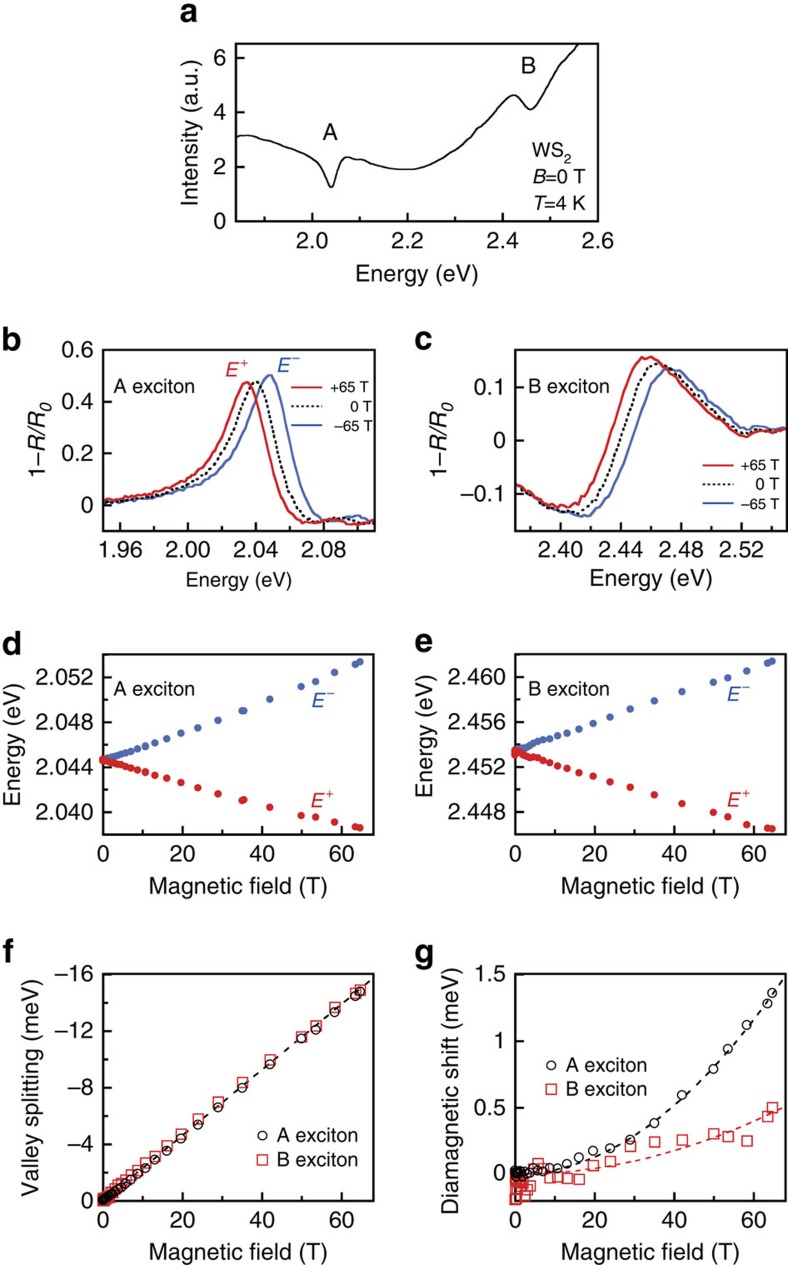
Figure 2a shows the reflection spectrum (raw data) from monolayer WS₂ at 4 K. Both the A and B exciton transitions are clearly visible and are superimposed on a smoothly varying background. Figure 2b shows the well-resolved Zeeman splitting of the A exciton in WS₂ at the maximum ±65 T applied magnetic field. Red, blue and (dashed) black curves show the normalized reflection spectra, 1−R/R₀ (where R₀ is a smooth background), at +65, −65 and 0 T respectively. A valley splitting of ∼15 meV, analysed in detail below, is observed. Moreover, because these measurements are based on magneto-reflectance spectroscopy (rather than photoluminescence), the valley splitting of the higher-energy B exciton in WS₂ can also be observed, as shown in Fig. 2c. For both the A and B excitons, the energy of the exciton transition in positive magnetic fields (hereinafter called E⁺) shifts to lower energy, while the exciton energy in negative fields (E⁻) shifts to higher energy, as labelled.

Figure 2. Valley Zeeman effect and diamagnetic shift in monolayer WS₂.

(a) Reflection spectrum of monolayer WS₂ at B=0 T and T=4 K. The A and B exciton resonances are labelled. (b) Normalized reflection spectra (1−R/R₀) at the A exciton resonance using σ⁺ polarized light. The dashed black trace was acquired at B=0 T. The red trace was acquired at +65 T, and corresponds to the σ⁺ transition in the K valley. The blue trace was acquired at −65 T, which is equivalent (by time-reversal symmetry) to the σ⁻ transition in the K′ valley at +65 T. The valley Zeeman splitting between these two peaks is clearly resolved. (c) Similar reflection spectra and valley Zeeman splitting of the B exciton. (d) Energies (E⁺ and E⁻) of the field-split A exciton versus magnetic field. (e) Same, but for the B exciton. (f) The measured valley Zeeman splitting (E⁺−E⁻) versus magnetic field, for both A and B excitons. The dotted line corresponds to a splitting of −4μ_B (−232 μeV T⁻¹). (g) The average energy, (E⁺ +E⁻)/2, for both the A and B excitons (the zero-field offset has been subtracted). A small quadratic diamagnetic shift is revealed. The dotted lines show quadratic fits to the data (ΔE_dia=σB²), where σ is the diamagnetic shift coefficient. We find that σ_A=0.32±0.02 μeV T⁻² and σ_B=0.11±0.02 μeV T⁻² for the A and B excitons, respectively.

The exciton resonances were fit using complex (absorptive+dispersive) Lorentzian lineshapes to extract the transition energy. The field-dependent energies of the split peaks in monolayer WS₂, E⁺(B) and E⁻(B), are shown in Fig. 2d,e for the A and B excitons, respectively. The splitting between the two valleys, E⁺−E⁻, is shown in Fig. 2f for both the A and B excitons. The measured valley Zeeman splitting is negative, and increases in magnitude linearly with applied field, with nearly identical rates of −228±2 μeV T⁻¹ for the A exciton and −231±2 μeV T⁻¹ for the B exciton. These values correspond to Landé g-factors of −3.94±0.04 and −3.99±0.04, respectively, thereby quantifying the valley Zeeman effect in the monolayer transition-metal disulphides, and also providing a measurement of the B exciton valley splitting in monolayer TMD materials.

The A exciton valley splitting that we measure in monolayer WS₂ is quite close to that reported recently from magneto-photoluminescence studies of its diselenide counterpart, monolayer WSe₂ (refs ^{13, 16}). For comparison, reported g-factors for all the monolayer TMDs are shown in Table 1. As discussed above, our measured values of g≃−4 agree surprisingly well with a simple two-band tight-binding model, wherein m_e=m_h and valley moment (Berry curvature) contributions to the exciton magnetic moment cancel out, so that the exciton Zeeman shifts derive solely from atomic orbital magnetic moments of the valence bands. However, Berry curvature contributions to the Zeeman splitting are expected in more general models⁴⁵ where m_e≠m_h. Deviations away from g=−4, observed, for example, in refs ^{13, 14}, have been explained along these lines (although, note that for tightly bound excitons, the total valley moment contribution can vary significantly in magnitude and sign, because this orbital moment must be averaged over a substantial portion of the Brillouin zone¹³).

Table 1. Summary of effective g-factors and diamagnetic shifts in monolayer TMDs.

Material	A exciton g-factor	B exciton g-factor	σA (μeV T−2)	σB (μeV T−2)
Monolayer WS2	−3.94±0.04		0.32±0.02
	−3.33±0.04 (bulk)	−3.99±0.04	0.64±0.02 (bulk)	0.11±0.02
	−3.2±0.3 (bulk)53
Monolayer MoS2	−4.0±0.2
	−4.6±0.08 (bulk)55	−4.65±0.17	—	—
	−3.1±0.1 (bulk)53
Monolayer WSe2	−3.7±0.2 (ref. 16)	—	—	—
	−4.37±0.15 (ref. 13)
	−1.57 to −2.86 (ref. 14)
	−4±0.5 (ref. 17)
Monolayer MoSe2	−3.8±0.2 (refs 12, 16)	—	—
	−4.1±0.2 (ref. 15)

Experimentally measured exciton g-factors corresponding to the valley Zeeman effect, and diamagnetic shift coefficients σ, in monolayer transition-metal dichalcogenide materials. Measurements from this work are indicated in boldface. For comparison, also included are selected measurements from bulk crystals.

In view of the above, it is therefore particularly noteworthy that we also measure g≃−4 for the B exciton in monolayer WS₂, despite the fact that its reduced mass almost certainly differs from that of the A exciton, as shown below from direct measurements of the diamagnetic shift (that is, m_h cannot equal m_e for both spin-up and spin-down valence bands). Note that early studies of bulk MoS₂ (refs ^{47, 48, 49}) also indicate that the B exciton mass significantly exceeds that of the A exciton. This suggests that contributions to the orbital moment from Berry curvature effects, expected when m_e≠m_h, may not play a significant role in determining the measured exciton magnetic moment and the valley Zeeman effect.

Non-local dielectric screening in monolayer TMDs

In addition to the reduced mass m_r, the characteristic size of the A and B excitons in monolayer TMDs is an essential parameter for determining material and optical properties. This is especially relevant because of non-local dielectric screening in these and other 2D materials, which fundamentally modifies the functional form of the attractive potential V(r) between electrons and holes²³,³⁶,³⁷. Rather than a conventional Coulomb potential, V(r) is believed to assume the following form:

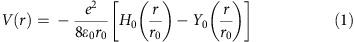where H₀ and Y₀ are the Struve function and Bessel function of the second kind, respectively, and the characteristic screening length 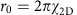, where χ_2D is the 2D polarizability of the monolayer material²³,³⁷. This potential follows a 1/r Coulomb-like potential for large electron–hole separations 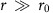, but diverges weakly as log(r) for small separations 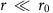, leading to a markedly different Rydberg series of exciton states with modified wavefunctions and binding energies that cannot be described within a hydrogen-like model²³,²⁴,²⁵,²⁷.

Diamagnetic shifts in monolayer WS₂

To this end, the use of very large 65 T magnetic fields allows us to measure the small diamagnetic shifts of excitons in monolayer TMDs so that the characteristic size of their wavefunctions can be directly inferred. In general²⁰,²¹,²², an exciton diamagnetic shift ΔE_dia is expressed as

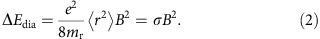Here σ is the diamagnetic shift coefficient, m_r is the in-plane reduced mass, r is a radial coordinate in a plane perpendicular to the applied magnetic field B (here for 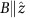, r is in the monolayer plane) and 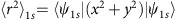is the expectation value of r² over the 1s exciton wavefunction 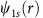. Equation (2) applies in the ‘low-field' limit where the characteristic cyclotron energies ħω_c (and also ΔE_dia) are less than the exciton binding energy, which is the case for excitons in TMDs even at ±65 T. Given m_r, σ can then be used to determine the r.m.s. radius of the 1s exciton in the monolayer plane, r₁:

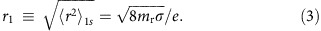This definition is entirely general and independent of V(r). (Note that for a standard Coulomb potential V(r)=−e²/(4πɛ_rɛ₀r) in two dimensions, 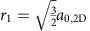, where a_0,2D=2πɛ_rɛ₀ħ²/m_re² is the classic Bohr radius for hydrogenic 2D excitons.)

Exciton diamagnetic shifts have eluded detection in recent magneto-photoluminescence studies of monolayer MoSe₂ and WSe₂ (refs ^{12, 13, 14, 15, 16}), likely due to the limited field range employed (|B|<10 T). Here the diamagnetic shift of the A exciton in monolayer WS₂ can be seen in 65 T fields via the slight positive curvature of both E⁺(B) and E⁻(B) in Fig. 2d. To directly reveal ΔE_dia, Fig. 2g shows the average exciton energy, (E⁺+E⁻)/2. Overall quadratic shifts are indeed observed, indicating diamagnetic coefficients σ_A=0.32±0.02 μeV T⁻² for the A exciton and a smaller value of σ_B=0.11±0.02 μeV T⁻² for the B exciton. These measurements were repeated on five different regions of the monolayer WS₂ sample, with similar results.

Exciton radii and binding energies

Importantly, knowledge of σ constrains not only the r.m.s. exciton radius r₁ (if the mass is known) but also the exciton binding energy if the potential V(r) is known. Theoretical estimates³,²³,³¹,³² for the A exciton reduced mass in monolayer WS₂ range from 0.15 to 0.22m₀, from which we can then directly calculate r_1,A=1.48–1.79 nm via equation (3). These values are in reasonable agreement with recent ab initio calculations of the 1s exciton wavefunction in monolayer WS₂ (ref. ²⁵), and further support a picture of 2D Wannier-type excitons with lateral extent larger than the monolayer thickness (0.6 nm) and spanning several in-plane lattice constants.

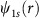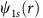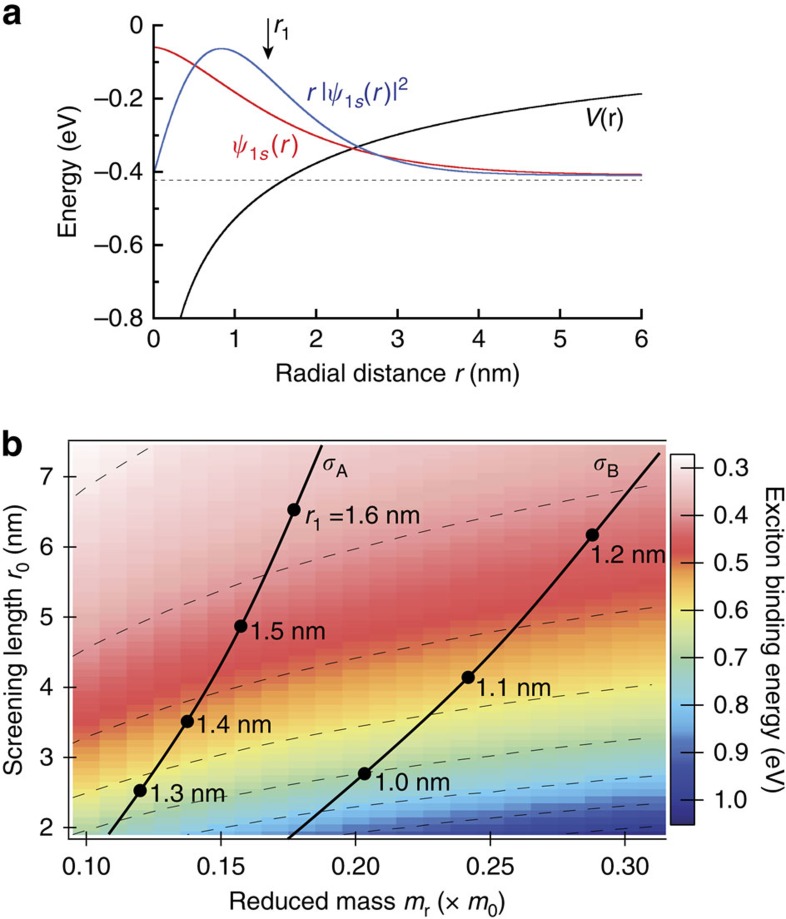
Moreover, σ, m_r and r₁ can then be used to calculate the A exciton wavefunction and its binding energy, by numerically solving the 2D Schrödinger equation for describing the relative motion of electrons and holes using the potential V(r) as defined in equation (1), and taking the screening length r₀ as an adjustable parameter to converge on a solution for that has the correct r.m.s. radius r₁. For example, using m_r,A=0.16m₀ for the A exciton in WS₂, and using the measured diamagnetic shift σ_A, we find that r_1,A=1.53 nm via equation (3). A wavefunction 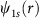with this r.m.s. radius, shown explicitly in Fig. 3a, is calculated if (and only if) the screening length r₀=5.3 nm, and the binding energy of this state is 410 meV. For comparison, this inferred screening length is somewhat larger than expected for a suspended WS₂ monolayer (where r₀=2πχ_2D=3.8 nm; ref. 23), but is less than the value of 7.5 nm used recently by Chernikov²⁴ to fit a non-hydrogenic Rydberg series of excitons in WS₂ from reflectivity data. Similarly, the 410 meV exciton binding energy that we estimate exceeds the value inferred by Chernikov (320 meV), but is less than the 700–830 meV binding energies extracted from two-photon excitation studies²⁵,²⁶ and reflectivity/absorption studies²⁸ of monolayer WS₂. We emphasize, however, that the exciton wavefunctions and binding energies that we calculate necessarily depend on the reduced mass m_r and the exact form of the potential V(r), which is sensitive to the details of the dielectric environment and choice of substrate material³³,⁵⁰.

Figure 3. Constraining exciton binding energies via the diamagnetic shift.

(a) A plot of the (non-hydrogenic) 1s A exciton wavefunction in monolayer WS₂, 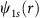, computed by numerically solving Schrödinger's equation using a reduced mass m_r=0.16 and the non-local dielectric screening potential V(r) defined in equation (1). The screening length r₀ was adjusted to give 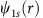such that the r.m.s. exciton radius  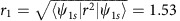nm, which is the value calculated from the measured diamagnetic shift σ_A=0.32 μeV T⁻². (Note that r₁ is an r.m.s. value, and does not correspond to the peak of the 2D radial probability density 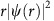.) (b) Colour surface plot of the calculated exciton binding energy, using V(r) from equation (1), over a range of reduced mass m_r and screening length r₀. Dashed lines show contours of constant binding energy. Solid lines indicate contours of constant diamagnetic shift corresponding to those measured in Fig. 2g for the A and B excitons in monolayer WS₂. The calculated r.m.s. exciton radius r₁ is indicated at various points along the contours.

More generally, Fig. 3b shows a colour-coded surface plot of the exciton binding energy, calculated within the framework of the non-local dielectric screening potential V(r) defined in equation (1), over a range of reduced masses m_r and effective dielectric screening lengths r₀. At each point, the 1s exciton wavefunction 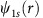, its binding energy, and its r.m.s. radius r₁ were calculated, from which we computed the expected diamagnetic shift coefficient 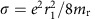. Importantly, the solid lines on the plot indicate the contours of constant diamagnetic shift that correspond to our experimentally measured values σ_A and σ_B. At intervals along these contours, r₁ is indicated. From this plot, it can be immediately seen that over the range of theoretically calculated masses (m_r,A=0.15–0.22m₀), excitons having the appropriate size to give the measured diamagnetic shift σ_A (that is, those lying along the σ_A contour) have binding energies in the range of 480–260 meV. Within this model, excitons with even larger binding energies (but still constrained to exhibit the correct diamagnetic shift) are anticipated if the reduced mass m_r is lighter and the effective screening length r₀ is smaller.

In addition, Fig. 3b also allows us to estimate the mass, binding energy and spatial extent of the B exciton in monolayer WS₂, for which a smaller diamagnetic shift of σ_B=0.11 μeV T⁻² was measured. Assuming that the local dielectric environment is similar for A and B excitons (that is, r₀ is unchanged), then parameters for the B exciton lie at a point on the σ_B contour that is directly to the right of those on the σ_A contour. Thus, if m_r,A=0.16m₀ and r_1,A=1.53 nm as discussed above, then the B exciton reduced mass is m_r,B=0.27m₀, its r.m.s. radius is r_1,B=1.16 nm and its binding energy is 470 meV. These values are qualitatively consistent with trends identified in early optical studies of bulk MoS₂ crystals⁴⁸,⁴⁹, in which B exciton masses and binding energies were found to exceed those of A excitons. These results highlight a further interesting consequence of the potential V(r), which is that exciton binding energies scale only weakly and nonlinearly with m_r, in contrast to the case for hydrogenic potentials.

Zeeman splitting and diamagnetic shifts in bulk WS₂

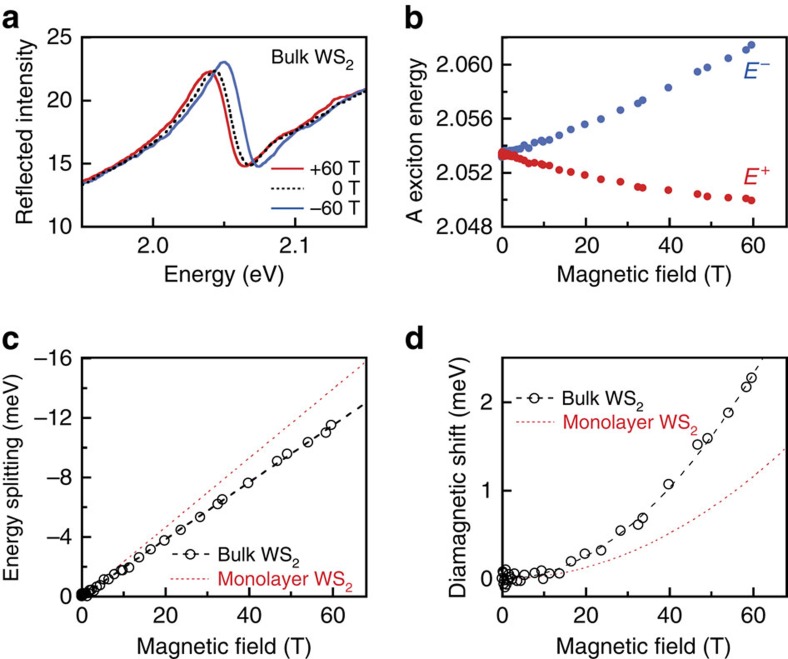
For direct comparison with monolayer WS₂, circularly polarized magneto-reflectance measurements were also performed on the exfoliated surface of a bulk WS₂ crystal (grown by chemical vapour transport at the Tennessee Crystal Center). Figure 4a shows the well-known⁵¹ A exciton resonance in bulk WS₂, which arises from the lowest-energy direct optical transition that is located at the K points of the Brillouin zone⁵² (this transition, with only slight modification in energy, eventually becomes the lowest overall transition when WS₂ is thinned to a single monolayer and becomes a direct-gap semiconductor¹,²). At low temperatures and in ±60 T magnetic fields, the Zeeman splitting of the bulk A exciton is readily resolved (Fig. 4a–c) and is found to increase linearly with field at a rate of −193 μeV T⁻¹ (g=−3.33). This value is in very close agreement with early magnetic circular dichroism measurements of g-factors in bulk WS₂ (ref. ⁵³), wherein it was suggested that deviations from g=−4 arise from the crystal-field mixing of p-type chalcogen atomic orbitals into the predominantly d-type character of the conduction and valence bands. Within this context, the value of g≃−4 that we measured in monolayer WS₂ (Fig. 2f) may suggest that such mixing effects, if present, may be suppressed in atomically thin WS₂.

Figure 4. Zeeman splitting and diamagnetic shift in bulk WS₂.

(a) Intensity of reflected σ⁺ light from the A exciton in bulk WS₂ at 4 K, using B=0, +60 and −60 T. (b) Energies of the Zeeman-split exciton transitions, E⁺ and E⁻. (c) The measured exciton splitting (E⁺−E⁻), corresponding to g=−3.33. For comparison, the red line shows the valley Zeeman splitting measured in monolayer WS₂ (cf. Fig. 2f). (d) The average energy (E⁺+E⁻)/2 showing a diamagnetic shift (0.64 μeV T⁻²) that is twice as large as that measured in monolayer WS₂ (red line; cf. Fig. 2g).

In addition, Fig. 4d shows that the measured diamagnetic shift of the A exciton in bulk WS₂ is 0.64 μeV T⁻², which is twice as large as in monolayer WS₂. Assuming an in-plane reduced mass of m_r=0.21m₀ in bulk WS₂ (ref. ⁵¹), we calculate via equation (3) an in-plane r.m.s. radius of r₁=2.48 nm for the bulk A exciton, which is substantially larger than that inferred for monolayer WS₂. This large r.m.s. radius indicates an effective dielectric screening constant ɛ_r≃7.0, in agreement with early work⁵¹, and from which the A exciton binding energy in bulk WS₂ can be estimated via the standard hydrogenic formulation, 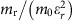× 13.6 eV=58 meV. This value agrees extremely well with early work on bulk WS₂ (ref. ⁵¹), and is close to that found in other bulk TMDs⁵⁴. Therefore, we find that the binding energy of the A exciton in WS₂ increases by approximately a factor of 7 on reducing the dimensionality of the host crystal from three-dimensional to 2D. Note, however, that these estimates depend on the assumed value of the reduced mass m_r, which has not yet been measured independently by, for example, cyclotron resonance studies.

Valley Zeeman effect in monolayer MoS₂

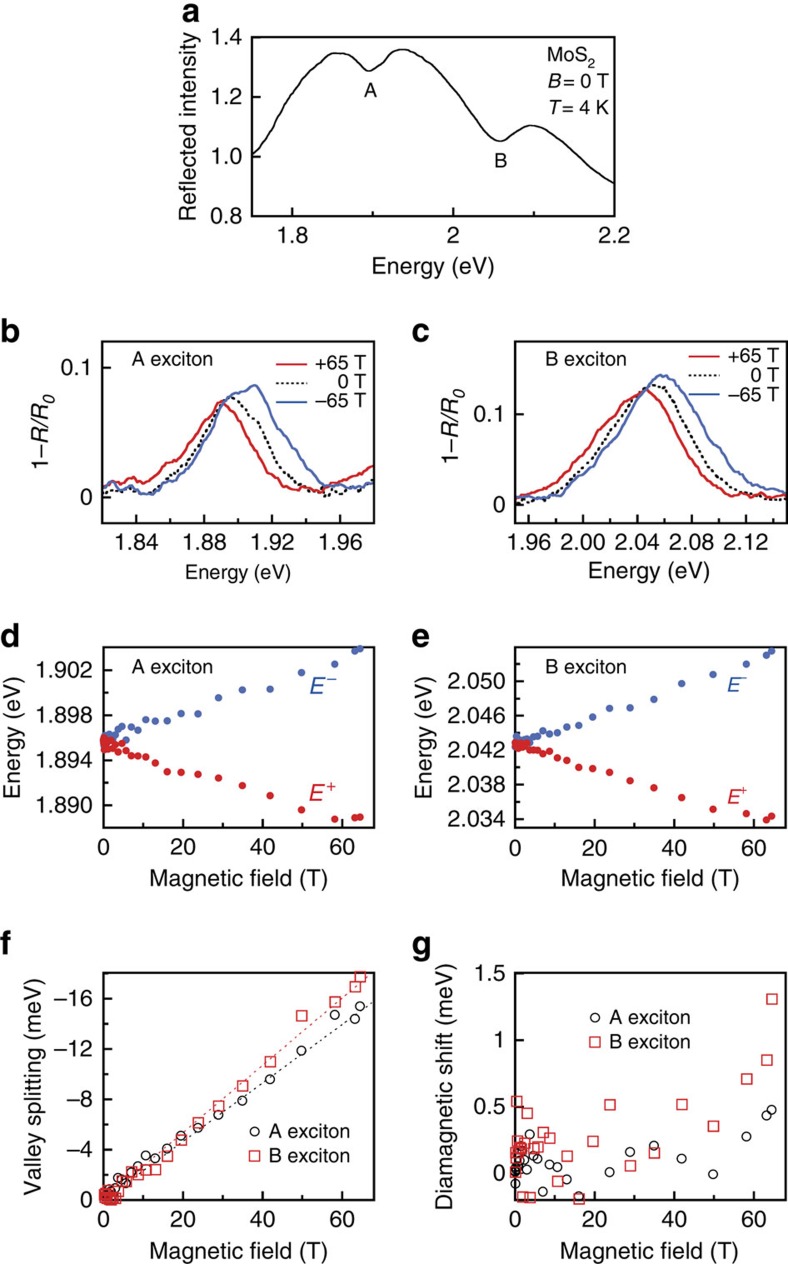
To complete this study of the monolayer transition-metal disulphides, we also performed high-field magneto-reflectance studies on large-area samples of monolayer MoS₂ (Fig. 5). The A and B exciton linewidths are broader and the optical reflection contrast is lower than for monolayer WS₂ (Fig. 5a). Nonetheless, a clear valley Zeeman splitting of both excitons is observed (Fig. 5b,c). The energies of the field-split exciton peaks are shown in Fig. 5d,e for the A and B excitons, respectively. Although the reduced signals and broader features lead to increased scatter in the fitted data, Fig. 5f shows that the measured valley splitting of the A and B excitons in MoS₂ increases approximately linearly with field at rates of −233±10 and −270±10 μeV T⁻¹, corresponding to g≃−4.0±0.2 and −4.65±0.17, respectively. For the A exciton, this value is very close to those inferred from low-field magneto-photoluminescence studies¹²,¹⁵,¹⁶ of their diselenide counterpart, monolayer MoSe₂ (Table 1). As discussed above for the case of monolayer WS₂, a g-factor of −4 for the A exciton agrees surprisingly well with expectations from a simple two-band tight-binding picture, and suggests that the valley Zeeman effect in MoS₂, much like MoSe₂, is largely uninfluenced by contributions from the valley orbital (Berry curvature) magnetic moment. We note, however, that the measured valley g-factor is somewhat larger for the B exciton in monolayer MoS₂. Unfortunately, the reduced signal levels from these monolayer MoS₂ samples led to correspondingly increased scatter in the fitted exciton energies, precluding an accurate determination of exciton diamagnetic shifts in monolayer MoS₂ (Fig. 5g).

Figure 5. Valley Zeeman effect in monolayer MoS₂.

(a) Reflection spectrum of monolayer MoS₂ at B=0 T and T=4 K. The A and B exciton resonances are labelled. (b,c) Normalized reflection spectra (1−R/R₀) at the A and B exciton resonances at B=0, +65 and −65 T. (d) Energies of the field-split A exciton transition. (e) Same, but for the B exciton transition. (f) The measured valley splitting (E⁺−E⁻) versus the magnetic field, for both A and B excitons. (g) The average energy of the two valley-split resonances, (E⁺+E⁻)/2, for both A and B excitons. Increased scatter in the data from this MoS₂ sample precludes any clear identification of the diamagnetic shift.

Discussion

In summary, we have presented a comprehensive study of valley Zeeman effect and diamagnetic shifts of excitons in the archetypal monolayer transition-metal disulphides WS₂ and MoS₂. Valley g-factors of the A excitons are approximately −4, which are similar to those obtained from transition-metal diselenides. Unexpectedly, the heavier B exciton in monolayer WS₂ also exhibits g≃−4, suggesting that the valley Zeeman effect is largely unaffected by the exciton reduced mass. The very large magnetic fields used in these studies also allowed initial measurements of the exciton diamagnetic shifts in a monolayer TMD—specifically, WS₂—from which r.m.s. exciton radii were directly computed (r₁=1.53 and 1.16 nm for the A and B excitons, respectively). Within a picture of non-local dielectric screening in these 2D semiconductors, these measurements of diamagnetic shifts allowed us to constrain estimates of the exciton binding energies, which we calculate (using a reduced A exciton mass of 0.16m₀) to be 410 and 470 meV for the A and B excitons, respectively, in monolayer WS₂. These studies highlight the utility of very large magnetic fields for characterizing new 2D material systems.

Additional information

How to cite this article: Stier, A. V. et al. Exciton diamagnetic shifts and valley Zeeman effects in monolayer WS₂ and MoS₂ to 65 Tesla. Nat. Commun. 7:10643 doi: 10.1038/ncomms10643 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-5, Supplementary Notes and Supplementary References