Modulating RNA Alignment Using Directional Dynamic Kinks: Application in Determining an Atomic-Resolution Ensemble for a Hairpin using NMR Residual Dipolar Couplings

Abstract

Approaches that combine experimental data and computational molecular (MD) dynamics to determine atomic resolution ensembles of biomolecules require the measurement of abundant experimental data. NMR residual dipolar couplings (RDCs) carry rich dynamics information, however, difficulties in modulating overall alignment of nucleic acids has limited the ability to fully extract this information. We present a strategy for modulating RNA alignment that is based on introducing variable dynamic kinks in terminal helices. With this strategy, we measured seven sets of RDCs in a cUUCGg apical loop and used this rich data set to test the accuracy of an 0.8 μs molecular dynamics simulation computed using the Amber ff10 force field as well as to determine an atomic resolution ensemble. The MD-generated ensemble quantitatively reproduces the measured RDCs but selection of a sub-ensemble was required to satisfy the RDCs within error. The largest discrepancies between the RDC-selected and MD-generated ensembles are observed for the most flexible loop residues and backbone angles connecting the loop to the helix, with the RDC-selected ensemble resulting in more uniform dynamics. Comparison of the RDC-selected ensemble with NMR spin relaxation data suggests that the dynamics occurs on the ps-ns timescales as verified by measurements of R_1ρ relaxation-dispersion data. The RDC-satisfying ensemble samples many conformations adopted by the hairpin in crystal structures indicating that intrinsic plasticity may play important roles in conformational adaptation. The approach presented here can be applied to test nucleic acid force fields and to characterize dynamics in diverse RNA motifs at atomic resolution.

Graphical abstract

Introduction

A growing number of studies are highlighting the dynamic nature of RNA and importance of conformational transitions in ribozyme catalysis, hierarchical assembly of ribonucleoprotein complexes, and in RNA-based gene regulatory switches^1–3. There is a growing interest in going beyond static representations of RNA structure toward a dynamic description that provides a statistical description of a conformational landscape^4–6. Determining atomic-resolution ensembles of biomolecules is challenging because the number of parameters that can be measured experimentally typically pale in comparison to the number of parameters that need to be specified^4–6. This has spurred the development of hybrid methods that combine experimental measurements with computational techniques such as Molecular Dynamics (MD) simulations. Despite advances in determining ensembles of proteins using such methods^7–9 there remain significant challenges in determining dynamic ensembles of nucleic acids⁵. NMR observables that report on dynamics at atomic resolution can be difficult to measure in great abundance in nucleic acids or can be difficult to interpret quantitatively due to their unique properties. Here, we address a major obstacle in measuring independent sets of NMR Residual Dipolar Couplings (RDCs)^10,11 in nucleic acids and demonstrate its application in testing an MD simulation as well as in determining a high-resolution ensemble for a hairpin containing a cUUCGg apical loop.

NMR RDCs measured in partially oriented samples provide rich information regarding the orientation distribution of inter-nuclear vectors in biomolecules relative to the magnetic field with broad timescale sensitivity extending from picoseconds to milliseconds^12–17. RDCs measured between two nuclei depend on $\langle \frac{3{\text{cos}}^2\theta -1}{2}\rangle$, where θ is the angle between the inter-nuclear vector and the magnetic field, and the angular bracket denotes a time average over all orientations sampled by the inter-nuclear vector over timescales faster than the inverse of the dipolar interaction. While the angular term normally averages to zero due to isotropic reorientation, partial alignment of a molecule, typically using an ordering medium^11,18, makes it possible to measure RDCs as additional contributions to the splitting of resonances. Studies have shown that by changing the partial alignment of the biomolecule solute relative to the magnetic field, it is possible to measure independent RDC datasets that can be applied to more rigorously characterize internal dynamics^{13–15,19,20}. In theory, up to five independent sets of alignments and RDC datasets can be measured in a target biomolecule^13,14,21. Several approaches have been developed to modulate the alignment of proteins. These include changing the steric or electrostatic properties of the alignment medium ^12–14,19, use of paramagnetic tags and metal ions to induce magnetic alignment^22–26, and conserved mutagenesis to modulate electrostatic properties²⁷.

In the case of nucleic acids, modulating alignment to obtain independent sets of RDCs remains an outstanding problem. In both DNA and RNA, the negative electrostatic charge distribution is quite uniform over the entire molecule. As a result the steric and electrostatic repulsion forces governing alignment are quite similar, making it difficult to modulate alignment by changing the ordering medium²⁸. In contrast, positively charged ordering media can result in unfavorable attractive interactions that can perturb the nucleic acid conformation and result in significant line broadening. Other approaches have been used to modulate alignment including self-induced magnetic alignment^29,30, variable linear elongation of helices^15,31, and installation of protein binding sites to modulate the overall shape when in complex with a protein³². In the case of self-induced alignment, the magnitude of alignment and resulting RDCs remain sub-optimal. The other approaches increase the size of the RNA and result in unfavorable line broadening. In all cases, the approaches typically yield one additional RDC dataset and do not offer a path for obtaining more independent alignments and sets of RDCs.

We recently showed that independent sets of RDCs can be obtained by elongating terminal helices in RNA by variable amounts^15,31,33. Variable elongation of two helices linked by a bulge in HIV-1 TAR allowed the measurement of nearly three independent sets of RDCs³³. The measured RDCs exhibited poor agreement with an HIV-1 TAR trajectory obtained from an 8.2 μs MD simulation computed using the CHARMM36 force field³⁴. The overall Root-Mean-Square-Deviation (RMSD) was 8.6 Hz as compared to RDC uncertainty of ~2–4 Hz and with Pearson’s correlation coefficient R = 0.84³³. Comparison of the MD-generated and RDC-selected ensembles using a recently introduced REsemble approach³⁵ indicates that the discrepancy between the MD trajectory and RDCs arises primarily due to differences in the global inter-helical dynamics across the flexible bulge, with good agreement observed for other local parameters such as base-pair parameters, sugar pucker, and backbone phosphodiester torsion angles^33,35. These discrepancies could arise from insufficient sampling of collective inter-helical motions in the MD, especially given that the simulation time remains short compared to the RDC timescale sensitivity (< milliseconds). They could also arise from improper modeling solvent and ion atmosphere especially since the TAR inter-helical motion are strongly dependent on the monovalent and divalent ion concentration³⁶ or other imperfections in the force field³⁵.

The above study highlights the need to study simpler RNA motifs in order to dissect various potential sources of error in determining ensembles using hybrid experimental-computational methods. Hairpins or stem-loop motifs^37,38 offer excellent RNA model systems to both benchmark MD simulations and to obtain important insights into functionally important RNA dynamics. The hairpin, which caps the A-form helix, is the most common secondary structure motif in RNA. Hairpins play critical roles in tertiary RNA-RNA interactions and serve as site for adaptive recognition by proteins and ribonucleoprotein complexes^37,38, and been used to benchmark computational simulations^39,40. The most common hairpins are tetraloops, which can be grouped into different classes, including GNRA, UNCG, CUYG, GANC, (A/U)GNN, and UUUM; where G=guanine, A=adenine, U=uracil, C=cytidine, N= any base, R is a purine, and Y is a pyrimidine, and M=adenine or cytidine. These tetraloop families have distinct stabilities, structural, and functional properties and provide excellent model systems for benchmarking nucleic acid force fields and for carrying out RNA structure-dynamics-function studies^37,38.

Although variable elongation provides a powerful RDC-based approach for studying inter-helical dynamics in RNA, it is less well suited for studying other motifs such as apical loops considered here. Variable linear elongation of the helix is not expected to significantly modulate the overall alignment of a hairpin. To overcome this problem, we developed a new strategy in which kinks are introduced into variably elongated terminal helices so to modulate the overall shape and alignment of the RNA. The introduced kinks have different level of internal dynamics, which allow for additional modulation of the hairpin alignment. We demonstrate this approach on a cUUCGg hairpin which is a representative example of the UNCG tetraloop family^37,38 (Figure 1A). The cUUCGg hairpin lacks a bulge motif and inter-helical dynamics and has a conformation that is minimally dependent on the concentration of monovalent or divalent ions^36,41. In addition, the cUUCGg tetra-loop is known for its high structural and thermal stability and is expected to exhibit a low level of internal dynamics. It therefore provides an excellent opportunity to test how accurately MD simulations can recapitulate local motions in RNA. Therefore even a μs timescale MD trajectory can potentially provide a reasonable approximation of the extent of RNA dynamics⁴⁰. By providing more parameters to alter shape and alignment (length of the elongation, topology, and position of kink) than conventional linear elongation^15,31,33, the kinked-elongation approach described here opens the door toward rigorously benchmarking nucleic acid force fields as well as for determining atomic resolution dynamic ensembles of diverse RNA motifs.

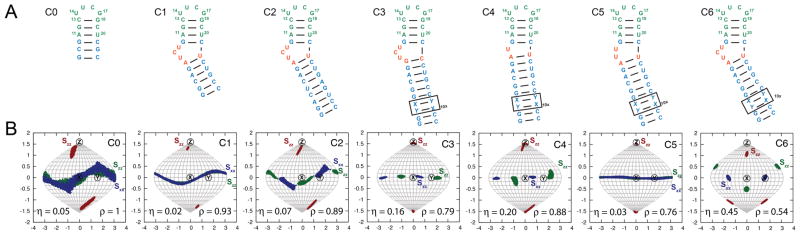
FIGURE 1.

Kinked elongated constructs of cUUCGg apical loop. (A) The alignment of the studied motif (green) is modulated by the kinked elongated strategy: helical parts (blue), bulge (orange). The constructs are labeled C0 to C6. (B) Sauson-Flamsteed projection maps depicting the order tensor frame (S _zz, S _yy, S _xx) relative to a frame of reference in which the helix axis of the upper helix is aligned parallel to the molecular z direction. Also shown is the asymmetry of alignment (η = |S_yy-S_xx|/ S_zz) and ρ values which represents the scalar product of the alignment tensor for a given construct with that of C0 (see Methods).

Results and Discussion

Modulating RNA Alignment using Variable Dynamic Kinked-Elongation

Our approach to modulate overall alignment of RNA relies on using bulges and internal loops to install directional dynamic kinks in an RNA terminal helix as shown for the cUUCGg hairpin in Figure 1A. Recent studies have shown that bulges and internal loops induce directional dynamic kinking of helices^42–45. The specific conformational available to given type of kink be computed based on secondary structure and consideration of simple topological forces including connectivity and steric constraints^42–46. Increasing the bulge length increases both the average bend angle as well as extent of inter-helical bending dynamics^15,47–49. Changing the position of the kink along the helix can also ‘phase-twist’ the directionality of the kink as has long been recognized in studies of DNA bending⁵⁰. These variations along with changes in the sequence of the kink can be exploited to modulate the overall shape of the RNA, and consequently, its overall alignment in ordered media.

Shown in Figure 1A are seven constructs (C0-C6) for the cUUCGg hairpin with variable kinked-elongations. In C0, the apical loop is appended to a linear 4 bp helix with sequence corresponding to the upper helix of the HIV-1 TAR with two G-C closing bps added for stability. C1, C2 and C6 all contain the HIV-1 TAR trinucleotide UCU bulge with lower A-U and upper G-C closing bps. They differ with respect to the length of the appended lower helix (six, nine, and 28 bps, respectively). C3 and C6 differ with respect to the lower closing bp (A-U for C6 and G-C for C3). The G-C closing bp in C3 has previously been shown to stabilize co-axial alignment of the two helices⁵¹. Finally C4 to C6 contain elongated helices appended to single U (C4), dinucleotide UU (C5), and trinucleotide UCU (C6) bulges, all closed by a lower A-U bp.

RDCs were measured in all constructs using Pf1 phage as an ordering medium^52,53(Methods). RDCs for C1, C2, C3, C5 and C6 have been reported previously in the context of studying the dynamics of the HIV-1 TAR bulge^15,31,51, but never used to analyze the dynamics of the cUUCGg apical loop. The data for C0 and C4 was measured to obtain additional independent sets of RDCs. The RDCs measured in the non-terminal Watson-Crick (WC) bps in the upper A-form helix (nucleotides A11, G12, C13, G18, C19 and U20) were subjected to an order tensor analysis^54,55 using an idealized A-form helix geometry as input coordinates⁵⁶. This allowed for the determination of the five elements of the order tensor describing overall alignment of the upper helix in Pf1 phage, modulated by the presence of the kinked elongation motif (see Supporting Table S1 and S2). Figure 1B shows the Sauson-Flamsteed projection maps depicting the orientation of the order tensor frame (S_xx, S_yy, S_zz) describing the average orientation of the RNA relative to the magnetic field along with the asymmetry of alignment η = |S_yy-S_xx|/S_zz which ranges between 0 and 1 for minimum and maximum symmetry, respectively. The order tensor is depicted relative to a reference A-form helix with helix axis oriented along the molecular z-direction.

The overall order tensor determined for the various constructs matched trends expected from the resulting overall shape and known dynamics properties of the installed kinks. For example, the order tensor for C0 is nearly axially symmetric (η ~ 0.05±0.09) with principal axis slighted tilted away from the helix (~23°) as expected based on structure-based prediction of alignment using PALES⁵⁷ (data not shown). As expected, elongating the kinked helix in C1, C2 and C6 results in increasingly larger deviations between the principal S_zz direction and reference helix axis and this is also accompanied by increasingly more asymmetric alignments (η=0.02±0.03, 0.07±0.04 and 0.45±0.05 respectively) (Fig 1B). Note that for a rigid kink, one would expect an axially symmetric order tensor when elongating the lower helix significantly, since the overall shape becomes more axially symmetric. The increase in asymmetry observed arises due to anisotropic inter-helical bending motions across the TAR bulge, as characterized in detail previously¹⁵. This highlights a unique feature of dynamic kinks: it makes it possible to access new alignment tensors characterized by both high asymmetry and S_zz deviating from the helical axis, both of which are otherwise difficult to accomplish for extended nucleic acids. These trends are accompanied by a decrease in correlation between these alignment tensors and the alignment tensor of C0, ρ varying from 0.93 (C1) to 0.89 (C2) and 0.54 (C6). The order tensor for C3 containing a closing G-C bp, which stabilizes coaxial alignment of helices⁵¹ results in less tilted S_zz direction and less symmetric tensor as compared to the kinked C6 containing an A-U closing bp (Fig 1B) resulting in a less independent tensor as compared to C0 (ρ=0.79 for C3 and 0.54 for C6). Finally increasing the length of the bulge across C4, C5, and C6 results in increasingly more tilted tensors particularly for C6, which also has the expected greater degree of asymmetry due to inter-helical bending. Interestingly, C5 exhibits very low asymmetry, possibly due to a more isotropic dynamics with a dinucleotide bulge or increased stacking of the two helices. The scalar product between the alignment tensors for these constructs and C0 (0.88 for C4 0.76 for C5 and 0.54 for C6) indicate that increasing the length of the bulge leads to more independent datasets.

Relative to the linear elongation, kinked elongation allows sampling of additional orthogonal dimensions in the overall order tensor as indicated by the scalar products between tensors being significantly below 1 (0.93, 0.89, 0.88, 0.79, 0.76 and 0.54). Compared to values reported for proteins, these scalar products suggest fairly correlated datasets but for comparison, aligning tRNA in phospholipid bicelles, negatively charged bicelles, fd bacteriophage or C₈E₅/octanol mixtures leads to at best, a scalar product of 0.87 as compared to Pf1 phage⁵⁸.

Using Independent RDC Datasets to Test an MD Simulation of the cUUCGg Hairpin

We used the seven RDC datasets measured on the cUUCGg to examine an ensemble of the cUUCGg hairpin obtained using an 0.8 μs MD simulation of a UUCG-capped HIV-1 TAR sequence, computed using the ff10 AMBER force field, which builds upon ff99 by modifying the potential describing the α and γ torsion angles⁵⁹ and the χ glycosidic torsion angle^60,61(Methods). To carry out this analysis, it is necessary to have the means of predicting RDCs for a given RNA conformation. In prior studies, we used structure-based approaches⁵⁷ to predict alignment and RDCs for individual conformers³³. Such approaches cannot be used for the present application since one generally does not have knowledge regarding the details of the dynamics at the installed dynamic-kink nor is this information of interest. We therefore used an alternative approach in which the order tensor for each construct is determined using the experimental RDC data and a Singular Value Decomposition (SVD) approach (Methods)^{15,54,62–64}. In prior studies^15,63, we used such an approach to determine the overall alignment tensor of elongated helices dominating alignment. This in turn allowed the interpretation of RDCs in terms of motions of shorter helices and bulge residues relative to the elongated helix. Here, we used an approach similar to that proposed by Blackledge and co-workers⁶⁴, in which an order tensor is determined for the upper helix and the apical loop. This increases the number of RDCs that can be applied toward the order tensor determination, and also relaxes the assumption of uniform local rigidity in the helix and the loop during the order tensor determination. In this approach, RDCs are calculated for a given trial ensemble by solving the following set of equations⁶⁴:

$$\left(\begin{array}{ccccc}\langle y_1^2-x_1^2\rangle & \langle z_1^2-x_1^2\rangle & \langle 2x_1{y}_1\rangle & \langle 2x_1{z}_1\rangle & \langle 2y_1{z}_1\rangle \\ ⋮& ⋮& ⋮& ⋮& ⋮\\ \langle y_l^2-x_l^2\rangle & \langle z_l^2-x_l^2\rangle & \langle 2x_l{y}_l\rangle & \langle 2x_l{z}_l\rangle & \langle 2x_l{z}_l\rangle \\ ⋮& ⋮& ⋮& ⋮& ⋮\\ \langle y_L^2-x_L^2\rangle & \langle z_L^2-x_L^2\rangle & \langle 2x_L{y}_L\rangle & \langle 2x_L{z}_L\rangle & \langle 2x_L{z}_L\rangle \end{array}\right)\left(\begin{array}{c}{A}_{yy}^c\\ A_{zz}^c\\ A_{xy}^c\\ A_{xz}^c\\ A_{yz}^c\end{array}\right)=\left(\begin{array}{c}{D}_1^c\\ ⋮\\ D_l^c\\ ⋮\\ D_L^c\end{array}\right)$$

where (x_l, y_l, z_l) are the normalized coordinates of the l th inter-nuclear vector corresponding to the lth normalized experimental RDC measured for construct $c({\mathit{D}}_{\mathit{l}}^{\mathit{c}})$, L is the total number of RDCs. The angular bracket denotes an average over the trial ensemble of structures due to internal motions. It is computed for a given trial ensemble by aligning structures to an A-form idealized helix using nucleotides G10, A11, G12, C19, U20 and C21. Note that the order tensor elements subsume any motional averaging contributions arising due to internal motions in the kink that modulate overall alignment. For a given trial ensemble, the five order tensor elements are determined for each construct (or alignment) that best reproduce the measured RDCs as implemented using SVD⁶⁴. In this manner, RDCs measured in the upper helix and the loop are used to determine the overall order tensor and all remaining regions of the RNA are treated as passive alignment modulation elements. The analysis further assumes that the internal local motions within the apical loop motif of interest do not modulate the overall alignment experienced by the upper helix-apical loop motif. This is a good assumption for compact tetraloops, which dynamics do not contribute to overall changes in shape. The analysis also assumes that the internal dynamics of the studied motif are not correlated with internal motions at the kinked-elongation site^15,47,51. Again this is a good assumption given that changing the kinked motif had minimal consequences on NMR spectra of the cUUCGg apical loop. With these assumptions, the approach can be applied a priori to any non-, straight- or kinked-elongated RNAs¹⁵. The order tensor elements obtained using this approach were very similar to those obtained by fitting the helical RDCs to the idealized A-form geometry but scaled up by a factor of ~1.10 (Table S3). This increase of the magnitude of the alignment is expected due to the explicit consideration of internal dynamics¹⁷.

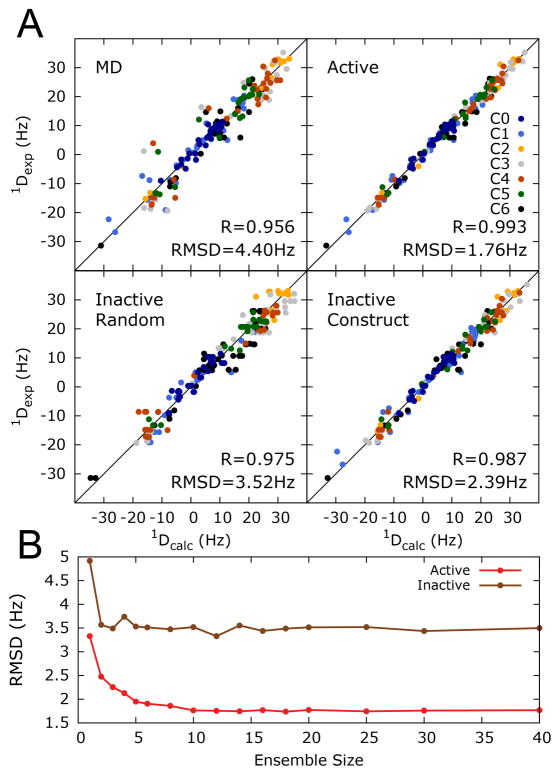
Interestingly, the entire conformational pool generated by the MD trajectory reproduces the RDCs measured in the tetraloop with an RMSD = 4.4 Hz and R = 0.96 (Fig 2A). Similar agreement was observed for another 3x200 ns ff10 AMBER simulation of cUUCGg without the TAR bulge reported recently (data not shown)⁴⁰. This agreement is significantly improved over that observed between RDCs probing the HIV-1 TAR inter-helical conformation and a 8.2 μs MD simulation computed using the CHARMM36 force field (RMSD = 8.6 Hz, R=0.84)³³. The improvement is unlikely due to the use of a different force field, since the same ff10 AMBER simulation poorly predicts the HIV-1 TAR helix-bulge-helix RDCs (RMSD = 10.3 Hz, R = 0.76) (Figure S1). However, the improvement should be treated with caution given that in the inter-helical study of TAR, the overall alignment tensor was computed directly based on shape with one adjustable scaling parameter per construct^33,57 whereas in the current study, all five order tensor elements are optimized to best reproduce the RDC data. It is worth noting that the approach proposed here cannot be applied to the study of inter-domain motion, as soon as the inter-domain dynamics influence the alignment properties of the system. Nevertheless, even if some differences can be expected from the use of different force-fields and order tensor calculation methods, these results support the hypothesis that MD trajectories are more accurate for local motifs lacking global motions or sensitivity to monovalent and divalent cations⁶⁵. It is also possible that the simpler cUUCGg motif allows for better sampling of the conformational space given that RDCs have broad sensitivity spanning ps-ms timescales.

FIGURE 2.

Constructing a cUUCGg tetraloop ensemble using RDCs derived from kinked-elongation and an MD simulation. (A) Agreement between measured RDCs color coded for different kinked-elongated constructs and values back predicted using the MD-generated (0.8μs MD simulation using the AMBER ff10 force field) and RDC-selected ensemble with N=10 conformers (Active). Also shown is the cross-validated agreement between measured RDCs and RDCs that left out from the sample and select analysis when randomly omitting ~13% of the data (Inactive Random) or entire RDC data set for an individual kinked-elongated construct (Inactive Construct). Shown in each case is the Root-Mean-Square-Deviation (RMSD) and Pearson’s correlation coefficient. (B) RMSD between measured and back-predicted RDCs as a function of number of conformers used in the sample and select analysis to construct ensemble. Values are shown when including all RDCs in the selection (active) and for RDCs randomly left out of the selection (inactive).

Constructing an RDC-Satisfying Ensemble of the cUUCGg Hairpin

Although the agreement with the RDCs is better for the cUUCGg hairpin, the RMSD remains slightly larger than measurement uncertainties (between ~2 and 4 Hz depending on construct)³³. Therefore, we used the experimental RDCs and the 10,000 conformer MD pool to construct an ensemble that reproduces RDCs within error. We used a Sample and Select (SAS) like approach⁶⁶ to select a subset of conformers based to their capability to reproduce experimental RDCs⁴⁷. A genetic selection algorithm was used to drive the search for the best-fit ensemble in which the alignment tensor for each construct is determined on the fly using a SVD approach as proposed by Blackledge and coworkers⁶⁷ (Methods). Based on the capability of the selected ensemble to reproduce both active (RDC data used in selecting ensemble) and inactive (RDC data left out during ensemble selection) data an ensemble size of 10 conformers was chosen, as no significant improvement in the data reproduction could be obtained by increasing further the number of conformer in the ensemble. Using a slightly different size would not affect significantly the analysis (Figure 2B and Methods). The selected ensemble reproduces the experimental RDCs to within 1.8 Hz RMSD (R=0.99) when using all RDCs in the selection. The ability to select an ensemble that satisfies the RDCs indicates that the necessary conformational space is sampled in the trajectory but with imperfect relative weights of various conformations.

To further assess the significance of the improvement in the RDC-selected ensembles, we performed cross validation analysis in which the agreement is assessed for RDCs that are left out from the selection either by randomly removing data (RMSD = 3.5 Hz and R=0.98) or removing entire datasets from individual constructs (RMSD = 2.4 Hz R=0.99) (Figure 2 and Methods). The cross-validated agreement remains better than that observed over the entire MD ensemble (RMSD = 4.4 Hz and R = 0.96) indicating that the small changes in the MD ensemble due to RDC-selection are significant. The cross-validated agreement is also improved relative to that of the previous study of the TAR bulge dynamics (RMSD = 4.0 Hz, R = 0.97), suggesting a high level of accuracy in describing the cUUCGg ensemble. Finally, the accuracy of the RDC-selected ensemble was cross-validated based on its capability to reproduce ¹H chemical shifts using the NUCHEMICS software⁶⁸. The RDC-selected ensemble yields a slight improvement (RMSD = 0.19 ppm) over that of the entire MD pool (RMSD = 0.21 ppm).

Comparison of RDC-Selected and MD Ensembles of the cUUCGg Hairpin

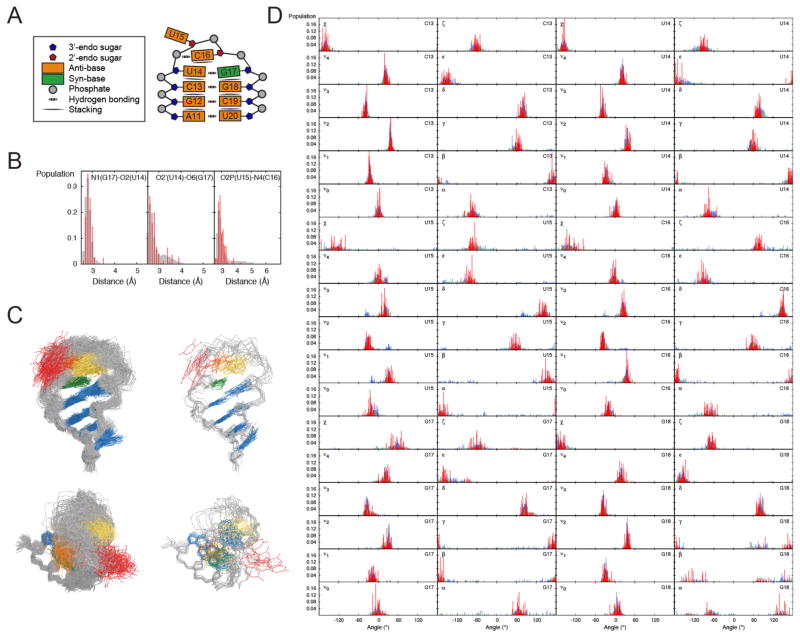
To evaluate the source of minor discrepancies between the measured RDCs and the MD ensemble, we compared the RDC-selected and MD-generated ensembles. High-resolution NMR and X-ray structures of the c13U14U15C16G17g18 hairpin show that c13-g18 forms a canonical WC closing bp (Fig 3A). U14 and G17 forms a trans Watson-Crick/sugar edge involving H-bonds between the carbonyl of U14 and the imino-proton of G17 and the 2′ hydroxyl group of U14 sugar and the carbonyl of G17 base, which adopts a syn conformation. C16 tends to stack onto U14 and its amino proton forms a unique H-bond with the U15-C16 bridging phosphate (Fig 3B). On the other hand, U15 is looped out and flexible. All residues adopt canonical C3′-endo sugar puckers with the exception of central residues U15 and C16, which adopt the C2′-endo sugar pucker.

FIGURE 3.

Comparison of the MD and RDC-selected ensembles for the cUUCGg tetraloop. (A) Schematic representation of the interactions and structural features of the cUUCGg loop. (B) Distance distributions between N1(G17)-O2(U14), O2′ (U14)-O6(G17) and O2P(U15)-N4(C16) that describe the H-bonding interaction between U14-G17 and U15-C16 in the MD (grey) and the RDC-selected ensemble (red) (C) Comparison of 100 randomly selected conformers from the MD (left) and RDC-selected ensemble (right), coordinates are included in the Supporting Information. (D) Comparison of dihedral angle distributions in the cUUCGg loop from the MD (grey), RDC-selected ensembles (red) and ensemble representing the cUUCGg structures in the PDB with (blue) and without (green) bound proteins and ligands.

Comparison of the RDC-selected and MD-generated ensemble reveals good agreement in many key aspects of the apical loop structure (Fig 3C, Supporting Information). For example, we observe minor differences in the distances of the H-bond described above, with the largest difference observed for the U15-C16 H-bond distance, which is slightly shorter following RDC-selection. In both the MD and RDC-selected ensembles, G17 is syn for >90% of the conformations, C16 is stacked on U14 for 25% (ensemble) to 39% (MD) of the conformations, and G17 stacked on C16 for <1% of the conformations. We also observe good agreement in glycosidic, sugar, and backbone torsion angle distributions. In both cases, the angular variability observed correlates with the structural stability of the hairpin (Fig 3D and S2). Thus, the most flexible residue is the flipped out U15 followed by the stacked C16 and with the smallest degree of flexibility observed for the U14-G17 bp. This is also in agreement with prior dynamics studies of this hairpin based on spin relaxation^69,70.

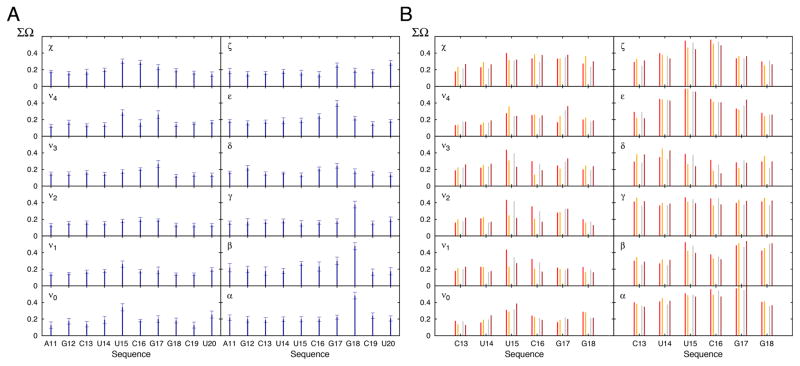
Nevertheless, there are some significant differences between the MD-generated and RDC-selected ensemble (Fig 3D). To help quantify these differences, we used the recently proposed REsemble approach to quantity the differences in angle distributions between the two ensembles (Figure 4A)³⁵. This approach allows to characterize the similarity between two ensembles in a manner that captures both the extent of overlap between the two distributions and extent of similarity between non-overlapping regions³⁵. For two distributions, ΣΩ varies between 1 and 0 for minimum and maximum similarity.

FIGURE 4.

Conformational variability in the MD-derived and RDC-selected ensemble of the cUUCGg hairpin. (A) Shown is the ΣΩ value between the MD and RDC-selected ensemble for all the backbone and sugar dihedral angles. A decrease in ΣΩ indicates an increase in similarity. Error bars are derived from Monte Carlo simulations (Methods). (B) ΣΩ value comparing the structural pool of the cUUCGg loop from the PDB (Methods) and the RDC-selected ensemble (red) or the MD trajectory (grey). Shown in orange and brown is the corresponding comparison when restricting the PDB structures to unbound RNA.

The ΣΩ values are shown in Figure 4A. The largest ΣΩ values are observed for sites that are flexible in both the MD and RDC-selected ensemble. The largest readjustments upon RDC selection were observed for the χ angles of U15 and C16, ε angle of G17, and the α, β and γ angles of G18 and the sugar pucker of U15 and G17 (Figure 3D and Table S4). In general, the RDC-selection tends to homogenize the angle distributions at several of these sites. For example, it decreases the breath of the χ angle distribution for the flipped out U15 and increases it for C16 likely due to decreased stacking with U14 (Fig 3D). The RDC selection tends to re-center the sugar pucker distribution towards the C3′-endo conformation (or C2′-endo for U15 and C16) while the MD more broadly samples the closely related alternate sugar pucker (Fig 3D and Table S5). The largest RDC-directed adjustments in backbone torsion angle distributions occur between G17 and G18, which are also the sites with the largest degree of backbone flexibility consistent with prior ³¹P NMR spin relaxation studies⁷¹. Interestingly, a recent study comparing an MD simulation of a similar cUUCGg tetraloop to NMR RDC and relaxation data also found discrepancies involving G17 and G18 that were attributed to improper behavior of the backbone angles⁴⁰. It is worth nothing that no RDC data were measured on the phosphodiester backbone and this observed changed in dynamics is indirectly driven by its coupling to other sugar and base parameters that affect the measured RDCs. The capability of the approach to indirectly capture these features has been verified using simulated data (Methods, Figures S3 and S4). Also it should be noted that the RDC-satisfying ensemble feature limited local motions within the helix itself (see below) consistent with prior studies⁵⁶.

RDC-Selected cUUCGg Ensemble and Relaxation-Dispersion Data Suggest Rapid Dynamic Sampling of Distinct Structures in the Protein Databank

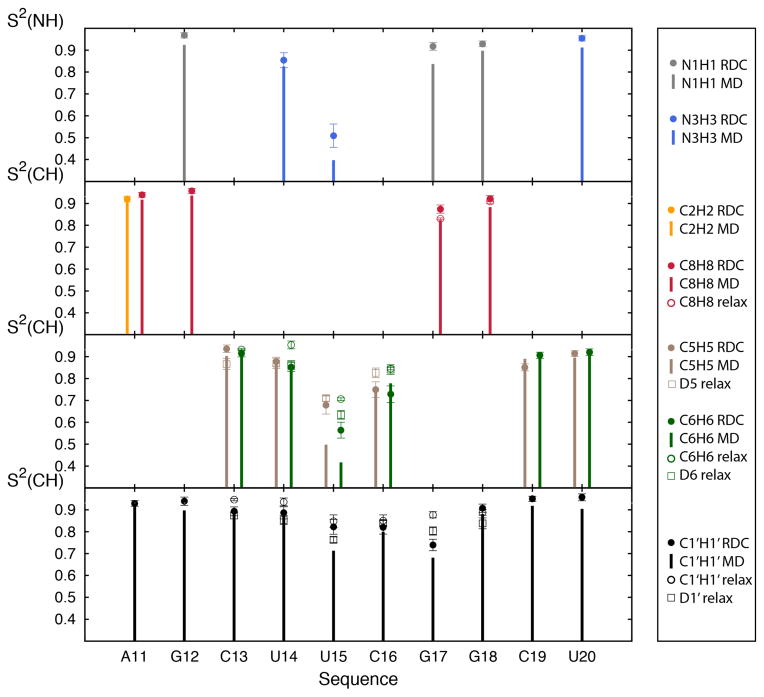
We computed the Lipari-Szabo order parameters for individual bond vectors in bases and sugars (S² which vary between 1 and 0 for minimum and maximum amplitude motions, respectively)⁷² for both the MD and RDC-selected ensemble, and compared the values with those measured previously by ¹³C⁶⁹ and ²H ⁷⁰ NMR spin relaxation. As expected, we observe relatively high order parameters (S² ~ 0.85–0.97) for the helical base pairs (Fig 5). The differences in apical loop S² values derived from the RDC-selected and MD ensemble mirror the trends seen from comparison of the torsion angles with the overall distribution of motions appearing more homogeneous in the RDC-selected ensemble as compared to the MD, possibly indicating that the conformational reorganization happens in a more concerted manner than described by the MD simulation. Once again, the differences in S² values are generally small (<0.1) with exception of the flexible nucleotide U15 for which differences are as large as ~0.2. The MD and RDC-selected ensembles yield S² values that are in good agreement with the experimentally measured values using ¹³C⁶⁹ and ²H⁷⁰ spin relaxation (Figure 5 and S5), suggesting that internal motions in cUUCGg occur primarily at the ps-ns timescale (note that the ¹³C relaxation study did not report the absolute value of S^{2 69}). The order parameters derived from a recent MD simulation also using the ff10 force-field on a related hairpin⁴⁰ are very close to those extracted from the RDC-derived profile (Fig S6). The order parameters from the hairpin are generally somewhat higher in the loop region than those extracted from the HIV-1 TAR MD simulation analyzed here, especially at residues U15 and G17, possibly due to a modulation of the motion by the surrounding sequence, in particular, the G12-C19 bp of HIV-1 TAR being replaced by an A12U19 in the tetra-loop or the use of slightly different initial structures.

FIGURE 5.

Conformational disorder in the cUUCGg tetraloop. Comparison of the order parameter (S²) of several bound vectors N1H1 (grey), N3H3 (blue), C2H2 (orange), C8H8 (red), C5H5 and D5 (brown), C6H6 and D6 (green) and C1′H1′ and D1′ (black). Bars correspond to the order parameters computed for the entire MD trajectory, filled circle to the order parameter computed for the RDC-selected ensemble, open circles to ¹³C spin relaxation order parameter measured on a related cUUCGg tetraloop⁶⁹ and open rectangles to ²H spin relaxation order parameter measured on a related cUUCGg tetraloop⁷⁰. The RNA sequence between the current and ²H relaxation study match only for residues 13 to 18, and differences in sequence could affect order parameters especially for residue 13 and 18. Error bars for the RDC-selected ensemble are obtained using Monte Carlo simulations (see Methods).

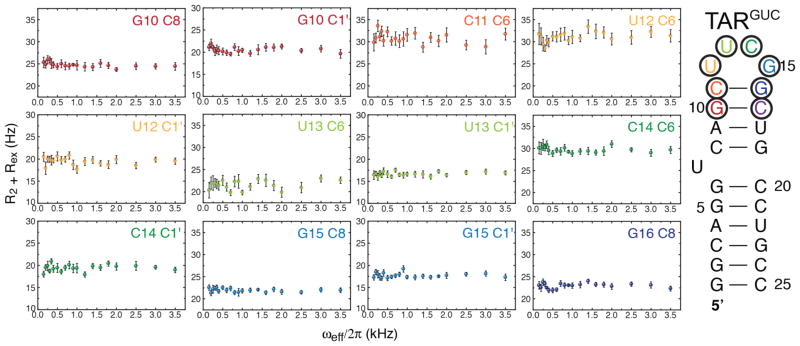
To further investigate slow motions in the cUUCGg loop we measured extensive on-resonance ¹³C spin R_1ρ relaxation dispersion^73,74 data targeting sugar and base carbons (Figure 6). These experiments were carried out using the same buffer conditions as the RDC measurements and employed a different RNA construct (TAR^GUC, Figure 6) which retains identical chemical shifts for the cUUCGg loop as the other constructs studied here (data not shown). None of the sites probed showed signs of relaxation dispersion and chemical exchange, suggesting that this tetra-loop does not undergo significant dynamics on the micro- to milli-second timescales, consistent with the above combined analysis of RDC and spin relaxation data.

FIGURE 6.

Absence of micro to milli-second motions in the cUUCGg tetraloop. On-resonance ¹³C R1ρ relaxation dispersion experiments on various sites in the cUUCGg tetraloop. No significant exchange contributions were found at any site of the construct used (color coded), at pH=6.4 and 298K (see Methods).

Finally, we compared the RDC-selected ensemble to the cUUCGg conformations captured in high resolution crystal structures obtained from the protein databank (Figure 3D and 4B) using the FRABASE database⁷⁵. These structures encompass unbound RNA and RNA in complex with proteins or small molecules (Table S6). Interestingly, despite the different nature of the descriptions, one dynamic ensemble and one collection of static structures, the distributions of local dihedral angles presents overall similar features, including high dispersion of the glycosidic torsion angles in the flexible U15 and C16 nucleotides and backbone torsion angles connecting G17 to G18. Nevertheless, there are cases where the collection of PDB structures samples sub-conformations that are not sampled by the RDC-selected ensemble or MD, particularly for the flexible U15 and to a lesser extent C16. Many of these differences arise form alternate sugar conformations in the PDB. This could possibly arise due to incomplete sampling in the MD, inaccuracies in the X-ray/NMR structure, differences in environmental conditions or crystal packing that affect the conformation. Indeed, we find much better similarity when considering sub-structures in the PDB that do not contain any ligand or protein. The similar ΣΩ values obtained when comparing the structural pool from the PDB to either the MD or the RDC-selected ensemble suggests that the comparison is mainly dominated by the difference in overall sampling rather than the precise distribution of population of the different angular degrees of freedom (Fig 4B). In general, we find that both the MD and RDC-selected ensembles encapsulate most of the conformations of this hairpin in the PDB, suggesting that intrinsic plasticity may play important roles in the conformational adaption of this loop.

Conclusion

We developed a kinked elongation strategy to measure independent RDC data sets on RNA motifs and used this approach to study the dynamics and test MD simulations of a cUUCGg tetra-loop. We observed much better agreement between the measured RDCs and values predicted from the MD simulation as compared to prior studies of inter-helical dynamics across a flexible bulge. The results are consistent with prior studies indicating that the discrepancies between MD simulation and measured RDCs are primarily due to inter-helical motions and not local motions within individual nucleotides. In the case of the cUUCGg apical loop, the largest discrepancies between the RDC data and the MD simulation are centered at the most flexible central residues in the loop, with the RDC-ensemble resulting in more uniform dynamics across the loop as compared to MD. Comparison of the RDC-ensemble with NMR spin relaxation data suggests that the dynamics in the loop occurs predominantly on the ps-ns timescales with limited motions occurring at the slow μs-ms timescales. The RDC-satisfying ensemble of the hairpin captures many of the conformations adopted by this motif in the protein databank indicating that intrinsic plasticity may play important roles in conformational adaptation. The approach presented here can immediately be applied to test force fields and characterize dynamics in diverse RNA motifs at atomic resolution.

Methods

Sample Preparation

The measurement of RDCs for C1, C2, C3, C5 and C6 were reported previously^15,31,51. The measurements were carried out using identical buffer (15 mM sodium phosphate, 25 mM sodium chloride, 0.1 mM EDTA, and ~10% D₂O) at pH ~ 6.4 and 298 K, with RNA concentration between ~0.6–1.2 mM and that of Pf1 phage ranging between 6 and 22 mg/mL depending of the level of elongation of the construct. The unlabeled RNA construct (C0) was purchased Thermo Fisher Scientific, dissolved in water, refolded, and exchanged into the same NMR buffer (15 mM sodium phosphate, 0.1 mM EDTA, 25 mM NaCl, pH 6.4, 10% D₂O). For measuring RDCs, the sample was concentrated by a factor of two and Pf1 phage solution (Asla Biotech) was added to reach a final phage concentration of ~25mg/mL. The RNA sample concentration was ~2 mM. Uniformly ¹³C/¹⁵N labeled C4 was prepared by in vitro transcription and purified using polyacrylamide gel electrophoresis (PAGES) following the procedure described previously¹⁵. The RNA sample was exchange into the same NMR buffer with final RNA concentration of ~0.75 mM and Pf1 phage concentration of ~8mg/mL.

The TAR^GUC RNA sample was prepared by in vitro transcription using T7 polymerase (Takara Bio, Inc.), uniformly ¹³C/¹⁵N-labeled NTPs (Isotec) and PAGE-purified DNA oligonucleotide (IDT, Inc.) containing the T7 promoter sequence, as previously described⁷⁶. The product was purified by 20% denaturing (8M Urea) polyacrylamide gel electrophoresis, extracted using an Elutrap electro-elution system (Whatman) and further purified by ethanol precipitation. The pellet was redissolved in NMR buffer (15 mM Sodium Phosphate pH 6.4, 25 mM Sodium Chloride, 0.1 mM EDTA) and extensively exchanged against the same buffer using an Amicon Ultra-4 centrifugal filter (NMWL 3 kDa). The final RNA concentration was ~1 mM.

Resonance Assignment of TAR^GUC

The assignment for the TAR^GUC was obtained at 298K using standard ¹H,¹³C- and ¹H,¹⁵N-heteronuclear single-quantum correlation (HSQC), HCN, and ¹H,¹H-Nuclear Overhauser effect spectroscopy (NOESY) experiments. All assignment were in excellent agreement with previously published results⁷⁷.

RDC Measurements

All NMR measurements were carried out at 298K on 600 MHz Varian or Bruker spectrometers equipped with a triple resonance cryogenic probes with pulse field gradients. The ¹H-¹³C J couplings and RDCs were measured in the base and sugar using transverse relaxation-optimized spectroscopy (TROSY) and HSQC experiments with the doublet encoded in the ¹³C dimension. The ¹H–¹⁵N couplings were measured using SOFAST imino-HMQC with the splittings encoded in the ¹H dimension. Data was processed using NMRPipe⁷⁸ and analyzed with Sparky⁷⁹.

Carbon R₁₃ Relaxation Dispersion

NMR experiments were performed on a Bruker Avance 600 MHz spectrometer equipped with a 5mm triple-resonance HCN cryogenic probe at 298 K. R_1ρ relaxation dispersion (RD) profiles were measured as described previously⁷⁴. On-resonance relaxation dispersion profiles were collected with the following series of relaxation delays [0, 4, 8, 12(2x), 16, 20, 26, 32 (2x) ms] for C6/C8 and [0, 4, 8, 12 (2x), 18, 26, 34, 42 (2x)] for C1′ spins, and applied spin-lock powers [100, 200, 250, 300, 350, 400, 500, 600, 700, 800, 900, 1000, 1200, 1400, 1600, 1800, 2000, 2500, 3000, 3500 Hz]. R_1ρ values were obtained from monoexponential decay fits of resonance intensities analyzed with Mathematica (Wolfram Research, Inc.) and plotted with Origin 8.5 (OriginLab). All data showed negligible R_1ρ dependence on spinlock power (R_ex) and was determined to have no detectable exchange using an F-test to discriminate between a two-state exchange model described by the Laguerre approximation equation⁸⁰ and a no exchange model (data not shown).

Order Tensors Analysis

For each construct, RDCs measured for nucleotides A11, G12, C13, G18, C19 and U20 were subjected to an order tensor fit assuming an idealized A-form helix geometry⁵⁶ with corresponding RNA sequence using the software RAMAH⁸¹. The scalar products between order tensors were computed as described by Sass at al⁸².

Molecular Dynamic Simulations

MD simulations were carried out using the UUCG capped HIV-1 TAR sequence C1 GGCAGAUCUGAGCUUCGGCUCUCUGCC (see Figure 1). Simulations were performed with the CPU and GPU versions of PMEMD MD engine from the AMBER simulation suite of programs^83–85. All simulations used the ff10 Amber force field for nucleic acids⁵⁹ and the χ glycosidic torsion angle^60,61,86, the TIP4P-Ew water model⁸⁷ together with the associated monovalent ion parameters⁸⁸.

The simulated system contained the HIV-1 TAR RNA construct, a total of 17386 water molecules, 71 cations (Na^-) and 45 anions (Cl^-), which corresponds to an approximate salt concentration of 0.140 M. The initial RNA conformations were taken from the structures with PDB ID 1ANR⁸⁹, 2KX5⁹⁰, 1LVJ⁹¹, and 1UUI⁹². The apical loop present in all these wild-type sequences was replaced with a UUCG tetraloop taken from the HIV-II TAR structure with the PDB ID 2KMJ. Four independent simulations were run for approximately 200ns, resulting in a total of 800ns total simulation time.

All the molecular dynamics simulations were run using periodic boundary conditions using rhombododecahedral symmetry. Prior to the production run a total of 20 ns of equilibration of water and ions was run where the RNA conformation was restrained, followed by 20 ns of equilibration where the restraints on the RNA were removed. The equilibration stage was run using constant temperature and pressure (NPT ensemble). Temperature was regulated using the Langevin thermostat with a collision frequency of 5ps⁻¹. Pressure was controlled using the Beredensen barrostat with using a relaxation time of 5ps. The production stage was run in the microcanonical ensemble (NVE). Numerical integration was performed using the leap-frog Verlet algorithm with 1 fs time steps. Covalent bond lengths involving hydrogen atoms were constrained using the SHAKE algorithm with a tolerance of 10⁻⁶.

RDC Ensemble Selection

RDC-satisfying ensembles were selected using a selection algorithm that is based on a sample and select principle implemented in the SVD-based ASTEROIDS approach developed by Blackledge and coworkers^67,93 but adapted for RNAs. The selection procedure is based on a genetic algorithm, used to select, without any possible repetition, an ensemble of size N within a pool of size M. In this study, the selected ensemble were typically of size N=10 and the initial starting pool contained M=10000 conformers. At each step in the selection procedure the set of P ensembles are generated either by random generation of new ensembles, by crossing of two ensembles from the previous round, or by mutating a previously obtained ensemble. For the initiation step the ensembles are simply randomly generated. In this study 6000 evolution steps where used with P=100 ensemble selected at each step. The selection in made by pooling the P ensembles in T different tournaments and keeping from each of the tournaments the best-suited members, i.e. the ensemble ensuring the best reproduction of the experimental data according to a classical χ² function:

$${\chi }^2=\sum _{i,j,k}\frac{{\left(D_{i,j,k}^{\mathit{calc}}-D_{i,j,k}^{\mathit{exp}}\right)}^2}{{\delta }_k^2}$$

where k represents different RDC types, i different nucleotides, and j different constructs. δ_k is a weighting factor that was fixed here to the theoretical range of the dipolar interaction:

$${\delta }_k=\frac{{\gamma }_I{\gamma }_S{\mu }_{0}h}{16{\pi }^3{r}_{IS}^3}$$

where γ_I and γ_S the gyromagnetic ratio of spins I and S, respectively. r_IS the inter-spin distance, μ₀ the permeability of vacuum and h the Planck constant. The procedure was repeated 10 times for each calculation, and the final ensemble that best fit the experimental RDC was selected as the final ensemble.

Indirect Analysis and Cross-Validations

10 new RDC datasets were generated by randomly removing 2 RDCs per nucleotide over the different constructs. Each new RDC dataset was submitted to the selection procedure. As for direct analysis, this procedure was repeated 10 times, and the ensemble with the best active χ² is kept and then used to back-calculate the removed RDCs.

For the cross-validation with the constructs the same procedure was applied but instead of randomly removing couplings the dataset for each different constructs were removed successively.

Monte Carlo Error Analysis

A Monte Carlo strategy was used to estimate uncertainties in order tensor and ensemble parameters. 250 pseudo-experimental RDC data sets were generated by independently noise corrupting the back-predicted RDCs from the best-selected ensemble (with ensemble size of 10). Errors bars were obtained by computing the standard deviation of the corresponding parameters over the 250 ensembles obtained using the different noise corrupted datasets.

Ensemble Analysis

The calculation of backbone and sugar dihedral angles were preformed using in-house programs following previously established convention. All order parameters where calculated using the following equation⁶⁴:

$$S^2=\frac{1}{2}\left(3\sum _{i=1}^3\sum _{j=1}^3{\langle {\mu }_i{\mu }_j\rangle }^2-1\right)$$

where μ_i represent the Cartesian coordinates of the ith normalized inter-nuclear vector, after alignment of all the conformers on an A-form idealized helix (using backbone heavy atoms of A11, G12, C13, G18, C19 and U20). Error bars were obtained through Monte Carlo analysis (vide supra).

REsemble analysis

The REsemble analysis was carried out as previously described³⁵.

Tests using simulated data

Two target ensembles were generated by randomly selecting 2000 structures from the MD pool using the following criteria:

• Case 1: Based on the β angle of nucleotide 18 and using a probability of acceptance centered at 160° and standard deviation 20°.

• Case 2: Based on the δ angle of nucleotide 17, using a probability of acceptance centered at −60° and standard deviation 30°.

From these two target ensembles, synthetic RDCs corresponding to the experimentally determined RDCs were generated assuming the order tensors in Table S1 and noise corrupted with noise corresponding to the weights used in the selection. The selection procedure was applied 100 times with an ensemble size of N=10.