Unveiling Inherent Degeneracies in Determining Population-weighted Ensembles of Inter-domain Orientational Distributions Using NMR Residual Dipolar Couplings: Application to RNA Helix Junction Helix Motifs

Abstract

A growing number of studies employ time-averaged experimental data to determine dynamic ensembles of biomolecules. While it is well known that different ensembles can satisfy experimental data to within error, the extent and nature of these degeneracies, and their impact on the accuracy of the ensemble determination remains poorly understood. Here, we use simulations and a recently introduced metric for assessing ensemble similarity to explore degeneracies in determining ensembles using NMR residual dipolar couplings (RDCs) with specific application to A-form helices in RNA. Various target ensembles were constructed representing different domain-domain orientational distributions that are confined to a topologically restricted (<10%) conformational space. Five independent sets of ensemble averaged RDCs were then computed for each target ensemble and a ‘sample and select’ scheme used to identify degenerate ensembles that satisfy RDCs to within experimental uncertainty. We find that ensembles with different ensemble sizes and that can differ significantly from the target ensemble (by as much as ΣΩ ~ 0.4 where ΣΩ varies between 0 and 1 for maximum and minimum ensemble similarity, respectively) can satisfy the ensemble averaged RDCs. These deviations increase with the number of unique conformers and breadth of the target distribution, and result in significant uncertainty in determining conformational entropy (as large as 5 kcal/mol at T = 298 K). Nevertheless, the RDC-degenerate ensembles are biased towards populated regions of the target ensemble, and capture other essential features of the distribution, including the shape. Our results identify ensemble size as a major source of uncertainty in determining ensembles and suggest that NMR interactions such as RDCs and spin relaxation, on their own, do not carry the necessary information needed to determine conformational entropy at a useful level of precision. The framework introduced here provides a general approach for exploring degeneracies in ensemble determination for different types of experimental data.

INTRODUCTION

There is great interest in developing methods for determining population-weighed dynamic ensembles of biomolecules using experimental data^1–8. The ensemble describes the energetic preferences of the many conformations that are typically sampled by a biomolecule in solution. This information in turn is critical for achieving a quantitative understanding regarding processes such as folding^9–10, enzymatic catalysis^11–14, and adaptive recognition^15–17. In particular, the ensemble description provides a route for determining the free energy and entropy contributions to such processes arising due to conformational changes in biomolecules^18–22. Common approaches used to determine dynamic ensembles of biomolecules seek to identify not a single static structure, but rather, an ensemble of population-weighted conformations that reproduces time-averaged experimental data within error²³. The data that has been used so far include several NMR interactions such as residual dipolar couplings (RDCs)^24–30, the Nuclear Overhauser effect (NOE)^31–32, paramagnetic relaxation enhancements (PRE)³³, chemical shifts (CS)^34–36, as well as X-ray diffraction³⁷ and small angle X-ray scattering (SAXS) and gold-SAXS data^38–39. These data can have distinct spatial and temporal sensitivities and have been applied to determine ensembles for biomolecules including globular well-folded proteins, DNA, RNA, and intrinsically disordered proteins^40–43. In particular, studies have examined the utility of RDCs in determining population-weighted ensembles of nucleic acids^7,24,28 and protein^1,2,25. These ensembles have provided important insights into functionally important motions including the role of dynamics in molecular recognition^7,28,25. Despite advances in using such experimental approaches for determining dynamic ensembles of biomolecules, the source and magnitude of the uncertainties in ensemble determination are not fully understood.

Despite advances in experimental approaches for determining dynamic ensembles of biomolecules, the source and magnitude of uncertainties in ensemble determination are not fully understood. Rather, many ‘degenerate’ ensembles can typically satisfy data to within experimental error. Such degeneracies have not yet been rigorously explored for ensemble determination though they have long been recognized as a major source of uncertainty even when determining single-static structures by NMR spectroscopy and X-ray crystallography^44–45. Bayesian approaches⁴⁶ make it possible to estimate uncertainties in the populations of conformers in an ensemble, but they require a prior distribution, and can be computationally expensive. Understanding the nature of the degeneracies associated with a given type of experimental data is not only important to avoid over interpreting data, but also, to guide the design of approaches for optimally addressing these sources of uncertainty.

One of the challenges in determining degeneracies in ensemble determination, and more generally, in evaluating the accuracy with which ensembles can be determined using various methods, is the lack of metrics that can be used to quantitatively compare the similarity between two ensembles, for example, a target ensemble that is used to predict experimental data, and ensembles that are generated that satisfy the data. Commonly used metrics such as Jensen-Shannon divergence (Ω²)^46–48 and the S-score⁴⁹ and measure the extent of overlap between two ensemble distributions but fail to quantify the extent of structural similarity between non-overlapping parts⁴⁸. Moreover, these measures of ensemble similarity can vary significantly depending on the size of the bin used to create the histogram distribution⁴⁸. Recently, we introduced an approach for overcoming this problem that relies on summing the square root of Jensen-Shannon divergence (Ω) over variable bin size⁴⁸. In particular, the normalized value of Ω summed over variable bin sizes (ΣΩ) is a metric that varies between 0 and 1 for perfect and zero similarity, respectively between two ensembles (see Methods). Here, we use ΣΩ and simulations to quantitatively examine degeneracies in determining ensembles with the use of NMR residual dipolar couplings (RDCs)^50–51 measured in partially aligned systems.

There has been great interest in recent years to harness the broad time-scale and rich spatial sensitivity of RDCs in determining dynamic ensemble of biomolecules^24–30. Here, we focus specifically on the problem of using RDCs to determine ensembles defining inter-domain orientation distributions. Domain-domain motions can significantly reorganize a biomolecule and play important roles in catalysis, ordered assembly of complexes, and adaptive recognition^52–54. While our study will focus on RNA A-form helices and RDCs, the conclusions deduced equally apply to any chiral domain and extend to other anisotropic interactions such as residual chemical shift anisotropies (RCSA)⁵⁵.

The determination of inter-helical ensembles for locally rigid A-form domains represents a best-case-scenario ensemble determination problem. First, one can pool together a large number of RDCs measured for various bond vectors within a domain to characterize what amounts to only three Euler angles describing the relative orientation of the two domains (Figure 1A). This is in contrast to determining an atomic resolution ensembles in which RDCs are parsed to determine distributions for many local degrees of freedom^{46, 49}. Second, a realistic and highly restricted range of inter-helical orientations can be defined a priori in an unbiased manner based on simple topological constraints encoded by the junctions linking helices^56–59. This obviates the need to rely on conformational pools derived from other methods such as molecular dynamics (MD) simulation in which correlations between various degrees of freedom can affect conformational sampling and data analysis. In addition, the topologically allowed conformational space is restricted to <10% of the total Euler space. This reduced conformational space captures realistic stereochemical constraints that serve to minimize degeneracies in ensemble determination. Our simulations also assume the theoretical maximum of five independent RDC data sets^60–63, originating from five alignment tensors that are assumed to be known a priori, and decoupling limit in which one domain fully dominates alignment, thus avoiding any complications arising due to correlations between internal motions and overall reorientation^{7, 28}. This framework allows us to hone in on the maximum information contained within second rank anisotropic interactions, and specifically, the twenty-five Wigner rotation elements that describe the information carried by five independent sets of RDCs in locally rigid domains⁶⁴.

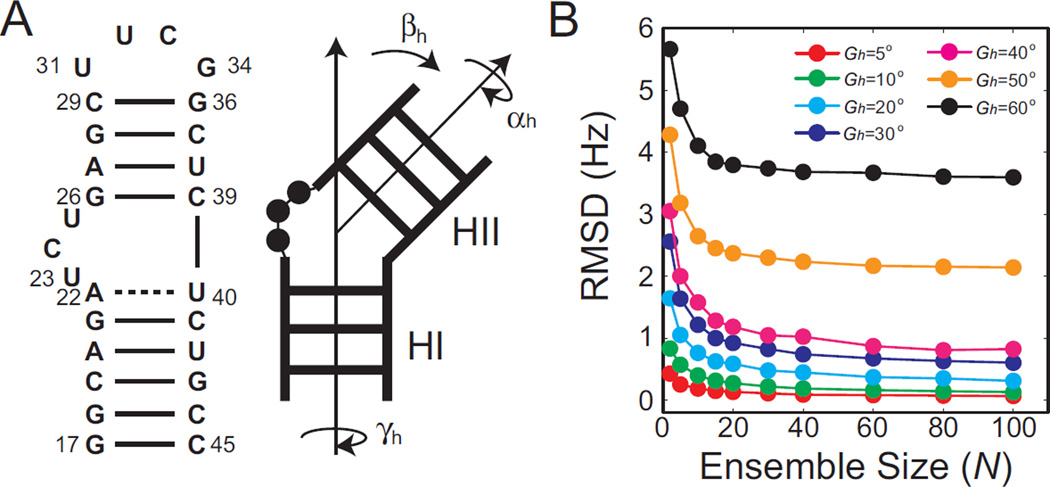
Figure 1. Defining an optimal grid size for binning histogram distributions of inter-helical angles.

(A) Secondary structure of the HIV-1 TAR used to model the two A-form helices linked by a bulge HJH motif and the inter-helical angles (α_h β_h γ_h) describing the relative orientation of the two A-form helices. (B) RMSD between five sets of RDCs calculated for ensembles derived from an MD simulation of HIV-1 TAR with variable size (N) and the RDC computed for corresponding grid-approximated conformational ensembles binned using variable grid size (Gh).

Our results reveal that ensembles with very different ensemble sizes and that can differ significantly from the target ensemble (by as much as ΣΩ ~ 0.4) can satisfy the ensemble averaged RDCs. These deviations increase with number of conformers in the target ensemble size, breadth of the distribution, and result in significant uncertainty in determining conformational entropy (as large as 5 kcal/mol at T = 298 K). Nevertheless, the RDC-degenerate ensembles are biased towards populated regions of the target ensemble, and capture other essential features of the distribution, including the shape.

METHODS

Conformational pool

All simulations for reconstructing ensembles employed a conformational pool of RNA inter-helical orientation consisting of two idealized A-form helices that are tethered together with a trinucleotide bulge helix-junction-helix (HJH) motif. The ‘lower’ helix was fixed and aligned with its helix axis oriented along the molecular z-direction. The ‘upper’ helix that was pivoted by placement of the phosphorus atom of the first nucleotide in the 3’ strand to the origin of the coordinate frame ^57–59 (Figure 1A). The orientation of the upper helix relative to the lower helix is then specified using three inter-helical Euler angles (α_h, β_h, γ_h) (Figure 1A). α_h and γ_h specify a rotation around the helical axis of the upper and lower helices respectively, and β_h is the inter-helical bend angle (Figure 1A). The topological pool of allowed inter-helical conformations was constructed as described previously⁵⁸ and consisted of all allowed inter-helical orientations subject to two topological constraints: i) helices cannot sterically collide with one another and ii) O3′(i) and P(i + 1) in the 3′ and 5′ helices across the bulge, respectively, cannot exceed the bulge linker length (4.9 Å per nucleotide)^57–59. First, a non-degenerate Euler grid is generated by incrementing each of the three angles by 5° (i.e. each conformation differs from its closest neighbor by a 5° change in one of the three Euler angles)^57–59. Note that each point on the grid represents a unique conformation. Next, all inter-helical orientations that fail to satisfy the above two topological constraints are discarded. For the trinucleotide bulge, only <10% of the space is topologically allowed. Note that for more complex RNA HJH motifs, the coarse grain model TOPRNA⁶⁵ can be used to construct the typologically allowed inter-helical conformations. Additional simulations were carried out using an unrestricted conformational pool (see DISCUSSION and Supplementary Materials). This conformational pool is constructed by Euler angles (α_h, β_h, γ_h) ranging from −180° to 180° without degenerate Euler degeneracy (α_h±180, ±β_h, γ_h±180)^57–59.

Grid Size

An optimum grid size of 5° for the conformational pool was selected that yields the lowest number of total conformations in the pool needed to reproduce a given set of RDC to within experimental uncertainty (<0.5 Hz). It was selected as following. A target ensemble containing N conformations was constructed by randomly selecting conformations from a 8.2µs MD simulation of HIV-1 TAR²⁸ (see Identifying RDC-satisfying ensembles using sample and select). Next, each conformer in the selected ensemble was binned to a 3D Euler grid with grid size G_h (see Measuring similarity between RDC-satisfying and target ensembles). The binning is preformed as described previously⁴⁸ by calculating the amplitude of single axis rotation that transforms the inter-helical orientation in a given conformer and every point on the grid, and the conformer is binned to the grid point with minimum amplitude single axis rotation i.e. to the grid point that is most similar to the selected conformer. In the case that more than one grid points show identical amplitude of single axis rotations, the grid point is set to be the one with smallest value of α²+β²+γ². For both target and grid-approximated ensemble, five sets of ensemble averaged RDCs were then computed (see Computing RDCs) assuming five independent sets of hypothetical alignment tensors anchored on the lower helix⁴⁸. The root-mean-square-deviation (RMSD) between the ensemble averaged RDCs for the target and grid-approximation was then computed and compared to RDC experimental uncertainty.

Building target ensembles

We examined RDC-satisfying ensembles for four types of target ensembles (i) Gaussian ensembles which are generated by restricting all three Euler angles in an Gaussian distribution with a specified standard deviation (σ= 10° or 30°) applied equally to all three Euler angles (ii) Random ensembles in which conformations are selected randomly from the topological pool (iii) discrete ensembles with N≤4 and (iv) ensemble of HIV-1 TAR inter-helical orientations obtained from an 8.2 µs MD trajectory generated using the CHARMM36⁶⁶ force field on Anton supercomputer⁶⁷. Ensembles (i)-(iii) were constructed using the topologically allowed inter-helical orientations for a 3-0 bulge⁵⁸. The Gaussian ensembles were constructed by randomly picking a conformation (α_m, β_m, γ_m) as the mean conformation and then randomly selecting conformers from the pool and accepting them with a probability calculated using three Gaussian distributions on three Euler angles respectively: $P_m=\frac{1}{\sigma \sqrt{\pi }}\text{exp}(-\frac{{(x-x_m)}^2}{{\sigma }^2})$ in which x=α, β, γ and x_m=α_m, β_m, γ_m and σ is the pre-defined width of the Gaussian target ensemble. A random number r varying between 0 and 1 is then generated and compared to all three Gaussian probabilities. The randomly selected conformation is accepted to construct the Gaussian target ensemble if and only if r is smaller than all three Gaussian probabilities. While the Gaussian target ensemble allows different conformations to carry different population weights, the random ensemble consists of distinct conformations with equal population weight.

Computing RDCs

Five synthetic RDC data sets corresponding to five perfectly orthogonal alignment tensors⁶⁴ were computed for all C-H vectors in the two helices of HIV-1 TAR assuming a standard A-form helical geometry⁶⁸. The five orthogonal alignment tensors were fixed on the reference lower helix and generated using the Gram-Schmidt procedure ⁶⁴. For each of the five alignment tensors, RDCs were computed using equation 1.

$$D_{\mathit{\text{ij}}}^{\mathit{\text{calc}}}=-\frac{{\mu }_0{\gamma }_i{{\gamma }_j}^h}{8{\pi }^3\langle r_{\mathit{\text{ij}}}^3\rangle }\langle \frac{3{\mathit{\text{cos}}}^2\theta -1}{2}\rangle =-\frac{{\mu }_0{\gamma }_i{{\gamma }_j}^h}{8{\pi }^3\langle r_{\mathit{\text{ij}}}^3\rangle }{\sum }_{k,l}{S}_{\mathit{\text{kl}}}\mathit{\text{cos}}{\varphi }_k\mathit{\text{cos}}{\varphi }_l$$ (1)

where γ_i and γ_j are the gyromagnetic ratios of spin i and j respectively; µ₀ is the magnetic permittivity of vacuum; h is the Plank’s constant; r_ij is the separation between spin i and j, and θ represents the angle between the internuclear vector connecting spin i and j and the external magnetic field; S_kl (k, l = x, y, z) are the elements of the alignment tensor represented in Cartesian form; ϕ_n is the angle between the bond vector and the corresponding n^th axis (n = x, y, z).

For all ensembles used in this study, RDCs were computed for each conformation in an ensemble and averaged over all conformations to generate ensemble-averaged RDCs. The averaged RDCs were then error-corrupted by adding to each RDC a number randomly selected from a normal distribution with standard deviation equal to the assumed RDC error.

Identifying RDC-satisfying ensembles using sample and select

We use the computed RDCs and sample and select (SAS) approach^8,24 to determine population-weighted inter-helical ensembles that satisfy RDCs to within experimental uncertainty. Here, RDCs were used to guide selection of N distinct conformations from a topological pool containing thousands of conformations such to identify ensembles that satisfy the measured RDCs. The initial N distinct conformations are randomly selected from the pool and the agreement between measured and predicted RDCs, χ², is computed using equation 2.

$${\chi }^2={\sum }_{i=1}^L{(D_i^{\mathit{\text{calc}}}-D_i^{\text{exp}})}^2/L$$ (2)

where L is the number of RDCs. Next, one of the conformations is replaced randomly by another conformation from the remaining conformations in the pool, and the agreement with measured RDCs is re-examined and the newly selected conformation is either accepted or rejected based on the Metropolis criteria: at each step (k) of the selection procedure, the change from step k to k+1 is accepted if χ² (k+1) < χ² (k); if χ² (k+1) ≥ χ² (k) with a probability P=exp((χ² (k)-χ² (k+1))/T), where T is an effective temperature that is linearly decreased using a simulated-annealing scheme^8,24. The initial effective temperature is set sufficiently high so that >99% of the conformations can be replaced and slowly decreased until the acceptance probability is smaller than 10⁻⁵. At each effective temperature, 200,000 steps were implemented followed by a decrease of effective temperature using T_i+1=0.9T_i. Using such a simulated annealing based approach, many SAS iterations are carried out until the penalty function shown in equation 2 is minimized, defined as achieving the best agreement with the measured RDCs at ensemble size N. The population-weighted ensemble is then constructed by combining the sub-ensembles from all SAS iterations.

Note that in the SAS analysis, a given conformation can only be selected once such that the reconstructed ensemble consists of equally populated conformations. Since the grid (G_h=5°) is significantly smaller than the RDC-distinguishable resolution (Figure 1B), ensembles with asymmetric population distributions can be obtained naturally by varying the number of neighboring conformations selected around a specific grid point. We avoid selecting the same conformation more than once to maximize sampling efficiency.

Measuring similarity between RDC-satisfying and target ensembles

The accuracy of RDC-determined ensembles was evaluated using a recently developed REsemble method⁴⁸. In this approach, one computes the similarity between a target and RDC-determined ensembles at different bin sizes using the square root of Jensen-Shannon divergence (JSD), Ω, as shown in equation 3^46–48.

$$\mathrm{\Omega }(w_i^T(m),w_i^P(m))=\sqrt{S\left(\frac{w_i^T(m)+w_i^P(m)}{2}\right)-\frac{1}{2}\left[S\right(w_i^T(m))+S(w_i^P(m)\left)\right]}$$ (3)

in which $\{w_i^T(m)\}\text{and}\{w_i^P(m)\}$ represent the population weights for the i^th bin in ensemble T and P, respectively for a given bin size, m. S(w_i)=−Σw_i(m)log₂w_i(m) in equation 3 is the information entropy. Ω varies between 0 and 1 for maximum and minimum similarity, and is equal to zero if and only if $\{w_i^T(m)\}=\{w_i^P(m)\}$. The sum of population overlap over all bin sizes normalized relative to values expected for worst prediction (e.g. random selection without guidance by RDCs) provides a convenient single-value measure of population overlap and structural similarity which we refer to as ΣΩ(w^T, w^P) that ranges between 0 and 1 for perfect and zero similarity, respectively,

$$\sum \mathrm{\Omega }(w^T,w^P)=\frac{{\sum }_m\mathrm{\Omega }(w_i^T(m),w_i^P(m))}{K}$$ (4)

in which K is the normalization factor. Note that ΣΩ(w^T, w^P) is also a metric, and therefore symmetric ΣΩ(w^T, w^P) = ΣΩ(w^P, w^T) and equal to zero if and only if two distributions are identical at all bin sizes or {w^T}={w^P}.

To measure the similarity between two ensembles, one has to have the ability to measure the similarity between distinct conformations within each ensemble. In the Euler conformational space, the straightforward Cartesian distance, ((α_hA- α_hB)² + (β_hA- β_hB)² + (γ_hA- γ_hB)²)^1/2 between two sets of Euler angles A and B defining two distinct inter-helical orientations does not provide a measure of structural similarity between the two conformations and in general, the Cartesian distance between Euler angles can be smaller than, equal to or larger than the actual difference between two conformations⁴⁸. Therefore we used the amplitude of single axis rotation to bin inter-helical orientations together and measure similarity between ensembles.

The binning grid points are constructed by picking a binning origin, defined by minimum value of each of the three Euler angle in the two ensembles upon comparison, and then incrementing each Euler angle by an amount defined by the bin size to cover the entire non-degenerate 3D Euler space. Next, the amplitude of a single axis rotation (ω) connecting a given conformation in the ensemble defined by Euler angles (α_h1, β_h1, γ_h1) and a point on the grid (α_h2, β_h2, γ_h2) is computed,

$$R({\alpha }_{h1},{\beta }_{h1},{\gamma }_{h1})=O(x,y,z,\omega )R({\alpha }_{h2},{\beta }_{h2},{\gamma }_{h2})$$ (5)

in which O(x, y, z, ω) represents a single axis rotation about a unit vector (x, y, z) with amplitude (ω) and the rotation amplitude ω is given by,

$$\omega =\mathit{\text{across}}\left(\frac{O_{11}+O_{22}+O_{33}-1}{2}\right)$$ (6)

in which O₁₁, O₂₂ and O₃₃ are the three diagonal elements of O(x, y, z, ω).

In this manner, the amplitude of the single axis rotation connecting a given conformation in an ensemble to every grid point is computed, and the conformation is binned to the grid point that leads to the minimum single axis rotation amplitude ω. In the case that more than one grid points show identical amplitude of single axis rotations, the grid point is set to be the one with the smallest value of α² + β² + γ². The population of each grid point is then calculated to be the number of conformations binned divided by the total number of conformations in the ensemble. In our case, binning of the target and the predicted ensemble led to two population distributions on the same set of binning grids for a given bin size, and the value of Ω between the two ensembles at the given bin size (bin size ranges from 0° to 180° in increments of 10°) is then calculated using equation 3.

Calculating ensemble conformational entropy

The conformational entropy S for population-weighted ensembles can be computed using equation 7:

$$S=-R{\sum }_i{p}_i\mathit{\text{log}}{p}_i$$ (7)

where R=1.987*10⁻³ kcal/mol/K is the gas constant and p_i is the population of the i^th conformation in the ensemble.

RESULTS

Defining an experimentally informed grid size for binning histogram distributions

It is generally not feasible to enumerate each and every conformation in an ensemble and experimentally determine its population weight. Two distinct conformations in the ensemble may not be distinguishable experimentally either because they differ in features that are not sensed by the data or because they do not differ sufficiently so as to give rise to experimental observations that differ within measurement uncertainty. Most ensemble determination approaches approximate the complex distribution into a discrete histogram distribution^43,46,48. Here, the histogram bin size should be small enough to ensure that it properly captures the target ensemble distributions in so far as accounting for the time-averaged experimental data. Bin sizes that are larger than optimum can result in rough approximations that fail to capture features of the ensemble that is sensed by the experimental data whereas smaller bin sizes push the resolution limit beyond that achievable by the data and unnecessarily increases the conformational space that needs to be sampled.

In the context of defining the relative orientation of two domains using RDCs, we can define a 3D Euler grid covering all of the unique and topologically allowed (see Methods) inter-helical orientations^56–59 (Figure 1A). The three Euler angles are incremented by a grid size given by G_h. Conformers in a given arbitrary ensemble can then be binned into their nearest points on the 3D grid, defined as the conformer that differs by the smallest amplitude single axis rotation⁴⁸ (see Methods). We then asked the question; how small of an Euler grid size is needed when binning inter-helical ensembles to account for an ideal set of five independent sets of RDCs? We computed five sets of independent ensemble averaged RDCs for target ensembles with varying size (number of unique conformations, N = 1 – 100) that were randomly selected from an 8.2µs MD simulation for HIV-1 TAR²⁸. We then binned all conformers in the ensemble to a set of grids with varying grid size G_h (grid-approximated ensemble, see Methods) and computed the expected RDCs for the grid-approximated ensemble. We then examined whether the RDCs for the target and grid-approximated ensembles are distinguishable based on typical RDC experimental uncertainty. These simulations assume alignment levels of S_zz ~10⁻³.

As expected, the RMSD between the target and grid-approximated ensemble RDCs decreases with the decreasing grid size. Thus, as the grid size decreases, the grid-approximated ensemble becomes more similar to the actual target ensemble resulting in similar ensemble-averaged RDCs. Conversely, as the grid size increases, the grid-approximated ensemble differs considerable from the target ensemble resulting in increasing RDC RMSD values. Note that large increase in RMSD between G_h = 40° and G_h > 40° can be attributed to a rapid drop in number of unique conformations that are used to bin the ensemble for this particular target ensemble (Figure 1B).

The RDC RMSD between the target and grid-approximated ensembles also decreases with increasing number of unique conformations in the target ensemble regardless of the size of G_h (Figure 1B). This is because as N increases, any perturbation in the predicted RDCs for a given grid-approximated conformer can be compensated for in part by opposite deviations in a second conformer. This mutual cancelation arises due to the fact that different conformers will effectively experience independent perturbations when binned into the grid, resulting in near random perturbations to the RDCs that increasingly cancel with increasing N resulting in a lower RDC RMSD. Therefore a much larger G_h can be afforded for a larger ensemble size, and the ‘resolution’ with which the ensemble can be determined using RDCs decreases. This result underscores an important inverse relationship between the number of unique conformations that can be used to approximate an ensemble and the corresponding bin size that can be afforded to create the histogram distribution.

For the simulations that follow, we assume a grid size of G_h=5°. This guarantees a sufficiently small bin size that ensures we are working well below the theoretical resolution limit of RDCs.

RDC-satisfying ensembles with predefined size

Next, we used the SAS scheme to identify the family of degenerate ensembles that reproduce five sets of independent RDCs, computed for a variety of target ensembles, to within experimental error. One of the unknowns during an ensemble determination is the size of the target ensemble defined as the number of unique conformations given some assumed bin size. In general, there can be a wide range of ensembles that differ in size that can satisfy experimental data. We initially avoided such size-related degeneracies and examined the degeneracies that arise when assuming the target ensemble size is known. Here, the ensemble size used in the SAS scheme was set equal to the target ensemble size from which the RDCs were derived. In this manner, we asked the question, how similar are the ensembles satisfying the RDCs to the target ensemble when restricting the size of the ensemble to be equal that of the target ensemble? In all cases, the pool grid size was set to G_h=5°.

We carried out these simulations for Gaussian and random target ensemble distributions containing a variable number of conformations (N = 1–100) derived from the topologically allowed pool (see Methods). The RDC-satisfying ensembles were then compared to the target ensemble using the REsemble approach⁴⁸. In particular, we computed ΣΩ which ranges between 0 and 1 for maximum and minimum similarity, respectively. For comparison, we also computed ΣΩ when comparing the similarity between the target ensemble and an ensemble of equal size that is selected randomly from the pool without guidance from the RDCs.

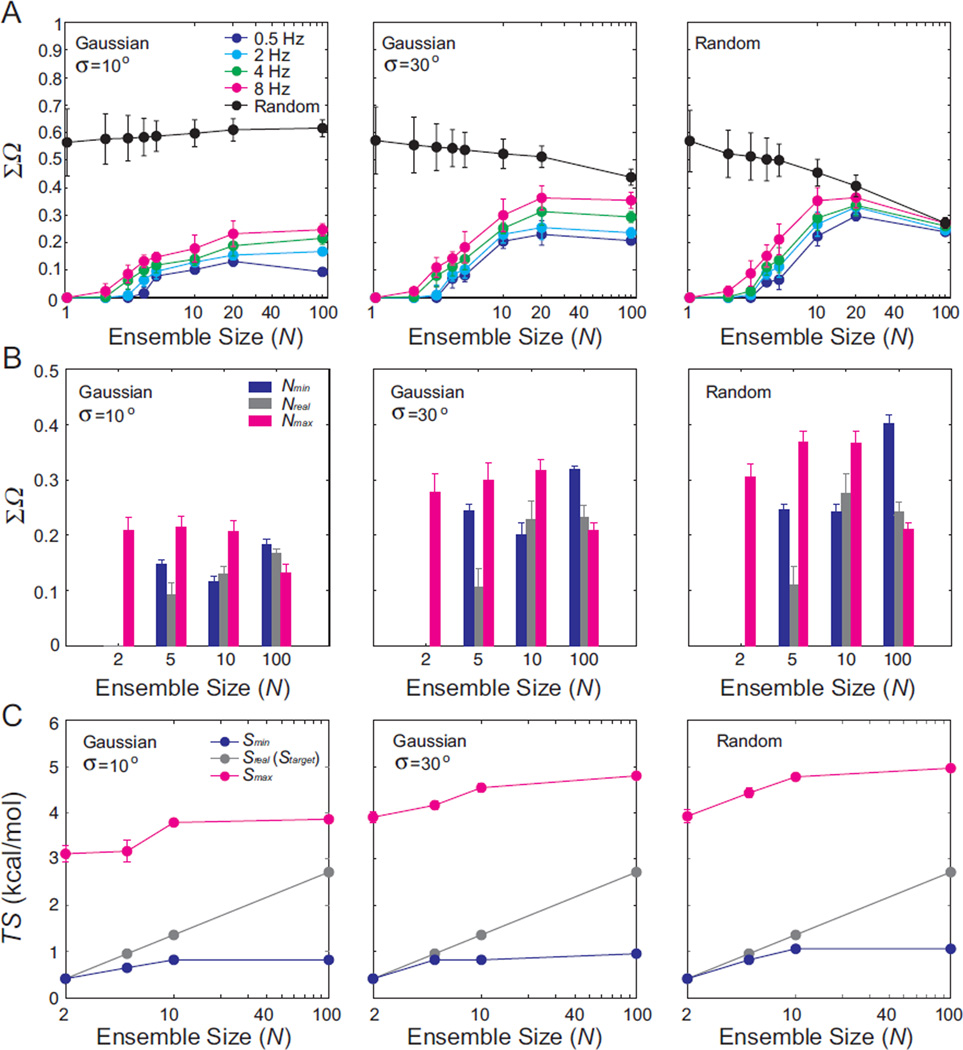
Shown in Figure 2 are the ΣΩ values for three different target ensembles. The results shown in Figure 2 represent averages and standard deviations over 100 independent SAS runs. Note that the similarity between RDC-satisfying ensembles obtained from independent SAS runs are well captured by the mean and standard deviation relative to the target ensemble. Overall we find good agreement between the RDC-satisfying and target ensembles with ΣΩ < 0.3 when assuming RDC uncertainty of 2 Hz, which can be compared to a 30° structural difference in a single structure (Figure S1). For comparison, ΣΩ > 0.3 and as large as ~ 0.6 when selecting ensembles randomly from the pool (Figure 2A, in black). The similarity between the RDC-satisfying and target ensemble generally decreases with increasing target ensemble size, conformational breadth, and RDC uncertainty. In some cases, we observe a decrease in ΣΩ in going from N=20 to N=100 particularly as the target ensembles increases in conformational breadth (Figure 2A, Table S1). This can be attributed to the fact that for target ensembles with broad distributions, there are fewer ensembles that can accomplish a given set of RDC averaging when restricting N to be large. Here, restricting the size of N increases the similarity between the RDC-satisfying and target ensembles (see section below). Note that sizeable ΣΩ values on the order of 0.3 are observed even when assuming negligible RDC uncertainty (<0.2Hz, data not shown). This indicates that at least some of the degeneracy manifests at levels far smaller than the typical RDC uncertainty.

Figure 2. Comparison of RDC-satisfying ensembles with target ensembles.

The similarity between RDC-satisfying ensembles with (A) prefixed and (B) variable ensemble size and target ensembles for three distinct distributions: Gaussian target ensemble with σ =10°, 30° and random target ensembles with RDC uncertainty. The values of ΣΩ represent the average over 100 simulations and the error bar represents the standard deviation. The similarity between the target ensemble and a randomly selected ensemble of equal size is also shown in black. (B) Results are shown for RDC-satisfying ensembles predicted using different ensemble sizes: N_min (blue), N_real(gray) and N_max (magenta) using 2Hz RDC uncertainty. The values of ΣΩ represent the average over 100 simulations and the error bars represent the standard deviation. (C) Comparison of conformational entropy for RDC-satisfying ensembles determined using N_min (blue), N_real (gray) and N_max (magenta) and for the target ensemble. Values represent the average of 100 simulations and error bars indicate the standard deviation.

RDC-satisfying ensembles without predefined size

In principle, ensembles with variable size can satisfy a given set of experimental data. In the SAS approach, one often selects the smallest sized ensemble (N_min) that can satisfy experimental data to construct the ensemble and larger ensemble sizes are usually ignored due to the risk of overfitting of the experimental data^2,26. However, the choice of N_min is arbitrary and larger N values often satisfy experimental data within uncertainty. These RDC degenerate families of ensembles cannot be ruled out on the basis of the data, and therefore, represent another set of degeneracies that need to be considered.

We therefore repeated the SAS analysis for some of the target ensembles shown in Figure 2 to identify the degenerate family of RDC-satisfying ensembles with variable size that reproduce RDCs within the assumed 2 Hz uncertainty. We identified RDC-satisfying ensembles with the following sizes: N_min which represents the smallest value of N that reproduces RDCs within uncertainty; N_real which represents the real target ensemble size; and N_max arbitrarily chosen to be 500 so long as it reproduces RDCs to within uncertainty. Note that for each target ensemble, the predicted ensemble using N_min was constructed from more SAS runs compared to the ensemble predicted using N_max so that the N_min and N_max RDC-satisfying ensembles have the same or very similar number of conformations. This avoids biased comparisons between N_min and N_max due to the different number of conformations.

Surprisingly, for all target ensembles examined, we were able to identify ensembles that satisfy the RDCs with N_max = 500. This was the case even for relatively small target ensembles with N=1 or 2 (Figure 2B and Figure S2, in this Figure we show all of the RDC RMSD plots). Conversely, ensembles with small N_min = 2–6 could be identified that satisfy RDCs for large sized target ensembles with N=100 (Figure 2B, S2). It should be noted that the variable sized ensembles reproduced the RDCs equally well with no obvious differences in frequency of outliers (Figure S3) in the commonly used “leave-out” cross-validation analysis^23,27,43. Here, four out of the five RDC data sets are used to generate ensembles and the RMSD between measured and predicted RDCs determined for the left out dataset (Figure S4).

Interestingly, the variability in N only slightly increases the maximum ΣΩ values (Figure 2B, Table S2) relative to the ΣΩ values observed when N is pre-fixed (Figure 2A). However, it results in large ΣΩ values even for small target ensemble sizes where the ΣΩ values were much smaller in the case that the ensemble size as assumed known (Figure 2A, B). In general, we find that for small target ensembles with N ≤ 10, the larger ΣΩ values arise due to N_max RDC-satisfying ensembles. Conversely, for target ensembles with N > 10, the largest ΣΩ values are generally observed with the smaller N_min satisfying ensembles. For these cases, lack of knowledge of N results in large uncertainty in the RDC-satisfying ensembles. The deviations generally increase with increasing conformational breadth of the target ensembles. This increase in ensemble uncertainty with breadth of the distribution has been noted previously^46,64. Interestingly, in some cases, especially for relatively large target ensembles (N=10, 100), the N_real RDC-satisfying ensembles do not best resemble the target ensemble. This can be attributed to the combinatorial increase of distinct ensembles that have to be sampled with large N_real and existence of degenerate ensembles that can satisfy RDCs to within experimental error. It should be noted that N_max was arbitrarily set to 500 and that the similarity may decrease even further with larger N_max values.

Conformational entropy

Next, we asked how well do the RDC-satisfying ensembles reproduce the conformational entropy of the target ensemble. We calculated the conformational entropy S of the ensembles (see Methods) predicted using N_min (S_min), N_real (S_real), and N_max (S_max), and compared these values to the entropy of the target (S_target). As shown in Figure 2C, the uncertainty in ensemble size described above results in a very large uncertainties in ensemble entropy. As expected, the N_max RDC-satisfying ensembles yield S_max that are significantly larger than S_target especially for small target ensembles whereas S_min is generally smaller particularly for larger target ensembles. Overall, the values of S_min and S_max yield large differences of TS values that range between 0.4–5.0 kcal/mol at T = 298K (Figure 2C, Table S3).

RDC-satisfying ensembles capture key feature of target ensembles

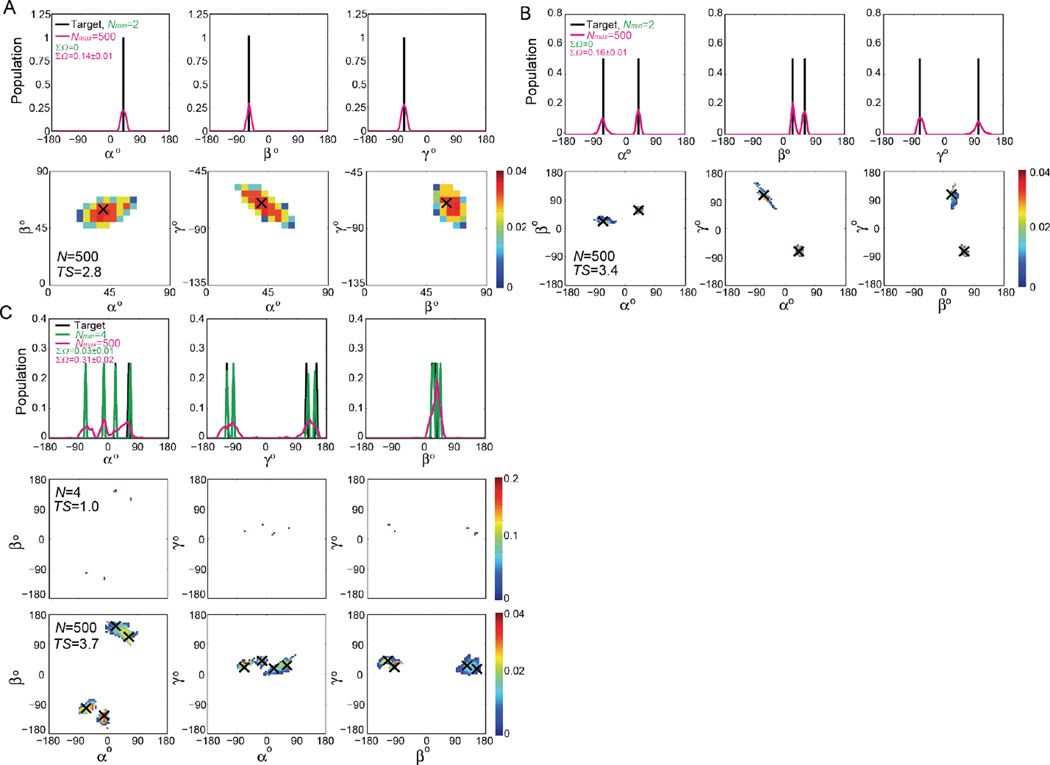
Next, we examined how the RDC-satisfying ensembles capture various features of the target ensembles. Shown in Figure 3 are representative examples of N_min and N_max RDC-satisfying ensembles for target ensembles with N=100 Gaussian σ = 10° (Figure 3A), σ = 30° (Figure 3B) and randomly selected target ensemble (Figure 3C). Shown are 1D populated weighted distributions comparing target ensemble, RDC-satisfying ensembles, the topological pool along with corresponding 2D distributions with color-coded population weights.

Figure 3. Comparison of RDC-satisfying and target ensembles: Gaussian and random target distributions.

1D and 2D population-weighted distributions of inter-helical angles ( α_h β_h γ_h) for N_min (green) and N_max (magenta) RDC-satisfying ensembles and corresponding target ensembles consisting of a Gaussian distribution with (A) σ = 10°, (B) σ = 30° and (C) randomly selected conformers from the pool. The value of ΣΩ comparing the RDC-satisfying and target ensemble and the TS values (in kcal/mol) are shown in the 2D distributions for each ensemble.

The N_min RDC-satisfying ensembles give rise to discretized ensembles that feature a smaller number of conformations in and around the most populated conformations in the target. Nevertheless, many conformers are erroneously lowly populated and there are also small differences in the population-distributions in and around the dominant target conformations. On the other hand, the N_max RDC-satisfying ensembles are broader, and while the most populated conformers are near the most populated conformers in the target ensemble, many conformers are also erroneously populated albeit typically to low levels that fall outside the target. On a quantitative level, the differences between the N_min and N_max RDC-satisfying ensembles ΣΩ(N_min-N_max) range between 0.2 and 0.4 and are comparable to the ΣΩ values observed when compared against the target ensembles. Visual inspection of these distributions shows that despite their obvious differences, both N_min and N_max RDC-satisfying ensembles recapitulate key features of the target distribution, including its breadth and shape (Figure 3).

We also carried out detailed simulations for more discrete smaller sized target ensembles with N=1, 2 and 4 conformations (Figure 4). In general, the RDC-satisfying ensembles are more similar to the target ensemble as compared to the ensembles with large size (Figure 4). The N_min ensembles nearly perfectly reproduce the target ensemble while N_max erroneous broadening around the dominant conformations (Figure 4). Interestingly, this broadening is not as significant as observed with target ensembles with much larger size (Figure 3) and there are fewer significantly populated conformations outside the dominant conformations. As expected, the differences between the N_min and N_max RDC-satisfying ensembles with ΣΩ(N_min-N_max) ranging between 0.1 and 0.3 are comparable to the ΣΩ values observed when compared against the target ensembles. The RDC satisfying ensemble capture salient feature of the distributions, including for example, whether the target ensemble is unimodal (Figure 4A), bimodal (Figure 4B) or tetramodal (Figure 4C).

Figure 4. Comparison of RDC-satisfying and target ensembles: Discrete distributions.

1D and 2D population-weighted distributions of inter-helical angles (α_h β_h γ_h) for N_min (green) and N_max (magenta) RDC-satisfying ensembles and corresponding target ensembles consisting of a discrete distributions with size (A)N=1, (B)N=2, and (C)N=4. The value of ΣΩ comparing the RDC-satisfying and target ensemble is shown in each case. The N_min RDC-satisfying ensembles perfectly overlap with the target ensembles and therefore only the N_max RDC-satisfying ensembles are shown in the 2D distributions with target conformations indicated using black crosses. The value of ΣΩ comparing the RDC-satisfying and target ensemble and the TS values (in kcal/mol) are shown in the 2D distributions for each ensemble.

It is important to note that even for N=1 target ensemble, the SAS scheme identifies an N_max = 500 ensemble that reproduces the RDCs within error (Figure S3). This ensemble features broadening around the conformer in the target resulting in standard deviation in β ~10° (Figure 4A). This highlights how RDCs can be misinterpreted in terms of dynamics. In particular, deviations in σ(β) < 10° are likely difficult to characterize using RDCs with uncertainty 2Hz and alignment levels of S_zz ~ 10⁻³.

Finally, we examined a more realistic target ensemble corresponding to 8000 conformations obtains from an 8.2 µs MD trajectory of HIV-1 TAR²⁸ generated using the CHARMM36 force field⁶⁶ and the Anton supercomputer⁶⁷ (see Methods). RDC-satisfying ensembles could be identified with N_min=4 and N_max=500 (Figure S5). The N_max=500 RDC-satisfying ensemble is more similar to the target ensemble (ΣΩ=0.12±0.02) as compared to the N_min=4 RDC-satisfying ensemble (ΣΩ=0.20±0.01) (Figure 5A). Despite these differences, the N_min=4 and N_max=500 capture salient features and dominant conformations in the target MD ensemble. As shown in Figure 5B–D, both ensembles capture the most populated region of the target ensemble that is not captured by the starting 3-0 junction-topology conformational pool although observable differences exist in lowly populated regions. While the N_min=4 ensemble is focused on the mostly populated conformations, the N_max=500 ensemble is broadened and samples many conformations around the populated regions. The target MD ensemble has an entropy TS = 3.9 kcal/mol at T= 298K. By comparison, the ensembles reconstructed using N_min=4 was 0.8 kcal/mol and that of N_max=500 was 4.6 kcal/mol at T = 298K. This uncertainty in free energy, particularly for larger and broader target ensembles, is way too large to allow meaningful insights into the role of conformational entropy in basic biological processes.

Figure 5. Comparison of RDC-satisfying and target ensembles: MD trajectory of HIV-1 TAR.

1D and 2D population-weighted distributions of the inter-helical angles (α_h β_h γ_h) for N_min (green) and N_max (magenta) RDC-satisfying ensembles and the corresponding target ensemble constructed by selecting conformers from an MD trajectory of HIV-1 TAR. The value of ΣΩ comparing the RDC-satisfying and target ensemble and the TS values (in kcal/mol) are shown in the 2D distributions.

It is worth noting that although our analysis assumes a topologically restricted inter-helical conformational space, similar results were obtained when using an unbiased unrestricted conformational pool spanning the entire Euler angle space (Figure S6). Although the ΣΩ values of the simulations using unrestricted pool are slightly larger than for the case using topologically restricted pool (Figure S6), the RDC-satisfying ensemble obtained from the entire pool capture salient features of different target ensembles (Figure S6). This is again consistent with degeneracies representing various degrees of broadening around the target conformations rather than having distinct minima along the landscape. Nevertheless, we note that the topologically allowed conformational pool may help reduce degeneracies in ensemble determination when using less than five independent RDC datasets and improve sampling particularly for systems with many inter-helical junctions.

Sparse RDC datasets

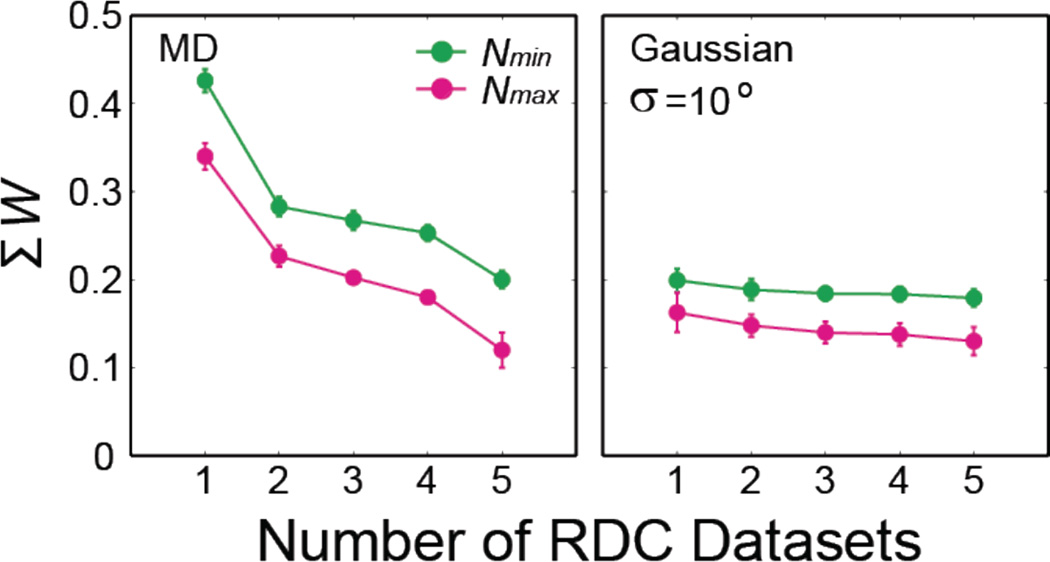
While our simulations assume a theoretical maximum of five independent datasets, in practice, such measurements are not easily accessible²⁸. We therefore also explored the more realistic scenario involving a smaller number of RDC datasets. As expected, reducing the number of independent RDC datasets resulted in RDC-satisfying ensembles that can differ even more significantly from target ensembles. However, in general, this decrease in similarity with decreasing number of RDC datasets was more significant for broad target ensembles such as the MD trajectory of HIV-1 TAR, where ΣΩ from N_max increases from 0.12±0.02 with five RDC datasets to 0.34±0.01 with only one RDC dataset as compared to the narrower Gaussian target ensemble with σ =10° where the corresponding ΣΩ increase is from 0.13±0.01 to 0.16±0.02 (Figure 6). These results indicate that it may be possible to determine inter-helical ensemble with reasonable accuracy for rigid molecules such as mutants of TAR¹⁶ and ligand-bound states of TAR^7,69–70 with experimentally accessible RDCs. Further simulations showed that even for flexible RNAs such as HIV-1 TAR, the ensembles predicted using N_min and N_max and experimentally accessible RDCs sample the ligand-bound states within experimental uncertainty, although ensembles predicted using N_min and N_max have different subtle details of conformational distributions (Figure S7).

Figure 6. Prediction of target ensembles using different number of independent RDC datasets.

Shown are the accuracy (ΣΩ) of predicted ensembles using N_min (green) and N_max(magenta) for the MD trajectory of HIV-1 TAR (left) and Gaussian target ensemble with σ = 10° (right).

DISCUSSION

For decades, structural biologists have struggled with the problem that while it may be feasible to find a structural model that satisfies experimental data obtained by NMR or X-ray diffraction, it is very difficult to enumerate all other models that satisfy the data equally well. Not too surprisingly, this problem is exacerbated when determining dynamic ensembles of biomolecules, given the large number of ensemble combinations that have to be tested. These degeneracies have not yet been actively examined in ensemble determination. Understanding the nature of the degeneracies is not only key to avoid over interpreting data, but also, to define approaches that can help improve ensemble determination, for example, by suitable combination of complimentary data. Prior studies^28,71 have estimated uncertainty in ensembles by using Monte Carlo type approaches. These approaches primarily provide an estimate of precision in ensemble determination and may not fully capture ensemble accuracy or the range of degenerate ensembles that equally satisfy the data such as the degenerate ensembles with different size and entropy uncovered in this work. In this work, we sought to develop a general framework for unveiling such ensemble degeneracies with specific application to NMR RDCs.

We designed our simulations to represent a ‘best-case-scenario’ ensemble determination problem where RDCs are calculated and predicted using five linearly independent alignment tensors. This allowed us to identify the degeneracies and sources of uncertainty that restrict the theoretical limits with which ensembles can be defined using the information contained in anisotropic interactions such as RDCs. We find that even under these ideal conditions, RDC-satisfying ensemble can vary significantly in size and differ from the target ensemble by ΣΩ ~ 0.4. This degeneracy increases with the breadth of the target ensemble and makes it difficult to extract quantitative thermodynamic information of interest. For example, the uncertainty translates into large errors in ensemble entropy, as high as ~5 kcal/mol or ~1.7 kcal/mol per degree of freedom. One can in principle gauge the amplitude of inter-helical motions and obtain estimates of the uncertainty in ensemble determination by using the RDC data to determine the generalized degree of order (GDO_int), which is the ratio of the degree of order measured in each of the two domains⁶⁴. Like any order parameter, the GDO_int varies between 0 (maximum motions) to 1 (minimum motions). As might be expected, systems with lower GDO_int represent broader ensembles, which are more susceptible to uncertainty including due to uncertainty in the ensemble size. Indeed, we find a good correlation between the uncertainty in the entropy S_max -S_min and the GDO_int of the target ensemble (data not shown). Therefore, the GDO_int can be used to obtain a priori information regarding the breadth of the distribution and potential uncertainties in parameters such as conformational entropy. In practice, the accuracy of inter-helical RNA ensembles determined with RDCs as the only source of constraints are likely to be less reliable, not only due to more limited RDCs, broader conformational space, but also because of inherent approximations that have to be assumed when computing RDCs for a candidate conformer^24,28. On the other hand, inclusion of RDCs on linker residues i.e. the helix junction motifs, may help further constrain the linker conformation and thereby facilitate definition of inter-helical ensemble²⁸. Further studies are needed to examine these effects and to evaluate how inclusion of other experimental data may help further improve determination of RNA ensembles.

In prior studies, we reported ensembles of HIV-1 TAR with size N=3⁷ and N=20^{24, 28}. In both cases, the ensembles come close to sampling seven distinct ligand bound conformations of TAR^7,24. This is consistent with our findings here that salient features of ensembles can be determined despite the uncertainty due to ensemble size. For completion, we also generated RDC-satisfying ensembles for HIV-1 TAR with N_min = 3 and N_max = 500. The ensembles sample similar conformational regions and come close to sampling ligand bond states (Figure S7).

In general, the RDC-satisfying ensembles are biased toward the populated regions of the target ensemble distribution, and capture other features, including the breadth and shape. We did not find any evidence for RDC-satisfying ensembles that do not strongly resemble the target ensemble. Rather, the degeneracies are better described as random broadening around the target conformations. Nevertheless, the RDC-satisfying ensembles can populate conformers that are never sampled in the real target ensemble or conversely, can result in depopulation of regions that are clearly populated in the target ensemble. These results emphasize the need to account for such uncertainty during the ensemble determination process.

The ensemble degeneracy, particularly due to variability in ensemble size, contributes significantly to uncertainty in conformational entropy. In this regard, it should be noted that spin relaxation data measured on amide backbones and methyl groups in proteins, which are based on the same basic NMR anisotropic interactions, have been used extensively to characterize conformational entropy in proteins^18–22. This represents a significantly smaller amount of data than used here. In particular, the five orthogonal sets of RDCs measured on locally rigid domains carries information described by 25 ensemble-averaged Wigner rotation elements^7,64. Here, all 25 Wigner elements are effectively applied in the ensemble determination. On the other hand, in studies that rely on measurements of spin relaxation data, one typically relies on a single Lipari-Szabo order parameter for one bond or methyl group - which effectively represents only one independent Wigner element^18–22. While our results suggest that it should not be feasible to determine entropy based on such parameters, it is possible that unique attributes of motions in proteins are such to permit estimation of entropy from such reduced parameters. Nevertheless, our study emphasizes the need to carefully evaluate the relationship between entropy and order parameters for different systems that may exhibit different dynamic attributes including nucleic acids studied here.

It is very likely the case that the ensemble degeneracies uncovered here will be common in other types of time-averaged experimental data. What is less clear is whether these degeneracies will be orthogonal, so that combining data together can help resolve uncertainties including those related to ensemble size. The framework introduced here can be generally applied to test intrinsic degeneracies in ensemble determination, and can be immediately applied to explore ideal combinations of data that can help overcome these sources of uncertainty.

CONCLUSION

Our results reveal that ensembles with variable size (or number of unique conformations) can satisfy the RDCs to within experimental uncertainty. This results in significant uncertainty in determining thermodynamic parameters of interest, such as conformational entropy. Nevertheless, the RDC-satisfying ensemble did not differ from the target ensembles by more than ΣΩ ~ 0.4 and are significantly more similar to the target ensemble as compared to those selected randomly from the pool. Future studies should quantitatively evaluate how inclusion of other types of experimental data including on the helix-junction-helix motif linkers can improve the accuracy and uniqueness with which ensembles can be determined. The framework introduced here can readily be applied to evaluate other types of data.