Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Feb 10;6:20684. doi: 10.1038/srep20684

Tumour-induced neoneurogenesis and perineural tumour growth: a mathematical approach

Georgios Lolas 1,3,a,*, Arianna Bianchi 2,*, Konstantinos N Syrigos 3
PMCID: PMC4748234  PMID: 26861829

Abstract

It is well-known that tumours induce the formation of a lymphatic and a blood vasculature around themselves. A similar but far less studied process occurs in relation to the nervous system and is referred to as neoneurogenesis. The relationship between tumour progression and the nervous system is still poorly understood and is likely to involve a multitude of factors. It is therefore relevant to study tumour-nerve interactions through mathematical modelling: this may reveal the most significant factors of the plethora of interacting elements regulating neoneurogenesis. The present work is a first attempt to model the neurobiological aspect of cancer development through a system of differential equations. The model confirms the experimental observations that a tumour is able to promote nerve formation/elongation around itself, and that high levels of nerve growth factor and axon guidance molecules are recorded in the presence of a tumour. Our results also reflect the observation that high stress levels (represented by higher norepinephrine release by sympathetic nerves) contribute to tumour development and spread, indicating a mutually beneficial relationship between tumour cells and neurons. The model predictions suggest novel therapeutic strategies, aimed at blocking the stress effects on tumour growth and dissemination.

A relationship between tumours and the nervous system has been suspected since the second century AD with the work of the Greek physician Galen1. Traditionally, the nervous system has not been considered to be actively involved in the process of metastasis. However, recent studies have demonstrated the presence of neurons in peritumoural regions of several human tumours, and the number of tumour-associated neurons has been correlated with metastases2,3. The relative importance of pre-existing versus newly-formed neurons to metastasis is not understood. Although pre-existing peritumoural neurons are likely to be sufficient for tumour spread, recruitment of neurons into the close proximity of a tumour may increase the propensity of tumours to metastasise. Increased nerve density and/or presence of intratumoural neurons should be regarded as an additional pathway for metastasis.

Significant progress has also been made in understanding the effects of stress- and depression-mediated release of chemicals by the nervous system on tumour cell dissemination4,5. On the one hand tumour cells produce factors that induce the formation of a neural network, and on the other the newly formed nerves release neurotransmitters that affect tumour growth and migration6,7. Following the terminology suggested by Entschladen and co-workers8, the formation of new nerve branches is herein called neoneurogenesis, in analogy to lymphangiogenesis and (blood) angiogenesis.

The present model aims to investigate how solid tumours induce peripheral nerve proliferation and how different types of nerves affect tumour growth and metastasis by releasing substances such as neurotransmitters. Also, we address the question of which role stress plays in cancer progression. This model was mainly inspired by recent works that focus predominantly on prostate cancer2,7,9. The study in Ayala et al.2 combines in vitro experiments with autopsy analysis of prostate cancer patients; Magnon and collaborators7 explore the effects of the nervous system on tumour progression by altering nerve structure and receptor activity in mice, after orthotopically implanting human tumour cells in the animals. Since the scope of our work does not include tumorigenesis, our model simulations start with a non-zero initial condition for primary tumour cells, reflecting the tumour cells implantation described in the study by Magnon et al.7. Our aim is to investigate the further evolution of these cells and their interactions with the pre-existing prostate-surrounding nerves. The model takes major inspiration from the work by Ayala et al.2, supporting the hypothesis of a symbiosis between nerves and tumour cells.

Biological background

Neurons, neurotransmitters and the Autonomic Nervous System (ANS)

Neurons (or nerve cells) are the core components of the nervous system. The electrical signals travelling inside a neuron are converted into signals transmitted by certain chemicals (neurotransmitters); these are then passed to another neuron across a synapse. A neurotransmitter released by a nerve binds to a receptor on another cell and, according to the receptor type, induces a certain action. The collection of all the neuronal structures that together control body functions below the level of consciousness (for instance, heart and respiratory rate, digestion and pupillary dilation) constitute the Autonomic Nervous System (ANS). The ANS is in turn made of three sub-systems; here we will focus only on two of them: the Sympathetic Nervous System (SNS, also called “fight or flight” system), which is responsible for quick response processes such as raising blood pressure or accelerating heart rate, and the Parasympathetic Nervous System (PNS, also known as “rest and digest” system), which governs slower responses such as gastrointestinal functions.

Tumour-induced neoneurogenesis

Tumours induce innervation around themselves3,10 and, in general, high levels of innervation in tumours correlate with a poor disease outcome2,7. Tumour cells have the ability to produce substances, such as Nerve Growth Factor (NGF), that stimulate the growth and improve the survival of nerve cells11,12. NGF also promotes tumour growth11 and inhibits aggregation of cancer cells and thus enhances tumour invasion, although this process is currently poorly understood13.

Tumours also release Axon Guidance Molecules (AGMs). These molecules were originally considered only for their role in the nervous system as guidance cues for axons. The term axon guidance denotes the process by which neurons send out axons along a precise path in order to reach the correct targets. The tip of an axon (or growth cone) is equipped with receptors that can sense (gradients of) chemicals, called guidance cues, which “tell” them where to expand14. In recent years, however, it was shown that many AGMs can also influence neuronal survival and migration and likely play an important role in cancer progression15. There are at least three different families of AGMs (semaphorins, slits and netrins), which seem to have different roles in nervous system development and cancer progression. They are also found in many different body tissues and can regulate cell migration and apoptosis (for a review of the role of AGMs in cancers, see Chédotal et al.16).

ANS effects on tumour progression

It was originally believed that the nervous system only indirectly affected cancer development, through perineural invasion (that is, the spread of tumours along nerve fibres17,18) and modulation of the immune function5. Indeed, neurotransmitters regulate the cytotoxicity of T lymphocytes and natural killer cells19 and induce leukocyte migration6,20; the consequent immunosuppression can favour tumour growth and progression, impairing the anti-tumour response5,21. However, it is the migratory effect of neurotransmitters that first suggested a direct link between nerves and tumour progression. One theory for the spread of metastases from a primary tumour to a certain organ claims that circulating cancer cells are attracted and settle in a specific region of the body due to the presence of factors such as chemokines or AGMs16,22. This assumption is in agreement with the well-known “seed and soil” hypothesis23. In particular, several studies have shown that neurotransmitters influence the migratory activity of cancer cells, perhaps by inducing a phenotypic change towards a more motile phenotype via intracellular signalling24, or simply by chemotaxis25. In addition, some neurotransmitters also induce tumour growth6. Indeed, tumour cells express many receptors, including serpentine receptors26 to which neurotransmitters are ligands. Neurotransmitters can induce several behavioural changes in tumour cells, mostly increasing their proliferation and/or migration (a summary of such effects can be found in Lang & Bastian6).

Mathematical model

We define the main domain of our study as a portion of the body containing the prostate and its near surroundings, thus including both the tumour and the neighbouring nerves. All the variables, with the exception of the migrating tumour cells (see below), are average concentrations/densities over this domain, which vary in time. We develop a compartmental model in which an extra domain is considered for the tumour cells which leave the main domain. A schematic of the model, showing the variables and their interactions, can be found in Fig. 1.

Figure 1. A schematic representation of the interactions among the model variables.

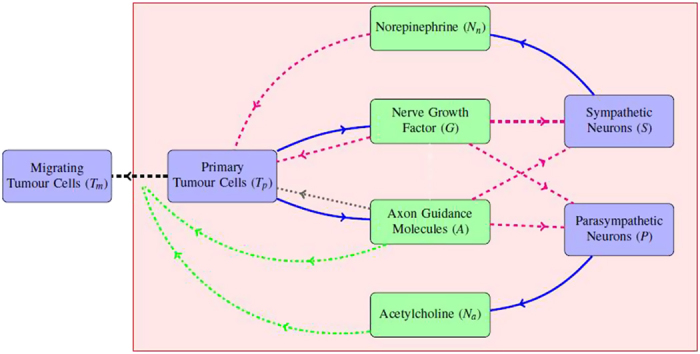
Figure 1

Open in a new tab

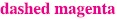Each variable corresponds to a rounded-corners rectangular box; note that cells are in Inline graphic while chemicals are in Inline graphic. The light red-shaded rectangular area represents the main domain, that is the prostate and its immediate surroundings. 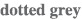Concerning the arrows, Inline graphic denotes production, Inline graphic denotes enhancement of growth and/or survival (and axon extension in the case of neurons), Inline graphic denotes migration enhancement, dashed black actual migration and Inline graphic denotes apoptosis induction.

We distinguish between primary tumour cells (Tp) and migrating tumour cells (Tm). The former are those that constitute the original tumour mass; when they detach and leave the orthotopic site of the tumour they are then designated migrating. The migrating cells are particularly dangerous because they have the potential to form metastases. Herein we do not explicitly account for the further development of the migrated tumour cells: our variable Tm represents an indication of potential metastasis formation.

NGF (G) is a neurotrophin (a kind of protein) which stimulates the growth and enhances the survival of both Sympathetic Nerve Cells (SNCs) and Parasympathetic Nerve Cells (PNCs). It has been found to be secreted by tumour cells. AGMs (A) also affect the survival and moreover the growth of both SNCs and PNCs. In reality, there are many kinds of AGMs, which can have completely different effects on nerve and tumour development. Here, for simplicity, we consider them as a single variable; taking into account the different types of AGMs would be one step towards improving the model in future.

The growth of both SNCs (S) and PNCs (P) is enhanced by NGF and AGMs. In addition, both types of nerve cell respond to a neurotransmitter called acetylcholine (Na), but only PNCs produce it; SNCs instead secrete epinephrine (also known as adrenaline) and norepinephrine (Nn, also called noradrenaline). Furthermore, norepinephrine enhances tumour cell survival, growth and chemotaxis whereas acetylcholine seems to stimulate tumour cell invasion and migration7. Note that norepinephrine is understood to be the main tumour-related sympathetic neurotransmitter; there are less documented effects of epinephrine on tumour cell growth and dissemination6.

Model equations

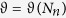It is well documented that tumour cells naturally undergo mitosis (see for instance Friberg & Mattson27). The model accounts for this by taking constant growth rates Inline graphic and Inline graphic for primary and migrating tumour cells, respectively. Only a fraction of primary tumour cells exhibit proliferation; this is due to the presence of a necrotic core, that we assume to be defined by the half inner radius of the (spherical) tumour mass28. This assumption leads to the conclusion that only 7/8 of the tumour volume (and thus primary tumour cells) proliferate. Primary tumour cells are also exposed to the chemicals present in the domain which influence the tumour development. Since tumour growth is enhanced by NGF, we assume that the growth rate of Tp is increased in a saturating manner by this factor. It has been shown that a classic logistic equation is often not suitable for modelling tumour growth29. Here we include an Allee effect in the growth term to take into account the fact that tumour cell populations tend to die out at low densities. The Allee effect is an ecological term describing a correlation between the size and the per capita growth rate of a population; its inclusion in cancer modelling was already suggested by Korolev et al.29. The use of ecological concepts in cancer biology and modelling is a promising development in tumour research30. Here we take the Allee threshold (in the sense of Korolev et al.29) to be a function Inline graphic that decreases as the norepinephrine level increases. This choice reflects the observation that norepinephrine enhances tumour cell survival31. Tumour cells also die at a constant rate dT. Interestingly, some AGMs (such as netrin-1) are also thought to control tumour cell apoptosis32; we model this phenomenon by adding a linear dependence on A to the death term. Finally, another relevant aspect of tumour cell dynamics is migration. Tumour cells can spontaneously disaggregate and move away from their original site. This process is enhanced by substances produced by nerve cells and distant organs, including AGMs33 and acetylcholine6,20. Hence, the densities of primary and migrated tumour cells are described by the following equations:

graphic file with name srep20684-m4.jpg
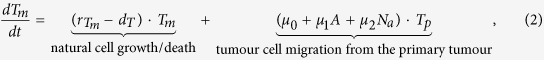graphic file with name srep20684-m5.jpg

where

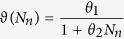graphic file with name srep20684-m6.jpg

(see the supplementary material for the motivation of the definition of 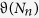Inline graphic).

We are interested in the effects that tumour-secreted NGF and AGMs have on the system; here the tumour secretion rate of these two growth factors is assumed to be constant8,24. We do not include other sources of NGF and AGMs in the main domain since these have a negligible effect on the dynamics that we want to study here (their effect on nerve growth in absence of tumour is implicitly included in the logistic growth of nerve cells – see below). As chemicals, both NGF and AGMs decay at constant rate dG and dA, respectively. They are also internalised by both tumour and nerve cells, which bind them to their surface receptors. Here we assume that SNCs and PNCs bind the proteins at the same rate (namely, γ2 for NGF and γ4 for AGM). The evolution equations describing NGF and AGM dynamics in the domain are therefore given by

graphic file with name srep20684-m8.jpg
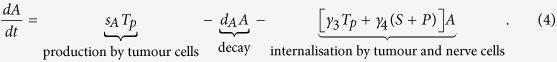graphic file with name srep20684-m9.jpg

We assume that in a normal (i.e. tumour-free) setting both SNCs and PNCs grow in a logistic manner and tend to their carrying capacities kS and kP, which are equal to their normal equilibrium values. However, when tumour cells are present nerve growth is enhanced by the secreted NGF34 and AGMs35. This additional growth is modelled by two saturating functions and is not subject to logistic limitation. This is due to the fact that, given the complex shape of neurons, it is difficult to estimate an actual maximum density. Nerve growth can also occur as axon elongation, which does not take a significant portion of space. Thus, the equations characterizing SNC and PNC rate of change are

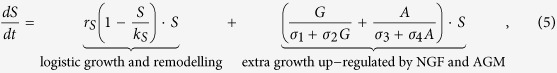graphic file with name srep20684-m10.jpg
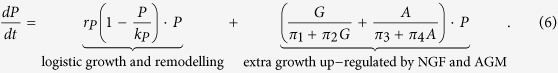graphic file with name srep20684-m11.jpg

Norepinephrine and acetylcholine are produced by SNCs and PNCs, respectively36, at respective net rates sn and sa that we assume to be constant. However, these two neurotransmitters are also released by other cell types37,38 and we include constant sources cn, ca in their equations. As chemicals, they decay at constant rates dn and da, respectively. Finally, they are absorbed by tumour cells6,7 at constant rates γ5 and γ6, respectively. The evolution equations for the neurotransmitters are then expressed by

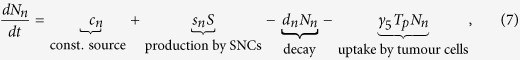graphic file with name srep20684-m12.jpg
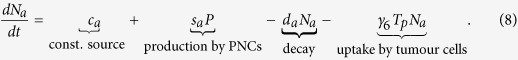graphic file with name srep20684-m13.jpg

Parameters and initial conditions

Parameters

Table 1 reports a list of all the parameters appearing in the model equations. Each parameter is supplied with its estimated value and units. A detailed description of the estimation of each parameter (together with used sources) can be found in the supplementary material. The parameter values were informed from the most relevant available datasets. Although these data are not “uniform” (in the sense that some are taken from experiments in vivo and others in vitro; some refer to human cell lines, others to rodents), we stress that, to the authors’ knowledge, no entirely homogeneous and complete experiment related to neoneurogenesis has been performed to date; thus a consistent estimation of the parameters is not possible. To test the robustness of the model to parameter alterations, we performed a parameter sensitivity analysis (see below).

Table 1. A list of all the parameters appearing in the model equations.
PARAMETER VALUE UNITS BIOLOGICAL INTERPRETATION
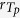Inline graphic 4.81 × 10−4 day−1 primary tumour cell basal growth rate
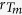Inline graphic 1 × 10−4 day−1 migrating tumour cell basal growth rate
τ1 134.27 pg day (mm3)−1 NGF-dependence of tumour cell growth rate
τ2 2.39 day NGF-dependence of tumour cell growth rate
kT 106 cells (mm3)−1 maximum tumour cell density (carrying capacity)
θ1 104 cells (mm3)−1 tumour cell Allee threshold in absence of norepinephrine
θ2 1 mm3 pg−1 norepinephrine-dependence of tumour cell Allee threshold
dT 1.27 × 10−2 day−1 tumour cell death rate
δ 1.29 × 10−2 mm3 pg−1 AGM-dependence of tumour cell apoptosis
μ0 0.22 day−1 spontaneous tumour cell migration rate
μ1 9.8 × 10−6 mm3 pg−1 day−1 AGM-dependence of tumour cell migration
μ2 2 × 10−3 mm3 pg−1 day−1 acetylcholine-dependence of tumour cell migration
sG 2.22 × 10−3 pg cell−1 day−1 NGF production rate by tumour cells
dG 22.18 day−1 NGF decay rate
γ1 5.57 × 10−5 mm3 cell−1 day−1 NGF internalisation rate by tumour cells
γ2 5 × 10−2 mm3 cell−1 day−1 NGF internalisation rate by nerve cells
sA 5.42 × 10−3 pg cell−1 day−1 AGM secretion rate by tumour cells
dA 2.4 day−1 AGM decay rate
γ3 10−5 mm3 cell−1 day−1 AGM internalisation rate by tumour cells
γ4 1.47 × 10−5 mm3 cell−1 day−1 AGM internalisation rate by nerve cells
rS 6 × 10−2 day−1 SNC basal growth rate
kS 0.26 cells (mm3)−1 SNC carrying capacity
σ1 1.29 × 102 pg day (mm3)−1 NGF-dependence of SNC growth rate
σ2 50 day NGF-dependence of SNC growth rate
σ3 7.79 pg day (mm3)−1 AGM-dependence of SNC growth rate
σ4 0.01 day AGM-dependence of SNC growth rate
rP 7 day−1 PNC basal growth rate
kP 0.03 cells (mm3)−1 PNC carrying capacity
π1 0.33 pg cell−1 day−1 NGF-dependence of PNC growth rate
π2 0.1 day NGF-dependence of PNC growth rate
π3 1 pg day (mm3)−1 AGM-dependence of PNC growth rate
π4 0.01 day AGM-dependence of PNC growth rate
cn 0.41 pg (mm3)−1 day−1 norepinephrine constant source
sn 1.6 pg cells−1 day−1 norepinephrine production rate by SNC
dn 1.66 day−1 norepinephrine decay rate
γ5 2 × 10−3 mm3 cell−1 day−1 norepinephrine uptake rate by tumour cells
ca 3.99 × 103 pg (mm3)−1 day−1 acetylcholine constant source
sa 0.73 day−1 acetylcholine production rate by PNC
da 49.91 day−1 acetylcholine decay rate
γ6 10−3 mm3 cell−1 day−1 acetylcholine uptake rate by tumour cells
Open in a new tab

Details can be found in the supplementary material.

Initial conditions

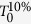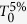In order to explore model predictions in different scenarios we will run simulations under different initial conditions on the primary tumour cells. In particular, Inline graphic and Inline graphic denote an initial density of primary tumour cells corresponding to 10% and 5% of the prostate volume, respectively (see the supplementary material for details). A relatively high percentage is used due to the fact that data concerning the tumour-nerve system evolution are only available for advanced stages of tumour progression (as in Ayala et al.2). We assume that a certain amount of tumour cells, corresponding to our initial data, has been implanted in previously tumour-free individuals (as done by Magnon et al.7, although there human tumour cells were implanted in mice). We also assume zero initial conditions for Tm, NGF and AGMs, because we are interested in the growth factors produced by the tumour (see above section). All the other values are assumed to be at their normal (tumour-free) level when the model simulation starts. A list of the initial values for all the model variables can be found in Table 2.

Table 2. Values of the model variables at t = 0.
INIT.VALUE VALUE UNITS
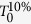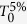
Tp(0) Inline graphic, Inline graphic cells/mm3
Tm(0) 0 cells/mm3
G(0) 0 pg/mm3
A(0) 0 pg/mm3
S(0) 0.26 cells/mm3
P(0) 0.03 cells/mm3
Nn(0) 0.5 pg/mm3
Na(0) 80 pg/mm3
Open in a new tab

For details, see the supplementary material.

Results

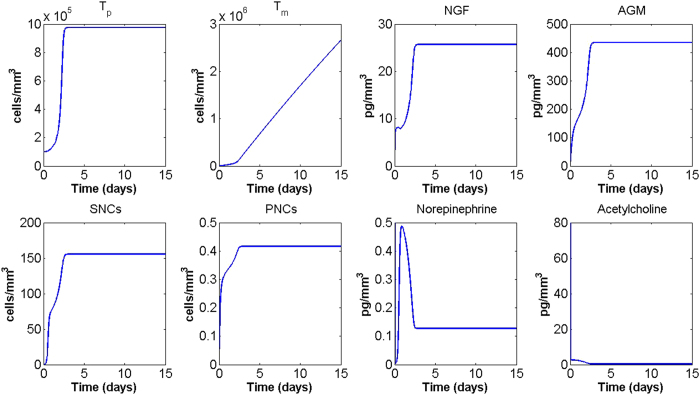
A simulation of the system of equations (1)–(8) with initial primary tumour cell density 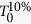Inline graphic (see above) is shown in Fig. 2, where the MatLab function ode45 was used to obtain the approximate solutions. The output of the model will be compared with the experimental observations reported in Ayala et al.2 and Magnon et al.7. Note that, to the authors’ knowledge, these are the only published experiments that specifically address tumour-nerve interaction dynamics; yet, these results are not completely consistent and therefore we will not carry out a quantitative comparison. Indeed, Ayala and collaborators2 use three different cell lines for in vitro experiments (human prostate cancer, mouse neuroblastoma and rat pheochromocytoma) and data from human patients for the nerve density analysis; Magnon and co-workers implanted human prostate cancer cells into mice to collect most of their data (only the assessment of nerve density in normal tissues surrounding tumour was done on human patients). Therefore, the only possible comparison between the model results and the experimental observations is of a qualitative, rather than a quantitative, nature.

Figure 2. Time-course of the model variables over a period of 15 days for 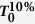Inline graphic.

Figure 2

Open in a new tab

Overall, the output is in good qualitative agreement with the experimental observations associated with aggressive human prostate tumour as reported by Ayala and collaborators2. Both sympathetic and parasympathetic nerves are, in the presence of tumour, significantly increased in the region around the prostate, and the number of tumour cells leaving the domain are constantly increasing, matching the metastases-formation report in Ayala’s and Magnon’s works2,7. Concerning the primary tumour mass, our model predicts that after an initial increase it reaches a non-zero equilibrium; this is in agreement with the results of Magnon and co-workers7, which reports an increase in tumour mass within the prostate. Also the fact that NGF and AGM levels stay high seems realistic: NGF levels are higher in inflammation and some studies report that semaphorin 7A and netrin-1 levels are significantly elevated in patients subject to chemotherapy and some kinds of cancers, respectively. Neurotransmitters reduce rapidly to a low non-zero level following the sudden implantation of tumour cells. On the other hand, our results are not in quantitative agreement with Magnon et al.7; in particular, the present model reaches an equilibrium approximately 5 days after tumour cells implantation, whilst in Magnon’s report7 it takes weeks to observe such significant changes. This may be due to the fact that the model does not take into account other elements of the prostate environment (such as lymphatic and blood vasculature) which compete with the nervous system for growth factors and space, thus potentially slowing down the dynamics. In particular, in order to incorporate blood and lymphatic vasculature role in neoneurogenesis, one could consider extra variables representing blood and lymphatic endothelial cells as well as tumour (lymph)angiogenic growth factors. Of particular interest is the relation between NGF and vascular endothelial growth factor in prostate cancer, as proposed by Nico et al.39 and Botelho et al.40. Including the immune system also has the potential to slow down the tumour’s growth; this could be modelled for instance by considering lymphocyte dynamics or macrophage plasticity41. The inclusion of such extra elements is not put in practice here; however, the considered variables are sufficient to confirm the experimental evidence of tumour-nerve bilateral interactions. Also, we did investigate how perturbations in the parameter values may affect the model output and how different initial conditions will determine cancer progression.

An interesting feature of the model is that a smaller initial condition for primary tumour cells, for instance 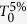Inline graphic, gives rise to completely different dynamics. In this case the primary tumour goes to zero after few days, while migrating tumour cells initially increase but then decrease to zero (Fig. 3). This behaviour is in accordance with the hypothesis that a tumour cell colony has to be bigger than a certain threshold in order to proliferate29. Note that the migrated tumour cells could cause tumour development in another site of the body where the conditions are more favourable. It is notable that the model is able to reflect this strong dependence of tumour progression on its initial conditions; this appears to be an important feature in modern cancer research inspired by ecological dynamics29. 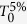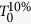Our Allee threshold, lying between Inline graphic and Inline graphic, appears to be unrealistically high but, to the authors’ knowledge, no measurement of this parameter is available for comparison. In this model tumour cell survival and growth are affected only by nerves, while in reality blood vessels also contribute to tumour maintenance by providing oxygen and nutrients; this may (partially) account for the high threshold.

Figure 3. Primary and migrating tumour cells density time-course for initial condition 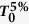Inline graphic.

Figure 3

Open in a new tab

Parameter sensitivity analysis

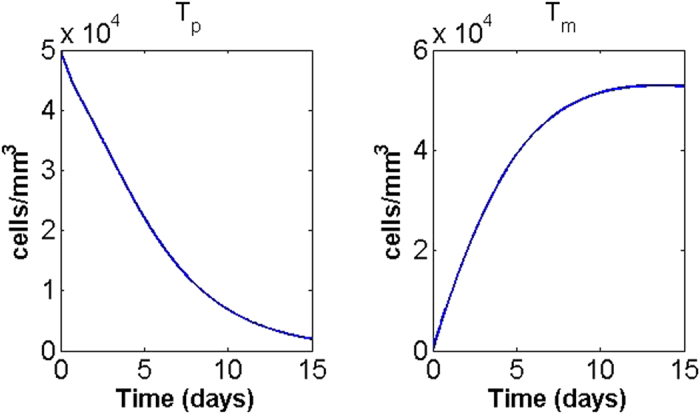
To test the robustness of the model, we performed a parameter sensitivity analysis by observing the effect that a 10% increase/reduction of each parameter value has on tumour cell densities at day 15. The model appears to be robust in the sense that final tumour cell densities are not greatly affected by perturbations in the parameter values. The only parameters that generate a change in the density of migrating tumour cells of 2% or more are reported in Fig. 4. Of these, only the tumour cell carrying capacity kT has a similar effect on primary tumour cells.

Figure 4. Parameter sensitivity analysis.

Figure 4

Open in a new tab

The graph shows the effects on migrating tumour cells at day 15 after an increase (Inline graphic) or decrease (Inline graphic) of 10% in the parameters. Here only the parameters which induced a percentage change of 2% or more are shown; they are: the tumour cell carrying capacity kT, the “basal” tumour cell Allee threshold θ1, and the spontaneous tumour cell migration rate μ0.

Stress and tumour progression

Many cancer patients exhibit stress and depression, which are known to have an effect on the immune system and consequently tumour growth5,42. Additionally, they may have a direct effect as stress is associated with increased release of norepinephrine by the hypothalamus and sympathetic nerves43. Here we simulate a stress condition by increasing the norepinephrine release rate sn by sympathetic nerves. Figure 5A shows the time course of primary and migrating tumour cells when sn is multiplied by 10 for initial condition 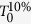Inline graphic. The plots show that when sn is increased, the primary tumour cell density settles quickly to a higher equilibrium, while tumour cell migration is enhanced. This is in accordance with the experimental observation that stress is related to higher cancer metastasis and perhaps higher mortality44,45. Again, our results agree qualitatively (but not quantitatively) with the experimental evidence.

Figure 5.

Figure 5

Open in a new tab

Primary and migrating tumour cells in stress conditions (simulated by multiplying sn by 10) for initial conditions (A) 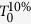Inline graphic and (B) 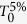Inline graphic respectively.

Another interesting prediction of our model is that for some initial conditions, such as 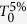Inline graphic, stress makes a crucial difference in tumour development. Here, if sn is taken to be its baseline value, recall the primary tumour tends to zero (Fig. 3); in stress conditions (simulated by multiplying sn by 10) the same initial condition leads to primary tumour growth and a constant increase of migrating tumour cells (Fig. 5B). This observation suggests that a stressful environment can affect tumour development and therapeutic efficacy, in accordance with many findings in the biological literature5,31. More experimental data are needed to precisely quantify this effect, however this already supports the potential for treatments targeting the sympathetic nervous system, as discussed by Cole & Sood46.

Blocking tumour acetylcholine receptors

Regarding parasympathetic neural activity, Magnon and collaborators7 report that impairing the cholinergic (acetylcholine) receptors on tumour cells does not significantly affect tumour growth in the orthotopic site, but markedly reduces tumour cell spreading and metastasis. To simulate this phenomenon, we set μ2 = 0; that is, we consider tumour cells to be non-responsive to acetylcholine. In this case, we see (simulation not shown) that the number of migrated tumour cells after 15 days is reduced by about 0.5% and a similar reduction is also observed in primary tumour cell density. Thus, the model corroborates the findings of Magnon et al.7 that cholinergic receptors on tumour cells are potential clinical targets in view of limiting cancer metastasis; again, for a quantitative assessment of the potential effectiveness of this treatment one would need to include more variables in the model.

Discussion

This work is the first mathematical confirmation of the major role played by the autonomic nervous system in promoting tumour development and progression of prostate cancer and highlights neoneurogenesis as a target for cancer drug development. In the present paper we develop a simple mathematical model for tumour neoneurogenesis and cancer progression based on recent experimental evidence; it results that, regardless of the presence of angiogenesis and lymphangiogensis, tumour-induced neoneurogenesis represents a symbiotic factor for prostate tumour. This work further expands our understanding of the process by which stress can regulate cancer aetiopathogenesis: previous research predominantly emphasised the role of the immune system in mediating stress effects on tumour growth and metastasis, while our model predicts that stress can directly affect primary tumour growth through the release of neurotransmitters. In addition, the effect of parasympathetic nerves is also captured by the model through the acetylcholine-induced tumour migration.

This model, though quite simple, gives good insights into tumour neoneurogenesis and offers many possibilities for expansion and improvement. First of all, the introduction of a spatial variable and thus the use of partial differential equations would allow a more precise description of the processes occurring during tumour neoneurogenesis. In particular, a spatial approach may be able to explain why sympathetic nerves tend to accumulate in normal tissues and only penetrate tumour edges, while parasympathetic nerves infiltrate tumour tissues7. Also, a more accurate description of the spatial component could allow for a distinction between axon elongation and nerve cell proliferation2.

The model could be further improved by considering different variables for different kinds of AGMs, which are known to have diverse effects on tumour cells16. In fact, circulating tumour cells are probably attracted to a specific organ by chemokines and AGMs; the fate of a new tumour cell cluster will depend on the sensitivity of the tumour cells to the specific factors and AGMs produced in the new environment.

One could also take into account the blood and lymphatic vasculatures. Guidance cues for axons also have a function in (lymph)angiogenesis47,48. Both angio-, lymphangio- and neoneuro-genesis promote metastasis formation, although in different ways; for instance, blood and lymphatic vessels offer pathways for tumour cells to disseminate, similar to perineural invasion17.

Another factor that could be included in the model is the immune system, which functions as a bridge between the tumour and nervous system and is the main cause of the indirect connections between the two (in addition, NGF also seems to be involved in immune response and inflammation49).

Additional Information

How to cite this article: Lolas, G. et al. Tumour-induced neoneurogenesis and perineural tumour growth: a mathematical approach. Sci. Rep. 6, 20684; doi: 10.1038/srep20684 (2016).

Supplementary Material

Supplementary Information
srep20684-s1.pdf (341KB, pdf)

Acknowledgments

The authors would like to thank Dr. Lasse Jensen, Dr. Kevin Painter and Prof. Michael Pepper for the useful technical discussions and suggestions.

Footnotes

Author Contributions G.L. and A.B. equally contributed to designing, developing and writing the present study. K.N.S. proofread the paper and provided comments and feedback from a medical perspective. All authors reviewed the manuscript.

References

  1. Thaker P. H. & Sood A. K. Neuroendocrine influences on cancer biology. Semin. Cancer Biol. 18(3), 164–170 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ayala G. E. et al. Cancer-related axonogenesis and neurogenesis in prostate cancer. Clin. Cancer Res. 14(23), 7593–7603 (2008). [DOI] [PubMed] [Google Scholar]
  3. Lü S., Zhou Y., Que H. & Liu S. Peptidergic innervation of human esophageal and cardiac carcinoma. World J Gastroenterol. 9(3), 399–403 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Lutgendorf S. K. et al. Social isolation is associated with elevated tumor norepinephrine in ovarian carcinoma patients. Brain Behav. Immun. 25(2), 250–255 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Vissoci Reiche E., Odebrecht Vargas Nunes S. & Kaminami Morimoto H. Stress, depression, the immune system, and cancer. The Lancet Oncology 5, 617–625 (2004). [DOI] [PubMed] [Google Scholar]
  6. Lang K. & Bastian P. Neurotransmitter effects on tumor cells and leukocytes. Prog Exp Tumor Res. Basel, Karger 39, 99–121 (2007). [DOI] [PubMed] [Google Scholar]
  7. Magnon C. et al. Autonomic nerve development contributes to prostate cancer progression. Science 341, 1236361 (2013). [DOI] [PubMed] [Google Scholar]
  8. Entschladen F., Palm D., Lang K., Drell T. IV & Zaenker K. Neoneurogenesis: Tumors may initiate their own innervation by the release of neurotrophic factors in analogy to lymphangiogenesis and neoangiogenesis. Medical Hypotheses 67, 33–35 (2006). [DOI] [PubMed] [Google Scholar]
  9. Syrigos K. N. Prostate cancer: Biology, diagnosis and management (Oxford University Press, USA, 2001). [Google Scholar]
  10. Palm D. & Entschladen F. Neoneurogenesis and the neuro-neoplastic synapse. Prog Exp Tumor Res. Basel, Karger 39, 91–98 (2007). [DOI] [PubMed] [Google Scholar]
  11. Dolle L., El Yazidi-Belkoura I., Adriaenssens E., Nurcombe V. & Hondermarck H. Nerve growth factor overexpression and autocrine loop in breast cancer cells. Oncogene 22(36), 5592–5601 (2003). [DOI] [PubMed] [Google Scholar]
  12. Ricci A. et al. Neurotrophins and neurotrophin receptors in human lung cancer. Am. J. Respir. Cell Mol. Biol. 25, 439–446 (2001). [DOI] [PubMed] [Google Scholar]
  13. Dollé L., Oliveira M., Bruyneel E., Hondermarck H. & Bracke M. Nerve growth factor mediates its pro-invasive effect in parallel with the release of a soluble E-cadherin fragment from breast cancer MCF-7/AZ cells. Journal of Dairy Research 72(Special Issue), 20–26 (2005). [DOI] [PubMed] [Google Scholar]
  14. Dickson B. Molecular mechanisms of axon guidance. Science 298, 1959–1964 (2003). [DOI] [PubMed] [Google Scholar]
  15. Mehlen P., Delloye-Bourgeois C. & Chedotal A. Novel roles for Slits and netrins: axon guidance cues as anticancer targets? Nat. Rev. Cancer 11(3), 188–197 (2011). [DOI] [PubMed] [Google Scholar]
  16. Chédotal A., Kerjan G. & Moreau-Fauvarque C. The brain within the tumor: new roles for axon guidance molecules in cancers. Cell Death and Differentiation 12, 1044–1056 (2005). [DOI] [PubMed] [Google Scholar]
  17. Entschladen F., Palm D., Drell T. L. IV, Lang K. & Zaenker K. S. Connecting a tumor to the environment. Current Pharmaceutical Design 13(33), 3440–3444 (2007). [PubMed] [Google Scholar]
  18. Villers A., McNeal J., Redwine E., Freiha F. & Stamey T. The role of perineural space invasion in the local spread of prostatic adenocarcinoma. The Journal of Urology 142(3), 763–768 (1989). [DOI] [PubMed] [Google Scholar]
  19. Lang K., Drell T. IV, Niggemann B., Zänker K. & Entschladen F. Neurotransmitters regulate the migration and cytotoxicity in natural killer cells. Immunology Letters 90, 165–172 (2003). [DOI] [PubMed] [Google Scholar]
  20. Entschladen F., Lang K., Drell T., Joseph J. & Zaenker K. Neurotransmitters are regulators for the migration of tumor cells and leukocytes. Cancer Immunol Immunother 51, 467–482 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Balkwill F. & Mantovani A. Inflammation and cancer: back to Virchow? The Lancet 357, 539–545 (2001). [DOI] [PubMed] [Google Scholar]
  22. Liotta L. An attractive force in metastasis. Nature 410, 24–25 (2001). [DOI] [PubMed] [Google Scholar]
  23. Fidler I. J. & Paget S. The pathogenesis of cancer metastasis: the ‘seed and soil’ hypothesis revisited. Nat. Rev. Cancer 3(6), 453–458 (2003). [DOI] [PubMed] [Google Scholar]
  24. Entschladen F., Palm D., Niggemann B. & Zaenker K. The cancer’s nervous tooth: Considering the neuronal crosstalk within tumors. Seminars in Cancer Biology 18, 171–175 (2008). [DOI] [PubMed] [Google Scholar]
  25. Drell T. IV, Joseph J., Lang K., Niggemann B., Zaenker K. & Entschladen F. Effects of neurotransmitters on the chemokinesis and chemotaxis of MDA-MB-468 human breast carcinoma cells. Breast Cancer Research and Treatment 80, 63–70 (2003). [DOI] [PubMed] [Google Scholar]
  26. Entschladen F., Drell T. IV, Lang K., Joseph J. & Zaenker K. Tumor-cell migration, invasion, and metastasis: navigation by neurotransmitters. Lancet Oncol. 5, 254–258 (2004). [DOI] [PubMed] [Google Scholar]
  27. Friberg S. & Mattson S. On the growth rates of human malignant tumors: implications for medical decision making. J Surg Oncol. 65, 284–297 (1997). [DOI] [PubMed] [Google Scholar]
  28. Ballangrud A. M., Yang W. H., Dnistrian A., Lampen N. M. & Sgouros G. Growth and characterization of LNCaP prostate cancer cell spheroids. Clin. Cancer Res. 5 (10 Suppl), 3171s–3176s (1999). [PubMed] [Google Scholar]
  29. Korolev K. S., Xavier J. B. & Gore J. Turning ecology and evolution against cancer. Nature Reviews Cancer 14(5), 371–380 (2014). [DOI] [PubMed] [Google Scholar]
  30. Pienta K. J., McGregor N., Axelrod R. & Axelrod D. E. Ecological therapy for cancer: defining tumors using an ecosystem paradigm suggests new opportunities for novel cancer treatments. Transl Oncol 1(4), 158–164 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Eng J. W. et al. A nervous tumor microenvironment: the impact of adrenergic stress on cancer cells, immunosuppression, and immunotherapeutic response. Cancer Immunol. Immunother. 63(11), 1115–1128 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Thiébault K. et al. The netrin-1 receptors UNC5H are putative tumor suppressors controlling cell death commitment. PNAS 100(7), 4173–4178 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Capparuccia L. & Tamagnone L. Semaphorin signaling in cancer cells and in cells of the tumor microenvironment–two sides of a coin. J. Cell. Sci. 122 (Pt 11), 1723–1736 (2009). [DOI] [PubMed] [Google Scholar]
  34. Lindsay R. M. Nerve growth factors (NGF, BDNF) enhance axonal regeneration but are not required for survival of adult sensory neurons. J. Neurosci. 8(7), 2394–2405 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wang K. H. et al. Biochemical purification of a mammalian slit protein as a positive regulator of sensory axon elongation and branching. Cell 96(6), 771–784 (1999). [DOI] [PubMed] [Google Scholar]
  36. Guyton A. C. & Hall J. E. in Textbook of medical physiology 11th edn, Ch. 60, 729–739 (Elsevier, 2006). [Google Scholar]
  37. Miller L. E., Justen H. P., Scholmerich J. & Straub R. H. The loss of sympathetic nerve fibers in the synovial tissue of patients with rheumatoid arthritis is accompanied by increased norepinephrine release from synovial macrophages. FASEB J. 14(13), 2097–2107 (2000). [DOI] [PubMed] [Google Scholar]
  38. Wessler I. & Kirkpatrick C. J. Acetylcholine beyond neurons: the non-neuronal cholinergic system in humans . Br. J. Pharmacol. 154(8), 1558–1571 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nico B., Mangieri D., Benagiano V., Crivellato E. & Ribatti D. Nerve growth factor as an angiogenic factor. Microvasc. Res. 75, 135–141 (2008). [DOI] [PubMed] [Google Scholar]
  40. Botelho F., Pina F. & Lunet N. VEGF and prostatic cancer: a systematic review. European Journal of Cancer Prevention 19(5), 385–392 (2010). [DOI] [PubMed] [Google Scholar]
  41. Magnon C. Role of the autonomic nervous system in tumorigenesis and metastasis. Molecular & Cellular Oncology 2(2), e975643 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Mravec B., Gidron Y. & Hulin I. Neurobiology of cancer: Interactions between nervous, endocrine and immune systems as a base for monitoring and modulating the tumorigenesis by the brain. Seminars in Cancer Biology 18, 150–163 (2008). [DOI] [PubMed] [Google Scholar]
  43. Kvetnansky R. et al. Sympathoadrenal system in stress. Interaction with the hypothalamic-pituitary-adrenocortical system. Ann. N. Y. Acad. Sci. 771, 131–158 (1995). [DOI] [PubMed] [Google Scholar]
  44. Chida Y., Hamer M., Wardle J. & Steptoe A. Do stress-related psychosocial factors contribute to cancer incidence and survival? Nat Clin Pract Oncol 5(8), 466–475 (2008). [DOI] [PubMed] [Google Scholar]
  45. Moreno-Smith M., Lutgendorf S. K. & Sood A. K. Impact of stress on cancer metastasis. Future Oncol 6(12), 1863–1881 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Cole S. W. & Sood A. K. Molecular pathways: beta-adrenergic signaling in cancer. Clin. Cancer Res. 18(5), 1201–1206 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Carmeliet P. & Tessier-Lavigne M. Common mechanisms of nerve and blood vessel wiring. Nature 436, 193–200 (2005). [DOI] [PubMed] [Google Scholar]
  48. Eichmann A., Makinen T. & Alitalo K. Neural guidance molecules regulate vascular remodeling and vessel navigation. Genes & Development 19, 1013–1021 (2005). [DOI] [PubMed] [Google Scholar]
  49. Woolf C. J., Safieh-Garabedian B., Ma Q. P., Crilly P. & Winter J. Nerve growth factor contributes to the generation of inflammatory sensory hypersensitivity. Neuroscience 62(2), 327–331 (1994). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep20684-s1.pdf (341KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES