Geometric Morphometrics on Gene Expression Patterns Within Phenotypes: A Case Example on Limb Development

Abstract

How the genotype translates into the phenotype through development is critical to fully understand the evolution of phenotypes. We propose a novel approach to directly assess how changes in gene expression patterns are associated with changes in morphology using the limb as a case example. Our method combines molecular biology techniques, such as whole-mount in situ hybridization, with image and shape analysis, extending the use of Geometric Morphometrics to the analysis of nonanatomical shapes, such as gene expression domains. Elliptical Fourier and Procrustes-based semilandmark analyses were used to analyze the variation and covariation patterns of the limb bud shape with the expression patterns of two relevant genes for limb morphogenesis, Hoxa11 and Hoxa13. We devised a multiple thresholding method to semiautomatically segment gene domains at several expression levels in large samples of limb buds from C57Bl6 mouse embryos between 10 and 12 postfertilization days. Besides providing an accurate phenotyping tool to quantify the spatiotemporal dynamics of gene expression patterns within developing structures, our morphometric analyses revealed high, non-random, and gene-specific variation undergoing canalization during limb development. Our results demonstrate that Hoxa11 and Hoxa13, despite being paralogs with analogous functions in limb patterning, show clearly distinct dynamic patterns, both in shape and size, and are associated differently with the limb bud shape. The correspondence between our results and already well-established molecular processes underlying limb development confirms that this morphometric approach is a powerful tool to extract features of development regulating morphogenesis. Such multilevel analyses are promising in systems where not so much molecular information is available and will advance our understanding of the genotype–phenotype map. In systematics, this knowledge will increase our ability to infer how evolution modified a common developmental pattern to generate a wide diversity of morphologies, as in the vertebrate limb.

Introduction

Geometric Morphometrics (GM) has emerged over the last few decades as the main tool for quantitative characterization, analysis, and comparison of biological form (Rohlf and Marcus 1993; Bookstein 1997a; Dryden and Mardia 1998; Lele and Richtsmeier 2001; Klingenberg 2002, 2010; Adams et al. 2013). However, the “morphometric revolution” has not yet attempted to directly analyze the shape of gene expression domains; that is, the region within a tissue where a gene is being expressed at a certain developmental time (Fig. 1). Since the genotype gives rise to the phenotype through gene expression and regulation, extending morphometrics to the analysis of gene expression patterns would help determine when and where genes are switched on/off within a structure and how development translates differences in gene expression into differences in morphology (Fig. 1). This is crucial to clarify the genetic and developmental phenomena underlying biological diversity and the evolution of phenotypes (Jernvall et al. 2000; Salazar-Ciudad and Jernvall 2010; Young et al. 2010; Hu et al. 2015).

Figure 1.

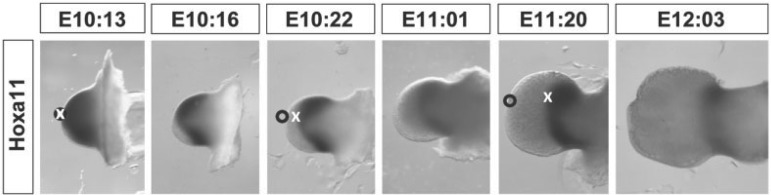
Gene expression domain of Hoxa11 within the developing limb. Example of time course WISH labeled limbs for Hoxa11 from approximately embryonic day 10.5 (E10:13: embryonic day 10 and 13 hours) to embryonic day 12 (E12:03: embryonic day 12 and 3 hours). Images are not at scale. The dissected limb buds show the expression of Hoxa11 as a black stain. Note that in 2 days of development, the limb bud shape changes from a bulge to a paddle-like limb, and this occurs as the size, shape and position of the Hoxa11 gene expression domain change every few hours of development. The annotations represent relative positions of the tissue boundary (black circle) and the gene expression domain (white cross) and illustrate one of the key distinctions between anatomical shapes and gene expression domains. The latter can literally “slide” through the former over time, due to active regulation of the gene. At E10:13 the distal boundary of Hoxa11 corresponds to the tissue boundary. But just 10 hours later, this is no longer true. Distal cells have switched off Hoxa11 expression, and the gene expression boundary has shifted proximally into the center of the limb. The main goal of our analysis is to accurately capture all these shape changes using a quantitative morphometric method and to associate the changes in the gene expression patterns with the changes in limb morphology. 162 × 51 mm (300 × 300 DPI).

To bridge this gap, we propose a quantitative morphometric method to perform accurate characterization of gene expression patterns within developing structures. Moreover, using the limb as a case example, we illustrate how variation in the expression patterns of two genes can be quantified, analyzed, and associated with limb morphological variation using standard geometric morphometric methods. The results of these analyses reveal the potential of the method to suggest underlying patterning mechanisms involved in limb morphological evolution. Our method will be valuable in systematics to further investigate the genetic and developmental processes correlated with diversification and adaptation.

From Anatomy to Gene Expression Patterns

It is essential to have detailed spatiotemporal representations of gene expression domains to understand the development and morphogenesis of complex biological structures (Sharpe 2003). Whole-mount in situ hybridization (WISH), a technique that localizes the expression of a specific gene in an entire piece of tissue by using a labeled complementary RNA strand (i.e., probe) (Rosen and Beddington 1993; de la Pompa et al. 1997; Correia and Conlon 2001), can be readily used to visualize gene expression domains in whole embryos. Yet, objective and accurate methods to quantify and compare gene expression patterns in a systematic manner are lacking. Visual inspection and manual analysis are the routine approaches for understanding gene expression patterns. This is severely limited—in the same way that verbal, non-quantitative descriptions of anatomy fail to capture important aspects of shape and size and have given way to quantitative morphometric techniques, such as GM.

The shape quantification of gene expression patterns will provide an important extra level of information not revealed by anatomical analysis. First, gene expression patterns can reveal information not present in the tissue alone because they typically take form of a molecularly defined subregion of a given tissue, whose boundaries may not correspond to rigorous histological definitions. Second, since gene expression is one of the key drivers for the changing cellular behavior that ultimately produces the adult anatomical form, patterns of gene expression may more directly represent the mechanisms responsible for producing the shapes of tissues.

Extending morphometric approaches from anatomy to gene expression patterns would thus provide a tool for: (i) characterizing changing gene expression patterns in their magnitude, proportion, and spatial locations over development, (ii) analyzing the variational properties of such gene expression domains, and (iii) linking changes in the shape of the gene expression patterns to the shape changes of the developing organ where the gene is actually expressed. Morphometric data have traditionally been used as a source of characters for phylogenetic analyses, either using morphometric characters for estimating phylogenies (MacLeod and Forey 2003), or mapping shape data onto phylogenetic trees constructed with independent data such as DNA sequences (Klingenberg 2010). Our method, which focuses on the link between the genotype to the phenotype through gene expression patterns, provides another input for phylogenetic studies. The comparative analysis of gene expression patterns in different species could be used to investigate the genetic and developmental processes underlying the evolution of anatomical phenotypes.

To successfully apply GM to gene expression patterns, three main challenges need to be addressed: the fuzzy boundaries of gene expression patterns, the lack of anatomical landmarks, and the high dynamics of change of gene expression patterns over time. Unlike anatomical structures, the contour of a gene expression pattern cannot always be clearly defined by its boundary. Where an expression domain extends to the edge of the tissue, the expression boundary is effectively the same as the tissue boundary. However, many genes show internal boundaries that do not match any visible anatomical or histological boundary, and critically these are often not sharp. Even genes which later represent sharp boundaries (or may in fact be responsible for the creation of a sharply defined anatomical feature), will typically pass through phases of development in which their boundaries are fuzzy spatial gradients. To handle the fuzziness of gene expression pattern boundaries, a threshold value of expression could be chosen to force the definition of a sharp (ON/OFF) boundary—that is, a single isocline. However, the decision of the threshold level is arbitrary and discards a valuable wealth of the spatial information of the pattern. Our method extracts gene expression domains at multiple expression levels using semiautomatic image processing and is able to analyze either on–off or gradient gene expression patterns.

The second challenge is that gene domains are often devoid of anatomical landmarks. Biological landmarks as traditionally defined must indicate corresponding points of physical tissue that can be reliably relocated with an acceptable degree of measurement error to enable comparison among individuals. However, the cells which make up the physical tissue can switch gene expression on or off during development. Consequently, the boundary of a gene expression domain can literally “slide” through the physical tissue over time. This highlights the fundamentally different nature of gene expression shapes versus anatomical shapes—the cells on the boundary of a gene domain at one time point may end-up far from the boundary a few hours later (Fig. 1). To deal with the lack of anatomical landmarks, our approach involves analyses of outlines or curves that do not require the researcher to establish an explicit correspondence of points to points in homologous structures, such as Elliptical Fourier analysis (EFA) (Kuhl and Giardina 1982; Lestrel 1989, 1997) and semilandmark-based GM methods (Bookstein 1997b).

The third challenge, that gene expression patterns may be highly dynamic and rapidly change in size, shape, and position in few hours over development, requires the use of many samples over even a small time-window of development. Despite being time- and resource-consuming, the advantages of analyzing large samples are to get better estimates of the mean shape of the gene expression domain at each developmental stage and, even more important, to obtain estimates of the shape variation of the gene expression domains. As we will show later, comparison of variation and covariation patterns at different time points is a key to further understand how development translates genetic variation into phenotypic variation.

A Case Example: The Mouse Limb

To illustrate the potential of our approach and how shape variation of gene expression patterns can be characterized and analyzed using a variety of existing GM methods, we used the mouse limb, which is a classical model system for studying biological patterning and development (Zeller et al. 2009). The mouse limb develops from a bulge of undifferentiated mesenchymal cells surrounded by a thin ectodermal layer that protrudes from the flank of the embryo around 9 d post fertilization. Over a period of only 2–3 days (d), this mass of cells grows into a limb bud with differentiated cartilage and muscles. Although limb patterning and morphogenesis is widely conserved among vertebrates and detailed knowledge about genes participating in these processes is available (Tabin and Wolpert 2007), the specific details of the genetic networks coordinating limb morphogenesis still remain obscure (Bénazet and Zeller 2009; Duboc and Logan 2009; Zeller et al. 2009; Zeller 2010).

Our study focuses on the analysis of the expression patterns of two genes relevant for limb proximodistal (P-D) patterning, Hoxa11 and Hoxa13 (Tabin and Wolpert 2007; Mariani 2010). These Hoxa genes are traditionally used as markers for the development of the zeugopod and the autopod, which will respectively develop into the upper limbs and the hands/feet (Tabin and Wolpert 2007; Mariani 2010). The expression of Hoxa11 and Hoxa13 is regulated by the expression of many other genes, mainly fibroblast growth factors (Fgfs) and sonic hedgehog (Shh), which are produced by the two main signaling centers in the limb bud (Towers and Tickle 2009; Zeller et al. 2009): the apical ectodermal ridge (AER), which is a thickening of the ectodermal layer along the boundary between the dorsal and ventral parts of the limb (Sun et al. 2002), and the zone of polarizing activity (ZPA), which is established at the posterior mesenchyme and is associated with anteroposterior (A-P) patterning (Capdevila and Izpisúa Belmonte 2001). Other molecules such as retinoic acid (RA) coming from the flank of the embryo also play an important role in limb patterning (Cooper et al. 2011).

Our approach can be used to accurately and more objectively represent gene expression patterns, but also to assess size and shape variation of gene expression patterns over development and to correlate the dynamic expression patterns of genes with the changing morphology of a growing organ. Throughout the rest of this article, we show how to perform and interpret this type of analysis using a large WISH-labeled sample of C57Bl6 mouse embryos between 10.5 and 12.5 postfertilization days (E10.5–E12.5), the period of greatest morphology diversity in limb development during which the P-D pattern is established.

Overall, our results define a genotype–phenotype temporal continuum in normal mouse limb development, providing a continuous representation of the limb morphology (phenotype) and the associated Hoxa11 and Hoxa13 gene expression domains over a concise temporal window (from E10:11 to E12:10). Our results are consistent with the available evidence on the molecular and developmental underpinnings of limb patterning—revealing functional, genetic, and developmental interactions between gene expression patterns and developing structures.

Materials and Methods

Here, we describe in detail the sample composition, the WISH protocol, the limb staging, and the multiple threshold method that we have devised to semiautomatically capture the shape of the limb and the gene expression domains from 2D pictures of the WISH-labeled limbs. Afterwards, we explain the different GM and multivariate statistical methods that were applied to (i) characterize the shape of Hoxa11 and Hoxa13 gene expression patterns, (ii) assess size and shape variation of limb buds and of Hoxa11 and Hoxa13 gene expression patterns, and (iii) estimate the shape covariation between the gene expression domains and the limb bud.

Samples

To provide a continuous temporal representation of embryonic normal mouse limb development between E10.5 and E12.5, we bred 13 litters of C57Bl6 mouse embryos and collected them at three different time points (E10.5, E11.5, and E12.5). The mouse embryos were labeled using WISH for either Hoxa11 or Hoxa13 gene expression as explained below. When available, all four right and left fore- and hind limbs of each specimen were dissected, photographed, staged, and processed for shape analysis. In total, we analyzed 75 limbs for Hoxa11 and 130 limbs for Hoxa13 (Table 1).

Table 1.

Sample size information by stage and gene

	Hoxa11	Hoxa13	Total
E10:11–E10:22	43 (15,28)	55 (21,34)	98 (36,62)
E10:23–E11:10	7 (6,1)	15 (10,5)	22 (16,6)
E11:11–E11:22	11 (9,2)	58 (34,24)	69 (43,26)
E11:23–E12:10	14 (6,8)	2 (2,0)a	16 (8,8)
Total	75	130	205

Note: Each stage comprises 12 h of embryonic development: (i) E10:11–E10:22 (from limbs of 10 d and 11 h, to limbs of 10 d and 22 h); (ii) E10:23–E11:10 (from limbs of 10 d and 23 h, to limbs of 11 d and 10 h); (iii) E11:11–E11:22 (from limbs of 11 d and 11 h, to limbs of 11 d and 22 h); (iv) E11:23–E12:10 (from limbs of 11 d and 23 h, to limbs of 12 d and 10 h). Sample sizes are provided for each gene and stage: first number indicates total sample size, whereas numbers in brackets specifies number of forelimbs and hindlimbs within each group. Right and left limbs account for approximately 50% of the sample within each group.

^aMain statistical analyses were not performed at this stage due to sample size limitation.

WISH and Imaging

Mouse embryos were dissected in cold phosphate-buffered saline (PBS; Sigma), fixed in 4% paraformaldehyde (PFA; Sigma), dehydrated in increasing series of MetOH/PBST (methanol/phosphate-buffered saline, 0.1% Tween 20; Sigma) and stored at −20°C for WISHs. Although the process of dehydration shrinks the tissue, the mouse embryos recovered their original size after rehydration in decreasing series of MetOH/PBST. After washing three times in PBST, embryos were permeabilized by treating them with proteinase K (Roche). WISHs (de la Pompa et al 1997) were performed using Hoxa11 and Hoxa13 RNA antisense probes labeled with digoxigenin-UTP (Roche). We used alkaline phosphatase coupled anti-digoxigenin (anti-DIG-AP, Roche) and NBT/BCIP staining (Roche) to reveal the in situ hybridizations. After WISH, dorsal-view pictures of dissected limb buds were taken using a Leica MX16F microscope with a magnification of 10x. All embryos underwent exactly the same protocol.

Staging

Individual limb buds were staged using our publicly available web-based staging system (http://limbstaging.crg.es, last accessed October 1, 2015) (Boehm et al. 2011). This morphometric tool allows the user to load 2D pictures of limb buds and draw a spline curve along the outline of the limb. The stage of the limb bud is then estimated after alignment and shape comparison of the spline with an existing data set of more than 600 limb buds between stages E10–E12 with a reproducibility of ±2 h. According to the staging estimates, the full time series of Hoxa11 and Hoxa13 labeled limbs were binned into four time periods (Table 1). These staging groups were used for further comparative ontogenetic analysis. The morphometric approach that we introduce here, however, does not depend on having such accurate fine-resolution staging system staging, and any other developmental criteria can be used to stage the specimens.

Multiple Thresholding

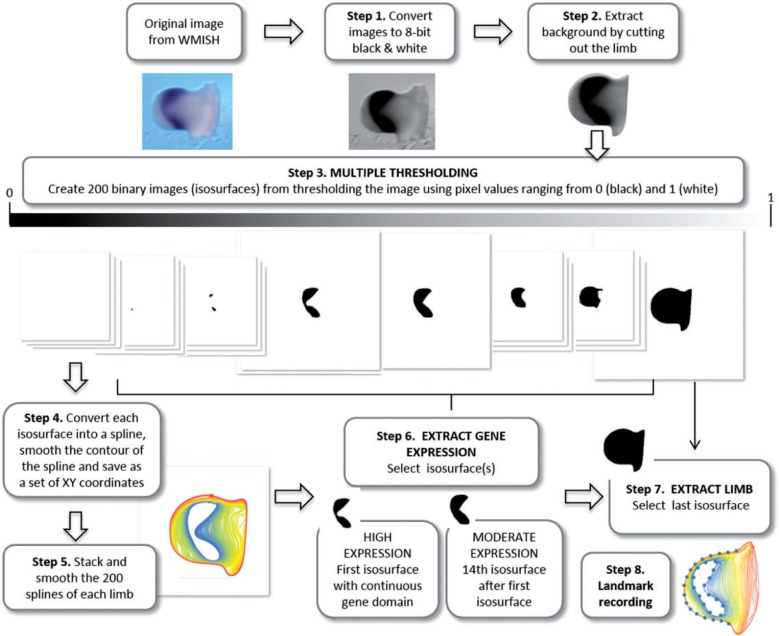
We segmented the shape of the limb bud and the shape of the Hoxa11 and Hoxa13 gene expression patterns from the 2D pictures of the WISH experiments using a semiautomatic pipeline based on R 3.0.0 (R Development Core Team 2013) and Fiji (Fiji is Just ImageJ) 1.48d scripts (Schindelin et al. 2012). This procedure allows the user to segment the limb outline and to perform a multiple thresholding of the gene expression domain (Fig. 2). Multiple thresholding captures the continuous gradient of gene expression by overlapping the isosurfaces thresholded for different pixel values representing the gene expression domain. Detailed description of this procedure is provided in Figure 2. The advantage of this method is that it is automatic and does not require adjustment of the brightness/contrast or the levels of the images. The gene segmentation is not thus affected by measurer subjectivity and/or manual digital image manipulation. Results from preliminary controls to check the potential experimental errors introduced by WISH labeling and imaging consistently showed that variation between developmental stages exceeded variation between experiments (data not shown). Color intensities can thus vary across experiments and specimens; however, as our multiple thresholding method is based on relative (not absolute) color intensities within each limb, the thresholds are comparable across specimens.

Figure 2.

Schematic pipeline of limb bud shape extraction and multiple thresholding of gene expression domains. In the first step of the multiple thresholding method, the original WISH images are converted into eight-bit grayscale images. The second step is to remove the background of the image by cutting out the limb. In step 3 the resulting image undergoes multiple thresholding: the image is automatically thresholded using 200 different values ranging from 0 (i.e. black pixel values) to 1 (i.e. white pixel values). Black pixels represent very high gene expression, whereas light gray represent very low gene expression. As a result 200 binary images are generated. The whole sequence of binary thresholded images (from now on called isosurfaces) captures the decreasing intensity of gray pixel values in the segmented limb images. In step 4 each isosurface is converted into a spline and saved as a set of xy coordinates. The fifth step stacks the 200 splines representing each limb and smoothes them to remove undesirable irregularities caused by high resolution automated spline extraction. The splines were smoothed by iteratively applying 25 times the smoothout function in R (Claude 2008), a procedure based on Haines and Crampton (2000) that reduces measurement error by averaging the xy coordinates of neighboring points. Note that when a gene is expressed as a gradient, many isosurfaces represent the expression domain and in step 6 the user needs to choose which level/s to analyze. We discarded the first isosurfaces containing scattered irregular patches with very strong gene expression, and selected as high gene expression level the first isosurface representing a continuous gene domain (step 6). Depending on the staining and the quality of the image, the number in sequence of the isosurface representing the high expression domain for each limb is different, but represents a homologous gene domain across the sample. As moderate expression we selected the 14th isosurface after the first one (step 6). The following isosurfaces representing very low levels of gene expression captured noisier signals of gene domains and were thus not considered for analysis. In step 7, the last isosurface is selected to extract limb bud shape. The isosurfaces representing the high and moderate gene expression domains and the limb bud are the starting point for the shape analysis, which begins in step 8 by recording landmarks on both the limb and the gene outlines. 208 × 174 mm (300 × 300 DPI).

Gene expression domains can then be extracted from the binary images generated by the multiple thresholding. If the gene domain shows a clear on–off expression pattern, only one binary image will represent the gene domain. If, as in our example, the gene domain shows a gradient expression pattern, a subset of binary images will provide a commensurate representation of the gradient (Fig. 2). In this case, the user can specify which levels of gene expression will be analyzed. For the current shape analysis of Hoxa11 and Hoxa13 domains, we defined two levels of gene expression: (i) a high gene expression, represented by the first isosurface displaying a continuous gene domain; and (ii) a moderate gene expression, represented by the 14th isosurface after the first isosurface (Fig. 2, step 6). Finally, the shape of the limb can be extracted from the last isosurface of the multiple thresholding output (Fig. 2, step 7).

Morphometric Analyses

The isosurfaces representing the shape of the limb and the gene expression domains were the starting point for three different sets of analyses: (i) Gene Shape Analysis, (ii) Limb Shape Analysis, and (iii) Limb/Gene Shape Analysis. For each analysis, we chose different GM and statistical methods to show different possible ways of analyzing gene expression patterns within developing structures and to highlight the advantages and disadvantages of each method.

Gene shape analysis

This set of analyses was performed to assess the shape variation of Hoxa11 and Hoxa13 gene expression domains independently from the limb bud shape. In this case, we used EFA (Kuhl and Giardina 1982; Lestrel 1989, 1997), a widely used method for systematic shape analysis of 2D closed outlines, such as our gene expression patterns (Fig. 2, step 6). We could have used a Procrustes-based semilandmark approach (Bookstein 1997b) as we have done with the limb shape, but we decided to use EFA to show that different geometric morphometric techniques can be used to analyze gene expression domains.

EFA is a morphometric method based on Fourier decomposition of outlines on a series of periodic trigonometric functions. These functions are characterized by increasing frequencies called harmonics: lower harmonics provide approximation for the coarse-scale trends in the original periodic function while the high-frequency harmonics are used to fit the fine-scale variations. One of the main advantages of Fourier analysis over other GM methods is that it does not require the presence of homologous landmarks and captures subtle shape differences by analyzing the complete geometric information of outlines. In comparison to other Fourier-based approaches, EFA does not require equally spaced points; virtually any outline can be fitted (Rohlf and Archie 1984; Crampton 1995; Haines and Crampton 2000) and the coefficients can be made independent of outline position and are normalized for size. The main disadvantages are that EFA cannot deal with open outlines or with more than a single outline at a time, and cannot be easily extended to 3D surfaces.

Due to the fuzziness of the Hoxa11 and Hoxa13 gene gradients, we analyzed two different expression levels (i.e., a high and a moderate expression level for each gene) to explore whether the analyses of gene domains at different expression levels just provided similar or else complementary additional information about the underlying biological mechanisms of limb development. Therefore, EFA was applied separately to the high and moderate Hoxa11 and Hoxa13 expression domains using the R package Momocs (Bonhomme et al. 2014). For each analysis, we pooled together the samples from the four staging groups (Table 1) and shape variation was expressed using the first 32 harmonics.

To explore the morphological variation of Hoxa11 and Hoxa13 expression domains, we performed a principal component analysis (PCA) on the variance–covariance matrix (Rohlf and Archie 1984; Crampton 1995) of the elliptical Fourier descriptors (EFDs) for each gene expression domain. Furthermore, to accurately describe the dynamical shape changes of the gene expression domains, we estimated the average shapes of the Hoxa11 and Hoxa13 expression domains for each staging group and compared them (Table 1). The differences between the average gene shapes of consecutive staging groups were visualized as thin plate spline (TPS) deformation grid splines (Bookstein 1997a).

Limb shape analysis

This set of analyses was performed to assess the shape variation of the limb bud without considering the gene expression patterns. Here, we opted for a Procrustes-based semilandmark analysis (Bookstein 1997b), which is an approach widely applied in structures devoid of homologous landmarks that allowed us to analyze the open contour of the limb bud. Semilandmarks are points located along a curve (Bookstein 1997b) or a surface (Gunz et al. 2005) that can be slid to corresponding equally spaced locations. The main advantage of Procrustes-based semilandmark analysis is that it can deal with several outlines simultaneously (either open or closed) and can be readily extended into 3D analysis (Mitteroecker and Gunz 2009).

In this study, the shape of the limbs was captured from the last isosurface produced by the multiple thresholding (Fig. 2, step 7). To define the open distal segment delimiting the limb bud contour, we manually recorded the $x$, $y$ coordinates of two anatomical landmarks that were used to define the start and end points of the limb bud (i.e., the maximum concavities at the posterior and anterior sides of the limb). Using R scripts (Claude 2008), we automatically recorded 19 equally spaced points between the start and end points of the limb bud outline and discarded the rest of the outline (i.e., the segment that lies to the right of these points in left limbs and to the left in right limbs) (Fig. 2, step 8).

The resulting configurations of 21 landmarks representing the limb bud shapes of all the samples generated in this study ($N=205$, Table 1) were analyzed using the Procrustes-based semilandmark approach. A general Procrustes analysis (GPA) (Rohlf and Slice 1990) was performed to superimpose the configurations of landmarks by shifting them to a common position, rotating, and scaling them to a standard size until a best fit of corresponding landmarks was achieved (Dryden and Mardia 1998). Semilandmarks were allowed to slide by minimizing the bending energy (Bookstein 1997b; Gunz et al. 2005; Mitteroecker and Gunz 2009). The resulting coordinates were the inputs for further statistical analysis to assess the patterns of limb morphological variation.

First, we performed a PCA that included the limbs from all four developmental stages to analyze the full ontogenetic trajectory of limb development. Second, we performed separate GP and PC analyses for each staging group to have a complete insight into the morphological variation within each developmental stage.

Limb/gene shape analysis

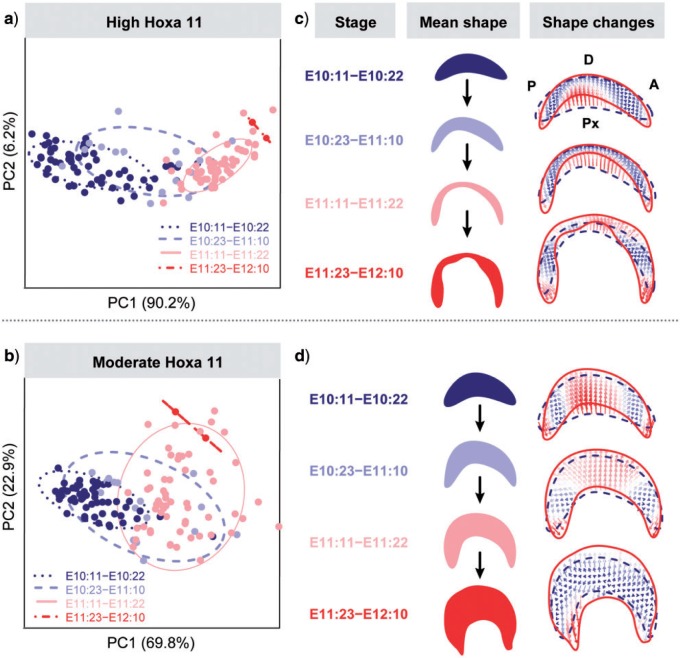
This set of analyses was performed to assess the dynamic shape changes of the limb bud in association with the Hoxa11 and Hoxa13 gene expression domains over limb development. In this case, we also used a Procrustes-based semilandmark analysis, because it is the only method that allowed us to analyze simultaneously the contours of the limb and the gene expression domains. Furthermore, it allowed us to assess not only the patterns of morphological variation, but also the patterns of covariation between the limb and the gene expression domains at each stage. This provided an extra level of information about the relationship between the gene expression of Hoxa11 and Hoxa13 and the actual morphology of the limb.

For each sample, we defined a configuration of 42 equally spaced points: 21 points located along the limb contour and 21 points located along the contour of the gene expression domain. The limb and the gene expression domains were represented by the same number of points to guarantee similar weighting of both features in the shape analysis. The start and end points of the limb bud outline were treated as fixed anatomical landmarks, whereas the remaining 40 points were treated as 2D curve semilandmarks that were slid to minimize the bending energy (Bookstein 1997b; Gunz et al. 2005; Mitteroecker and Gunz 2009).

To assess shape variation in limb and gene expression during the whole sequence of limb development, we performed GPA and PCA using the samples from all four staging groups for Hoxa11 ($N=75$) and for Hoxa13 ($N=130$). We also explored the morphological variation within each stage by performing separate GPA and PCAs for each stage.

To evaluate the patterns of covariation between the limb and the Hoxa11 and Hoxa13 expression domains, we used partial least squares (PLS) (Rohlf and Corti 2000). This method quantifies the covariation patterns between subsets of landmarks defined within the structure under study. In our study, we defined two different assemblages of the limb/gene configuration of landmarks to explore different scenarios of limb development. First, we separated the landmarks of the limb contour and the landmarks of the contour of the gene expression domains into two different subsets of landmarks to quantify the covariation between the limb and the Hoxa11 and Hoxa13 gene expression domains (Fig. 7c). Second, we divided the limb/gene configuration of landmarks into two subsets of landmarks that represented the anterior and the posterior regions of the limb (Fig. 7d). To have comparable results, the subsets of landmarks systematically had the same number of landmarks ($P=21$).

Figure 7.

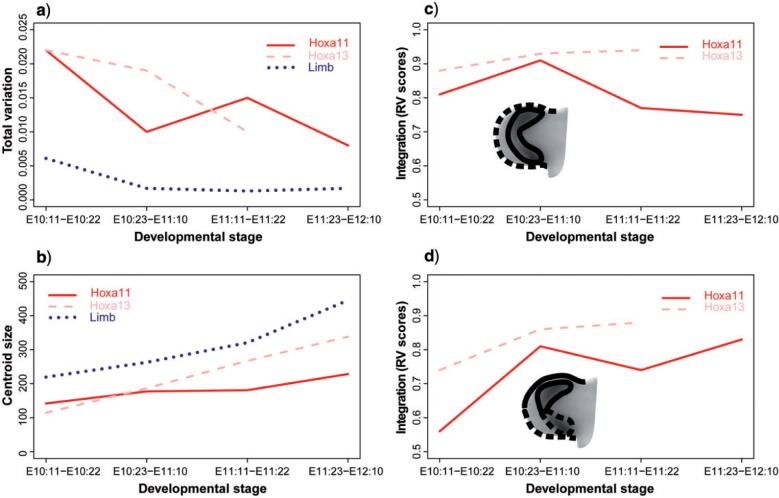
Comparison graphs between genes and stages. a) Total shape variation. b) Size of the limbs and size of the Hoxa11 and Hoxa13 expression domains. Since the patterns of increasing size were similar at moderate and high levels for both Hoxa11 and Hoxa13 gene expression domains, note that average scores from high and moderate gene expression levels have been plotted; for actual scores see Table 2. c) RV coefficients of the Limb/Gene modularity hypothesis. d) RV coefficients of the Anterior/Posterior modularity hypothesis. No values are available for the last stage of Hoxa13 analyses due to small sample size. 254 × 165 mm (300 × 300 DPI).

The Two-Block PLS analysis estimates the covariation between the two blocks of landmarks by performing a singular value decomposition of the covariance matrix between the subsets of landmarks (Rohlf and Corti 2000). As a result, PLS produces orthogonal pairs of new axes derived as linear combinations of the original variables: the first pair of axes has the largest interblock covariance, the second pair the next largest covariance, etc. (Rohlf and Corti 2000). In our analysis, each PLS analysis was applied to the adjusted coordinate data obtained after a joint Procrustes fit of the two configurations of landmarks. The amount of covariation was measured by the RV coefficient, which is a multivariate analog of the squared correlation (Klingenberg 2009).

Finally, along with shape analyses, we also performed size analyses. For each sample, we estimated the size of the limb and the size of the high and moderate gene expression domains. Size was computed as the square root of the summed distances between each landmark coordinate and the centroid of the configuration of landmarks defining each structure (i.e., the so-called centroid size) (Dryden and Mardia 1998). We then estimated the average sizes of the limb and the gene expression domains for each staging group, and tested for statistical significant differences between consecutive stages using a Welch Two-Sample $t$-test.

In all limb/gene shape and size analyses, Hoxa11 and Hoxa13 labeled limbs were analyzed separately and for both genes we analyzed high- and moderate gene expression levels and compared the results. All the analyses were performed using R (R Development Core Team 2013; http://www.R-project.org, last accessed October 1, 2015); geomorph (Adams and Otárola-Castillo 2013), a package available at CRAN (http://cran.r-project.org/web/packages/geomorph, last accessed October 1, 2015), and MorphoJ (Klingenberg 2011).

Results and Discussion

We here present our results and discuss the genetic and developmental interactions that might be underlying our morphometric results.

Gene Expression Domains: Shape Variation and Temporal Dynamics

We first analyzed the shape changes of Hoxa11 and Hoxa13 gene expression domains between E10.5 and E12.5 using EFA. The gene expression patterns were thus analyzed independently from the limb bud shape and the relative position of the gene domain within the limb was disregarded. Nevertheless, the EFA analysis of the gene shape changes provided direct information about the temporal dynamics of each gene.

Overall, the PCA computed over the whole sample of gene expression domains allowed us to analyze and compare the shape variation of the Hoxa11 and the Hoxa13 domains at different developmental stages and with different expression levels. Results revealed high morphological variation within developmental stages and different shape patterns of Hoxa11 and Hoxa13 expression throughout mouse limb embryonic development. Our results also underscored that the use of different expression levels may lead to different conclusions and that it is impossible to know a priori which level will provide the most useful information, advocating for simultaneously analyzing several levels of expression.

Hoxa11

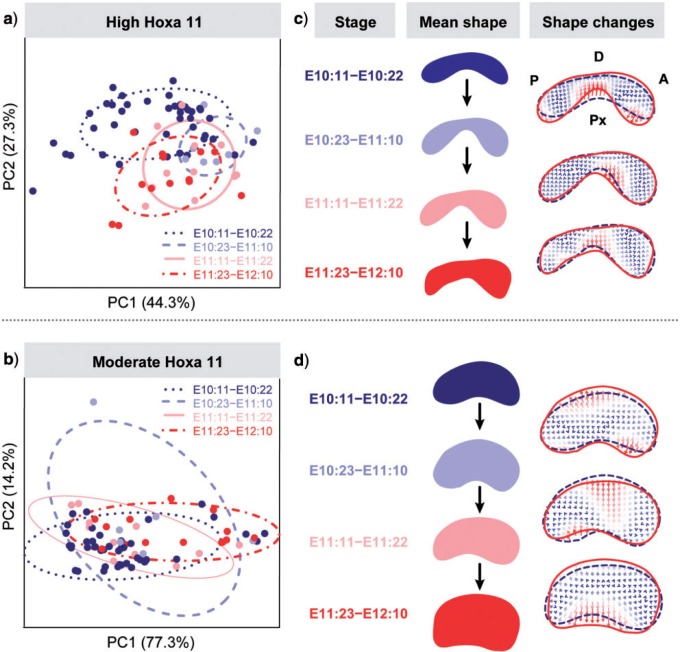
The PC analyses showed high amounts of shape variation and considerable overlap between staging groups. This indicates low morphological differentiation of the Hoxa11 gene expression domain over development and shows that despite continuously changing position (Fig. 1), the Hoxa11 domain does not significantly change in shape with time (Fig. 3a,b). Only when the high expression of Hoxa11 was considered, the earliest stage (E10:11–E10:22) showed some differentiation along PC2 (Fig. 3a). Accordingly, the greatest (i.e., most intense) shape change for high Hoxa11 expression occurred between the two earliest stages (E10:11–E10:22 and E10:23–E11:10), and afterward no major shape changes were observed (Fig. 3c). Hoxa11 thus revealed an early high dynamic period of shape change followed by a relative stasis, suggesting strong genetic regulation of Hoxa11 during the first 12 h of limb development. During this period a gene regulatory network must control Hoxa11 and modulate its expression to conform to the typical shape of the Hoxa11 expression pattern: a bean-shape domain with an A-P asymmetry, which might correspond with the starting expression of Hoxa13, a well-known repressor of Hoxa11 (Sheth et al. 2014). Later, if there is regulation, it must be addressed to maintain the already established shape of Hoxa11.

Figure 3.

EFA results of Hoxa11 domain over the full temporal sequence of mouse limb development. a,b) PCA scatterplots based on Hoxa11 high (a) and moderate (b) expression domains showing low morphological differentiation among developmental stages. c,d) Mean shapes representative of each developmental stage, and shape change comparison between consecutive stages using thin-plate spline (TPS) interpolation grids for Hoxa11 high (c) and moderate (d) gene expression domains. TPS allows expressing the shape differences (i.e. the mismatch of coordinates between average shapes) by distorting an orthogonal grid from a departing shape (the reference configuration, represented by the dashed outline) onto a second shape (i.e., a target configuration, represented by the solid outline). Gene domains display posterior (P) side to the left and anterior (A) side to the right, whereas distal (D) side is to the top and proximal (Px) side to the bottom. c) Comparison of gene mean shape changes for Hoxa11 high expression shows that the gene expression domain starts with a flat bean-shape and it rapidly changes by restricting the expression of Hoxa11 in the center of the domain and by expanding the expression toward the anterior and posterior edges of the gene domain. During the first half of embryonic day 11 (E10:23–E11:10) an asymmetry emerges, where the postero-distal edge of the Hoxa11 domain is flatter than the more rounded antero-distal edge, and this shape feature is maintained until the latest stage. Further comparison of the average shapes showed fluctuations around the already established shape of the Hoxa11 expression domain. d) Comparison of gene mean shape changes for Hoxa11 moderate expression shows that in comparison with the high expression Hoxa11 domains (c), the average gene shape sequence departs from a bigger but similar bean shaped Hoxa11domain. However, the shape changes occurring between consecutive stages only show an overall growth of the moderate Hoxa11 domain and do not show any specific shape changes over developmental time. 187 × 180 mm (300 × 300 DPI).

The analysis of the moderate expression of Hoxa11 was not able to capture the details of the earliest differentiation shown by the analysis of the high Hoxa11 expression level. The PCA of the moderate expression of Hoxa11 showed even higher variation within groups and a complete overlap along PC1 between early and late stages of limb development (Fig. 3b,d); whereas the average shape comparison indicated no significant morphological differentiation of moderate Hoxa11 expression over time, but random fluctuations around the same shape (Fig. 3d).

Hoxa13

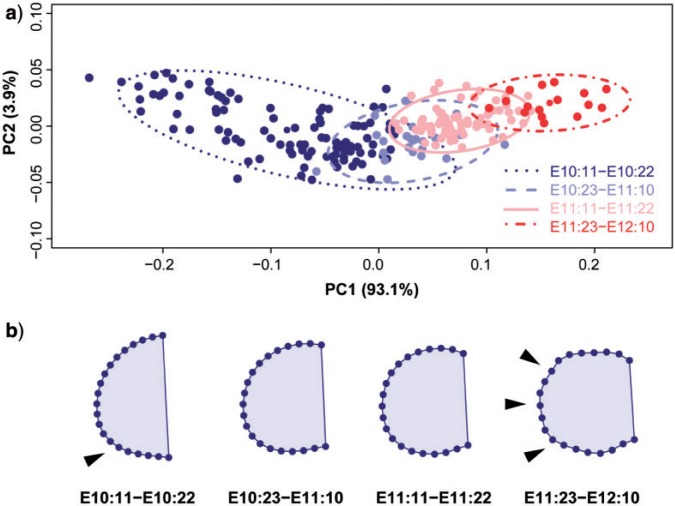
The high and the moderate expression levels of the Hoxa13 domain showed similar results and pointed out a completely different pattern of shape change and variation in comparison with Hoxa11. The PCA described a simple linear ontogenetic trajectory where the Hoxa13 expression domains were ordered according to the limb's ontogenetic stage (Fig. 4a,b), with PC1 explaining more than 90% of the total morphological variation. Instead of alternating dynamic and static periods of shape change, Hoxa13 showed a continuous morphological differentiation over time and a continuous shape change from a bean shape toward an arc shape (Fig. 4c), where the moderate expression of Hoxa13 (Fig. 4d) looked like a blown-up version of the high expression domain (Fig. 4c). The observed shape changes are probably strongly influenced by the FGF signaling from the AER and the continuous growth of the limb.

Figure 4.

EFA results of Hoxa13 domain over the full temporal sequence of mouse limb development. a,b) PCA scatterplots based on Hoxa13 high (a) and moderate (b) expression domains showing differentiation among stages, in which groups are ordered following a temporal sequence from earliest to latest stages. c,d) Mean shapes representative of each developmental stage, and TPS grids showing shape changes between consecutive stages after thin-plate spline interpolation of Hoxa13 high (c) and moderate (d) gene expression domains. Gene domains display posterior (P) side to the left and anterior (A) side to the right, whereas distal (D) side is to the top and proximal (Px) side to the bottom. In both high and moderate expression levels, the Hoxa13 domain starts with a boomerang-shape that keeps expanding toward the anterior and posterior edges of the gene domain. 186 × 180 mm (300 × 300 DPI).

Limb Bud: Morphological Variation over Development

After assessing the gene expression patterns in isolation using EFA, we assessed the shape changes of the limb bud itself using a Procrustes-based semilandmark analysis to understand the variational properties and the spatiotemporal dynamics of limb development from E10.5 to E12.5, without considering the gene expression domains.

A limb bud ontogenetic trajectory was described by the first two PCs, which together explained 97% of the total morphological variation (Fig. 5a). PC1 distributed the limbs throughout the morphospace according to their stage following a temporal sequence: from the earliest stage occupying the negative extreme of PC1 to the latest stages occupying the positive extreme of PC1. The continuous limb shape changes occurring through time along PC1 (Fig. 5) mainly express allometric shape changes over development (with more than 85% of shape variation explained by limb size); whereas PC2 axis reflects changes in asymmetry (Fig. 5a). The earliest and the latest limb buds are quite symmetrical and present positive values along PC2, whereas intermediate limbs show the most marked asymmetry and present negative values along PC2 (Fig. 5a). Given our current knowledge on the molecular and developmental processes underlying limb morphogenesis, it is likely that the early A-P asymmetry established at E10:11–E10:22 (Fig. 5b) is the result of gene regulation exerted from the ZPA; whereas the late appearance of digits occurring at E11:23–E12:10 (Fig. 5b) is a consequence of a Turing-based mechanism controlled by Wnt and Bmp and regulated by Fgf and Hox morphogen gradients (Sheth et al. 2012; Raspopovic et al. 2014).

Figure 5.

PCA on Procrustes-based semilandmark analysis of limb bud shape. a) Scatterplot of PC1 and PC2 scores. b) Corresponding sequence of mean shapes for each staging group showing shape changes from earliest (left) to latest (right) stages of mouse limb development. Limb buds are oriented distally to the left, proximally to the right, anteriorly to the top and posteriorly to the bottom. Graphs show how the limb bud starts as a wide bulge with an incipient A-P asymmetry that is already established by the second half of embryonic day 10 (see arrow). During development, this asymmetry becomes more prominent and the limb bud becomes narrower at its proximal edge. By the first half of embryonic day 12, the digits appear (see arrows). 172 × 137 mm (300 × 300 DPI).

Another interesting result from the PCA of the limb buds is the greater dispersion of the earliest stage (Fig. 5a), which suggests that early limb development is much more variable than the rest of development. This was confirmed by performing separate PCAs for each staging group. Comparison of the total amount of morphological variation within each developmental stage showed that the first staging group is 3.5 times more variable than the rest of the staging groups. The fact that the total amount of variation clearly drops and remains constant at later stages (Table 2, Fig. 7a) clearly suggests canalization of limb shape over development (Waddington 1942). Developmental canalization, besides providing the robustness of limb development to produce similar final phenotypes regardless of early variability of its environment or genotype (Waddington 1942), would contribute to the establishment of limb patterning by allowing a high rate of morphological change at the initial states and drastically reducing it at later stages of development.

Table 2.

Results from separate PCA and PLS analyses by gene, level of expression, and developmental stage

Gene expression	Developmental stage	Total variation	Limb/gene	A-P
			RV	RV
High Hoxa11	E10:11–E10:22	0.026	0.83	0.51
	E10:23–E11:10	0.005	0.89	0.71
	E11:11–E11:22	0.009	0.67	0.64
	E11:23–E12:10	0.005	0.73	0.87
Moderate Hoxa11	E10:11–E10:22	0.018	0.78	0.61
	E10:23–E11:10	0.014	0.94	0.90
	E11:11–E11:22	0.020	0.86	0.83
	E11:23–E12:10	0.011	0.77	0.79
High Hoxa13	E10:11–E10:22	0.025	0.88	0.72
	E10:23–E11:10	0.019	0.94	0.84
	E11:11–E11:22	0.008	0.95	0.88
Moderate Hoxa13	E10:11–E10:22	0.018	0.88	0.77
	E10:23–E11:10	0.018	0.92	0.88
	E11:11–E11:22	0.012	0.93	0.89

Note: Total amount of shape variation within each subsample is provided as the sum of the eigenvalues of the corresponding PCA. PLS analyses were performed after a single Procrustes superimposition in which the landmarks from the two subsets were fitted simultaneously and thus the relative size and position of the two blocks were considered in the analyses as integration factors. PLS results are provided as RV coefficients computed for both sets of a priori defined modules (Limb/Gene and Anterior/Posterior limb regions). RV coefficients can range from 0 (i.e., complete independence) to 1 (i.e., total interdependence between blocks).

Morphological Variation and Covariation Patterns of Limb and Gene Expression Domains

After fully assessing the shape changes of the Hoxa11 and Hoxa13 gene expression patterns, as well as of the limb buds in isolation, we next wanted to understand how gene dynamic variations linked to changes in the size and shape of the limb bud itself. This was achieved by simply combining within the same configuration of landmarks points from both the limb bud and the gene expression domain. This type of analysis is crucial for revealing the interactions between gene expression and phenotypic changes and thus to further understand the genetic regulation controlling limb development.

Even though Hoxa11 and Hoxa13 are paralogs located in the same genetic cluster and have similar functions in limb proximodistal patterning (Sheth et al. 2014), our analyses revealed that for Hoxa11 and Hoxa13 the patterns of size (Table 3, Fig. 7b) and shape change (Fig. 6) show clearly distinct trajectories over time.

Table 3.

Size comparison between consecutive developmental stages

Centroid size	Stage comparison	t	df	P-value
Limb	E10:11–E10:22/E10:23–E11:10	−8.65	34.68	<0.0001
	E10:23–E11:10/E11:11–E11:22	−9.42	61.73	<0.0001
	E11:11–E11:22/E11:23–E12:10	−14.483	25.669	<0.0001
High Hoxa11	E10:11–E10:22/E10:23–E11:10	−5.63	23.76	<0.0001
	E10:23–E11:10/E11:11–E11:22	1.66	13.67	0.1200
	E11:11–E11:22/E11:23–E12:10	−6.597	22.999	<0.0001
Moderate Hoxa11	E10:11–E10:22/E10:23–E11:10	−4.36	11.90	0.0009
	E10:23–E11:10/E11:11–E11:22	0.21	11.59	0.8388
	E11:11–E11:22/E11:23–E12:10	−8.653	22.599	<0.0001
High Hoxa13	E10:11–E10:22/E10:23–E11:10	−5.86	17.69	<0.0001
	E10:23–E11:10/E11:11–E11:22	−6.35	19.57	<0.0001
	E11:11–E11:22/E11:23–E12:10	−8.239	2.092	0.0126
Moderate Hoxa13	E10:11–E10:22/E10:23–E11:10	−5.40	17.41	<0.0001
	E10:23–E11:10/E11:11–E11:22	−5.84	20.29	<0.0001
	E11:11–E11:22/E11:23–E12:10	−8.71	4.79	0.0004

Note: Results from Welch Two-Sample $t$-test are provided.

Figure 6.

PCA results based on semilandmarks representing the associated shape of the limb and the gene expression domains. Solid lines depict the ontogenetic trajectories, whereas the shapes associated with negative and positive extremes of PC1 describe the start and ending points of the ontogenetic trajectory. a) Limb and Hoxa11 high expression domain. PC1 and PC2, which accounted for more than 83% of morphological variation, describe a complex ontogenetic trajectory with an inflexion point occurring around E11. The PC1 axis mainly expressed allometric shape changes through time (with 85.3% of shape variation explained by limb centroid size); whereas PC2 axis reflected changes in limb asymmetry. The ontogenetic trajectory starts with the first developmental stage (E10:11–E10:22) occupying the negative extreme of PC1 and exhibiting a wide range of variation both on PC1 and PC2. The shape associated with the most negative values of PC1 and the most positive values of PC2 shows that the earliest limbs are fairly symmetrical and present a posteriorly located Hoxa11 gene domain. During the second half of embryonic day 10 an incipient asymmetry is established. Over time, the limb bud grows, elongates and achieves a maximum asymmetry at the first half of day 11. Afterward, the second (E10:23–E11:10) and third (E11:11–E11:22) developmental stages considerably overlap at average values of PC1, showing that during embryonic day 11 shape remains fairly constant. From the second half of day 11, the limb bud keeps growing and reestablishing the symmetry. Finally, the ontogenetic trajectory finishes at the first half of day 12 with another period of morphological differentiation occurring at embryonic day 12 (E11:23–E12:10), in which limbs show dissimilar shapes, with the first appearance of digits and a proximally located Hoxa11 domain, and not overlapping with limbs from previous stages and occupying the positive extreme of PC1. b) Limb and Hoxa11 moderate expression domain. PC1 accounted for 69.5% of total morphological variation and was highly and significantly associated with limb growth and allometric shape changes. No other PCs separated any other known groups and the associated shape changes are similar to those earlier described for Hoxa11 high expression. c) Limb and Hoxa13 high expression domain. Results show a simple ontogenetic trajectory starting with an asymmetric limb and a large distal posteriorly located Hoxa13 domain. While the limb grows and changes shape, the Hoxa13 domain expands toward the anterior region following the limb contour. d) Limb and Hoxa13 moderate expression domain. A similar shape pattern was displayed by the moderate expression domain of Hoxa13. 189 × 189 mm (300 × 300 DPI).

Size variation

We estimated the size of the limb and the size of the gene expression domains at each developmental stage. When we compared the changes in limb size between consecutive stages, we found that the limb grows continuously throughout development. Statistically significant limb size differences were thus found between all pairs of consecutive stages (Table 3). Regarding the gene expression domains, Hoxa11 and Hoxa13 showed a clearly distinct pattern of increase in size: whereas Hoxa13 follows the limb growth curve and keeps growing throughout development, the Hoxa11 expression domain only grows at the earliest and the latest stages, remaining constant and uncoupled from the limb growth at intermediate stages (Fig. 7b). Statistical testing supported these results: significant size differences in the Hoxa13 domain were found between all pairs of consecutive stages, whereas size differences in Hoxa11gene expression domains were not significant between intermediate stages (Table 3).

Shape variation

Our analyses showed that although the Hoxa11 expression domain remains fairly constant in size and shape after a 12-h period of strong morphological changes in early development (Figs. 3 and 7b), it continuously changes in position from the distal toward the proximal region of the limb bud throughout development (Fig. 6a,b). By contrast, the Hoxa13 expression domain constantly remains at a distal position, attached to the limb bud (Fig. 6c,d), but changing gradually in shape and size through development (Fig. 6c,d and 7b).

Similar descriptions of Hoxa11 and Hoxa13 spatiotemporal dynamics had been previously reported after visual assessment of temporal sequences of WISH-labeled limbs. However, for the first time, our analyses reveal the variational properties underlying such gene expression patterns. The amount of morphological variation within developmental stages and the degree of differentiation among groups can reveal some clues about limb development. Our results show that variation within groups is high, leading to substantial overlap between developmental stages. This result highlights the importance of quantitative analysis accounting for variation using large samples of specimens, which are usually the exception rather than the norm in developmental studies. Since the shapes of limbs at different stages may be undistinguishable from one another due to growth variation, qualitative analysis based on just one or few specimens per stage can provide misleading results and incomplete overviews of the developmental processes underlying morphogenesis.

Despite the high variability during limb development, our results underscore that variation is not random, but structured and gene-specific. The PCA based on the full sequence of the Hoxa11 and Hoxa13 labeled limbs (Fig. 6) showed that PC1 successfully captured growth and development, so that the staging groups were ordered following temporal criteria, and together with PC2 described a clear ontogenetic trajectory (Fig. 6). However, the amount of within-group variation and the degree of overlap between consecutive stages differs among the developmental periods and between the Hoxa11 and Hoxa13 domains. For instance, the analysis of the high Hoxa11 expression level revealed a complex ontogenetic trajectory during limb development (Fig. 6a), with highly variable and dynamic shape changes occurring during the earliest stage, lower variation and morphological differentiation at intermediate stages, and late but more constrained differentiation occurring at the last stage of limb development. In the case of Hoxa13, the analyses described a simple ontogenetic trajectory (Fig. 6c,d), showing consecutive staging groups largely overlapping over a continuous morphological gradient of shape change through development. Finally, the PCA results from the stage-specific analyses confirmed the tendency toward developmental canalization for both genes, showing a decrease in total variance over time for the associated shapes of limb with Hoxa11 and Hoxa13, as previously shown for the limb alone (Table 2, Fig. 7a).

Taking into account all this detailed morphometric information, we can look for independent biological evidence regarding the molecular and cellular processes underlying the observed variation patterns. Periods in which highly dynamic changes occur can be indicators of two developmental processes highly relevant for limb development: they can either reveal specific key moments of up- or downregulation of gene expression, or periods during which significant tissue shape changes occur that drive changes in gene expression patterns. Our results support previous evidence (Marcon et al. 2011) and suggest that the simple ontogenetic trajectory of the limb associated with the Hoxa13 domain follows the expected pattern of a gene expression pattern that is likely driven by cellular tissue movements occurring during limb elongation. Since the Hoxa13 expression domain keeps its expression boundary “attached” to the limb tissue boundary, remaining under the direct influence of the AER and Fgf signaling and tracking the changes in limb size (Fig. 7b) and shape (Fig. 6c,d), our results indicate that after genetic activation, no major up- or downregulation events would be necessary to control Hoxa13 gene expression over development.

By contrast, our results suggest that cell proliferation and tissue movements alone would not be sufficient to explain the complex gene expression pattern revealed for the Hoxa11 expression domain. First, the dynamic gene expression pattern of Hoxa11 is uncoupled from limb growth (Fig. 7b). Second, more fine-tuned genetic regulation of cells switching on and off would be required to trigger Hoxa11 activation and to alternate the periods of strong morphological differentiation and relative stasis revealed by the morphometric analyses (Figs. 3c and 6a), and yet allow a constant change in position of the Hoxa11 domain toward the distal limb region (Fig. 6a,b).

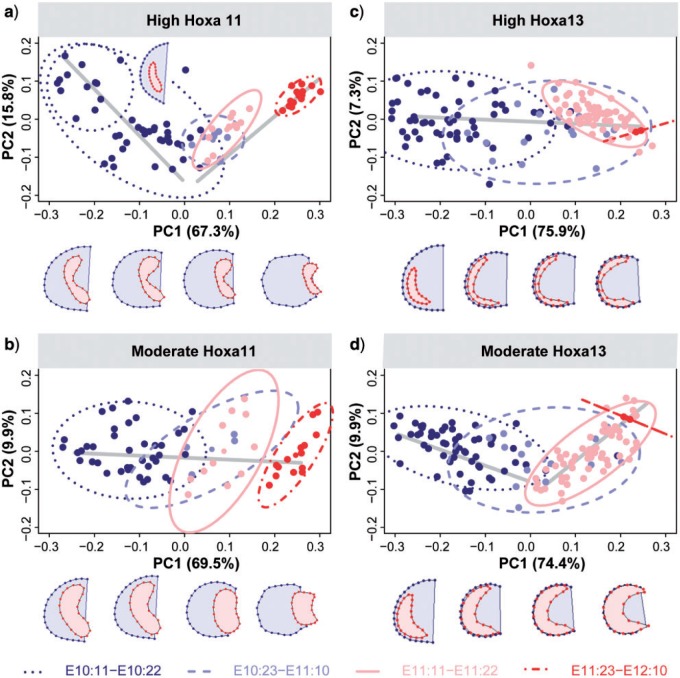
Shape covariation

Finally, our approach was also able to directly assess the association between the gene expression domains and limb bud shape. Results from the PLS analyses will complement our previous results by quantifying at each developmental stage the statistical covariation between the limb and the gene domains.

Limb morphogenesis results from precise gene expression controlled by the spatiotemporal orchestration of several signaling pathways relevant for limb and digit patterning. Thus, some genes directly regulate whether cells will proliferate, migrate, differentiate, or undergo apoptosis, while other genes will not. Although Hoxa11 and Hoxa13 are two genes expressed within the developing limb, and they are relevant for limb morphogenesis, we have no a priori knowledge whether there is a direct covariation between the shape of limb and the shapes of the Hoxa11 and Hoxa13 domains, and whether the intensity of this covariation changes over time or not. We expect that the relative degree of covariation will be a predictor for how directly a specific gene controls morphogenetic processes, versus other biological processes.

The PLS analyses explored these covariation patterns, and by comparing the dynamic interactions between the limb and the Hoxa11 and Hoxa13 domains over time, we have identified key time points for pattern formation in normal limb development. Our analyses showed that for both high and moderate expression levels, Hoxa11 and Hoxa13 expression domains were strongly correlated with limb morphology, especially in the earliest stages (Table 2, Fig. 7c,d). However, Hoxa11 has a tendency to reduce integration and thus become independent from limb shape over time (Fig. 7c), which could result either from less mechanistic integration and/or decreasing variation. By contrast, Hoxa13 shows a tendency to maintain a consistently high integration with limb shape over time (Fig. 7c), which could result from its close alignment with the limb bud outline. When the integration is so high such that the RV coefficients are close to 1, the shape of the gene expression domains is almost perfectly predictable from the limb bud shape. In the case of Hoxa11, this only holds between E10.5 and E11. The tight association between the limb bud and the Hoxa11 domains dilutes over time, and in limbs older than 12 d the shape changes occurring in the limb bud shape, such as the appearance of digits, cannot be associated with shape changes in the Hoxa11 domain. On the contrary, the limb bud shape and the Hoxa13 domain maintain the high integration over time, even increasing it, and they are almost predictable one from the other throughout development (Fig. 7c), supporting the tighter association between Hoxa13 and the limb bud growth and associated tissue movements.

Besides the integration between the limb and the gene expression domains, we also assessed a second integration scenario, by testing the association between the anterior and posterior regions of the limb. For both Hoxa11 and Hoxa13 expression domains (Fig. 7d), the integration between the anterior and posterior regions of the limb is low at the early stages but increases with time throughout development (Table 2, Fig. 7d). Interestingly, the low morphological integration at the earliest stages (Table 2), evidenced as an A-P compartmentalization of the limb early in development, is likely the result from molecular signaling from the ZPA. It is well established that patterning along the A-P axis of the developing vertebrate limb is controlled by asymmetric expression of the Shh gene, which is restricted at the ZPA in early development and decreases over time (reviewed in Towers and Tickle 2009; Zeller et al. 2009). There is thus a direct correspondence between the spatiotemporal expression pattern of Shh and the early A-P morphological modularity of the limb suggested by the PLS analyses (Table 2). The influence of the ZPA and Shh signaling could also explain the sequence of symmetric/asymmetric phases of limb development revealed by the ontogenetic trajectories of our morphometric analyses (Figs. 5 and 6). Our results thus highlight the interactions between Hoxa11 and Hoxa13 and suggest further interactions with other gene signaling pathways (Figs. 3–7).

Conclusions

Despite the potential of GM to track development (Klingenberg 2010; Young et al. 2010; Martínez-Abadías et al. 2013; Mayer et al. 2014), GM has hardly been applied to gene expression patterns (Airey et al. 2006) and limited progress has been made in quantifying genetic expression and correlating it with phenotypic variation (Jernvall et al. 2000; Salazar-Ciudad and Jernvall 2010). Although variation is common and widespread in development, and phenotypic variation is the substrate for natural selection, there is a lack of quantitative studies assessing size and shape variation of gene expression patterns over development (Xu et al. 2015). Our study shows how GM can be extended to the analysis of nonanatomical shapes, such as gene expression domains.

Besides illustrating how a full-quantitative shape analysis can provide very detailed descriptions of associated phenotypic and genetic changes occurring during development, our method demonstrates how we can further improve our understanding of morphogenesis. By using GM methods, we can assess the size and shape variation of gene expression domains in association with the shape change patterns of a developing organ. The resulting variational patterns can be considered as “phenotypic indicators” of the effect of the genetic and/or developmental processes regulating morphogenesis. A PCA over a large sample including several stages of development can describe an ontogenetic trajectory, estimate the proportion of total morphological variation that is due to size variation and growth, and suggest other genetic or environmental factors that would explain the variation and morphological differentiation among staging groups. By assessing the degree of variation and overlap between groups, we can extrapolate the spatiotemporal dynamics and identify periods of high changes versus periods of relative stasis or continuous change. The comparison of the amount of total shape variance by staging groups can reveal developmental canalization over time, indicating whether a system heads toward a stable specific outcome, even if there is high variability during earlier developmental stages.

The simultaneous analysis of the shapes of the gene expression and the developing organ through the PLS and the modularity analyses can directly assess the morphological integration between them and estimate the degree of predictability of the gene expression domain from the shape of the developing organ. If morphological integration is assessed at several consecutive developmental stages, comparison of results between different time points will reveal whether the magnitude or the pattern of integration is constant or changes through time and this may help to identify key time points for pattern formation. Similarities on covariation patterns will indicate a constant spatial–temporal interaction between genes and the developing organ; whereas changes in covariation patterns will suggest disruption and changes in gene regulation that are potentially relevant for pattern formation.

The correspondence between our results and already well-established developmental processes underlying limb patterning and morphogenesis (for a review, see Towers and Tickle 2009; Zeller et al. 2009; Zeller 2010) supports the conclusion that this type of systematic analysis of phenotypic and genetic shape can extract features which likely have a biological or mechanistic explanation. Our method is thus a powerful tool to extract features of development that cannot be simply perceived by eye that can be especially useful to suggest developmental mechanisms for unknown genes or systems where not so much molecular information is available, as in the case of the limb bud. A system like this that accurately quantifies and tracks the relationship between gene expression patterns and morphology can be used to test predictions of causative relationships bringing us closer to attaining a genotype–phenotype map for development.

Assumptions and Limitations

The application of GM to gene expression patterns is, however, not straightforward. The main assumption of our method is that WISH is a reliable indicator of quantitative gene expression and that GM can be used to accurately capture and analyze the shape of gene expression domains. Our preliminary analyses indicated that variance due to WISH and imaging procedures were negligible in comparison to variation due to growth and development. However, our results highlight that the conclusions are very sensitive to which genes and expression levels are selected. Optimally, several genes and several expression levels should be analyzed to fully understand the development of a complex biological structure.

The main limitation of our method is the intrinsic shape of the gene expression domain. Not every gene expression domain can be represented as a unique shape continuously changing over time. Some gene expression domains have inherently ill-defined shapes, lack homologous landmarks, and/or dramatically change their shape even over short periods of time (Mayer et al. 2014; Xu et al. 2015). For example, Sox9, an early chondrogenesis marker, first appears in mouse embryo limbs as a single expression domain by E10, and in just 2.5 h it differentiates into an increasing number of separate domains, revealing the formation of limb bones and digits (Raspopovic et al. 2014). GM cannot deal with such changing shapes, especially those involving the emergence or loss of structures. In those cases, our method could only be applied within stages, not across several time points, and EFA could not be applied if the gene expression domain comprises more than a single domain. Finally, our method is limited to genes that can be labeled by WISH.

We have proposed a semiautomatic approach to segment the limbs and the gene expression domains from 2D WISH-labeled pictures. Our approach will have to be adjusted to be applied to other structures, but the same principles may apply. Afterward, our morphometric approach will be ready to use with available user-friendly free software, such as MorphoJ and R packages especially suited to GM (geomorph, Momocs). Potentially, this approach can also be extended to analysis of 3D shapes and gene expression patterns, as well as to different organs, genes, and animal models (Hu et al. 2015; Xu et al. 2015), but further progress is required for a complete automation of the process and to make the method available for 3D data.

Potential Applications in Systematics

Systematic and phylogenetic studies routinely use genetic (molecular) or phenotypic (morphology) data to infer the relationships between species and to reconstruct the history of evolutionary transformations. Instead, our method focuses on an intermediate level, which links genotype to phenotype through the dynamics of gene expression patterns (as spatial control of gene expression directs morphogenesis). It thus addresses an important part of the relationship between molecular and morphological evolution. Increasingly, detailed comparisons between gene expression patterns of different species are explored, but in a manual or non-quantitative manner. Our method allows such studies to be put on a more rigorous and quantitative footing. Here, we discuss first the most direct case of limb evolution, and then provide examples of other systems in which genetic differences contribute to novel phenotypic variants through development and which could benefit from our method.

The main utility of our approach in systematics relies on its potential to analyze genetic and developmental processes that are correlated with diversification and adaptation. The increasingly important comparisons of gene expression patterns between different species helps to investigate how evolution has modified a common developmental pattern to generate a wide diversity of morphologies, as in the vertebrate limb. Due to remarkable developmental plasticity, vertebrate limbs have evolved many successful adaptations for performing such different tasks as running, swimming, and flying (Cooper et al. 2014). Recent research has started unveiling the molecular and developmental mechanisms underlying the diversification of limb morphology (Dai et al. 2014), including modes of evolutionary digit loss (Cooper et al. 2014), and key evolutionary innovations such as the evolution of flight in mammals (Cooper et al. 2012; Wang et al. 2014). These studies qualitatively assessed limb shape and gene candidate expression patterns (Shh, Ptch1, Hoxd9-13, Meis2, Tbx3, Fam5c, etc.) in model (mice) and nonmodel mammal species (jerboas, horses, camels, pigs, opossums, bats). The main conclusion, based on obvious shape differences between species, is that the evolution of the limb morphology depends on the complex integration of multiple gene regulatory networks. However, considering that small changes in gene expression may have large effects on morphology (Honeycutt 2008) and that continuous changes in underlying developmental or genetic parameters map to continuous changes in the phenotype (Young et al. 2010; Harjunmaa et al. 2014), subtle but significant differences in gene expression patterns should also be analyzed. Our method can exactly tackle this issue: applied to data such as that published by Cooper et al. (2014) (see e.g., Fig. 2 and Extended Data Fig. 2), our quantitative method would provide formal and accurate testing of shape differences in the limb and the gene expression patterns between species. Furthermore, by comparing the correlation patterns between the gene expression patterns and the associated limb morphology over time, our method would help to disentangle two types of expression changes: those which are associated with anatomical shape change, versus those which occur independently of anatomical changes, and thus represent alterations at a purely regulatory level. This in turn can help to reveal the mechanisms that generated the differing limb morphologies in mammals, and potentially reveal when two distinct examples of a similar phenotypic change (e.g., digit reduction) were in fact driven by different underlying molecular changes (a specific type of convergent evolution, in which the same phenotypic outcome was achieved in distinctly different ways).

Examples other than the limb have also been studied recently. Changes in single or few signaling molecules can explain variation in such different systems and organisms such as tooth form in mammals (Harjunmaa et al. 2014), facial shape in birds and reptiles (Bhullar et al. 2015; Hu et al. 2015; Xu et al. 2015), morphological diversification of the feeding apparatus in African cichlids (Hu and Albertson 2014), as well as wing shape in Drosophila and other dipterans (Cicin-Sain et al. 2015). Using a similar quantitative but landmark-free approach, Xu et al. (2015) and Hu et al. (2015) showed significant correlations between the expression pattern of Shh in the forebrain and the shape of the frontonasal ectodermal zone (FEZ), which lead to facial phenotypic differentiation between two orders of birds (Anseriformes vs. Galliformes). Further investigating the appearance of the avian rostrum in the fossil record as well as FEZ gene expression domains (FGF and WNT signaling pathways) in nonmodel birds and reptiles (emus, alligators, lizards, and turtles), Bhullar et al. (2015) proposed an autapomorphic median gene expression region in Aves that could be experimentally altered to transform bird beaks into skeletal patterns similar to ancestral dinosaur palates. All these cases provide clear examples in which our method could be applied and demonstrate the utility of combining comparative anatomy, computational and experimental developmental biology in systematics and phylogeny. Some of these cases collected gene expression patterns in 3D, and our method could also be extended into the third dimension.

Considering that the type of data required for applying our method (i.e., gene expression profiling in model and nonmodel species) is already being generated, its application should be straightforward with the generation of larger samples. This is time- and resource-consuming, but the effort should be well justified by the benefits of the approach.

Our method could compare the distribution of variation in gene expression within species to the divergence in gene expression among species (Sears 2014). Moreover, the covariation patterns between the shape of a developing organ and the shape of associated candidate gene expression domains could be compared among species by combining our method with phylogenetic techniques (Klingenberg and Marugán-Lobón 2013; Adams and Felice 2014). Overall, we believe that the application of morphometrics to gene expression patterns will help us understand a wide range of evolutionary processes—from habitat adaptation to great evolutionary transformations.

Funding

The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement Beatriu de Pinós Grant 2010_BP_B_00183-1 and Marie Curie Fellowship FP7-PEOPLE-2012-IIF 327382. We acknowledge support of the Spanish Ministry of Economy and Competitiveness, ‘Centro de Excelencia Severo Ochoa 2013-2017’, SEV-2012-0208.