Abstract
We prove that maximum likelihood phylogenetic inference is consistent on gapped multiple sequence alignments (MSAs) as long as substitution rates across each edge are greater than zero, under mild assumptions on the structure of the alignment. Under these assumptions, maximum likelihood will asymptotically recover the tree with edge lengths corresponding to the mean number of substitutions per site on each edge. This refutes Warnow's recent suggestion (Warnow 2012) that maximum likelihood phylogenetic inference might be statistically inconsistent when gaps are treated as missing data, even if the MSA is correct. We also derive a simple new proof of maximum likelihood consistency of ungapped alignments.
Keywords: Kullback–Leibler divergence, maximum likelihood, missing data, multiple sequence alignment, phylogeny
Phylogenetic inference is a fundamental bioinformatics problem. The amount of sequence data available is increasing and researchers design methods that try to extract all information from large data sets. One desirable property of a phylogenetic method is statistical consistency: as the number of sites tends to infinity, the inferred tree should converge to the true tree that generated the data. It is now widely accepted that standard phylogenetic methods, such as distance methods or maximum likelihood, achieve statistical consistency under Markov models of evolution without insertions and deletions (see Felsenstein (2004) or RoyChoudhury (2014) for a discussion).
In practice, phylogenies are usually built from multiple sequence alignments (MSAs) that contain insertions and deletions (indels). Most phylogenetic methods treat indels as missing data and do not attempt to model the indel process. It has been widely assumed that statistical consistency of standard phylogenetic methods extends to this setting, though to our knowledge no proof of this has been published. Recently, Warnow (2012) called this assumption into question by presenting an example of an evolutionary process where methods treating indels as missing data will fail to achieve consistency. More specifically, Warnow pointed out that for alignments that contain indels but no substitutions, methods that neglect indels will give equal support to all tree topologies, whereas an explicit model of the indel process can achieve statistical consistency. Although such evolutionary regimes are rare in nature, Warnow claimed that this example might be representative of a larger class of models where consistency may not hold, even when the alignment is correct.
Here, we prove that the “no substitutions” scenario highlighted by Warnow is in fact the only case where standard phylogenetic inference methods fail to achieve statistical consistency on correct MSAs. Specifically, we prove that for any evolutionary process where each edge in the tree has a nonzero substitution rate, standard maximum likelihood inference is consistent on MSAs, under minimal assumptions on the indel process.
Preliminaries
Trees, Alignments, and Substitutions
A phylogenetic tree on leaves is a tree (not necessarily binary) whose leaves are uniquely labeled with elements of the taxon set . Each edge in has an associated positive length. For any two leaves , the distance is defined as the sum of lengths of all edges on the path from to . For a taxon set , is the unique tree obtained by removing all vertices of that do not lie on a path between some two leaves in , suppressing all degree-two vertices in the remaining tree, and adjusting the edge lengths so that for every choice of and in .
A MSA is an matrix with entries from the set , where is the number of taxa and is the number of sites in the alignment. Characters in the same column of are descended from a common ancestral site. represents a “gap” in the alignment, indicating that taxon has no sites that are homologous to any site in column . This can happen as a result of a deletion on a branch leading to taxon or an insertion on any branch that does not lie between and the root of the tree.
For a taxon set , a site category is the set of columns in whose nongap characters occur precisely in taxa from . For sets and , we denote by the restriction of to rows in and columns in . In particular, is the restriction of to the rows in and columns in , and therefore contains no gaps. By slight abuse of notation, we will write to refer to the characters in the -th column of .
We need to make some minimal assumptions about the evolutionary process in order to prove our main result. We assume the sequences evolve along the edges of the tree under a continuous-time Markov chain where substitutions and indels are independent of each other, starting from an unobserved ancestral sequence at the root of the tree. We also assume that for each insertion, the inserted nucleotides are drawn independently from the equilibrium distribution of the substitution model. For simplicity of presentation, we assume the Jukes–Cantor model for nucleotide substitution (Jukes and Cantor 1969), with substitutions independent between sites, though our proof could be generalized to more complicated models (see Section 5).
The assumption of independence between indel and substitution processes appears to be crucial. In a recent paper, McTavish et al. (2015) showed that distance methods are inconsistent when some sites are invariant with respect to both substitutions and indels. Other authors have also reported biases in reconstructed phylogenies when patterns of missing data were correlated with the substitution process (Grievink et al. 2013; Roure et al. 2013). Similar problems have been discussed in statistics literature (Allison 2001).
Given a tree with specified branch lengths and an evolutionary model, we can compute the probability of a pattern of nucleotides arising at the leaves of , for example using Felsenstein's pruning algorithm (Felsenstein 2004). In standard phylogenetic analyses, gaps at site are treated as missing data. This is equivalent to computing the likelihood where is the set of taxa that do not have gaps at site .
For a sequence alignment , the likelihood of given tree is the product of per-site likelihoods for each site in the alignment. Taking the logarithm of the likelihood, we can write
It is often convenient to use the normalized per site log-likelihood .
The maximum likelihood phylogeny is the tree that maximizes the likelihood of the alignment:
Finally, we define a metric on the space of all phylogenies on as follows: let . It can be easily verified that this is indeed a metric, as long as all edge lengths are positive. We note that this is not true in the case discussed by Warnow, where all edges have zero length as the substitution rate is zero across the tree. When zero-length edges are allowed, it is possible to find trees and with distinct topologies such that , which violates the definition of a metric.
Consistency of ML has been stated in several papers (Yang 1994; Rogers 1997). A formal statement of consistency can be written as follows:
Theorem 1 Let be an ungapped -column MSA generated from tree . Then with probability 1 as .
Several proofs of Theorem 1 have been proposed, but some were later found to be incorrect. The proofs of Yang (1994) and Rogers (1997) show that for any tree , we have with probability 1 as . Unfortunately, this is insufficient to prove consistency, since it does not preclude the possibility that the sequence does not converge to . This was noticed recently by RoyChoudhury (2014), who provides a more detailed discussion of these two proofs. Felsenstein (1973) argued that consistency follows from the result by Wald (1949), who proved statistical consistency for maximum likelihood estimators under very general conditions. However, Felsenstein's claim was disputed by Yang (1994) and Farris (1999), since Wald's proof relies on several technical assumptions which are not straightforward to verify for phylogenetic trees. These arguments were in turn countered by more recent works Swofford et al. (2001); RoyChoudhury (2014). Chang (1996) proved that ML is consistent for a more complicated model where each branch in the tree has its own substitution matrix. Although Chang's model includes the basic time-homogeneous model as a special case, the proof of identifiability for Markov models of evolution is somewhat complicated due to its generality. Chang's proof also requires the true tree to be binary, though the author does mention that the result could be extended to nonbinary trees. To our knowledge, no simple, correct proof has been published for the basic scenario where sequences evolve according to a fixed time-reversible model, constant across sites and edges.
We will use the following property to establish our result:
Lemma 1. For any , as .
This states that as the number of alignment columns tends to infinity, it is almost certain that an ungapped MSA has a higher likelihood on than any other tree that is “distinct enough” from . We prove this lemma towards the end of the article.
The Indel Process
We assume that the process starts from an ancestral sequence of length . The expected length of the alignment is proportional to and we have whenever . For simplicity, we will write from now on. We make the following two mild assumptions about the structure of the alignment:
- Assumption 1. For each pair of taxa, let be the number of columns such that and . Then, with probability 1,
Assumption 2. For each , either or as , with probability 1.
Assumption 1 states that every pair of taxa has infinitely many shared nongapped sites as the size of the MSA tends to infinity. Assumption 2 states that every possible site category either is not observed or is observed infinitely many times as the size of the MSA tends to infinity. These two assumptions hold for a large class of Markov models of sequence evolution, including for example the TKF model (Thorne et al. 1991), the “long indel” model (Miklós et al. 2004) and the recently introduced Poisson indel process (Bouchard-Côté and Jordan 2013). These models assume that sequences evolve according to a continuous-time Markov chain where the insertion and deletion rates are uniform across the sequence. This uniformity directly implies Assumption 2. Assumption 1 is a consequence of the fact that, under these models, each site of the ancestral sequence has a positive probability of not undergoing a deletion between any two leaves of the tree, as long as indel rates on every branch are finite. Note that the only case when we have as for some sets occurs when there are no deletions. In that case, an insertion remains present in all descendant lineages. Thus, the sets for which coincide with the clades in the tree.
Consistency for Gapped Alignments
We can now state and prove consistency of ML inference of phylogeny for gapped alignments. The key intuition behind the proof is that the likelihood of a gapped alignment can be represented as a sum of likelihoods of a finite number of gapped alignments created by restricting to different site categories. We use Lemma 1 to prove that consistency for these ungapped alignments is enough to ensure consistency of the whole gapped alignment.
Theorem 2 Under Assumptions 1 and 2, maximum likelihood phylogenetic inference is consistent. More precisely, if is an -column alignment containing gaps, with probability 1 as .
Proof. The log-likelihood of the alignment given tree can be written as the product of per-site likelihoods:
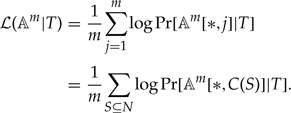 |
Since gaps are treated as missing data, we can write equivalently
For each taxon set , is an ungapped alignment.
By Lemma 1, for all we have
| (1) |
for all such that . By Assumption 1, for any tree such that , there exists at least one set such that and as . We can use this to bound the probability of any tree distinct from having higher likelihood:
By the union bound, iterating over all subsets of , we get
From Equation (1), we see that the above sum tends to zero as . It follows that for all . Consequently, we have as , as desired. █
A New Proof of ML Consistency for Ungapped Alignments
In this section, we present a new and simple proof of Theorem 1, consistency for maximum likelihood on ungapped alignments.
A pattern at site is a tuple denoting the characters at alignment positions , respectively. The probability of seeing each at a site is specified by tree , and let be the empirical frequency of pattern in the alignment. It is easy to see that with probability 1 as . For a fixed pair of taxa , we will write for the fraction of columns in such that and , and denote by a pattern such that , and is a tuple containing the characters of at taxa other than and . Likewise, we will write for the probability of jointly observing character at and character at given that .
The following lemma provides an upper bound on the log-likelihood of the data given a misspecified tree .
Lemma 2. Let be a tree such that there exist with . Then
where is the Kullback-Leibler (KL) divergence between pairwise character distributions and ,
Proof. Let be the probability of under tree . The normalized log-likelihood can be written as
Our goal is to bound when is constrained so that . We can write
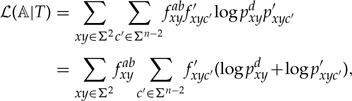 |
where and . Since , we have and hence
| (2) |
To get an upper bound on , we find the values of that maximize the expression in Equation (2) subject to for each . By Gibbs' inequality (MacKay 2003), this occurs when for all , and therefore
Using , we get
 |
as desired. █
We note that the bound in Lemma 2 is quite loose, as it does not incorporate the constraint that the pattern probabilities must be consistent with some phylogenetic tree .
The next lemma ensures that, given enough data, there exist no high-likelihood trees that are bounded away from the true tree :
Lemma 3. Given any taxon pair and any , and writing , we have
| (3) |
and
| (4) |
with probability 1.
Proof. Applying Lemma 2 to all trees such that , we get
which is equivalent to
The term is the normalized log-likelihood of given . It can be easily verified that, under the Jukes–Cantor model, this is a concave function of , with the maximum at where is the fraction of sites that differ between and (Felsenstein 2004). Because tends to with probability 1, will tend to . From the concavity of , we get
with probability 1 as . This, together with the observation that as , proves Inequality 3.
The proof of Inequality 4 proceeds analogously. █
Lemma 3 provides us with the means to prove Lemma 1 and hence Theorem 1:
Proof of Lemma 1. By repeatedly applying Lemma 3 for all pairs of taxa, we obtain
with probability 1. On the other hand, we have with probability 1, which proves Lemma 1.
Proof of Theorem 1. The proof proceeds analogously to the proof of Theorem 2 in the previous section. By repeatedly applying Lemma 1, we get
for all which implies as , as desired. █
Conclusions
We have shown that standard maximum likelihood phylogenetic inference is statistically consistent even in the case where gaps are treated as missing data, as long as substitution rates across edges are nonzero. The problematic scenario highlighted by Warnow is not representative of the vast majority of data sets where substitutions are common. Given the widespread use of maximum likelihood in phylogenetic inference, this result should be reassuring to practitioners. Although it has been observed that alignment gaps can be used to reconstruct accurate phylogenies (Thatte 2006; Dessimoz and Gil 2010), our result shows that neglecting the information in gaps should not lead to incorrect inferences when sufficiently long sequences are available.
The methods used for the proof for gapped alignments have also permitted the construction of a new proof for ungapped alignments, which we consider simpler than other existing proofs.
Our proofs of consistency could be generalized to more complex evolutionary models. More flexible models of evolution, such as the general time-reversible model (Tavaré 1986) require inferring model parameters as well as the tree. To adapt our proof of Theorem 1 to this setting, one would have to define a suitable distance measure on the joint space of trees and substitution rate matrices. We leave this for future work.
In most practical scenarios, MSAs contain errors. Indeed, there are reasons to believe that this problem is more serious for large alignments, and manual curation requires a prohibitive amount of effort. Investigating whether MSAs introduce systematic biases in the long sequence limit is an interesting question for future research.
Acknowledgments
We would like to thank Simon Tavaré for discussions. We would also like to thank Associate Editor Dr. Edward Susko and the anonymous reviewers whose suggestions helped improve the article.
Funding
J.T. was supported equally by the Cancer Research UK Cambridge Institute and the European Molecular Biology Laboratory. N.G. was supported by the European Molecular Biology Laboratory.
References
- Allison P.D. 2001. Missing Data. Sage University Papers Series on Quantitative Applications in the Social Sciences, 07-136. Sage Publications, Thousand Oaks, CA, United States.
- Bouchard-Côté A., Jordan M.I. 2013. Evolutionary inference via the Poisson indel process. Proc. Natl Acad. Sci. USA 110:1160–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang J.T. 1996. Full reconstruction of Markov models on evolutionary trees: identifiability and consistency. Math. Biosci. 137:51–73. [DOI] [PubMed] [Google Scholar]
- Dessimoz C., Gil M. 2010. Phylogenetic assessment of alignments reveals neglected tree signal in gaps. Genome Biol. 11:R37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farris J.S. 1999. Likelihood and inconsistency. Cladistics 15:199–204. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1973. Maximum likelihood and minimum-steps methods for estimating evolutionary trees from data on discrete characters. Syst. Biol. 22:240–249. [Google Scholar]
- Felsenstein J. 2004. Inferring phylogenies. Sunderland: Sinauer Associates. [Google Scholar]
- Grievink L.S., Penny D., Holland B.R. 2013. Missing data and influential sites: choice of sites for phylogenetic analysis can be as important as taxon sampling and model choice. Genome Biol. Evol. 5:681–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes T.H., Cantor C.R.Munro H.N. 1969. Evolution of protein molecules. Mammalian protein metabolism. New York: Academic Press; p. 21–132. [Google Scholar]
- MacKay D.J. 2003. Information theory, inference and learning algorithms. Cambridge University Press: Cambridge, United Kingdom. [Google Scholar]
- McTavish E J., Steel M., Holder M.T. 2015. Twisted trees and inconsistency of tree estimation when gaps are treated as missing data—the impact of model mis-specification in distance corrections. Mol. Phylogenet. Evol. 93:289–295. [DOI] [PubMed] [Google Scholar]
- Miklós I., Lunter G., Holmes I. 2004. A long indel model for evolutionary sequence alignment. Mol. Biol. Evol. 21:529–540. [DOI] [PubMed] [Google Scholar]
- Rogers J.S. 1997. On the consistency of maximum likelihood estimation of phylogenetic trees from nucleotide sequences. Syst. Biol. 46:354–357. [DOI] [PubMed] [Google Scholar]
- Roure B., Baurain D., Philippe H. 2013. Impact of missing data on phylogenies inferred from empirical phylogenomic data sets. Mol. Biol. Evol. 30:197–214. [DOI] [PubMed] [Google Scholar]
- RoyChoudhury A. 2014. Consistency of the maximum likelihood estimator of evolutionary tree. arXiv preprint arXiv:1405.0760.
- Swofford D.L., Waddell P.J., Huelsenbeck J.P., Foster P.G., Lewis P.O., Rogers J.S. 2001. Bias in phylogenetic estimation and its relevance to the choice between parsimony and likelihood methods. Syst. Biol. 50:525–539. [PubMed] [Google Scholar]
- Tavaré S.Miura R.M. 1986. Some probabilistic and statistical problems in the analysis of dna sequences. Lectures on Mathematics in the Life Sciences. Providence: American Mathematical Society; p. 57–86. [Google Scholar]
- Thatte B.D. 2006. Invertibility of the TKF model of sequence evolution. Math. Biosci. 200:58–75. [DOI] [PubMed] [Google Scholar]
- Thorne J.L., Kishino H., Felsenstein J. 1991. An evolutionary model for maximum likelihood alignment of DNA sequences. J. Mol. Evol. 33:114–124. [DOI] [PubMed] [Google Scholar]
- Wald A. 1949. Note on the consistency of the maximum likelihood estimate. Ann. Math. Stat. 20:595–601. [Google Scholar]
- Warnow T. 2012. Standard maximum likelihood analyses of alignments with gaps can be statistically inconsistent. PLoS Curr. doi:10.1371/currents.RRN1308. [DOI] [PMC free article] [PubMed]
- Yang Z. 1994. Statistical properties of the maximum likelihood method of phylogenetic estimation and comparison with distance matrix methods. Syst. Biol. 43:329–342. [Google Scholar]


