Another Look at the Mechanisms of Hydride Transfer Enzymes with Quantum and Classical Transition Path Sampling

Abstract

The mechanisms involved in enzymatic hydride transfer have been studied for years, but questions remain due, in part, to the difficulty of probing the effects of protein motion and hydrogen tunneling. In this study, we use transition path sampling (TPS) with normal mode centroid molecular dynamics (CMD) to calculate the barrier to hydride transfer in yeast alcohol dehydrogenase (YADH) and human heart lactate dehydrogenase (LDH). Calculation of the work applied to the hydride allowed for observation of the change in barrier height upon inclusion of quantum dynamics. Similar calculations were performed using deuterium as the transferring particle in order to approximate kinetic isotope effects (KIEs). The change in barrier height in YADH is indicative of a zero-point energy (ZPE) contribution and is evidence that catalysis occurs via a protein compression that mediates a near-barrierless hydride transfer. Calculation of the KIE using the difference in barrier height between the hydride and deuteride agreed well with experimental results.

Graphical abstract

The origins of enzymatic rate enhancement are of interest due to the importance of enzymatic reactions in biology and the appeal of incorporating these mechanisms in proteinaceous or nonproteinaceous engineered catalysts. While long-time scale motion of enzymes, for example, allosteric regulation, has long been accepted as an important part of their function, faster motions have only recently been accepted as a part of catalysis.^1–3 These fast motions, usually on the fs to ps scale, include rate-promoting vibrations, which are protein fluctuations that induce a compression of the active site of the protein, thereby lowering the barrier to reaction.^4–13 Enzymes involving hydrogen transfer are especially susceptible to fast protein motion because the possibility of tunneling makes the reaction dependent on the width of the barrier as well as the height. For many years, tunneling was not thought to be a major factor in enzymes, but it is now accepted that almost all enzymes involving hydrogen transfer have some contribution from quantum tunneling.^3,14,15

One enzyme that has received much attention from researchers is yeast alcohol dehydrogenase (YADH) as an enzyme where hydrogen tunneling may play an important role.^16–18 YADH catalyzes the oxidation of alcohols to aldehydes using the coenzyme nicotinamide adenine dinucleotide (NAD).¹⁹ It natively functions on small, primary alcohols, especially ethanol, but many investigations utilize benzyl alcohol as the substrate, which makes hydride transfer rate-limiting and allows for analysis of that step.²⁰ One of the main pieces of evidence pointing toward tunneling in this enzyme is the elevated Swain–Schaad exponent (SSE).^16,17 The SSE relates the rate of reaction with different isotopes based on reduced mass considerations, and elevation beyond the semiclassical limit can be evidence of tunneling.^21,22 However, this elevation can also be from other sources, such as changes in the tunneling ready state (TRS), that is, the ensemble of active site geometries at the point of particle tunneling.¹⁸

The participation of fast protein motion and the possibility of isotopically dependent reaction paths make it necessary to carefully choose a method that can account for these requirements. Therefore, we modified the CHARMM molecular dynamics program^23,24 to include propagation according to adiabatic centroid molecular dynamics (CMD).^25–30 In enzymes involving hydrogen transfer, a method is required beyond traditional QM/MM because this standard method contains quantum mechanics only in the energy surface; the propagation of atoms remains classical. Previously, the only CHARMM modules that properly included the effects of quantum dynamics were the CHARMMRATE module (within the ensemble-averaged variational transition state framework¹⁷) and the QUB module (using centroids to quantize the classical path for the calculation of free energies³¹). The focus of these modules is to calculate free-energy barriers and other average properties of the system. To achieve this, the effect of coupled degrees of freedom is included through a statistical correction. This is appropriate for average properties when equilibrium solvation holds but does not provide a full atomistic description of the quantum dynamics.

To take advantage of our detailed description of quantum dynamics, we utilized transition path sampling (TPS) to generate reactive trajectories.^32,33 Because the reaction coordinate of an enzyme is difficult to determine a priori, TPS has the significant advantage over other methods in that an initial guess for the reaction coordinate is perturbatively altered to generate an ensemble of trajectories. With sufficient trajectories, a TPS ensemble should contain a representative selection of all of the energetically accessible reaction paths. We performed a TPS analysis of the hydride transfer in the oxidation of benzyl alcohol inside of YADH. Application of CMD to the transferring hydride (CMD1) resulted in an average root-mean-squared (RMS) radius of 0.30 Å for the hydride, showing that there is delocalization of the particle.

The activation free energy of the entire enzymatic complex has been traditionally used for gaining insight on the degree of hydride tunneling via computational methods. We propose that this energy does not provide the most direct investigation of tunneling. Rather, the free-energy barrier, which is the work performed on the transferred particle by the fluctuating environment within the short transfer period, should be used, a quantity that is different than the activation free energy of the whole system but that is the one relevant for tunneling. Because this is a fully atomistic calculation, it is capable of including the effects of possible fast protein motions coupled to the reactive event with a time scale similar to the chemical barrier crossing, an effect that (if it exists) would have been omitted in computational studies that treat the protein as an ensemble average. For example, a recent study³⁴ that suggests that protein dynamics play no important part in the reaction projects the protein system, with many thousand degrees of freedom, onto a two-dimensional surface. Our group has found indications of direct coupling of protein dynamics to reaction in horse liver alcohol dehydrogenase (HLADH)³⁵ and felt it likely that similar dynamics occurs in YADH as well. Using these methods, the average classical barrier for hydrogen transfer (Table 1) was found to be very low, such that the hydride can easily overcome the barriers without tunneling. It is worth noting again that this value, as well as the other free-energy barriers that we have calculated, are different from other measurements because of the difference in what we are calculating, that is, the free-energy barrier for hydride transfer from the reactive configuration.

Table 1.

Comparison of the Average Properties of YADH Trajectory Ensembles with and without CMD

method	free-energy barrier (kcal/mol)	D–A distancea (Å)
Classical	0.97	2.78 ± 0.06
CMDb	0.28	2.72 ± 0.09
CMD3c	0.32	2.69 ± 0.27
CMD-Dd	1.05	2.70 ± 0.04

^aAverage minimum in the D–A distance in the neighborhood of the reaction.

^bCMD applied to the transferring hydride.

^cCMD applied to the transferring hydride and the secondary hydrogen, which rehybridize during the reaction.

^dCMD applied to the transferring deuteride, which replaced the hydride as the transferring particle.

The average barrier using the CMD method was lower than the average classical barrier, as expected, but the small difference between them is consistent with a zero-point energy (ZPE) contribution, not particle tunneling. Examination of the minimum donor–acceptor (D–A) distances reveals an insignificant change in the average distance of the CMD ensemble compared to the classical ensemble. This is expected as the small energy barrier is not large enough to greatly influence that aspect of the transition state.

In addition to the application of CMD to the transferring particle, a TPS ensemble was generated where CMD was applied to the transferring particle and the two secondary hydrogen atoms that rehybridize during the reaction (CMD3). Probes of the quantum effects using secondary kinetic isotope effects (KIEs) have suggested that there is some coupled motion between the secondary and primary positions during the reaction.^16,17 Secondary KIEs have alternatively been interpreted as being due solely to the contribution of the secondary particles to the ZPE.¹⁸ In the CMD3 ensemble, all three centroid hydrogen particles had an average RMS radius of 0.30 Å. Generation of trajectories for the CMD3 ensemble was more difficult than generation of trajectories for the CMD1 ensemble due to the significantly more time-consuming generation of trajectories and the lower reactive probabilities for similar perturbations. The average barrier for CMD3 was 0.04 kcal/mol higher than the average barrier for CMD1, showing that the addition of quantum dynamics to the secondary particles had an insignificant effect on the barrier to hydride transfer. The average minimum D–A distance in the CMD3 ensemble was similar to the classical and CMD1 ensembles.

In order to compare the results of our methods with an experimental metric, we obtained a TPS ensemble with deuterium instead of hydrogen as the transferring particle (CMD-D). This allows for an approximate comparison with the primary KIE. The CMD method was also applied in this ensemble to correctly incorporate the quantum effects of the deuterium. The average RMS radius of deuterium for a typical trajectory was 0.22 Å, significantly lower than the hydride as a result of the increase in particle mass. The decreased delocalization of the deuteride, in addition to the change in ZPE, should cause an increase in barrier height in the deuterium ensemble relative to the CMD1 ensemble. This was indeed the case (Table 1). The experimentally determined primary H/D KIE is 3.4,²⁰ which, if one were to use the simple approximation that the KIE is due entirely to the different free-energy barriers in the hydride transfer step, corresponds to a difference of 0.72 kcal/mol. The difference in barrier height between the CMD1 and CMD-D ensembles, 0.77 kcal/mol, agrees fairly well with this experimental measure. The average minimum D–A distance in the deuterated ensemble was similar to the hydrogen ensembles. If tunneling played a major role in the reaction, one would expect the deuterated ensemble, with reduced quantum effects, to transfer at a shorter distance than the CMD or CMD3 ensemble. The fact that they have similar distances is further evidence for the negligible degree of tunneling in this enzyme.

It is also worthwhile to examine the distribution of barrier heights in YADH, shown in Figure 1a. CMD3 is omitted from this figure due to the small number of trajectories. In every ensemble, there are trajectories that have a barrierless particle transfer. In these trajectories, the free-energy barrier of the reaction is entirely in bringing the system to the reactive state, which allows the hydride to move from the donor well to the acceptor well freely. It is important to note that because the protein motion is on a similar time scale as the particle transfer, many methods that only include the degrees of freedom transverse to the reaction coordinate statistically, that is, only through partition functions, would be inappropriate for this system.^14,36 It is known from the Grote–Hynes theory that this equilibrium solvation assumption fails if there is no separation of time scales between the reaction coordinate and a transverse degree of freedom; in the absence of such time scale separation, this transverse degree of freedom has to be described with time-evolved dynamics coupled to the reaction coordinate³⁷ and cannot be captured statistically with partition functions.

Figure 1.

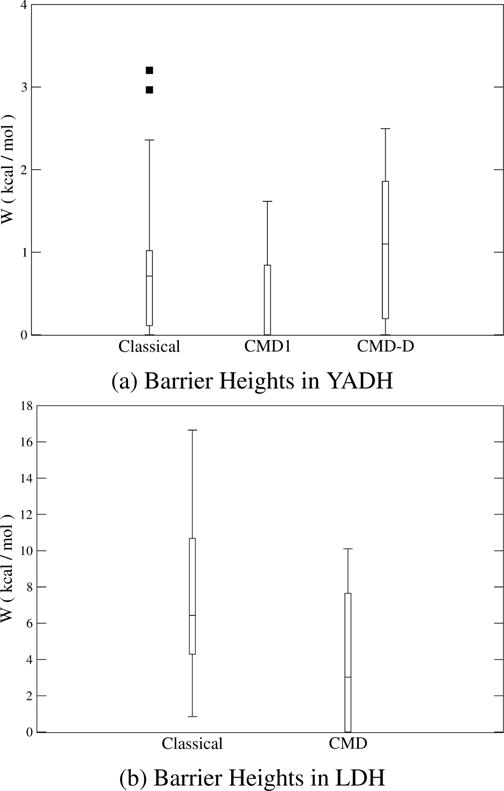
Box plots showing the distribution in the amount of work needed for barrier crossing in YADH and LDH. The horizontal line marks the median value; the box around it marks the first and third quartiles; the whiskers mark the last data points within 1.5 of the interquartile range; solid squares represent data outside of this range.

The barriers in the YADH calculations were surprisingly small. To verify that the results were not an artifact of the centroid implementation or the preparation of YADH but represent true barriers, we performed a similar calculation along the reverse direction of the reaction, in a similar enzyme, human heart lactate dehydrogenase (LDH), to check whether larger barriers are obtained. The LDH catalyzes interconversion of lactate and pyruvate. Though LDH and YADH both perform similar reactions, chemical differences between the two systems affect their direct comparison. First, LDH calculations were performed with its native substrate, while YADH calculations were performed with benzyl alcohol, a nonideal substrate. Second, in part because of the form of substrates with which the protein was crystallized, YADH was examined in the substrate oxidation direction, while LDH was examined in the direction of substrate reduction. Third, while the mechanism in YADH involves an equilibrium proton transfer, followed by a rate-determining hydride transfer, LDH involves an approximately simultaneous proton and hydride transfer.

Two reactive trajectory ensembles were generated for LDH using TPS, one classical and one with CMD applied to both transferring particles. The average RMS radius of both the hydride and the proton was 0.30 Å, similar to the centroid hydrogen in YADH. The average classical barrier in LDH is higher than that in YADH (Table 2). This barrier is still low enough to be surmounted without tunneling, and a difference with CMD of 4.07 kcal/mol is consistent with a ZPE contribution, not tunneling. The distribution of barrier heights (Figure 1b) in each ensemble is extensive. In the classical LDH ensemble, barriers range from 0.85 to 16.65 kcal/mol, a range that extends from a height where tunneling will not play a significant role to a height where quantum effects could be important. The wide range of the calculated work is a strong indication that the barrier depends on the instantaneous positions of the surrounding residues. There is some evidence for tunneling in LDH in the difference between the average D–A distances of the classical and CMD calculation. An increase of 0.09 Å upon application of the centroid method corresponds to delocalization of the hydride during the reaction, allowing the transfer to occur over a longer distance. In conclusion, both the barriers of the reaction and the qualitative features of the transfer step are consistent with expectations for this enzyme. This gives us confidence that the results for YADH were not artifacts of the computational method.

Table 2.

Comparison of the Average Properties of LDH Trajectory Ensembles with and without CMD

method	free-energy barrier (kcal/mol)	D–A distancea (Å)
Classical	7.77	2.77 ± 0.02
CMDb	3.61	2.85 ± 0.03

^aAverage minimum in the D–A distance in the neighborhood of the reaction.

^bCMD was applied to the transferring hydride and proton.

Returning to YADH, an indication of the influence of the D–A distance on the reaction barrier was the large barrier in a biased trajectory that we created for YADH, which had a small harmonic restraint as a penalty for D–A compression. Even with this penalty, the 500 fs trajectory showed D–A compression, and the distance at the moment of transfer was 3.44 Å. In the biased trajectory, the hydride had to surmount a barrier of 28.78 kcal/mol to react, significantly higher than any barrier in the TPS ensemble. Without the protein guiding the search through conformational space for a reactive conformation, the reaction would be limited to an entropically expensive unguided search for a rare D–A compression. It is worth emphasizing again that it is this motion on the same time scale as the barrier crossing that causes barrier reduction.

We applied CMD to two dehydrogenases using TPS to generate ensembles of reactive trajectories. TPS with CMD allows an atomistic description of the reactive event, in contrast to many methods that utilize equilibrium solvation techniques that make an implicit adiabatic and statistical assumption about motions that are coupled to the reaction coordinate, an assumption that may not be appropriate for all enzymes. Our technique provides mechanistic detail, with the inclusion of any fast protein dynamics. We argued that information about tunneling is not inferred from activation free energies that include the entire system but from the activation free energy on the transferred hydride calculated as an ensemble average of individual trajectories. This calls into question previous experimental markers thought to indicate tunneling. The analysis of the work on the transferring hydride showed that YADH has a small contribution from quantum effects, while LDH has a larger contribution, including possibly a small contribution from quantum tunneling. We found that for certain trajectories where the transfer distance is small, the transfer is barrierless, raising the possibility that an entropic search for these configurations is crucial for catalysis.