Principles of cryo-EM single-particle image processing

Abstract

Single-particle reconstruction is the process by which 3D density maps are obtained from a set of low-dose cryo-EM images of individual macromolecules. This review considers the fundamental principles of this process and the steps in the overall workflow for single-particle image processing. Also considered are the limits that image signal-to-noise ratio places on resolution and the distinguishing of heterogeneous particle populations.

Introduction

‘Any sufficiently advanced technology is indistinguishable from magic’. From the perspective of Arthur C. Clarke's Third Law [1], cryo-EM single-particle reconstruction (SPR) might rightly be considered a very advanced technology. One starts with a set of perhaps 100 000 hopelessly noisy-looking images of single macromolecular ‘particles’, and by a seemingly magical process —typically requiring thousands of CPU-hours on a computer cluster —the end result can be one or more 3D density maps from which atomic structures can be determined.

The success of SPR is made possible by two astonishing phenomena. First, in many cases individual rapidly frozen macromolecules are so consistent in conformation that the positions of atoms are superimposable within a few angstroms from copy to copy. This consistency allows information to be combined from images of ensembles of these particles to provide the final density map. Second, even the very noisy images obtained from low-dose imaging of the cryo-EM specimen can contain in themselves enough information to allow the orientation of the underlying particles to be determined. These two phenomena, coupled with recent advances in image acquisition technology, statistical estimation theory and algorithm development, are allowing single-particle cryo-EM methods to move rapidly into the mainstream of structural biology.

The goal of this review article is to provide an overview of the processing that takes particle images to density maps. The emphasis is on the statistical methods that are embodied in the program Relion [2], which has been used for the majority of recent high-resolution reconstructions. Not addressed here is the process of fitting of atomic models to density maps, nor the very important issue of validating these models. For practical details, more rigorous theory and more complete reviews of the literature, the reader is encouraged to consult the recent reviews by Cheng et al. [3], Elmlund and Elmlund [4] and Nogales and Scheres [5].

Figure 1a shows one of the cryo-EM micrographs obtained by Liao et al. [6] in their pathbreaking work on the TRPV1 ion channel. Owing to electron-counting technology and motion correction, these micrographs have particularly good signal-to-noise ratios (SNRs) and contain information beyond 3.4 Å resolution. The formation of an individual particle image (Fig. 1b–d) can be modeled as a projection of the 3D molecular density, which in turn is modified by the contrast-transfer function (CTF) of the defocused microscope. The recorded image is very grainy due to the random counting noise from the low dose of electrons used. An ensemble of thousands of high-quality particle images like this can contain the information to make an atomic-resolution reconstruction of the particle density, but the atomic-resolution information in an individual particle image cannot be evaluated. This is because the spectral SNR of a particle image is below unity —there is more noise than signal— for details finer than about 16 Å (Fig. 1e) in this dataset. In general,

The high-resolution content of an individual particle image cannot be measured.

Fig. 1.

Cryo-EM micrograph and a particle image. (a) One quarter of a micrograph from the TRPV1 dataset of Liao et al. [6] with selected particles marked by boxes. (b), Boxed image (256 pixels on a side, pixel size 1.22 Å) of the particle marked with a thick box in (a). (c) Corresponding projection of the 3D map of the TRPV1 protein, computed according to the angles assigned to this particle image by the Relion reconstruction program [2]. TRPV1 is a membrane protein, here solubilized by amphipols, and the viewing direction is approximately in the membrane plane; the transmembrane region is at the lower right. (d) Simulated noiseless particle image, obtained by operating on the projection image with the fitted contrast-transfer function. Note the arcs extending from the particle due to signal delocalization from the substantial defocus δ = 2.2 µm. The electron wavelength is λ= 2 pm at 300 keV, and image features of characteristic size (resolution) d = 3.5 Å are expected to be delocalized by about λδ/d = 120 Å; hence the need for a large boxed image size. (e) Average particle spectral signal-to-noise ratio [7] computed from Fourier ring correlations between phase-flipped particle images and map projections. For display, images in (a) and (b) were Gaussian filtered with half power at 20 and 11 Å, respectively. Data are from micrograph 21 and particle image 4 in the EMPIAR database entry, http://dx.doi.org/10.6019/EMPIAR-10005.

The only way to characterize the quality of single-particle data is by collecting statistics on sets of images, for example by computing averages or variances. The relevant averages are 2D class averages, or a 3D reconstruction; for measuring the variance, the power spectrum of an image stack can be computed, whereas the variance and covariance of 3D reconstructed volumes can also be computed. These measures of data quality are much less direct than what is possible from crystallographic experiments, where the raw data are diffraction patterns and the presence of high-resolution spots directly indicates high-quality data.

Theory of SPR

Before going into more technical topics, we first will consider the basics of SPR. Conceptually, there are two pieces to SPR. One, which is common to computed tomography in its many forms, is the construction of a 3D map from projection images. The other, unique to SPR, is the prerequisite step of determining projection angles from the projection images themselves.

Basics of 3D reconstruction

The goal is to determine the 3D density of an object from a set of 2D tomographic projections. Suppose a 3D density map M is represented as values on a 3D grid of size n × n × n. There is a density value associated with each voxel of the map. The value of each pixel of a projection image I can be obtained as the sum of the density values on a line passing through the map. A cryo-EM particle image is, at root, a projection image like this.

There are various methods for 3D reconstruction from projection images [8] although an instructive and widely used method makes use of the Fourier slice theorem. This theorem can be summarized in the following way.

A density map having n³ voxels has an equivalent representation, called its Fourier transform (FT). The FT is also an n × n × n array of numerical values. We denote the FT of M by $\hat{M}$; it contains all the information of the original map. The FT has the special property that if all of its voxels outside a sphere of radius R are set to zero, the remaining nonzero voxels contain the information of the original map, but only up to a resolution R (expressed in appropriate spatial-frequency units such as Å⁻¹). There is likewise a Fourier transform for 2D images; the FT of an image I we will call $\hat{I}$.

The Fourier slice theorem is a statement about the relationship between a 3D map and a 2D projection image of that map. It says: if projection image I is obtained by projecting M along a particular direction p, then the values of $\hat{I}$ will be identical to the values of $\hat{M}$ on a slice through that Fourier volume; that slice is taken on a plane that passes through the Fourier origin and is normal to p.

The Fourier slice theorem suggests a strategy for building up a 3D density map from projection images. The steps are as follows:

1. Obtain a large set of projection images I_j, with P_j being the corresponding projection vectors.

2. Compute the Fourier transforms ${\hat{I}}_j$.

3. In the 3D Fourier space, for each p_j, define a plane p_j that includes the origin and is perpendicular to p_j.

4. Assign voxels of $\hat{M}$ by constraining the values on each slice plane P_j to be equal to the values of ${\hat{I}}_j$.

5. Convert $\hat{M}$ back to M by the inverse Fourier transform.

That is all there is to it, except for details. One is the technical problem of interpolation, as the grid of pixels on the Fourier image I_j does not necessarily match the grid of voxels selected by a slice. Good solutions to this problem have been found. A second, more fundamental issue is the problem of inconsistent values: what should we do when pixels from two images ${\hat{I}}_j$ and ${\hat{I}}_k$ correspond to the same voxel in the 3D Fourier volume, but the pixel values are not equal? The solution is some sort of weighting scheme for merging information in assigning voxel values.

Third, what happens if the set of slice planes does not adequately cover the Fourier volume, but leaves some voxels unassigned? The results are phenomena known as the ‘missing wedge’, ‘missing cone’ and ‘preferential orientation’ artifacts, which give rise to anisotropic resolution in the reconstruction.

Finally, there is the issue of CTF correction. Cryo-EM images are typically acquired using defocus contrast. This is a primitive form of phase-contrast imaging where the microscope's objective lens is intentionally focused beyond the specimen by a distance of a few microns. The resulting image can be modeled by an ideal phase-contrast image that is modulated by a variable scaling of its Fourier components. The scaling factors are called the CTF. It is not possible to remove the effects of the CTF from an image, because at certain frequencies the CTF is zero and therefore no information is present at all at these frequencies. However, it is straightforward to include CTF effects in 3D reconstruction. The value at a given Fourier voxel is assigned according to a weighted average of all of the relevant Fourier pixels of the contributing images. The weights are chosen to be positive, negative or zero depending on the sign and magnitude of the CTF at the image pixel position, so that images having the strongest contrast make the largest contribution to the voxel value. In this way,

CTF effects are readily handled when information is combined from multiple images.

Determination of particle orientations

For each projection image, we must know the projection vector so that we can insert the Fourier values in the correct plane. In standard SPR, the projection vectors are completely unknown, because the individual particles are oriented randomly. It is the determination of the particle orientations that is the difficult part of SPR. Generally, it is carried out by projection-matching (see, for example, [9]). One starts with an initial estimate of the 3D map. Reference images are obtained by computing the projection of this map in an extensive set of projection directions. Then a given single-particle image is compared with each reference, and the projection vector of the best-matching reference is the one assigned to this particle image.

The refinement of a SPR then proceeds iteratively. Given an initial 3D model, projection vectors are assigned to all of the particle images, and then a 3D reconstruction is performed. This serves as the new 3D model, and the process is iterated perhaps a few dozen times.

The projection-matching process is not very complicated, but it takes vast amounts of computer time. It is instructive to see how steeply the computational intensity scales with resolution. Suppose that we determine for a roughly spherical particle of diameter D a map with minimum feature size (resolution) d. Each single-particle image should then be at least n × n pixels in size, with n = 2D/d. Although to adequately sample the Fourier volume for a particle of s-fold symmetry, one needs only about $\pi n/s$ projection directions; to assign an appropriately precise projection direction to each particle image, we must instead test $\pi n^2/s$ projection directions for each one.

Because the location of each particle in the micrograph is not known exactly—say up to an uncertainty of t pixels—the comparison of a particle image with each reference projection requires the testing of t² translational shifts and also $\pi n$ different in-plane rotations; and each one of these comparisons requires n² operations, one for each pixel. For m particle images, the number of computer operations is then very roughly

$$n_c=t^2{\pi }^2{n}^{5}m/s.$$

Since n is proportional both to particle size and to resolution, we find that

The computational complexity of SPR increases very steeply with the particle size and the resolution.

For a particle of diameter D = 120 Å and a target resolution d = 3 Å, the minimum image size would be n = 80. Given a dataset of m = 30 000 particles with s = 4 and t² = 25, n_c = 6 × 10¹⁵. This corresponds to about 1600 CPU-hours at 10⁹ CPU operations per second.

This rough estimate does not account for oversampling of image data or the extra overhead involved in the statistical weighting of images in reconstructions. On the other hand, this estimate also does not take into account computational gains from algorithmic improvements, and indeed none of the widely used refinement programs require as much computer time as we have estimated here. The complexity of the in-plane rotation and image comparison steps can be reduced from $\pi n^3$ to n² log n or fewer operations through the use of polar Fourier transforms [10] spherical harmonics [11] or steerable basis functions [12]. The number of references to be compared with each image can be reduced substantially through local search strategies ([2,13]; and many others). The cost of comparisons can be decreased through reduced representations of images and volumes [14]. In the end, it appears that the complexity can be reduced substantially, but it seems unlikely that n_c can be reduced below the order of n³m/s.

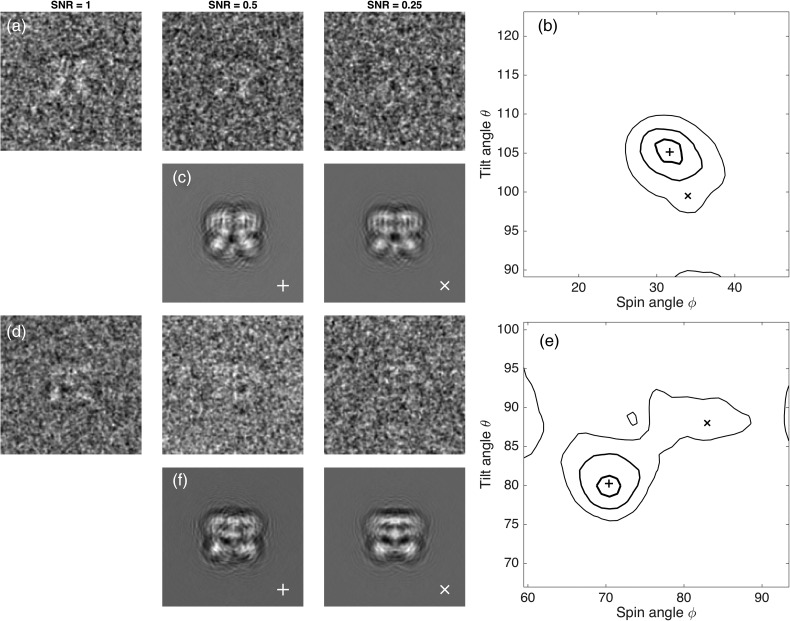
Even in the case of a relatively small particle with D = 120 Å, orientation assignments that preserve information at d = 3 Å must be accurate to small angles, within ${\sin }^{-1}(d/D)\approx {1.5}^{\circ }$ to avoid mixing of information between adjacent Fourier voxels. Can projection matching perform this well? Figure 2 shows the result of a simulation of projection-matching based on two particles in the micrograph of Fig. 1. In view of the 3.4 Å reconstruction obtained by Liao et al. [6] from this dataset, it is no surprise that angles were retrieved with an acceptable error of 1.7° when the simulated images had the same noise level as the experimental particle images. When simulated with higher noise yielding half the SNR, the angle errors doubled to 3°; errors of this size would limit the resolution of a 3D reconstruction to about 6 Å. With another 2-fold reduction in SNR, the angle errors became very large, too large for even low-resolution 3D reconstruction. From this simulation, it appears that the signal in these images was just sufficient to allow a high-resolution reconstruction to be obtained.

Fig. 2.

Angle assignment errors. Two particles from the micrograph in Fig. 1 were chosen as representative. They are approximately side views with tilt angles θ = 160° and 80° and spin angles $\varphi ={31}^{\circ }$ and 70°. Sets of 10 000 simulated particle images were computed with noise variance either matching that of the actual particles (labeled SNR = 1) or variance that is larger by a factor of 2 or 4, yielding the relative SNR values of 0.5 or 0.25. In rows (a) and (d), images with reversed contrast (protein is white) are shown after Gaussian filtering at 15 Å. Orientation angles were obtained by projection-matching for each image. (b and e) Contours enclosing 50% of the estimated angle values are shown for the two particles at three SNR values. In each plot, the thickest contour line corresponds to SNR = 1, where the standard deviation of errors in both angles was 1.7°. At SNR = 0.5, the errors had a standard deviation of 3° while at SNR = 0.25 angle errors of 10° or more were common, as shown by the thin contour lines. In rows (c and f), simulated noiseless images corresponding to central (+) and outlying (X) angle assignments demonstrate the subtlety of differences between projections at these angles. Angles, CTF parameters and estimated SNR were taken from particles 17 and 4 in the same dataset as that used in Fig. 1.

It is astonishing that projection-matching can perform so well. Visually, it would seem impossible to distinguish, on the basis of even the SNR = 1 particle images in Fig. 2a and d, the pairs of very similar reference projections shown in Fig. 2c and f. Nevertheless, the accuracy of projection-matching degrades very rapidly at lower SNR levels.

Statistical weighting of projections

Maximum-likelihood and other statistical approaches to the SPR problem are able to deliver good results despite moderate errors in orientation assignments. They do this by avoiding the direct assignment of an orientation to a particle image, but instead use a ‘fuzzy’ assignment based on computed probabilities of orientations. The probabilities of the orientations for a particle image are used as weights in applying the information from that image in the 3D reconstruction [2]. Furthermore, some particle images have more signal or for other reasons give more reliable orientations than others; it is advantageous in the 3D reconstruction to assign stronger weights to them based, for example, on correlation coefficient values [13].

Model bias

From a mathematical standpoint, SPR is a very challenging, nonlinear optimization problem. The goal is to obtain the 3D structure, that is the roughly 10⁶ voxel values in a 3D density map, from perhaps 10⁹ very noisy pixels in a dataset of particle images. To solve the structure, ideally one would examine all possible density maps and pick the single one that best matches the dataset, given a scoring function such as the squared error or the likelihood. A complete search of all possible 3D maps is currently impossible, and at present the main approaches are local optimization algorithms: they start with an initial model of the structure, and iteratively refine it. The iterations improve the value of the scoring function, but there is no guarantee that at convergence the score that is obtained is the global optimum. Of interest in this respect is the employment of techniques like stochastic hill-climbing [15]; these allow what is otherwise a conventional least-squares optimization to escape from being trapped in a local minimum. Even these algorithms however are not guaranteed to find the global minimum squared error. In practice, we are faced with this phenomenon:

Model bias means that the final structure is influenced by the initial model.

When the data quality is high, convergence to the global optimum is quite reliable and initial models such as smooth ellipsoids or random densities result in correct structures. However, when the SNR of the images is low or when preferential particle orientation causes the strong over-representation of certain projection directions, model bias can be severe. Model bias in SPR results from misassignment of particle orientations and can be avoided —or identified —by several methods.

First, one can start with an ab initio model derived from the particle images. Orientations can be assigned on the basis of ‘common lines’ on intersecting planes in the 3D Fourier transform [16,17], and models can be generated by the global, simultaneous assignment of angles [18] or by stochastic clustering approaches [19]. Alternatively, one can initiate the refinement process with a reliable model obtained by a data-collection technique that directly provides orientation-angle values. Random conical tilt reconstruction [20] and subtomogram averaging [21] are methods where calibrated tilts of the specimen stage provide good starting models.

Another approach is, post hoc, to test the reliability of angle assignments using tilt-pair analysis [22]. The introduction of a known magnitude of stage tilt should result in angle assignments shifting by the same amount, and verification of these shifts greatly increases the confidence that angle assignments are valid. Finally, one comfort is that the gross misassignment of angles generally results in low-resolution reconstructions. Thus, it is to be hoped that an interpretable, high-resolution map is unlikely to suffer from model bias.

The image-processing pipeline

Having described the SPR process, we now turn to other steps involved in obtaining density maps from micrographs.

Particle picking

A cryo-EM micrograph contains randomly arranged particles along with non-particles—bits of frost, deformed particles, protein aggregates and so on. Traditionally, the particle locations are identified or ‘boxed’ using a particle-selection program having both interactive and automatic functions. An example is E2Boxer [23] where the user can click on the obvious particles in a displayed micrograph; from the coordinates, the program extracts small square regions (boxes) of the micrograph, which are then collected into a ‘stack’ of particle images. Programs typically include an auto-picker function where 2D or 3D particle models are used to identify particles automatically. A remarkably successful generic 2D model is the ‘difference of Gaussians’, where a broad 2D Gaussian function of negative amplitude is subtracted from a narrow 2D Gaussian of positive amplitude [24]. The result is a pattern of a circular white object with a dark surround, similar in overall appearance to the (inverted-contrast) image of a particle with its surrounding undershoot of image intensity caused by the CTF. More sophisticated 2D particle models are created as rotational averages from a manually picked particle set or from projections of an initial 3D particle model. The models are used as references to build correlation-coefficient or likelihood maps in which the peaks are taken to identify particles. The user controls one or more threshold values, which set the discrimination of particles from non-particles.

With model-based auto-picking comes the danger of 2D model bias. Specifically, if a detailed particle model is used as the reference to identify particles, then the particle stack will, through biased selection of positions in the micrograph, consist of images that best match the reference. Even if the micrograph contains no particles, the selected boxes of noise can show features of the reference when averaged together [25]. Fortunately, if there are true particles with high SNR in the micrograph, they will predominate in the automatic picking process. At the present state of the art, it seems that machines are always less reliable than humans at picking particles, and thus:

If you cannot see and recognize the particles, most likely there are not any.

CTF determination

Compensation for the CTF of particle images can be performed at the reconstruction stage, as we considered above. The CTF is a function that oscillates rapidly, with some Fourier components transferred with positive contrast and others with inverted contrast. With 1 µm of defocus, the first zero of the CTF, for 300 keV imaging, is at the spatial frequency of (14 Å)⁻¹. (In the following, we shall just denote the frequency by its reciprocal, 14 Å in this case.) At twice the resolution (7 Å), the CTF has gone through four reversals, and at four times the resolution (3.5 Å) it has gone through 16 reversals. If the defocus is greater, the density of reversals increases proportionately, so that at 4 µm of defocus the number of reversals at each resolution is quadrupled. Higher defocus is advantageous for visualizing, picking and determining the orientation of small particles because it preserves more of the signal at the lowest spatial frequencies, roughly 200 Å to 20 Å, which are best for recognizing and orienting particles. However, with high defocus the increased density of contrast reversals requires a more precise modeling of the CTF. Astigmatism, which turns the circular rings in the CTF into ellipses, must also be modeled correctly [26]. The overall precision required can be appreciated in that a defocus error of 124 nm yields a complete reversal in the polarity of the CTF at 3.5 Å; thus errors of this size can cause the signal to vanish when information from different images are combined. Fortunately, there are several programs that quickly and accurately determine the CTF parameters from micrographs [27] for use in subsequent image processing and reconstruction steps.

2D Classification of particle images

Both the low SNR of individual cryo-EM images and the distortion due to CTF effects make it difficult to evaluate the images in a particle stack. The clustering of similar particle images (a process commonly termed 2D classification) and calculation of class-average images is a good way to see what a dataset contains; secondary-structure elements such as alpha-helices are routinely visible in the class images from high-resolution data.

The clustering of similar particle images was first introduced by van Heel and Frank [28] and the problem has received much attention; for a recent comparison of methods, see Zhao and Singer [12]. Described here is the maximum-likelihood 2D classification implemented in Relion [2]. One starts with a set of random ‘reference’ images. Then for each particle image, probabilities are computed with respect to its rotation, translation and the degree of matching to each reference. Translated and rotated particle images are formed, and their 2D Fourier transforms, appropriately weighted by the CTFs, are combined to form the overall average images. These averaged images are taken to be a new set of references, and the procedure is iterated a few dozen times. The result is a set of representative averaged images that underlie the dataset.

2D classification is very similar to SPR. In both cases, each particle image is aligned and tested against a set of reference images, and then the reference set is updated. The only difference is that in SPR, the updating of the references occurs through the process of 3D reconstruction; this enforces a strong self-consistency constraint, as all the references come from the same 3D volume. On the other hand, 2D classification lacks this constraint.

SPR and 2D classification are similar processes, except that the former includes the constraint of consistency with a unique 3D structure.

Starting with random seeds and having no self-consistency constraint, the process of 2D classification does not converge to a unique or reproducible set of class-average images; at best one takes the set to be representative of the variety of images contained in the dataset. Classification is useful, however, as artifactual images (frost balls for example) tend to be grouped together in the classifications, so their exclusion is readily done by marking all members of an aberrant class as ‘bad’ particles and excluding them from further processing.

2D classification gives an early impression of heterogeneity in a dataset. Sometimes, it is possible to recognize views of particles in different conformations or different sizes, and use the 2D class identities to sort the individual particle images in a process called ‘supervised classification’. The class average images also portray the variety of viewing directions available in a dataset. For example, it is straightforward to distinguish ‘top’ from ‘side’ views of symmetric particles, and the symmetry point group is sometimes apparent. Top views of particles having cyclic symmetries show rotational symmetry, whereas the corresponding side views can have internal mirror symmetry.

3D Classification, heterogeneity and the identifiability problem

One of the astonishing features of SPR is that many macromolecules can be frozen such that atomic positions are consistent within a few angstroms from copy to copy. Nevertheless, the general experience with high-resolution structures shows that every population of particles has some heterogeneity, and by selecting a consistent subset of particle images higher resolution can be obtained. Subtle differences in structures can be discovered and sorted through simultaneous SPR using multiple 3D models, a process called 3D classification. Because it is sometimes possible to distinguish different macromolecular species as well as different conformations in 3D classification, in cryo-EM structure determination there is also the promise of purification in silico, where the particles in a biochemically impure specimen are sorted out by computer.

The classification of 3D models is similar in principle to the 2D classification of images. When implemented in the process of SPR using statistical weighting, the set of probabilities computed for each particle image also includes the probability that the image arises from each of several different 3D densities. After multiple iterations of refinement, the assignment of each particle image to a particular 3D model is usually unambiguous, and separate reconstructions can be made from the separately assigned particle stacks. 3D classification does not work as well as one might hope: the number of 3D models must be given in advance, and minority structures often fail to be discovered. It is common to use repeated rounds of classification to define a population of particle images yielding the best-resolution structure. In the end, there seems to be much room for improvement in the automatic sorting of particle-image populations, with one promising alternative approach being that of Shatsky et al. [29].

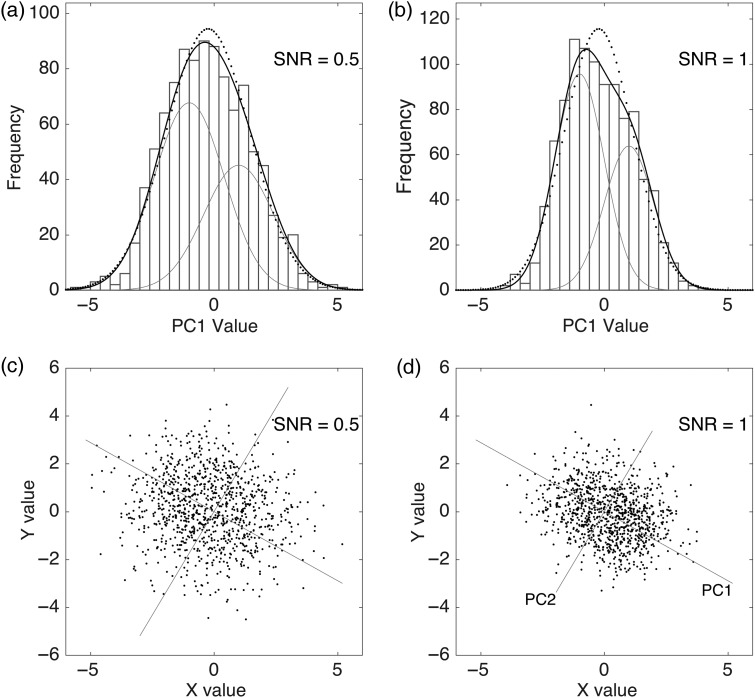
One expects there to be limits to the power of classification, having to do with the inability to distinguish, on the basis of noisy particle images, among similar reference images arising from different 3D maps. Distinguishing these images is an example of the identifiability problem of statistics. Consider the 1D problem of distinguishing between one or two populations in sets of random numbers. Figure 3a demonstrates the case where the large standard deviation of the distributions —the noise—is sufficient to make the overall two-population distribution indistinguishable from that of a single population. A small reduction of the noise (increasing the SNR by a factor of 2) allows the two components to be distinguished and their mean values to be determined (Fig. 3b). The same principle holds in SPR, where small improvements in SNR can make all the difference in distinguishing the members of heterogeneous populations of particles.

The ability to identify and separate heterogeneous particle populations depends critically on the signal-to-noise ratio of the images and on the magnitude of differences among the populations.

Fig. 3.

Illustrations of the identifiability problem in 1D and 2D. (a) Although a set of values comes from two populations of random numbers, the resulting distribution is essentially indistinguishable from a one-population distribution (dotted curve). (b) When the noise is variance is halved (SNR is increased), the two populations become distinguishable in the histogram. (c) Two populations in a two-dimensional space, also not distinguishable. (d) With twice the SNR, the principal component PC1 becomes visible, along which the two populations are separated. It is the projection of the values along PC1 that are depicted in (b).

An individual particle image can be represented as a point in a high-dimensional space where the number of dimensions is equal to the number of pixels in the image. Classification of images is then equivalent to discovering clusters of points in this space. Finding the clusters is simplified by finding the principal components, that is, the axes of major variation in an ensemble of images (Fig. 3c and d).

Variance, covariance and manifolds

As an important first step in the analysis of heterogeneity, the variance of a 3D map can be computed [30] to identify the 3D locations of ‘hot spots’ of variation. Theoretically more useful would be the covariance of a 3D map, which tells how variations in the density at one voxel correlate with variations in another voxel. For example, evidence for a conformational variation in which a structural element is found either in location A or location B would come from a negative covariance between the two locations in the map. Computation of the entire covariance is entirely unwieldy (the covariance matrix of a 10⁶-voxel map will have 10¹² entries) but techniques have been developed recently to identify the principal components of the covariance [31–33]. The principal components describe individual degrees of freedom. A simple hinge motion is described by one degree of freedom, and actual conformational fluctuations are expected to be described well by just a few degrees of freedom. The principal components of the covariance then provide an informative linear approximation to the possible deformations of the structure. A complete modeling of the degrees of freedom, including nonlinear effects, can be done by constructing the appropriate low-dimensional manifold in the space of all 3D volumes. This is a procedure called nonlinear embedding, and it is beginning to be applied to the cryo-EM heterogeneity problem [34].

What are the prospects for further improvements in SPR?

SNR is the fundamental limiting factor in SPR. We saw in Fig. 2 that a decrease in SNR reduces the precision of orientation determination of particles; indeed, beyond a certain limit, attempts at reconstruction will fail entirely. With Figure 3, we argued that distinguishing populations in a heterogeneous mixture of particles also becomes impossible at low SNR. Increasing the size of datasets and the use of statistical SPR methods can compensate somewhat for decreases in SNR, but even with these methods SPR rapidly becomes impractical.

SNR, evaluated as image power to noise power in single-particle images, scales roughly proportionally to molecular weight [35]. For most of the past decade high-resolution structures obtained through SPR were restricted to complexes with molecular weights well above 1 MDa. Only particles of this size yielded images with sufficient signal to allow particle orientations to be determined accurately. It was with the advent of electron-counting cameras, which brought a severalfold increase in SNR, the structure of smaller structures such as the 400 kDa TRPV1 ion channel became possible. At the time of writing, the smallest near-atomic cryo-EM structure is that of gamma secretase [36], a 120 kDa membrane-protein complex. The particle's irregular shape was helpful, no doubt, in making orientation determinations more accurate, but nevertheless this structure represents a very impressive benchmark regarding particle size for SPR. One wonders if it will be possible to obtain structures of even smaller, hard-to-crystallize proteins such as G-protein-coupled receptors having molecular weights on the order of 50 kDa. Are there ways in which image SNR can be increased further, so that orientation determination can be made more reliable?

Electron-counting cameras can be improved somewhat. The Gatan K2 electron-counting camera used by Liao et al. [6] and Bai et al. [36] has a detection quantum efficiency that ranges from about 0.7 at low spatial frequencies to 0.4 at typical resolution limits [37]. Improvements bringing these numbers toward unity will give proportional increases in SNR.

The SNR of micrographs can be improved through the use of minimal ice thickness and zero-loss energy filtration of the image-forming electrons. The classical theory of cryo-EM image formation makes the assumption that specimens are very thin and only a minority of electrons undergo scattering events. Unfortunately, inelastic scattering (which happens at triple the rate of the desirable elastic-scattering events) becomes substantial in specimens more than a few tens of nanometers thick. Inelastic scattering has two deleterious effects. First, once an electron is inelastically scattered, it cannot participate in the phase-contrast image formation, and thus the image contrast is reduced. Second, the inelastically scattered electrons contribute to the shot noise in the recorded image. An energy filter is a device that removes the inelastically scattered electrons before they reach the camera, so that this second effect is eliminated, giving an improvement in SNR. Indeed, energy-filtered imaging was used for the gamma-secretase structure [36].

The SNR of acquired images is fundamentally limited by electron dose, which in turn is constrained by radiation damage to the specimen. Radiation damage is the breaking of chemical bonds and the creation of molecular fragments, some of which remain immobilized in the ice. Traditional low-dose images are obtained at a dose of roughly 20 electrons per square angstrom of specimen area to avoid the loss of high-resolution information as damage occurs. One very approximate way to model the effect of radiation damage on particle images is a linear-filter model that assumes that the high-resolution Fourier components are attenuated whereas the low-resolution components remain largely unchanged [38–40]. To the extent that this model is valid, images can have their SNR improved by the appropriate weighting of the frames acquired in movie-mode imaging. Strong beam-induced movement during the first 1–2 e/Ų of exposure typically makes the first movie frames unusable and these frames, unfortunately, are best discarded. High-resolution information is preferentially obtained from the remaining early frames of a movie, whereas low-resolution information, so important for particle picking and orientation determination, is accumulated from entire movies with total doses much higher than 20 e/Ų. Procedures of this sort are already being used to improve image SNR, but there may be room for improvement, based on a more complete understanding of beam-induced movement and radiation-damage effects.

Finally, it should be remembered that defocus-contrast is a poor way to obtain phase-contrast images in the electron microscope. A substantial gain in SNR is promised by in-focus phase-plate imaging, for example through the use of the Volta phase plate of Danev et al. [41]. In phase-plate imaging, the oscillating CTF, having an average squared magnitude of ½, is replaced with a constant contrast-transfer close to unity magnitude; meanwhile, the shot noise level remains the same. Technical problems remain, including the knotty one of precise focusing of the microscope when a phase plate is in use, but in principle a factor of two increase in SNR is possible.

In summary, there is still room for considerable improvement in cryo-EM technology. One can predict:

Future SNR improvement by a factor of 3–4 seems possible, making practical the structure determination of some proteins below 50 kDa in size.

Contributing to these improvements will be advances in specimen preparation, instrumentation and algorithms for single-particle image processing.

Funding

The study was funded by National Institutes of Health (R01-NS021501).