The Impact of Physiological Crowding on the Diffusivity of Membrane Bound Proteins

Abstract

Diffusion of transmembrane and peripheral membrane-bound proteins within the crowded cellular membrane environment is essential to diverse biological processes including cellular signaling, endocytosis, and motility. Nonetheless we presently lack a detailed understanding of the influence of physiological levels of crowding on membrane protein diffusion. Utilizing quantitative in vitro measurements, here we demonstrate that the diffusivities of membrane bound proteins follow a single linearly decreasing trend with increasing membrane coverage by proteins. This trend holds for homogenous protein populations across a range of protein size and for heterogeneous mixtures of proteins of different sizes, such that protein diffusivity is controlled by the total coverage of the surrounding membrane. These results demonstrate that steric exclusion within the crowded membrane environment can fundamentally limit the diffusive rate of proteins, regardless of their size. In cells this “speed limit” could be modulated by changes in local membrane coverage, providing a mechanism for tuning the rate of molecular interaction and assembly.

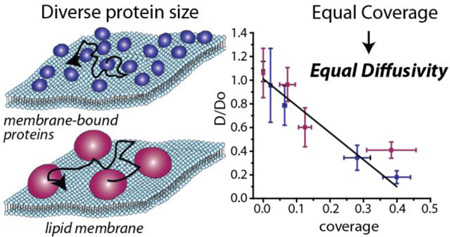
GRAPHICAL ABSTRACT

The diffusivities of membrane bound proteins follow a linearly decreasing trend with increasing membrane coverage, regardless of protein size.

INTRODUCTION

Diffusion of membrane proteins is a key step in the assembly of macromolecular structures on membrane surfaces including signaling complexes, focal adhesions, viral buds, endocytic pits, and cell-cell junctions¹. Therefore it is critically important to understand the chemical and physical parameters that influence membrane protein diffusivity within the highly crowded cellular membrane environment. Specifically, the soluble domains of transmembrane and peripheral membrane-bound proteins cover more than 30% of the plasma membrane surface in cells^2,3 and even larger portions of specialized membranes such as synaptic vesicles⁴ and the inner mitochondrial membrane,⁵ leading to protein-protein collisions and interactions that are expected to slow diffusion over membrane surfaces^6,7. Indeed, the diffusivities of transmembrane and peripheral membrane-bound proteins measured in live cells are typically at least an order of magnitude lower than diffusivities measured under dilute in vitro conditions⁸. However, in addition to molecular crowding, cellular structures such as lipid rafts, cortical actin, focal adhesions, and endocytic structures also modify membrane protein diffusion, frequently introducing anomalous behavior⁹. In live cells it is difficult to differentiate the influence of these structures from the influence of the crowded environment itself.⁸

In contrast, in vitro systems of purified lipids and proteins have the potential to isolate the impact of molecular crowding on diffusion. Specifically, a recent in vitro study revealed a monotonic decline in the diffusivity of transmembrane proteins with a wide range of molecular weights with increasing protein coverage¹⁰, though coverage was below 5%, much less than physiological levels. Similarly, the diffusivity of peripheral membrane-bound avidin declined with increasing coverage, displaying anomalous diffusive behavior at relatively low levels of membrane coverage¹¹. However the potential of avidin for lateral self-association¹² complicates use of this data to understand crowded diffusion in general. Taken together, while in vitro studies have provided critical insights, we presently lack a systematic understanding of the influence of protein crowding on the diffusivity of diverse peripheral membrane-bound proteins at physiological concentrations.

RESULTS AND DISCUSSION

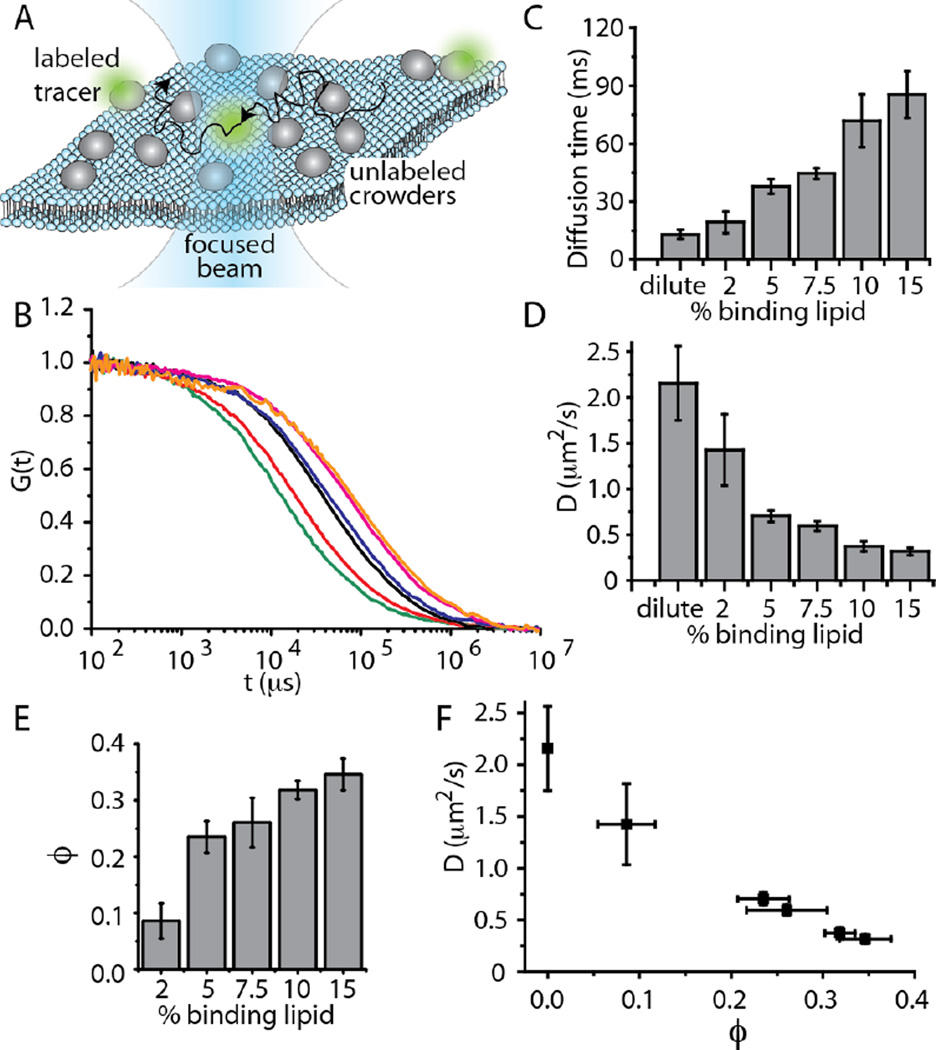
To address this gap, here we use fluorescence correlation spectroscopy (FCS) to study the diffusivity of peripheral membrane-bound proteins as a function of membrane coverage and protein size. To vary membrane coverage we used increasing concentrations of Ni-NTA lipids to bind 6-histidine-tagged proteins to the membrane surface. These lipids form a strong bond with histidine which leads to low dissociation rates over periods much longer than diffusive timescales¹³. FCS is an established technique for measuring the diffusivity of membrane components both in vitro and in live cells¹⁴. In our FCS experiments a small number of fluorescent-labeled tracer proteins (less than one per diffraction limited focal area) diffuse among an increasing concentration of identical, unlabeled peripheral membrane-bound proteins (see Experimental section). As tracer proteins diffuse through the focal area, they create fluctuations in the fluorescence signal, which is auto-correlated to reveal the characteristic timescale of diffusion, Fig. 1A.

Figure 1.

Diffusivity decreases linearly with increasing membrane coverage by transferrin. (A) Fluorescence correlation spectroscopy (FCS) measurement scheme. Peripheral membrane-bound proteins diffuse freely over the surfaces of supported lipid bilayers. The diffusivity of a small population of labeled tracer proteins is measured by autocorrelating fluctuations in the intensity of fluorescence emission as they diffuse through a laser beam focused at the membrane surface. (B) Autocorrelation curves for increasing concentration of Ni-NTA lipids, which serve as protein binding sites: dilute (green), 2 mol% NTA (red), 5 mol% NTA (black), 7.5 mol% NTA (blue), 10 mol% NTA (pink), 15 mol% NTA (orange). (C) As binding site density increased, diffusive time constant increased, (D) diffusivity decreased, and (E) protein coverage increased. (F) Diffusivity decreased approximately linearly with increasing membrane coverage. The detailed procedure used to measure membrane coverage is described in the Experimental section. In all plots, error bars represent the standard deviation of multiple trials. The number of trials for each individual data point is listed in the Experimental section.

We began by examining membrane surfaces decorated with the model protein transferrin, which has a molecular weight of 78 kDa and is expected to occupy approximately 24 nm² on the membrane surface, based on crystallographic data. Normalized correlation data from FCS revealed an increasing characteristic diffusion time with increasing concentration of Ni-NTA binding sites on the membrane surface (Fig. 1B). The data were originally fit with a single component diffusion model, but residuals of a few percent remained and for some curves the slope was slightly overestimated, Figure S1. These fitting problems were largely corrected by using a correlation function for anomalous diffusion, as described in Materials and Methods, Figures S2. However, the anomalous diffusion component did not increase with increasing protein coverage, Figure S3, suggesting that the source of the anomalous behavior was likely not the protein crowding process. Possible explanations for the anomalous behavior include inhomogeneity in the fluidity of the membrane and interactions between the membrane and the underlying substrate ¹⁵. Nonetheless, we cannot rule out the possibility that anomalous protein diffusion may be present and contributing to the results. Fitting the data quantified the increase diffusion time with increasing binding sites (Fig. 1C), resulting in a trend of decreasing diffusivity (Fig. 1D).

Next we used calibrated, photon-counted confocal scans of the membrane surfaces to measure the concentration of peripheral membrane-bound proteins as the concentration of Ni-NTA binding sites increased (see Methods), Fig. 1E. Protein coverage increased from less than 10% to nearly 40% as the concentration of Ni-NTA lipids increased from 2–15%. The trend appears to saturate, likely owing to reduced accessibility of membrane binding sites as protein coverage increased. Combining data on diffusivity and membrane coverage reveals a decreasing trend that is approximately linear, within the experimental uncertainty, Fig. 1F.

We asked to what extent steric exclusion effects could explain this trend. A simple Boltzmann lattice model^3,16, in line with more detailed models in the literature ¹⁷, predicts that the diffusivity of non-interacting spherical particles, which cannot simultaneously occupy the same space, will decrease linearly with increasing molecular coverage, Equation 1, where ϕ is fractional coverage, where D₀ is the diffusivity under dilute conditions, and α is a constant³.

$$\mathrm{D}={\mathrm{D}}_0(1-\mathrm{\alpha }\mathrm{\varphi })$$ Equation 1

Expressing ϕ as the product of the projected area per protein, A_P, and the number of proteins per membrane area, m, gives Equation 2.

$$\mathrm{D}={\mathrm{D}}_0(1-\mathrm{\alpha }{\text{mA}}_{\mathrm{P}})$$ Equation 2

Theoretical studies based on the Smoluchowski equation have predicted that crowded diffusion of hard spheres in 2D is well described using a value of 2 for α^16,18. Fitting Equation 2 to the data with A_P as a free parameter yields a value of 31 nm² for A_P, in reasonable agreement with crystallographic data, 24 nm². These results suggest that steric exclusion among non-interacting spheres provides a reasonable approximation of the influence of crowding on diffusion of membrane bound transferrin proteins at physiological levels of membrane coverage (see Supplementary Fig. S4 and associated discussion).

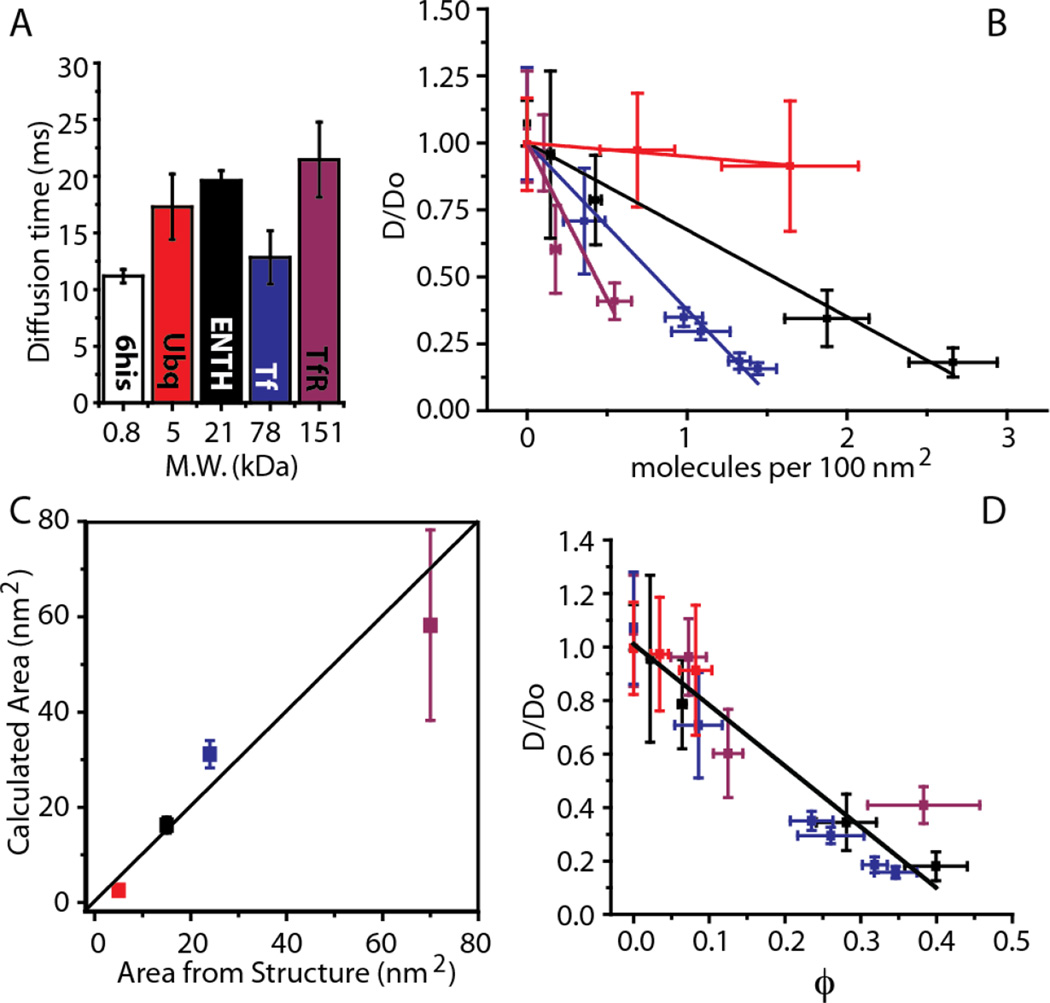
A prediction of this model is that diffusivity and membrane coverage should be linearly related, regardless of protein size, such that a few large proteins should impact diffusivity equally to a larger number of smaller proteins. To test this prediction we examined three additional proteins of increasing size including ubiquitin (5 kDa), the ENTH domain of Epsin1 (21 kDa), and the ectodomain of Transferrin Receptor dimer, TfR (151 kDa). Based on their structures, these proteins are expected to occupy increasing areas on the membrane surface: ubiquitin (5 nm²), ENTH (16 nm²), TfR (70 nm²). We have previously used the data on ENTH as a standard of comparison to large intrinsically disordered proteins¹⁹. We began by measuring the diffusion time of each membrane bound protein under dilute conditions as well as the diffusivity of the labeled membrane tag, 6-histidine, alone, Fig. 2A. All diffusivities are in the 1–10 µm²/s range as expected from literature reports^20,21. These diffusivities are 1–2 orders of magnitude below those expected for 3D diffusion of globular proteins in solution²², suggesting that viscous drag within the membrane dominates hydrodynamic drag on the protein. Therefore, it is not surprising that no clear trend exists between diffusion time and protein molecular weight under dilute conditions. Variations likely arise from protein-membrane interactions that modify the drag within the membrane as the protein diffuses.

Figure 2.

A single decreasing trend relates diffusivity and membrane coverage for membrane bound proteins with diverse sizes. All legend colors are as in panel A. (A) Characteristic diffusion time under dilute conditions is not a function of molecular size. (B) Normalized diffusivity versus the concentration of membrane bound proteins. The diffusivity data were normalized by the fitted values of D_o. The Experimental section contains a detailed description of the linear fit and goodness of fit calculations. (C) Experimentally calculated molecular area (vertical axis) versus predicted molecular area based on crystallographic structures (horizontal axis) (D) Normalized diffusivity versus membrane coverage. In all plots, error bars represent the standard deviation of multiple trials. The number of trials for each individual data point is listed in the Experimental section.

For each model protein, diffusivity decreased with increasing membrane bound concentration, Fig. 2B. The rate of this decrease became larger with increasing protein size, as predicted by Equation 2. Fitting this model to the data yielded estimates of the area occupied by each protein in reasonable agreement with crystallographic data, Fig. 2C. Further, plotting the data as a function of membrane coverage reveals that the diffusivities of all proteins collapse onto a single, approximately linear trend with a slope of about −2, in agreement with theory, Fig. 2D. These results demonstrate that the impact of physiological levels of molecular crowding on the diffusivity of peripheral membrane-bound proteins can be described to the first order by a steric exclusion model, which predicts a linear decline in diffusivity with increasing coverage, regardless of protein size. Notably these results, in agreement with equation 1, indicate that under crowded conditions, protein diffusivity is influenced by both the interaction with the membrane, which determines D₀, and the protein size and membrane-bound concentration, which determine ϕ.

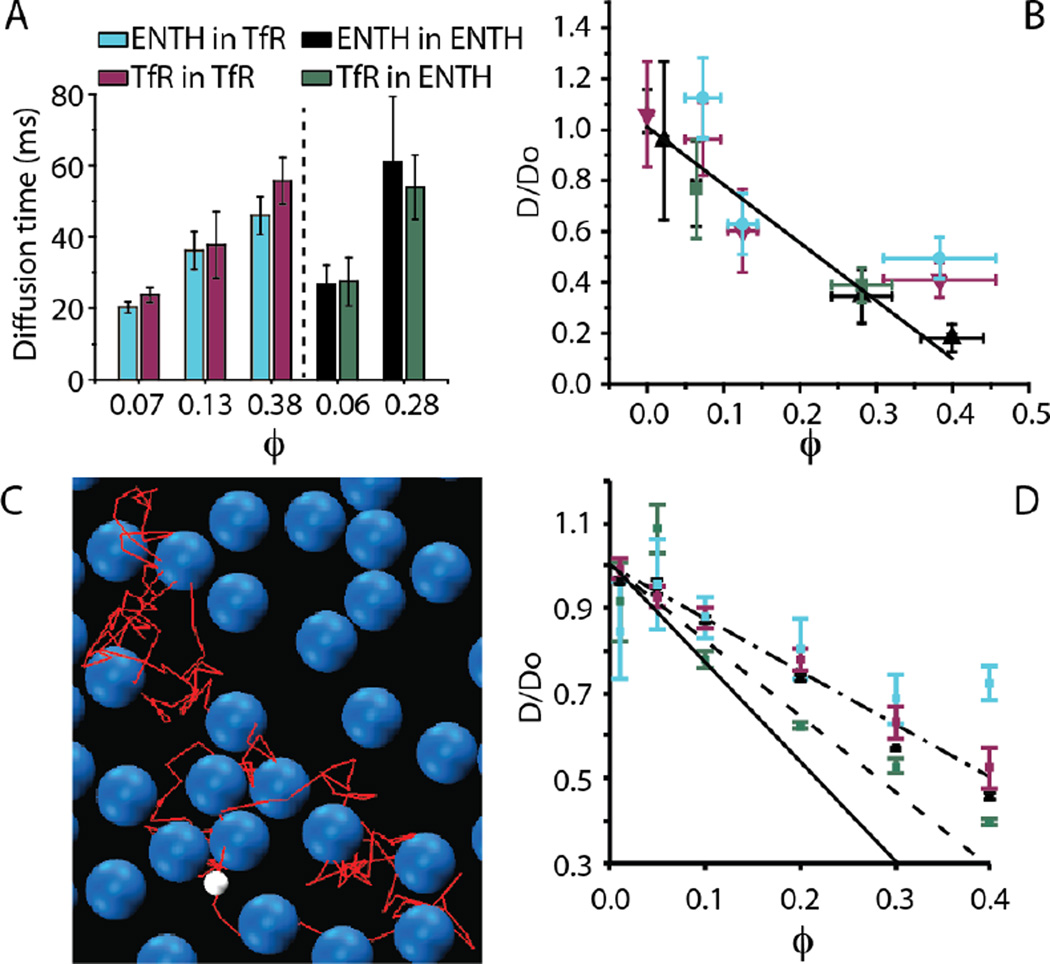
Cellular membranes host proteins of diverse size. As a first step toward examining these complex mixtures, we sought to determine how the impact of crowding on diffusion changes when the tracer protein and the surrounding proteins that make up the crowded environment have different sizes. Interestingly, the results reveal that diffusion of large and small tracer proteins is impacted approximately equally by a crowded field of surrounding proteins at a given coverage, Fig. 3A. Specifically, when the membrane is crowded to a given coverage by ENTH proteins, the diffusivity of a tracer protein is approximately the same, whether the tracer is another ENTH protein or a larger TfR protein (Fig. 3A, right). Similarly, when the membrane is crowded by a given concentration of TfR proteins, the diffusivity of a tracer protein is approximately the same, whether the tracer is another TfR protein or a smaller ENTH protein (Fig. 3A, left). Plotting the normalized diffusivity of these proteins as a function of membrane coverage for both the heterogeneous and homogenous cases, Fig. 3B, all data fall roughly along the same linear trend that best fit the homogenous data in Figure 2D. These results suggest that the influence of crowding on the diffusivity of a peripheral membrane-bound protein can be predicted simply by measuring the coverage of the surrounding membrane by other proteins, regardless of the size of these crowders (Supplementary Fig. S4).

Figure 3.

A steric exclusion model predicts the influence of heterogeneous protein crowding on diffusivity. See panel A for legend. (A) Comparisons of the diffusive time constant for homogeneous and heterogeneous experiments performed at the same membrane coverage. (B) Normalized diffusivity as a function of membrane coverage for homogenous and heterogeneous crowding. See the Experimental section for details of the linear fit. (C) Coarse-grained molecular dynamics simulation of heterogeneous 2-D crowding for the case that the tracer protein is ENTH and the crowding proteins are TfR. The white sphere represents a small ENTH tracer protein. The blue spheres represent larger TfR crowding proteins. The red line represents the path of the tracer protein leading to the current position. (D) MD simulation-derived relationship between normalized diffusivity and coverage for homogenous and heterogeneous crowding, LJ ε=1k_BT. Dash-dot line: best fit to plotted simulation points. Solid line: ε=10k_BT for TfR-sized particles. Dashed line: hard sphere potential from Cichocki and Hinsen. In all plots, error bars represent the standard deviation of multiple trials. The number of trials for each individual data point is listed in the Experimental section.

While the simple Boltzmann lattice model agrees reasonably with our data, it neglects interactions among proteins, which may modify the dependence of diffusivity on coverage. Furthermore, it cannot accommodate mixtures of proteins of different sizes. Toward addressing these limitations, molecular dynamics simulations were carried out in which protein interactions were modeled with a Lennard-Jones (LJ) potential and two walls were used to restrict the diffusion to a pseudo 2-D environment, Fig. 3C. Langevin dynamics were used to control the temperature at 300K. The results indicate that for homogenous systems of either small proteins, similar in size to ENTH, or large proteins, similar in size to TfR, the diffusion constant decreases linearly as the surface coverage increases, in agreement with equation 2, Fig. 3D. Similarly, under heterogeneous conditions in which (i) a small tracer protein diffuses among large crowders or (ii) a large tracer protein diffuses among small crowders, an approximately linear decline in diffusivity is observed with increasing membrane coverage, Fig. 3D. A LJ potential minimum energy well depth, ε, of roughly one k_BT was utilized in these simulations to represent nonspecific interactions between the particles, yielding a slope of −1.2, dash-dot line, Fig. 3D. Strengthening particle interactions increased the slope, which reached a value of −2.3 for ε=10kBT (solid line Fig. 3D and Supp. Fig. S5), though quantitative agreement between the data and the highly simplified model is not expected. Simulations in the literature using a hard sphere potential have also yielded a linear trend (slope of −1.8 ¹⁷, dashed line Fig. 3D), though differences in the simulation approach prohibit detailed quantitative comparison to our results. Regardless of the strength of particle interaction, normalized diffusivity declined linearly with increasing coverage in agreement with our data. The robustness of this linear decline arises from steric exclusion, which is, to the first order, independent of particle size and interaction (Supplementary text²³). However, the slope of the decline likely depends on the strength of protein and lipid interactions. Notably, our MD simulation is highly simplified and does not include a number of physical factors which are likely to influence membrane protein diffusion, such as the viscosity of the membrane, lipid-protein interactions, and protein-protein binding events. As such, while the results of the model provide insight into the influence of steric exclusion on diffusion, they do not provide quantitative predictions of protein diffusivity.

CONCLUSIONS

The major conclusion of this work is that steric exclusion effects can largely explain the influence of physiological levels of protein crowding on the diffusivity of peripheral membrane-bound proteins in vitro. Specifically we have found that the average diffusive rate of a peripheral membrane-bound protein is controlled by the coverage of the surrounding membrane by other proteins, regardless of protein size and even when proteins of different sizes are bound simultaneously to the membrane surface. Notably, in living cells a diverse range of other processes not present in these in vitro studies are likely to influence diffusion of membrane proteins. These processes include protein-protein binding, variations in membrane physical and chemical properties, and protein interaction with cellular structures such as the cytoskeleton, lipid rafts, endocytic structures, and many others. Nonetheless, our results quantitatively confirm the ability of physiological levels of protein crowding to modulate protein diffusion on membrane surfaces, reducing diffusivity by an order of magnitude as membrane coverage increases. This idea has been frequently predicted by theory^16,23,24 and suggested by biochemical perturbations of membrane protein density in cells^6,7, but never precisely measured as a function of physiological levels of protein coverage on membrane surfaces. In providing these measurements, our results imply that changes in the local coverage of the membrane by proteins could be used to set a “speed limit” on the local rate of diffusion, impacting rates of reaction and molecular assembly. Utilizing this mechanism, cellular structures that modify membrane coverage by sequestering and releasing membrane protein constituents could locally tune the dynamics of protein assembly on membrane surfaces. Such structures could include cytoskeletal networks, lipid rafts, endocytic pits, and others.

EXPERIMENTAL MATERIALS AND METHODS

Chemical reagents

MOPS (3-(N-morpholino)propanesulfonic acid), and HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), Tween 20, Sodium bicarbonate, PBS tablets, TCEP (Tris(2-carboxyethyl)phosphine hydrochloride, Imidazole, and NHS-Atto488, were purchased from Sigma Aldrich. NaCl, KCl, DMSO (Dimethyl sulfoxide), PMSF (Phenylmethanesulfonyl fluoride), β-ME (β-mercaptoethanol), sucrose were purchased from Fisher Scientific. Texas Red-DHPE was purchased from Invitrogen. All lipids were purchased from Avanti Polar Lipids (Alabaster, AL), including: Ni-NTA DOGS (1,2-dioleoyl-sn-glycero-3-[(N-(5-amino-1-carboxypentyl)iminodiacetic acid)succinyl] (nickel salt))) and POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine). All chemical reagents were used without further purification.

Proteins and purification

Ubiquitin with a 6-histidine tag was purchased from R&D Biosystems. Tranferrin and Transferrin Receptor were generously provided by the laboratory of Dr. Anne Mason at the University of Vermont. Transferrin has a single 6× histidine tag, while Transferrin Receptor is expressed as a native dimer and therefore has two 6× histidine tags. ENTH was purified as previously described ²⁵ with the following modifications: ENTH was expressed in BL21(DE3) pLysS cells (Invitrogen) over night at 18°C and was purified from bacterial extracts by incubation with Ni-NTA agarose in 25 mM HEPES, pH 7.4, 150 mM NaCl, 1mM PMSF, and 5 mM β-ME. Bacteria cells were lysed with 1% Tween20 and sonication. After extensive washing, proteins were eluted from Ni-NTA agarose by gradually increasing to a final buffer concentration of 200 mM imidazole. Eluted proteins were concentrated and dialyzed to completion with 25 mM HEPES, pH 7.4, 150 mM NaCl, and 5 mM β-ME at 4°C. Proteins were stored as small aliquots at −80°C.

Protein labeling

To perform labeling reactions, the protein buffer was exchanged to 150 mM sodium bicarbonate, 20 mM KCl, 1 mM TCEP, pH 8.4 buffer using a 10 KDa molecular weight cut off centrifugal filter (Millipore). The labeling reactions were performed using amine-reactive, NHS-ester functionalized dyes (Atto-Tec). The protein concentration was approximately 1 mg/mL. The dye, dissolved in anhydrous DMSO, was added to the protein solution, and the reaction proceeded at room temperature for about 30 minutes. The reactive dye concentration was adjusted experimentally to achieve the desired labeling ratio of approximately 1 dye :1 protein. After labeling reactions, the unreacted dye was removed from Transferrin, and Transferrin receptor with 20 kDa size exclusion spin columns (Princeton Bio Separations). For ubiquitin, the protein was purchased in a lyophilized state eliminating the need for buffer exchange. The unreacted dye was removed from Ubiquitin and ENTH by size exclusion chromatography with Sephadex G-25 (GE Healthcare Life Sciences) and the protein was concentrated using a centrifugal filter (Millipore).

Supported lipid bilayer preparation

Small Unilamellar Vesicles (SUVs) were prepared by drying down lipid films in clean glass conical tubes. The tubes were put under vacuum for 2–3 hours. Then the lipid film was resuspended in phosphate buffered saline (PBS) to create a 0.5 mM solution of liposomes. The liposomes were sonicated with a horn sonicator for 16 minutes in 4-minute intervals separated by 2 minute cooling periods in an ice bath. Ultraclean coverslips were used as the substrate for supported lipid bilayer (SLB) preparation. Silicone gaskets (Grace Biolabs) formed a well on the coverslip surface. PBS was used to initially hydrate the coverslip; then a 0.5 mM solution of SUVs was pipetted onto the coverslip, followed by a 15-minute incubation period during which the SLB formed. The SLB was washed repeatedly with experimental buffer (20 mM MOPS 200 mM NaCl pH 7.35 with TCEP as needed to prevent protein aggregation). After washing, protein solution was pipetted onto the SLB and incubated for the experiments described below.

Fluorescence correlation spectroscopy (FCS)

SUVs consisting of POPC lipids and increasing percentages of DOGS-Ni-NTA lipids were used to prepare SLBs. A small concentration of Atto488 labeled protein (2 nM to 8 nM depending on the protein and mol% DOGS-Ni-NTA) was pre-bound to the SLB surface for approximately 30 minutes. The SLB was washed to remove excess fluorescent protein. Then a 2 µM solution of unlabeled protein was added to the SLB to create a crowded membrane surface and incubated until equilibrium was reached (15 minute incubation for ENTH and Ubiquitin, 30 minute incubation for transferrin and TFR). FCS measurements at the membrane surface were acquired using a custom-built time correlated single-photon counting (TCSPC) confocal microscope that has been described previously ²⁶. The diameter of the laser focus was determined by collecting intensity scans of fluorescent beads of sub-diffraction limited size at 35 nm steps. A Gaussian function was fit to the intensity profile of the beads. The standard deviations obtained from the Gaussian fits were averaged for all beads, and the diameter of the laser focus was defined as two standard deviations (~330 nm). FCS curves were collected for 250–1000 seconds using autocorrelation through Becker and Hickl data acquisition software. Experimental n values for FCS curves are as follows: for transferrin, n = 11 curves, 2 SLBs (2% DOGS-Ni-NTA, uncrowded); n =17 curves, 4 SLBs (2% DOGS-Ni-NTA); n = 9 curves, 2 SLBs (5% DOGS-Ni-NTA); n =7 curves, 2 SLBs (7.5% DOGS-Ni-NTA); n = 12 curves, 2 SLBs (10% DOGS-Ni-NTA); n = 10 curves, 2 SLBs (15% DOGS-Ni-NTA); for transferrin receptor, n = 10 curves, 2 SLBs (2% DOGS-Ni-NTA, uncrowded); n = 12 curves, 3 SLBs (2% DOGS-Ni-NTA); n = 10 curves, 2 SLBs (7.5% DOGS-Ni-NTA); n = 7 curves, 2 SLBs (15% DOGS-Ni-NTA); for ubiquitin, n = 8 curves, 3 SLBs (2% DOGS-Ni-NTA uncrowded); n = 10 curves, 3 SLBs (5% DOGS-Ni-NTA); n = 13 curves, 2 SLBs (15% DOGS-Ni-NTA); for ENTH, n = 9 curves, 2 SLBs (2% DOGS-Ni-NTA, uncrowded); n = 14 curves, 2 SLBs (1% DOGS-Ni-NTA); n = 12 curves, 2 SLBs (2% DOGS-Ni-NTA); n = 19 curves, 3 SLBs (5% DOGS-Ni-NTA); n = 15 curves, 2 SLBs (7.5% DOGS-Ni-NTA) for the 6× his-tag, n = 12 curves, 2 SLBs (2% DOGS-Ni-NTA, uncrowded); for ENTH crowded by TFR, n = 9 curves, 2 SLBs (2% DOGS-Ni-NTA); n = 12 curves, 2 SLBs (7.5% DOGS-Ni-NTA); n = 9 curves, 2 SLBs (15% DOGS-Ni-NTA); for TFR crowded by ENTH, n = 14 curves, 3 SLBs (2% DOGS-Ni-NTA); n = 8 curves, 2 SLBs (5% DOGS-Ni-NTA).

The autocorrelations obtained were fit with the standard 2D autocorrelation function,

$$G(t)=(1+\beta e^{-\frac{t}{{\tau }_c}})*\left(\frac{C}{1+\frac{t}{{\tau }_D}}\right)+1$$ Equation S1

as well as a 2D autocorrelation function for anomalous diffusion,

$$G(t)=(1+\beta e^{-\frac{t}{{\tau }_c}})*\left(\frac{C}{1+{\left(\frac{t}{{\tau }_D}\right)}^{\gamma }}\right)+1$$ Equation S2

where C is 1/N_p, and N_p is the average number of diffusing proteins in the excitation region. τ_D is the diffusion time. γ is the anomalous diffusion exponent¹¹. Corrections for short time processes such as intersystem crossing are included in β and τ_C, which are held constant in the fitting as 0.05 and 5 µs respectively. They have little effect on fitting the longer time processes of interest here. The autocorrelation curves were fit with graphing and data analysis software OriginLab 9.0 using a custom nonlinear explicit curve fitting function that is defined by equation S1. This curve-fitting model uses the Levenberg-Marquardt algorithm to iterate the parameters fitted by the software. As described above and in Supplementary Figures S1–S3, fitting the data with equation S2 corrected for residual misfits present when fitting with equation S1. Therefore, the values of τ_D reported in the manuscript figures were derived from fitting the data with equation S2.

Membrane coverage measurements

To measure the number of labeled proteins bound to the SLB surface per area for experiments measuring crowded diffusion rates, we executed the following steps, which are similar to a procedure we have employed previously¹⁹ : (i) determine the average brightness (number of photons per time) per single dye molecule on a sparsely covered surface, (ii) measure the average number of photons collected from the crowded membrane surface within the confocal spot size, (iii) divide this value by the average brightness of a single molecule to determine the number of molecules diffusing within the confocal spot size on the crowded membrane, (iv) measure the confocal spot size, (v) divide the number of molecules per confocal spot by the area of the confocal spot to arrive at a measure of the number of labeled molecules per membrane area on the crowded surface.

(i) Determine the brightness per single dye molecule

The calibrated single molecule fluorescence for Atto488 was determined by binding a dilute concentration of Atto488 labeled proteins to the surface of an SLB. Collecting FCS data on protein diffusion over the membrane surface, the correlation amplitude provides a measure of the number of molecules diffusing within the laser focus. Then, a nanopositioning piezoelectric stage coupled with Becker and Hickl electronics for TCSPC was used to sample the fluorescence intensity (photons per time) within the laser focus at an array (32 × 32) of positions on the SLB surface, typically 200 nm apart. Dividing the average value from these measurements by the number of molecules within the laser focus (from the amplitude of the FCS correlation) provides a measure of the average brightness of individual fluorophores (photons per time).

(ii) Measure the total number of photons collected from the crowded membrane surface within the confocal spot size

For the case of ENTH and transferrin a 2 µM solution of 95 parts dark protein: 5 parts Atto488 labeled protein was incubated with an SLB composed of POPC lipids with varying molar % of DOGS-Ni-NTA lipids. For TFR a 300 nM solution of 20 parts dark and 10 parts labeled was used, and for ubiquitin a 2 µM solution of 1 part dark and 1 part labeled was used. ENTH and ubiquitin were bound to the SLB for 15 minutes (30 minutes for transferrin and TFR) before being washed thoroughly to remove unbound protein. Then the brightness of the membrane surface (photons per time within the confocal spot) was measured as described in part i.

(iii) Calculate the number of molecules diffusing within the confocal spot size on the crowded membrane

The overall membrane brightness (average of 32×32 array trials of point brightness measurements) was divided by the average brightness of a single molecule to determine the number of labeled molecules diffusing within the confocal spot size. Since a known percentage of the peripheral membrane-bound molecules were labeled, the total density of peripheral membrane-bound molecules was calculated by dividing by the ratio of unlabeled to labeled protein.

(iv) Measure the confocal spot size (as described above)

The diameter of the laser focus was determined by collecting intensity scans of fluorescent beads of sub-diffraction limited size at 35 nm steps. A Gaussian function was fit to the intensity profile of the beads. The standard deviations obtained from the Gaussian fits were averaged for all beads, and the diameter of the laser focus was defined as two standard deviations (~330 nm).

(v) Divide the number of molecules per confocal spot by the area of the confocal spot to arrive at a measure of the number of labeled molecules per crowded membrane area

Experimental n values for photon counting scans are as follows: for transferrin, n = 20 scans 2 SLBS (2% DOGS-Ni-NTA); n = 22 scans 2 SLBS (5% DOGS-Ni-NTA); n =20 scans 2 SLBS (7.5% DOGS-Ni-NTA); n = 21 scans 2 SLBS (10% DOGS-Ni-NTA); n = 17 scans 2 SLBS (15% DOGS-Ni-NTA); for transferrin receptor, n =20 scans 2 SLBS (2% DOGS-Ni-NTA); n = 29 scans 2 SLBS (7.5% DOGS-Ni-NTA); n = 30 scans 2 SLBS (15% DOGS-Ni-NTA); for ubiquitin, n = 19 scans 2 SLBs (5% DOGS-Ni-NTA); n = 19 scans 2 SLBS (15% DOGS-Ni-NTA); for ENTH, n = 11 scans, 1 SLB (1% DOGS-Ni-NTA); n = 10 scans, 1 SLB (2% DOGS-Ni-NTA); n = 10 scans, 1 SLB (5% DOGS-Ni-NTA); n = 12 scans, 1 SLB (7.5% DOGS-Ni-NTA).

Calculation of goodness of fit for linear fits

To compute the linear trends in Figures 2B, 2C, 2D, and 3B, OriginLab 9.0 software was used to produce a linear fit (unweighted least-square method) for the respective data points. In Figure 2B, 4 linear fits were performed for ubiquitin (R² of 0.99), ENTH (R² of 0.98), TfR (R² of 0.74), and transferrin (R² 0.97). The x error bars represent trial repeats as described in the section “Membrane Coverage Measurements”. The y error bars represent trial repeats as described in the section “Fluorescence Correlation Spectroscopy (FCS)”. In Figure 2C a single linear fit (R² of 0.88) was used to visualize the correlation between experimentally calculated protein area coverage vs. predicted area coverage from crystallographic data. To experimentally calculate the molecular area, the linear fit of each protein in Figure 2B was used to define the parameters in Equation 2 such that the only unknown variable is membrane area (A_p) – the fitted slope is divided by the fitted intercept and finally divided by the constant α (value of 2 from literature). The y error bars are error propagated from molecule/area uncertainty in trial repeats described in “Membrane Coverage Measurements”. In Figure 2D a single linear fit (R² of 0.90) was used for all data points to approximate an experimental slope of −2 for □□□This linear fit was then plotted onto Figure 3B to visualize how closely the trend of heterogeneous protein crowding follows the trend of homogenous protein crowding.

Diffusion simulations

Stochastic Dynamics (SD) or Langevin Dynamics was used to simulate protein diffusion using the TINKER v7 ²⁷ molecular modeling software package. Two types of proteins were modeled for the computational study, a “Big” and “Small” protein of diameters 10 nm and 4 nm, imitating TFR and ENTH respectively. Each protein was represented as a spherical particle with Lennard-Jones interaction. Solvent frictional force was captured via a friction coefficient acting on the velocity as implemented through TINKER SD routine. Parameters were determined by conducting three-dimensional SD simulations and adjusting the parameters to reproduce known 3D protein diffusion constants (~10⁻⁶ cm²/s). Since our data indicate that all proteins diffuse at similar rates under dilute conditions (Fig. 2A), each protein was set to the same mass (19 kDa) and epsilon value (0.5 kcal/mol ~ 1 k_BT), while the protein diameters varied as mentioned above (10 nm and 4 nm). The friction coefficient was set to 0.1 ps⁻¹. The protein diameters of 10 nm and 4 nm were set equal to “sigma” (σ) in the Lennard-Jones potential. A geometric combining rule was used for the Lennard Jones interaction for both radius and epsilon $(r_{ij}=2\sqrt{r_i}\sqrt{r_j},{\epsilon }_{ij}=\sqrt{{\epsilon }_i}\sqrt{{\epsilon }_j})$. To simulate a pseudo 2-D system, the protein particles were contained between two parallel “walls” consisting of stationary particles tightly spaced that did not allow proteins to diffuse across them. Four types of systems were studied: homogenous (i) large or (ii) small proteins and heterogeneous systems of (iii) small surrounded by large (Figure 3C) or (iv) large surrounded by small proteins. Six crowding conditions of ϕ = 1,5,10,20,30, and 40% were simulated for each system. Area occupancy, ϕ, is defined as the percent of the 2-D area taken up by proteins (projected as a 2-D circle with diameter of σ for each protein). The number of molecules in each system varied according to the area occupancy. For the large protein homogeneous system, the protein counts were 10,10,10,20,20,40 for the 1,5,10,20,30, and 40% area occupancy, respectively. For the small protein homogenous system, the protein count was 10,40,100,100,100,100. For the heterogeneous mixtures, the big protein count in the small environment was 1,1,10,10,10,10, while the small protein count in the big environment was 1 small protein for all % area occupancy. For the heterogeneous systems, the ratio of the number of tracer proteins to the number of crowding proteins was 1:100. Owing to solvent drag, the small proteins diffused more rapidly than the large proteins in our simulations. For example, for the 10% crowded case (ϕ = 10%), the small proteins diffuse approximately 6 times faster than the large proteins. However, since hydrodynamic drag has a similar impact on the protein intrinsic diffusivities, D₀, this effect does not significantly impact the reported ratios, D/D₀. In the vertical direction (perpendicular to the 2D plane of diffusion), the protein “walls” held a clearance of 11 nm from the box edge. Simulations ran for 10 µs with a 5 ps time-step with analyzed frames saved every 100 ps. Each system was simulated approximately 10 times, though systems with larger error bars were simulated with additional runs (typically 5–10 additional runs with the extreme of 55 runs for the 5% crowding by a big protein in a small environment). Diffusion values were determined by first averaging the mean square displacement (MSD) over all runs for All simulations converged, following a linear regime of diffusion. The reported diffusion constant values were the diffusion values with a time interval, Δt, of 1.5 µs. The reported error of the diffusion constants was computed as the standard error from the individual simulation runs of each system. Notably, in all experiments protein coverage did not exceed 40%, such that protein remained mobile on the membrane surface. Further increases in protein density substantially above this level would be expected to promote formation of a solid phase. ²⁸