Twin differentiation of cognitive ability through phenotype to environment transmission: The Louisville Twin Study

Abstract

The Louisville Twin Study is one of the most intensive twin studies of cognitive ability. The repeated measurements of the twins are ideal for testing developmental twin models that allow for the accumulation of gene-environment correlation via a phenotype to environment (P=>E) transmission process to explain twins’ divergence in mean ability level over time. Using full-scale IQ scores from 566 pairs of twins (MZ=278; DZ=288), we tested whether a P=>E transmission model provided better representation of actual developmental processes than a genetic simplex model. We also addressed whether the induced gene-environment correlation alters the meaning of the latent nonshared environmental factors with a simple numerical method for interpreting nonshared environmental factors in the context of P=>E transmission. The results suggest that a P=>E model provided better fit to twins’ FSIQ data than a genetic simplex model and the meaning of the nonshared environment was preserved in the context of P=>E.

The Louisville Twin Study (LTS) is one of the oldest longitudinal twin studies in the United States and has been an invaluable source for advancing knowledge of the biometric influences on cognitive and psychosocial development. The LTS also consists of the most intensively studied group of twins over time (Wilson, 1983), with full cognitive testing of twins from the ages of 3 months to 15 years (Eaves, Long, & Heath, 1986; McArdle, 1986; Wilson, 1986; Zonderman, 1986). With the recent resuscitation of the LTS, we have reanalyzed the FSIQ data using a reciprocal effects modeling framework (Dickens & Flynn, 2001) to explain whether the accumulation of gene-environment correlation via a phenotype to environment (P=>E) transmission process drives twins’ divergence in mean ability level over time.

The purpose of this report is to: (1) present the rationale for why inclusion of P=>E transmission parameters in standard genetic simplex models does a better job explaining cognitive developmental processes than genetic simplex models alone; (2) test whether P=>E transmission models provide superior fit to LTS twins’ FSIQ data than a genetic simplex model; and (3) present a simple numerical method for interpreting latent nonshared environmental components in the context of P=>E transmission that hamper traditional interpretation of the nonshared environment in conventional twin models.

Reciprocal Effects Models

Dickens and Flynn (2001) originally presented their version of the reciprocal effects model (for another version of reciprocal effects models see Bronfenbrenner & Ceci, 1994; Bronfenbrenner, 1994) to explain how small changes in social environments could snowball into massive population-based gains in mean IQ points within a couple of generations (20–30 years). Reciprocal effects models, however, also have important implications for individual development, as they provide an ecological framework for how organisms interact with their physical and social environments. People do not randomly select environments, but maneuver and position themselves into environments and milieus where they can thrive, as well as react to environments provided to them (e.g., by caregivers). That is, people select into certain environments (e.g., niches) to reinforce innate or learned abilities, like athletic ability, or remove themselves from unsupportive environments to minimize failures. Similarly, environmental factors rarely evoke random behavior from people, but rather reinforce a set of selected behaviors. For example, middle-aged sports players often select out of player status and into coaching status as they age to maintain their overall “baseball” skills. As the process unfolds over time, the mean effect of organisms’ environments on behavior, thus, gradually increases over time.

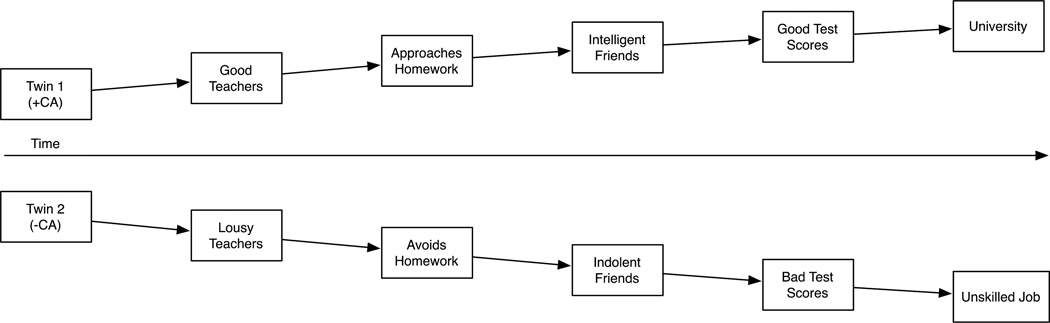
The niches people select into, we submit, are highly individualized. Even siblings matched for part of their genetic ancestry and family environments can wind up with very different cognitive and psychiatric profiles for the reason that one sibling was slightly smarter (and elicited more supportive responses from family, friends, and educators) than a co-sibling (Beam & Turkheimer, 2013). Figure 1 illustrates an elementary example for how an initial genetic advantage for cognitive ability spurs different developmental trajectories between siblings. The cumulative biologic and environmental effects over time, as a result of a single initial difference, sets one twin on an academic trajectory but the co-twin not. Small phenotypic differences between siblings, thus, can cause siblings to “drift apart” via their selection into and evocation of subsequent environmental differences. These differences are hypothesized to set twins on unique developmental trajectories.

Figure 1.

Theoretical description of “sibling drift.” +CA = initial genetic advantage for cognitive ability relative to co-twin; -CA = initial genetic disadvantage for cognitive ability relative to co-twin.

Statistically, there are three consequences of reciprocal effects models when applied to within-family differentiation. First, biological siblings and twins raised in the same family should diverge over time. Second, the statistical phenomenon known as gene-environment correlation (rGE) should accumulate with the passage of time (i.e., the strength of the match between twins and their nonshared environments increases). Third, the correlations among nonshared environmental factors – that is, any environmental experience that makes twins and siblings dissimilar from one another – should increase over time.

Why P=>E Models Matter

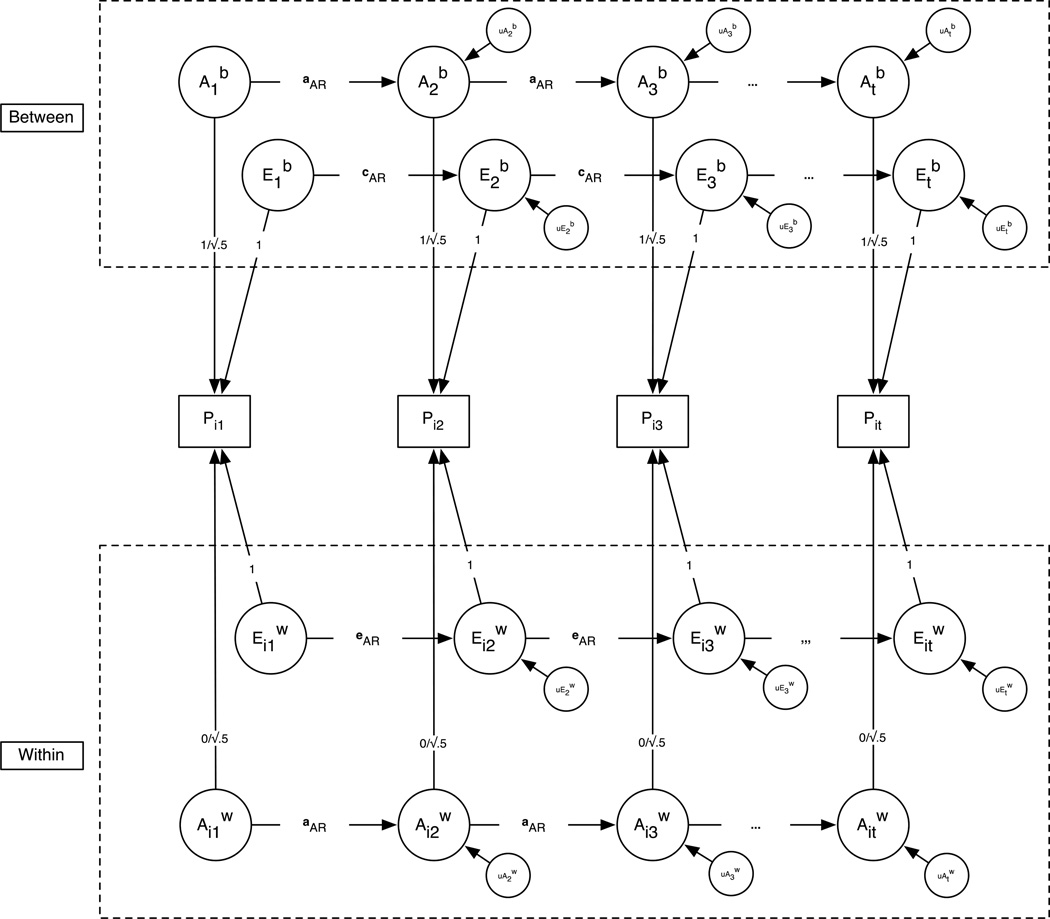
The purpose of P=>E transmission models is to more accurately approximate the causal processes underlying human development – namely, the process that produces behavioral diversification within members who share common genetic ancestries and social histories. We take the view that developmental behavior genetics has done well elucidating that individual biometric processes might change (or not) over time, but that explaining why people with common genetic and environmental backgrounds develop differently requires further investigation. Fig. 2, which represents a generic genetic simplex model for t measurement occasions as a multilevel structural equation model, illustrates that the development of a phenotype, P, is the sum of the total additive genetic (both between, $a_t^b$, and within, $a_t^w$, effects) and environmental (both between, $e_t^b$, and within, $e_t^w$, effects) variance components underlying P. While genetic simplex models can be used to delineate the biometric components underlying individual differences in cognitive ability, the P=>E model presented in Fig. 3 can be used to explain why people diverge developmentally. Explained in greater detail below, the important conceptual point for the moment is that the path projecting from P to the subsequent within-family environmental component, $e_t^w$, represents the influence people have on their own environments. This subsequent environmental component, in turn, evokes responses from people that further increase the selected behavior, as indicated by the within-time effect of $e_t^w$ on P in Fig. 3.

Figure 2.

Generic ML-SEM genetic simplex model. Biometric components of P_it, phenotypic CES-D scores for twin i at time t, are estimated between- and within-families; $A_t^b$ = between-family genetic effect at time t; $E_t^b$ = between-family (common) environmental effect at time t; $A_t^w$ = within-family genetic effect at time t; $E_t^w$ = within-family (nonshared) environmental effect at time t; $u{A}_t^b$ = unique between-family genetic effect at time t; $u{E}_t^b$ = unique between-family environmental effect at time t; $u{A}_t^w$ = unique within-family genetic effect at time t; $u{E}_t^w$ = unique within-family environmental effect at time t; a_ar, c_ar, and e_ar = auto-regression coefficient between adjacent components; the between-family and within-family genetic loadings for the MZ twins are 1 and 0, respectively, to meet the assumption that MZ twins share 100% of their genes; the between-family and within-family genetic loadings for the DZ twins are both √5 to meet the assumption that DZ twins share 50%, on average, of their segregating genes.

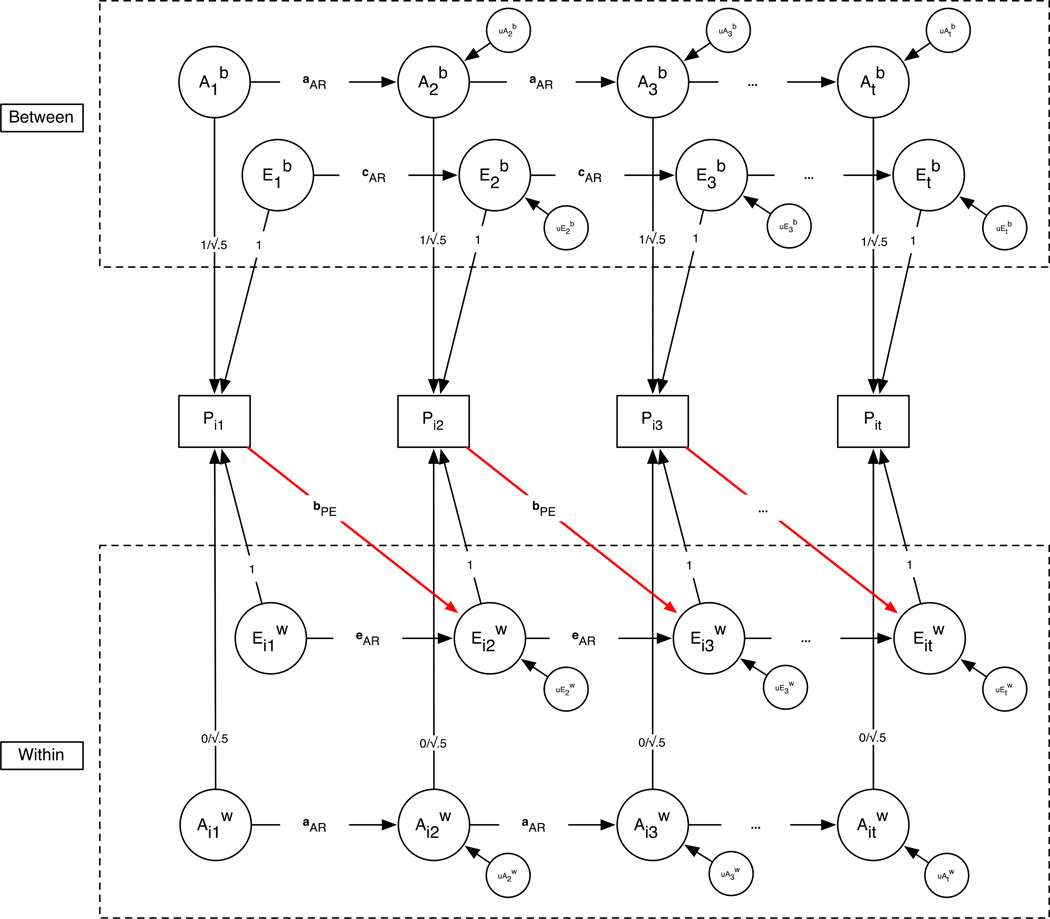
Figure 3.

Generic ML-SEM genetic simplex model with P=>E. The red line represents that the P=>E parameter, b_PE, which was only estimated at the within-family level in the DZ group.

Developmental processes can be notoriously difficult to identify in longitudinal twin data. Wilson’s (1983) theory of developmental synchronies was, as was Eaves et al.’s (1986) theory of developmental change, crucial for helping behavior geneticists advance research on underlying mechanisms of development. Wilson, however, concluded that “Intelligence as ultimately realized in adolescence is powerfully affected by developmental genetic processes that steadily move each zygote toward a targeted end point” (p.312, Wilson, 1983) while Eaves et al. (1986) concluded, based on a series of genetic simplex models, that “‘memory’ for previous environmental effects will tend to eradicate genetic effects in the long run if the genetic effects do not induce comparable permanent phenotypic changes with lasting effect” (p.159, Eaves et al., 1986). The relative importance of genetic and environmental mechanisms underlying cognitive development was hardly settled with the same set of data (that is, the extent to which genetic and environmental effects are responsible for stability and change in cognitive development)! We agree with Eaves et al. that their (and to some extent all) models were “still far from all-embracing” (p.144), in part because of the assumption that genetic and environmental components operate orthogonally to one another.

P=>E models matter because they model developmental processes from an ecological perspective rather than purely statistical perspectives. A basic tenet of P=>E transmission models is that genes require corresponding supportive environments to have influence on development (Bronfenbrenner & Ceci, 1994). In other words, genes without sufficient match to suitable environments lose influence on development (Fischbein, 1978; Tucker-Drob, Rhemtulla, Haren, Turkheimer, & Fask, 2011; Turkheimer, Beam, Finkel, & Davis, this issue; Turkheimer, Haley, Waldron, D’Onofrio, Gottesman, 2003). P=>E models incorporate matching processes between people and their environments that give rise to gene-environment covariance (CovGE), a measure of the match between genes and environments. People select their environments, and environments evoke consistent behavioral responses from people that reinforce specific behaviors. The inclusion of CovGE in longitudinal twin models adds considerable complexity to twin models and has been mostly futile: “The fact that so many attempts to specify CovGE have come to grief is because their authors have thought in statistical rather than biological terms” (p.7, Eaves, Krystyna, Martin, & Jinks, 1977). P=>E models better approximate these biological terms, but the difficulty lies in the violation of basic statistical assumptions of conventional twin models – that is, the widely accepted (though fundamentally wrong) assumption that genetic and environmental effects are independent sources of developmental influence. We address how violation of the independence assumption complicates the interpretation of environmental components later in this report.

Different P=>E transmission models

Others have developed and applied longitudinal P=>E models to child cognitive and psychiatric twin data from the Netherlands Twin Registry to explain how biosocial processes produce behavioral diversification (de Kort et al., 2014; Dolan, de Kort, van Beijsterveldt, Bartels, & Boomsma, 2014). While a study that compares and contrasts each P=>E version would be fruitful for understanding how people select environments and how environments evoke behavior, such a study falls outside the scope of the current report on reviving the LTS. The version we present in the following report, however, differs from their version (hereafter referred to as the “NTR-P=>E”) in 2 key ways. First, we use a multilevel structural equation modeling (ML-SEM) approach to keep the unit of analysis as the individual whereas the unit of analysis in the NTR-P=>E is the twin pair. When the unit of analysis is the twin pair, sibling effects (i.e., how a twin’s behavior influences a co-twin’s environment) can be modeled. While the ML-SEM we use does not permit sibling effects, ML-SEM provides a more straightforward approach to test within-individual niche picking that “gives rise to within-individual GE covariance, as it involves an individual’s choice or preference for certain environments, based on personal interest, talent, and personality” (p.82, de Kort, Dolan, & Boomsma, 2012).

Second, the ML-SEM P=>E approach we have developed only generates underlying within-family rGE estimates where it contributes to within-family differentiation. As there are no genetic differences between identical (MZ) twins, within-family niche-picking processes cannot generate rGE that would explain why one identical twin selects one environment whereas the co-identical twin selects a different environment. Only within-family genetic differences, transmitted indirectly via nonidentical (i.e., fraternal or DZ) twins’ (and siblings’) phenotypes, can produce within-family environmental differences in downstream development. The ML-SEM approach permits estimating P=>E effects that generate within-family rGE only in sibling groups where genotype is not perfectly correlated.

The “nonshared environment” in P=>E models

As noted above, P=>E transmission violates the independence assumption in twin models. Whereas genetic simplex models meet “the (nontrivial) assumption that genes and environment are independent, with the result that phenotypic variances and covariances are simply the sum of their genetic and environmental components” (p.145, Eaves et al., 1986), P=>E models do better at meeting the developmental assumption that “changes in individual development over the lifespan cannot be ascribed to singular causes (e.g., hereditary factors) operating in isolation” (p.347, Gottlieb, 2003). Better developmental models, however, complicate the interpretation of the latent variables in the model. Genetic simplex models and P=>E models, thus, make trade-offs between ease of interpretation and ecological validity, with P=>E being more ecologically valid than genetic simplex models but more difficult to interpret.

Under standard conventional genetic simplex models, the interpretation of the additive genetic, common (shared) environmental, and nonshared environmental factors are preserved. Nonshared environmental factors are interpreted as any environmental factor that makes identical twins from the same family dissimilar from one another, including measurement error. Despite efforts to distinguish nonshared environmental components from measurement error via latent variables and explicitly modeling measurement error (McGue & Christensen, 2002; Plomin & Spinath, 2004), the interpretation of the nonshared environment in P=>E models, however, is still less straightforward and offers a different challenge than taking measurement error into account. As de Kort et al. (2014) stated, “Statistically, the alternative P=>E model has the disadvantage of lacking orthogonality of the decomposition of variance, which complicates the interpretation of the variance components” (p.98), particularly at measurement occasions after the first.

No attempts, however, have been made to interpret nonshared environmental (NSE) factors in the context of CovGE in P=>E models. We present a simple and straightforward numerical method for interpreting nonshared environmental factors at measurements t >1 in P=>E models. The meaning of the nonshared environment in P=>E models (which we refer to as NSE’ hereafter) can be approximated by numerically comparing the model estimated NSE’ matrix to the nonshared environmental matrix in the genetic simplex model. The NSE’ matrix can be subtracted from the NSE matrix, with differences close to zero implying that the meaning of NSE’ is similar to the standard interpretation of NSE.

In the remainder of this paper, we present our reanalysis of the LTS cognitive ability data from ages 4–15 to test the alternative hypothesis that ML-SEM P=>E models provide superior fit to the data than a standard genetic simplex model. The underlying CovGE generated by the P=>E process would provide support for the reciprocal effects argument that individual niche selection explains behavioral diversification of nonidentical twins over time. We then examine the model estimated NSE’ matrix generated in the P=>E model to the model estimated NSE matrix generated in the genetic simplex model to draw conclusions about whether conventional interpretations of the nonshared environment hold in the context of P=>E transmission.

Method

Participants

The Louisville Twin Study began in the 1950s as the first longitudinal twin and family study to shed light on the heritability of rates of growth and age-related changes in physical, cognitive, and psychological development (Zonderman, 1986). Twins and their parents (as well as siblings) were recruited through Board of Health records in Louisville, Kentucky, with efforts made to recruit families representative of Louisville’s socioeconomic demography. Twins were brought in for cognitive testing at regular intervals from 3 months of age to approximately 15 years of age. Recruitment and data collection were ongoing in the LTS, with intermittent lapses in data collection due to funding crises. The last wave of measurement ended in 2003; a new wave of data collection has yet to restart with the majority of twins now middle-aged. Zygosity was determined through blood typing on 22 (or more) red cell antigens (Wilson, 1983).

For the present study, we used cognitive testing data (full-scale IQ scores) from 1,129 individual twins (554 MZ twins and 575 DZ twins) from 566 families (MZ pairs = 278; DZ pairs = 288). Missing data is an issue in the LTS, particularly in the latter study years. For the purposes of this report, we used any twins’ available FSIQ data (additional data have been recovered since NIA funded efforts in 2014 to resuscitate the LTS) and handled missingness with full information maximum likelihood estimation (FIML). It is worth noting, however, that FIML was implemented under the assumption that data were missing at random (MAR), however, missing data patterns are probably missing not at random (MNAR). With the resuscitation of the LTS, we plan to address missingness more thoroughly in future reports.

Ages of Measurement

Twins were initially recruited into the LTS at 3 months of age and tested every 3 months for the first year of life. Twins were tested every 6 months during their second and third years of life. Twins were tested annually from the ages of 4 to 9, with 3-year follow-up testing at ages 12 and 15. Exploratory data analysis suggested two discrete periods of development, potentially separated grossly by the twins transition to formal elementary school education: the first from 3 months to 3.5 years and the second from age 4 and beyond. As the focus of this report is to highlight the advantages of the LTS cognitive ability data to test the hypothesis that development occurs according to the reciprocal exchange between people and their environments (Beam & Turkheimer, 2013), we restricted our analysis to the 8 measurements from age 4 to age 15.

Measures of Mental Development

Wilson (1983) presented a thorough explanation of the measures of mental development used in the LTS, which we briefly summarize here. At ages 4, 5 and 6 years, twins were administered The Wechsler Preschool and Primary Scale of Intelligence (WPPSI; Wechsler, 1967). Twins measured later in the study were administered the McCarthy Scales of Children’s Abilities (McCarthy, 1972) at ages 4 and 5, as it captured a broader sample of children’s behavior than the WPPSI. The Wechsler Intelligence Scale for Children (WISC), and the revised version of the WISC (WISC-R; Wechsler, 1974) was administered at all other ages. All scores were standardized with a mean of 100 and a standard deviation of 15. The use of different intelligence scales means that slightly different cognitive ability constructs were measured over time. Developmental trends in FSIQ scores, thus, may be affected slightly by heterogeneity in the scales used to index cognitive ability.

Data Analysis

Descriptive statistics of the twins FSIQ scores were calculated at each age in R 3.2.0 (R Core Team, 2015) using the package “psych” (Revelle, 2015). Twin correlations were calculated at each age and plotted over time for MZ and DZ twins so that patterns of difference between each zygosity group could be compared. We then explored the stability of within-family differences in MZ and DZ twins’ FSIQ scores from ages 4 to 15. Twins were rank ordered within each family from lowest to highest FSIQ scores at age t. Means of twins with lower FSIQ scores (the “low” FSIQ twin) and twins with higher FSIQ scores (the “high” FSIQ twin) were calculated at age t and all subsequent waves. Mean longitudinal trajectories for the low and high twins were then plotted. The procedure was conducted at each age of measurement, resulting in 7 different trajectories (t – 1 measurements) to examine stability of within-family differences of FSIQ scores.

Next, we fit a genetic simplex model and P=>E models to the twins’ FSIQ data. We parameterized both models using ML-SEM, which wide-formats the twins’ repeated FSIQ measurements but nests each twins’ data within family (i.e., family data are in long format). At each age of measurement, twins’ FSIQ scores were decomposed into between-family and within-family genetic and environmental components based on twins’ degree of consanguinity according to standard mixed-effects (i.e., multilevel) approach (McArdle & Prescott, 2005). Genetic and environmental effects are estimated at the between-family level and the within-family level to model the genetic and environmental factors that contribute to twins’ similarity of development (between-family) and genetic and environmental factors that contribute to twins’ dissimilarity of development (within-family).

In the genetic simplex model (see Fig. 2), the 6 conventional twin assumptions are maintained. First, additive genetic (A) effects at each measurement, t, were decomposed between-family and within-family based on the assumption that MZ twins share 100% of their genotype and DZ twins share 50% of their genotype, on average. The total A effect is divided into between-family (A^b) and within-family (A^w) genetic effects, with appropriate loadings assigned to each to meet the proportion of genotype shared between by twin pairs. A^b constitutes the total A effect in the MZ group (there are no within-family genetic differences) whereas A^b and A^w each contribute one-half of the total A effect in the DZ group.

Second, common environmental (E^b) effects at each measurement, t, constitute any between-family environmental process contributing to twins’ developmental similarity. Third, nonshared environmental (E^w) effects at each measurement, t, constitute any within-family environmental process contributing to twins’ developmental dissimilarity, including measurement error.

Fourth, A (that is, A^b + A^w), E^b, and E^w effects are assumed to be independent of one another. Fifth, the equal environments assumption assumes that E^b effects influence MZ and DZ twins’ trait similarity equally. Sixth, twins’ are the product of parents’ random mating.

The genetic simplex model (Fig. 2) correlates variables over time via first-order autoregressive (AR-1) effects between adjacent ages of measurement for the between-and within-family genetic and environmental factors (t > 1):

$$A_t^b=a_{\mathit{\text{ARt}},t-1}{A}_{t-1}^b+u{A}_t^b,\text{and}{E}_t^b=c_{\mathit{\text{ARt}},t-1}{E}_{t-1}^b+u{E}_t^b,\text{and}{A}_{\mathit{\text{it}}}^w=a_{\mathit{\text{ARt}},t-1}{A}_{\mathit{\text{it}}-1}^w+u{A}_{\mathit{\text{it}}}^w,\text{and}{E}_{\mathit{\text{it}}}^w=e_{\mathit{\text{ARt}},t-1}{E}_{\mathit{\text{it}}-1}^w+u{E}_{\mathit{\text{it}}}^w.$$

The autoregressive coefficients (a_ARt,t−1, c_ARt,t−1 and e_ARt,t−1) were constrained so that AR-1s were fit for the two different intervals between measurements (1-year and 3-year intervals). There were, thus, a total of 6 AR-1s estimated. All variances and disturbances (labeled $u{A}_t^b,u{E}_t^b,u{A}_{\mathit{\text{it}}}^w$, and $u{E}_{\mathit{\text{it}}}^w$ in Fig. 2) were freely estimated, with boundaries set to 0 to prevent estimation of negative variances. The AR-1s for $A_{\mathit{\text{it}}}^w$ were not estimated in the MZ group, as there is no within-family genetic variation.

In the P=>E model (see Fig. 3), 7 additional parameters were estimated in the DZ group to model the effect of within-family phenotypic differences on twins’ subsequent nonshared environmental effects. The P=>E parameters necessarily violate the fourth assumption of conventional twin models noted above by inducing within-family covGE. The P=>E effects are indicated by the regression paths labeled b_PE in Fig. 3 and are interpreted as the mean effect of twins’ total within-family phenotypic score at t −1 on the nonshared environment at t:

$$E_{\mathit{\text{it}}}^w=b_{\mathit{\text{PEt}},t-1}{P}_{\mathit{\text{it}}}^w+u{E}_{\mathit{\text{it}}}^w.$$

The effect was only estimated in the DZ group for the reason that b_PEt,t−1 is redundant with e_ARt,t−1 in the MZ group. (The within-family phenotypic variables are the nonshared environmental factors in the MZ group.) In the DZ group, P=>E is expected to contribute to increased stability of phenotypic differences of twins within the same family, above and beyond stability generated by the within-family genetic and nonshared environmental AR-1 process.

Finally, the P=>E parameters necessarily change the meaning of the nonshared environment at measurements t > 1 by indirectly correlating the $E_{\mathit{\text{it}}}^w$ components and the $A_{\mathit{\text{it}}}^w$ components, which can be verified by path tracing rules. We addressed the change in meaning of the nonshared environment by numerically comparing the model estimated NSE correlation matrix generated by the genetic simplex model to the NSE’ correlation matrix generated by the P=>E model. Differences between the matrices close to 0 suggest that inclusion of the P=>E parameter does not appreciably change the meaning of the nonshared environment when the independence assumption is violated.

All ML-SEM models were estimated in Mplus 7.3 (Muthén & Muthén, 2014) using FIML estimation to handle missing data. All models were overidentified. At the between-family level, there are 44 df available per zygosity group (88 df in total); at the within-family level, there are 36 df available per zygosity group (72 df in total). The genetic simplex model consisted of 28 between-family parameter estimates and 20 within-family parameter estimates. We estimated 2 separate P=>E models: a 7-parameter P=>E model and a 2-parameter P=>E model. The 7-parameter model allowed all P=>E to be freely estimated whereas the 2-parameter model constrained all P=>E pathways for 1-year measurement intervals to be the same and P=>E pathways for 3-year measurement intervals to be the same. As noted above, all P=>E parameters were estimated in addition to the parameters in the genetic simplex model and only at the within-family level in the DZ group.

Model fit was evaluated using the Root Mean Square Error of Approximation (RMSEA; Browne & Cudeck, 1992). The conventional model fit cutoff value of 0.05 was used to evaluate whether the model was “good” or not. Additionally, the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) were used to evaluate model fit (Burnham & Anderson, 2004). Both the AIC and BIC take into account the tradeoff between model parsimony and model complexity, with lower values indicative of better absolute model fit.

Results

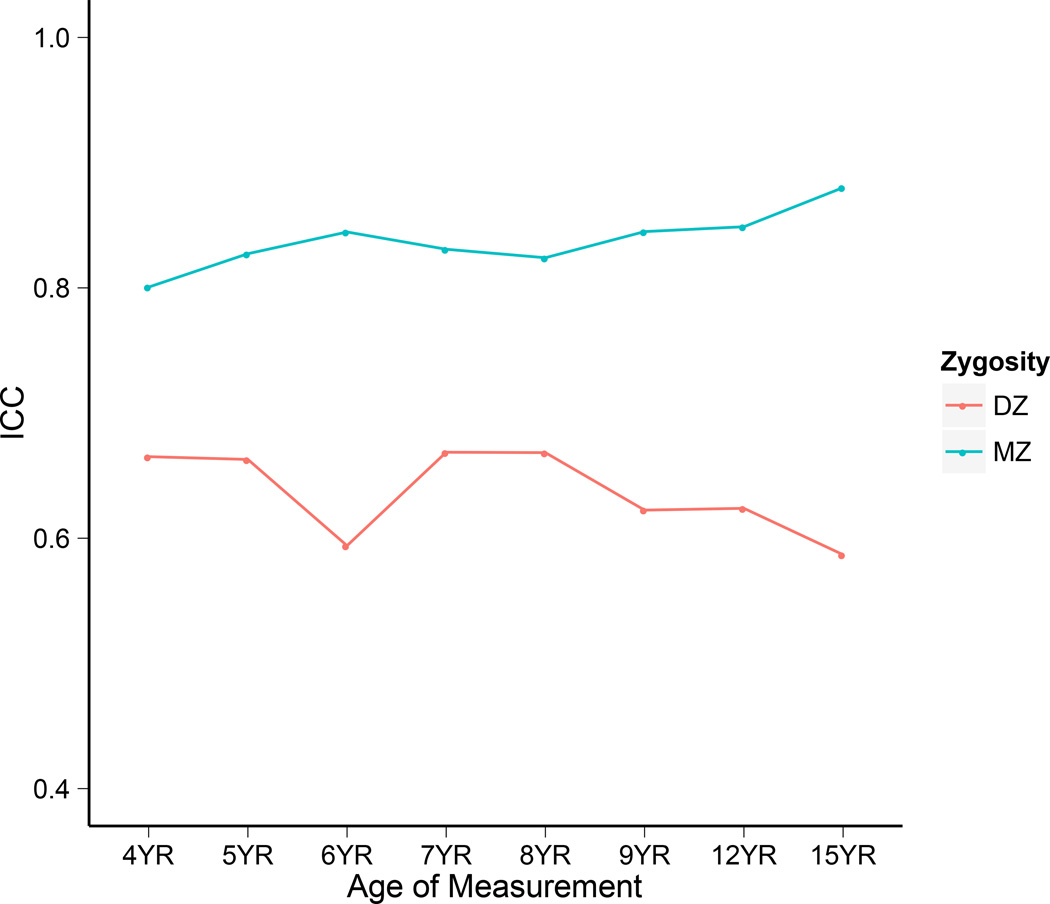
Table 1 presents the means and standard deviations of the FSIQ scores at each age of measurement. The standardized FSIQ scores approximately increase to the instrument standardized mean of 100 and SD of 15 after age 4. Fig. 4 presents a plot of the twin correlations. The MZ twin correlations are greater than DZ twin correlations, but not at least twice as great indicating the presence of total additive genetic (A) and common environmental (E^b) effects, in addition to nonshared environmental effects (E^W) on twins’ FSIQ scores. Comparison of the MZ and DZ twin correlations from ages 4 to 15 suggests that the MZ twins increase in similarity despite slight decreases in similarity at ages 6, 7, and 8 years. Conversely, the DZ twins decreased in similarity despite a single slight increase in similarity from age 6 to age 7. The divergence pattern between the MZ and DZ twin correlations over time suggests that the DZ twins may decrease in similarity because of differential exposure to environmental reinforcers (Fischbein, 1978), a pattern we have found to be captured by reciprocal effects processes that are not accounted for in genetic simplex models (Beam & Turkheimer, 2013).

Table 1.

Means and standard deviations of FSIQ scores from 4 to 15 years of age

Age of Measurement	Mean	SD	N
48 months (4 years)	90.84	15.07	829
60 months (5 years)	96.32	14.72	781
72 months (6 years)	100.45	13.65	783
84 months (7 years)	97.83	14.01	757
96 months (8 years)	101.68	14.20	848
108 months (9 years)	102.38	14.77	618
144 months (12 years)	99.16	14.40	182
180 months (15 years)	99.64	13.95	609

Figure 4.

MZ and DZ intraclass correlations (ICCs) of FSIQ scores from age 4 to age 15.

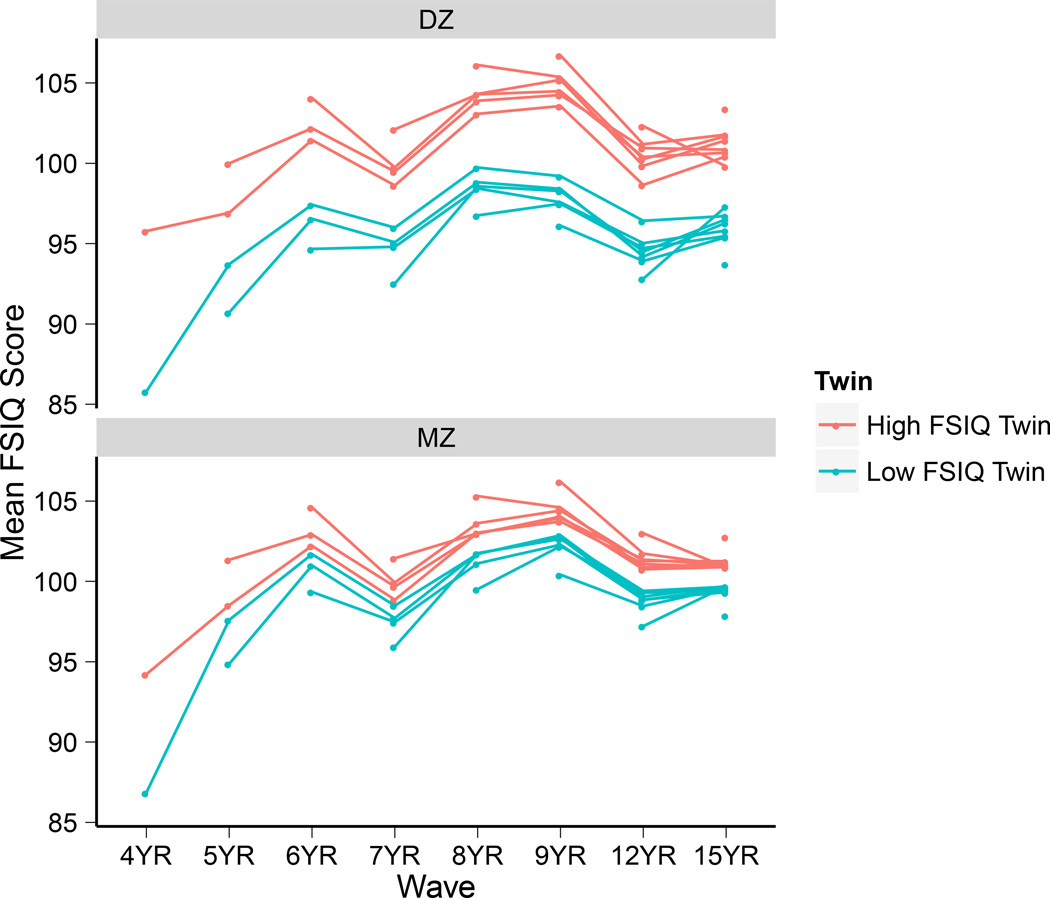
For space considerations, we do not present the raw longitudinal correlations. These correlations have been presented and analyzed elsewhere (Wilson, 1983) and reanalyzed (Eaves et al., 1986) to illustrate that the LTS FSIQ scores follow an autoregressive pattern from infancy through adolescence. Instead, we present the systematic relation of mean FSIQ scores from age 4 to age 15 of low FSIQ and high FSIQ twins raised in the same family (Fig. 5). We draw the reader’s attention to 2 features of the plot. First, low FSIQ and high FSIQ MZ and DZ twins appear to track one another closely, which illustrates Wilson’s (1983) developmental synchronies finding. Second, the low FSIQ and high FSIQ DZ twins do not follow the same course of development as closely as the MZ twins. Although the differences between the high FSIQ DZ twin and the low FSIQ DZ twin are not dramatic, they nevertheless demonstrate modest support for divergence between DZ twins’ scores over time. When combined with the divergence pattern of MZ and DZ twin correlations in Fig. 4, the tendency for the trajectories of the high FSIQ and low FSIQ DZ twins to diverge at times (often before reconverging, for example, see from 8 to 12 years in the line plot that begins at age 4 of the DZ twins) may be attributed to the tendency of twins to be matched to differentially supportive environments based on their within-family phenotypic differences.

Figure 5.

Stability of within-family differences in DZ and MZ twins’ FSIQ scores. At each wave, t, twins were rank ordered from low to high FSIQ scores within their families. Means at each wave ≥ t were calculated for “low” FSIQ and “high” FSIQ twins, and then plotted over time. The procedure was repeated until all t were exhausted.

We proceeded to test the P=>E model against a genetic simplex model to determine whether a reciprocal effects process captured the divergence patterns observed in Fig.4 and Fig. 5. There was one modification to the genetic simplex model that needs to be noted. In preliminary model fitting, a single common genetic factor fit the covariances among the genetic factors better than a model with 2 AR-1s (both AR-1s were greater than 1). There was 1 additional degree of freedom in all ML-SEMs (9 parameters rather than the 10 originally specified in the genetic simplex model). The 7 parameter P=>E model provided better fit to the FSIQ twin data than the genetic simplex model whereas the 2 parameter P=>E model did not provide better fit to the data than the genetic simplex model (Table 2).

Table 2.

Model fit of genetic simplex and P=>E models

Model	X2	df	Model Comparison	ΔX2	Δdf	p	RMSEA	AIC	BIC
1. Genetic Simplex	271.85	123	-	-		-	0.05	12349.50	12535.58
2. P<=>E model (7 parameters)	256.91	116	1	14.94	7	0.037	0.05	12348.57	12569.85
3. P<=>E model (2 parameters)	268.21	121	1	3.64	2	0.162	0.05	12349.86	12545.99

Note. RMSEA = Root Mean Square Error of Approximation; AIC = Akaike Information Criterion test; BIC = Bayesian Information Criterion test.

The ML parameter estimates are presented in Table 3. Three of the 7 P=>E parameters (b_PE) were significantly different from zero – b_PE60, b_PE96, and b_PE108. The two positive b_PE parameters indicate that the within-family phenotypic differences in FSIQ at one year of measurement predicted more disparate within-family environmental exposure at the subsequent year of measurement. Conversely, the negative b_PE108 parameter is interpreted as DZ twins converging toward one another at a rate faster than the MZ twins, a finding inconsistent with our hypothesis that the reciprocal exchange between twins and their environments would cause twins within the same family to diverge from one another over time.

Table 3.

Maximum likelihood parameter estimates

Parameter	FSIQ ML Estimate	S.E.
Variances
var(A)	0.91	0.12
var(A48)	0.33	0.07
var(uA60)	0.15	0.04
var(uA72)	0.02	0.02
var(uA84)	0.05	0.03
var(uA96)	0.02	0.02
var(uA108)	0.08	0.03
var(uA144)	0.01	0.03
var(uA180)	0.12	0.05
var(E48b)	0.70	0.14
var(uE60b)	0.07	0.06
var(uE72b)	0.03	0.03
var(uE84b)	0.16	0.03
var(uE96b)	0.06	0.02
var(uE108b)	0.01	0.02
var(uE144b)	0.14	0.04
var(uE180b)	0.01	0.04
var(E48w)	0.41	0.04
var(uE60w)	0.30	0.03
var(uE72w)	0.20	0.02
var(uE84w)	0.24	0.02
var(uE96w)	0.24	0.02
var(uE108w)	0.20	0.02
var(uE144w)	0.18	0.02
var(uE180w)	0.15	0.02
Autoregressions
Car (1-year)	0.96	0.02
eAR(1-year)	0.33	0.03
Car (3-year)	0.95	0.03
eAR (3-year)	0.60	0.05
P=>E Effects
bPE48	−0.02	0.05
bPE60	0.10	0.04
bPE72	−0.03	0.05
bPE84	0.04	0.05
bPE96	0.12	0.05
bPE108	−0.10	0.04
bPE144	0.06	0.05

The model estimated rGEs are provided in Table 4. The large standard errors suggest that these estimates are imprecise and should be interpreted with caution. The majority of estimates between A_Common and the nonshared environmental factors (column 1) are positive and consistent with implications of reciprocal effects models – people select into and are reinforced by environments that are positively correlated with their genetically-influenced phenotypes.

Table 4.

Model estimated gene-environment correlations (rGE)

	ACommon	A48	A60	A72	A84	A96	A108	A144	A180
E46	0	0	0	0	0	0	0	0	0
E80	−.02 (.06)	−.01 (.04)	0	0	0	0	0	0	0
E72	.11 (.06)	−.01 (.02)	.03 (.02)	0	0	0	0	0	0
E84	.00 (.08)	.00 (.01)	.01 (.01)	−.01 (.01)	0	0	0	0	0
E96	.06 (.07)	.00 (.00)	.00 (.00)	.00 (.00)	0.01 (.02)	0	0	0	0
E108	.18 (.07)	.00 (.00)	.00 (.00)	.00 (.00)	0.01 (.01)	.02 (.02)	0	0	0
E144	−.05 (.09)	.00 (.00)	.00 (.00)	.00 (.00)	0.00 (.00)	.01 (.01)	−.04 (.02)	0	0
E180	.05 (.09)	.00 (.00)	.00 (.00)	.00 (.00)	0.00 (.00)	.01 (.01)	−.03 (.01)	.01 (.01)	0

Note. Standard errors are given in parentheses. A = additive genetic factor; E = nonshared environmental factor; common = common factor.

Finally, we addressed whether inclusion of the P=>E parameters appreciably altered the meaning of the nonshared environmental factors. The model estimated NSE correlations generated by the genetic simplex model are presented in the lower triangles of Table 5 and Table 6 for the MZ and DZ twins, respectively. For clarity of presentation, we present the model estimated NSE and NSE’ correlations separately for MZ and DZ twins. The NSE correlations in the lower triangle of Table 5 and the lower triangle of Table 6 are the same and come from the genetic simplex model (Model 1). The correlations in the upper triangle of Table 5 and Table 6 come from the 7-parameter P=>E model (Model 2) and differ between the MZ and DZ groups because only the P=>E parameters were estimated in the DZ group. The difference between the NSE correlation matrix and the model estimated NSE’ correlation matrix generated by the 7 parameter P=>E model is presented in the upper triangle of the same tables. For both MZ and DZ twins, the differences are close to zero, suggesting that the numerical interpretation of the nonshared environment in the P=>E model is a good approximation of the analytic interpretation of the nonshared environment in conventional twin models that meet the independence assumption among genetic and environmental factors.

Table 5.

Model estimated NSE and difference between NSE and NSE’ correlations in the MZ twins

	E48	E60	E72	E84	E96	E108	E144	E180
E48	-	0.01	0.02	0.00	0.01	0.01	0.00	0.00
E80	0.37	-	0.01	0.01	0.01	0.00	0.00	0.01
E72	0.16	0.42	-	0.01	0.02	0.00	0.00	0.00
E84	0.05	0.14	0.33	-	0.02	0.01	0.00	0.00
E96	0.02	0.05	0.12	0.35	-	0.02	0.00	−0.01
E108	0.01	0.02	0.04	0.13	0.38	-	−0.02	−0.04
E144	0.00	0.01	0.02	0.07	0.20	0.54	-	−0.03
E180	0.00	0.01	0.01	0.04	0.12	0.32	0.60	-

Note. Values in the lower triangle are model estimated NSE correlations in the genetic simplex model. Values in the upper triangle are the difference between the model estimated NSE correlations in the genetic simplex model and the model estimate NSE’ correlations in the 7 parameter P=>E model (NSE – NSE’).

Table 6.

Model estimated NSE and difference between NSE and NSE’ correlations in the DZ twins

	E48	E60	E72	E84	E96	E144	E144	E180
E48	-	0.02	−0.01	0.00	0.00	0.00	−0.01	0.00
E80	0.37	-	−0.06	−0.01	0.00	0.00	0.00	0.00
E72	0.16	0.42	-	0.03	0.00	−0.03	0.00	−0.01
E84	0.05	0.14	0.33	-	−0.02	−0.04	−0.02	−0.02
E96	0.02	0.05	0.12	0.35	-	−0.09	−0.04	−0.04
E108	0.01	0.02	0.04	0.13	0.38	-	0.05	−0.02
E144	0.00	0.01	0.02	0.07	0.20	0.54	-	−0.05
E180	0.00	0.01	0.01	0.04	0.12	0.32	0.60	-

Note. Values in the lower triangle are model estimated NSE correlations in the genetic simplex model. Values in the upper triangle are the difference between the model estimated NSE correlations in the genetic simplex model and the model estimate NSE’ correlations in the 7 parameter P=>E model (NSE – NSE’).

Discussion

Wilson (1983) attributed the end point of cognitive development to genetic processes to a degree that he attributed people’s environments also to be genetically influenced. He concluded: “It is undoubtedly true that niche picking occurs, but it is important to note that it is driven by developmental genetic processes that propel each offspring in a particular direction” (p.312). Viewed from a reciprocal effects modeling framework ( Dickens & Flynn, 2001; Dickens, Turkheimer, & Beam, 2011), we submit that the match between people and their environments facilitates the genetic expression required to propel organisms in their particular directions (Bronfenbrenner & Ceci, 1994). The significant P=>E effects found in the 7-parameter model support the argument that people’s behavior (i.e., the cumulative effect of people’s genetic and environmental histories), not their genotype, shape their environments (Turkheimer, 2004) while at the same time these environments evoke from people increased behavioral responses.

Second, although developmental synchronization between LTS twins is well-documented in the LTS (Wilson, 1983), the current report highlights that twins also diverge from their family mean. In this way, the significant P=>E effects found in the ML-SEMs provide support for the first consequence of the reciprocal exchange between people and their environments. That is, this reanalysis of the LTS cognitive ability data indicate that P=>E effects partially explain within-pair divergence of the DZ twin twins at some moments from the ages of 4 to 15. Sibling synchronization and sibling drift are not mutually exclusive phenomena but occur in tandem. Even though twins traverse similar developmental trajectories, it appears that the smarter twin is a good degree more likely to remain the smarter twin over the course of child and adolescent development, as illustrated in Fig. 5. In other words, common familial backgrounds probably do make siblings alike, as Wilson already observed, but within the confines of the twins’ family, there is room for behavioral diversification attributed to person-environment matching processes.

While this reanalysis of the LTS provided some support for the first consequence of the reciprocal effects modeling framework, there was very modest support for the second consequence – that is, increasing rGE over time. The pattern of increasing rGE from ages 7 to 9 is in the predicted direction, but the standard errors of the correlations are large and unreliable. Thus, we cannot rule out the possibility that the significant rGE correlations we observed are a statistical artifact and not a true effect. The fact that de Kort et al. (2014) observed significant phenotype-to-environment effects in the cognitive scores of Dutch children, however, engender confidence that the generated rGE is a real effect but that we lacked power to detect small correlations.

Finally, we observed significant stable nonshared environmental differences over time in both the MZ and DZ twins attributed to a constant nonshared environmental effect and a first-order autoregressive process. While a consequence of reciprocal effects models is increasing nonshared environmental correlations over time, we cannot conclude that the stability of nonshared environmental effects is attributed to P=>E processes. The evidence against a reciprocal effects modeling framework consists of nearly equivalent model-estimated nonshared environmental correlation matrices with and without the presence of the P=>E parameter in the DZ twins. Person-environment matching should strengthen the correlation among environments as matching unfolds over time.

On the other hand, P=>E may produce twin drift away from the family mean despite relatively constant nonshared environmental differences. Statistically, the linear effects of P=>E processes are additive, not multiplicative. Thus, mean increases in cognitive ability mean of the high FSIQ twin (and corresponding decreases in the cognitive ability mean of the low FSIQ twin) may occur without corresponding increases among nonshared environmental correlations. Future research will need to uncover the conditions under which significant P=>E processes lead to greater observed pair difference regardless of increasing nonshared environmental correlations over time.

As others and we have pointed out elsewhere (Beam et al., de Kort et al., 2014; Dolan et al., 2014), P=>E effects necessarily change the meaning of the nonshared environmental factors. We provided a simple numerical check to evaluate whether P=>E alters the meaning of the nonshared environment by subtracting the model estimated NSE’ correlation matrix generated by the P=>E model from the model estimated NSE correlation matrix generated by the genetic simplex model without P=>E. The differences were near zero, which suggests that the traditional analytical meaning of the NSE seems to be well preserved in the context of P=>E estimation. Our conclusion, however, is not based on formal hypothesis testing of significant differences between the estimated NSE and NSE’ matrices and so should be interpreted cautiously. Future simulation studies on the effects of different magnitudes of P=>E parameters on estimated NSE matrices is needed to conclude whether the meaning of the nonshared environmental factors can be retained in the context of P=>E parameterization. For the time being, in cases where longitudinal twin researchers add P=>E effects in their models, we advise conducting this simple comparison between the model estimated NSE and NSE’ matrices to facilitate latent variable interpretation in the context of P=>E transmission.

The current reanalysis of the LTS cognitive ability data was completed as part of the recent resuscitation of the Louisville Twin Study. The major strength of this reanalysis 29 years after Eaves et al.’s (1986) study of same data is to move beyond developmental models that melt down phenotypic variance into the sum of genetic and environmental effects. The P=>E modeling approach used here addresses Eaves et al.’s limitation of a genetic simplex model that was “extremely simple” by adding parameters that capture the reciprocal exchange between people and their environments. The P=>E parameter adds subtle complexity meant to capture how people attempt to apply more control over their environments during development as well as react to environmental demands (Dickens & Flynn, 2001). The significant P=>E finding in the LTS is consistent with de Kort et al.’s (2014) analysis of cognitive development in the NTR. The increased nuance of P=>E models reveals that it is possible to incorporate transactional mechanisms in twin models that capture the genuine complexities of cognitive development.

The primary shortcoming of the current study is that we have reanalyzed a portion of the LTS cognitive ability data that possesses a large amount of missing data. The amount of missingness is made visible in Table 1 by the fluctuation in sample size across the ages of measurement. The resuscitation of the LTS, however, has uncovered a large portion of mental testing data that was collected but never entered for analysis, particularly at older ages where missingness is greatest. As these data are cleaned and become available for future analyses, we expect that the P=>E effects observed in this report will become more apparent.

Another limitation is that estimates of the environmental autoregressive structures and the P=>E effects for the 3-year age intervals may not be meaningful. The negative b_PE108 estimate, for example, should be interpreted with caution, as phenotypic behavior from 3 years prior may not bear much influence on current environmental exposure, particularly in the years between childhood and pre-adolescence.

A final limitation is that we did not explore sex differences in the P=>E models. There were two reasons we did not. First, neither Wilson (1983) nor Eaves et al. (1986) compared differences between male and female twins. In an effort to maintain an analytic framework to draw comparisons between their studies and ours, we chose not to test for sex differences. Second, for the reason that P=>E parameters are difficult to detect even in large samples (Dolan et al., 2014), we pooled gender to maximize the available power to reject the null hypothesis with P=>E included in the model.

The overall goal of this P=>E project is to explore the ecological niches people carve out for themselves at different developmental stages. Much of human experience is about gaining control of behavior (cognition, weight, anxiety, for example) to be more or less effective in life. The resuscitation of the LTS will help further the development of longitudinal twin models useful for advancing knowledge on cognitive and psychosocial developmental processes. Furthermore, the LTS population is now middle-aged, which poises us to collect follow-up data on the surviving study participants to shed light on how early developmental processes influence cognitive health and decline, adult psychopathology, and general well-being in the second half of the lifespan.