Large Cross-National Differences in Gene × Socioeconomic Status Interaction on Intelligence

Abstract

A core hypothesis in developmental theory predicts that genetic influences on intelligence and academic achievement are suppressed under conditions of socioeconomic privation and more fully realized under conditions of socioeconomic advantage: a Gene × Childhood Socioeconomic Status (SES) interaction. Tests of this hypothesis have produced apparently inconsistent results. We performed a meta-analysis of tests of Gene × SES interaction on intelligence and academic-achievement test scores, allowing for stratification by nation (United States vs. non–United States), and we conducted rigorous tests for publication bias and between-studies heterogeneity. In U.S. studies, we found clear support for moderately sized Gene × SES effects. In studies from Western Europe and Australia, where social policies ensure more uniform access to high-quality education and health care, Gene × SES effects were zero or reversed.

One of the most important, but contentious, topics of the nature-nurture debate is the source of individual differences in intelligence (Galton, 1869; Jensen, 1969). Historically, the debate pits a hereditarian perspective, which views individual differences in intelligence as primarily genetic, against a sociological perspective, which views such differences as primarily rooted in environmental experience. Reports of recovery from IQ deficits among children rescued from severely adverse circumstances (e.g., Nelson et al., 2007) support a role for environmental experience on intellectual development. Yet these findings are seemingly undermined by ubiquitous reports that heritability estimates from twin and pedigree studies of intelligence are large (Bouchard & McGue, 1981) and increase with age (Briley & Tucker-Drob, 2013), findings generally supported by heritability estimates from genome-wide data on unrelated individuals (Davies et al., 2011; Plomin et al., 2013). Understanding this apparent paradox is a central goal in research on cognitive development. One hypothesis that has been offered as a rapprochement between hereditarian and sociological views is that natural potentials for adaptive functioning are more fully expressed in the context of more nourishing environmental experiences (Bronfenbrenner & Ceci, 1994). Known as the Scarr-Rowe hypothesis of Gene × Socioeconomic Status (SES) interaction (Turkheimer, Harden, D’Onofrio, & Gottesman, 2009), it was originally described by Scarr-Salapatek (1971) as follows: “IQ scores within advantaged groups will show larger proportions of genetic variance and smaller proportions of environmental variance than IQ scores for disadvantaged groups. Environmental disadvantage is predicated [sic] to reduce the genotype-phenotype correlation in lower-class groups” (p. 1286).

The Scarr-Rowe hypothesis thus predicts that the heritability of intelligence will be lower among individuals raised under conditions of greater childhood socioeconomic disadvantage. The first support for this hypothesis came from a small sample of school-age Philadelphia, Pennsylvania, twins, for whom data on sex but not zygosity were available and for whom only census-level SES, not family-level SES, was available (Scarr-Salapatek, 1971). These findings were sharply criticized for methodological flaws, with Eaves and Jinks (1972) concluding that “evidence previously analysed is insufficient to support the conclusions drawn” (p. 84). After a 28-year period of virtually no new research on the topic, Rowe, Jacobson, and Van den Oord (1999) reported higher heritability of vocabulary IQ at higher levels of parental education among a population-based American sample of adolescent twin and sibling pairs. Some subsequent U.S. research has replicated the interaction (Bates, Lewis, & Weiss, 2013; Harden, Turkheimer, & Loehlin, 2007; Tucker-Drob, Rhemtulla, Harden, Turkheimer, & Fask, 2011; Turkheimer, Haley, Waldron, D’Onofrio, & Gottesman, 2003). Other studies, however, have failed to replicate the finding (Bartels, van Beijsterveldt, & Boomsma, 2009; Kremen et al., 2005; Soden-Hensler, 2012; van der Sluis, Willemsen, de Geus, Boomsma, & Posthuma, 2008), including a study using the largest sample to date (Hanscombe et al., 2012).

A number of factors might explain the inconsistencies among findings. First, reports of Gene × SES interaction on IQ might be false positives resulting from poorly powered studies conducted against a backdrop of bias toward publishing and citing positive findings. Alternatively, Gene × SES interactions might be true effects, but researchers could fail to replicate them because of low power or poor methodology. Finally, multiple authors have suggested that Gene × SES interactions may differ in strength across different populations or societies (Bates, Hansell, Martin, & Wright, 2015; Bates et al., 2013; Hanscombe et al., 2012; Tucker-Drob, Briley, & Harden, 2013; Turkheimer & Horn, 2014). Those supporting this type of explanation have pointed to higher social stratification in access to education (Hauser, 1970) and relatively modest social health (Adler & Newman, 2002) and social-welfare support (DeNavas-Walt & Proctor, 2014) in the United States compared with Australia and Western Europe.

In this meta-analysis, we sought robust and reliable answers to three questions. First, does the range of studies from the United States support a positive estimate of Gene × SES interaction on achieved IQ? Second, do studies on participants outside the United States show a similar greater-than-zero Gene × SES effect? Third, can a single estimate adequately account for all of the observed effect sizes, or are separate estimates necessary to represent effect sizes from the United States and from Western Europe and Australia? To answer these questions, we collected the world’s literature on Gene × SES effects on IQ, undertaking or commissioning from the original authors a number of reanalyses of the data and uncovering previously unpublished studies.

Method

We conducted a meta-analysis of the world’s literature on Gene × SES interaction effects on cognitive ability, seeking to (a) determine the true effect size, (b) examine bias in reporting effects, and (c) examine moderators of effect size, including age of subjects, nation (United States vs. non–United States), test type (achievement or knowledge test score vs. intelligence test score), SES assessment (education, income, wealth, and occupational status), and year of publication. We used sophisticated methods for estimating random-effects meta-regressions in nested data (i.e., in a meta-analytic data set that contained multiple effect sizes per study). Because this methodology required that all effect sizes and standard errors be calculated using a consistent modeling approach, we typically (a) obtained the raw data and reanalyzed it ourselves, (b) were provided with parameter estimates from reanalyses by the original study authors (all authors contacted complied with our request), or (c) reanalyzed the published subgroup covariance matrices (see Table 1).

Table 1.

Studies of Gene × Socioeconomic Status Interaction Included in the Meta-Analysis

Study	Original report	Twin pairs	Effect sizes	Country	Phase of life	Data acquisition and analysis
Brisbane Adolescent Twin Study (BATS)	Bates, Hansel, Martin & Wright (2015)	1,176	1	Australia	Adolescence	Raw data were analyzed by current authors
Cognitive Ability, Self-Perceived Motivation, and School Achievement (CoSMoS)	Spengler, Gottschling, & Spinath (2011)	542	1	Germany	Adolescence	Data were reanalyzed by original authors
Early Childhood Longitudinal Study-Birth Cohort (ECLS-B)	Rhemtulla & Tucker-Drob (2012); Tucker-Drob, Rhemtulla, Harden, Turkheimer, & Fask (2011)	750	6	United States	Early childhood	Raw data were analyzed by current authors
Florida State Twin Registry (FSTR)	Soden-Hensler (2012)	466	1	United States	Middle childhood	Results were reported in original article
Midlife in the United States (MIDUS)	Bates, Lewis, & Weiss (2013)	851	1	United States	Adulthood	Raw data were analyzed by current authors
Minnesota Twin Family Study (MTFS)	Kirkpatrick, McGue, & Iacono (2015)	2,494	1	United States	Adolescence	Data were reanalyzed by original authors
National Collaborative Perinatal Project (NCPP)	Turkheimer, Haley, Waldron, D’Onofrio, & Gottesman (2003)	319	3	United States	Early childhood	Raw data were analyzed by current authors
National Longitudinal Study of Adolescent Health (Add Health)	Jacobson & Vasilopoulos, 2012; Rowe, Jacobson, & Van den Oord (1999)	1,909	2	United States	Adolescence and early adulthood	Data were reanalyzed by original authors
National Merit Twin Study	Harden, Turkheimer, & Loehlin (2007)	839	2	United States	Adolescence	Raw data were analyzed by current authors
Netherlands Twin Register–Adult (NTR-A)	van der Sluis, Willemsen, de Geus, Boomsma, & Posthuma (2008)	314	4	The Netherlands	Early and middle adulthood	Data were reanalyzed by original authors
Netherlands Twin Register–Child (NTR-C)	Bartels, van Beijsterveldt, & Boomsma (2009)	3,132	1	The Netherlands	Middle childhood	Data reported in article were reanalyzed by current authors
Swedish Twin Registry	Fischbein (1980)	215	2	Sweden	Middle childhood	Data reported in article were reanalyzed by current authors
Twins Early Development Study (TEDS)	Asbury, Wachs, & Plomin (2005); Hanscombe et al. (2012)	8,716	16	England	Childhood and adolescence	Data were reanalyzed by original authors
Vietnam Era Twin Registry (VET)	Grant et al. (2010); Kremen et al. (2005)	3,203	2	United States	Early and middle adulthood	Data were reanalyzed by original authors

Note: The number of twin pairs for van der Sluis et al. (2008) was approximated by dividing the reported number of individual participants by 2. The number of pairs for the ECLS-B was rounded to the nearest 50 in accordance with data-security regulations.

Study identification

We identified published studies of Gene × SES interaction on objective measures of intelligence and academic achievement by searching databases, reviewing citations to and in identified studies and citations from narrative reviews, and consulting with colleagues. We used Google Scholar to search for studies using combinations of the following search terms: twin, gene, socioeconomic status, education, income, achievement, intelligence, cognition, and interaction. Previous narrative reviews of this literature that we consulted were articles by Turkheimer and Horn (2014), Turkheimer et al. (2009), Nisbett et al. (2012), and Tucker-Drob et al. (2013). We also consulted a table of previous studies included in Hanscombe et al. (2012).

Through consulting with colleagues, as well as reviewing recent abstracts from the meetings of the Behavior Genetics Association and the International Society for Intelligence Research, we additionally identified a number of unpublished findings. K. C. Jacobson (a coauthor of an article by Rowe et al., 1999) conducted a Gene × SES analysis of a later wave of the National Longitudinal Study of Adolescent Health (Jacobson & Vasilopoulos, 2012). E. M. Tucker-Drob (an author of articles by Tucker-Drob et al., 2011, and Rhemtulla & Tucker-Drob, 2012) conducted a Gene × SES analysis of a later wave of the Early Childhood Longitudinal Study-Birth Cohort (ECLS-B) data. Soden-Hensler (2012) reported Gene × SES results in an unpublished dissertation that we identified in our electronic literature search. T. C. Bates provided results from a manuscript submitted for publication (Bates et al., 2015). M. Spengler shared an unpublished manuscript (Spengler, Gottschling, & Spinath, 2011), and updated her analyses with additional data for the purposes of inclusion in the current meta-analysis.

Inclusion and exclusion criteria

Studies included in the final meta-analytic data set are listed in Table 1. To qualify for inclusion in our meta-analysis, studies needed to meet the following five criteria. First, intelligence or achievement had to be continuously measured using an objective performance-based test or tests. Second, inference of genetic influence had to be made using siblings (preferably twins) with varying degrees of genetic relatedness. Third, the degree of genetic relatedness had to be known to a high degree of certainty (for twins, this meant that zygosity was diagnosed through either physical similarity ratings or genotyping). Fourth, an ordered categorical or continuous measure of family SES during childhood (a single or composite measure of parental education, family income, or parental job prestige) had to have been examined as a moderator of genetic variance in intelligence or achievement. Finally, participants could not have been specifically selected on the basis of their psychiatric or medical diagnoses, patient status, or (low or high) intelligence or achievement test scores. Thus, studies were excluded if (a) they used a categorical measure of intelligence or achievement; (b) the measure of intelligence or achievement was not derived from an objective test or tests; (c) only sex, but not genetic relatedness or zygosity information, was available for the twin pairs; (d) only adulthood SES was measured; (e) SES was measured at the school or neighborhood level but not at the family level; or (f) participants were selected on the basis of their test scores, medical or psychiatric diagnoses, or patient status. We did not exclude studies on the basis of the age at which intelligence or achievement was measured.

When the original studies reported separate effect sizes for each of multiple cognitive measures, we included the effect sizes for each measure. When studies reported effect sizes for multiple measures of SES, we used the effect sizes associated with the composite SES measure, if available. If a composite measure was not available, we used effect sizes associated with parental education (midparent education was preferred to maternal or paternal education) or family income. If both parental education and family income were available, but a composite score was not, we used effect sizes from both. We made one exception for the Twins Early Development Study (TEDS) sample (Hanscombe et al., 2012), which used three different SES measures from three different waves of data collection (composite of parental education and occupation at 18 months and 7 years, and income at 9 years). Because each measure provided information about SES during a different period of childhood, we deemed it best to retain effect sizes from all three SES indices.

Excluded studies

Some notable examinations of Gene × SES interaction did not meet our inclusion criteria. Data from Scarr-Salapatek (1971) were excluded because the study relied on data from participants for whom only sex but not zygosity was available and for whom only census-level SES, but not family-level SES, was available.

Using kinship data from the National Longitudinal Survey of Youth (NLSY), Van Den Oord and Rowe (1997) relied on full siblings, half siblings, and cousins to estimate genetic effects on academic achievement at different levels of a variety of measured environments, including parental education. A classification algorithm was used to determine sibling types from indirect parentage information. Genetic inference in this design rested on comparisons between sibling types that differed markedly in some of the same variables that were hypothesized to be moderators of heritability. For instance, A. K. Cheung, Harden, and Tucker-Drob (2014) report that, in the NLSY data set, full siblings, compared with half siblings, were nearly twice as likely to be Caucasian and over twice as likely to have college-educated parents. We therefore decided that the NLSY kinship data were not appropriate for examining Gene × SES interaction.

Nagoshi and Johnson (2005) examined SES differences in familial resemblance for cognitive abilities in the Hawaii Family Study of Cognition. However, as these authors did not capitalize on data from relatives of different degrees of genetic relatedness or from adoptees, their data could not be used to distinguish genetic from environmental sources of familial variance.

Friend, DeFries, and Olson (2008) and Friend et al. (2009) tested for differences in the heritability of categorical outcomes: reading disability and high reading ability, respectively. The samples employed in these studies were also specifically selected on the basis of the outcome under study, that is, at least one twin meeting criteria for proband status, and were thus excluded from our meta-analysis.

Finally, in a poster presented at the 2014 Behavior Genetics Association meeting, Prescott, McArdle, Achorn, Kaiser, and Lapham (2014) estimated biometric models of Gene × SES interaction using archival twin and sibling data from Project Talent of 1960. However, we excluded their findings because, as in Scarr-Salapatek (1971), only sex, not zygosity, was available from participants, and genetic inference required reliance on differences in intraclass correlations across same-sex twins, opposite-sex twins, and nontwin siblings.

Obtaining effect-size estimates

Because our analysis plan required that the results from each study be estimated from the same model, we often either reanalyzed data to which we had access or obtained reanalyzed data from the original study authors. For each study, we obtained a full set of parameter estimates and associated standard errors for an untrimmed version of Purcell’s (2002) biometric model of latent Gene × Measured Shared Environment interaction, where the measured shared environment is the SES index, and the phenotype is the index of intelligence or achievement. This model, displayed in Figure S1 in the Supplemental Material available online, is an extension of the standard ACE model, which decomposes phenotypic variation into additive genetic effects (A), shared environmental effects (C), and nonshared environmental effects (E). The parameters produced are the main effects of A, C, E, and SES, along with A × SES, C × SES, and E × SES interactions. These parameters are termed a, c, e, s, and a′, c′, and e′, respectively. Of central interest is the A × SES interaction, labeled a′. To ensure that effect sizes were placed on a metric that was comparable across studies, we z-transformed phenotypes and continuous SES measures (using the mean and standard deviation from data pooled across all twins and siblings of all relatedness types) prior to fitting the Purcell model.

For studies that provided separate mean and covariance matrices for each level of an ordered categorical SES variable, we used parametric cross-group constraints to obtain estimates of a, c, e, s, a′, c′, and e′ that were directly comparable with those obtained from the Purcell (2002) model applied to continuous SES data. To do this, we determined the SES z score for each discrete group by using the proportion of participants in each category to calculate normal distribution thresholds for group membership, and then computing the mean z score between the calculated thresholds following the assumption of a continuous normal underlying SES distribution. This assumption was reasonable because the studies that did employ continuous measures of SES typically transformed their SES measure to normality if it was not already approximately normally distributed.

Conducting a meta-analysis of effect sizes

After compiling a meta-analytic database of study-specific effect sizes, we fit random-effects meta-regression models in Mplus (Muthén & Muthén, 2012) using the general procedure described by M. W. L. Cheung (2008), separately for each parameter of interest (a, c, e, s, a′, c′, and e′). Random-effects models do not require the traditional assumption that all effect sizes were derived from the same population with a single true effect size. Rather, they allow for population variation in the true effect size above and beyond variation attributable to sampling error. In practice, this means that standard errors and significance levels for meta-analytic parameters for random-effects models are more conservative than they would be for fixed-effects models. We included multiple effect sizes per sample (e.g., for different intelligence measures, different waves, or different measures of SES), weighted meta-regression models by the reciprocal number of effect sizes included for the corresponding sample and by the inverse of each parameter’s sampling variance, and implemented a sandwich estimator that corrects standard errors for nonindependence of data points derived from the same sample.

Results

Summary of meta-analytic data set

As displayed in Table 1, our meta-analytic data set consisted of 43 effect sizes from a total of 24,926 pairs of twins and siblings (approximately 50,000 individuals) participating in 14 independent studies. Data were relatively evenly split across U.S. (18 effect sizes, 8 studies, 10,831 twin or sibling pairs) and non-U.S. (Western Europe and Australia; 25 effect sizes, 6 studies, 14,095 twin or sibling pairs) samples. Because all variables were placed on a z scale, the magnitude of the Gene × SES interaction parameter (a′) represents the expected difference in the regression effect of the additive genetic factor on intelligence for each standard-deviation difference in SES.

Gene × SES effects in U.S. and non-U.S. samples

In an unconditional meta-analytic model, the meta-analytic mean for the Gene × SES interaction was nonsignificant (a′ = .029, SE = .019, p = .136), but there was substantial heterogeneity in the effect (the standard deviation of the random effect was .048; SE = .019, p = .011). When a dummy-coded nation variable (0 = non–United States, 1 = United States) was added to the metaregression model, there was a significant difference between Gene × SES effect sizes from the United States compared with those from Western Europe and Australia (b = 0.101, SE = 0.032, p = .001). There was a significant Gene × SES effect for U.S. studies (a′ = .074, SE = .020, p < .0005) but a trivial and nonsignificant Gene × SES effect for non-U.S. studies (a′ = −.027, SE = .022, p = .223). In this model, the standard deviation of the random effect was .029 (SE = .012, p = .022), which indicates residual heterogeneity in the Gene × SES effect. Estimates from this model, as applied to all seven parameters, are presented in Table 2.

Table 2.

Meta-Analytic Results: Estimates From Meta-Regression Models for all Structural Equation Model Parameters

Meta-regression parameter	s	a	a′	c	c′	e	e′
United States	.300 (.027)	.636 (.044)	.074 (.020)	.548 (.070)	−.046 (.032)	.479 (.033)	−.025 (.016)
Europe	.280 (.022)	.672 (.045)	−.027 (.022)	.507 (.052)	−.029 (.012)	.471 (.034)	.063 (.065)
Difference	.020 (.033)	−.036 (.065)	.101 (.032)	.042 (.086)	−.017 (.028)	.008 (.047)	−.088 (.068)
τ	.073 (.016)	.097 (.013)	.029 (.012)	.158 (.018)	.007 (.195)	.115 (.018)	.137 (.069)

Note: The bottom row (τ) shows the standard deviations of the random effects, which represent residual heterogeneity in effect sizes. Standard errors are given in parentheses.

The source of residual heterogeneity in a′ primarily stemmed from the non-U.S. studies (τ = .033, SE = .017, p = .047). Among U.S. studies, heterogeneity was not significant (τ = .014, SE = .040, p = .735). Post hoc analysis revealed that, exclusive of effect sizes from The Netherlands, residual heterogeneity was nil in the non-U.S. group (τ = .005, SE = .517, p = .993), and there continued to be a significant difference between Gene × SES effect sizes from the United States compared with those from Western Europe and Australia (b = 0.069, SE = 0.012, p < .0005). The model excluding studies from The Netherlands still indicated that there was a significant Gene × SES effect for U.S. studies (a′ = .068, SE = .021, p = .001) but no Gene × SES effect for non-U.S. studies (a′ = −.001, SE = .033, p = .979).

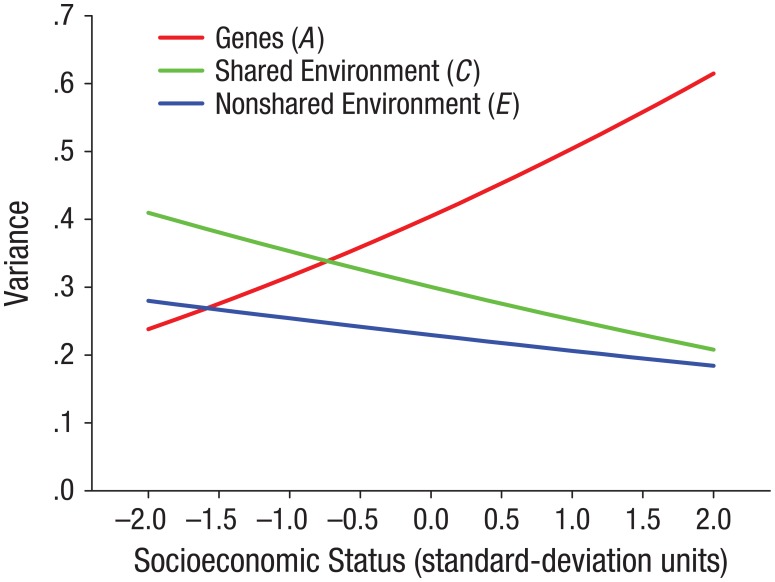
Figure 1 presents genetic and environmental variance components as a function of SES, as implied by the meta-analytic parameter estimates for the United States. Genetic variance in intelligence increases from .24 at 2 standard deviations below the mean SES to .61 at 2 standard deviations above the mean SES. As instantaneous proportions of variance, these correspond to heritability estimates of 26% at 2 standard deviations below the mean SES and 61% at 2 standard deviations above the mean SES. There is also some indication that the shared and nonshared environmental variance components decrease with SES, although these interactions were not statistically significant.

Fig. 1.

Variance in cognitive-test performance for the U.S. sample accounted for by genetic and environmental factors, graphed as a function of socioeconomic status (SES). Cognitive test scores were standardized to a z scale within each data set prior to model fitting. This plot is very close to (but not identical with) a plot in which the y-axis represents the instantaneous proportion of variance for each level of SES.

Additional moderator analyses

We next tested additional moderators of the a′ effect size. In our first moderation model, we compared effect-size estimates for studies that measured cognition in adulthood (ages > 20 years; 7 effect sizes) to those that measured cognition in childhood (ages < 20 years; 36 effect sizes). Because there were a small number of studies of adult cognition, we restricted the remaining moderator analyses to the childhood subsample. We examined each of the following study characteristics as moderators of the a′ effect size in turn, each time controlling for whether or not effect sizes came from U.S. samples: childhood age, single versus composite measure of SES, achievement or knowledge test score versus intelligence test score, and single measure of cognitive ability versus composite cognitive measure. None of these moderators was statistically significant. Results are presented in Table 3.

Table 3.

Results From the Additional Moderation Tests of the Gene × Socioeconomic Status (SES) Interaction (a′ Effect Size)

Meta-regression parameter	Moderation Model 1 (full sample)	Childhood subsample (age < 20 years)
		Baseline model	Moderation Model 2	Moderation Model 3	Moderation Model 4	Moderation Model 5
United States	.076 (.021)	.078 (.022)	.123 (.034)	.092 (.026)	.085 (.038)	.060 (.025)
Europe	−.026 (.022)	−.026 (.023)	.008 (.024)	−.009 (.017)	−.023 (.017)	−.028 (.023)
Difference	.102 (.032)	.104 (.035)	.114 (.034)	.101 (.034)	.108 (.043)	.087 (.037)
Older than 20 years	−.011 (.016)	—	—	—	—	—
Childhood age	—	—	−.003 (.002)	—	—	—
SES: single indicator (1) vs. composite (0)	—	—	—	−.031 (.031)	—	—
Test scores: Achievement or knowledge test (1) vs. intelligence test (0)	—	—	—	—	−.015 (.045)	—
Measure of cognitive ability: single (1) vs. composite (0)	—	—	—	—	—	.046 (.033)
τ	.029 (.012)	.033 (.013)	.030 (.013)	.031 (.012)	.032 (.012)	.027 (.016)

Note: The bottom row (τ) shows the standard deviations of the random effects, which represent residual heterogeneity in effect sizes. Standard errors are given in parentheses.

Finally, we examined whether there were childhood age differences in the a parameter, which represents the main effect of genes. Consistent with previous meta-analyses of Gene × Age interactions (e.g., Briley & Tucker-Drob, 2013; Haworth et al., 2009), there was significant support for age differences in the a and c parameters, which indicates that genetic variance increases and shared environmental variance decreases with age (Fig. S2 in the Supplemental Material). This finding, which replicates previously documented age trends in genetic and environmental variance components, indicates that studies in the current meta-analysis are representative of the wider literature.

Probing for publication bias

Funnel asymmetry

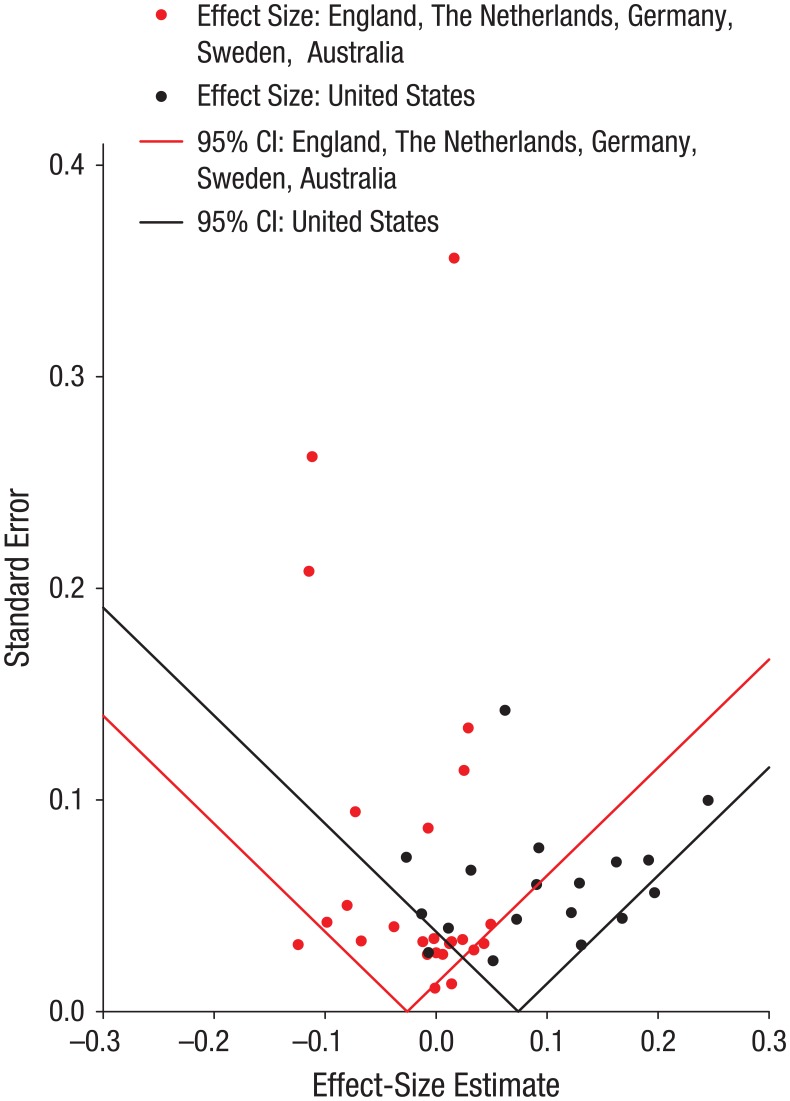
Figure 2 presents diagnostic funnel plots of Gene × SES interaction effect sizes, separately for U.S. studies and for European and Australian studies. This type of figure is named a funnel plot because when there is no (within-group) heterogeneity in population effect sizes, 95% of the meta-analytic effect sizes should fall within the inverted triangle-shaped region, with greater horizontal spread around estimates with higher standard errors. Biased reporting is indicated when data points are scattered asymmetrically around the point estimate; commonly, effects with large standard errors (i.e., studies with low power) will be conspicuously absent from the region of the funnel nearer to the null. Evidence for bias was lacking. The only conspicuously empty area of the U.S. funnel is toward the apex, which indicates an absence of effect sizes from U.S. studies with small standard errors. An alternative version of this funnel plot, with data points replaced by study acronyms, can be found in Fig. S3 in the Supplemental Material.

Fig. 2.

Funnel plot of effect-size estimates for the Gene × Socioeconomic Status interaction in the U.S. and non-U.S. samples. Each plotted point represents the standard error and effect-size estimate for a study included in the meta-analysis. The triangle-shaped regions indicate where 95% of the data points should lie if there is no (within-group) heterogeneity in population effect sizes. CI = confidence interval.

Formal tests of funnel asymmetry also revealed no evidence of publication bias. In the U.S. studies, neither the standard error nor the square standard error was related to a′ effect sizes, both when estimated with ordinary least squares (ps = .368 and .578, respectively) or weighted least squares (ps = .123 and .211, respectively, with the weighting based on the reciprocal sampling variance). Similarly, in the non-U.S. studies, neither the standard error nor the square standard error was related to a′ effect sizes, both when estimated with ordinary least squares (ps = .291 and .505, respectively) or weighted least squares (ps = .232 and .560, respectively, with the weighting based on the reciprocal sampling variance). In the entire meta-analytic data set, controlling for a dummy-coded variable representing U.S. versus non-U.S. studies, we found that neither the standard error nor the square standard error was related to a′ effect sizes, both when estimated with ordinary least squares (ps = .595 and .651, respectively) or weighted least squares (ps = .951 and .998, respectively, with the weighting based on the reciprocal sampling variance).

p-curve analysis

We submitted the a′ effect sizes to a p-curve analysis (Simonsohn, Nelson, & Simmons, 2014) using the online p-checker app (Schönbrodt, 2014), which tests whether the distribution of statistically significant p values is right skewed, as would be expected if the data reflect a true nonnull effect. In the absence of a right-skewed distribution (i.e., when the distribution of significant p values is either uniformly distributed or left skewed), one cannot rule out the null hypothesis of no true effect.

When only U.S. studies were entered into the p-curve analysis, p-checker indicated that the p curve was, in fact, right skewed, which indicates that these studies contain evidential value (z = −3.427, p < .001). It also indicated that the p curve was not flatter than one would expect if studies were powered at 33% (z = 1.253, p = .895). If significant, this would have indicated that results had no evidential value. Finally, there was no evidence of left skew (z = 3.427, p = 1.000), which would have indicated p-hacking or selective reporting.

In contrast, when only non-U.S. studies were entered into p-curve analysis, p-checker did not indicate significant right skew (z = −1.264, p = .103), which indicates that there was no evidence for a nonnull a′ effect outside of the United States. It also indicated that the p curve is not flatter than one would expect if studies were powered at 33% (z = .122, p = .548), and that there was no evidence of left skew (z = 1.264, p = .897).

Robustness checks

We conducted a series of further analyses to verify the robustness of our results. First, we ensured that the results persisted after removing effects sizes from the TEDS and the Minnesota Twin Family Study (MTFS; Kirkpatrick, McGue, & Iacono, 2015) from analyses. The TEDS, which uses a UK sample, was the largest sample in the meta-analysis and reported a null Gene × SES effect. The MTFS, which reported a significant Gene × SES result, was the second largest study from the U.S. studies included in the meta-analysis and reported the smallest standard error for the Gene × SES effect of all the U.S. studies. Thus, it was possible that the difference between results for Western Europe and Australia and results for the United States was simply driven by a difference between TEDS results and the U.S. results, or a difference between TEDS and MTFS results more specifically. We ruled these possibilities out. A model that excluded all effect sizes from TEDS still yielded a null Gene × SES effect in non-U.S. samples (a′ = −.052, SE = .035, p = .133), a significant Gene × SES effect in the U.S. sample (a′ = .076, SE = .019, p < .0005), and a significant difference between U.S. and non-U.S. studies for the Gene × SES effect (difference = .128, SE = .040, p = .002). A model that excluded all effect sizes from both TEDS and MTFS yielded a null Gene × SES effect in non-U.S. samples (a′ = −.052, SE = .034, p = .127), a significant Gene × SES effect in the U.S. sample (a′ = .083, SE = .023, p < .0005), and a significant difference between U.S. and non-U.S. studies (difference = .135, SE = .042, p = .001).

Second, we ensured that results persisted in a model that excluded effect sizes from our own primary investigations of Gene × SES interaction, specifically, those from the ECLS-B and the Midlife in the United States (Bates, Lewis, and Weiss, 2013) studies in the United States, which reported a positive Gene × SES effect, and those from the Brisbane Adolescent Twin Study (Bates et al., 2015) in Australia, which reported a null Gene × SES effect. This model yielded a null Gene × SES effect in non-U.S. samples (a′ = −.033, SE = .028, p = .240), a significant Gene × SES effect in the U.S. sample (a′ = .074, SE = .025, p = .003), and a significant difference between U.S. and non-U.S. samples (difference = .107, SE = .039, p = .006). A very similar pattern occurred when (rather than excluding our own primary investigations) we controlled for a dummy-coded indicator of whether results came from our own primary investigations.

Third, we ensured that results persisted in a model that excluded all effect sizes from primary investigations of Gene × SES interaction authored by Turkheimer, whose 2003 article is the most highly cited and reports the largest Gene × SES effect of all articles included in the meta-analysis. A model that excluded these effect sizes (reported in Harden et al., 2007; Tucker-Drob et al., 2011; Turkheimer et al., 2003) yielded a null Gene × SES effect in non-U.S. samples (a′ = −.027, SE = .022, p = .220), a significant Gene × SES effect in the U.S. sample (a′ = .058, SE = .020, p = .003), and a significant difference between U.S. and non-U.S. samples (difference = .085, SE = .030, p = .005). A very similar pattern was obtained when (rather than excluding primary investigations by Turkheimer) we used a dummy-coded indicator to control for whether results came from primary investigations by Turkheimer, and also when we controlled for a dummy-coded indicator of whether results came from primary investigations by Turkheimer, Bates, or Tucker-Drob.

In conclusion, all robustness checks indicated the presence of a significantly positive Gene × SES interaction in the United States but not in Western Europe and Australia, with the difference between U.S. and non-U.S. studies being statistically significant. These results cannot be attributed to a few select studies with either disproportionately large samples or disproportionately large (or small) effect sizes.

Cross-national differences in racial diversity

One possibility that we were unable to fully test in our meta-analytic data set is the extent to which the Gene × SES interactions detected in the United States were driven by the greater racial and ethnic diversity of the U.S. sample compared with the non-U.S. samples. Evidence from individual studies included in the meta-analysis, however, suggests that this is not the case. For instance, Tucker-Drob et al. (2011) reported that Gene × SES effects persisted in a nationally representative sample of American children even when race, and its interaction with the biometric components, was controlled. Additionally, Harden et al. (2007) reported evidence for Gene × SES interaction in a positively selected sample of U.S. adolescents that contained very few racial minorities. Kirkpatrick, McGue, and Iacono (2015) similarly report evidence for Gene × SES interaction in a sample containing very few Black and Hispanic participants.

Implications of meta-analytic effect-size estimates for reproducibility

Our meta-analytic finding of a Gene × SES interaction in the United States was based on a total sample size of more than 10,000 pairs of U.S. twins and siblings. It is instructive to estimate the minimum sample size necessary to achieve sufficient power to reproduce the Gene × SES interaction effect in the United States. We performed a simulation study in which we generated data using a model in which all effect sizes (s, a, c, e, a′, c′, and e′) were set to the meta-analytic estimates for the United States (reported in Table 2) and analyzed each data set with the unconstrained Gene × Environment model represented in our Figure S1 (Purcell, 2002). One-third of participants were assumed to be monozygotic, and two-thirds were assumed to be dizygotic (as would be expected in an unselected sample of same-sex and opposite-sex twins). We increased the sample size in increments of 100 pairs, conducting 100 replications per sample size, until at least 80 of the 100 replications produced an a′ estimate that was significant at p < .05 (i.e., power was estimated at a minimum of 80%).

Results indicated that a minimum of 3,300 twin pairs is needed to achieve at least 80% power. In contrast, when the same procedure was implemented using parameter estimates for Full-Scale IQ scores from Turkheimer et al. (2003), an early and highly publicized study that reported a much larger Gene × SES interaction than was indicated by the current meta-analysis, results indicated that a minimum sample size of only 500 twin pairs is needed to achieve at least 80% power. It therefore appears that the inconsistency of previous U.S. studies to replicate Gene × SES effects on intelligence may have stemmed from low power associated with overly optimistic expectations regarding the magnitude of the true interaction effect.

Discussion

This meta-analysis of published and unpublished data provided clear answers to our three questions. First, studies from the United States supported a moderately sized Gene × SES interaction on intelligence and academic achievement (a′ = .074; Fig. 1). Second, in studies conducted outside the United States (in Western Europe and Australia), the best estimate for Gene × SES magnitude was very slightly negative and not significantly different from zero. Third, the difference in the estimated magnitude of the Gene × SES effect between the U.S. and the non-U.S. studies was itself significant.

Beyond nation, we did not identify any other significant moderators of Gene × SES effects. We examined whether test performance was measured in childhood or adulthood, childhood age of testing, whether the tests measured either achievement and knowledge or intelligence, whether a single or composite indicator of SES was used, and whether the tests were of single ability or a composite cognitive measure. None of these additional moderators achieved statistical significance, and the cross-national difference in the Gene × SES effect remained when each of these possible moderators was entered into the meta-analytic model. Thus, the cross-national difference identified does not appear to be an epiphenomenon of cross-national differences in the age ranges examined or the particular intelligence or achievement outcomes measured.

We did not find evidence of publication or reporting bias in our meta-analytic data set. Both visual and formal tests of funnel-plot asymmetry were not significant, both when applied to the overall meta-analytic data set and when separately applied to effect sizes from U.S. and non-U.S. samples. Moreover, p-curve analysis, which is based on the shape of the distribution of p values for effect sizes surpassing the p < .05 significance threshold, indicated no evidence for p-hacking (i.e., questionable research practices). Consistent with the cross-national difference identified in our primary meta-analysis, p-curve analysis further showed evidential value for a nonzero Gene × SES effect in U.S. studies but did not reveal evidence for a nonzero Gene × SES effect in non-U.S. studies. Robustness checks indicated that results were not driven by a small number of studies with either disproportionately large samples or disproportionately large (or small) effect sizes. Variation in Gene × SES effect sizes in U.S. studies—ranging from near zero to extremely large—was no greater than would be expected by sampling variability alone.¹

We also replicated the well-established phenomenon that genetic influences on intelligence increase and shared environmental influences on intelligence decrease with childhood age (e.g., Briley & Tucker-Drob, 2013; Haworth et al., 2009). This replication further demonstrates that the studies that met inclusion criteria for our meta-analysis on Gene × SES effects are representative of the wider body of behavioral genetic research on intelligence. Interestingly, as can be seen by comparing Figures 2 and S2, these Gene × Age trends closely parallel the U.S. Gene × SES effect. Genes account for considerably more variation in intelligence both at higher ages and in higher U.S. socioeconomic contexts. Indeed, both phenomena may reflect a process of increased and accumulated effects of gene-environment transactions with the increased opportunity that comes with both social class and age (Tucker-Drob et al., 2013; Turkheimer & Horn, 2014).

The results indicate that Gene × SES effects are not uniform but can rather take positive, zero, and even negative values depending on factors that differ at the national level. The finding that low SES was associated with attenuated genetic influences on intelligence in the United States resolves an important debate. The finding that this interaction is observed only in the United States, together with the indication that the effect may even reverse in sign (The Netherlands), suggests that further research on between-nations variability in the effects of family SES on cognitive development is particularly important. Candidate mechanisms that might underlie such variability include national differences in how concepts of letter and number that underpin literacy and numeracy are imparted (Ramani & Siegler, 2008), educational quality more broadly (Taylor, Roehrig, Soden Hensler, Connor, & Schatschneider, 2010), medical and educational access (Bates et al., 2013; Tucker-Drob et al., 2013), and macrosocietal characteristics, such as upward social mobility (Ritchie, Bates, & Plomin, 2014) and income support (Duncan, Morris, & Rodrigues, 2011). Our results suggest that large-scale genetically informed research that incorporates careful measurement and consideration of both proximal and national social factors may provide a unique key to understanding the impact of specific policies on individual differences in intellectual development and academic achievement.