Abstract
We develop a multi-group epidemic framework via virtual dispersal where the risk of infection is a function of the residence time and local environmental risk. This novel approach eliminates the need to define and measure contact rates that are used in the traditional multi-group epidemic models with heterogeneous mixing. We apply this approach to a general n-patch SIS model whose basic reproduction number R0 is computed as a function of a patch residence-times matrix ℙ. Our analysis implies that the resulting n-patch SIS model has robust dynamics when patches are strongly connected: there is a unique globally stable endemic equilibrium when R0 > 1 while the disease free equilibrium is globally stable when R0 ≤ 1. Our further analysis indicates that the dispersal behavior described by the residence-times matrix ℙ has profound effects on the disease dynamics at the single patch level with consequences that proper dispersal behavior along with the local environmental risk can either promote or eliminate the endemic in particular patches. Our work highlights the impact of residence times matrix if the patches are not strongly connected. Our framework can be generalized in other endemic and disease outbreak models. As an illustration, we apply our framework to a two-patch SIR single outbreak epidemic model where the process of disease invasion is connected to the final epidemic size relationship. We also explore the impact of disease prevalence driven decision using a phenomenological modeling approach in order to contrast the role of constant versus state dependent ℙ on disease dynamics.
Keywords: Epidemiology, SIS-SIR Models, Dispersal, Residence Times, Global Stability, Adaptive Behavior, Final Size Relationship
1. Introduction
Sir Ronald Ross must be considered the founder of mathematical epidemiology [62] despite the fact that Daniel Bernoulli (1700-1782), was most likely the first researcher to introduce the use of mathematical models in the study of epidemic outbreaks [8, 28] nearly 150 years earlier. Ross’ appendix to his 1911 paper [62] not only introduces a nonlinear system of differential equations aimed at capturing the overall dynamics of the malaria contagion, a disease driven by the interactions of hosts, vectors and the life-history of Plasmodium falciparum, but also includes a tribute to mathematics through his observation that this framework may also be used to model the dynamics of sexually transmitted diseases [62]. Ross’ observation has motivated the use of mathematics in the study of the impact of human social interaction on disease dynamics [9, 18, 21, 23, 22, 34, 40, 45, 46, 47, 71]. In particularly, Ross’ work introduced the type of framework needed to capture and modify the dynamics of epidemic outbreaks; new landscapes where public policies could be tried and tested without harming anybody, complementing and expanding the role that statistics plays in epidemiology. Suddenly scientists and public health experts had a “laboratory” for assessing the impact of transmission mechanisms; evaluating, a priori, efforts aimed at mitigating or eliminating the deleterious impact of disease dynamics.
The study of the dynamics of communicable disease in metapopulation, multi-group or age-structure models has also benefitted from the work of Ross. Contact matrices have been used in the study of disease dynamics to accommodate or capture the dynamics of heterogeneous mixing populations [1, 19, 29, 38]. The spread of communicable diseases like measles, chicken pox or rubella is intimately connected to the concept of contact, “effective” contact or “effective” per capita contact rate [25, 38]; a clear measurable concept in, for example, the context of sexually transmitted diseases (STDs) or vector-borne diseases. The values used to define a contact matrix emerge from the a priori belief that contacts can be clearly defined and measured in any context. Their use in the context of communicable diseases is based often on relative rankings; the result of observational subjective measures of contact or activity levels. For example, since children are believed to have the most contacts per unit of time, their observed activity levels are routinely used to set a relative contact or activity scale. Traditionally, since school children are assumed to be the most active, they are used to set the scale with the rest of the age-specific contact matrix usually completed under the assumption of proportionate (weighted random) mixing (albeit other forms of mixing are possible [2, 9, 18, 20, 29, 38] and references therein). In short, mixing or contact matrices are used to collect re-scaled estimated levels of activity among interacting subgroups or age-classes; a phenomenological estimation process based on observational studies and surveys [59]. Our belief that contact rates cannot, in general, be measured in satisfactory ways for diseases like influenza, measles or tuberculosis, arises from the difficulty of assessing the average number of contacts per unit of time of children in a school bus, or the average number of contacts per unit of time that children and adults have with each other in a classroom or at the library, per unit of time. The issue is further confounded by our inability to assess what an effective contact is: a definition that may have to be tied in to the density of floating virus particles, air circulation patterns, or whether or not contaminated surfaces are touched by susceptible individuals. In short, defining and measuring a contact or an effective contact, turns out to be incredibly challenging [59]. That said, experimental methods may be used to estimate the average risk of acquiring, for example, tuberculosis (TB) or influenza, to individuals that spend on the average three hours per day in public transportation, in Mexico City or New York City.
In this paper we propose the use of residence times in heterogeneous environments, as a proxy for “effective” contacts per unit time. Catching a communicable disease would of course depend on the presence of infected/infectious individuals (a necessary condition), the level of “risk” within a given “patch” (crowded bars, airports, schools, work places, etc), and the time spent in such environment. Risk of infection is assumed to be a function of the time spent in pre-specified environments; risk that may be experimentally measured. We argue that characterizing a landscape as a collection of patches defined by risk (public transportation, schools, malls, work place, homes, etc) is possible, especially if the risk of infection in such “local” environments is in addition a function of residence times and disease levels. Ranking patch-dependent risks of infection via the values of the transmission rate (β) per unit of time, may therefore be possible and useful. The reinterpretation of β and the use of residence times move us away from the world of models that account for transmission via the use of differential susceptibility to the world where infection depends on local environmental risk.
Consequently, we introduce a residence times framework in the context of a multi-group system defined by patch-dependent risk (defined by β). We study the role of patch residence times on disease dynamics within endemic and single outbreak multi-group scenarios. Specifically, the study of the impact of patch residence times (modeled by a matrix of constants) on disease dynamics within a Susceptible-Infected-Susceptible (SIS) framework is carried out first, under the philosophy found in [10, 11, 13, 15, 17, 21, 34, 48]. Individuals move across patches as a function of their assessment of relative levels of infection in each area (studies using alternative classical approaches are found in [15, 16, 35, 69]). The concept of modeling disease dynamics where the population is structured into several communities goes back to Rushton and Mautner [63]. They considered an SI model with a constant population size in each community and derived solutions for their model. Multi-group models have surged in the literature to model sexually transmitted diseases. Lajmanovich and Yorke [56] proposed an SIS model in the study of gonorrhea in a heterogeneous population. They obtained conditions to prove the global stability of both the disease free equilibrium and the endemic equilibrium (EE). Nold [60] proposed some extensions, allowing a more general contact form, of the model in [56]. Other multi-group models with different settings (including differential infectivity in each group) have been considered in [30, 39, 49, 52, 53, 54, 57, 65, 67]. Hethcothe and Thieme [39] proved the uniqueness and the local stability of the EE if R0 > 1 for an SIRS multi-group model. Lin and So [57] proved the global stability of the EE if the effective contact rates between groups are small. Recently, authors in [30, 66] revisited the Lajmanovich and Yorke’s model [56]. Guo et al. in [32, 33] used a combination of Lyapunov functions and elements of graph theory to prove the global stability of the EE of an SIR and SEIR multi-group models. Shuai and van den Driessche [66] used a similar approach to study the asymptotic behavior of equilibria for some epidemic multi-group models. Typically, a sharp threshold property [66], for which the disease dies out if R0 ≤ 1 and persists if R0 > 1, holds if the transmission (and contact) matrix B = (βij)1≤i,j≤n is irreducible.
In this paper, we explore the disease dynamics when the residence times matrix ℙ could be irreducible or not. First, we prove that the irreducibility of the residence times matrix ℙ lead to a sharp threshold property. This property also holds when ℙ is replaced by the irreducible matrix ℙDℙt where D is a particular diagonal matrix and the residence times matrix ℙ could be rectangular. Then we study the disease dynamics at patch level by relaxing the irreducible condition on the residence times matrix ℙ. Generalizations are explored through simulations of the two-patch SIS model with state-dependent residence times within our framework. The results are compared to the disease dynamics generated by constant residence times. More specifically, the paper is organized as follows: Section 2 introduces a general n patch SIS model that accounts for residence times. Theoretical results on the role of residence times matrix (ℙ) on disease dynamics are carried out using the residence times dependent basic reproduction number R0(ℙ). The patch-specific reproduction numbers (ℙ), i = 1, …, n are defined to determine the disease persistence at the patch level. The usage of R0(ℙ) allows us to explore the cases when the network configuration of patches is the non-strongly connected. In addition, we also apply our framework to a SI model and a SIS model without demographics. Section 3 explores, through simulations, the dynamics of the SIS model under a state-dependent residence times matrix in a two-patch system; ℙ ≡ ℙ(I1, I2). That is, when the decisions to spend time in a patch are a function of patch-disease prevalence. Section 4 highlights our framework in the case of a two patch single outbreak SIR model following the work of Brauer [10, 17], and discusses the role of ℙ on the final epidemic size. Section 5 collects our observations, conclusions and discusses future work. The detailed proofs of our theoretical results are provided in the Appendix.
2. A general n-patch SIS model with residence times
A general n-patch SIS model with residence time matrix ℙ is derived. The global analysis of the model is carried out via the basic reproduction number R0. We also include patch-dependent disease persistence conditions.
2.1. Model derivation
We model disease dynamics within an environment defined by n patches (or risk areas) and so, we let Ni(t), i = 1, 2, …, n denote resident population at Patch i at time t. We assume that Patch i residents spend pij ∈ [0, 1] time in Patch j, with , for each i = 1, …, n. In extreme cases, for examples, we may have, for pij = 0, i ≠ j, that is Patch i residents spend no time in Patch j while (or equivalently pii = 0) would imply that Patch i residents spend all their time in Patch j (with j = 1, …, n and j ≠ i) even though their patch is (labelled) i. In the absence of disease dynamics, the population of Patch i residents is modeled by the following equation:
| (1) |
where the parameters bi, di represent the birth rate, and the natural per capita death rate in Patch i, respectively. Hence, the Patch i resident population approaches the constant as t→∞.
In the presence of disease, we assume that disease dynamics are captured by an SIS model, thus, the Patch i resident population is divided into susceptible and infected classes, represented by Si, Ii, respectively, with Si + Ii = Ni. We further assume that (a) there is no additional death due to disease; (b) the Patch i Infected resident population recovers and goes back to the susceptible class at the per capita rate γi; (c) the residence time matrix collects the proportion of times spent by i-residents in j-environments, i = 1, …, n and j = 1, …, n. The disease dynamics are therefore described by the following equations:
| (2) |
We model Si infection within Patch j in the following way:
- Since each pij entry of ℙ denotes the proportion of time that Patch i residents spent mingling in Patch j, we have that:
- – There are Nipij = Sipij + Iipij Patch i residents in Patch j on the average at time t.
- – The total Patch j, the total effective population is , of which are infected. Hence, the proportion of infected individuals in Patch j is and well defined, as long as there exists a k such that pkj > 0; so that the population in Patch j is nonzero.
-
Hence, the [Si infected per unit of time in Patch j] can be represented as the product of the following three items:The transmission takes on a modified frequency-dependent form that depends on how much time individuals of each epidemiological class spend in a particular area, and where βj differs by patch to reflect spatial differences in potential infectivity. More precisely, βj is assumed to be a patch-specific measure of disease risk per unit of time with its effectiveness tied in to local environmental and sanitary conditions. Therefore,
provided that there exists k such that pkj > 0.(3)
Model (2) can be rewritten as follows:
| (4) |
with, the dynamics of the Patch i resident total population modeled by the equation: (t) = bi − diNi(t), where Si + Ii = Ni, which implies that as t→+∞. Theory of asymptotically autonomous systems for triangular systems [24, 70] guaranties that System (4) is asymptotically equivalent to:
| (5) |
for i = 1, 2, …, n, with residence times matrix satisfying the conditions:
HP1. At least one entry in each column of ℙ is strictly positive; and
HP2. The sum of all entries in each row is one, i.e., = 1 for all i.
Remarks on Model (5)
Time scales: We assume that the disease dynamics occurs at the comparable time scale as to the demographic dynamics, and individuals enter or leave the patches at the relative faster time scale, e.g., daily, or even hourly. The case when there is no demographics in the context of a single epidemic outbreak scenario, has been considered in Section 4.
In our current modeling framework, we assume that the residence times matrix ℙ is a n×n matrix. This approach could generalize the concept of k social groups and l patches by letting n = max{k, l}, pij|i>k = 0 and pij|j>l = 0. The consequence of this generalization is that ℙ could have zero rows (when k < l = n) or columns (when l < k = n). The alternative treatment has been provided in the subsection 2.3 (thanks to the referee).
We do not assume that the residence times matrix ℙ being irreducible, instead, we assume that it satisfies relaxed conditions HP1-HP2. More specifically, we will explore the following two cases: (1) the global dynamics of Model (5) when the residence times matrix ℙ is irreducible; (2) the persistence of disease dynamics at the patch level under conditions of HP1 and HP2 in the following subsection which includes the scenario when ℙ is not irreducible.
2.2. Equilibria, the basic reproduction number and global analysis
To analyze the system, we investigate the basic reproduction number of the system with fixed residence times to better understand its properties in the absence of behavioral responses to risk. We let B = (β1, β2, …, βn)t define the risk of infection vector; βi a measure of the risk per susceptible per unit of time while in residence in Patch i.
Letting S = (S1, S2, …, Sn)t, I = (I1, I2, … In)t, and . Then System (5) can be rewritten in the following compact (vectorial) form:
| (6) |
with state space in . The set Ω = {I ≥ 0ℝn, I ≤ } is a compact positively invariant that attracts all trajectories of System (6). This implies that the populations involved are “biologically” well-defined since solutions of (6) will converge to and stay in Ω. We therefore restrict the dynamics of (6) to the compact set Ω.
The analysis of System (6) is naturally tied in to the basic reproductive number R0 [27, 68]; the average number of secondary cases produced by an infected individual during its infectious period while interacting with a purely susceptible population. R0 is given by (see the detailed formulation in Appendix):
| (7) |
where V = −diag(dI + γI), dI = (d1, d2, …, dn)t and γI = (γ1, γ2, …, γn)t.
The basic reproduction number R0 is used to establish global properties of System (6). For the relevant literature on global stability for multi-group or metapopulation models, see [5, 51, 55, 56, 65] and the references therein. We define the disease free equilibrium (DFE) of System (6) as I∗ = 0ℝn and the endemic equilibrium (when R0 > 1) as where all components are positive. By using the same approach as in [51, 56], we arrive at the following theorem regarding the global dynamics of Model (6).
Theorem 2.1.
[Global dynamics of Model (6)] Suppose that the residence times matrix ℙ is irreducible, then the following statements hold:
If R0 ≤ 1, the DFE I∗ = 0ℝn is globally asymptotically stable. If R0 > 1 the DFE is unstable.
If R0 > 1, there exists a unique endemic equilibrium which is GAS.
Remarks
The detailed proof of Theorem 2.1 is provided in Appendix B. These results imply that System (6) is robust, that is, disease outcomes are completely determined by whether or not the reproduction number R0 is greater or less than one. The results of Theorem 2.1 while powerful, do not provide easily accessible insights on the impact of the residence matrix ℙ on the levels of infection within each patch.
Direct insights on the effects of ℙ, are derived by focusing on the levels of endemicity within each patch. The following two definitions help set the stage for the discussion:
The basic reproduction number for Patch i in the absence of movement (pii = 1 or , SIS model, is defined as , which determines whether or not the disease will be endemic in Patch i. In short disease will die out if ≤ 1 with a unique endemic equilibrium, that is GAS, if > 1.
- The basic reproduction number associated with Patch i, under the presence of multi-patch residents, is defined as follows:
We explore the role that (ℙ) plays in determining the impact of all residents on disease dynamics persistence in Patch i in the following theorem.
Theorem 2.2.
[The endemicity of disease in Patch i] Assume that the residence times matrix ℙ satisfies Condition HP1 and HP2 but that some of its entries can be zeros.
If (ℙ) > 1, then the disease persists in Patch i.
- If the following conditions hold:
then we have
Thus, when Condition H holds and < 1, then endemic levels of disease cannot be supported in Patch i. That is,
Remarks
The detailed proof of Theorem 2.2 is provided in Appendix C. The results of Theorem 2.2 give insights on the role that the infection risk (measured by B) and the residence time matrix (ℙ) have in promoting or suppressing infection. Further, a closer look at the expression of the general basic reproduction number in Patch i, namely
leads to the following observations:
- The movement between patches, modeled via residence time matrix ℙ, can promote endemicity: For example, if ≤ 1, i.e., there is no endemic disease in patch i. Then, the presence of movement connecting Patch i to possibly all other patches can support endemic disease levels in the following ways:
- Via the presence of high risk patches, that is, there exists a patch j such that is large enough. For example, letting pkl = 1/n for all k, l with the total population in each patch being the same ( = K for all k; K a constant) then and consequently, if , then Patch i will promote the disease at endemic levels.
- Whenever individuals spend more time in high risk than in low risk patches. For example, in the extreme case, pij = 1 with , we have that (ℙ) > 1, and thus, endemic disease levels in Patch i can be supported. Patch j (j = 1, …, n and j ≠ i) can therefore be considered the source and Patch i (i ≠ j) the sink [3, 4, 5, 6, 55, 56, 65, 64].
- Under the assumption > 1, for an isolated Patch i, conditions that lead to disease extinction in the same Patch i under the movement can be identified. According to Theorem 2.2, Condition J should be satisfied and so the expression of (ℙ) reduces to
Therefore, the only way to have the value of (ℙ) be less than one, would be when the amount of time spent in Patch i is such that . Therefore, we conclude that the synergy between the residence time matrix ℙ and the existence of sufficient low risk patches (i.e., βj ≪ βi) can suppress a disease outbreak in Patch i.
2.3. Social groups versus patch environments
We assume that there are n social groups interacting in m different patch environments. Let pij be the proportion time of social group i spent at patch environment j, then the residence time matrix ℙ = is a n×m matrix. Following the same modeling approach of the system (5), Model 5 is rewritten as the following form:
| (8) |
where
Model (8) is isomorphic to those considered in [30, 32, 33, 66], which could be rewritten in the simplified form (6) as Model (5). Denote the disease transmission matrix B = (bik)1≤i,k≤n, then we also have the form of B = ℙdiag(B)diag()−1ℙt which is symmetric. We could see that Theorem 2.1 still holds if the irreducibility of ℙ is replaced by the irreducibility of B. We should also expect similar results of Theorem 2.2 for Model (8) when B is not irreducible.
The difference between the models in the aforementioned papers (e.g., [30, 32, 33, 66]) and our model (8) is that: In the former models, the disease transmission coefficient βij involves the contact rate between group j and group i, see the case of bilinear incidence [32, 33, 66] and proportional of βij for the frequency-dependent incidence [30, 32]. In our case, the disease transmission matrix B = (bik)1≤i,k≤n is symmetric and incorporates the environmental risks in different patches and the proportion of times that different social groups spent in each patch.
Now we apply the approach above to a SIS model without demographics and a SI model with the disease induced death rate ci for each social group i as follows.
- A SIS model without demographics (i.e., assume that the total population size Ni at each patch i is constant and the natural death rate di = 0) could be rewritten in the form of:
whose simplified form is(9)
where is symmetric, and G = (γiδik)1≤i,k≤n with δik being the Kronecker delta. The basic reproduction number of Model (9) is ρ(BG−1) which determines whether the disease persists or dies out. Both our theorem 2.1 and 2.2 could be applied to Model (9) - A SI model with the disease induced death rate ci for each social group i could be rewritten in the form of:
whose simplified for(10)
where C = (ciδik)1≤i,k≤n, and is still symmetric but depending on the total population size Nl in each patch. Notice that = −clIl, we expect the total population at each patch approaches zero as time is large enough. This is confirmed by simulations. Simulations also suggest that the infection dynamics have similar patterns as the prevalence of the SIR model studied in Section 4, and the limit of Ii(t)/Ni(t) goes to 1 for each patch as time is large enough.
3. Two patch models: state-dependent residence times matrix
We now extend the analysis of disease dynamics to the case where susceptible individuals respond to variations in risk in an automatic way. In particular, we consider the case when susceptible individuals make programmed responses to variations in disease risk, and do not choose their response to optimize an index of wellbeing (see for example [10, 13, 15, 17]). While this may not be a very good approximation of disease risk management in real systems, it enables us to explore the implications of certain types of phenomenologically modeled behavioral responses by assuming, for example, that the proportion of time spent in a particular patch depends on the numbers of infected individuals on that particular patch; that is ℙ ≡ ℙ(I1, I2).
Possible properties of the proportion of time spent by resident of Patch i into Patch j, i ≠ j, (pij) may include: increases with respect to the growth of infected resident in patch i (Ii), or decreases with respect to infected resident in patch j (Ij). Mathematically, we would have that
In a two-patch system, the use of the relationship pij (I1, I2) + pji(I1, I2) = 1, reduces the above four conditions on ℙ, to the following conditions:
Examples of functions pij(I1, I2) with these properties include,
and
where σij are such the .
More complex behavioral response formulations may also depend on the states of total populations N1 and N2, but the current specification captures important components of risk (infections) and allows us to retain the asymptotic equivalence property applied in the case of fixed residence times. Hence, using the same notation as in System (6) leads to the following two dimensional system with ℙ = ℙ(I1, I2):
| (11) |
where
and
where X(I1, I2), Y(I1, I2) and Z(I1, I2) are positive functions of I1 and I2.
The basic reproduction number R0 is the same as in the previous section since it is computed at the infection-free state, i.e.
where, in this case, we have that and σij = pij(0, 0), ∀{i, j} = {1,2}.
The properties of positiveness and boundedness of trajectories of System (6) are preserved in System (11). In addition, System (11) has a unique DFE equilibrium whose local stability is determined by the value of the R0: the DFE is locally asymptotically stable if R0 < 1 while it is unstable if R0 > 1.
Let us consider whether System (11) can have a boundary equilibrium such as (0, ) or (, 0). The assumption that System (11) has such a boundary equilibrium (0, ) with > 0 implies that Y(0, ) = 0. Since p11(0, I2) = and p22(0, I) = σ22, we deduce that
This indicates that Y(0, I2) = 0 if and only if σ21 = 0 and σ12 = 0, which requires that:
A similar arguments can be applied to the boundary equilibrium (, 0). Therefore, we conclude that System (11) will have a boundary equilibrium ((0, ) or (, 0)) only in the trivial case of isolated patches, that is, where there is no movement between two patches. This conclusion differs from the state-independent residence matrix model (6), since for example, the two-patch model (6), according to Theorem 2.1, boundary equilibrium (0, ) or (, 0) can exist when p11 = p22 = 0 (p12 = p21 = 1).
To illustrate the difference between the state-dependent residence matrix model (11) and the state-independent residence matrix model (6), we look at the situation when σ11 = σ22 = 0, σ12 = σ21 = 1 (p11 = p22 = 0, p12 = p21 = 0 for the state-independent residence matrix model (6)). Under the condition of σ11 = σ22 = 0, σ12 = σ21 = 1, we have Model (11), that
and
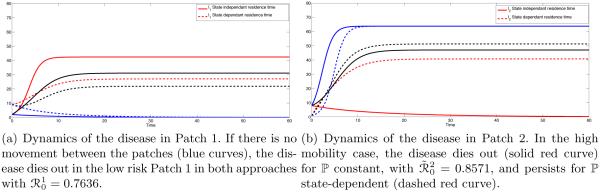
This difference has significant impact on disease dynamics (see Fig 1(a) and Fig 1(b), red curves).
Figure 1.
Coupled Dynamics of I1 and I2 for constant pij (solid) and state dependent pij (dashed). The red lines is case of high mobility, i.e. p12 = p21 = σ12 = σ21 = 1. The black lines represent the symmetric case, i.e: p12 = p21 = σ12 = σ21 = 0.5 and the blue line represent the polar case, i.e.: p12 = p21 = σ12 = σ21 = 0.
In Fig 1(b), we see that the infection in Patch 2 (high risk) persists in the state-dependent case whereas it dies out when ℙ is constant. That is due to the fact that pii(I1, I2) will not equal zero whereas pij (I1, I2) with i ≠ j may. For the constant residence times matrix, the dynamics of the disease in each patch is also independent, where people in patch i infect only susceptible in patch j with i ≠ j. In Fig 1(b) (red solid curve), we observe that the disease dies out in Patch 2 with = 0.8571. For the state-dependent case, unless there is no disease in both patches or one disease-free Patch, the proportion of time residents spend in their own patch is nonzero. This leads the disease to persist in both patches if R0 > 1 (see Fig 1(b), red dashed curves). However, even in this case, the disease dies out in both patches if R0 < 1 (See Fig 3, red curves, for instance).
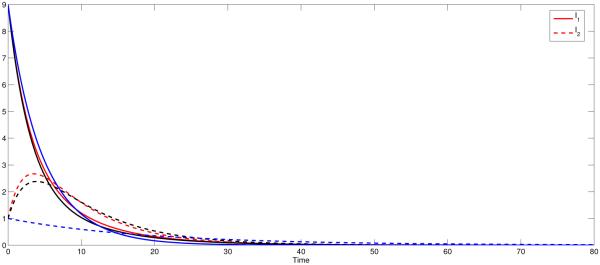
Figure 3.
Dynamics of I1 and I2 for varying σij for the state-dependent pij (I1, I2) where R0 < 1. This is obtained by using the values β1 = 0.2 and β2 = 0.3. In all the three cases, the disease dies out in both patches. The black curves represent the symmetric case (p12 = p21 = σ12 = σ21 = 0.5 ), the blue line represent the polar case (p12 = p21 = σ12 = σ21 = 0) and red curves represent high mobility case (p12 = p21 = σ12 = σ21 = 1).
3.1. Applications and comparisons: the two patch cases
The analytical results of the global dynamics on the asymptotic behavior of Model (11) are still unresolved. Hence, we ran simulations to gain some insights on the role of ℙ(I1, I2) on endemic dynamics. We observe that trajectories converge towards an endemic equilibrium whenever R0 > 1; however, there are substantial differences in the transient dynamics generated by state-dependent ∙(I1, I2) when compared to those generated with a constant residence times matrix.
Unless stated otherwise, we suppose the following generic values for the simulations: β1 = 0.3, β2 = 1.2, b1 = 9, d1 = 1/7, b2 = 9, d2 = 1/10 and γ1 = γ2 = 1/4. We carried out numerical simulation for a range of residence times matrices. It is observed that:
For the symmetric case where p12 = p21 = 0.5, the disease is endemic in both patches as predicted by Theorem 2.1 since R0 = 2.0466. For the state-dependent case, simulations suggest (Fig 1(a) and Fig 1(b), black dashed curves) that trajectories tend to be endemic in both patches. However, the level of endemicity is lower than the constant case in Patch 1 (low risk patch) and is greater in Patch 2 (high risk patch).
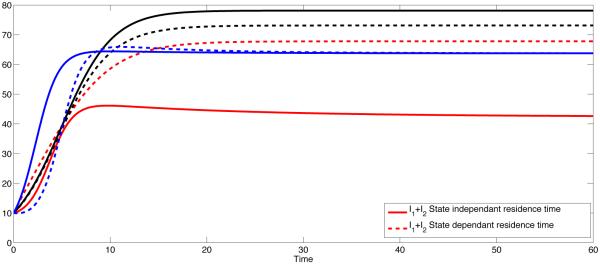
Fig 2 sketches the overall prevalence in both patches with three different scenarios of residence times matrix ℙ, both the constant and state-dependent case. The disease persists since the overall R0 > 1 in all three cases.
The case where there is no movement between patches, that is, p12 = p21 = 0 (p11 = p22 = 1) and σ12 = σ21 = 0 (or p12(I1, I2) = p21(I1, I2) = 0), corresponds to the case where the system behaves as two isolated patches. In this case the disease dies out or persists in Patch i if is above or below unity in both approaches. This is illustrated on Fig 1(a) and Fig 1(b) where the disease dies out in Patch 1 (Fig 1(a), blue solid line) where = 0.7636 and the disease persists in Patch 2 (Fig 1(b), blue solid curve) where = 3.4286. For the state dependent case (dashed blue curves on on Fig 1(a) and Fig 1(b)) the outcome is similar to the constant residence times case.
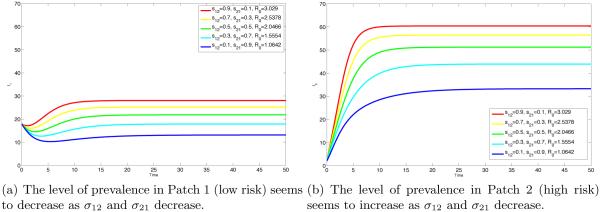
In Fig 4(a) and 4(b), we explore the cases where there is symmetry (σij = σji) with σij = pij (0, 0). We supposed in this case that Patch 2 has higher risk (β2 = 1.2) and Patch 1 has lower risk (β1 = 0.3). As can be intuitively deduced, the prevalence in Patch 1 is at its highest in the case of “high mobility” (σ12 = σ21 = 1), and decreasing as σij decreases (with i ≠ j). Conversely, prevalence in Patch 2 is at its highest under very “low mobility” (σ12 = σ21 = 0) and decreases as σij increases. Note that σij, with i ≠ j is proportional to pij (I1, I2) which is the actual residence time.
We continue to explore the asymmetric case (σij ≠ σji), that is, there is more mobility towards one patch. In Fig 5(a), the prevalence in Patch 1 (low risk) is at its highest if there is “high mobility” from Patch 1 to Patch 2 (σ12 = 1) and no mobility from Patch 2 to Patch 1 (σ21 = 0), the prevalence decreases along with σ12. If the programmed response of residents of Patch 1 is to reduce their mobility (σ12 = 0) then, even if the mobility of residents in the high risk Patch 2 is extremely high (σ21 = 1), still the prevalence in Patch 1 is at its lowest. Similar remarks hold for Fig 5(b) regarding the prevalence in Patch 2 (high risk) under different mobility schemes.
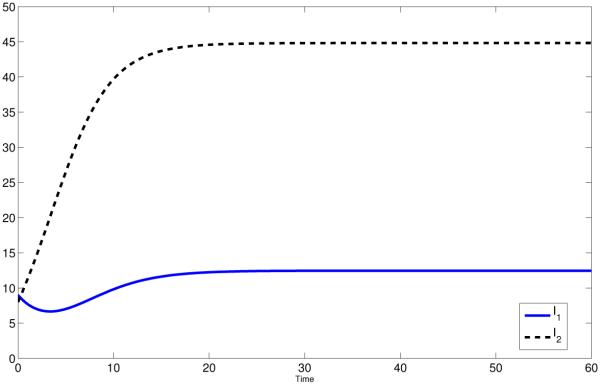
Finally, Figure 6 presents the dynamics of the infected in both patches for the (conventional) case where p12 = 0 (and p11 = 1). This case is particularly interesting since the residence time matrix ℙ is not irreducible (hence the hypothesis of Theorem 2.1 fails) but (ℙ) = 1.8929 > 1. As predicted by Theorem 2.2, the disease in Patch 2 is persistent. Also, it is worth noticing that in Fig 6, I1 persists as well even though (ℙ) = 0.4455 < 1, as the condition (ℙ) > 1, for i = 1, 2, is sufficient but not necessary for persistence in Patch i.
Figure 2.
Coupled Dynamics of I1+I2 for constant pij (solid) and state dependent pij (dashed). The overall prevalence is higher if the residence times is symmetric (solid and dashed black curves). The black curves represent the symmetric case (p12 = p21 = σ12 = σ21 = 0.5 ), and the blue lines represent the polar case (p12 = p21 = σ12 = σ21 = 0) and red curves represent high mobility case (p12 = p21 = σ12 = σ21 = 1).
Figure 4.
Dynamics of I1 and I2 for varying σij for the state-dependent pij (I1, I2) approach.
Figure 5.
Dynamics of and I1 and I2 for varying σij, but non-symmetric, for the state-dependent pij (I1, I2).
Figure 6.
Dynamics of I1 and I2 where p12 = 0. In this case the residence time matrix ℙ is not irreducible, the disease in Patch 2 persists nonetheless as predicted by the theorem 2.2.
4. Final epidemic size
The study of the role of residence time matrices on the dynamics of a single outbreak within a Susceptible-Infected-Recovered (with immunity) or SIR model without births and deaths is relevant to the development of public disease management measures [14, 26, 36]. Under the parameters and definitions introduced earlier, and making use of the same notation, we arrive at the following system of nonlinear differential equations:
| (12) |
where Ri denotes the population of recovered immune individuals in Patch i, αi is the recovery rate in Patch i and Ni ≡ Si + Ii + Ri, for i = 1, 2.
The basic reproduction number R0, is by definition the largest eigenvalue of 2×2 (n×n for the general case) next generation matrix,
It has been shown (see [37], for example) that not everybody gets infected during an outbreak, and so, estimating the size of the recovered population (the final epidemic size in the absence of deaths or departures) is tied in the solutions of the final size relationship, given in this case, by the system:
| (13) |
where
The relationship (13) is obtained by using the fact that, in (12), we have . This implies that limt→∞ Ii(t) = 0 (for i = 1, 2), since Si and Ii are positive and integrating Si in (12), we obtain, after some tedious algebra Expression (13). The references [10, 12] give more details on the computation of the final size relationship. We would like to point out that the next generation matrix and the matrix K defining the final epidemic size have the same eigenvalues.
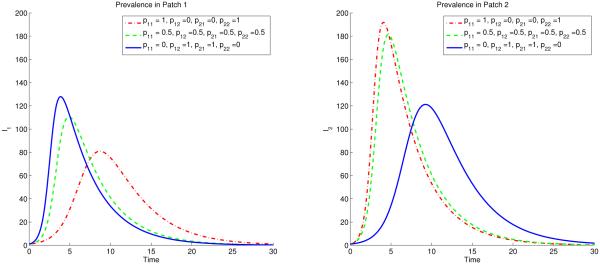
The residence time matrix ℙ plays an important role as evidenced by the dependence of the final epidemic size relation as in Fig 7. As we can notice in Fig 7, the prevalence in low risk Patch 1 is highest in the high mobility scheme where as in high risk Patch 2, the high mobility leads to the lowest prevalence. Also, as stated before ( Ii(t) = 0, for i = 1, 2) with any typical outbreak model, the disease ultimately dies out from both patches [38].
Figure 7.
The prevalence in patch 1 (low risk) reaches its highest when in extreme mobility case (solid blue line) and is lowest when there is no mobility between the patches. The opposite of this scenario happens in patch 2 (high risk).
5. Conclusion and Discussions
Heterogeneous mixing in multi-group epidemic models is most often defined in terms of group specific susceptibility and average contact rates captured multiplicatively by the transmission parameter β. However, contact rates, in general, cannot be measured in satisfactory ways for diseases like influenza, measles or tuberculosis, due to the difficulty of assessing the average number of contacts per unit of time of susceptible populations in different locations for varied activities. In this paper we propose the use of residence times in heterogeneous environments, as a proxy for “effective” contacts over a certain time window; and develop a multi-group epidemic framework via virtual dispersal where the risk of infection is a function of the residence time and local environmental risk. This novel approach eliminates the need to define and measure contact rates that are used in the traditional multi-group epidemic models with heterogeneous mixing.
Under the proposed framework, we formulate a general multi-patch SIS epidemic model with residence times. We calculate the basic reproduction number R0 which is a function of a patch residence-times matrix ℙ. Our global analysis shows that the model is robust in the sense that the disease dynamics depend exclusively on the basic reproductive number when the residence times matrix ℙ is “constant” (Theorem 2.1). We proved that the disease free equilibrium is globally asymptotically stable (GAS) if the basic reproduction number R0 ≤ 1 and that a unique interior endemic GAS equilibrium exists if R0 > 1. This results holds as long as the residence time matrix ℙ is irreducible, that is, the graph of the patches is strongly connected.
If the residence time matrix ℙ is not irreducible, that is, the network of the patches is not strongly connected, Theorem 2.1 does not apply. For these cases, our further analysis (Theorem 2.2) provides accessible insights on the impact of the residence matrix ℙ on the infection levels within each patch. Our results imply that the infection risk (measured by B) and the residence time matrix (ℙ) can play an important role in the endemicity at the patch level. More specifically, the right combinations of the environmental risk level (B) and dispersal behavior (ℙ) can either promote or suppress infection for particular patches. For example, we are able to apply Theorem 2.2 to the two patch case when residents of Patch 1 visit Patch 2 but not conversely. Theorem 2.2 allows us not only to characterize the patch-specific disease dynamics as a function of the time spend by residents and visitors to the patch of interest, but also to classify patches as sources or sinks of infection, a role that depends on risk (B) and mobility (ℙ).
The entries of residence times matrix ℙ could be prevalence dependent, i.e., not constant anymore. The disease dynamics are expected to be different than the cases when ℙ is constant. To explore these differences, we study a two patch model with the state-dependent residence times matrix ℙ, and assume that each entry pij (I1, I2) of the residence times P(I1, I2) is negatively correlated with the prevalence in Patch j. When the residence times P(I1, I2) is prevalence dependent, our analysis and simulations suggest that (1) its disease dynamics may be prone to persistent by comparing to the case when ℙ is constant (e.g. Fig 1, 2); and (2) the disease endemic level could be rather complicated (e.g. Fig 3, 4, 5, 6).
We have extended our framework to a two-patch SIR single outbreak model to explore how the residence time matrix ℙ may affect the final endemic size. We first derived the final epidemic size relationship in order to capture the size of the outbreak. Our analysis and simulations support that the residence time matrix ℙ plays an important role in the final epidemic size. For example, as observed in Fig 7, the prevalence in low risk Patch 1 is highest in the high mobility scheme where as in high risk Patch 2, the high mobility leads to the lowest prevalence.
In both conventional and phenomenological approaches to residence times used in this paper, humans behavior and responses to disease risk are automatic: ℙ is constant and predefined functions of health status. Recent studies [31, 42, 43, 44, 61] have incorporated behavior as a feedback response coupled with the dynamics of the disease. A model of the decision to spend time in patch i = 1, 2 based on individuals’ utility functions that include the possibility of adapting to changing contagion dynamics in the above two patch setting, using previous work [31, 58], is the subject of a separate study.
Acknowledgements
These studies were made possible by grant #1R01GM100471-01 from the National Institute of General Medical Sciences (NIGMS) at the National Institutes of Health. The contents of this manuscript are solely the responsibility of the authors and do not necessarily represent the official views of DHS or NIGMS. Research of Y.K. is partial supported by NSF-DMS (1313312). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. The authors are grateful to two anonymous referees for helpful comments and suggestions which led to an improvement of this paper.
Appendix A. Computation of R0
Proof
The general SIS model with residence time is described by the system (6)
The right hand member of the above system be can clearly decomposed as F + V where
The Jacobian matrix at the DFE of F and V are giving by:
The basic reproduction number R0 is given by the spectral radius of the next generation matrix −FV−1 [27, 68]. Hence, we deduce that
Appendix B. Proof of Theorem 2.1
The proof uses the method in [51] which is based on Hirsch’s theorem [41].
Theorem B.1 (Hirsch [41])
Let = F (x) be a cooperative differential equation for which is invariant, the origin is an equilibrium, each DF (x) is irreducible, and that all orbits are bounded. Suppose that
Then all orbits in tend to zero or there is a unique equilibrium p∗ in the interior of and all orbits in tend to p∗.
Proof of Theorem 2.1.
Equation (6) can be written as:
| (14) |
where F = diag()ℙdiag(B)diag()−1ℙt and V = −diag(dI + γI), as defined in Appendix A. Let us denote by X(I) the semi flow induced by (14). Hence
| (15) |
where W (I1, I2) = diag(ℙdiag(B)diag()−1ℙtI). Since ℙ is irreducible and I ≤ , DX(I) is clearly Metzler irreducible matrix. That means, the flow is strongly monotone. Plus, DX(I) is clearly decreasing with respect of I. Hence, by Hirsch’s theorem either all trajectories go to zero or go to an equilibrium point ≫ 0. From the relation (15), we have DX(0) = F + V where F and V are the one defined previously in Appendix A. However, since F a nonnegative matrix and V is Metzler, we have the following equivalence
where α(F + V) is the stability modulus, i.e: the largest real part of eigenvalues, of F + V and ρ(−FV−1) the spectral radius of −FV−1. Hence, the DFE is globally asymptotically stable if R0 = ρ(−FV−1) < 1. And if R0 > 1, i.e: α(F + V) > 0, the DFE is unstable [68]. Since, we have proved that DX(I) is a Metzler matrix, to prove the local stability of the endemic equilibrium ≫ 0, we only need to prove that it exists w ≫ 0 such that DX()w < 0 [7]. The endemic equilibrium ≫ 0 satisfies the equation
Hence,
Hence, with w = , we deduce that is locally stable. With the attractivity of guaranteed Hirsh’s theorem, we conclude that the endemic equilibrium ≫ 0 is globally asymptotically stable if R0 > 1.
Finally, if R0 = 1, we have α(F + V) = 0. It exists c ≫ 0 such that (F+V )tc = 0. By considering the Lyapunov function V = 〈c|I〉. This function is definite positive and its derivation along the trajectories if (14) is
| (16) |
Plus = 0 only at the DFE. Hence the DFE is GAS if R0 = 1. This completes the proof of the theorem 2.1.
Appendix C. Proof of Theorem 2.2
Proof
Since Model (6) has the compact global attractor Ω, then according to Theorem (2.1), we can expect that limt→∞I(t) < , thus for time large enough, we can have we have − Ii > 0, therefore
which indicates follows when (ℙ) > 1
Then apply the average Lyapunov Theorem [50], we can conclude that lim inft→∞ Ii(t) > 0, i.e., the disease in the residence Patch i is persistent if (ℙ) > 1.
If pij > 0 and pkj = 0 for all k = 1, .., n, and k ≠ i, this implies that if there is a portion of the residence Patch i population flowing into the residence Patch j, then there is no other residence Patch k where k ≠ j, i.e.,
which also implies that
then we can conclude that Model (6) can have an equilibrium since under these conditions,
Therefore, if the conditions pkj = 0 for all k = 1, .., n, and k ≠ j whenever pij > 0 hold, then we have
Therefore, Ii = 0 is the invariant manifold for Model (6).
On the other hand, when these conditions hold, then we have
Therefore, if , then we have the following inequality:
Therefore, we have limt→∞ Ii(t) = 0, i.e., there is no endemic in the residence Patch i.
Contributor Information
Derdei Bichara, SAL MATHEMATICAL, COMPUTATIONAL AND MODELING SCIENCE CENTER, ARIZONA STATE UNIVERSITY, TEMPE, AZ 85287. derdei.bichara@asu.edu.
Yun Kang, SCIENCES AND MATHEMATICS FACULTY, COLLEGE OF LETTERS AND SCIENCES, ARIZONA STATE UNIVERSITY, MESA, AZ 85212. yun.kang@asu.edu.
Carlos Castillo-Chavez, SAL MATHEMATICAL, COMPUTATIONAL AND MODELING SCIENCE CENTER, ARIZONA STATE UNIVERSITY, TEMPE, AZ 85287. ccchavez@asu.edu.
Richard Horan, DEPARTMENT OF AGRICULTURAL, FOOD AND RESOURCE ECONOMICS, MICHIGAN STATE UNIVERSITY, EAST LANSING, MI 4882, horan@msu.edu.
Charles Perrings, SCHOOL OF LIFE SCIENCES, ARIZONA STATE UNIVERSITY, TEMPE, AZ 85287. Charles.Perrings@asu.edu.
References
- [1].ANDERSON RM, MAY RM. Directly transmitted infections diseases: control by vaccination. Science. 1982;215:1053–1060. doi: 10.1126/science.7063839. [DOI] [PubMed] [Google Scholar]
- [2].ANDERSON RM, MAY RM. Dynamics and Control. Oxford science publications; 1991. Infectious Diseases of Humans. [Google Scholar]
- [3].ARINO J. Disease in metapopulations model. 2008. draft.
- [4].ARINO J, DAVIS J, HARTLEY D, JORDAN R, MILLER J, VAN DEN DRIESSCHE P. A multi-species epidemic model with spatial dynamics. Math. Med. Biol. 2005;22:129–142. doi: 10.1093/imammb/dqi003. [DOI] [PubMed] [Google Scholar]
- [5].ARINO J, VAN DEN DRIESSCHE P. The basic reproduction number in a multi-city compartmental model. Lect. Notes Contr. Inf. Sci. 2003;294:135–142. [Google Scholar]
- [6].ARINO J, VAN DEN DRIESSCHE P. Disease spread in metapopulations. In: Zhao X-O, Zou X, editors. Nonlinear dynamics and evolution equations. Vol. 48. AMS; Providence, R.I.: 2006. pp. 1–13. Fields Instit. Commun. [Google Scholar]
- [7].BERMAN A, PLEMMONS RJ. Classics in Applied Mathematics. Vol. 9. Society for Industrial and Applied Mathematics (SIAM); Philadelphia, PA: 1994. Nonnegative matrices in the mathematical sciences. Revised reprint of the 1979 original. [Google Scholar]
- [8].BERNOULLI D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole. Mem. Math. Phys. Acad. R. Sci. Paris. 1766:1–45. [Google Scholar]
- [9].BLYTHE SP, CASTILLO-CHAVEZ C. Like-with-like preference and sexual mixing models. Math. Biosci. 1989;96:221–238. doi: 10.1016/0025-5564(89)90060-6. [DOI] [PubMed] [Google Scholar]
- [10].BRAUER F. Epidemic models with heterogeneous mixing and treatment. Bull Math Biol. 2008;70:1869–1885. doi: 10.1007/s11538-008-9326-1. [DOI] [PubMed] [Google Scholar]
- [11].BRAUER F, CASTILLO-CHAVEZ C. Basic models in epidemiology. In: Steele J, Powell T, editors. Ecological Time Series. N. Y. Raven Press; 1994. pp. 410–477. [Google Scholar]
- [12].BRAUER F, CASTILLO-CHáVEZ C. Texts in Applied Mathematics. Vol. 40. Springer-Verlag; New York: 2012. Mathematical models in population biology and epidemiology. [Google Scholar]
- [13].BRAUER F, CASTILLO-CHAVEZ C, VELASCO-HERNáNDEZ JX. Kirschner D, editor. Recruitment effects in heterosexually transmitted disease models. dvances in Mathematical Modeling of Biological Processes. 1996;3:1:78–90. International Journal of Applied Science and Computation. [Google Scholar]
- [14].BRAUER F, FENG Z, CASTILLO-CHAVEZ C. Discrete epidemic models. Math. Biosci. Eng. 2010;7:1–15. doi: 10.3934/mbe.2010.7.1. [DOI] [PubMed] [Google Scholar]
- [15].BRAUER F, VAN DEN DRIESSCHE P. Models for transmission of disease with immigration of infectives. Math. Biosci. 2001;171 doi: 10.1016/s0025-5564(01)00057-8. [DOI] [PubMed] [Google Scholar]
- [16].BRAUER F, VAN DEN DRIESSCHE P, WANG L. Oscillations in a patchy environment disease model oscillations in a patchy environment disease model. Math. Biosci. 2008;215:1–10. doi: 10.1016/j.mbs.2008.05.001. [DOI] [PubMed] [Google Scholar]
- [17].BRAUER F, WATMOUGH J. Age of infection epidemic models with heterogeneous mixing. Journal of Biological Dynamics. 2009;3:324–330. doi: 10.1080/17513750802415822. [DOI] [PubMed] [Google Scholar]
- [18].CASTILLO-CHAVEZ C, BUSENBERG S. A general solution of the problem of mixing of subpopulations and its application to risk-and age-structured epidemic models for the spread of aids. Mathematical Medecine and Biology. 1991;8:1–29. doi: 10.1093/imammb/8.1.1. [DOI] [PubMed] [Google Scholar]
- [19].CASTILLO-CHAVEZ C, COOKE K, HUANG W, LEVIN SA. Results on the dynamics for models for the sexual transmission of the human immunodeficiency virus. Appl. Math. Lett. 1989;2:327–331. [Google Scholar]
- [20].CASTILLO-CHAVEZ C, HETHCOTE H, ANDREASEN V, LEVIN S, LIU W. Epidemiological models with age structure, proportionate mixing, and cross-immunity. Journal of Mathematical Biology. 1989;27:233–258. doi: 10.1007/BF00275810. [DOI] [PubMed] [Google Scholar]
- [21].CASTILLO-CHAVEZ C, HUANG W. Mathematical approaches for emerging and reemerging infectious diseases: models, methods, and theory (Minneapolis, MN, 1999) Vol. 126. Springer; New York: 2002. Age-structured core group model and its impact on STD dynamics; pp. 261–273. IMA Vol. Math. Appl. [Google Scholar]
- [22].CASTILLO-CHAVEZ C, HUANG W, LI J. Competitive exclusion in gonorrhea models and other sexually transmitted diseases. SIAM J. Appl. Math. 1996;56:494–508. [Google Scholar]
- [23].CASTILLO-CHAVEZ C, HUANG W, LI J. Competitive exclusion and coexistence of multiple strains in an SIS STD model. SIAM J. Appl. Math. 1999;59:1790–1811. [Google Scholar]
- [24].CASTILLO-CHAVEZ C, THIEME HR. Asymptotically autonomous epidemic models. In: Arino O, Kimmel M, editors. Mathematical Population Dynamics: Analysis of Heterogeneity, Volume One: Theory of Epidemics. Wuerz; 1995. A. D.E. [Google Scholar]
- [25].CASTILLO-CHAVEZ C, VELASCO-HERNáNDEZ JX, FRIDMAN S. Modeling contact structures in biology. In: Levin SA, editor. Frontiers in Mathematical Biology. Vol. 100. Springer-Verlag; 1994. ch. 454-491. [Google Scholar]
- [26].CHOWELL D, CASTILLO-CHAVEZ C, KRISHNA S, QIU X, ANDERSON KS. Modelling the effect of early detection of ebola. The lancet. 2015;15:148–149. doi: 10.1016/S1473-3099(14)71084-9. [DOI] [PubMed] [Google Scholar]
- [27].DIEKMANN O, HEESTERBEEK JAP, METZ JAJ. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- [28].DIETZ K, HEESTERBEEK J. Daniel Bernoulli’s epidemiological model revisited. Math. Biosci. 2002;180:1–21. doi: 10.1016/s0025-5564(02)00122-0. [DOI] [PubMed] [Google Scholar]
- [29].DIETZ K, SCHENZLE D. A celebration of statistics. Springer; New York: 1985. Mathematical models for infectious disease statistics; pp. 167–204. [Google Scholar]
- [30].FALL A, IGGIDR A, SALLET G, TEWA J-J. Epidemiological models and lyapunov functions. Math. Model. Nat. Phenom. 2007;2:62–68. [Google Scholar]
- [31].FENICHEL E, CASTILLO-CHAVEZ C, CEDDIA MG, CHOWELL G, GONZALEZ PARRA P, HICKLING GJ, HOLLOWAY G, HORAN R, MORIN B, PERRINGS C, SPRINGBORN M, VALAZQUEZ L, VILLALOBOS C. Adaptive human behavior in epidemiological models. PNAS. 2011 doi: 10.1073/pnas.1011250108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].GUO H, LI M, SHUAI Z. Global stability of the endemic equilibrium of multigroup models. Can. Appl. Math. Q. 2006;14:259–284. [Google Scholar]
- [33].GUO H, LI M, SHUAI Z. A graph-theoretic approach to the method of global Lyapunov functions. Proc. Amer. Math. Soc. 2008 [Google Scholar]
- [34].HADELER K, CASTILLO-CHAVEZ C. A core group model for disease transmission. Math Biosci. 1995;128:41–55. doi: 10.1016/0025-5564(94)00066-9. [DOI] [PubMed] [Google Scholar]
- [35].HEIDERICH KR, HUANG W, CASTILLO-CHAVEZ C. Mathematical approaches for emerging and reemerging infectious diseases: an introduction, I. V. M. Appli. Vol. 125. Springer-Verlag New York, Inc.; 2002. Nonlocal response in a simple epidemiological model; pp. 129–151. [Google Scholar]
- [36].HERNANDEZ-CERON N, FENG Z, CASTILLO-CHAVEZ C. Discrete epidemic models with arbitrary stage distributions and applications to disease control. Bull Math Biol. 2013;75:1716–1746. doi: 10.1007/s11538-013-9866-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].HETHCOTE HW. Qualitative analyses of communicable disease models. Math. Biosci. 1976;28:335–356. [Google Scholar]
- [38].HETHCOTE HW. The mathematics of infectious diseases. SIAM Rev. 2000;42:599–653. [Google Scholar]
- [39].HETHCOTE HW, THIEME HR. Stability of the endemic equilibrium in epidemic models with subpopulations. Math. Biosci. 1985;75:205–227. [Google Scholar]
- [40].HETHCOTE HW, YORKE J. Lect. Notes Biomath. Vol. 56. Springer-Verlag; 1984. Gonorrhea : transmission dynamics and control. [Google Scholar]
- [41].HIRSCH M. The dynamical system approach to differential equations. Bull. AMS. 1984;11:1–64. [Google Scholar]
- [42].HORAN DR, FENICHEL EP. Economics and ecology of managing emerging infectious animal diseases. Amer. J. Agr. Econ. 2007;89:1232–1238. [Google Scholar]
- [43].HORAN DR, FENICHEL EP, MELSTROM RT. Wildlife disease bioeconomics. International Review of Environmental and Resource Economics. 2011;5:23–61. [Google Scholar]
- [44].HORAN DR, FENICHEL EP, WOLF CA, GRAMING BM. Managing infectious animal disease systems. Annu. Rev. Resout. Econ. 2010;2:101–124. [Google Scholar]
- [45].HSU SCHMITZ S-F. Effect of treatment or/and vaccination on hiv transmission in homosexual with genetic heterogeneity. Math. Biosci. 2000;167:1–18. doi: 10.1016/s0025-5564(00)00021-3. [DOI] [PubMed] [Google Scholar]
- [46].HSU SCHMITZ S-F. A mathematical model of hiv transmission in homosexuals with genetic heterogeneity. Journal of Theoretical Medecine. 2000;2:285–296. [Google Scholar]
- [47].HSU SCHMITZ S-F. The influence of treatment and vaccination induced changes in the risky contact rate on hiv transmisssion. Math. Pop. Stud. 2007;14:57–76. [Google Scholar]
- [48].HUANG W, COOKE K, CASTILLO-CHAVEZ C. Stability and bifurcation for a multiple-group model for the dynamics of hiv/aids transmission. SIAM J. Appl. Math. 1992;52:835–854. [Google Scholar]
- [49].HUANG W, COOKE KL, CASTILLO-CHAVEZ C. Stability and bifurcation for a multiple-group model for the dynamics of hiv/aids transmission. SIAM Journal on Applied Mathematics. 1992;52:835–854. [Google Scholar]
- [50].HUTSON V. A theorem on average Liapunov functions. Monatshefte für Mathematik. 1984;98:267–275. [Google Scholar]
- [51].IGGIDR A, SALLET G, TSANOU B. Global stability analysis of a metapopulation sis epidemic model. Math. Pop. Stud. 2012;19:115–129. [Google Scholar]
- [52].JACQUEZ JA, SIMON CP. The stochastic si model with recruitment and deaths i. comparison with the closed sis model. Math Biosci. 1993;117:77–125. doi: 10.1016/0025-5564(93)90018-6. [DOI] [PubMed] [Google Scholar]
- [53].JACQUEZ JA, SIMON CP, KOOPMAN J. The reproduction number in deterministic models of contagious diseases. Comment. Theor. Biol. 1991;2 [Google Scholar]
- [54].JACQUEZ JA, SIMON CP, KOOPMAN J, SATTENSPIEL L, PERRY T. Modeling and analyzing HIV transmission : the effect of contact patterns. Math. Biosci. 1988;92 [Google Scholar]
- [55].KUNIYA T, MUROYA Y. Global stability of a multi-group sis epidemic model for population migration. DCDS series B. 2014;19 [Google Scholar]
- [56].LAJMANOVICH A, YORKE J. A deterministic model for gonorrhea in a nonhomogeneous population. Math. Biosci. 1976;28:221–236. [Google Scholar]
- [57].LIN X, SO JW-H. Global stability of the endemic equilibrium and uniform persistence in epidemic models with subpopulations. J. Aust. Math. Soc., Ser. B. 1993;34:282–295. [Google Scholar]
- [58].MORIN B, CASTILLO-CHAVEZ C. Sir dynamics with economically driven contact rates. Natural Resource Modeling. 2003;26:505–525. doi: 10.1111/nrm.12011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].MOSSONG J, HENS N, JIT M, BEUTELS P, MIKOLAJCZYK R, MASSARI M, SALMASO S, TOMBA GS, WALLINGA J, HEIJNE J, SADKOWSKA-TODYS M, ROSINSKA M, EDMUNDS WJ. Social contacts and mixing patterns relevant to the spread of infectious diseases. Plos Medecine. 2008;5:381–391. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].NOLD A. Heterogeneity in disease-transmission modeling. Math. Biosci. 1980;52:227. [Google Scholar]
- [61].PERRINGS C, CASTILLO-CHAVEZ C, CHOWELL G, DASZAK P, FENICHEL EP, FINNOFF D, HORAN RD, KILPATRICK AM, KINZIG AP, KUMINOFF NV, LEVIN S, MORIN B, SMITH KF, SPRINGBORN M. Merging economics and epidemiology to improve the prediction and management of infectious disease. Ecohealth. 2014 doi: 10.1007/s10393-014-0963-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].ROSS R. The prevention of malaria. John Murray; 1911. [Google Scholar]
- [63].RUSHTON S, MAUTNER A. The deterministic model of a simple epidemic for more than one community. Biometrika. 1955:126–132. [Google Scholar]
- [64].SATTENSPIEL L, DIETZ K. A structured epidemic model incorporating geographic mobility among regions. Math Biosci. 1995;128:71–91. doi: 10.1016/0025-5564(94)00068-b. [DOI] [PubMed] [Google Scholar]
- [65].SATTENSPIEL L, SIMON CP. The spread and persistence of infectious diseases in structured populations. Math. Biosci. 1988;90:341–366. Nonlinearity in biology and medicine (Los Alamos, NM, 1987) [Google Scholar]
- [66].SHUAI Z, VAN DEN DRIESSCHE P. Global stability of infectious disease models using lyapunov functions. SIAM Journal on Applied Mathematics. 2013;73:1513–1532. [Google Scholar]
- [67].SIMON CP, JACQUEZ JA. Reproduction numbers and the stability of equilibria of SI models for heterogeneous populations. SIAM J. Appl. Math. 1992;52:541–576. [Google Scholar]
- [68].VAN DEN DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- [69].VELASCO-HERNáNDEZ JX, BRAUER F, CASTILLO-CHAVEZ C. Effects of treatment and prevalence-dependent recruitment on the dynamics of a fatal disease. IMA J Math Appl Med Biol. 1996;13:175–192. [PubMed] [Google Scholar]
- [70].VIDYASAGAR M. Decomposition techniques for large-scale systems with nonadditive interactions: Stability and stabilizability. IEEE Trans. Autom. Control. 1980;25:773–779. [Google Scholar]
- [71].YORKE JA, HETHCOTE HW, NOLD A. Dynamics and control of the transmission of gonorrhea. Sex Transm Dis. 1978;5:51–56. doi: 10.1097/00007435-197804000-00003. [DOI] [PubMed] [Google Scholar]