Repeated stimulation of cultured networks of rat cortical neurons induces parallel memory traces

Abstract

During systems consolidation, memories are spontaneously replayed favoring information transfer from hippocampus to neocortex. However, at present no empirically supported mechanism to accomplish a transfer of memory from hippocampal to extra-hippocampal sites has been offered. We used cultured neuronal networks on multielectrode arrays and small-scale computational models to study the effect of memory replay on the formation of memory traces. We show that input-deprived networks develop an activity⇔connectivity balance where dominant activity patterns support current connectivity. Electrical stimulation at one electrode disturbs this balance and induces connectivity changes. Intrinsic forces in recurrent networks lead to a new equilibrium with activity patterns that include the stimulus response. The new connectivity is no longer disrupted by this stimulus, indicating that networks memorize it. A different stimulus again induces connectivity changes upon first application but not subsequently, demonstrating the formation of a second memory trace. Returning to the first stimulus does not affect connectivity, indicating parallel storage of both traces. A computer model robustly reproduced experimental results, suggesting that spike-timing-dependent plasticity and short time depression suffice to store parallel memory traces, even in networks without particular circuitry constraints.

In vivo, consolidation of declarative memory can be subdivided into two specific processes (Squire et al. 1984). Rapidly after learning, memories are temporarily stored in hippocampus, a process generally referred to as synaptic consolidation. During the second phase, systems consolidation, memories are slowly transferred to the neocortex. This stage of memory encoding probably requires repeated activation of cortical areas by the hippocampus (Sutherland and McNaughton 2000; Frankland and Bontempi 2005; Karlsson and Frank 2009; Nakashiba et al. 2009). Long-term potentiation is generally assumed to be the underlying process in synaptic consolidation (Bramham and Messaoudi 2005). However, whether and to what extent the signs of reactivation play a functional role in consolidating respective neural memory representations or merely reflect use-dependent phenomena of inert neural activity is presently not clear (Gais and Born 2004). At present, no empirically supported mechanism to accomplish a transfer of memory from hippocampal to extra-hippocampal sites has been offered (Nadel et al. 2007) and the “algorithms” that create memory traces remain unclear, forming a major obstacle in the search for memory traces.

Studies of artificial neural networks suggested that the stabilization of reverberating neural activity underlying short-term memory produces long-term memory (Gerard 1949; Hebb 1949). Later basic theories proposed that activity patterns in artificial recurrent excitatory networks are dictated by attractors, local minima in the energy landscape that are associated with certain activation patterns. External input substantially changes the set of attractors of a network (Amit 1989), and thus the palette of activation patterns, which may reflect memory traces. However, these theories cannot be straightforwardly validated in biological networks, because simultaneous activity of multiple neurons is difficult to record in vivo and consequently, it is hard to provide accurate estimates of the synaptic coupling in vivo.

Dissociated cortical neurons cultured on multielectrode arrays provide a useful platform to study network aspects of neuronal tissue, including memory. A week after seeding cultures become spontaneously active, to reach a mature state after ∼3 wk (van Pelt et al. 2004; Stegenga et al. 2008). Beyond 3 wk, activity patterns and connectivity stabilize, but a slow drift of observed activity patterns (on timescales of hours to days) remains (Stegenga et al. 2008). Activity patterns are determined by a certain connectivity, and conversely, activity patterns affect connectivity through plasticity mechanisms like spike-timing-dependent plasticity (STDP). Networks develop an activity–connectivity balance, where activity patterns support current connectivity, connectivity appears relatively constant, and activity may fluctuate within a fixed set of possible patterns. Responses to electrical stimulation usually differ from spontaneously occurring patterns and therefore disturb the activity–connectivity balance, yielding a change in connectivity.

We hypothesize that networks will develop a new activity–connectivity equilibrium, such that the new spontaneous activity patterns include the network response to the applied stimulus. If so, the first application of a certain stimulus should activate new patterns, and induce connectivity changes. Repeated application of that same stimulus should not lead to further connectivity changes as the stimulus response becomes part of the spontaneous repertoire, and imposes no further drive away from the equilibrium. This reasoning provides a tool to verify the hypothesis without a priori knowledge of the actual encoding of memory traces.

Results

We investigated the effect of repeated stimuli on connectivity in 21 experiments in 20 cultured cortical networks on multielectrode arrays, and in 36 simulations with a computer model of a 100-neuron cortical network.

Experiments

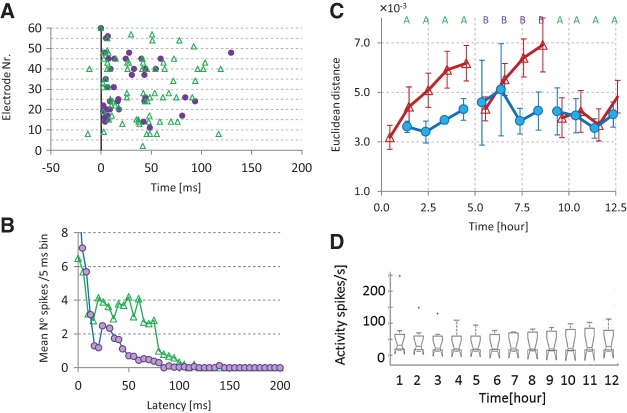
In all experiments, long-term recordings were subdivided into data blocks. We determined the connectivity Matrix S for each data block (see Materials and Methods) to assess connectivity changes. Without external input, functional connectivity was quite stable: on average, strengths of functional connections varied <25% of their mean value for the duration of our experiments (5–10 h). In stimulation experiments, all evaluation periods between the stimulation periods contained multiple data blocks, each having their own connectivity S, with a certain distance to the initial connectivity. We calculated the mean distance to the initial connectivity, ED₀, for all evaluation periods. Figure 1A shows the temporal evolution of ED₀ in control cultures (n = 4, dashed line) and cultures that received 15 min of tetanic stimulation (see Materials and Methods) after every hour of no stimulation (n = 13, solid line). There is no significant difference between the starting points of both curves (t-test P > 0.38). One-way ANOVA showed that ED₀ significantly increased in stimulated cultures (P < 0.03), whereas control cultures showed no significant change (P > 0.4).

Figure 1.

Connectivity changes in control recordings and repeatedly stimulated cultures. Long-term recordings were divided into data blocks, in each data block we calculated the connectivity matrix and we calculated the Euclidean distance from the initial connectivity matrix (ED₀). (A) Connectivity changes in control recordings (○, dashed line; n = 4) and repeatedly (tetanus) stimulated cultures (Δ, solid line; n = 13). Horizontal axis indicates stimulation periods (15 min of tetanic stimulation), the intervals in between denote 1 h of spontaneous activity. The average distance in the first evaluation period reflects spontaneous fluctuations. Error bars indicate SEM and reflect differences between experiments. (B) Connectivity changes during repeated low-frequency stimulation (0.2 Hz for 15 min, n = 4). From the periods of spontaneous activity (1 h each) between stimulation periods, we calculated connectivity matrices and the distances from the initial connectivity (dashed line, ○) and from the connectivity before the last stimulation period (solid line, ♦). Error bars indicate SEM and reflect differences between experiments. (C) Average area under the PSTH of all stimuli within each stimulation period. On average there were no significant changes in the number of stimulus induced action potentials throughout the experiments (ANOVA P = 0.97). Total time along horizontal axis in B and C was ∼12 h.

Low-frequency stimulation (0.2 Hz, during 15 min) yielded comparable results, ED_0,norm increased significantly in stimulated cultures (ANOVA, P < 0.003). The distance between the connectivity before and after the first period of stimulation (ED_stim[1]) was much larger than ED_stim around subsequent stimulation periods (Fig. 1B, solid line). After normalization, all distances except ED_stim[2] were significantly smaller than ED_stim[1] (t-test: P < 0.03). The distance across stimulation periods did not drop to zero, but as shown in Figure 1B, the remaining connectivity differences did not yield an increasing distance from the initial connectivity (ED₀, dashed line). Figure 1C shows the mean area under the post-stimulus time histogram (PSTH) upon each stimulus pulse. The mean amount of action potentials in response to stimulation did not change during the experiment (P = 0.97, one-way ANOVA). Finally, we estimated similarity between events (stimulus responses or spontaneous network bursts recorded before or after the stimulation period) using the EC measure (see Materials and Methods). Stimulus responses tended to have higher similarity to post-stimulation spontaneous bursts than to prestimulation burst, but the difference was not significant.

In seven cultures, we investigated the effect of stimulation at a second electrode. Both electrodes were selected to yield clearly detectable network responses (see Materials and Methods), without further restrictions related to their location. The distance between the stimulation electrodes ranged from 200 µm (adjacent electrodes) to 1.34 mm (see Table 1). Results obtained with adjacent stimulation electrodes were similar to those obtained with larger distances between the stimulation electrodes, but we did not specifically search for possible distance dependencies. Similarity between responses to stimulation at one electrode, as assessed by event correlation (EC, see Materials and Methods), averaged 0.61, and was much higher than EC between the first stimulations at different electrodes. Figure 2A,B shows an example of two responses to stimulation at different electrodes A and B, with EC(A[1], B[1]) = 0.32.

Table 1.

Overview of cultures used

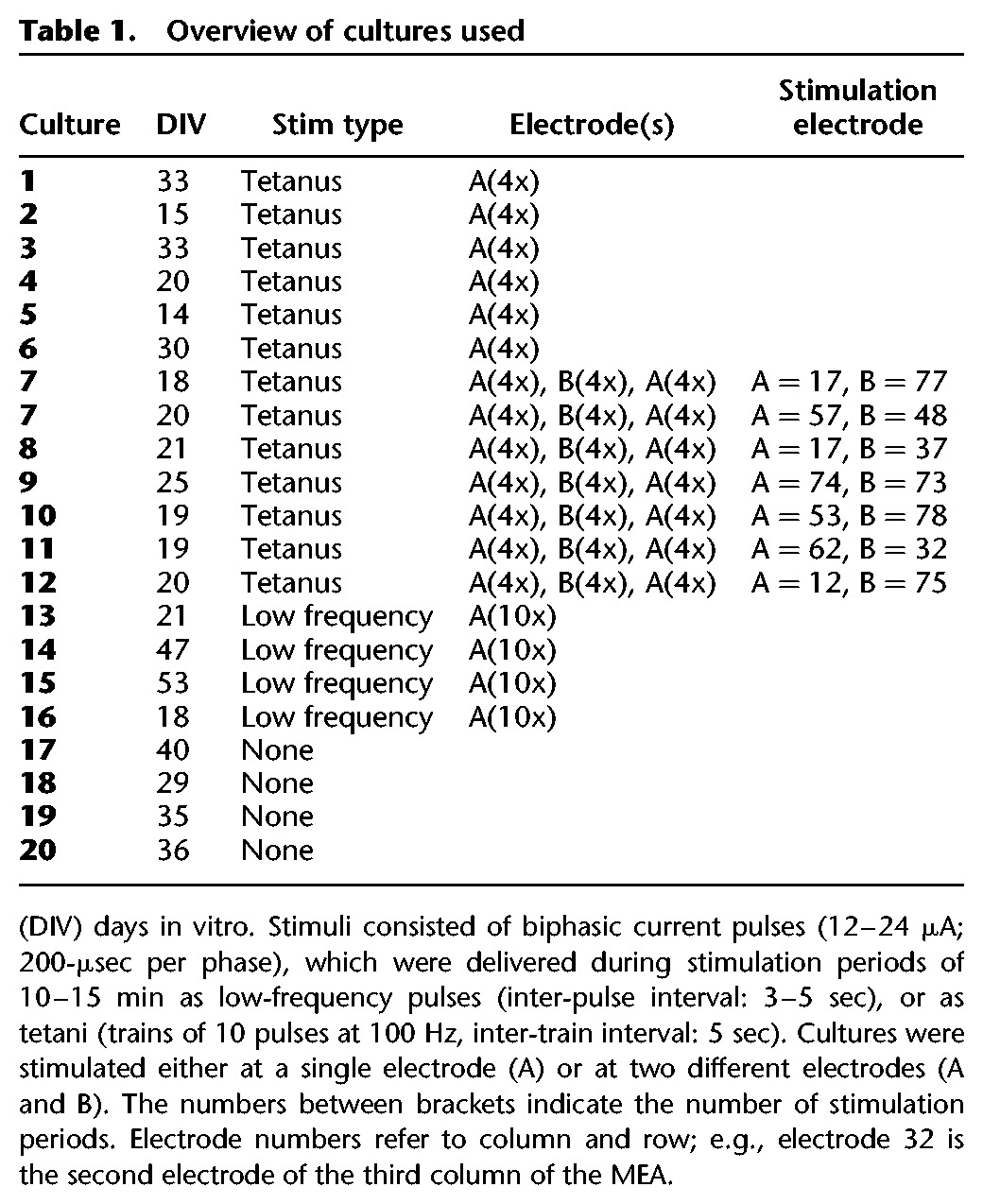
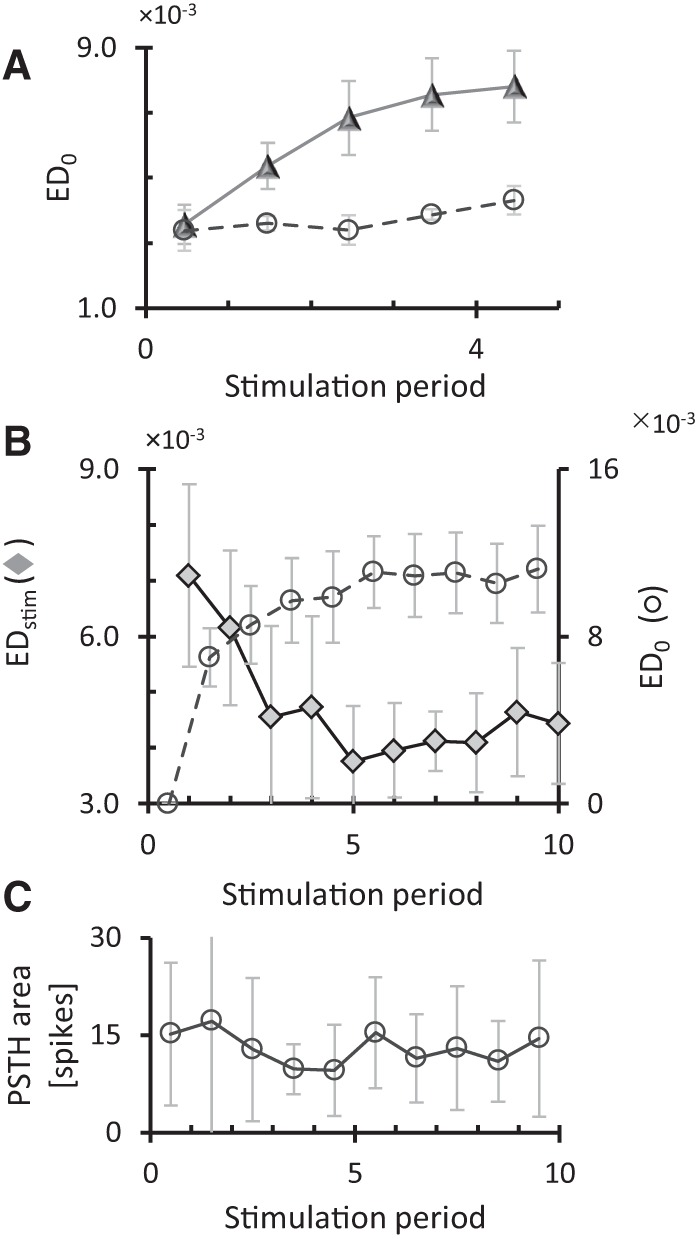
Figure 2.

Network response to two different stimuli. (A) Example raster plots of responses to stimulus A (Δ) and B (•) EC = 0.32. (B) Mean stimulus response to both stimuli (n_A = 20, n_B = 20) in that experiment. (C) Euclidean distance from the initial connectivity matrix without stimulation (•, n = 4 experiments), or across periods of tetanic stimulation at electrode A or B, as indicated (Δ, n = 7 experiments). For comparison, all distances are calculated to the last connectivity matrix before stimulation at that particular electrode (A or B). (D) Box plot of the spontaneous array wide firing rate. On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points considered to be not outliers, and the outliers are plotted individually. The firing rate remained unchanged during these experiments (one-way ANOVA, P > 0.99).

Periods of spontaneous activity were divided into 16.7 ± 1.4 data blocks to determine the temporal development of functional connectivity (see Materials and Methods). In all experiments, connectivity changes across stimulation periods leveled off when the first electrode was stimulated during four stimulation periods.

Subsequent switch to another electrode again yielded large connectivity changes upon the first stimulation followed by smaller changes after successive stimuli at that electrode. Finally, returning to the first stimulation electrode did not induce connectivity changes larger than spontaneous fluctuations. Figure 2C shows connectivity changes in response to stimulation at electrode A or B, with respect to the connectivity just before the first application of that stimulus (i.e., switching to a new stimulation electrode was associated with a new reference for ED₀). Differences across first stimulation periods at either electrode were substantially larger than those across subsequent stimulation periods, or periods of equal duration of no stimulation. Returning to stimulus A, we found no connectivity changes larger than spontaneous fluctuations. On average, the array wide spontaneous activity remained constant during the experiments (ANOVA: P > 0.99, see Fig. 2D).

Computer modeling

A model of 100 neurons coupled by synapses with short-term facilitation (STF) and depression (STD) and STDP, robustly reproduced the in vitro finding that networks develop an activity–connectivity balance. We used several network realizations, two different implementations of STDP, various patterns of synaptic noise, and low-frequency or tetanic stimulation. With additive STDP, the percentage of extreme synaptic weights (>90% of their maximum or <10%) increased during the whole simulation and averaged 73% at the end of the simulation. With tetanic stimulation, the fraction of synapses with an extreme value decreased during all stimulation periods in all simulations, although in some periods this decline was small. Whereas low-frequency stimulation and additive STDP often led to many synapses with extreme values, the combination of the multiplicative STDP model and tetanic stimulation generally yielded unimodally distributed synaptic strengths.

Activity and connectivity robustly stabilized in all networks explicitly tested (n = 5). To quantify the stability of connectivity, we calculated the temporal development of ED₀. Connectivity stabilized as the slope of the ED₀ curve against time approached zero (see Materials and Methods). The slope dropped below 0.5% within ∼30 min. In all other models connectivity also stabilized, before we applied stimulation.

The models also reproduced the experimental finding that a first external stimulus induced large connectivity changes, reflected by large ED_stim values. Connectivity changes in response to low-frequency stimulation were substantially larger than those in response to tetanic stimulation. Although the differences were much smaller, we saw a similar trend in the experimental data. Subsequent stimuli did not induce large connectivity changes (tetanic stimulation), or to a rapidly decreasing extent (low-frequency stimulation), as illustrated in Figure 3A.

Figure 3.

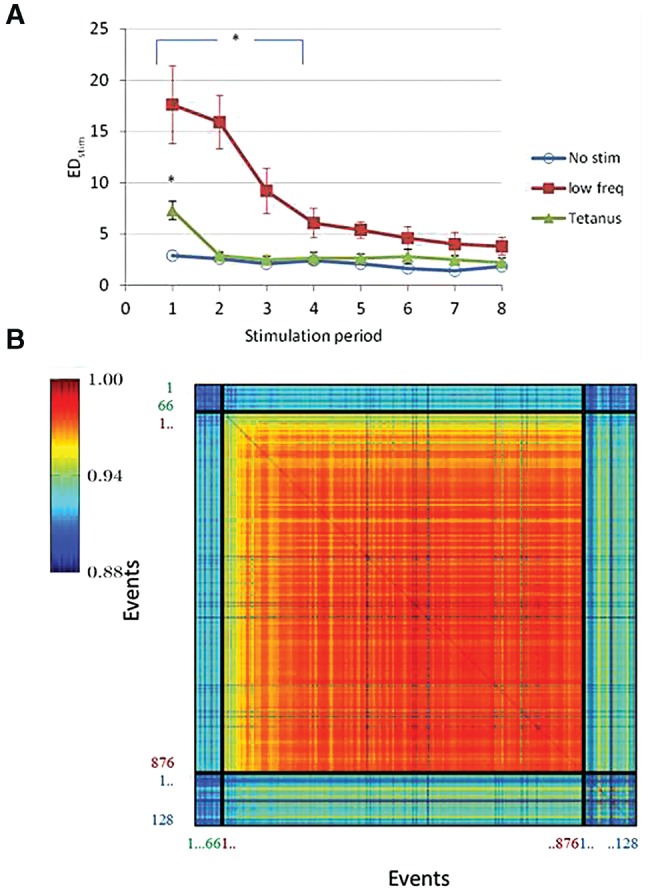
Connectivity changes following repeated stimulation in the computer model. (A) Squares show the effect of low-frequency stimulation (0.2 Hz for 15 min), triangles show tetanic stimulation. Both curves indicate connectivity changes across stimulation periods, averages ± SDs of four simulations are shown. No stimulation (circles) was simulated once. Significant differences (ANOVA and Tukey HSD test, P < 0.01) are indicated by an asterisk. (B) Typical example of the similarity between all events in a simulation: 66 prestimulation bursts (labeled in green), 876 stimulus responses (labeled in red), and 128 post-stimulation bursts (labeled in blue). The figure shows color-coded values of all EC (n,m), 0 < n, m ≤ (66 + 876 + 128). Twenty-four of the 900 stimulations did not evoke a network response.

In 12 simulations, we stimulated the network model for 2 h at 0.125 Hz. To investigate the similarity between stimulus responses and spontaneous pre- and post-stimulation burst patterns, we calculated the events correlations EC (see Materials and Methods). The example in Figure 3B shows that stimulus responses progressively resembled their neighbors, indicating a stabilization of the response. Furthermore, the average similarity of stimulus responses to post-stimulation spontaneous bursts was significantly higher than that to prestimulation bursts (one-sided Wilcoxon signed rank, P < 0.001).

A typical example of the responses to two different stimuli A and B (Fig. 4A) shows that the main difference occurred in the first part of the response. The later part of the response was generally relatively similar for different stimuli. Overall similarity of the response to these two stimuli was 0.95, which would be indicated as green in Figure 3B. Provided that synaptic strengths did not reach extreme values after application of the first stimulus (which in general was the case when tetanic stimulation was applied), a second, different stimulus also induced large connectivity changes at first, but not after subsequent stimulation periods. Return to the first stimulus did not induce ED_stim values that significantly exceeded spontaneous fluctuations. Figure 4 also displays ED₀ (solid line, open circles) for easy comparison with Figure 2C.

Figure 4.

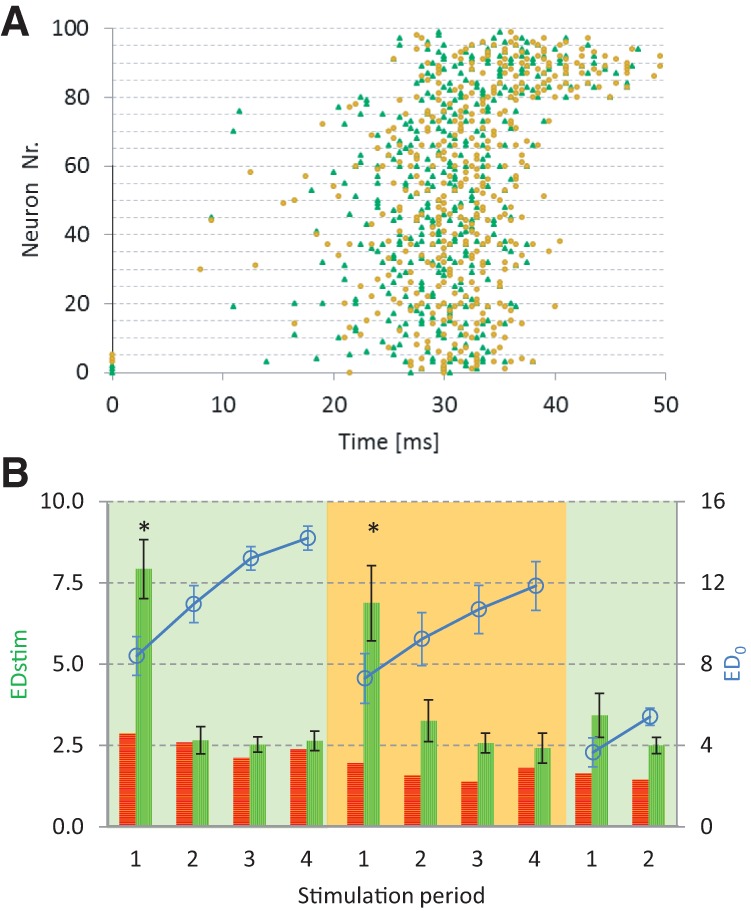
Response to two different stimuli in simulated network. (A) example of stimulus response rasterplots (similarity: EC(A[1], B[1]) = 0.95). Neurons (0,1,2) (stim A, Δ), or (3,4,5) (stim B, •) were stimulated at t = 0. Neurons 80–99 were inhibitory. (B): Euclidean distances between connectivities across subsequent stimulation periods (vertically hatched bars). First, stimulus A was applied four times, then four times stimulus B and then again stimulus A (n = 4 simulations), horizontally hatched bars indicate distances between equidistant periods without stimulation (n = 1). Significant differences (ANOVA + Tukey's HSD, P < 0.05) are indicated by an asterisk.

Discussion

Spontaneous neuronal activity patterns reflect connectivity and closely timed spikes in coupled neurons may potentiate or depress the efficacy of transmission in the connecting synapse. Without external input, dissociated cortical networks develop rather stable firing patterns (Stegenga et al. 2008), as well as a stable connectivity (le Feber et al. 2007). This implies that the occurring patterns do not affect connectivity, and therefore, activity and connectivity are in balance. Activity and connectivity are maintained because these networks are easily excitable and highly recurrent (le Feber et al. 2014), which leads to bursting firing patterns, with many action potentials within the time window of STDP. Self-stabilizing activity is also obtained in artificial recurrent neural networks, and stable patterns are referred to as attractors (Amit and Brunel 1997). Although activity patterns in cultures stabilize after 3 wk, a slow drift of observed activity patterns (on timescales of hours to days) remains (Stegenga et al. 2008). A similar slow drift of self-sustained activity patters is observed in continuous attractor network models (Carter and Wang 2007).

Computer simulations robustly reproduced the experimentally observed stabilization of connectivity. To realize sufficient ongoing network activity and network bursts, the degree of connectivity (the relative number of connections per neuron) and the level of synaptic noise in the model were higher than biologically plausible. The relatively high degree ensured that all network models were highly recurrent and, combined with relatively high synaptic noise, produced bursting activity patterns. The current study confirms that isolated recurrent networks develop a stable connectivity. In biological networks, the development toward this stable connectivity is governed by the “rules” of STDP (le Feber et al. 2009), indicating that this process depends on synaptic plasticity.

An external input usually initiates deviating patterns, which may drive the network away from the existing balance. In vitro, we used a single stimulation electrode to directly (non-synaptically) activate multiple neurons (Marom and Shahaf 2002; Wagenaar et al. 2004; Reinartz et al. 2014), and in simulations, we directly activated a set of neurons, which was usually sufficient to trigger a network burst. Stimuli were applied either as low-frequency pulses or as tetani. Tetanic stimulation has been shown to affect connectivity in a wide range of frequencies (20–250 Hz), inter-train intervals (2–10 sec), and numbers of pulses per train (10–100, see e.g., Jimbo et al. 1998, 1999; Ruaro et al. 2005). The exact parameter setting does not seem very critical, as long as the amplitude is sufficient to induce a network response. This view is supported by the current finding that low-frequency and tetanic stimulation yielded very similar results. Following a period of external stimulation, networks developed a new balance due to the mutually affective forces between activity and connectivity, with activity patterns including the stimulus response pattern. In simulations, adaptation of network connectivity was reflected by gradually changing stimulus responses during the early phase of the stimulation period toward a stabile response in the second half of the stimulation period. Furthermore, in all simulations the similarity between stimulus responses, particularly stabile stimulus responses, and post-stimulation bursts was significantly higher than that between stimulus responses and prestimulation bursts. This indicates that the stimulus response patterns appeared in the post-stimulation spontaneous activity. We saw a similar but non-significant trend in the experimental data. Indirect support that the new equilibrium includes the stimulus response patters, comes from the observation that subsequent application of the same input no longer affects connectivity. Although the connectivity changes across stimulation periods did not drop to zero, the remaining connectivity changes did not yield an increasing distance from the initial connectivity and therefore probably reflect fluctuations around a stable point. Apparently, the stimulus no longer formed a reorganizing force to drive connectivity further away from the initial state. The small values of ED, in the order of 10⁻³, reflect the strengths of functional connections, which usually ranged from 10⁻⁴ to 10⁻² (e.g., le Feber et al. 2007) and should therefore not be interpreted as minor connectivity changes. Investigation of artificial neural networks showed that external input usually changes the set of attractors in a network (Amit 1989). The changes in the connectivity matrix S probably reflect such a change in the set of attractors, and the correspondingly adapted activity patterns can be interpreted as memory traces.

Nakazawa et al. (2004) defined four key features of a memory trace: (1) the memory trace should form in an experience-dependent manner, (2) the trace should be specific to the information that is acquired, (3) the trace must outlast the period during which the animal is exposed to the information, and (4) the subsequent presentation of at least part of the original cues should reactivate the trace. The connectivity changes in this study comply with conditions 1–3 and probably also with the fourth condition. Connectivity changes occur upon external stimulation, which can be seen as experience-dependent formation. Different inputs induce different connectivity changes and therefore the trace is specific to the acquired “information,” and connectivity changes clearly outlasted the stimulation period. The current study focused on the formation of memory traces, and not on memory recollection. Therefore, compliance with the fourth criterion could only be deduced from indirect evidence. The finding that stimulus responses stabilized, probably means that subsequent presentation of the cue reactivated the trace and did not interfere with the established activity–connectivity equilibrium. Marom and coworkers showed that repeated stimulation of cultured cortical networks induced site-specific responses that enabled deduction of the stimulation site during up to 24 h (Shahaf et al. 2008; Kermany et al. 2010). This further supports the view that presentation of the original cue reactivates the trace.

From the waning effect of a repeated stimulus on connectivity, we can conclude that inputs are stored in network connectivity, but the encoding scheme remains unclear. Our findings imply that there is no univocal relationship between the stimulus and its encoding, as it depends not only on the stimulus but also on connectivity at the moment of arrival of the stimulus. Simulations showed that stimulus responses and spontaneous patterns developed toward each other, until the stimulus response no longer exerted a driving force away from the existing equilibrium. Spontaneous appearance of response patterns may be interpreted as a memory trace. Similar findings were obtained in vivo by Yao et al. (2007), who showed that response patterns to visual stimuli in cat visual cortex also appeared in spontaneous patterns. Their study, however, did not address network connectivity, and a mechanism to explain the appearance of the response patterns in the post-stimulation spontaneous activity patterns was not determined.

Stimulation at a second, different electrode, induced connectivity changes similar to the first stimulus. Again, large connectivity changes occurred across the first stimulation period, and much smaller changes upon subsequent periods. This pattern indicates that the network also memorized the second input. Moreover, it confirmed that the network was still able to adapt to external inputs, and that the unaffected connectivity after several repetitions of the first stimulus was not due to impeded network plasticity. This strongly supports the view that there was no longer a driving force away from the existing connectivity.

Returning to the first stimulus did not affect network connectivity, indicating that the first memory trace was not erased by application of the second stimulus. Instead, both memory traces existed in parallel, at least for the 4-h periods in our experiment. The longer-term characterization of memory traces remains subject to further study, but should be feasible with the current approach. We were able to detect memory traces after a few hours, whereas memory transfer from hippocampus to cortex probably takes at least several days (Wang et al. 2006; Rudy and Sutherland 2008). This accelerated formation of detectable traces may be related to model artifacts, like the relatively small network size. Alternatively, it may be easier to track memory traces through functional network connectivity than by extensively searching for certain patterns in recorded spontaneous activity. Thus, newly formed memory traces may be detected earlier. The simplicity and relatively long duration of our cues possibly further accelerated the formation of memory traces. In general, longer stimulation periods led to faster establishment of a new balance (data not shown), indicating that the duration of the stimulus may influence the time required before a memory trace can be detected.

The computational model, with three incorporated plasticity mechanisms: STF, STD, and STDP, perfectly reproduced these experimental findings. STD has been shown to destabilize attractors in artificial neural networks (Sandberg et al. 2003), but it is added to the computational model to avoid endless bursts of activity, in analogy to the presumed mechanism of burst termination in cultured networks (Eytan and Marom 2006). The implemented STDP enabled network connectivity to adapt to different inputs. However, occasionally stimulation leads to connectivity close to the borders of the connectivity space, with many synapses near their maximum strength or zero. In such cases, more extensive stimulation was required to pull the network out of this state toward another equilibrium. In simulations, tetanic stimulation was more suitable than low-frequency stimulation for retaining connectivity away from these borders. Network activation in the computer model tended to potentiate strong synapses and to depress weaker synapses. Second and subsequent pulses of a tetanus coinciding with an induced network burst, frequently forced synapses away from their extreme values, and kept networks in a state more susceptible to memorizing new inputs. Possibly, addition of a third, homeostatic plasticity mechanism that has been demonstrated in in vitro networks, synaptic scaling (Turrigiano et al. 1998), to the computer model could avoid these artifacts. Larger network models imposed a very high computational load and were not necessary to reproduce the experimental findings. However, it has been shown that the storage capacity of artificial neural networks, or the number of possible stable states (attractors), scales linearly with the number of synapses per neuron (Amit 1989) and, therefore, parallel storage of memory traces may even be better facilitated in larger networks.

We conclude that cultured cortical networks memorize external inputs. A second input did not erase the first memory trace, but both traces were stored in parallel. Three synaptic plasticity mechanisms, STDP, STF, and STD were sufficient to enable parallel memorization of different inputs, in networks without specific circuitry constraints.

Materials and Methods

Cell culturing and stimulation

We obtained cortical cells from newborn Wistar rats at postnatal Day 1. All surgical and experimental procedures complied with Dutch and European laws and guidelines and were approved by the Utrecht University Animal Experiments Review Committee. After trypsin treatment cells were dissociated by trituration. About 400,000 dissociated neurons (400 µL suspension) were plated on a multielectrode array (MEA; Multi Channel Systems), precoated with polyethyleneimine. This procedure resulted in an initial cell density of ∼5000 cells/mm², with aging cell densities gradually decreased to ∼2500 cells/mm². Neurons were cultured in a circular chamber with inner diameter d = 20 mm, glued on top of an MEA, which contained 60 titanium nitride electrodes with a 30-µm diameter and 200-µm pitch (Fig. 1A). The culture chamber was filled with ∼700 µL R12 medium (Romijn et al. 1984). MEAs were stored in an incubator, under standard conditions of 37°C, 100% humidity, and 5% CO₂ in air. For recording, we firmly sealed the culture chambers with watertight but O₂ and CO₂ permeable foil (MCS; ALA scientific), and placed the cultures in a measurement setup outside the incubator. During recording, we kept the CO₂ level of the environment ∼5% and we maintained humidity. For details about the recording setup see Stegenga et al. (2008). Recordings began after an accommodation period of at least 20 min.

We used 20 different cultures for 21 experiments, which were performed 27 ± 10 d after plating of the cells (see Table 1). Cultures were electrically stimulated with biphasic current pulses, of 200 µsec per phase. Figure 5B shows an example of 5 min of recorded activity. Each tick after one of the electrodes 0–59 indicates an action potential recorded at that channel. The first 75 sec of this recording contained low-frequency stimulation, indicated by ticks at channel 60. Figure 5C shows examples of a stimulus response (left) and a spontaneous network burst (right).

Figure 5.

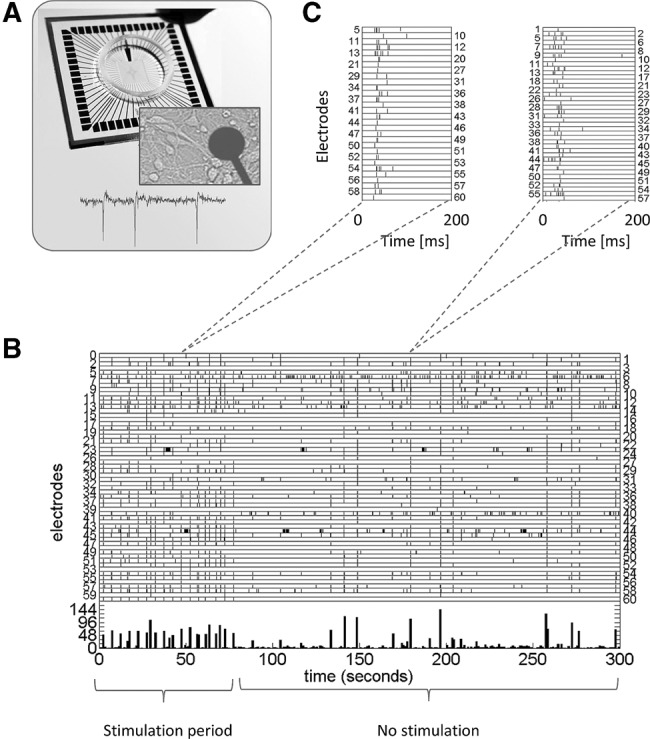
Multielectrode array (MEA) and recorded activity. (A) MEA, zoom at one of the electrodes and several neurons, and an example of extracellularly recorded action potentials. (B) Raster plot of recorded activity. Vertical axes indicate all electrodes, action potentials are shown as ticks in the row corresponding to the recording electrode. Ticks in row 60 indicate stimulus pulses. (C) Examples of a stimulus response (left) and a spontaneous network burst (right).

All electrodes were probed at several amplitudes in random order, to find suitable electrodes for stimulation. There were no constraints related to the location of the stimulation electrodes. The amplitude was set to a level that usually (>50% of stimuli) triggered a network burst in response to a stimulus pulse at the selected electrode (12–24 µA). At these currents, voltages remained sufficiently low to avoid electrolysis. Pulses were applied at a single electrode, either as low-frequency pulses for 10 min (inter-pulse interval: 3–5 sec), or as tetani (trains of 10 pulses at 100 Hz, inter-train interval: 5 sec, duration: 10–15 min). Subsequent stimulation periods were separated by 1 h of no stimulation. Periods of no stimulation were used to record spontaneous activity, needed to infer functional connectivity. In low-frequency stimulation experiments, we calculated the area under the PSTH to quantify the network stimulus response. In tetanus experiments, this was not possible because the mean stimulus response time window largely exceeded the inter-pulse interval. In tetanus experiments, we monitored the array wide activity level during periods of no stimulation to verify that the cultures did not deteriorate during the experiments.

First experiments showed quickly decreasing connectivity changes in response to repeated periods of stimulation at a certain electrode. After 3–4 stimulation periods at a certain electrode only minor connectivity changes were found, not or hardly exceeding spontaneous fluctuations (see Fig. 1B). In experiments with separate periods of stimulation at different electrodes, we aimed to reach this “saturation point” for each electrode, while keeping the total experimental time as short as possible to avoid spontaneous connectivity changes, preferably <15 h (Stegenga et al. 2008). Multiple stimulation site experiments contained four stimulation periods at one electrode, then four periods of stimulation at a second electrode and finally four stimulation periods at the first electrode, and lasted ∼12–13 h.

Connectivity analysis

We used periods of spontaneous activity, including population bursts as well as periods of more dispersed firing, to analyze network connectivity. Long-term recordings were divided into data blocks of 2¹³ spiking events. The 1-h epochs between subsequent stimulation periods were long enough to obtain multiple data blocks in all experiments, and short enough to keep the total experimental time below 15 h. In each data block, we used conditional firing probabilities (CFPs) to determine functional connectivity (le Feber et al. 2007). For all possible pairs of active electrodes (>250 spikes/data block) we calculated CFPs as the probability to record an action potential at electrode j at t = τ (τ > 0), given that one was recorded at electrode i at t = 0. If a CFP curve was not flat (for exact criteria see le Feber et al. (2007), the two neurons were functionally connected. Functional connections were characterized by two parameters: their strength and latency. These parameters may be used to follow the development of a functional connection in time.

In each data block, the strengths of all connections were combined into a connectivity matrix S, where S(i,j) contains the strength of the functional connection from i to j. The magnitude of changes between subsequent data blocks was assessed by the Euclidean distance (ED) between connectivity matrices at time t and time t₀ (Equation 1).

$$\mathrm{E}{\mathrm{D}}_{t_0}\left(t\right)=\sqrt{\sum _{i=1}^n\sum _{j=1}^n{\left[S_{ij}\right(t)-S_{ij}(t_0\left)\right]}^2}$$

t₀ was always smaller than t and chosen as:

• The first data block of a recording, or in the case of stimulation (possibly at multiple electrodes), the last data block before stimulation at that specific electrode. These distances were indicated by ED₀; or

• the last data block that was separated from t by a stimulation period. These distances were indicated by ED_stim.

The total number of functional connections widely differed between cultures, and consequently, absolute ED values covered a wide range. Therefore, we normalized all ED curves per culture to their mean value before statistical testing.

Activity pattern analysis

During phases of no stimulation, network bursts were extracted using the algorithm by Eckmann et al. (2008) and categorized as pre- and post-stimulus bursts. To assess the similarity between stimulus responses and spontaneous bursts, we adopted a method by Segev et al. (2004), which was adapted to yield normalized values between 0 and 1. In short, at all electrodes signals were represented as point processes and convoluted with a normalized Gaussian. We calculated cross correlations per electrode, and used the maximum mean cross correlation (at one certain latency) as a measure of similarity (events correlation; EC).

Computer modeling

We used a 100-neuron computer model to verify that (1) without external input networks established a stable connectivity, (2) external input disrupted this equilibrium, (3) networks reached a new stable connectivity, and (4) this new equilibrium was no longer disrupted by external input.

To simulate the firing activity, we used a (pulse-coupled) spiking neural network model as described in Gritsun et al. (2010, 2011). We used a set of neuronal parameters that adequately reproduced the dynamics of cortical neurons (Izhikevich 2003), for details see “Neuron model.” This set contained a mixture of all neuronal cell types that exist in the cortex, which gave our simulations a certain degree of robustness against variations of cell properties. However, it should be noted that our results might be affected by changes in cell properties. On average, each neuron had 50 connections. This implicates that the probability that any pair of two neurons were monosynaptically connected was 50%. This very high connection probability was necessary to enable the neurons to trigger each other, and ensured a highly recurrent network. The connections were modeled by synapses that expressed STF and STD as described by Markram et al. (1998). In addition to the model by Gritsun et al., synapses also expressed additive (Song et al. 2000) or multiplicative STDP (Van Rossum et al. 2000), implemented with a symmetric implementation of a nearest neighbor pairing scheme. We applied parameter values obtained by Gupta et al. (2000) and Markram et al. (1998) to describe the phenomenological synaptic model of short-term plasticity, including STD and STF, for details on the synapse model see “Synapse model.”

Ongoing spontaneous activity was initiated by white synaptic noise as implemented by Gritsun et al. (2012), see “Synaptic noise and model sensitivity.” Synaptic noise was set to a level high enough to ensure that all models displayed spontaneous activity, including network bursts. This indicated that neurons were not solely driven by noise input, but were able to trigger each other. Connectivity matrices containing the strengths of all synapses were stored every minute to observe the development of connectivity under various conditions of stimulation or no stimulation. To validate the solidity of our findings, we repeated all experiments in multiple simulations, based on different network realizations (different set of neurons and a different connectivity matrix), different noise realizations (with the same stochastic characterization), and different STDP models (see “Synaptic noise and model sensitivity”). A more thorough sensitivity analysis of this type of models can be found in Gritsun et al. (2010, 2011, 2012). The model was implemented in Matlab and C++, codes are available upon request.

We aimed to start stimulation only in networks with stabilized connectivity. To quantify the stability of connectivity, we calculated ED₀ for all connectivity matrices. Connectivity stabilized as the slope of the ED₀ curve against time approached zero. Connectivity was considered stable when this slope dropped below 1% of the slope based on the first five data points. Before computer models were stimulated, we ensured that sufficient time was allowed to develop a stable connectivity. This stable connectivity was used as the reference to calculate ED₀.

To simulate electrical stimulation, we simultaneously activated a random set of three (all excitatory) or nine neurons (two inhibitory and seven excitatory), which was in general sufficient to trigger a network response. This approach is conceptually congruent with experimental stimulation, where even stimulation through a single electrode activates a set of nearby neurons and neurons that have an axon passing close to the stimulation electrode, which together may trigger a reverberating network response. Stimulation was applied as either low-frequency stimuli (0.2 Hz, for 15 min at 9 neurons, see Fig. 3A, or 0.125Hz for 2 h at 3 neurons, see Fig. 3B) or tetani, as described under cell culturing and stimulation. To calculate ED_stim in simulations, we used the mean weights of all synapses during the last 15 min before stimulation and the first 15 min after stimulation. ED_stim values that significantly exceeded those of connectivity matrices without stimulation in between were indicative of a disturbed balance, whereas ED_stim values in the range of spontaneous fluctuations confirmed that the stimulus was compatible with the connectivity.

Neuron model

The structure of the network was based on the network model by Gritsun et al. (2010). Eighty percent of the neurons in the model were excitatory and 20% were inhibitory. Each neuron i spiked when the intracellular potential f_i reached the threshold of 30 mV:

$$x_i\left(t\right)=\{\begin{array}{cc}1& \text{if}{f}_i\ge 30\text{mV}\\ 0& \text{otherwise}\end{array}$$

Each time step the postsynaptic potentials (psp_ij) of all presynaptic neurons were added to the membrane potential v_i:

$$f_i(v_i,\mathrm{ps}{\mathrm{p}}_{ij})=v_i\left(t\right)+{\sum }_{j=1}^n\mathrm{ps}{\mathrm{p}}_{ij}$$

with n the number of neurons.

The membrane potential was described using two differential equations as described in Izhikevich (2003):

$$\frac{\mathrm{d}{v}_i}{\mathrm{d}t}=0.04v_i^2+5v_i+140-u_i+I$$

$$\frac{\mathrm{d}{u}_i}{\mathrm{d}t}=a_i(b_i{v}_i-u_i)$$

with a resetting of the variables v and u after spiking:

$$\text{if}{v}_i\ge 30\text{mV},\text{then}\{\begin{array}{c}{v}_i\leftarrow c_i\\ u_i\leftarrow u_i+d_i\end{array}$$

Here, v_i and u_i are the membrane potential and the recovery current. The recovery current represents the activation of K⁺ and the inactivation of Na⁺ currents. The time scaling of recovery was described by a_i, with lower a_i resulting in slower recovery. b_i described the sensitivity of u_i for subthreshold variations of v_i c_i and d_i describe the after-spike reset value of v_i and u_i · c_i represents the fast high-threshold K⁺ conductance and d_i the slow high-threshold K⁺ and Na⁺ conductances. I was the input to the neuron with arbitrary units and can be used for synaptic currents or injected DC currents. All models contained a mixture of the different inhibitory (fast spiking and low-threshold-spiking neurons) and excitatory neuron types (regular spiking, intrinsically bursting, and chattering neurons). The mixture was created by assigning the following values to the parameters for excitatory neurons:

$$\begin{array}{rl}(a_i,b_i)& =(0.02,0.2)\\ (c_i,d_i)& =(-65,8)+(15,-6){r_i}^2\end{array}$$

and to the inhibitory neurons:

$$\begin{array}{rl}& (a_i,b_i)=(0.02,0.25)+(0.08,-0.05)r_i\\ & (c_i,d_i)=(-65,2)\end{array}$$

in which r_i is a random variable uniformly distributed over [0;1]. In Equation (7) r_i was squared to create a bias toward RS neurons (Izhikevich 2004).

Synapse model

Upon the arrival of new synaptic input the postsynaptic potential was increased (excitatory input) or decreased (inhibitory), the amplitude of this change reflected the synaptic efficacy (se_ij). Otherwise, the PSP declined to baseline with time constant τ_syn. We took τ_syn = 5 msec for both excitatory and inhibitory neurons, based on the time constants of the AMPA and the GABA_A synaptic conductances (5.3 and 5.6 msec, respectively (Dayan and Abbott 2000)).

$$\frac{\mathrm{dps}{\mathrm{p}}_{ij}}{\mathrm{d}t}=-\frac{\mathrm{ps}{\mathrm{p}}_{ij}}{{\tau }_{\mathrm{syn}}}+\mathrm{s}{\mathrm{e}}_{ij}{\mathrm{e}}_{ij}\delta (t-t_j^{\mathrm{sp}}-l_{ij})$$

where, $t_j^{\mathrm{sp}}$ is the time of spiking of the postsynaptic neuron, e_ij is 1 when the presynaptic neuron (j) was excitatory, −1 when this neuron was inhibitory, and 0 if there was no connection between the neurons.

The latency (l_ij) is defined as the total delay between generation of the action potential in neuron j and arrival of the postsynaptic potential in neuron i. i_ij is normally distributed between 3.5 and the maximal latency (D_max). D_max is estimated to be 25 msec in cortical cultures (Gritsun et al. 2010). We maintained this value of D_max, even in the current, much smaller network model to avoid that a small D_max of a few milliseconds, combined with the time step of 1 msec would give all neuron pairs approximately the same latency.

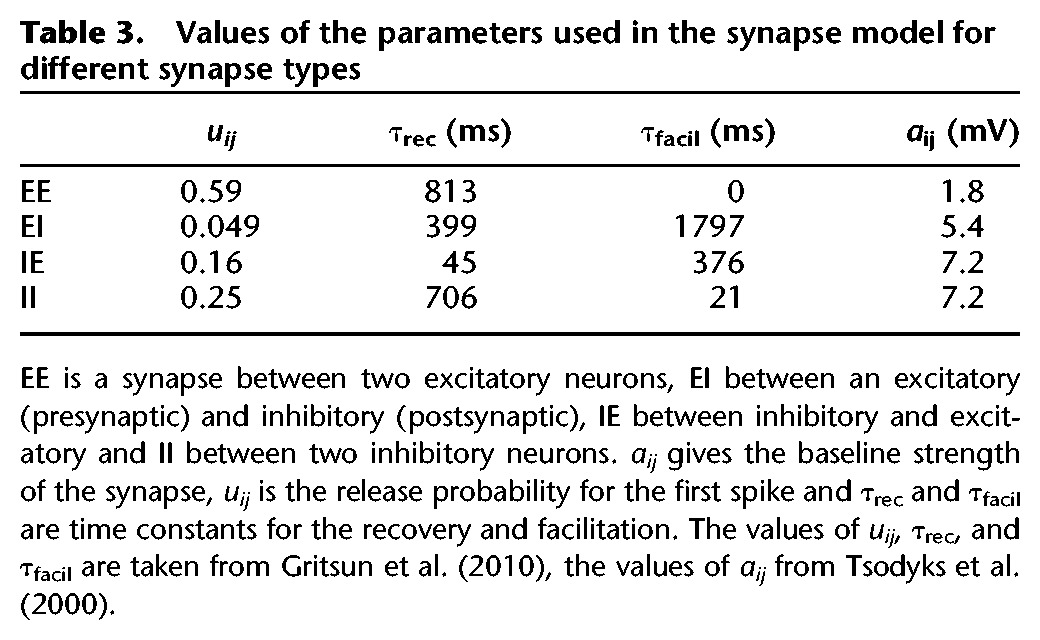
The synaptic efficacy represented different processes of synaptic plasticity: $\mathrm{s}{\mathrm{e}}_{ij}=F\cdot a_{ij}\cdot r_{ij}\cdot y_{ij}\cdot w_{ij}$, in which r_ij, y_ij, and w_ij are variables giving the relative strength of the synapse. r_ij is related to the fraction of neurotransmitter available and represents short-term depression, y_ij represents STF, and w_ij is a factor determined by STDP. Initial values are shown in Table 2. F and a_ij are parameters that give the baseline strength of the synapse. The value of a_ij depends on the type of synapse as shown in Table 3. With these values of a_ij, the value of se corresponds to biologically plausible EPSP values if F = 1. F, a compensation factor to achieve bursting patterns in the small network with few inputs per neuron was equal for all synapses and was set to a value necessary for bursting.

Table 2.

Initial values of the variables

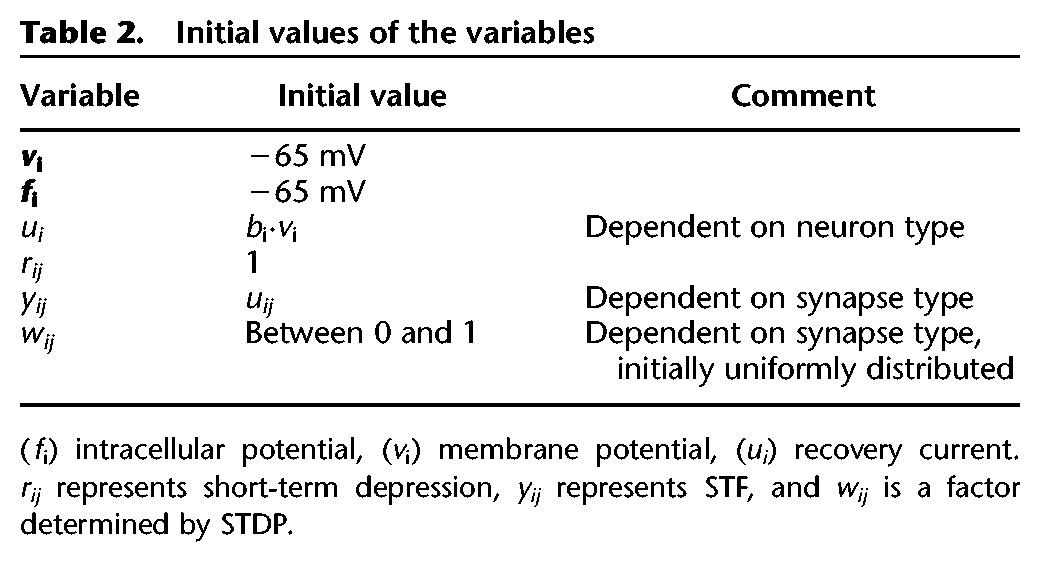
Table 3.

Values of the parameters used in the synapse model for different synapse types

Short-term plasticity

STF and depression were implemented using the model of Markram et al. (1998).

With presynaptic spikes, r and y were updated according to the following equations:

$$r_{ij}^k=r_{ij}^{k-1}\left(1-y_{ij}^k\right){\text{e}}^{-\mathrm{\Delta }{t}_{\mathrm{STP}}/{\tau }_{\mathrm{rec}}}+1-{\text{e}}^{-\mathrm{\Delta }{t}_{\mathrm{STP}}/{\tau }_{\mathrm{rec}}}$$

$$y_{ij}^k=y_{ij}^{k-1}{\text{e}}^{-\mathrm{\Delta }{t}_{\mathrm{STP}}/{\tau }_{\mathrm{facil}}}+u_{ij}\left(1-y_{ij}^{k-1}{\text{e}}^{-\mathrm{\Delta }{t}_{\mathrm{STP}}/{\tau }_{\mathrm{facil}}}\right)$$

In these equations, Δt_STP is the time difference between the previous and the current presynaptic spike, u_ij is the release probability for the first spike and τ_rec and τ_facil are time constants for the recovery and facilitation, respectively. k is the running variable for the spikes. For instance, r^k_ij refers to the fraction of neurotransmitter available with the current spike in the synapse between neuron j and i. Table 3 shows the values for u_ij, τ_rec, and τ_facil.

Spike-timing-dependent plasticity

Both the additive and the multiplicative STDP model update w at every pre- and postsynaptic spike: $w_{ij}^{k+1}=w_{ij}^k+\mathrm{\Delta }w$. STDP was only implemented in excitatory connections; if the presynaptic neuron was inhibitory, w was constant and equal to 0.5. Both models were based on measurements of EPSC. This means that they actually model how the EPSC instead of the EPSP is influenced by STDP. However, it was assumed that these were linearly correlated; so these equations could also be used to model the influence of STDP on the EPSP.

The additive STDP model (Song et al. 2000) used the following update rules:

$$\mathrm{\Delta }{w}_{ij}=\{\begin{array}{cc}{A}_{-}{\mathrm{e}}^{\mathrm{\Delta }{t}_{\mathrm{STDP}}/{\tau }_{-}}& \mathrm{if}\mathrm{\Delta }{t}_{\mathrm{STDP}}<0\\ A_{+}{\mathrm{e}}^{-\mathrm{\Delta }{t}_{\mathrm{STDP}}/{\tau }_{+}}& \mathrm{if}\mathrm{\Delta }{t}_{\mathrm{STDP}}\ge 0\end{array}$$

with A₊ = 0.005, A₋ = −1.05 A₊, and τ₋ = τ₊ = 20 msec. Δt_STDP is the time difference between the presynaptic and the postsynaptic spike, Δt_STDP = t_post−(t_pre + l_ij). Furthermore, we limited w_ij to 0 ≤ w_ij ≤ 1 to avoid instability.

The value of A_– followed from the restriction that the product of the probability of potentiation and amount of potentiation should equal the product of the probability of depression and amount of depression. The probability of a postsynaptic spike just after a presynaptic spike is higher than a presynaptic spike just after a postsynaptic spike, because presynaptic spike can initiate postsynaptic spike, but not vice versa. Thus, the mean amount of depression should be lower than the mean amount of potentiation (Song et al. 2000).

The multiplicative model (Van Rossum et al. 2000) was almost equal to the additive model, except that the weight update of the depression depended on the weight. The same parameter values were used, but the value of A₋ was adapted to depend on the current weight.

This gave the following update rules for the multiplicative model:

$$\mathrm{\Delta }{w}_{ij}=\{\begin{array}{cc}{A}_{-}{w}_{ij}{\mathrm{e}}^{\mathrm{\Delta }{t}_{\mathrm{STDP}}/{\tau }_{-}}& \mathrm{if}\mathrm{\Delta }{t}_{\mathrm{STDP}}<0\\ A_{+}{\mathrm{e}}^{-\mathrm{\Delta }{t}_{\mathrm{STDP}}/{\tau }_{+}}& i\mathrm{f}\mathrm{\Delta }{t}_{\mathrm{STDP}}\ge 0\end{array}$$

Here, we took A₋ = −0.0105, assuming that w_ij averaged ∼0.5. In this, STDP model boundaries were not necessary.

Synaptic noise and model sensitivity

Synaptic noise initiated network spiking and bursting behavior. Synaptic noise was injected as white noise added to the synaptic current I (see Equation 4). This approach avoided an undesired influence of the time step size on the solution of the differential equations.

The mean value of the synaptic noise (µ) was 0. Simulations with different values of the compensation factor of the synaptic strength (F), the standard deviation of the noise (σ), and the maximal latency (D_max) were done to assess the influence of these parameters on the number of bursts, the duration of these bursts and the spike frequency during these bursts. This was done with the additive as well as the multiplicative STDP model. The simulation time was 5 min and the initial weights of the synapses (w) were uniformly distributed between 0 and 1. The neuron parameters (a, b, c, and d) and the connectivity matrix (L) were equal in all simulations, except for the simulations in which D_max was varied, when all latencies increased or decreased proportionally to D_max. Simulations with the following parameter values were performed:

• F ranged between 4 and 10 with steps of 1. These simulations were done with σ = 2.0 or σ = 2.5. D_max was 25 msec.

• σ Varied between 2.0 and 3.0 with steps of 0.1. F was 5 and D_max was 25 msec.

• D_max was 3.5, 5, 10, 15, 20, and 25 msec. In all these simulations, F = 5 and σ = 2.1.