Simultaneous Pharmacokinetic Modeling of Gentamicin, Tobramycin and Vancomycin Clearance from Neonates to Adults: Towards a Semi-physiological Function for Maturation in Glomerular Filtration

Abstract

Purpose

Since glomerular filtration rate (GFR) is responsible for the elimination of a large number of water-soluble drugs, the aim of this study was to develop a semi-physiological function for GFR maturation from neonates to adults.

Methods

In the pharmacokinetic analysis (NONMEM VI) based on data of gentamicin, tobramycin and vancomycin collected in 1,760 patients (age 1 day–18 years, bodyweight 415 g–85 kg), a distinction was made between drug-specific and system-specific information. Since the maturational model for clearance is considered to contain system-specific information on the developmental changes in GFR, one GFR maturational function was derived for all three drugs.

Results

Simultaneous analysis of these three drugs showed that maturation of GFR mediated clearance from preterm neonates to adults was best described by a bodyweight-dependent exponent (BDE) function with an exponent varying from 1.4 in neonates to 1.0 in adults (Cl_GFR = Cl_drug*(BW/4 kg)^BDE with BDE = 2.23*BW^−0.065). Population clearance values (Cl_drug) for gentamicin, tobramycin and vancomycin were 0.21, 0.28 and 0.39 L/h for a full term neonate of 4 kg, respectively.

Discussion

Based on an integrated analysis of gentamicin, tobramycin and vancomycin, a semi-physiological function for GFR mediated clearance was derived that can potentially be used to establish evidence based dosing regimens of renally excreted drugs in children.

INTRODUCTION

Children may differ from adults in their response to drugs due to differences in pharmacokinetic (PK) and/or pharmacodynamic (PD) relationships (1–3). A prerequisite to developing rational dosing schemes for the pediatric age range (from neonates to adults), is to understand how developmental changes influence this PK and PD relationship (4). Given the large number of drugs used and the wide range in age and bodyweight in the pediatric population, a major effort would be needed to obtain this information for all drugs used in children. Therefore novel approaches to support pediatric data analysis, to develop predictive pharmacokinetic models and to develop rational dosing schemes in children are required. A promising approach would be the characterization of maturation in important metabolic and excretion routes across the pediatric life-span from preterm neonates to adults (4,5). On the basis of model drugs, these maturation functions can be derived and subsequently be used to predict the PK for other drugs that are metabolized or excreted through the same pathway (6,7).

Glomerular filtration rate (GFR) is responsible for the elimination of a large number of water-soluble drugs and drug metabolites. In adults, GFR is well defined with a value of around 120 ml/min (8). Concerning the pediatric age range, it is known that nephrogenesis starts at week 5–6 of gestation and continues until 36 weeks of gestation (8–11). Furthermore, during the first weeks of life, a rapid increase is seen in GFR which is mainly due to hemodynamic changes (8). Adult levels, as expressed per body surface area, are reached at approximately 6–12 months of age (8). However, partly due to the expression of GFR per body surface area, the application of these functions in the analysis of renally excreted drugs in different age categories is complicated underlining the need for novel functions quantifying GFR across the pediatric lifespan. GFR can be determined on the basis of the concentrations of endogenous (creatinine) or exogenous compounds (inulin, radio-isotopes). Nevertheless, several limitations are linked with each of these methods in the pediatric age range. Therefore the most pragmatic method to assess maturation in GFR is the determination of the clearance of a (model) drug that is almost entirely eliminated through GFR and that is widely used in clinical practice across the pediatric age range (12–14). The advantage of the use of clearance of renally excreted drugs as a measure to determine GFR, is that this information can be gathered in daily clinical practice. The latter is of course of major importance in the pediatric and neonatal age range to keep the burden for each patient to a minimum.

The aim of this analysis was to develop a semi-physiological function to describe maturation in GFR on the basis of simultaneous population pharmacokinetic modeling of gentamicin, tobramycin and vancomycin, which are almost entirely eliminated through GFR. Since this analysis is based on three different drugs, a novel system-based pharmacology approach was applied (5). More specifically, within the model a distinction was made between drug-specific and system-specific properties (5). Consequently, the pediatric covariate model on clearance was considered to contain system-specific information on the developmental changes in GFR and therefore the same covariate model on clearance was implemented for all three drugs. The population values for clearance and volume of distribution and the covariate model on volume of distribution were considered as drug-specific values and estimated for each drug separately.

METHODS

Patients and Data

Data of gentamicin, tobramycin and vancomycin were included in this analysis, which were available from previously published studies (15–18) and from retrospective data collection at the intensive care units of the Erasmus MC-Sophia Children’s Hospital, Rotterdam, the Netherlands. In total, data from 1,812 subjects were available, which were divided into four different age categories according to FDA guidelines (19): 1) neonates (0–1 month), 2) children 1 month–2 years, 3) children 2–12 years, 4) children 12–18 years. Fifty-two patients (N=14 neonates, N=22 patients aged between 1 and 23 months, N=15 patients aged between 2 and 11 years, N=1 patients aged between 12 and 18 years) with creatinine values three times higher than the age-related reference values (20–24), were excluded from the analysis as they were considered to be patients with severe renal dysfunction. Beside peak and trough samples taken before and 1 h after initiation or completion of the dose, there were often samples available at other time points. Available data are briefly discussed below while more details on the studies can be found in the original articles (15–18). An overview of the different datasets is given in Table I.

Gentamicin (15,16)

For gentamicin, data of two different studies were combined into one dataset resulting in a total of 1,705 samples available from 717 patients (682 neonates, 26 infants 1–24 months, five children 2–12 years, four children 12–18 years, with a bodyweight range between 440 g and 80 kg).

Tobramycin (17)

A total of 1,273 tobramycin concentrations available from 614 patients were included in this analysis (463 neonates, 67 infants 1–24 months, 48 children 2–12 years, 36 children 12–18 years, with a bodyweight range between 485 g and 85 kg). This tobramycin dataset consisted of data of preterm and term neonates aged up to 4 days of age obtained from a study performed by de Hoog et al. (17) and data of patients ranging between a postnatal age of 9 days and 18 years of age obtained from a retrospective analysis performed at the intensive care units of the Erasmus MC-Sophia’s Children Hospital, Rotterdam, the Netherlands. Patients were included in the retrospective data analysis when they were younger than 18 years and when bodyweight, age and serum creatinine concentration (not exceeding three times the age-related reference value as explained above) was available.

Vancomycin (18)

For vancomycin 1,168 concentrations were available from a total of 429 patients (283 neonates, 87 infants 1–24 months, 42 children 2–12 years, 17 children 12–18 years, with a bodyweight range between 415 g and 85 kg). Two hundred and sixty nine preterm neonates between 1 and 30 days of age were included from a study performed by Allegaert et al. (18) and 160 patients ranging between 4 days and 17 years of age were obtained from a retrospective analysis performed at the intensive care units of the Erasmus MC-Sophia Children’s Hospital, Rotterdam, the Netherlands. For the retrospective data analysis, the same criteria as explained under tobramycin were used.

Table I.

Overview of the Study and Patient Characteristics (Median (Range))

Drug	Gentamicin	Tobramycin	Vancomycin
Number of subjects	717	614	429
Number of blood samples	1,705	1,273	1,168
Age	Median 2 days (1 day–15 years)	Median 3 days (2 days–18 years)	Median 16 days (1 day–17 years)
Subjects (n) per age group (range)
1 (1–28 days)	682 (GA 23–43)	463 (GA 23–43)	283 (GA 23–34)
2 (1–23 months)	26	67	87
3 (2–11 years)	5	48	42
4 (12–18 years)	4	36	17
Bodyweight	2,600 g (440 g–80 kg)	2,010 g (485 g–85 kg)	1,800 g (415 g–85 kg)
Serum creatinine (μmol/L)	72 (12–104)	72 (5–130)	51 (7–144.1)

GA Gestational age (weeks)

Pharmacokinetic Modeling

The population pharmacokinetic analysis was performed with the non-linear mixed effect modeling software NONMEM 6.2. (Globomax LLC, Hanover, MD, USA) using the first-order conditional estimation method with the interaction option (FOCEI). Tools like S-Plus version 6.2.1 (Insightful software, Seattle, WA) with NM.SP.interface version 05.03.01 (© by LAP&P Consultants BV, Leiden, The Netherlands), PsN and R (version 2.10.1) were used to visualize and evaluate the model. Four different steps were used to develop the model: (i) choice of the structural model, (ii) choice of the statistical sub-model, (iii) choice of the covariate model, (iv) model validation.

Structural and Statistical Model

For the structural model, both one and two compartment models were tested. Concerning the statistical model, the inter-individual variability was assumed to be log-normal distributed in an individual i (post hoc value) and is given by the following equation:

$${\theta }_i={\theta }_{TV}\times e^{{\eta }_i}$$ (1)

in which θ_TV is the typical value of the parameter and η_i is assumed to be a random variable with mean value zero and variance ω². For the intra-individual variability and residual error (statistical submodel), proportional (Eq. 2), additive (Eq. 3) and combination (Eq. 4) error models were tested:

$${\mathit{\Upsilon }}_{ij}=C_{\mathit{pred},ij}\times \left(1+{\epsilon }_{ij}\right)$$ (2)

$${\mathit{\Upsilon }}_{ij}=C_{\mathit{pred},ij}+{\epsilon }_{ij}$$ (3)

$${\mathit{\Upsilon }}_{ij}=C_{\mathit{pred},ij}\times \left(1+{\epsilon }_{1,ij}\right)+{\epsilon }_{2,ij}$$ (4)

where Y_ij is the jth observation in the ith individual, C_pred,ij is the predicted concentration and ε_ij is a random variable from a normal distribution with a mean of zero and estimated variance of σ².

Discrimination between structural and statistical models was based on different diagnostic tools (25). A difference in objective function (OFV) of 3.9 points or more was considered as statistically significant (p<0.05 based on χ² distribution). Furthermore, the goodness-of-fit plots (observed versus individual predicted concentrations, observed versus population predicted concentrations, conditional weighted residuals versus time, conditional weighted residuals versus population predicted concentrations) of all data, stratified by drug and age categories were used for diagnostic purposes. Finally the total number of parameters, visual improvement of individual plots, correlation matrix, confidence intervals of parameter estimates, ill-conditioning (26) and shrinkage (27) were assessed. Ill-conditioning was tested by calculating the condition number by dividing the largest eigenvalue by the smallest eigenvalue.

Covariate Model

The pharmacokinetic model was developed by simultaneously analyzing the data of gentamicin, tobramycin and vancomycin. On the basis of a systems-based pharmacology approach, within the model a distinction was made between system-specific and drug-specific information (5,6). Using this approach, it was assumed that the covariate model contains system-specific information derived from the developmental changes in clearance across the pediatric age range from neonates to adults of the underlying physiological systems, in this case GFR. As a result, the covariate relationships on clearance for all three drugs were not tested separately for each drug but the same covariate relationship was tested on clearance of all three drugs (7). The population value for clearance and volume of distribution and the covariate models on volume of distribution were considered to contain drug-specific information and were therefore estimated by NONMEM for each drug separately.

The following covariates were tested: bodyweight, age, serum creatinine concentrations (< three times the age-related upper limit of the reference value in order to exclude severe renal dysfunction) and co-administration of ibuprofen, indomethacin, diuretics, amoxicillin and aminoglycosides. Since during the first 5 days of life serum creatinine values are considered to reflect maternal renal function (10,28), these creatinine values were excluded from the analysis. According to the origin of the data (15–18), serum creatinine was measured using the enzymatic or uncompensated Jaffé method. In order to evaluate the influence of creatinine as a covariate on clearance different approaches were used:

1. Evaluation of creatinine value normalized to age. According to the measuring technique, enzymatic or Jaffé respectively, different age-related reference values were used (20–24).

2. Evaluation of creatinine clearance. Different formulas were used to estimate creatinine clearance (mL/min) in the ith individual: Cockroft-Gault formula, Schwartz formula and Modification of Diet in Renal Disease (MDRD) formula.

Cockroft-Gault:

$${CL}_{cr}i=\frac{(140-\mathit{age})\times \mathit{weight}}{72\times S_{Cr}}(\times 0.85\text{if}\text{female})$$ (5)

where age is expressed in years, weight in kg and Scr is the serum creatinine (mg/dL).

Schwartz formula:

$${CL}_{Cr}i=\frac{k\times \mathit{length}}{S_{Cr}}$$ (6)

where k=0.33 for preterm babies in the first year of life, k=0.445 for full term infants and k=0.55 for infants and children between 1 and 12 years of age, Scr is the serum creatinine (mg/dL) and length was expressed in cm and was determined using the growth charts of the World Health Organization.

MDRD formula:

$${CL}_{Cr}=180\times S_{Cr}^{-1.154}\times {\mathit{age}}^{-0.203}(\times 0.742\text{if}\text{female})$$ (7)

where age is expressed in years and S_Cr in mg/dL.

Creatinine clearance was tested as covariate on clearance using the above mentioned formulas as well as the combination of the Schwartz formula<12 years of age and the Cockroft-Gault or MDRD formula>12 years of age.

Continuous covariates were separately entered into the model using a linear or power function, as shown in Eq. 8

$$P_i=P_p\times {\left(\frac{{\mathit{COV}}_i}{{\mathit{COV}}_{\mathit{median}}}\right)}^k$$ (8)

where P_i indicates the individual or post hoc value of the parameter for the ith subject, P_p is the population value of the parameter and COV is the appropriate covariate. In case of a power function, k represents the exponent value, while for a linear relationship k is fixed to 1. For creatinine, linear or power functions were tested in the denominator since a negative relationship was seen between creatinine concentrations and clearance.

In addition, as it often has been reported that the exponent k (Eq. 8) on clearance is higher in neonates and young children (scaling exponent >1) (29,30) compared to older children and adults (scaling exponent <1), a recently developed bodyweight-dependent exponent function (BDE) was tested in which the scaling exponent varied with bodyweight (31–33). In an analysis undertaken by Wang et al. (31), this BDE model (Eq. 9) was first used, in which the exponent for propofol clearance was found to vary between 1.35 for neonates and 0.57 for adults. The bodyweight-dependent exponent function (BDE) used in this analysis is given in Eq. 9:

$${CL}_{\mathit{GFR}}={CL}_{\mathit{Drug}}\times {\left(\frac{BW}{4kg}\right)}^{\mathit{BDE}}\text{and}\mathit{BDE}=L1\times {BW}^M$$ (9)

in which CL_GFR is clearance in the ith individual with bodyweight BW; CL_drug is the clearance of the drug (gentamicin, tobramycin, vancomycin) in a full term neonate with a bodyweight of 4 kg; BW is bodyweight of an individual i; L1 is the intercept in the scaling exponent and M is the exponent which allows the scaling exponent to change with bodyweight.

The significance of a covariate was statistically evaluated by the use of the objective function. In the forward inclusion a p value <0.005 was considered as statistically significant while a more stringent p value <0.001 was used in the backward deletion. In addition, the reduction in interindividual variability in the parameter studied was evaluated upon inclusion of the covariate in the model. When two or more covariates were found to significantly improve the model, the covariate that reduces the objective function the most was retained into the model and served as a basis for subsequent inclusion of additional covariates. The choice of covariate model was further evaluated as discussed previously under structural and statistical model whereby the results of the model validation were also considered.

Model Validation

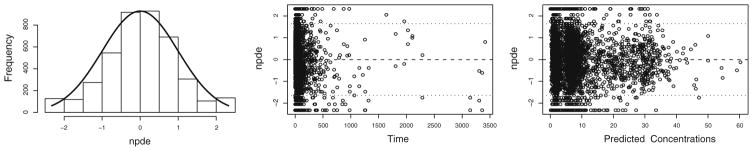
Validation of the model was performed using the normalized prediction distribution error method (34,35). The dataset was simulated 500 times in NONMEM and the observed and simulated concentrations were compared using the NPDE package in R. A histogram of the NPDE distribution and the scatterplots showing the NPDE versus time and versus predicted concentrations were subsequently used to evaluate the final model.

RESULTS

Patients and Data

The analysis was based on a total number of 4,146 observations from three different drugs (gentamicin, tobramycin and gentamicin) collected in 1,760 patients varying in age between 1 day and 18 years of age and with a bodyweight that varied between 0.415 and 85 kg. A summary of the clinical characteristics is given in Table I.

Pharmacokinetic Modeling: System-based Approach

In the pharmacokinetic analysis based on the simultaneous analysis of gentamicin, tobramycin and vancomycin data, a two compartment model parameterized in terms of clearance (CL), intercompartmental clearance (Q), volume of distribution of the central compartment (V1) and volume of distribution of the peripheral compartment (V2) was superior over a one compartment model. Since no covariance step could be obtained, the model was simplified by equalizing Q and V2 to CL and V1, which was supported by the results of the two compartment model. The interindividual variability was only included on clearance values of gentamicin, tobramycin and vancomycin as it could not be estimated on volume of distribution of the three drugs, probably because of overparameterization. The residual variability was best described using a combined error model.

As mentioned in the methods section, the model consisted of drug-specific and system-specific parameters. The covariate model on clearance for these three drugs was considered system-specific information while the population values for clearance and volume of distribution and the covariate model on volume of distribution was considered as drug-specific information. Concerning the system-specific part of the model, a power function on the basis of bodyweight as covariate in which the exponent varied with bodyweight (Eq. 9) was found to best describe the developmental changes in clearance of the three different drugs across the entire pediatric life-span. As shown in Eq. 9, clearance was standardized to a full term neonate with a bodyweight of 4 kg, while it is emphasized that given the nature of this function also the median weight of the population or 70 kg could have been chosen. Implementation of this bodyweight-dependent exponent model on clearance of the three different drugs caused a drop in objective function of 3,607 points (p<0.005). The scaling exponent BDE was found to change in neonates from 1.42 for a neonate of 1,000 g to 1.34 for a neonate of 2,500 g to 1.3 for a neonate for 4,000 g to 1.0 in adults of 18 years old with a bodyweight of 70 kg. A higher objective function (104 points) was found when bodyweight was implemented using a power function (Eq. 8) on clearance of the three drugs. Bodyweight was also identified as most important covariate on volume of distribution of the central compartment for all three drugs. Bodyweight was implemented using a power function for gentamicin and tobramycin, while a linear function was identified for vancomycin causing in total a drop in objective function of 2,438 points (p < 0.005). By implementing these covariates, a large part of the interindividual variability on clearance of gentamicin (62%), tobramycin (87%) and vancomycin (77%) was explained. Although the influence of creatinine on the clearance of the three different drugs was thoroughly evaluated using different methods as described in section “Methods”, creatinine nor creatinine clearance was not identified as a covariate in the final pharmacokinetic model. This may be explained by two different reasons: 1) only children with creatinine concentrations below 3 times the age-related reference values were included, 2) two different methods (Jaffé and enzymatic method) were used to measure creatinine in the different studies. Consequently when serum creatinine values are considered to be normal with one technique, this holds not true for the other technique.

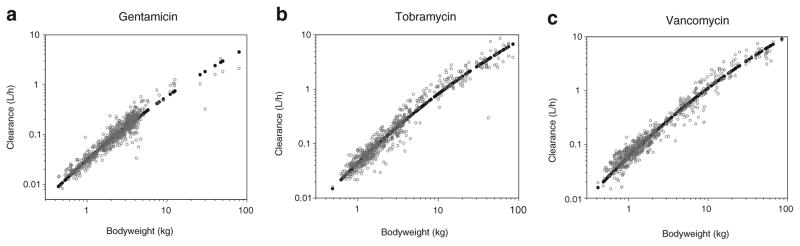
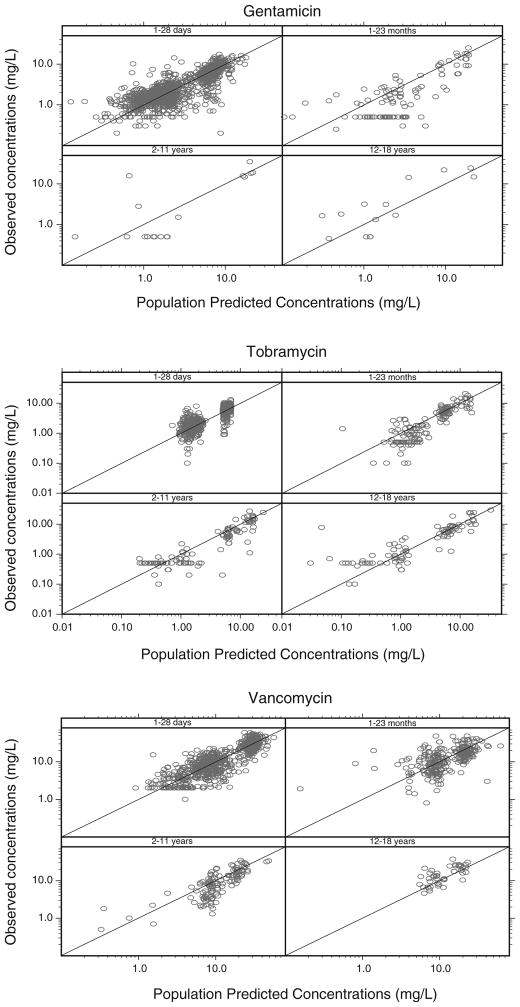
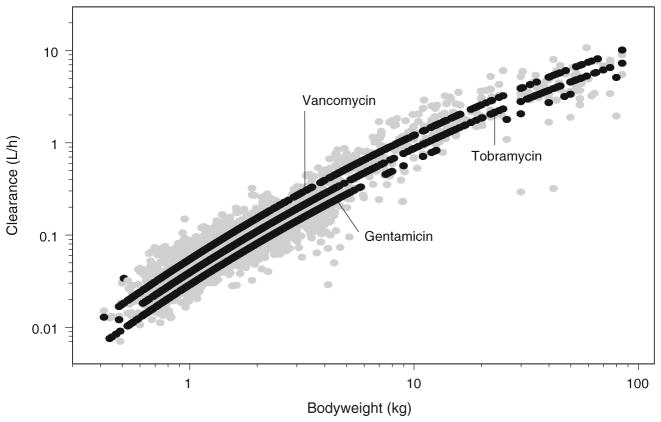
The parameter estimates of the final pharmacokinetic model with the system-specific function for GFR mediated clearance are given in Table II. The individual post hoc and population predicted clearance values versus bodyweight are illustrated in Fig. 1a, b, c. These figures show that for each drug the individual post hoc values are equally distributed around the population clearance values even though one function is used to capture maturational changes in clearance of each of the three drugs. The observed versus population predicted concentrations per drug and per age category are depicted in Fig. 2 while in Fig. 3 the individual and population predicted clearance values of the final system-specific pharmacology model are illustrated versus bodyweight. Based on the correlation matrix, a high correlation was seen between L1 and M (>95%). The condition number (428) was far below the critical value of 1,000 which indicates that the model was not overparameterized.

Table II.

Population Parameter Estimates of the Final System-Specific Pharmacology Model with the System-Specific Function for GFR Mediated Clearance and Drug-Specific Information on Gentamicin, Tobramycin and Vancomycin

Parameter	Final pharmacokinetic covariate model (CV%)
Fixed effects
System specific parameters: ${CL}_{\mathit{GFR}}={CL}_{\mathit{Drug}}\times {\left(\frac{BW}{4kg}\right)}^{\mathit{BDE}}\mathit{BDE}=L1\times {BW}^M$ (Eq. 9)
L1	2.23 (6.23)
M	−0.065 (−12.1)
Drug specific parameters:
CLgenta 4 kg (L/h)	0.21 (2.01)
CLtobra 4 kg (L/h)	0.28 (2.47)
CL vanco 4 kg (L/h)	0.39 (2.72)
V1genta 4 kg (L)	1.45 (2.94)
V1tobra 4 kg (L)	1.90 (1.99)
V1vanco 4 kg (L)	2.22 (2.63)
V1genta=V4 kg×(BW/4 kg)k2 (Eq. 8)
k2	0.759 (4.35)
V1tobra=V4 kg×(BW/4 kg)k3 (Eq. 8)
k3	0.735 (2.56)
V1vanco=V4kg×(BW/4 kg)k4 (Eq. 8)
k4	1 FIX
Qgenta=CLgenta	–
Qtobra=CLtobra	–
Qvanco=CLvanco	–
V2genta=V1genta	–
V2tobra=V1tobra	–
V2vanco=V1vanco	–
Interindividual variability
ω2 on CLgenta	0.143 (12.5)
ω2 on CLtobra	0.158 (16.5)
ω2 on CLvanco	0.171 (10)
Residual variability
σ2 (proportional)	0.0886 (5.21)
σ2 (additive) (mg/L)	0.0494 (22.7)

CL clearance, CL_{4 kg} clearance for a full term neonate of 4 kg, Q intercompartmental clearance, V1 volume of distribution of the central compartment, V2 volume of distribution of the peripheral compartment, BW bodyweight (g), L1 coefficient of the bodyweight dependent exponent function, M bodyweight dependent exponent, k2 the exponent of bodyweight on V1 of gentamicin, k3 the exponent of bodyweight on V1 of tobramycin, k4 the exponent of bodyweight on V1 of vancomycin

Fig. 1.

Individual post hoc (grey) and population predicted (black) clearance values (L/h) versus the most predictive covariate bodyweight for the three different drugs using the final system-specific pharmacology model (a, b, c).

Fig. 2.

Observed versus population predicted concentrations of the final system-specific pharmacology model for gentamicin, tobramycin and vancomycin, split by four age categories.

Fig. 3.

Individual (grey) and population predicted (black) clearance values for gentamicin, tobramycin and vancomycin versus bodyweight (kg) for the final system-specific pharmacology model.

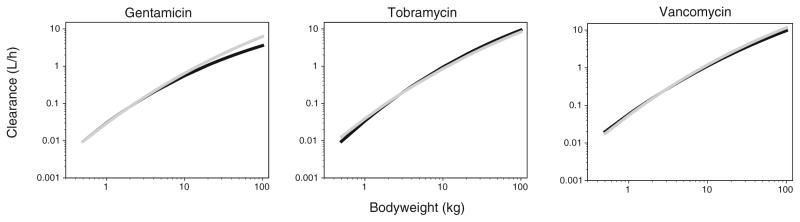
To evaluate the performance of this system-specific pharmacology model, it was compared with independent reference models which were developed separately for each drug using a systematic covariate analysis. In accordance to the system-specific pharmacology model, a bodyweight dependent exponent model was found to best describe the developmental changes in clearance for each drug. Furthermore bodyweight was also found as covariate on volume of distribution. Figure 4 illustrates the population predicted clearance values versus bodyweight for the final system-specific pharmacology model and the independent reference models for the three different drugs.

Fig. 4.

Population predicted clearance values versus bodyweight for the final system-specific pharmacology model (grey) and independent reference models (black) for the three different drugs.

Model Validation

The system-specific model was internally validated using the normalized prediction distribution error method. The results of the NPDE analysis of the final system-specific model (Fig. 5) show that the model can predict the median concentrations accurately, even though a slightly over prediction of the variability was also seen. Finally, no trend was observed between the NPDE versus time and versus predicted concentrations.

Fig. 5.

NPDE results of the final system-specific pharmacology model for the three different drugs. Left panel: Histogram of the NPDE distribution with the solid line representing a normal distribution, middle panel: NPDE versus time, right panel: NPDE versus predicted concentrations.

DISCUSSION

In order to support data analysis, to develop predictive models and to develop rational drug dosing schemes in children, new approaches are needed. One of the approaches, which is applied in the current investigation, is to characterize the developmental changes of important metabolic and excretion pathways from neonates until adults by the use of model drugs. Since maturation of renal function is age dependent, resulting in differences in glomerular filtration rate at different stages of development, the aim of this study was to characterize the maturation of GFR throughout the pediatric age range on the basis of three different renally excreted model drugs. To perform this analysis a system-specific pharmacology model (5) was developed in which a distinction was made between drug-specific and system-specific information. In this model, the developmental changes in clearance of all three drugs from preterm neonates to adults were considered system specific information and were characterized on the basis of one bodyweight-dependent exponent model (31–33) in which the exponent was found to vary with bodyweight from 1.4 in neonates to 1.0 in adults for all drugs. While this approach resulted in adequate description of the data for the entire pediatric life-span (Fig. 3), it is emphasized that the description of the developmental changes in renal clearance, performed in this analysis can also be viewed as empirical because an (advanced) allometric function is used. We prefer however the use of the term semi-physiological because this approach meets in the middle of a standard population pharmacokinetic analysis and a full physiologically based pharmacokinetic analysis because both drug specific and system specific information are estimated in one model.

The performance of this system-specific pharmacology model was compared with independent reference models which were developed separately for each drug using a systematic covariate analysis. In Fig. 4 clearance values are plotted versus bodyweight for the system-specific pharmacology model and for the independent reference models for the three different drugs. While for tobramycin and vancomycin, similar clearance values are observed over the entire pediatric age range, a difference between the two approaches is observed for gentamicin at the higher clearance values. For example the estimates for clearance for a neonate of 4 kg were for gentamicin 0.21 and 0.20 L/h, for tobramycin 0.28 and 0.29 L/h and for vancomycin 0.39 and 0.38 L/h for the system-specific and independent reference model, respectively. For a child of 20 kg, the estimates for clearance were 1.38 and 1.07 L/h for gentamicin, 1.84 and 2.08 L/h for tobramycin and 2.56 and 2.29 L/h for vancomycin, while for an individual of 60 kg the estimates for clearance were 4.00 and 2.54 L/h for gentamicin, 5.34 and 6.07 L/h for tobramycin and 7.43 and 6.34 L/h for vancomycin for the system-specific and independent reference model, respectively. This difference for gentamicin in the higher clearance values between the two different approaches can probably be explained by the fact that for gentamicin data of only 9 individuals were available in the age range between 2 and 18 years (Fig. 2). Compared to the independent reference model of gentamicin, in the system-specific pharmacology model this information is supported by information on tobramycin and vancomycin for which much more information was available between in the age range between 2 and 18 years. It is therefore anticipated that for gentamicin the system-specific pharmacology model may be more reliable than the independent reference model for the higher bodyweight ranges.

In this analysis, the developmental changes in GFR were described from neonates until adults using only bodyweight as covariate on clearance. In an article of Rhodin et al. (36), maturation of renal function was described from premature neonates to adults using a pooled dataset of 8 different studies in which GFR was evaluated based on clearance of Cr-EDTA, mannitol, inulin, iohexol and sinistrin. Both bodyweight and postmenstrual age were identified as covariates to describe the maturational changes in GFR. Bodyweight was included on clearance using an allometric function with an exponent of 0.75 while postmenstrual age was included using a sigmoidal hyperbolic function. In our analysis which was based on a systematic covariate analysis on the basis of statistical principles, bodyweight was identified as most important covariate on clearance. More specifically, it was found that bodyweight was best implemented on clearance using a bodyweight-dependent exponent model in which the exponent based on bodyweight was found to range from 1.4 in neonates to 1 in adults (Fig. 6). These findings confirm the results of previous studies in which it was also shown that the scaling exponent on clearance is higher in neonates and young children compared to older children and adults (29,30,32). Moreover the difference in scaling exponent signifies that the largest increase in clearance of these different drugs, which in their turn reflect GFR, is seen in the first weeks of life until 1 year after birth (8) (Fig. 1). As suggested before, this can be due to hemodynamic changes leading to an increase in renal blood flow and decrease in vascular resistance (9,37).

Fig. 6.

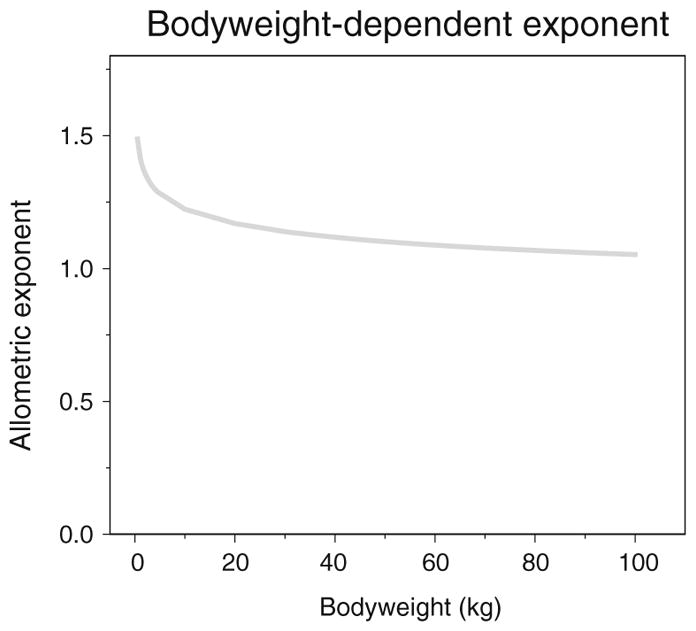
The relationship between the allometric exponent in the final system-specific pharmacology model and bodyweight (kg) in the bodyweight-dependent exponent model (Eq. 9).

Previously, a pharmacokinetic model was developed describing the developmental changes in clearance of amikacin in preterm and term neonates on the basis of birth bodyweight and postnatal age, representing antenatal and postnatal maturation of the kidney, respectively (29). In that model, that proved of predictive value for other renally excreted antibiotics in neonates (38,39) a decrease in clearance was seen when ibuprofen was co-administered. Since the combination of birth weight and postnatal age is not applicable for older children, bodyweight and age were studied as covariates. In the current study in which clearance of three different renally excreted drugs was described from neonates until adults, bodyweight was included on clearance using the bodyweight-dependent exponent model, because it proved superior over age. Although the final system-specific pharmacology model based on bodyweight was able to describe the observed concentrations without bias in all age categories, including neonates, for all drugs (Fig. 2), it needs to be evaluated whether the model based on birth weight and postnatal age (29) for the neonatal population would be superior in precision over the current model. Finally ibuprofen was not identified in this current study as a covariate on clearance. Probably this is due to the limited available information on co-administration of ibuprofen or indomethacin. Although it can not be excluded that separate models are needed to describe more accurately the developmental changes in neonates, in the current study we were able to successfully describe the developmental changes over the entire pediatric age range.

In this analysis, an influence of serum creatinine or creatinine clearance could not be identified, even though different approaches were tested (methods). This seems an unexpected finding because patients with creatinine values up to three times the age-related reference values (20–24) were included in the analysis. Potentially, this result may in part be explained by the fact that two different methods (Jaffé and enzymatic method) were used to measure creatinine concentrations in the different studies. Due to interferences with proteins, ketoacids, cephalosporins and bilirubin, the Jaffé method overestimates creatinine concentrations compared to the enzymatic method (40–42). In adults it is seen that serum creatinine concentrations are overestimated by the Jaffé method by about 30% compared to the enzymatic method (43,44). In neonates and children this overestimation could not be exactly quantified or changes continuously (22,45). Moreover, this difference in creatinine measurement also affects the formulas used to calculate creatinine clearance to estimate GFR (42). Consequently these formulas need to be adapted based on the used measuring technique. Finally, the numbers of patients with a three times increased serum creatinine concentration across the entire age range was low (5%), which should be considered when interpreting this result. Therefore, it seems that care should be taken to apply the model to children with a creatinine concentration between the two- and three times the age-related reference value. We should however notice that the final system-specific pharmacology model is able to describe the observed concentrations of all different age ranges of the three drugs adequately and without bias, even though creatinine was not included in the final model. Moreover without inclusion of creatinine on clearance, a large part of the interindividual variability was explained for the three drugs (gentamicin: 62%, tobramycin: 87%, vancomycin: 77%).

This analysis based on the use of three different renally excreted drugs to characterize GFR from neonates until adults has in addition to a number of advantages (e.g. information can be obtained directly from clinical practice causing no additional burden for patients) also some restrictions. First of all, it should be emphasized that the model developed in this study describes the developmental changes in GFR in patients without severe renal impairments. To evaluate maturation of GFR in patients with an impaired renal function, new studies need to be performed. Furthermore, it should be taken into account that data are obtained from patients staying at the intensive care units for which factors of critical illness or augmented renal clearance may have an influence on renal function.

In conclusion, in this study, we were able to develop a system-specific pharmacology model describing maturation in GFR from neonates to adults based on three different renally excreted drugs using a bodyweight-dependent exponent function. In a next step, it will be evaluated whether this model can be used to predict other renally excreted drugs, which has been shown before for a neonatal GFR model (29,39). In addition, it would be useful to analyze the sensitivity of this relationship to other model parameterizations and to characterize the exact influence of differences in pharmacokinetic and physicochemical properties. Furthermore, besides the extension of this system-specific pharmacology model to other renally excreted drugs the possibility to describe the developmental changes in tubular processes across the entire pediatric age using this system-specific GFR model can be explored when analyzing clearance of a drug undergoing both GFR and tubular excretion. By applying a more system-based approach the development of pharmacokinetic models will be advanced and the development of evidence-based and individualized dosing regimen in children be facilitated.

CONCLUSIONS

In this study the developmental changes in GFR mediated clearance in neonates, infants, toddlers, children and adolescents were described by describing the pharmacokinetics of three renally excreted drugs, gentamicin, tobramycin and vancomycin. Based on a distinction between drug-specific and system-specific parameters, a semi-physiological function for GFR mediated clearance was derived that can potentially be used to facilitate sparse data analysis and evidence based dosing regimens of renally excreted drugs in children..

ABBREVIATIONS

BDE

Bodyweight-dependent exponent

BW

Bodyweight

GFR

Glomerular filtration rate

NPDE

Normalized prediction distribution error method

PD

Pharmacodynamics

PK

Pharmacokinetics

PNA

Postnatal age