Learning to learn about uncertain feedback

Abstract

Unexpected outcomes can reflect noise in the environment or a change in the current rules. We should ignore noise but shift strategy after rule changes. How we learn to do this is unclear, but one possibility is that it relies on learning to learn in uncertain environments. We propose that acquisition of latent task structure during learning to learn, even when not necessary, is crucial. We report results consistent with this hypothesis. Macaque monkeys acquired adaptive responses to feedback while learning to learn serial stimulus-response associations with probabilistic feedback. Monkeys learned well, decreasing their errors to criterion, but they also developed an apparently nonadaptive reactivity to unexpected stochastic feedback, even though that unexpected feedback never predicted problem switch. This surprising learning trajectory permitted the same monkeys, naïve to relearning about previously learned stimuli, to transfer to a task of stimulus-response remapping at immediately asymptotic levels. Our results suggest that learning new problems in a stochastic environment promotes the acquisition of performance rules from latent task structure, providing behavioral flexibility. Learning to learn in a probabilistic and volatile environment thus appears to induce latent learning that may be beneficial to flexible cognition.

Our environment is both noisy and volatile, and we track the resulting uncertainty to guide our choices (Behrens et al. 2007). Monkeys and humans successfully make choices and switch strategies in tasks with both features (Pleskac 2008; Rudebeck et al. 2008; Walton et al. 2010; Collins and Koechlin 2012; Donoso et al. 2014; McGuire et al. 2014). In these studies, increasingly sophisticated models, often derived from Bayesian principles, explain behavior and its neural correlates in well-trained subjects. But subjects are trained before data are acquired, and the training process, during which subjects learn to learn about the different causes of unexpected feedback, is surprisingly understudied. In these tasks, an unexpected negative feedback might be due to the noise, or more formally the stochasticity of an event or outcome. Such feedback should be ignored for optimal performance. Unexpected feedback may also be due to a change in the settings or rules of our volatile environment. This should induce a switch of choice strategy. Although we do not know how we learn to learn about these features, learning to learn appears to provide tuning of cognitive control processes required for efficient adaptation (Collins and Frank 2013).

The way in which we learn is likely to modify our response to stochastic elements of the environment. This is especially true in many naturalistic settings, such as foraging. By learning to be more efficient we may make the environment more changeable by depleting resources quicker and so increasing the need to switch strategies—this is a common problem for optimal choice in foraging situations (Ollason 1980; McNamara and Houston 1985). Hence improved learning can increase volatility, and in the context of increased volatility, stochastic outcomes become less easy to detect and ignore (Payzan-LeNestour and Bossaerts 2011).

This predicts that the response to stochasticity should modify with learning to learn. The strategies employed by human subjects are shaped by a priori information about the types of environmental uncertainty in the task (Hertwig et al. 2004; Payzan-LeNestour and Bossaerts 2011). Across nature, learning in stochastic (as opposed to deterministic) environments leads to greater behavioral flexibility as measured by remapping tasks (Gallistel et al. 2001; Biernaskie et al. 2009; Tebbich and Teschke 2014). So, in these cases, subjects learn to learn about uncertain tasks and, in doing so, acquire abstract information about latent task structure, even when not necessary (Kornell et al. 2007; Gershman et al. 2010; Collins and Frank 2013). Deep neural networks can now acquire such latent structure and generalize it across a range of tasks (Mnih et al. 2015), suggesting that this acquisition process could be crucial to behavioral flexibility. We sought to show that learning to learn in a stochastic and volatile environment drives the acquisition of latent information. Importantly, this latent information should impact performance and strategy (Collins and Frank 2013) in ways that identify the nature of the learning to learn process.

Learning to learn was established in deterministic tasks in primates by the seminal work of Harlow on “learning sets” (Harlow 1949). Monkeys acquire a learning set that provides optimal performance on tasks of simple associative learning, as well as reversal learning (Murray and Gaffan 2006). Learning set is posited as a memory-dependent performance rule, for example “win-stay lose-shift” based on previous feedback (Murray and Gaffan 2006). But as soon as feedback is determined by any probabilistic rule, optimal performance would require choice driven by more than the single previous outcome—it is unclear whether simple “win-stay lose-shift” is then adapted or modified in order to track a longer feedback history.

Monkeys with learning set flexibly transfer between new learning and remapping learning (Schrier 1966). This flexibility derives from “win-stay lose-shift,” as in deterministic tasks the rule applies equally to new and remapped associations. Hence, monkeys naïve to remapping or reversal learning are able to remap their knowledge very efficiently. These deterministic tasks are a special case, but if such benefits of learning to learn are generalizable to more realistic stochastic settings, transfer effects to remapping tasks should also be observable in such settings.

In this study, therefore, we follow the evolution of responses to stochasticity across learning to learn in a paradigm in which the level of volatility is driven by changing performance. We tracked the progress of monkeys as they acquired new problems in a stochastic environment. Each time monkeys successfully learned a problem, a new problem was presented for learning, imposing volatility in addition to the stochastic nature of the task. We followed how the monkeys learned to learn over a large number of problems, and showed that as volatility increased with learning, monkeys acquired an exploratory response to the stochastic environment, even though the task did not require this. We then tested whether learning to learn in a volatile environment permitted flexible choosing, as learning set does in deterministic settings. Monkeys repeatedly remapped what they learned. Despite their naivety to remapping, the monkeys were immediately able to do so optimally.

Results

Adaptive responses to standard and unexpected feedback differ through learning

Our study proceeded in two major steps. In the first, monkeys performed an “Identity Task” (IT, Fig. 1B), in which they learned pairs of object–response associations in a probabilistic environment on a 90/10 schedule—that is 10% of trials received “Trap” feedback where the opposing feedback was given compared to the rule currently in force. We refer to this probabilistic feedback as the stochasticity of the environment. A pair of these associations formed a problem. Monkeys serially learned a long sequence of new problems, changing problem after learning the current one to a performance criterion. Each new problem was incidentally signaled by a change in the identity of the stimuli, the first trial of the new problem being a Switch trial. We measured the learning of the monkeys on individual problems by the number of errors to reach the criterion. But in addition to this learning, monkeys also “learned to learn,” by reducing the number of errors to criterion over many problems (Fig. 2A), and learning to rapidly adapt to new stimuli after a Switch (Supplemental Fig. S1). This process eventually stabilized to consistently <50 errors to criterion (vertical dotted lines). We call this the “stabilized period” even if some learning still occurred, as shown by the continuous improvement of percentage correct per problem (Fig. 2B).

Figure 1.

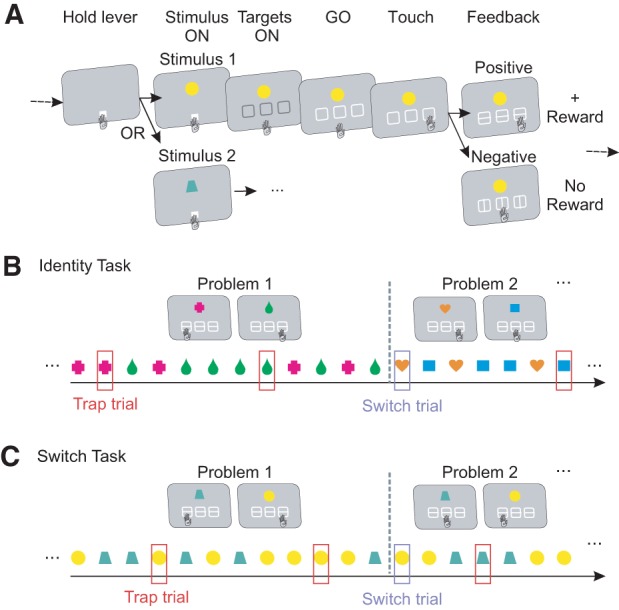
Task design. (A) Structure of a single trial—common to both tasks. The monkey holds a touch screen “lever” to initiate the task, and then selects one of the three targets in response to a central stimulus. Monkeys learn about two stimuli concurrently. Positive or negative visual feedback is horizontal or vertical bars, respectively. Positive feedback was followed by the delivery of a juice reward. (B) Identity Task. Each problem comprised two mappings, between each of the two stimuli and a single target. One stimulus at a time was randomly presented. On Trap trials, misleading feedback was given: positive feedback with a juice reward after an incorrect choice; negative feedback with no reward after a correct choice. Trap trials occurred pseudorandomly with P = 0.1. After a performance criterion (17/20 correct responses), the problem changed (Switch trial), and two new mappings with two new stimuli were randomly selected. (C) Switch Task. Identical to the Identity Task, except that stimuli remained the same when the problem changed. Only the mappings between stimuli and responses changed. Thus, Switches between problems were not visually detectable.

Figure 2.

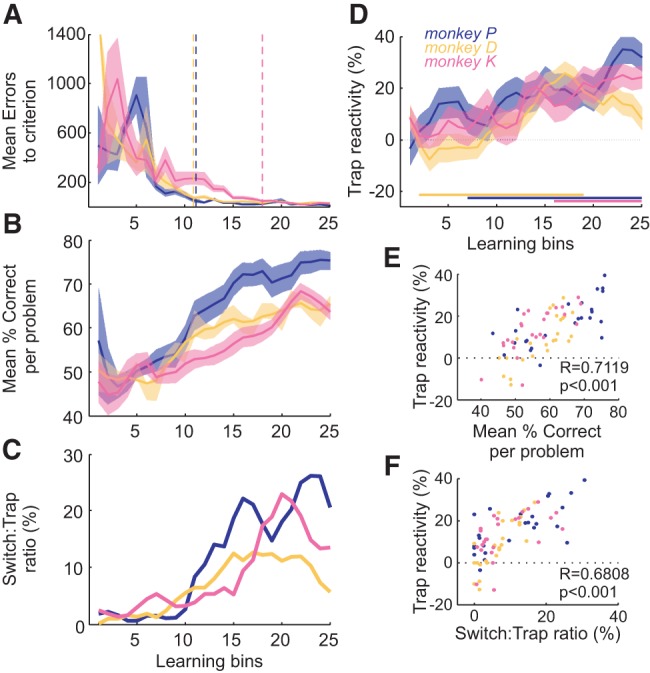
Acquisition of the Identity task. (A) Mean errors to criterion across learning bins, showing significant learning. Vertical dotted lines indicate the stabilization point of the curve for each monkey (see Materials and Methods). Shaded area is standard error of the mean (sem). (B) The mean percentage of correct responses to criterion for problems of each learning bin. (C) The ratio of Switch over Trap trials (taken as an index of the volatility), for each learning bin. (D) The value of the Trap reactivity across learning bins. Trap reactivity is the difference in performance before and after the Trap trial. It increases from an initial value around zero, especially later in learning (horizontal bars). (E) Correlation between Trap reactivity and percentage correct. (F) Correlation between Trap reactivity and the switch:trap ratio. In all figures: monkey P, blue; monkey D, yellow; and monkey K, pink.

Reward maximization in this task would require the monkeys to learn the rule, ignore the Trap trials, and switch rule only in the presence of new stimuli. While theoretically optimal performance like this is obtainable in deterministic tasks, achieving optimality in a stochastic environment is costly. In order to understand how the monkeys adapted to feedback noise over learning, we studied their response to the uninformative Trap trials.

Trap reactivity refers to the change in performance after a Trap feedback compared to performance before it (example in Fig. 4A). Initially monkeys appeared to take very little notice of Trap feedback (Fig. 2D), showing Trap reactivity around 0. This potentially maximized rewards, as Trap trials are uninformative about the rule and unpredictable. Trap reactivity then increased significantly over problems in all monkeys (Fig. 2D, glm, interaction Trials × Learning_Bins, P < 0.001). This increase was strongly correlated with performance (correlation between Trap reactivity and percentage of correct responses per learning bin, R = 0.7119, P < 0.001, Fig. 2E), a counter-intuitive result. Optimal responding demands that monkeys decrease Trap reactivity as they improve at the task, given that a Trap feedback is never predictive of a switch. But significantly improving performance is also increasing the level of volatility (Fig. 2C), as monkeys reach criterion and switch quicker. This is a naturalistic situation—in foraging, increased efficiency of foraging also requires increased shifting between patches. In IT, by analogy, learning increases the ratio of switches to Traps, making Traps harder to distinguish from switches. In this context an increase in Trap reactivity is less counter-intuitive (correlation between Trap reactivity and switch:trap ratio per learning bin, R = 0.6808, P < 0.001, Fig. 2F).

Figure 4.

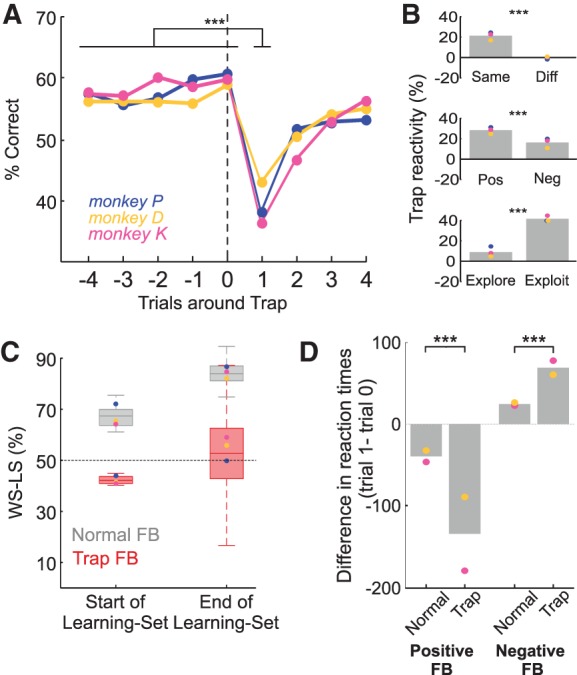
Trap reactivity on IT. (A) Percentage correct around Trap trial (trial 0) for all monkeys. Trap reactivity is the drop of performance between trials 0 and 1. (B) (Top) Trap reactivity is modulated by the stimulus of the trial, specifically being present only when the subsequent trial is on the same stimulus as the Trap trial. (Middle) Trap reactivity is greater for “Positive” Traps (positive feedback after incorrect choice) than “Negative” Traps (negative feedback after correct choice). (Bottom) Trap reactivity is greater during exploitation compared to exploration period (See Experimental procedure). (C) Proportion of trials upon which Win-Stay Lose-Shift (WS-LS) strategy is applied after feedback in the Identity Task, split between normal and Trap feedback. Fifty percent represents a random (not WS-LS) strategy. Box plots represent group data, circles each monkey's mean. WS-LS is significant and increasing across learning for normal feedback, but absent for Trap feedback. (D) Effect of feedback on reaction times (RTs). Plot shows the difference (trial 1—trial 0) in RTs before and after the feedback in question. Full circles indicate a significant (P < 0.001) difference between trials 0 and 1 in every case. Feedback on trial 0 can be positive or negative, and that feedback can either be Trap feedback or “normal.” (Left panel) Post-correct speeding, which is further increased by Trap feedback. (Right panel) Post-error slowing, again increased by Trap feedback. In all figures, Monkey P, blue; monkey D, yellow; and monkey K, pink. Gray bars represent averages of all monkeys. Stars indicate the significant difference between conditions. (***) P < 0.001; (*) P < 0.05; ns: nonsignificant.

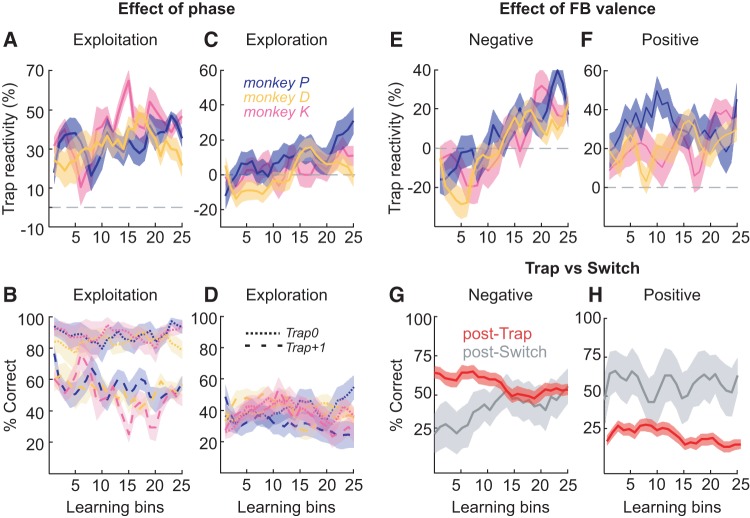
Trap reactivity increased even when the monkeys were performing each problem well, when only exploitation periods were considered (glm on exploitation trials only, interaction Trials × Learning_Bins, P < 0.001) (Fig. 3A). This effect was robust to variation in the criterion used for selecting exploration/exploitation periods (Supplemental Fig. S2). Importantly, the increase in Trap reactivity was not driven by an increase of general performance with learning, but by a decrease of performance on trial Trap+1 (Fig. 3B). Trap reactivity also increased during exploration periods, although less strongly (glm on exploration trials only, interaction Trials × Learning_Bins, P < 0.01) (Fig. 3C). Further, the increase in Trap reactivity could not be accounted for by the increase in correct trials with learning. Even when we considered only the Trap trials in the form of surprising negative feedback after a correct choice (“Negative Trap”), the effect persisted (Separate glms for positive and negative Trap feedback. Interaction Trials × Learning_Bins, P < 0.01 and P < 0.001, respectively) (Fig. 3E,F). This increasing reactivity to unexpected feedback with learning was specific to Trap feedback. We compared Trap reactivity across learning bins with Switch reactivity (taken here as the mean performance on the trials following a switch). While performance after a Trap decreased with learning (accounting for the increase of Trap reactivity) (Separate glms for positive and negative Trap feedback on performance at Trap+1, factor Learning_Bins, P < 0.001 in both cases), performance on the trials following a Switch trial increased after a negative feedback and remained high and stable across learning after a positive feedback (Separate glms for negative and positive Switch feedback on performance at Switch+1,+2 and+3, factor Learning_Bins, P < 0.01 and P > 0.05) (Fig. 3G,H). This shows that monkeys are increasing the volatility in part by becoming efficient at switching, and it is specifically while they do this that they also increase their Trap reactivity; they learn to switch well, but they also learn to switch to unexpected outcomes. It should be noted that Switch reactivity here is performance on the three trials after a Switch, whereas Trap reactivity remains performance at Trap+1. The Switch here provides new stimuli with no reward history (unlike the Trap), and so an appropriate response to it requires integrating feedback from more than one trial. A difference between the effects on performance of Trap and Switch is also obtained; however, if we check this result only on trial Switch+1 (Supplemental Fig. S3, separate glms for positive and negative Trap feedback on performance at Trap+1, factor Learning_Bins, P > 0.05 in both cases).

Figure 3.

Modulations of Trap reactivity and performance with learning set on IT. (A–D) Effect of phase on Trap reactivity across learning: (A) in exploitation and (C) in exploration. Effect of phase on performance at the trial of the Trap (Trap0, dotted line) and at the next trial (Trap+1, dashed line): (B) in exploitation and (D) in exploration. (E,F) Effect of feedback valence on Trap reactivity across learning: (E) after a negative Trap feedback (received after a correct response) and (F) after a positive Trap feedback (after an incorrect response). (G,H) Comparison of performance at trial Trap+1 (red) and Switch+1 to Switch+3 trials (gray) after a (G) negative or (H) positive feedback (concatenated data from the 3 monkeys). In all figures: monkey P, blue; monkey D, yellow and monkey K, pink.

In the stabilized period at the end of the IT, Trap reactivity was highly significant and persistent (reverse Helmert contrast comparing performance at trial Trap+1 versus previous trials, P < 0.001, for the three monkeys) (Fig. 4A). Performance was also lower two trials after a Trap (reverse Helmert contrast, trial Trap+2 versus previous trials, P < 0.001, for the three monkeys) but then returned to initial pretrap levels (reverse Helmert contrast, trial Trap+3 versus previous trials, ns, for the three monkeys) (Fig. 4A). The Trap reactivity acquired by the monkeys had a number of properties. Trap reactivity was stimulus specific—that is specific to the stimulus associated with the Trap feedback (glm, interaction Trials × Stimulus_Similarity, P < 0.001) (Fig. 4B, top). Trap reactivity showed a stronger value in response to a positive Trap (after an incorrect response) compared to a negative Trap (glm, interaction Trials × FB_Valence, P < 0.001) (Fig. 4B, middle). Trap reactivity was also stronger in exploitation than exploration (glm, interaction Trials × Phase, P < 0.001) (Fig. 4B, bottom), demonstrating that monkeys were not shedding their Trap reactivity each time they mastered a problem. This shows that Trap reactivity is a strategy adapted to the overall environmental volatility in the whole task, and not simply a signal of exploration on an individual problem.

Monkeys apply different choice strategies following normal or Trap feedback, further supporting this argument. In deterministic studies of learning set, a Win-Stay Lose-Shift (WSLS) structure is latent within the task. Adopting a WSLS strategy provides an optimal performance rule, and this is posited as the rule acquired in learning set (Murray and Gaffan 2006; Wilson et al. 2010). WSLS, however, becomes nonoptimal in nondeterministic designs—in our case because Trap feedback should be ignored. Nevertheless, our monkeys acquired a significant WSLS strategy for normal feedback (binomial test, P < 0.05), but significantly more so than for Trap feedback, which approached chance levels of WSLS (glm on win-stay lose-shift values, main effect of Normal_or_Trap, P < 0.001). Indeed, the monkeys showed significantly greater acquisition of WSLS for normal feedback (same glm, interaction Normal_or_Trap × Learning_Bins, P < 0.05) (Fig. 4C). This shows that in the main our monkeys learn the stochastic task as other monkeys have learned the deterministic one (Harlow 1949; Izquierdo et al. 2004; Murray and Gaffan 2006)—using normal feedback to apply WSLS. But in addition the monkeys clearly learned to differentiate unexpected feedback (Trap and Switch trials), and applied a different strategy to that class of feedback. Specifically, on Trap trials monkeys are not using WSLS (Fig. 4C, low WSLS after Trap), but they are significantly changing response (Fig. 4A, Trap reactivity). Their strategy after Trap feedback therefore appears to be more random than these alternatives—and could thereby be interpreted as exploratory.

Different responses to feedback and Trap reactivity were also reflected in reaction times (RTs, Fig. 4D). RT decreased in the trial following positive feedback (two-sample Kolmogorov–Smirnov test, P < 0.05, for both (normal or trap) cases, for monkey D and K. Monkey P's data could not be analyzed due to technical problems); and increased after negative feedback (two-sample Kolmogorov–Smirnov test, P < 0.05). These post-correct speeding and post-error slowing effects were accentuated significantly after Trap trials (multifactor ANOVA on RT differences, factor Normal_or_Trap: P < 0.001, in both negative and positive cases).

Over the course of learning to learn about a task in a probabilistic environment, monkeys both adapted their responses to the task contingencies, but also modified their response to unexpected feedback, even though such a response was not the most rewarding strategy. Instead of learning to ignore Trap feedback, they became reactive to all unexpected feedback, Trap or Switch. This result suggests a fundamental influence of a probabilistic learning environment on the way in which animals learn about tasks. The explorative value of unexpected feedback, we propose, drives a performance rule that although not necessary for the initial task (cf. Collins and Frank 2013), is nevertheless important in promoting generalization of the learning.

Adaptive responses to feedback promote flexible decisions

In a second step, we sought to test how having learned to learn with both stochasticity and volatility would serve the monkeys when moving to a task of higher complexity with less information.

To test this we transferred the monkeys to the Switch Task (ST). Here the identity of stimuli was fixed each day, and did not change between problems. Only the rule that associated stimuli to responses changed (Fig. 1C), requiring monkeys to remap what they knew about the current objects and the responses without any cue to the change of rule. Reversal learning is a specific form of remapping task—here remapping was more complicated than simple reversal given there were three options and two objects. It should be stressed that these monkeys, naïve to cognitive testing at the start of the experiment, had never relearned a new rule for the same stimulus. We sought to compare monkeys’ performance when starting ST with their initial performance on IT. Monkeys made many errors when first exposed to IT (Fig. 2A). Monkeys performing classical reversal learning for the first time (Harlow 1949; Izquierdo et al. 2004) show high error rates, just as when they start to learn simple discrimination problems. But importantly monkeys’ initial error rates in reversal learning are lower if they have previously acquired a deterministic learning set (Schrier 1966). ST and IT maintained the same parameters in terms of volatility and stochasticity of the environment, potentially promoting good performance after transfer. Monkeys worked to the same performance criterion, and worked on a 90/10 schedule, receiving 10% Trap trials.

Monkeys maintained low and stable errors to criterion when starting the ST compared with their performance at the end of the IT. That is, their transfer from new problem learning to remapping learning was perfect, regardless of the fact that these monkeys had never remapped a response to a stimulus in their lives (no significant difference between errors to criterion at the end of IT and the start of ST, Kruskal–Wallis test, H = 0.89, 1 d.f., P = 0.34) (Fig. 5A). This performance did not improve further, so the monkeys started this task with immediately asymptotic learning (linear regression over bins of problems, P > 0.05 for the three monkeys). We propose that this high level of performance was reached because a learning to learn process on IT prepared monkeys to transfer to the new and more complex task.

Figure 5.

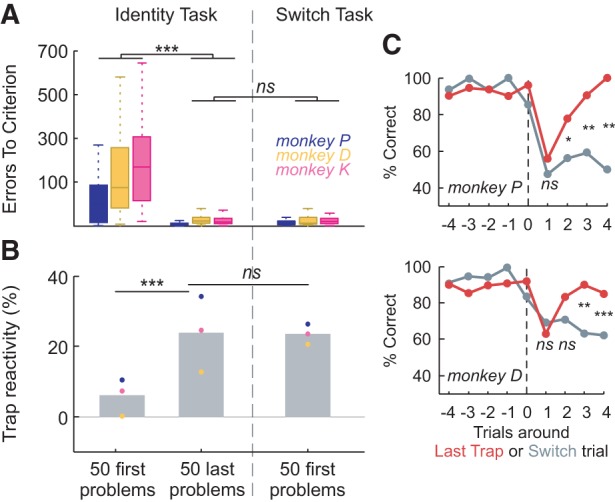
Switch task. (A) Excellent transfer from IT to the ST. Errors-to-criterion for the 50 first problems and the 50 last problems of the IT; and for the 50 first problems of the ST. (B) Trap reactivity is unchanged by task transfer, having increased during learning, suggesting that Trap reactivity acquired in IT is adaptive to ST. Gray bars represent averages of all monkeys. (C) Contrast of behaviors around Last Trap trials and Switch trials. Monkey P (top) shows performance that distinguishes the two forms of unexpected feedback from trial 2—the earliest possible moment. Monkey D's performance (bottom) distinguishes at trial 3. In this case only, the performance after Switch is calculated on the basis of the rules of the previous problem, to provide a comparable score between Switch and Trap. P-values compare the performance at LastTrap versus Switch. (*) P < 0.05; (**) P < 0.01; (***) P < 0.001; ns: nonsignificant.

We cannot specifically attribute high-level performance on ST after transfer to the learning of IT in a stochastic and volatile setting. This is because we do not have a control group that acquired a deterministic version of IT and then transferred to the same stochastic ST as described here. It is very unlikely, given the rich literature of training on remapping tests, that monkeys with such a training regime would also show good and asymptotic transfer to ST, but without such a control group we cannot make that claim. We can nevertheless draw two conclusions. First, monkeys with our stochastic training regime are capable of asymptotic task transfer. Second, there is at least some evidence to support an assertion that this is because of the stochastic nature of IT. Specifically, a number of results support the assertion that Trap reactivity has driven efficient transfer. Trap reactivity on the ST closely matched that of the IT, even though unexpected feedback in the ST could be a signal of either a Trap or a change in rule. As such it is important for the monkeys to discriminate Trap from Switch trials. Trap reactivity was still present (reverse Helmert contrast, on performance at trial Trap+1 versus previous trials, P < 0.001, for monkeys P and D) (Supplemental Fig. S4A) and maintained at the level of the IT (glm, no significant interaction Trials × Task, for the 50 last problems of IT versus 50 first problems of ST (Fig. 5B), with no change over problems (glm, no significant interaction Trials × Learning_Bins). Trap reactivity had the same properties: a stronger effect on trials with the same stimulus as the Trap trial (glm, interaction Trials × Stimulus_Similarity, P < 0.001) (Supplemental Fig. S4B); and a stronger effect after positive compared to negative Trap feedback (glm, interaction Trials × FB_Valence, P < 0.001) (Supplemental Fig. S4C). Trap reactivity was still significantly stronger in exploitation trials than exploration (glm, interaction Trials × Phase, P < 0.001) (Supplemental Fig. S4D). We also observed post-correct speeding and post-error-slowing (two-sample Kolmogorov–Smirnov test, P < 0.05, for both (normal or trap) cases, for each monkey, except monkey K showing no significant post-negative feedback slowing) (Supplemental Fig. S4E). In terms of RTs, monkeys reacted differently to Trap compared with normal feedback only when the feedback was positive (multifactor ANOVA on reaction time differences, factor Normal_or_Trap: P < 0.05 and nonsignificant, for positive and negative cases, respectively).

Trap reactivity is an adapted strategy for using unexpected feedback to differentiate Switch from Trap trials. The only way to distinguish Trap from Switch trials in ST is to maintain a record of the feedback history a number of trials after unexpected feedback. Exploratory responses during this period will make adaptation to Switch even more efficient. Monkeys were immediately capable of doing this in ST, suggesting that they had learned to learn in this fashion during IT. Monkeys very quickly discriminated the two situations (at trial +2 for monkey P, and trial +3 for monkey D; glm, Performance at Switch versus Trap trial +3, P < 0.001 for monkeys P and D, Monkey K was excluded from analysis due to an insufficient number of trials), indicating that they were able to efficiently integrate the feedback history (Fig. 5C). In fact, Traps and Switches were theoretically dissociable after two trials, when the continued presence of the unexpected feedback can first be assessed, given that Trap trials never occur on two successive trials. As such, from the start of ST, monkeys were distinguishing volatility from stochasticity optimally or near optimally, despite the fact that the ST contained far fewer cues to aid the monkeys. The pattern of target selection after a Last Trap or a Switch did differ between the two tasks (Supplemental Fig. S4F). This shows that monkeys were indeed sensitive to the lack of switch cue, but adapted their behavior so rapidly that there were no significant differences in errors to criterion. There were no differences in reaction times in trials following a Last Trap compared to a Switch (two-sample Kolmogorov–Smirnov test comparing distributions for Last Trap versus Switch trials, nonsignificant).

Discussion

Three monkeys acquired a probabilistic task with signaled rule switches. In doing so they increased their response to misleading information provided by Trap feedback. Hence monkeys’ performance was good and stable, but they were not maximizing their rewards for this specific task. This form of responding appeared, however, to be adapted to the changing volatility over learning and continued stochasticity of the reward environment, suggesting that learning to learn led to a choice that was driven by a process that takes these latent variables into account. Monkeys that learned in this way transferred without cost to a more complex version of the task with remapping of previously learned associations and unsignaled rule switches. Good transfer is therefore possible even from tasks that provide stochastic feedback.

The data from the IT show that over the course of learning to learn about a task in a probabilistic environment, monkeys will both adapt their responses to the task contingencies, but also modify their response to unexpected feedback, even in cases where such a response is not necessarily the most rewarding strategy. This result demonstrates the fundamental influence of a probabilistic learning environment on the way in which animals learn about tasks. Trap reactivity continued to increase even when errors-to-criterion was relatively stabilized. Stabilization of learning to learn is therefore an important concern in training animals for neuroscience experiments, where we wish to separate learning effects from elements of the acquired task (Costa et al. 2014). This consideration is also important in situations where learning to learn might be used in wider applications (e.g., Bavelier et al. 2012). If latent information is being acquired, for example about the structure of the task (Collins and Frank 2013), classical measures of learning might not capture this ongoing process, introducing a risk of cutting short the learning to learn process before the attendant advantages can be obtained.

What is the specific process occurring as the monkeys learn to learn? From a modeling perspective, adapting responses to Trap feedback could be akin to a matching of the learning rate for unexpected feedback to the volatility of the environment, a process reflected in decision-making after learning in humans (Courville et al. 2006; Behrens et al. 2007; Payzan-LeNestour and Bossaerts 2011). But the emergence of a significant difference in response strategy after different forms of feedback (Fig. 4C) is striking, suggesting that monkeys are genuinely learning to detect unexpected outcomes and explore after them. It is unclear whether a simple modulation of model learning rate could account for such a categorical change in strategy, but this provides evidence for at least two levels of information acquisition during learning to learn. First, as in deterministic tasks, monkeys are increasing their proportion of WSLS on normal feedback trials. Second, by acquiring the information about the statistics of unexpected outcomes, something that can only be learned by integrating across many trials, monkeys learn to maintain an exploratory strategy to these trials. What is particularly striking in the results from IT is that monkeys are not obliged to acquire this exploratory strategy on this task—there is a clear signal to explore in the change of stimuli—yet they nevertheless do.

It is of note that monkeys’ final level of Trap reactivity in IT represents the final Trap/Switch ratio in the task. The fact that Trap reactivity is present in exploitation, increases with experience, and correlates with percentage correct reinforces the idea that it is a learning-driven strategy. The explorative value of unexpected feedback, we propose, drives a latent performance rule that is not necessary for the initial task (cf. Collins and Frank 2013), but yet is robustly acquired, and might potentially be important in promoting generalization of the learning. Whether this acts as an account of the role of probabilistic environments in other species remains an open question (Gallistel et al. 2001; Biernaskie et al. 2009; Tebbich and Teschke 2014).

Generalization of learning was expressed in the transfer from new learning (IT) to remapping (ST). While there is some evidence for this process being driven by the acquired Trap reactivity, the aim of this study was to follow learning in a stochastic environment, and so we do not make the specific claim that good transfer was because learning was in a stochastic as opposed to deterministic environment.

Nevertheless, our findings do show very clearly that remapping can be performed at asymptotic levels without prior remapping experience. Classically such remapping, and the special case of reversal learning, has been associated with a process of cognitive inhibition, in which subjects make large numbers of errors on initial remapped problems, and subsequently acquire the ability to inhibit efficiently their previous learning. Here the monkeys performed their first ever remapping problems just as well as they had been performing new discriminations, a remarkable result considering the difficulty usually induced by initial remapping (Harlow 1949; Izquierdo et al. 2004). The result argues either that monkeys do not need inhibition to complete the task, or that in learning to learn the IT they acquired the ability to inhibit. Monkeys never have cause to unlearn or ignore any of their previous stimulus learning during the IT, as stimuli are never repeated, and so it is unlikely that they have learned to inhibit specific stimulus-response associations. But rather, because monkeys treat unexpected feedback in the same manner in IT and ST, we hypothesize that this reactivity promotes a rapid differentiation of Trap feedback from Switch feedback in ST, the crucial prerequisite for efficient performance. A deterministic to stochastic transfer experiment would confirm this hypothesis, contributing to a growing body of evidence that questions the importance of the cognitive process of inhibition (Stuss and Alexander 2007).

Accounts of learning set in deterministic tasks have shown that instead of inhibiting, monkeys are applying the prospective memory-dependent WSLS performance rule as a result of their learning set (Murray and Gaffan 2006; Wilson et al. 2010). This rule explains the capacity to remap with only prior experience of serial discriminations (Schrier 1966), as the rule applies equally to both tasks. Both of these functions—learning set and inhibition—have been closely associated with frontal cortex and damage to it (Browning et al. 2007; Miller and Cummings 2007), but when the two explanations were explicitly contrasted, the learning set mechanism was clearly predictive of performance after lesions in monkeys (Wilson and Gaffan 2008), again calling into question the cognitive inhibition process.

Our data link into this work on learning set in that both processes require the integration of temporally discontinuous information into coherent structures of action, a process strongly associated with prefrontal cortex (Browning and Gaffan 2008; Fuster 2008; Wilson et al. 2010). In the case of deterministic learning set, these structures need to link two consecutive trials in order to apply the performance rule. In our data, the capacity to link a longer series of outcomes over time, and to extract from those outcomes a performance rule that generalizes to all unexpected feedback, is crucial to adapting responses to volatility (Behrens et al. 2007). This process is also likely to be dependent on frontal cortex mechanisms, and more specifically the mid cingulate cortex (Kennerley et al. 2006; Quilodran et al. 2008). Our study has shown the complex time-course of this process, laying the groundwork for longitudinal electrophysiological investigation of the physiological mechanisms. Learning to learn in a probabilistic environment therefore drives formation of these extended temporal structures, inducing latent learning effects.

Materials and Methods

Subjects and materials

Three rhesus monkeys (Macaca mulatta), two females and one male, weighing 7, 8, and 8.5 kg (monkeys P, K, and D, respectively) were used in this study. Ethical permission was provided by the local ethical committee “Comité d’Éthique Lyonnais pour les Neurosciences Expérimentales,” CELYNE, C2EA 42, under reference C2EA42-11-11-0402-004. Animal care was in accordance with European Community Council Directive (2010) (Ministère de l'Agriculture et de la Forêt) and all procedures were designed with reference to the recommendations of the Weatherall report, “The use of non-human primates in research.” Laboratory authorization was provided by the “Préfet de la Région Rhône-Alpes” and the “Directeur départemental de la protection des populations” under Permit Number: #A690290402.

Monkeys were trained to perform the task seated in a primate chair (Crist Instrument Co., USA) in front of a tangent touch-screen monitor (Microtouch System, Methuen, USA). An open-window in front of the chair allowed them to use their preferred hand to interact with the screen (all three monkeys were left-handed). Presentation of visual stimuli and recording of touch positions and accuracy was carried out by the EventIDE software (Okazolab Ltd, www.okazolab.com).

Behavioral tasks

Principle of the task

The task is an adaptation for monkeys of the task described for human subjects in Collins and Koechlin (2012). Across successive trials, a problem consisted in the monkey concurrently finding, by trial and error, the correct mappings between stimuli and targets, within a set of two stimuli (stimulus 1 and 2) and three targets (target A, B, and C) (Fig. 1). For example, a problem would consist in concurrently finding the two associations: “stimulus 1 with target A” and “stimulus 2 with target C.” Monkeys learned problems to a behavioral criterion. The task contained stochasticity, in the form of unreliable feedback, and volatility, in the form of switches between problems.

Monkeys initially learned a version of the task in which the volatility was made evident by changes in stimulus (Fig. 1B). During this version, we tracked the monkeys’ learning about stochasticity and volatility of the environment. We then studied how this learning was applied in a second version of the task in which volatility was unsignaled (Fig. 1C).

Procedure of the task

Trial procedure

The structure of a single trial and a single problem was always the same, regardless of the form of the task. Monkeys initiated each trial by touching and holding a lever item, represented by a white square at the bottom of the screen (Fig. 1A). A fixation point (FP) appeared. After a delay period, a stimulus was displayed at the top of the screen (Stim ON signal), and was followed after a delay by the appearance in the middle of the screen of three targets (Targets ON signal). Stimuli consisted of square bitmap images of either an abstract picture or a photograph, of size 65 × 65mm. Targets were three empty gray squares, of the same size as the stimulus. After a further delay all targets turned white, providing the GO signal following which monkeys were permitted to make their choice by touching a target. Monkeys maintained touch on the chosen target for a fixed amount of time in order to receive visual feedback on that choice. Feedback consisted of horizontal (positive) or vertical (negative) bars within each of the three targets. A positive feedback was followed by the delivery of ∼1.8 mL of 50% apple juice. After the completion of a trial, a new stimulus was picked within the set of two stimuli and monkeys were allowed to begin a new trial. Timing for each event gradually increased across learning to progressively train monkeys to hold their hand on the screen without moving after each action.

Problem procedure

A problem consisted of the monkeys learning about two stimuli concurrently. For a given trial, one of the two stimuli was pseudorandomly selected (50% of each stimulus over 10 consecutive trials). The two concurrent stimuli were never associated to the same target. Hence, there were six possible mappings of the two stimuli and the three targets. Each mapping was randomly selected (with the constraint that the two mappings of a problem had to be different from each other), so that the two mappings of a problem could never be predicted nor learned. The only way to find them was to proceed by trial and error based on feedback provided after each choice.

After reaching a performance criterion (defined as a total of 17 correct responses out of 20 successive trials), the problem changed and two new mappings were randomly selected. We refer to this change of problem as a “Switch.” Switches only occurred after the performance criterion was reached and after a correct response. These Switches provide the volatility in the environment of the task.

In addition to and separate from this volatility, a stochastic reward environment was created by providing misleading feedback (called “Trap feedback”) on 10% of trials. Trap trials occurred pseudorandomly once every 10 trials, with the constraint that there were at least two consecutive normal trials between each Trap trial. Trap feedback was the inverse of that determined by the current mapping—as such Trap feedback after a correct response consisted of negative feedback (see below) and no reward; Trap feedback after an incorrect response consisted of positive feedback and a reward.

Task version

We trained the monkeys in two successive steps: (1) the Identity Task (IT) (Fig. 1B) and (2) the Switch task (ST) (Fig. 1C). The two tasks were strictly identical at the level of individual trials and at the level of the problems, and both tasks contained 10% Trap trials, thus monkeys learned each task directly in a probabilistic environment.

The single but crucial difference between the two tasks was the nature of the Switch between problems. In the initial IT, when the problem switched, both the identity of the stimuli and the responses were changed. That is, after a problem Switch, monkeys learned about new objects and new rules. Stimuli were always novel to the monkey in a new problem. In contrast, in the ST, monkeys worked on the same pair of stimuli throughout the session. As such only the responses were changed—the stimuli remain the same across problems, and so the monkeys were learning about new rules for the same objects after a problem Switch. Thus, Switches between problems were visually detectable in the Identity Task whereas the only way to detect a Switch in the Switch task was by trial and error using feedback on subsequent trials.

Task motivation

In order to motivate and maintain performance at a stable level throughout each daily session, animals were asked to complete a fixed number of problems each day (number varying throughout learning between 100 and 350 trials). Upon successfully completing this number of problems, monkeys received a large reward bonus (50 mL of fruit juice, calculated based on the effectiveness in motivating the monkey).

Behavioral and statistical analyses

Principles of analyses

The major behavioral measure in these tasks was errors to criterion, the number of errors made by the monkey to reach the performance criterion of 17 correct answers out of 20 successive trials. In addition, we studied the mean percentage of correct responses on specific subclasses of trials. In particular, we focused on trials around the Trap and Switch by aligning on these events and calculating percentage correct for the surrounding trials. Trap or Switch trials were referred to as trial Trap0 and Switch0, respectively.

Behavioral analyses focused on two major questions: first the learning of volatility, in the form of improvement in performance across problems and hence the formation of a learning set. Second the learning of stochasticity, in the form of changes in response to the Trap trials, which provided unreliable feedback on 10% of trials.

Analysis of volatility: learning set and errors to criterion

We analyzed the data from IT both during acquisition of the learning set and during the subsequent stable performance. Data were analyzed up until the endpoint where the monkey had completed 400 problems with <50 errors to criterion. Monkeys did not learn at the same rate, but to render performance equivalent in terms of learning progression, we separated the data into 25 bins, referred to as learning bins. Therefore, the bins for each monkey did not contain exactly the same number of problems, but after the 25 bins all 3 monkeys had reached the same behaviorally defined level of stable performance (Fig. 2A).

We then split these data into an acquisition phase and a stable phase. The acquisition phase was completed when the learning set had been acquired to the point of stabilization of the errors to criterion per problem i.e., when the learning curve became flat. As a marker of this transition we determined the “stability point” (dashed lines on Fig. 2A). This was determined for each monkey by a sliding linear regression (window of 40 points) on the errors to criterion curve in order to detect when the slope would become nonsignificant at P < 0.05. Data after the stability point were deemed to be in the stable period.

Analysis of stochasticity: Trap trials and logistic regression

Effect of Trap feedback on performance

In order to initially test the effect of a Trap feedback on performance, we used Reverse Helmert coding. This compares each level of a categorical variable to the mean of the previous levels, by using a specific contrasts matrix within a generalized linear model of the binomial family. We compared performance at the trial following a Trap (trial Trap +1) with the mean performance of the trials before and including the Trap (trials Trap 3, 2, 1, and 0). In order to test for the subsequent recovery of performance, we compared performance at trial Trap +2 and Trap +3 with the mean performance of trials Trap 3, 2, and 1.

Modulation of Trap reactivity

We observed modulations of performance after Trap trials (hereafter named Trap reactivity). Trap reactivity was modulated by a number of different factors, showing the different influences on the learning of stochasticity. To evaluate these modulations, trial-by-trial performance was fitted with logistic regressions. Models were of the form: Y_i = β · X_i, where X corresponds to fixed-effects design matrix. We also measured the score of win-stay lose-shift strategy after a Trap or a normal feedback (with a score of 1 for a change or a maintenance of previous response after an incorrect or a correct feedback, respectively, and a score of 0 for the reverse pattern of responses) and evaluated modulations of this strategy using the same binomial models as for the performance. We also observed modulation of the counts of different targets types selected after a Trap or a Switch trial. We fitted these counts with a glm using a Poisson regression for the model “Target” (see above). All models were applied to the two tasks, except the “Trap or Switch” model that was applied on ST data only. All statistical procedures were performed using R (R Development Core Team 2008, R foundation for Statistical computing) and the relevant packages (MASS, car).

Different combinations of the following factors were included as explanatory variables to calibrate the different models: (1) “Monkey” (three levels: monkey P, K, or D); (2) “Trials” (trial 1 pre-Trap or trial 0 Trap; and trial+1 post-Trap) referring to the trial before and the trial after a Trap trial; (3) “Learning_bins” corresponding to 25 bins of trials in the IT. The size of the groups differed for each monkey; (4) “Trap_Valence” (positive or negative) referring to the valence of the Trap feedback (positive after an incorrect response, or negative after a correct response); (5) “Stimulus_Similarity” (same or different), referring to the fact that the considered trial tested the same stimulus or not as the Trap trial; (6) “Phase” (exploration or exploitation), referring to the phase within the problem. We used the following criterion: “exploration” trials were trials associated with a performance of no more than 3/5 correct over a sliding window of five trials, whereas “exploitation” trials were those with a performance of 4/5 or more; (7) “Trap_or_Switch,” referring to the identity of trials being either around a Trap or around a Switch trial. Here, only the last trap trial before each Switch trial was considered. Similarly, a factor “Normal_or_Trap” was used for distinguishing the effects of normal versus Trap feedback; and (8) “Target_type” (“Good,” “Second,” or “Exploratory”), referring to the type of target selected. “Good” indicates the correct target for the stimulus in the current trial; “Second” indicates the other correct target of the problem, which is incorrect in the current trial; and “Exploratory” indicates the third target, which is never correct in the current problem).

We tested the data using five different models to understand the different influences on the learning of volatility:

“Learning-Set” model. This model tested whether Trap reactivity was modulated across learning. It included the factors “Monkey,” “Trials,” and “Learning_bins,” and was applied selectively on trials that had the same stimulus as the Trap trial. A possible confounding factor of a learning effect on Trap reactivity was the valence of the Trap feedback. At the beginning of learning, monkeys made more errors and thus received positive feedback on Trap trials more often than at the end of learning. The effect of learning on Trap reactivity could partially be the consequence of this unequal number of positive versus negative Trap feedback, and on the unequal relevance of each feedback valence. To account for this possibility, we applied the “Learning-Set” model on a subset of data with only positive Trap trials and on another subset with only negative Trap trials. An influence of learning on Trap feedback reactivity would be represented as a significant “Trials × Learning_bins” interaction. Significant interactions “Trials × Learning_bins” in both models would indicate that the effect of learning is not independent from the valence of the Trap feedback.

“Trap reactivity modulation” model. This model tested the influence of the behavioral context on established Trap reactivity, and contained the factors “Monkey,” “Trials,” “Trap_Valence,” and “Phase.” This model was tested on the stable period of performance after the stability point. Similarly, we tested in a separate model this influence of the factor “Stimulus_Similarity.”

“Trap or Switch” model. This model tested how fast monkeys were able to differentiate between a Trap trial and a Switch trial on the ST, when there was no stimulus change to signal the difference. It included the factors “Monkey,” “Trials,” and “Trap_or_Switch.” To render the trials included as equivalent as possible, we included only data around each Switch and the Trap that immediately preceded it (“Last Trap”). We also selected only trials with the same stimulus as the Trap or Switch, and only in the stable period. For procedural reasons unrelated to the current experiment, Monkey K provided limited data on the ST. There were thus insufficient trials to power this analysis, and that monkey's data were excluded.

“WSLS” model. This model tested modulations of the win-stay lose-shift strategy after a normal compared to a Trap trial, as a function of learning bins. We thus used the factors “Normal_or_Trap” and “Learning_Bins”.

“Target” model. This model tested how fast monkeys were able to differentiate between a Trap trial and a Switch trial, in terms of proportions of targets selected by monkeys. We thus compared counts of each type of target selected after a Trap or Switch. We included the factors “Target_type,” “Trap_or_Switch,” and “Monkey.”

Model selection

Models were selected using a standard procedure of constructing the model starting with all possible interactions between the included factors as described above. In a stepwise manner we evaluated the contribution of each level of fixed effect. We used the drop1 function, repeatedly testing the effect of dropping the highest-order interaction fixed-effect term on the fit (Zuur et al. 2008). Models were selected using AIC, and changes in AIC between models were tested using a χ² test (P < 0.05). The principle of model selection was identical for all models. It should be noted that the factor Monkey was included in these models, accounting for individual differences between monkeys and improving fit.

Reaction times

Reaction times were calculated as the time between the GO signal and the lever release (in order to further select a target on screen). Measures beyond 2 sec were not included in the analysis. Due to a technical fault in the software, reaction time measurements for monkey P were inaccurate during the first task (IT), and were excluded from analyses. This fault was corrected for the second task (ST).