Computational high-resolution optical imaging of the living human retina

Abstract

High-resolution in vivo imaging is of great importance for the fields of biology and medicine. The introduction of hardware-based adaptive optics (HAO) has pushed the limits of optical imaging, enabling high-resolution near diffraction-limited imaging of previously unresolvable structures^1,2. In ophthalmology, when combined with optical coherence tomography, HAO has enabled a detailed three-dimensional visualization of photoreceptor distributions^3,4 and individual nerve fibre bundles⁵ in the living human retina. However, the introduction of HAO hardware and supporting software adds considerable complexity and cost to an imaging system, limiting the number of researchers and medical professionals who could benefit from the technology. Here we demonstrate a fully automated computational approach that enables high-resolution in vivo ophthalmic imaging without the need for HAO. The results demonstrate that computational methods in coherent microscopy are applicable in highly dynamic living systems.

A number of ophthalmoscopes capable of imaging various regions of the living eye have been developed over the years. Focusing primarily on the cornea and retina, these instruments enable the diagnosis and tracking of a wide variety of conditions involving the eye. In particular, optical coherence tomography (OCT)^6,7 has become a standard of care for diagnosing and tracking diseases such as glaucoma and age-related macular degeneration, with research extending into applications such as diabetic retinopathy⁸ and multiple sclerosis⁹. When imaging the retina, imperfections of the eye cause patient-specific optical aberrations that degrade the image-forming capabilities of the optical system and possibly limit the diagnostic potential of the imaging modality. As a result of these aberrations, it is known that in the normal uncorrected human eye, diffraction-limited resolution can typically only be achieved with a beam diameter less than 3 mm, resulting in an imaging resolution of only 10–15 µm (ref. 7). With the correction of ocular aberrations, a larger beam could be used (up to ~7 mm in diameter), achieving a resolution of 2–3 µm (at 842 nm)³—this is the accomplishment of hardware-based adaptive optics.

Traditionally, HAO incorporates two additional pieces of hardware into an imaging system: a wavefront sensor (WS) and a deformable mirror (DM). The WS estimates the aberrations present in the imaging system (in this case the eye) and the DM corrects the wavefront aberrations. Together, these two pieces of hardware are part of a feedback loop to maintain near diffraction-limited resolution at the time of imaging. Further complicating the system is the need for optics that ensure that the plane introducing the wavefront aberrations (in the case of ophthalmic imaging, this is the cornea) is imaged to the WS and the DM, as well as software to calibrate and coordinate all the hardware involved. In all, the addition of an HAO system can more than double the cost of the underlying imaging modality and, without the possibility of post-acquisition corrections, the full dependence on hardware requires that optimal images are acquired at the time of imaging, potentially lengthening the time required to image the patient/subject. Although much time has been spent on the development of HAO systems, due to these difficulties, commercialization has only now begun with the introduction of the first HAO fundus camera (rtx1, Imagine Eyes).

As a result of these difficulties, alternative (computational) approaches to HAO in the human eye have been considered, such as blind or WS-guided deconvolution^10,11. Restricted to incoherent imaging modalities, however, these techniques were only capable of manipulating the amplitude of backscattered photons. By using the full complex signal measured with OCT⁷, many groups have previously developed computational techniques that extend standard blind or guided deconvolution to correct optical aberrations in a manner that is closer to HAO by directly manipulating the phase of the detected signal. Although the acquired phase is more sensitive to motion than the amplitude, it provides the potential for higher-quality reconstructions. These techniques have been demonstrated on a variety of tissue phantoms and highly scattering ex vivo tissues^12–15, although, due to the sensitivity of the measured phase to motion^16,17, only recently was in vivo skin imaging achieved^18–20. In vivo imaging of the skin leveraged direct contact with the sample, which greatly reduced the amount of motion. Although possible, direct contact with many tissues such as the eye is undesirable as it often causes discomfort to the patient. Without direct contact, the motion of the living eye, even under conscious fixation²¹, presents a significantly more difficult imaging scenario. The resulting magnitude and variety of motions far exceed those of previous studies.

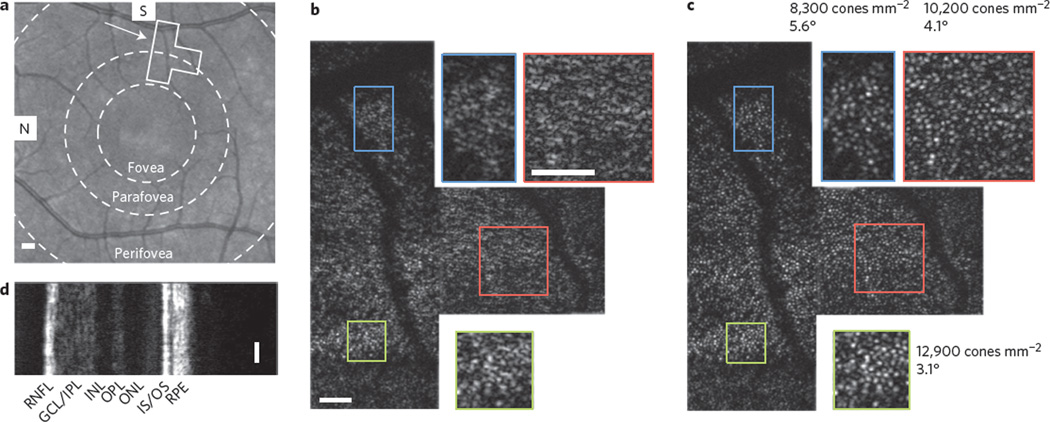
Here, in combination with an automated computational aberration correction algorithm (Supplementary Section II) and a phase stabilization technique (Supplementary Section III), an en face OCT system (Supplementary Figs 1 and 2) has been designed to rapidly acquire en face sections through biological samples⁴. In vivo retinal imaging was performed on a healthy human volunteer, and an area extending between the perifoveal and parafoveal regions (2.8° to 5.7° from the fovea) was chosen for OCT imaging, as outlined and indicated by the arrow on the scanning laser ophthalmoscope (SLO) image in Fig. 1a. The individual was asked to fixate on an image in the distance and, due to the natural drift of the eye²¹, images were acquired and stitched together in a small area centred about the fixated region (see Methods). The resulting en face OCT mosaic, acquired through the inner-segment/outer-segment (IS/OS) junction in the retina, is shown in Fig. 1b. Due to the presence of optical aberrations, microscopic anatomical features such as the cone photoreceptors are not distinguishable in Fig. 1b.

Figure 1. Computational aberration correction and imaging of the living human retina.

a, SLO image of the retina centred on the foveal region. The boxed region outlines the position of the en face OCT mosaic. The concentric circles outline three major macular zones: the fovea, parafovea and perifovea. b, Raw en face OCT mosaic. Zoomed insets on the top and bottom (1.9×) show no recognizable features. c, Same mosaic as in b, after computational aberration correction. Throughout the field-of-view, cone photoreceptors are now visible with variable densities²². d, SD-OCT cross-section acquired simultaneously with the en face OCT data. Scale bars represent 1° in the SLO image and 0.25° in all SD- and en face OCT images. S, superior; N, nasal; RNFL, retinal nerve fibre layer; GCL/IPL, ganglion cell layer/inner plexiform layer; INL, inner nuclear layer; OPL, outer plexiform layer; ONL, outer nuclear layer; IS/OS, inner segment/outer segment; RPE, retinal pigment epithelium.

Figure 1c shows the results of the fully automated two-step algorithm (when applied to Fig. 1b), which was developed to both measure and correct low- and high-order aberrations (Supplementary Section II). The first step corrected large bulk aberrations via a computational aberration sensing method¹⁴ to reveal individual cone photoreceptors. The second automated step fine-tuned the aberration correction by using selected cone photoreceptors as guide-stars¹⁵. It was found that both techniques were necessary to optimize the resolution of the final result in Fig. 1c (Supplementary Fig. 3). After correction, cone photoreceptors are clearly visualized throughout the entire field-of-view. Two insets are magnified 1.9 times to show further detail. As expected and quantified in three regions of Fig. 1c, a decrease in cone packing (12,900 cones mm⁻² down to 8,300 cones mm⁻²) was observed radially from the central fovea²². Finally, a simultaneously acquired spectral-domain (SD) OCT cross-section (Fig. 1d) provided the traditional cross-sectional view of the retina. Note that three more figures are presented in Supplementary Figs 7–9 from additional subjects (including imaging of foveal cones).

The successful reconstructions of even highly packed cone photoreceptors (bottom insets in Fig. 1) were probably a result of the combined confocal and coherence gating in the fibre-based OCT system²³. By placing the optical focus near the IS/OS junction, the preceding layers (from the nerve fibre layer down to the inner photoreceptor segment) contributed little to the collected signal⁵ (this results from both the confocal gate and also the lower scattering coefficient of the surface layers). The strong, almost specular reflection from the IS/OS junction then dominated any multiple-scattered photons resulting from the surface layers (explored further in Supplementary Figs 5 and 6). Furthermore, if any multiple scattering occurred between photoreceptors in the IS/OS junction, these photons would appear at a deeper depth (longer time-of-flight) and, as a result of the coherence gate, similarly would not contribute to the collected signal resulting from the photoreceptor layer (for further discussion see Supplementary Section IV).

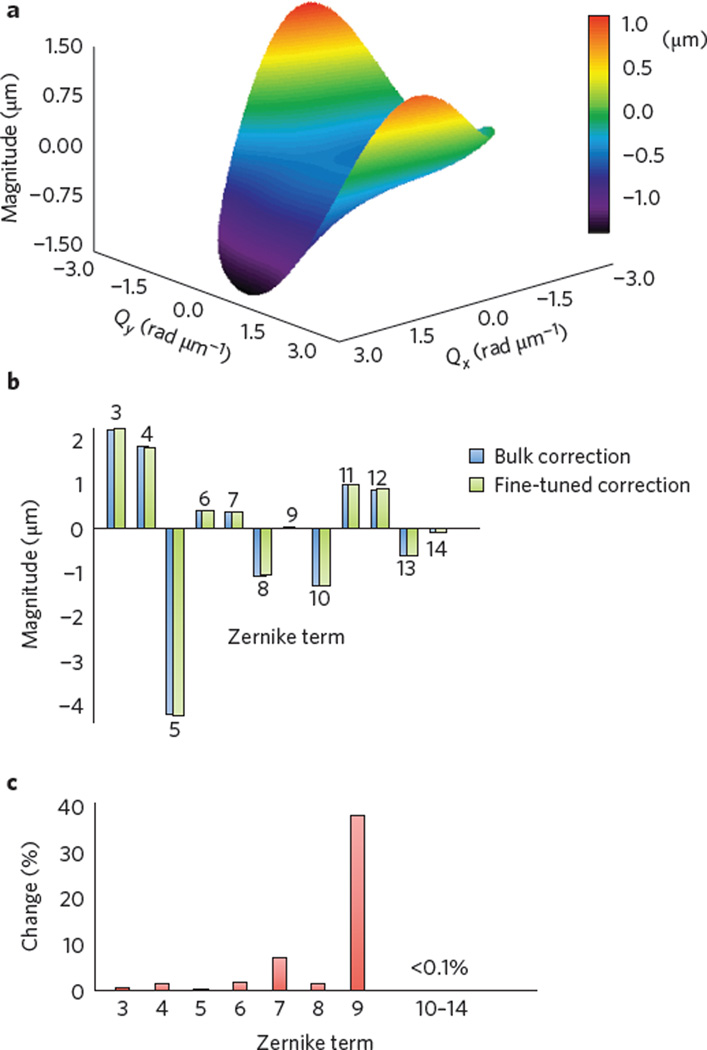
This computational approach to wavefront shaping has an advantage when compared to hardware approaches in that a wide variety of corrections are possible. Separate frame-by-frame wavefront corrections in addition to multiple wavefront corrections for a single frame are both possible for the compensation of time- and spatially-varying aberrations, respectively. This is aptly demonstrated by the mosaic in Fig. 1, where a separate wavefront correction was used for each of the nine constituent frames. A representative quantitative measure of the wavefront error is shown in Fig. 2 and is further discussed in the Methods. The shape of the surface plot (Fig. 2a), the decomposition of the function into Zernike polynomials (Fig. 2b), and the change in Zernike terms after fine-tuning (Fig. 2c) highlight the ability of this technique to computationally correct high-order aberrations that may otherwise require a large-element deformable mirror to correct in hardware¹⁴. In Fig. 2a, Qx and Qy represent angular spatial frequency along the x- and y-axes, respectively. Due to the double-pass configuration and possible aberrations in the system, it should be noted that, similar to a WS in a typical HAO system, this wavefront error does not directly represent the ocular aberrations of the individual’s eye and therefore may deviate from the known average aberrations in the healthy population²⁴.

Figure 2. Computational wavefront correction.

a, Surface plot of a computational wavefront correction applied to an acquired en face OCT frame. b, Zernike polynomial decomposition of the wavefront correction shown in a, after the bulk aberration correction step and after the fine-tuning step (both fully automated). The presence of high-order Zernike polynomial terms highlights the flexibility of computational aberration correction. c, Per cent change of each Zernike term after fine-tuning. Although small, the fine-tuning further enhances the resolution and image quality (Supplementary Fig. 3).

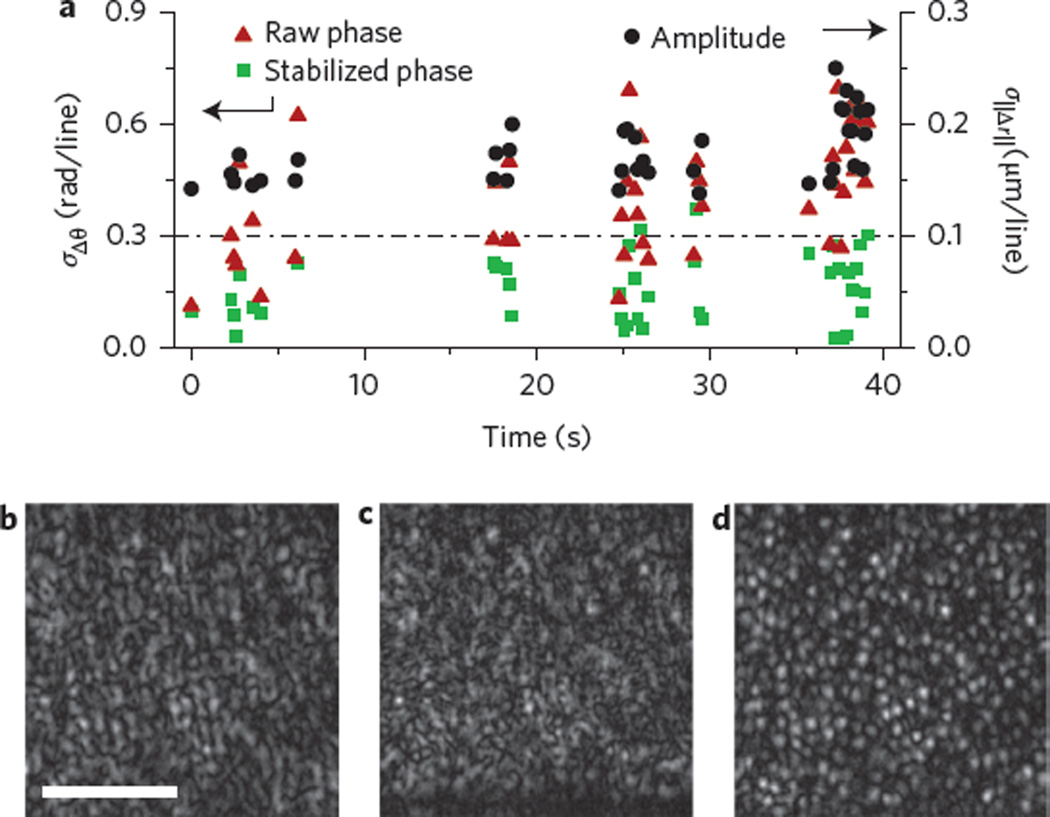
Finally, we considered motion, which could severely diminish the ability of these computational techniques to correct aberrations^16,19. During normal fixation, it is know that the eye presents three main types of motion: microsaccades, drift and tremors²¹. The fast but temporally rare microsaccades, in addition to the slow and constant drift, did not present significant instabilities due to the fast imaging speed. We found that the fast and constant ocular tremors and subject motion were the most disruptive types of motion. Small patient motion along the optical axis primarily corrupted the measured phase, while the transversely directed motion of the ocular tremors affected both the phase and amplitude of the data equally^16,19. Figure 3a presents a quantitative analysis of both types of stability. Although there were no apparent motion artefacts in the en face OCT images presented in Fig. 1b, the phase showed large variations (Supplementary Fig. 4). Due to this unavoidable sub-wavelength motion, a phase stabilization technique (see Supplementary Section III) was developed to automatically correct the phase so as to obtain reliable aberration correction. To quantitatively verify the stability of the acquired data, Fig. 3a shows the phase stability measures (see Methods) of frames (with an average signal-to-noise ratio (SNR) greater than 8 dB) when imaging the living human retina before phase stabilization and after phase stabilization. After stabilization, the phase stability was found to be below the previously determined stability requirements for aberration correction^16,19 (dashed horizontal line in Fig. 3a). The amplitude stability (see Methods) was also measured, but due to insufficient SNR, this measure only represented an upper bound of the amplitude stability. The true stability was thus known to be better than that shown in Fig. 3a and, in combination with the reconstructions shown in Fig. 3c,d, we believe the amplitude stability requirements are also sufficiently met. Finally, with phase stabilization, the aberration-corrected image in Fig. 3d revealed the cone photoreceptors, whereas the original OCT image (Fig. 3b) and the non-phase stabilized aberration-corrected image (Fig. 3c) do not show any obvious photoreceptors.

Figure 3. Quantitative stability analysis and correction.

a, Acquired data above a chosen SNR (8 dB) were analysed using two metrics of stability: phase and amplitude analyses. Initial phase analysis (‘raw’ phase) shows that most frames are not sufficiently stable for aberration correction (points that lie above the dashed line). After a phase stabilization algorithm (‘stabilized’ phase), most frames were sufficiently stable. Due to insufficient SNR, the amplitude analysis only represents an upper bound for the true stability, which explains why the data are above the necessary threshold. From this analysis, in combination with the mosaics shown in Fig. 1, we conclude that the amplitude stability was also sufficient for computational aberration correction. b, Cropped en face OCT image. c, Aberration-corrected image without phase stabilization. d, Aberration-corrected image with phase stabilization. Scale bar, 0.5°.

Microscopic optical imaging of human photoreceptors in the living retina, both near (Supplementary Fig. 9) and far (Supplementary Figs 1, 7–9) from the fovea, has been demonstrated for the first time without the need for a DM or other aberration correction hardware. Optimal aberration correction was facilitated by a phase stabilization algorithm in combination with rapid image acquisition. Computationally corrected images of large low- and high-order aberrations resulted in en face images of the photoreceptor layer that closely match the image quality typically achieved with HAO OCT systems. Phase-corrected computational reconstructions were free of motion artefacts, as supported by quantitative stability analyses. The highly dynamic nature of the eye has required that the robustness of computational imaging methods be extended far beyond what has previously been shown to be tolerable, suggesting that the computational optical imaging techniques presented here hold great potential for complementing or, for some uses, replacing HAO for in vivo cellular-resolution retinal imaging. Additionally, by further combining both hardware and computational technologies, even higher and previously unobtainable resolutions may be possible.

Methods

Experimental set-up

En face OCT imaging was performed with a superluminescent diode (SLD) centred at 860 nm and with a full-width at half-maximum (FWHM) bandwidth of 140 nm providing a theoretical axial resolution of 2.3 µm in air, or 1.6 µm in the retina, assuming an average index of refraction of 1.40 for the human retina⁷. Due to possible dispersion mismatch and losses through the acoustic optic modulators, the experimentally measured axial resolution was 4.5 µm (FWHM) in tissue. As shown in Supplementary Figs 1 and 2, light was delivered to the eye (10%) through a 90/10 fibre-based beamsplitter. Supplementary Fig. 2a shows the sample arm of the en face OCT system, where light exiting the fibre in the sample arm was collimated with a 15 mm focal length lens (AC050-015-B, Thorlabs), reduced in size with a reflective beam compressor (BE02R, Thorlabs), passed through a crystal to match the dispersion introduced by the acoustic optic modulators (AOMs) in the reference arm (described later), and was incident on a 4 kHz resonant scanner (SC-30, EOPC). The resonant scanner provided scanning along the fast-scan axis. The beam was then expanded 2.5× via a 4–f system using lenses with focal lengths f = 100 mm (AC254-100-B, Thorlabs) and f = 250 mm (AC254-250-B, Thorlabs), reflected off a dichroic mirror, and was incident on a pair of galvanometer scanners (PS2-07, Cambridge Technology). These scanners were used to scan along the slow axis. Due to the configuration of the resonant scanner, the fast axis was not orthogonal to either galvanometer scanner and thus both were used to scan orthogonally to the fast axis. Finally, the beam was expanded 1.33× via a second 4–f system using lenses with focal lengths f = 60 mm (AC254-060-B, Thorlabs) and f = 80 mm (AC254-080-B, Thorlabs). The beam incident on the eye was calculated to be ~7 mm in diameter.

The reference arm was configured in a transmission geometry. Light exiting the fibre was first collimated before passing through two AOMs, one driven at 80 MHz and the other at 80.4 MHz. The net modulation on the optical beam was 0.4 MHz. The beam was then passed through dispersion-compensating glass, which balanced the dispersion from the extra glass and human eye in the sample arm. Dispersion compensation in en face OCT was crucial, as it could not be easily compensated in post processing as in SD-OCT. The light returning from the sample (90%) and the light from the reference arm were then combined in a 50/50 beamsplitter and measured on a balanced, adjustable gain photodiode (2051-FC, Newport). Fibre-based polarization controllers were also placed in the sample and reference arms to maximize transmission through the reference arm and interference at the 50/50 beamsplitter.

The measured signal from the photodiode was modulated at 0.4 MHz by the AOMs (1205C, Isomet) and was detected using a high-speed DAQ card (ATS9462, AlazarTech). Processing included digitally band-pass filtering the measured signal in the Fourier domain around the 0.4 MHz modulation frequency and correcting for the sinusoidal scan of the resonant scanner by interpolating along each fast-axis line. The interpolation was necessary because resonant scanners are only capable of performing sinusoidal scan patterns. After interpolation and cropping the fly-back from the galvanometer scanners, the field-of-view consisted of 340 × 340 pixels. The system acquired at a frame rate of approximately 10 en face frames per second (FPS). To reduce motion of the participant, data were acquired using a pre-triggered technique where the press of a button would save to disk the previous 200 frames of data. In this way, once good data were seen on the real-time GPU-processed OCT display, the data could be reliably acquired. Further processing is described in the next sections.

Supplementary Fig. 2b shows a schematic of the SD-OCT system sample arm. For conciseness, the source, detector, reference arm and Michelson interferometer are not shown. The subsystem used an SLD centred at 940 nm with a bandwidth of 70 nm (Pilot-2, Superlum), resulting in an axial resolution of 4.5 µm in tissue. A 50/50 fibre-based beamsplitter was used to deliver light to a static reference arm and to the sample arm depicted in Supplementary Fig. 2b. The sample arm light was first collimated with a multi-element lens system, resulting in a small-diameter beam of ~1.5 mm. After passing through the dichroic mirror (DMLP900, Thorlabs), the light was incident on the same galvanometer scanners used for the slow-axis scanning in the en face OCT system and was expanded by the same 1.33× 4–f lens system mentioned already. The smaller beam resulted in much lower resolution and larger depth-of-field. This assisted in alignment of the participant with the en face OCT system. The SD-OCT signal was measured with a spectrometer (BaySpec) and a 4,096-pixel line-scan camera (spL4096-140 km, Basler). The spectrum, which was spread on the camera (over ~1,024 pixels) did not fill the entire line sensor, although all 4,096 pixels were acquired and processed. Acquisition of the SD-OCT data was synchronized so that one B-scan corresponded to a single frame of the en face OCT system. The combined SD and en face OCT beams were aligned collinear to each other so that the SD-OCT frame was spatially located along the centre of the en face OCT frame.

Imaging procedure

Experiments were conducted under Institutional Review Board protocols approved by the University of Illinois at Urbana-Champaign. Imaging was performed in a dark room to allow for natural pupil dilation (that is, without pharmaceutical agents). The participant’s head was placed on a chin and forehead rest, which allowed for three-axis position adjustments. The chin cup (4641R, Richmond Products) provided repeatable placement of the subject’s head and the forehead rest was constructed from a rod padded with foam. The subjects were asked to look in the direction of a fixation target in the distance (a computer monitor) and relax their eyes. The final f = 80 mm lens defined the working distance of the system as the subject’s eye was placed at the pivot of the scanned beam (80 mm from the final lens).

The operator of the system then moved the subject’s head forward and backward to find the IS/OS junction in the live view of the SD-OCT and en face OCT images. Once the desired data were seen on the live feed, a physical button was pressed that commanded the LabVIEW software to save the previous 200 frames of data (~10–20 s). This pretriggering technique ensured that the desired data were captured.

Subject details

Subject #1 (images shown in the main text, Fig. 1) was a male volunteer (28 years of age) with no known retinal pathologies. Subject #2 (for images see Supplementary Section V and Supplementary Figs 7 and 9) was a male volunteer (27 years of age) with no known retinal pathologies. Subject #3 (for images see Supplementary Section V and Supplementary Fig. 8) was a male volunteer (25 years of age) with no known retinal pathologies.

Compilation of mosaic

After aberration correction, the data were reviewed manually and data with sufficient SNR and visible cones were set aside. It is approximated that of the data with sufficient SNR, more than 90% successfully had visible photoreceptors. The data that were set aside were then manually aligned in PowerPoint to compile the mosaic. The edges around each frame were softened to reduce the appearance of mosaicing artefacts, although the overlap of each frame was often 40% and presented excellent agreement in cone photoreceptor positions between frames. An SLO image of the participant was then acquired on a commercial ophthalmic OCT system (Spectralis, Heidelberg Engineering). The blood vessels from the en face OCT data were then registered to the SLO image to determine the precise location of imaging.

Stability analysis

Stability was assessed in a manner similar to what has previously been explained¹⁹. The analysis here differs slightly due to the two-dimensional nature of our acquisition. Specifically, repeated lines were acquired with a human retina in place. This was performed by scanning with the resonant scanner and holding the galvanometer mirrors stationary. The phase stability was assessed by considering phase fluctuations along the temporal axis. In the absence of any motion, the phase would be constant in time. Phase differences along the temporal axis were obtained by complex-conjugate multiplication and the complex signal was averaged along the fast axis. This cancelled out any transverse motion and measured purely axial motion, as previously discussed¹⁹. The standard deviation of the resulting angle across time was then plotted in Fig. 3 for each frame with an average SNR above 8 dB. The variance of the noise was calculated on a frame with the retina not present and the average signal was calculated by averaging the amplitude of the entire en face frame of the retina. Amplitude stability was measured by calculating the cross-correlation coefficient (XCC) between the first line and all other lines along time. In the presence of high SNR and no motion, the XCC should be close to 1. When motion occurs, the XCC will decrease and from this, physical displacements could be measured. The standard deviation of the incremental displacements is what was finally plotted in Fig. 3.

Wavefront measurement and decomposition

After the above aberration correction algorithm was run on a frame, a single phase filter in the Fourier domain was calculated to transform the OCT data to aberration-corrected data. The angle of the phase filter, however, was calculated modulus 2π. Therefore, an implementation of Costantini’s two-dimensional phase unwrapping algorithm was used to calculate the complete phase. The central wavelength (860 nm) was then used to convert the phase to micrometres. The wavefront was decomposed into the American National Standards Institute (ANSI) standard Zernike polynomials by first restricting the square wavefront correction to a circular aperture. Next, an orthonormal family of Zernike polynomials was generated on a circular aperture. Each generated Zernike polynomial was individually multiplied and integrated against the wavefront correction to obtain the desired Zernike polynomial coefficients.