Membrane tubule formation by banana-shaped proteins with or without transient network structure

Abstract

In living cells, membrane morphology is regulated by various proteins. Many membrane reshaping proteins contain a Bin/Amphiphysin/Rvs (BAR) domain, which consists of a banana-shaped rod. The BAR domain bends the biomembrane along the rod axis and the features of this anisotropic bending have recently been studied. Here, we report on the role of the BAR protein rods in inducing membrane tubulation, using large-scale coarse-grained simulations. We reveal that a small spontaneous side curvature perpendicular to the rod can drastically alter the tubulation dynamics at high protein density, whereas no significant difference is obtained at low density. A percolated network is intermediately formed depending on the side curvature. This network suppresses tubule protrusion, leading to the slow formation of fewer tubules. Thus, the side curvature, which is generated by protein–protein and membrane–protein interactions, plays a significant role in tubulation dynamics. We also find that positive surface tensions and the vesicle membrane curvature can stabilize this network structure by suppressing the tubulation.

The Bin/Amphiphysin/Rvs (BAR) superfamily proteins regulate the membrane shape of cell organella as well as membrane fusion and fission; therefore, BAR protein dysfunction is implicated in neurodegenerative, cardiovascular, and neoplastic diseases¹,²,³,⁴,⁵,⁶,⁷. However, the manner in which these proteins assemble on the biomembrane and cooperate to reshape the membranes is not well understood. The extension of membrane tubes from liposomes and specific adsorption of the BAR superfamily proteins onto tube regions have been observed in in vitro experiments¹,²,³,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵. Frost et al. have experimentally determined that F-BAR proteins are adsorbed on flat regions of lipid membranes using electron microscopy⁹. Although the assembly seems to constitute the nucleus of the tubule formation, the tubule protrusion process has not been experimentally observed. Recently, Tanaka-Takiguchi et al. reported that the formation dynamics of tubules from a liposome can differ significantly for different F-BAR proteins¹³. That is, FBP17 and CIP4 simultaneously generate many tubule protrusions over the entire liposome surface, while PSTPIP1 and Pacsin2 generate only a few protrusions from a narrow region of the surface. In particular, the tubules induced by CIP4 and PSTPIP1 have the same radius. Thus, the tubule nucleation process depends on the protein type. However, it is not known what causes this difference in tubule nucleation behaviour. Tanaka-Takiguchi et al. also reported that the full length of Pacsin2 induces tubulation, but its F-BAR domain region alone does not¹³. In contrast, Wang et al. reported the tubulation is induced by F-BAR domain of Pacsin1 more than by the full-length protein¹⁰.

In the last decade, interactions between laterally isotropic objects on biomembrane, such as transmembrane proteins and adsorbed spherical colloids, have been intensively investigated¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²². In contrast to such studies, however, the interactions between anisotropic adhesives have not yet been explored so far. The BAR domains are banana shaped and generate an anisotropic curvature different from the isotropic spontaneous curvature C₀²³. This anisotropic nature has recently been receiving increasing theoretical interest. The classical Canham–Helfrich curvature free energy²⁴,²⁵ has been extended to anisotropic curvatures²⁶,²⁷,²⁸. Dommersnes and Fournier have derived a many-body potential of long-range interactions between point-like anisotropic inclusions and found linear assemblies and egg-carton membrane structures using Monte Carlo simulations²⁹,³⁰. In addition, the adsorption and assembly of BAR domains have been investigated using atomic and coarse-grained molecular simulations³¹,³²,³³,³⁴. For example, Simunovic et al. have simulated a linear aggregation of N-BAR domains parallel to the domain axis³³,³⁴. However, the relationship between this aggregation and tubulation remains unclear. Further, tubular formation has been simulated using a dynamically triangulated membrane model³⁵,³⁶ and, also, meshless membrane models³⁷,³⁸. Despite these numerous advancements, the present understanding of the physics of membrane shape deformation due to anisotropic curvature is still far from complete.

In this paper, we focus on the effects of the spontaneous (side) curvature C_side of a protein rod perpendicular to its longest axis on the assembly behaviour. The side curvature has not been focused upon in previous studies, but here we reveal that it strikingly changes the assembly dynamics. The excluded volume or van der Waals attraction between proteins and the membrane can effectively generate positive or negative C_side. We simulate flat membranes and vesicles using an implicit-solvent meshless membrane model³⁸,³⁹,⁴⁰,⁴¹,⁴², which allows a large-scale simulation. A BAR domain is modelled as a banana-shaped rod, which is assumed to be strongly adsorbed onto the membrane. The rod length corresponds to 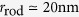(the BAR domain lengths range from 13 to 27 nm²). To investigate the membrane-curvature-mediated interactions, no direct attractive interaction is considered between the rods. Our previous studies showed that parallel and perpendicular assemblies occur separately through membrane-mediated attractive interactions at low protein density³⁸, and that polyhedral shapes are formed at high protein density⁴² for vesicles and membrane tubes.

Results

Tubulation from Flat Membrane

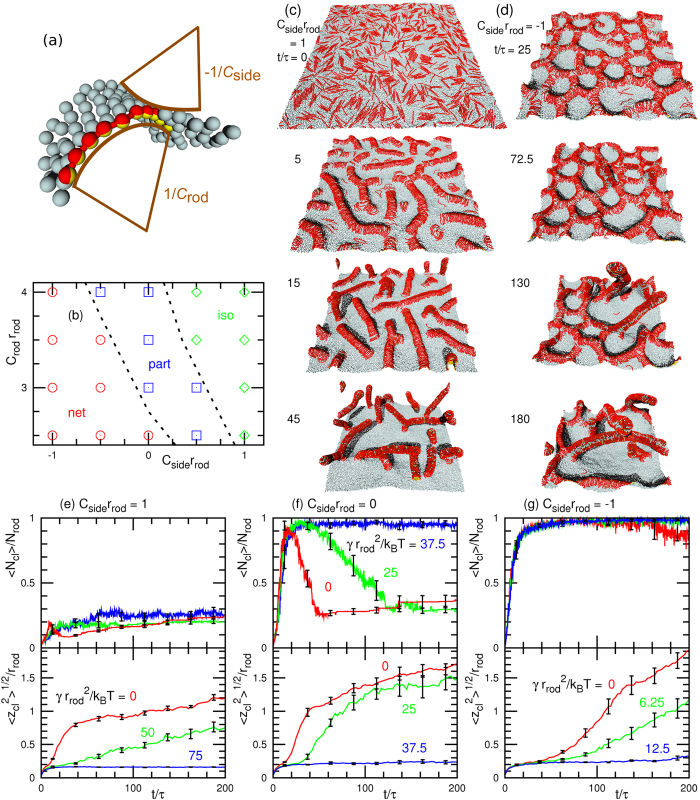
First, we investigate the tubulation from a tensionless flat membrane (surface tension γ = 0) at a high rod density, ϕ_rod = 0.4 (see Fig. 1). The protein rods are initially equilibrated with the rod curvature C_rod = 0 and C_side = 0. Once the spontaneous curvatures are altered at t = 0, the rods begin to assemble perpendicularly to the rod axis. For a positive spontaneous curvature of C_sider_rod = 1 (C_sideC_rod > 0), many tubules simultaneously protrude via the bending of straight rod assemblies (see Fig. 1(c) and Supplemental Movie 1). Branches of the rod network are formed on the membrane for a short time only. When the tubulation is initiated, neighbouring branches are broken through lateral shrinkage of the rod assembly.

Figure 1. Tubulation dynamics from flat membrane for high rod density, ϕ_rod = 0.4 (N_rod = 1,024).

(a) Protein rod with spontaneous rod and side curvatures, C_rod and C_side, respectively. The protein rod is displayed as a chain of spheres, the halves of which are coloured red and yellow. The orientation vector lies along the line of the yellow to red hemispheres. The light blue spheres represent membrane particles. (b) Dynamic phase diagram of tubulation from a tensionless flat membrane. The red circles represent percolated network formation before tubulation. The green diamonds indicate that the tubules are formed from isolated clusters. The blue squares represent partial network formation, and the dashed lines are guides for the eye. (c,d) Sequential snapshots of tubulation from tensionless flat membrane for C_sider_rod = (c) 1 and (d) −1 at C_rodr_rod = 4. (e–g) Time evolution of mean cluster size 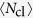and mean cluster height 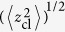for C_sider_rod = (e) 1, (f) 0, and (g) −1 at C_rodr_rod = 4. Error bars calculated from eight independent runs are displayed at several data points.

For a negative curvature C_sider_rod = −1, the rods form a percolated network covering the entire membrane area [see the top snapshot in Fig. 1(d)] and a tubule protrudes under membrane undulation (see the second snapshot in Fig. 1(d) and Supplemental Movie 2). Subsequently, tubule growth occurs along the network. Thus, the tubulation dynamics is altered remarkably by a relatively small C_side. Negative and positive C_side values stabilize and destabilize the network branches, respectively. The tubulation at C_sider_rod = −1 is significantly slower than that at C_sider_rod = 1 and much fewer tubules protrude: the average protrusion time of the first tubule are 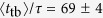and 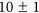for C_sider_rod = −1 and 1 at C_rodr_rod = 4, respectively.

Such characteristic dynamics is distinguishable from the time evolution of the mean cluster size 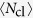and the root mean square cluster height 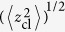, as shown in Fig. 1(e–g). For C_sider_rod = −1, the majority of the rods belong to one large percolated cluster during the tubulation. In contrast, for C_sider_rod = 1, 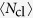decreases as the tubules are formed and the rod assemblies are divided; subsequently, 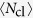slowly increases owing to tubule fusion. Branched tubules are formed by this fusion [see the bottom snapshot in Fig. 1(c) and the late stage of Supplemental Movie 1]. Based on the evolution of 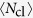, the tubulation pathways are categorized into three groups [see Fig. 1(b)]: tubulation via percolated-network formation (net), via partial-percolated-network formation (part), and without percolation (iso). When a percolated network does not cover the entire membrane surface or a large cluster of 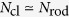is maintained for a period shorter than 20τ, we categorize the tubulation pathway as part. (A typical dynamics is shown in Supplemental Movie 3). For the entire parameter range explored in Fig. 1(b), the final structures are tubules. As C_rod decreases, the tubulation decelerates and a smaller number of large tubules are formed. The tubules are nucleated and grow from the network vertices at C_rodr_rod = 2.5 or 0.3 and C_sider_rod = −1 (see Fig. 2). The tubule radius R_tb is roughly determined by C_rod as R_tb ~ 1/C_rod. At C_rodr_rod = 4, the tubule with circumference 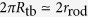consists of two hemicylinders of the rod assembly.

Figure 2. Snapshot of tubulation from tensionless flat membrane at C_rodr_rod = 2.5, C_sider_rod = −1, and ϕ_rod = 0.4.

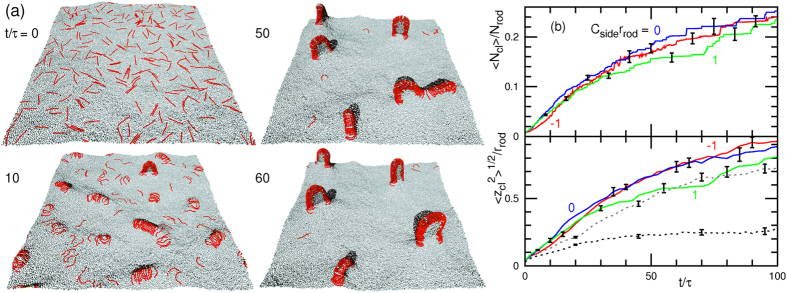
Our simulation results show that the network formation suppresses the tubulation. To confirm this more clearly, the effects of C_side on the rod–membrane interaction are investigated. A percolated network is not formed during the tubulation at a low ϕ_rod of 0.1. Rather, the rods assemble into linear clusters and, subsequently, the large clusters 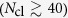transform into tubules (see Fig. 3 and Supplemental Movie 4). Although the initial cluster formation is slightly slower for negative curvature, i.e., C_sider_rod = −1, no qualitative difference is detected in the tubulation dynamics [see Fig. 3(b)]. Thus, we conclude that the suppression of the tubulation at high rod density is caused by the mesoscale network formation.

Figure 3. Membrane tubulation from flat membrane for low ϕ_rod = 0.1 (N_rod = 256), at C_rodr_rod = 4.

(a) Sequential snapshots at C_side = 0 and γ = 0. (b) Time evolution of 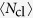and 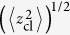. The solid lines represent the data for C_sider_rod = −1, 0, and 1 at γ = 0. The gray and black dashed lines represent the data for 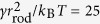and 37.5 at C_side = 0, respectively. Error bars calculated from eight independent runs are displayed at several data points.

Recent experiments have demonstrated that positive surface tension can suppress tubulation by BAR proteins¹⁵ and budding by clathrin coats⁴³. In our simulation, the positive tension and network formation cooperate to suppress tubulation [see Figs 1(e–g) and 3(b)]. At ϕ_rod = 0.4, the critical tension decreases with increasing C_side: 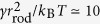and 70 for C_sider_rod = −1 and 1, respectively, where k_BT denotes the thermal energy. These are experimentally measurable magnitudes ( 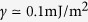and 0.7 mJ/m², respectively). The assembly of rods into a clustered network is not suppressed by the applied tension. In contrast, network structure breaking does not occur at higher tensions [see Fig. 1(f)]. Thus, the network formation is stabilized by the positive tensions.

When a positive tension γ is imposed for the coexisting states of network and tubules as shown in the second snapshot of Fig. 1(d), the tubules continue to grow at 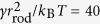. However, the tubules shrink at 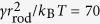. Thus, at the critical tension 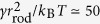, the tubule elongation force f_tb by the rod assembly is balanced with the expansion of the projected membrane area by the surface tension as 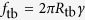. This tension is higher than that required to suppress the tubule protrusion from the flat membranes 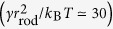, because a nucleation barrier exists for the protrusion.

Geometrical Analysis

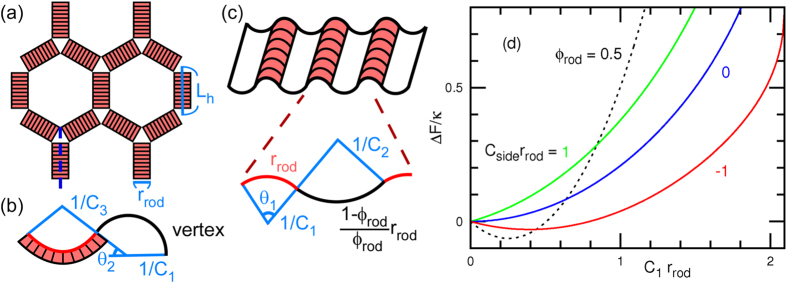
To clarify the effects of C_side on the network formation, the difference between the free energy of a hexagonal array of the rod assembly and that of a striped array is estimated using a simple geometric model (see Fig. 4). Here, a percolated network is modelled as a hexagonal array with side length L_h [Fig. 4(a)], while an unbranched rod assembly is modelled as a striped array [Fig. 4(c)]. The rod assemblies have rectangular shapes with widths equal to the rod length r_rod. Our analysis shows that the hexagonal network can have lower energy for C_side < 0. This explains why the membranes are trapped in the branched network as a local free-energy minimum.

Figure 4. Energy analysis of network structure using simple geometric model.

(a–c) Schematic representation of geometric model. (a) Top view of hexagonal array at C₁ = 0. (b) Side view of hexagonal array along the dashed line in (a). (c) Bird’s-eye and front views of striped array. (d) Free-energy difference 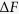between hexagonal and striped arrays of rod assembly. The solid lines represent the data for C_sider_rod = −1, 0, and 1 at ϕ_rod = 0.4. The dashed line represents the data for C_sider_rod = −1 and ϕ_rod = 0.5.

In the striped array, the rod assemblies are aligned in parallel with intervals of (1 − ϕ_rod)r_rod/ϕ_rod. The rod assemblies are curved upwards and the other regions are curved downwards, as shown in Fig. 4(c). To maintain the continuity of the normal vector of the membrane, the curvatures have the relation C₂ = ϕ_rodC₁/(1 − ϕ_rod). The curvature energy F_st of the striped array per the area 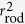is given by

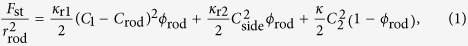where κ_r1 and κ_r2 are the bending rigidities of the rod assembly parallel and perpendicular to the rod axis, respectively. In our simulation, κ = 15k_BT, κ_r1 = 40k_BT, and κ_r2 = κ⁴².

In the hexagonal array case, the membrane surface is divided into the following three regions: Region I: A rectangular rod assembly with length 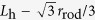and width r_rod; Region II: A triangular membrane with side length r_rod at the vertex; and Region III: A hexagonal membrane with side length 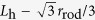. On a flat membrane, the areas of these regions are given by 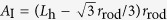, , 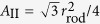and 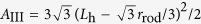, respectively. To simplify the calculation, it is assumed that each region has constant curvatures and its area is independent of these curvatures. Region I has curvatures C₁ along the rod axis and –C₃ perpendicular to the rod axis [along the dashed line in Fig. 4(a)], such that it has a saddle shape. Regions II and III are triangular and hexagonal spherical caps with radii 1/C₁ and 1/C₄, respectively. To maintain the continuity of the normal vector of the membrane, 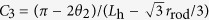and 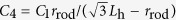. The angle θ₂ is given by 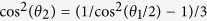, where 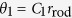, since the vertices of three rod assemblies make contact with each other on the spherical cap and maintain three-fold rotational symmetry. At θ₂ = 0, C₁ has a maximum value of 2π/3r_rod. As the area fraction of region I is 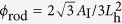, L_h is obtained as

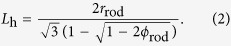The curvature energy F_hex of the hexagonal array per 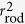is given by

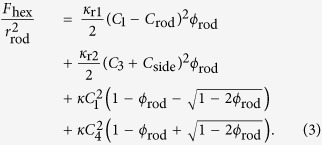The energy difference 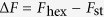is shown in Fig. 4(d). The first terms in equations (1) and (3) cancel since both arrays have the same curvature C₁ along the rods. Hence, 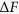is independent of C_rod and κ_r1. In the hexagonal array, the curvature energy of the rod assembly is reduced for C_side < 0, and F_hex is smaller than F_st for small C₁. Thus, the branched network can be stabilized by a negative C_side during the formation of the rod assembly.

In our simulation, networks are formed in a wider range of C_side for smaller values of C_rod [see Fig. 1(b)]. This dependence can be explained by an effective increase in the area fraction ϕ_rod. The rod assembly region contains more membrane particles with decreasing C_rod (see light blue particles in rod network and tubules in Fig. 2). Thus, the area of region I increases. At ϕ_rod = 0.5, the minimum of 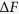is twice that at ϕ_rod = 0.4, although the area fraction is only 25% larger [see the dashed line in Fig. 4(d)]. Thus, the effective increase in the rod region enhances the network formation.

As ϕ_rod decreases, L_h of the hexagonal array increases [see equation (2)]. However, it is difficult for the hexagonal network with long L_h to form spontaneously, since the tubule formation begins before the rod assembly reaches L_h. The simulation results for ϕ_rod = 0.1 indicate tubulation from clusters with 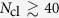at 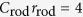. Thus, the formation threshold of the percolated network is 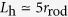, where 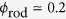. In the simulation at ϕ_rod = 0.2, the clusters are typically percolated only in one direction at C_rodr_rod = 4 and C_sider_rod = −1, which supports this estimation of the critical density.

Shape Transformation of Small Vesicles

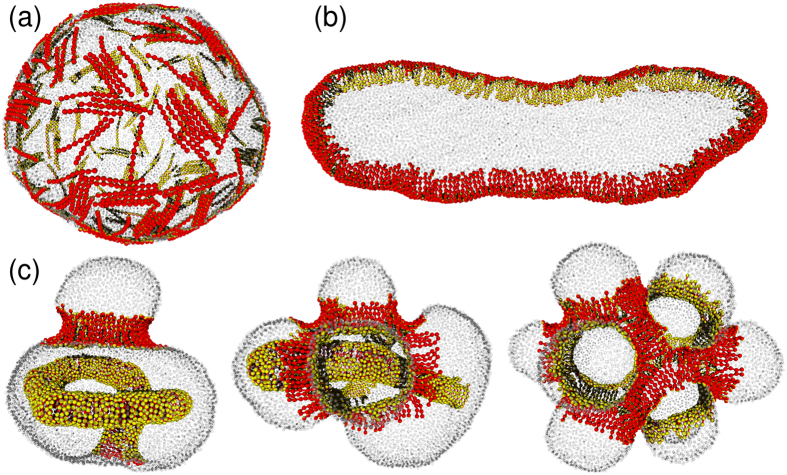
Next, we investigate the tubulation from a vesicle of radius R_ves = 3.07 r_rod at ϕ_rod = 0.3 (see Fig. 5) and demonstrate that the original membrane curvature C_ves = 1/R_ves = 0.33/r_rod changes the tubulation dynamics. For the positive curvature C_rodr_rod = 4, no tubulation is obtained for C_sider_rod = −1, 0, and 1. Instead, the vesicle deforms to an elliptic disk and the rods surround the disk rim [see Fig. 5(b)]. A discoidal bud is often transiently formed, but the rearrangement of the rod assemblies results in disk formation even for C_sider_rod = −1 (see Supplemental Movie 5). Thus, outward tubulation and network formation are suppressed in small vesicles.

Figure 5. Snapshots of vesicles at ϕ_rod = 0.3 and N_rod = 288.

(a) Spherical shape in thermal equilibrium at C_rod = 0 and C_side = 0. (b) Elongated discoidal shape in thermal equilibrium at C_rodr_rod = 4 and C_sider_rod = −1. (c) Three metastable shapes at C_rodr_rod = −4 and C_sider_rod = 1. The membrane particles are displayed as small transparent spheres for clarity.

In contrast, for the negative curvature C_rodr_rod = −4, tubulation into the inside of the vesicle is obtained (see Fig. 5(c) and Supplemental Movie 6). A percolated network with C_sideC_rod < 0 has a significantly longer lifetime than in the flat membrane case [see the middle and right snapshots in Fig. 5(c)]. The coexistence of tubules and a ring is also obtained [see the left snapshot in Fig. 5(c)]. The ring stabilizes an outward bud. For C_rod < 0, the rods bend the membrane towards the interior (opposite to the original membrane curve), such that the rods locally form a saddle shape in which the two principal curvatures have opposite signs. The network and ring structures are stabilized by the positive (opposite) C_side > 0, but not by C_side < 0.

Discussion

We have revealed that, in addition to the spontaneous curvature along the protein rods C_rod, the perpendicular spontaneous curvature C_side significantly influences the protrusion of membrane tubules. The percolated-network structure of the rod assembly has a long lifetime for C_side < 0, because the saddle membrane shape at branches of the rod network is stabilized by the opposite curvature of C_side with respect to C_rod. Thus, the network formation decelerates the tubulation significantly, despite having a minor effect on the equilibrium property. Both positive surface tensions and membranes originally bending in the same direction as C_side < 0 can stabilize the network structure. Our findings provide new insights into the regulation of biomembrane shapes by curvature-inducing proteins.

Here, we employ Langevin dynamics, in which hydrodynamic interactions are neglected. Since the static stability of the network branch is the key factor, we do not expect the obtained C_side dependence to be qualitatively changed by the hydrodynamic interactions. However, the network formation condition may be modified. The diffusion coefficient of the proteins on the membrane depends on the protein size, and fast protein diffusion compared to the membrane deformation speed likely enhances the network formation.

The F-BAR domain of Pascin is considered to have a nonzero side curvature, since it has an S-shape on the membrane surface in the addition to the curvature perpendicular to the membrane¹⁰. Pascin induces membrane tubes in a wide range of diameter¹⁰,¹⁴. In the present simulations, we did not obtain such a behaviour. It may require a larger side curvature or attractive interactions between the rods. The rod assembly with large side curvatures is an interesting problem for further studies.

An assembly of F-BAR proteins, Cdc15, has been observed along the contractile ring of cell division⁴⁴. Their adsorption to the inner leaflet of the plasma membrane is considered to yield a ring structure similar to that shown in Fig. 5(c). Our study suggests that the side curvature may play an important role in the formation of neck-like structures during cell division and membrane budding in endo/exocytosis.

Methods

We employ one of the meshless membrane models⁴¹, in which a fluid membrane is represented by a self-assembled one-layer sheet of membrane particles. A membrane particle has an excluded volume with diameter σ and an orientational degree of freedom. The solvent is implicitly accounted for by an effective potential between the membrane particles. The mechanical properties of the fluid membrane can be varied over a wide range. The details of the meshless membrane model and protein rods are described in refs ^38,41, respectively. In this study, we employ the parameter set used in ref. 38 for a membrane with isotropic spontaneous curvature C₀ = 0. The membrane has mechanical properties typical for lipid membranes: Bending rigidity κ/k_BT = 15 ± 1, tensionless membrane area per particle , area compression modulus 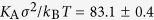, and edge line tension .

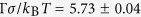A BAR protein is modelled as a curved rod consisting of a chain of N_sg membrane particles with r_rod = 10σ and N_sg = 10. The rod has anisotropic spontaneous curvature C_rod along its length and spontaneous curvature C_side perpendicular to its length. When two protein rods come into contact, C_side is applied between the rods. When the rod is surrounded by membrane particles, the spontaneous curvature C_side/2 is applied between the rod and neighbouring membrane particles. A molecular dynamics with a Langevin thermostat is employed⁴¹,⁴⁵. The simulation results are displayed with a time unit of 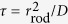, where D is the diffusion coefficient of the membrane particles in the tensionless membranes. We use total particle numbers N = 25,600 and 9,600 for flat membranes and vesicles, respectively. The rod density is defined as ϕ_rod = N_rodN_sg/N.

The mean square cluster height 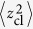is calculated as follows. A rod is considered to belong to a cluster when the distance between the centres of mass of the rod and one of the rods in the cluster is less than r_rod/2. The height variance of each cluster is calculated as 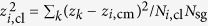, where N_i,cl is the number of rods belonging to the i-th cluster, z_i,cm is the z component of the centre of mass of the cluster, and the summation is taken over all rod segments in the cluster. Finally, 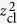is calculated as the average of 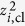for all clusters.

Additional Information

How to cite this article: Noguchi, H. Membrane tubule formation by banana-shaped proteins with or without transient network structure. Sci. Rep. 6, 20935; doi: 10.1038/srep20935 (2016).