Micelle-Encapsulated Quantum Dot-Porphyrin Assemblies as in Vivo Two-Photon Oxygen Sensors

Abstract

Micelles have been employed to encapsulate the supramolecular assembly of quantum dots with palladium(II) porphyrins for the quantification of O₂ levels in aqueous media and in vivo. Förster resonance energy transfer from the quantum dot (QD) to the palladium porphyrin provides a means for signal transduction under both one- and two-photon excitation. The palladium porphyrins are sensitive to O₂ concentrations in the range of 0–160 Torr. The micelle-encapsulated QD-porphyrin assemblies have been employed for in vivo multiphoton imaging and lifetime-based oxygen measurements in mice with chronic dorsal skinfold chambers or cranial windows. Our results establish the utility of the QD-micelle approach for in vivo biological sensing applications.

INTRODUCTION

Metabolic profiles of tumors may provide a spatiotemporal map of key markers for the growth of tumors and for their response to therapy. Three key parameters that represent the metabolic status of a tumor are glucose, pH, and oxygen, as these serve as direct measures of tumor consumption, metabolism, and respiration, respectively.^1,2 Since tumors primarily exploit glycolysis for energy needs, the tumor microenvironment is characterized by low extracellular pH arising from both lactic acid and carbonic acid; the latter is derived from dissolved CO₂ as a product of aerobic respiration.² These species tend to accumulate in the tumor due to inefficient removal pathways, resulting in a further decrease in pH (6.6–6.8).³ Additionally, tumor vasculature exhibits abnormal structure and function, resulting in leaky vessels and heterogeneous blood flow.⁴ Vascular hyperpermeability and the lack of functional lymphatic vessels induce an elevation of interstitial fluid pressure in solid tumors. This forms physiological barriers to the delivery of therapeutics.⁵ Moreover, the vascular abnormalities result in characteristically low oxygenation (hypoxia) in tumors. Hypoxia is a master regulator of tumor progression, through stimulation of angiogenesis (the formation of new blood vessels), metastasis, stem-like cell phenotype, reduced tumor cell apoptosis (programmed cell death), and immune suppression.^5–8 It induces the production and activation of growth factors, cytokines, and enzymes that promote these cell phenotypes. This hostile microenvironment, characterized by acidosis and hypoxia, also reduces the effectiveness of chemotherapy and radiation therapy, which depend on oxygen for cytotoxicity.^4,9 Both pH and pO₂ affect tumor cell metabolism, tumor cell proliferation and viability, and glucose and oxygen consumption rates.² Together, tumor acidosis and hypoxia incapacitate immune cells, render tumor cells invasive and metastatic, and induce the expression of angiogeneic factors, which trigger and stimulate tumor growth.^10–12

A new therapeutic strategy–established over the past decade–is to target angiogenesis, as tumors require blood vessels for growth and metastasis.^5,13–18 Certain antiangiogenic therapies can transiently “normalize” the abnormal tumor vasculature, thereby increasing the flow of both oxygen and therapeutics as well as removal of wastes and metabolites.¹⁹ The “vascular normalization” hypothesis posits that restoring the balance between pro- and antiangiogenic factors in the tumors by using antiangiogenic drugs can result in a time window in which tumor vasculature resembles normal vessels. It has been demonstrated that such therapies can engender normalization of the leaky, distended, and tortuous tumor vasculature.²⁰ Upon normalization, blood flow, and thus oxygen and drug distribution, is increased; this represents an opportunity to treat the tumor with a substantial dose of chemotherapeutics to have a superior impact on tumor progression.²¹ However, in order to optimize it, the normalization process must be efficiently monitored, and the drug doses must be high enough to induce normalization, but not excessive to prune the vasculature.²²

Although measurements of gene expression, drug delivery, and physiological parameters have yielded valuable insights into tumor angiogenesis and other pathophysiological processes, these techniques are either destructive or have poor spatial resolution. More desirable are nondestructive and noninvasive techniques that are able to monitor dynamic processes within a tumor. The spatial resolution of the technique should be on the order of 1–10 μm to monitor events at the cellular and subcellular level. Intravital microscopy (i.e., imaging of living organisms) allows dynamic processes to be observed and physiological functions to be determined quantitatively.^4,9 Specifically, multiphoton laser scanning microscopy (MPLSM) enables noninvasive 3-D optical imaging with significant depth penetration and ~1 μm spatial resolution.^23–26 Although much research has focused on imaging tumor angiogenesis and microenvironment, there have been few studies that monitor dynamic changes in the functional parameters of pH and pO₂.^4,9 Understanding how pH and O₂ levels change as a function of disease progression or therapy is critical to develop novel targeted therapeutics. For MPLSM imaging to be realized, new noninvasive sensors, with sufficiently high quantum yields to generate sufficient signal for deep tissue imaging, must be developed that are small enough to penetrate into the tumor and monitor dynamic changes with high resolution.¹⁹

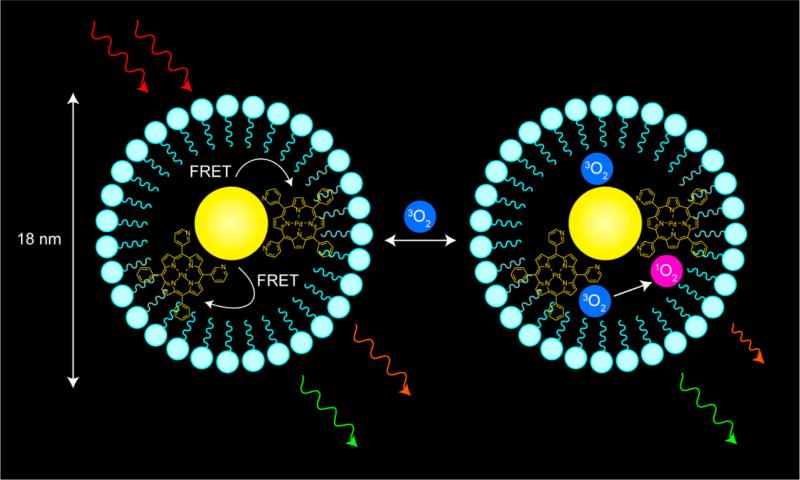
To this end, we have developed optical chemosensors that exploit a quantum dot (QD) scaffold. The QD serves both as a photon antenna for multiphoton absorption as well as an internal emission intensity standard for ratiometric sensing.²⁷ Quantum dots have been used as two-photon donors in Förster resonance energy transfer (FRET)-based donor–acceptor dyad configurations,^28–30 complementing biological FRET sensing schemes that employ organic fluorophores as two photon antenna.^31–33 Self-referencing pH sensors^34–36 and a higher-pressure (160–760 Torr) oxygen sensor³⁷ have also been developed to probe biological microenvironments. Recently, we developed supramolecular QD/palladium(II) porphyrin (1, Chart 1) assemblies for lower-pressure (0–160 Torr) oxygen sensing under one- and two-photon excitation.³⁸ Herein, we report the water solubilization of these assemblies by encapsulating a preassembled QD-porphyrin construct within a phospholipid micelle. Encapsulation of QDs in lipid or amphiphilic polymer micelles is an established method of solubilizing them in aqueous buffer.^39–52 Whereas micelles have been used for biological imaging, micelle-encapsulated QDs have been only used to sense nitric oxide.⁵³ We now exploit the micelle approach to sense oxygen ratiometrically under two-photon excitation. Using the sensing scheme outlined in Figure 1, we have established the utility of the micelle approach for in vivo imaging and sensing for the first time.

Chart 1.

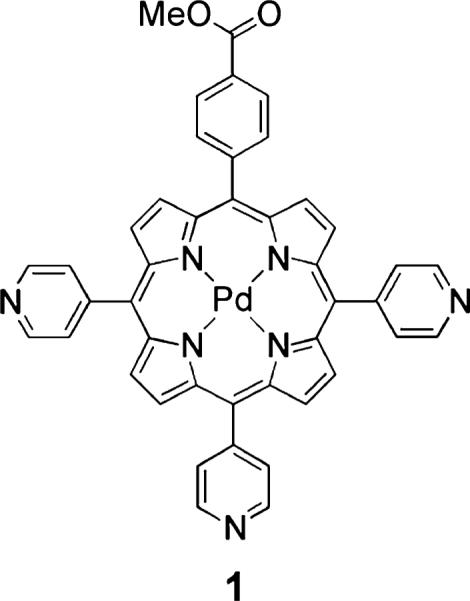
Figure 1.

Schematic representation of the oxygen sensing method developed in this study. The quantum dot-porphyrin assembly encapsulated in a lipid micelle is irradiated under two-photon excitation using NIR (700–1000 nm) light. Through FRET, the porphyrin is promoted to an excited electronic state. Oxygen can freely diffuse into the micelle and reversibly quench porphyrin emission; the lifetime and intensity of the emission are a quantitative measure of O₂ concentration.

EXPERIMENTAL SECTION

Materials

The following chemicals were used as received: propionic acid, chloroform (CHCl₃), dichloromethane (CH₂Cl₂), toluene, methanol (MeOH), ethanol (EtOH), ethyl acetate (EtOAc), acetonitrile (MeCN), pyrrole, 4-pyridinecarboxaldehyde, methyl 4-formylbenzoate, 2′,7′-dichlorofluorescein (fluorescein 27), 1,3-diphenylisobenzofuran (DPBF), and tris(2,2′-bipyridyl)dichlororuthenium-(II) hexahydrate ([Ru-(bpy)₃]Cl₂) from Sigma-Aldrich; sodium bicarbonate (NaHCO₃), sodium hydroxide (NaOH), and sodium sulfate (Na₂SO₄) from Mallinckrodt; palladium(II) acetylacetonate (Pd(acac)₂) from Strem; pyridine from EMD; silica gel 60 Å 230–400 mesh ASTM from Whatman; 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000] ammonium salt, 25 mg/mL solution in chloroform from Avanti Polar Lipids Inc.; Dulbecco's phosphate-buffered saline (PBS) without calcium and magnesium from Mediatech Inc.; chloroform-d (CDCl₃) from Cambridge Isotope Laboratories; and argon from Airgas. Cadmium selenide core–shell QDs obtained from QD Vision were twice precipitated from toluene using EtOH and redissolved in toluene prior to use. Compound 1 was prepared as previously reported.³⁸

5-(4-Methoxycarbonylphenyl)-10,15,20-tris(4-pyridyl) porphyrin (1-H₂)

The free-base porphyrin was prepared with a variation to the Adler–Longo porphyrin synthesis.^54,55 The modification affords usable (>350 mg) amounts of porphyrin with minimal chromatography. In a three-neck round-bottom flask, 100 mL propionic acid and 100 mL toluene were brought to reflux. An aldehyde solution was prepared by dissolving 1.62 g methyl 4-formyl-benzoate (9.87 mmol) and 2.7 mL 4-pyridinecarboxaldehyde (3.1 g, 29 mmol) in 7 mL toluene. A pyrrole solution was prepared by dissolving 2.6 mL pyrrole (2.5 g, 37 mmol) in 7 mL toluene. These two solutions were simultaneously added to the refluxing solvent dropwise via syringe. After the addition was complete, the solution was refluxed for 1.5 h. The reaction mixture was then cooled to room temperature, and solvents were removed by rotary evaporation. The crude residue was dissolved in 100 mL CHCl₃, and a saturated solution of NaHCO₃ was carefully added; the biphasic mixture was stirred until bubbling had subsided. The organic layer was washed with water, dried over Na₂SO₄, and brought to dryness. The crude reaction mixture was purified on a silica gel column using CH₂Cl₂ to elute all of the fast-moving porphyrin isomers (B₄, AB₃, and cis-/trans-A₂B₂ isomers). After these four products eluted, the solvent was changed to 100% EtOAc and then 10% MeOH in EtOAc to elute the desired A₃B porphyrin. A second silica gel column, using EtOAc as the sole eluent, was necessary to fully purify the desired product, affording 387 mg (5.8% yield, based on the amount of B aldehyde) of the title compound. ¹H NMR (500 MHz, CDCl₃, 25 °C) δ = −2.90 (bs, 2H), 4.12 (s, 3H), 8.16 (m, 6H), 8.30 (m, 2H), 8.47 (m, 2H), 8.82–8.89 (bm, 8H), 9.06 (m, 6H) (Figure S1).

Preparation of Sensors

Toluene stock solutions of 1 (~100 μM) and QD (~10 μM) were prepared. The concentration of the QD stock solution was calculated using ε₃₅₀ = 4.34 × 10⁵ M⁻¹ cm⁻¹, as estimated using an empirical formula based on the first absorbance feature (λ = 501 nm).⁵⁶ To prepare the sensor QD1-MC, an aliquot of the QD stock (typically containing ~10 nmol of QDs) was dissolved in 4 mL of chloroform, and an appropriate volume of the porphyrin stock was then added to give 10 mol equiv of porphyrin per QD. The resultant mixture was stirred overnight at room temperature in a 20 mL scintillation vial to allow equilibration of the porphyrin on the QD surface. Solvent was removed by rotary evaporation, and the residue was dissolved in 750 μL of the lipid solution (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000] ammonium salt 25 mg/mL solution in chloroform). Solvent was removed by rotary evaporation and 4 mL PBS were added. The mixture was then sonicated for 5 min using a Microson XL 2000 ultrasonic liquid processor (Qsonica LLC) with an output power of 2 W to give an orange, nonturbid solution. Aggregates were removed by filtering the solution through a 0.45 μm and then 0.22 μm syringe filter (Millipore). Solutions for in vivo imaging were prepared by combining four independent batches and concentrating the solution using 50,000 MW centrifuge filters to a final volume of 500–700 μL. The porphyrin-free construct QD-MC was prepared using the same micelle formation protocol outlined above for QD1-MC.

Physical Measurements

¹H NMR spectra were recorded on a Varian Inova-500 spectrometer at the MIT Department of Chemistry Instrumentation Facility (DCIF) and internally referenced to the residual solvent signal (δ = 7.26 for CHCl₃ in CDCl₃).⁵⁷ UV–vis absorption spectra were acquired using a Cary 5000 spectrometer (Agilent). Steady-state emission and excitation spectra were recorded on a SPEX FluoroMax-3 spectrofluorimeter. Porphyrin emission quantum yields were referenced relative to a freeze–pumped–thawed sample of [Ru(bpy)₃]Cl₂ in MeCN (Φ = 0.094).⁵⁸ The quantum yield of QD was determined using fluorescein 27 in 0.1 M NaOH (Φ = 0.87, η = 1.335)⁵⁹ as the standard. Samples for phosphorescence quantum yield measurements, vacuum lifetime (τ_o) measurements, and nonquenched steady-state emission spectra were prepared by subjecting solutions to three cycles of freeze–pump–thaw to pressures below 10⁻⁵ Torr. Gel filtration chromatography (GFC) was performed on an Akta Prime system (GE) with a Superose 6 cross-linked dextran column, using PBS as the eluent; the UV absorbance at 280 nm was monitored over the course of the column. Dynamic light scattering (DLS) measurements were made using a Zetasizer Nano S90 (Malvern). Bright-field transmission electron micrographs (TEM) were recorded using a JEOL 2100 transmission electron microscope. Dark-field scanning transmission electron micrographs (STEM) were recorded on a JEOL 2010 TEM/STEM. For spectroscopic measurements conducted at 37 °C, a TC 125 temperature controller (Quantum Northwest) equipped with a circulating water bath was used to maintain the sample temperature. Samples were equilibrated at 37 °C for 1 h before any measurements were made.

Solution oxygen measurements were made using an Ocean Optics NeoFox Phase Measurement system equipped with a FOXY-HPT-1-PNA fiber optic probe. The sensor was calibrated using a two-point calibration: an air-equilibrated PBS solution and a PBS solution purged with argon for 1 h. The probe was recalibrated before each set of data was collected; the measured lifetime of the sensor was used to determine the amount of dissolved oxygen in the sample. For these calibration measurements, the solubility of oxygen (20.94%) from 1 atm of air in pure water as a function of temperature was calculated using the empirical equation⁶⁰ as advocated by the National Institute of Standards and Technology (NIST):⁶¹

$$\ln c=-52.16764+\frac{84.59929}{\tau }+23.41230\ln \tau$$ (1)

where c is in units of mL of gas at STP per liter of solution and τ = T/100, where T is the temperature in K. A variation of this equation assumes 1 atm of O₂.⁶² At 25 and 37 °C, c = 5.951 and 4.999, respectively. Using the ideal gas law, the solubility of oxygen in pure water was calculated to be 265 and 223 μM at 25 and 37 °C, respectively. For PBS buffer, the concentration of oxygen was adjusted by⁶⁰

$$k_{\mathrm{sc}\propto }=\left(\frac{1}{c_2}\right)\log \left(\frac{c^0}{c}\right)$$ (2)

where k_scα is the salt effect parameter, c₂ is the concentration of solute, c° is the solubility of oxygen in pure water, and c is the solubility of oxygen in the electrolyte solution. Since the primary component of this buffer is NaCl, the concentration of the salt, c₂ = 137 mM in the buffer⁶³ and k_scα = 0.145 L mol⁻¹ for NaCl⁶⁰ was used in eq 2 to furnish the solubility of oxygen in PBS to be 255 and 213 μM at 25 and 37 °C, respectively. For the solubility of oxygen in blood, the molar concentration of oxygen was converted to a partial pressure using c = αP, where c is the concentration of dissolved oxygen, P the partial pressure of oxygen, and α is the solubility parameter, taken to be 0.031 mL L⁻¹ Torr⁻¹ or 122 μmol L⁻¹ Torr⁻¹ for blood at 37 °C.⁶⁴

The presence of singlet oxygen was determined by monitoring the decrease in absorbance of DPBF at 410 nm upon steady-state photolysis as a function of time. White light, produced using a Newport 67005 xenon lamp operating at 200 W, was passed though a Newport 74100 monochromator, to furnish 414 nm light with a photovoltage of ~60 mV, as measured using a silicon amplified detector (DET-L-SIVU-R-C, Newport) connected to a Newport Merlin radiometry system. Samples were irradiated for a total of 60 min; absorption spectra were recorded every 5 min using a CCD array UV–vis spectrophotomer (SI Photonics, Inc.). A solution of the sensitizer (~4 mL) was prepared such that the absorbance at the irradiation wavelength was matched (A₄₁₄ = 0.195): QD1-MC in PBS and Ru(bpy)₃Cl₂ in MeOH as a reference. A stock solution of DPBF was prepared (5.7 mg in 12 mL MeOH, 1.8 mM). An aliquot (100 μL, 0.18 μmol) of the DPBF solution was added to the sensitizer solution. Control samples were prepared by adding 100 μL DPBF solution to ~4 mL of solvent (MeOH or PBS).

Nanosecond time-resolved emission measurements of porphyrin lifetimes were acquired using a previously reported system.^65,66 Pump light was provided by the third harmonic (355 nm) of a Quanta-Ray Nd:YAG laser (Spectra-Physics) operating at 10 Hz. The pump light was passed through a BBO crystal in an optical parametric oscillator (OPO) yielding a visible frequency that was tuned to 450 nm. Excitation light was attenuated to 1–3 mJ per pulse for all experiments using neutral density filters. Emitted light was first passed through a series of long pass filters to remove excitation light then to a Triax 320 monochromator (Jobin Yvon Horiba) and dispersed by a blazed grating (500 nm, 300 grooves/mm) centered at 685 nm. The entrance and exit slits of the monochromator were set to 0.36 mm in all experiments herein, corresponding to a spectral resolution of 4.5 nm. The signal was amplified by a photomultiplier tube (R928, Hamamatsu) and collected on a 1 GHz digital oscilloscope (9384CM, LeCroy); acquisition was triggered using a photodiode to collect scattered laser excitation light.

Femtosecond time-resolved emission measurements of QD lifetimes were acquired using a Libra-F-HE (Coherent) chirped-pulse amplified Ti:sapphire laser system, as previously described.³⁸ Excitation pulses of 450 nm were produced via fourth harmonic generation of the idler using a BBO crystal; the pulse power was attenuated to 0.4–1 mW at the sample. Emission lifetimes were measured on a Hamamatsu C4334 Streak Scope streak camera, which has been described elsewhere.⁶⁷ The emission signal was collected over a 140 nm window centered at 480 nm using 100 and 2 ns time windows; delays for these time windows were generated using a Hamamatsu C1097–04 delay unit. A 495 nm long pass filter was used to remove laser excitation light. Two-photon emission spectra were generated using this Libra-F-HE (Coherent) laser system. Excitation pulses of 800 nm were used directly from the Libra output; the pulse power was attenuated to 5–8 mW using neutral density filters, and the beam was focused onto the sample using a 200 mm focal length lens. The emission spectrum was collected using a Hamamatsu C4334 Streak Scope streak camera in a 140 nm window centered at 480 nm.

Two-photon lifetime measurements were made using a custom-built MPLSM in the Edwin L. Steele Laboratory, Department of Radiation Oncology at Massachusetts General Hospital, as previously described.⁶⁸ Additions to the MPLSM system⁶⁹ were made such that lifetime measurements could be performed; these modifications have been previously described.³⁸ The 850 nm laser output was adjusted using a 10RP52-2 zero-order half-wave plate (Newport) and a 10GL08AR.16 Glan-Laser polarizer (Newport) to attenuate the power to 700 mW for air samples and 400 mW for freeze–pumped–thawed samples. The beam was passed through a 350–50 KD*P Pockel cell (Conoptics) that switched the triggering pulses from a DG535 digital delay generator (Stanford Research Systems); the output of the Pockel cell was ~10% of the incident power during the “off” cycle. The excitation cycle was 1.60 μs in duration for air samples and 15.36 μs in duration for freeze–pumped–thawed samples. A 750DCXR short pass dichroic mirror (Chroma Technology), a HQ690/90m-2p bandpass filter (Chroma Technology), and a focusing lens were used in front of the GaAs H7421-50 photomultiplier tube (Hamamatsu) to collect phosphorescent emission. Photon counting was performed using a SR430 multichannel scaler (Stanford Research Systems) to histogram the counts in 1024 or 2048 bins of 40 ns for air samples or 2.56 μs for freeze–pumped–thawed samples.

In Vivo Experiments

The MPLSM system described above was used to collect two-photon in vivo images of severe combined immunodeficient (SCID) mice with surgically implanted dorsal skinfold chambers (DSC)⁷⁰ or cranial windows (CW).⁷¹ Prior to imaging, mice were anesthetized with Ketamine/Xylazine (10/1 mg/mL) and subsequently treated with 150–200 μL of the concentrated sensor solution via retro-orbital injection. This sensor dosage was determined empirically, balancing the desire to inject a minimal amount of sensor while dosing a sufficient quantity to view blood vessels upon systemic injection. At this dosage, the sensor remained in circulation long enough to perform continuous imaging for several hours without the need to inject additional sensor. For imaging, 850 nm excitation light was used at a power of 400 mW. Collected light was split into three channels: green for QD emission using either a 565 or 570 nm long pass dichroic mirror and a HQ535/40m-2p bandpass filter (40 nm bandwidth centered at 535 nm), yellow using a 585 nm long pass dichroic mirror alone, and red for porphyrin emission using a HQ690/90m-2p bandpass filter. For in vivo porphyrin emission lifetimes, the excitation cycle was 15.36 μs in duration, and photon counts were collected in 1024 bins of 2.56 μs.

Energy-Transfer Analysis

The efficiency of energy transfer from the QD to the porphyrin was evaluated using Förster analysis:^72,73

$$E=\frac{m{k}_{\mathrm{D}\to \mathrm{A}}}{m{k}_{\mathrm{D}\to \mathrm{A}}+{\tau }_{\mathrm{D}}^{-1}}=\frac{m{R}_0^6}{m{R}_0^6+r^6}$$ (3)

where k_D→A is the rate of energy transfer, r is the distance between the donor and acceptor, R₀ is the Förster distance, or the distance at which the energy transfer efficiency is 50%, and m is the number of acceptor molecules per donor. This quantity (E) can be measured experimentally:

$$E=1-\frac{{\tau }_{\mathrm{D}\to \mathrm{A}}}{{\tau }_{\mathrm{D}}}$$ (4)

where τ_D is the lifetime of the QD alone and τ_D→A is the lifetime of the QD with surface-bound porphyrin. R₀ is determined from the spectral overlap integral:

$$R_0^6=\frac{9000\left(\ln 10\right){\kappa }^2\Phi }{128{\pi }^{5}N{n}^4}{\int }_0^{\infty }{F}_{\mathrm{D}}\left(\lambda \right){\epsilon }_{\mathrm{A}}\left(\lambda \right){\lambda }^4\mathrm{d}\lambda$$ (5)

where κ² is the relative orientation factor of the dipoles, taken to be 0.476 for static donor–acceptor orientations,^73,74 Φ_D is the quantum efficiency of the donor, N is Avogadro's number, n is the index of refraction of the medium, which is taken to be 1.334 for PBS,⁷⁵ F_D(λ) is the normalized intensity of the donor, and ε_A(λ) is the extinction coeffcient of the acceptor at wavelength λ. The average number of porphyrins attached to the QD, m, was determined from the optical cross sections of the spectra of QD, the porphyrin, and the corresponding assembly. The absorption spectrum of the assemblies was taken as the sum of the individual absorbance spectra of the donor and acceptor, as previously demonstrated.³⁸ The value for m and the concentration of the assemblies was calculated using the individual donor and acceptor absorption spectra, their known ε values, and Beer's law.

RESULTS AND DISCUSSION

Sensor Preparation

Micelle encapsulation represents a scalable method of synthesizing water-soluble QD nanosensors and circumvents laborious multistep polymer syntheses required for coating QDs for covalent conjugation to a chemosensor. Figure 1 shows the porphyrin-QD micelle construct used in this study. A lipid functionalized with a PEG-2000 chain for water solubility was used to prepare these micelles. This particular phosphoethanolamine lipid was selected based on the studies of Dubertret, Norris, and coworkers, who demonstrated that single QDs may be encapsulated within the micelle when the QD is sufficiently large (diameter >3 nm).³⁹ TEM images revealed that the QDs used in this study are ~3.5 nm in diameter (Figure S2), suggesting that the volume of the micelle can accommodate a single QD donor in the presence of multiple porphyrin acceptors, analogous to the organic-soluble constructs.³⁸

Whereas the vast majority of synthetic procedures for micelle formation involve heating and evaporation of an organic solvent^{39,41,43,44,50} or dissolution of an organic film in aqueous media or a similar method of phase transfer,^{40,42,45,46,49,51,52} sonication offers an alternative method to assemble micelles. In contrast to other protocols,⁴⁷ we were able to rapidly (~5 min) and facilely produce micelle nanosensors of a consistent size by conducting sonication at room temperature. The lower sonication temperatures for micelle formation are afforded by the QD, which serves as a template for micelle formation as evidenced by the inability to form micelles in the absence of QD. Additionally, when a porphyrin solution in the absence of QD was treated in an identical manner, the solution remained turbid and inhomogeneous. Gel filtration chromatography (GFC) (Figure S3) and DLS (Figure S4) establish a Gaussian distribution of particles. In order to determine the size of these constructs, micelles containing the QD alone (QD-MC) were imaged using dark-field STEM and bright-field TEM (Figure 2); additional images are provided in Figures S5 and S6. The STEM images demonstrate that the micelles are largely well dispersed and the particles are 4.69 ± 0.81 nm, measuring 46 independent QDs over 10 different images. This is corroborated by the bright-field data, which show that the QDs are 3.80 ± 0.64 nm in diameter, measuring 39 independent QDs over 10 different images. In instances of aggregation, the bright-field data confirm that the QDs are individual particles (Figures 2b and S6). Both imaging techniques give the same size particles within error, confirming that single QDs are encapsulated in the majority of micelles. Based on DLS, the average particle size (i.e., hydrodynamic diameter) for a typical QD-MC is 16.8 ± 0.7 nm, and micelles with the porphyrin (QD1-MC) are slightly larger at 18.2 ± 0.7 nm. The size of QD-MC is consistent with micelles containing single QDs reported by Dubertret, Norris, and co-workers (10–15 nm), as measured by TEM using phosphotungstic acid to stain the phospholipid layer.³⁹ Our observation of slightly larger particles is likely due to the radial extension of the PEG-2000 chains in solution, rather than the incorporation of multiple QDs within a single micelle. Presumably, the appended porphyrins on the surface of the QD increase the radius of the assembly relative to the QD alone, resulting in a larger micelle size. These QD-micelle constructs are only a few nanometers larger than our previously reported polymeric conjugates with dihydrolipoic acid-polyethylene glycol (DHLA-PEG)⁷⁶ or poly imidazole ligands (PIL),⁷⁷ both of which exhibit particle sizes of ~11.5 nm by DLS.

Figure 2.

(a) Dark-field STEM and (b) bright-field TEM images of QD-MC, demonstrating that the individual QDs are observed. While the micelles may aggregate, the TEM grid is clearly visible between individual particles, indicating that the vast majority of micelles contain a single QD.

The QD-micelle constructs are stable for over 2.5 years when stored at 4 °C. Both dilute and concentrated (i.e., those used for in vivo imaging) samples of QD-MC remained nonturbid, green solutions that are highly fluorescent, as observed using a hand-held UV lamp as the excitation source. Concentrated samples of QD1-MC developed a fine orange precipitate over time. The supernatant from this sample has an absorption spectrum that is identical to that of a freshly prepared sample (Figure S7). If the entire sample and pellet were resuspended in PBS buffer and filtered through 0.2 μm syringe filter, the absorption spectrum showed a decrease in porphyrin absorption relative to QD absorption (λ < 375 nm). Moreover, the sample shows green QD fluorescence when excited with a hand-held UV lamp. This phenomenon is not observed for freshly prepared samples of QD1-MC, where QD emission is not visible by eye. These observations suggest that the pellet is largely free porphyrin that has been released from degraded micelles. The QDs, however, remain in solution, accounting for the green fluorescence of the sample and increased absorption at λ < 375 nm. Although dilute solutions of QD1-MC did not have a visible precipitate after 2.5 years, an increase of QD absorption and visible green fluorescence were observed.

Photophysical Properties

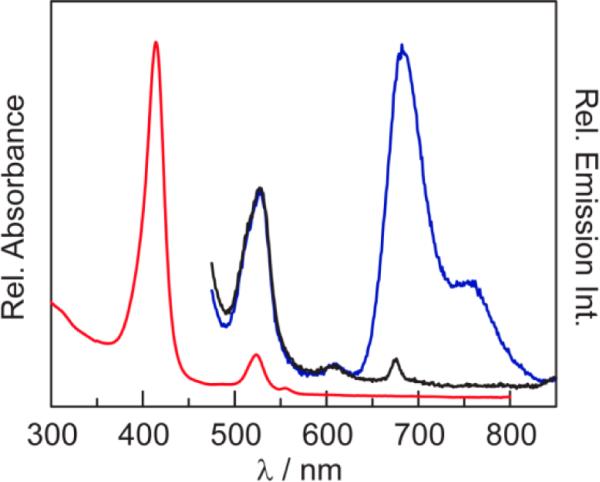
The absorption spectrum of QD1-MC, shown in Figure 3, is dominated by the Soret and two Q bands of porphyrin 1, which is superimposed onto the absorption spectrum of the QD. These spectral features are comparable to those of QD1 in toluene (Table S1). The emission spectrum of QD1-MC exhibits the luminescence features of the QD (λ_em,max = 527 nm) as well as the triplet (λ_em,max = 682 and 754 nm) and singlet (λ_em,max = 608 nm) transitions of 1.^38,78,79

Figure 3.

Steady-state absorption (red line) and emission spectra of QD1-MC (λ_exc = 450 nm) in PBS buffer. Whereas the emission intensity of the phosphor is almost completely quenched in the presence of air (~160 Torr O₂) (black line), it is pronounced under vacuum (blue line). The emission of the QD in QD1-MC (λ_em,max = 523 nm) is unchanged in air and vacuum, thereby establishing a ratiometric sensor.

The emission quantum yield of the QD is perturbed by the micelle, decreasing from Φ = 0.72 for the QD in toluene³⁸ to Φ = 0.42 for QD-MC in PBS (Figure S8). However, QD-MC has a superior quantum yield relative to micelles assembled from the same lipid with heating (Φ = 0.24),³⁹ suggesting that synthesis of the micelle using sonication as opposed to heating may be beneficial to furnish higher QD quantum yields. The high emission quantum yields, together with the high two-photon absorption cross sections of QDs,^80–82 enable emission spectra to be obtained under two-photon excitation in toluene.³⁸ Similar spectra are difficult to obtain in PBS, which was found to effectively generate white light under excitation by the tightly focused femtosecond laser beam (5–8 mW of focused 800 nm light). As a result, two-photon emission could be detected easily only for QD-MC owing to its high quantum yield (Figure S9), where the green emission of the sample exceeded the generated white light. Owing to FRET, the two-photon emission spectrum of QD1-MC is obscured by the generated white light continuum. However, two-photon emission from all samples could be detected using MPLSM (vide infra).

The energy-transfer efficiency and QD quenching of QD1-MC were compared to the toluene soluble construct QD1. At 10 equiv of porphyrin 1, a 97% decrease in QD emission intensity, relative to the QD alone, was observed. This is consistent with the 94% FRET efficiency determined from QD lifetime measurements.³⁸ A summary of the FRET parameters is presented in Table S2. The emission spectrum of QD1 shows that the QD and porphyrin emission features have approximately equal intensity. For convenience, these data have been reproduced in Figure S10. Upon micelle encapsulation, QD emission is further attenuated, as demonstrated in Figure 3 for equal porphyrin loadings. Indeed, the QD emission intensity of QD1-MC is reduced by 98% relative to QD-MC at equivalent QD loadings (Figure S11). The lifetime of the QD similarly reflects very efficient energy transfer. Whereas the lifetime of the QD in the micelle (13 ns) increases relative to toluene (Table S3), likely due to a modulation of the surface states of the QD,^38,83 the QD lifetime in QD1-MC is dramatically diminished (~80 ps). This is a direct result of energy transfer. Using eq 4, we calculate the FRET efficiency to be 99% (Table S2), which is consistent with the observed decrease in emission intensity. The increased quenching efficiency in QD1-MC relative to QD1 is attributed to the increased spectral overlap (Figure S12) in the micelle construct as a result of the 10 nm red shift of QD emission in the micelle (see Tables S1 and S2). Additionally, the excitation spectrum of QD1-MC (Figure S13) exhibits increased emission relative to 1 in the 300–400 nm region, where QD absorbance dominates, indicating that the QD is the donor in the FRET process.

From this value of efficiency, eq 3 yields an average QD-porphyrin distance of 2.67 nm. Based on the bright-field TEM data presented in Figure S6, the radius of the QD is 1.90 nm. Using the crystal structure of an analogous A₃B porphyrin with a single 4-pyridyl substituent,³⁸ the distance between the pyridyl nitrogen and the palladium center is 0.77 nm. Thus, the QD to porphyrin center-to-center distance based on structural metrics is 2.67 nm, which matches the average donor–acceptor distance (r) determined by FRET analysis.

Using the absorption spectrum of QD1-MC, we measure an average of eight porphyrins per QD. This value is lower than the 10 equiv excess of porphyrin to QD, but it is consistent with our photophysical studies of QD1 (10 equiv 1) in toluene, which showed that the phosphorescence lifetime exhibited biexponential kinetics attributed to bound and free porphyrin in a 75:25 ratio.³⁸ This demonstrates that ~8 equiv of porphyrin are encapsulated within the micelle. Presumably, the rest of the hydrophobic porphyrin intercalates in the excess lipid used to prepare the micelles. This porphyrin population, associated with excess lipid, is subsequently washed away from the micelles.

The excited-state lifetimes of porphyrin in QD1-MC under both one- and two-photon (λ_exc = 450 and 850 nm, respectively) excitation were measured, and the results are presented in Table 1. Under one-photon excitation, the porphyrin excited-state decay is biexponential. Relative to the lifetime of free porphyrin 1 (τ(1) = 154 μs),³⁸ a longer and shorter lifetime component is observed for porphyrin in the micelle. This behavior has been observed previously for QD1, which exhibits a long lifetime component of τ(QD1) = 590 μs and a short lifetime component of (τ(QD1) = 149 μs (Table S4).³⁸ This biexponential decay has been attributed to the porphyrin under dynamic equilibrium with the QD surface. The longer component is due to porphyrin associated with the QD, residing within the passivating ligand that coats the QD surface. The shorter lifetime component is due to the free porphyrin, which is under dynamic equilibrium with the surface-bound porphyrins. Similarly, in QD1-MC, biexponential decays are obtained with lifetimes on the order of QD1. Figure S14 shows a representative decay trace for a freeze–pump–thawed sample of QD1-MC and demonstrates that the biexponential fit is superior to the monoexponential one. The long lifetime is ascribed to porphyrin associated with the QD surface within the micelle and the short lifetime is consistent with free porphyrin residing within the oleate groups of the micelle. Consistent with this behavior is the observation of a monoexponential decay of QD1-MC under two-photon excitation. The observed difference in one- and two-photon lifetimes is typically ascribed to differences in vibronic coupling between one- and two-photon excitation.^84,85 A signature for differences in vibronic coupling is a small shift in the emission maximum owing to varying Franck–Condon factors, which will affect both the radiative and nonradiative decay pathways and, hence, lifetimes. Linear polyenes exhibit a shift of 50–80 cm⁻¹ in emission energy under one- and two-photon excitation and an attendant difference in lifetime.⁸⁶ Noting that the earliest descriptions of porphyrin electronic structure were successfully based on a cyclic polyene model,⁸⁷ we observe a 64 cm⁻¹ energy difference in the porphyrin emission maximum in QD1 under one- and two-photon excitation. On this basis, we ascribe the difference in one- and two-photon lifetimes in Table 1 as the difference in oscillator strength arising from vibronic coupling. Because the QD is the two photon antenna, only porphyrins at the surface of the QD can be excited via FRET. The free porphyrin within the micelle cannot be excited, and hence emission decay from this population is absent under two-photon excitation conditions. In this regard, the two-photon experiment is ideal for in vivo sensing for self-assembled chemosensors, as the experiment naturally selects for a single population of chemosensors which are associated with the QD. Background signal from unassociated chemosensors is absent, since this population cannot directly be excited under two photon conditions.

Table 1.

Porphyrin Lifetimes for QD1-MC under One- and Two-Photon Excitation

samplea	λexc/nm	τ1 (μs)b	A1 (%)c	τ2 (μs)b	A2 (%)c
QD1-MC	450 (1-hν)	411 ± 27	48	29 ± 5	52
QD1-MC	850 (2-hν)	233 ± 18	100	–	–

^aFreeze–pumped–thawed (<10^–5 Torr) solutions of PBS at 25 °C.

^b95% confidence interval.

^cRelative contribution to the biexponential fit.

Oxygen Sensing

The porphyrin luminescence is significantly quenched by oxygen, as shown in Figure 3. Under 450 nm excitation, where the QD is the primary photon absorber, there is a 10-fold diminishment in the intensity of the T(0,0) transition of the aerated sample relative to the same sample in fpt solutions. A similar trend is observed in the lifetime of QD1-MC in aerated PBS buffer owing to oxygen quenching. We note that the quenched lifetime of QD1-MC is 10× greater than that of QD1 in aerated toluene (see Table S4), suggesting that the micelle provides a modest barrier of O₂ versus that observed for freely diffusing O₂ in solution. This phenomenon has also been previously observed for Pd porphyrins in asolectin vesicles.⁸⁸ Under MPLSM excitation with 850 nm light, the sensitivity of the porphyrin emission to oxygen in QD1 and QD1-MC is similar. This suggests that two-photon excitation mechanism of the porphyrin via FRET from the QD is the same for both sensor constructs.

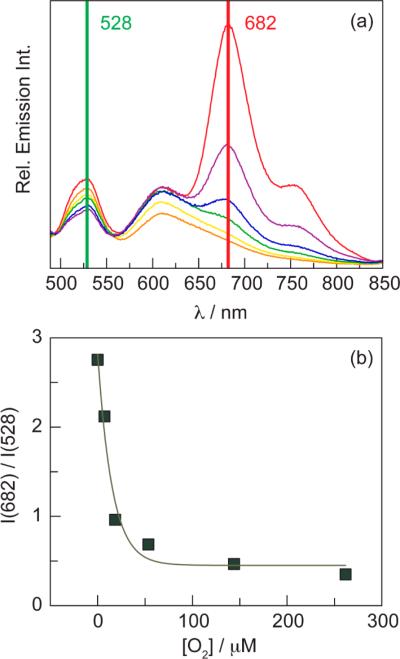
Emission spectra of QD1-MC were recorded after exposure to dissolved oxygen at different concentrations (Figure 4a). The nominal O₂ dependence of the QD emission at 528 nm arises as a consequence of only freeze–pump–thawing the sample (Figure S15) and is not observed for typical samples. This phenomenon has also been observed with the organic soluble construct QD1 (see Figure S10b). Since the sensor contains two fluorophores, ratiometric oxygen sensing may be realized by using the porphyrin to QD emission intensity ratio. An in vitro ratiometric calibration curve (Figure 4b) was constructed by plotting the 682 to 528 nm intensity ratio as a function of [O₂]. The data exhibit an exponential relation; this has also been observed for a ratiometric O₂ sensor consisting of a platinum porphyrin as the oxygen-sensitive phosphor and a QD as an intensity reference embedded in a polymer hydrogel.⁸⁹

Figure 4.

(a) Steady-state emission spectra of QD1-MC (λ_exc = 450 nm) in PBS buffer with various oxygen concentrations: 0 (red line), 5 (purple line), 20 (blue line), 55 (green line), 145 (yellow line), and 260 (orange line) μM O₂. (b) In vitro ratiometric intensity calibration curve constructed from data obtained in (a). The data were fit to an exponential function: y = 0.45 + 2.36 exp(−0.065x), where x is the oxygen concentration in μM and y is the 682 nm/528 nm intensity ratio.

The rate constant for oxygen quenching of porphyrin emission in QD1-MC was determined by Stern–Volmer analysis of the lifetime variance with the concentration of oxygen. A representative example of the decay traces as a function of oxygen concentration in the range of biological sensing (vide infra) is presented in Figure S16. Decay traces are fit to a biexponential decay (Table 1). The long and short lifetime components each obey Stern–Volmer behavior:

$$\frac{{\tau }_{\mathrm{o}}}{\tau }=1+k_{\mathrm{q}}{\tau }_0\left[{\mathrm{O}}_2\right]$$ (6)

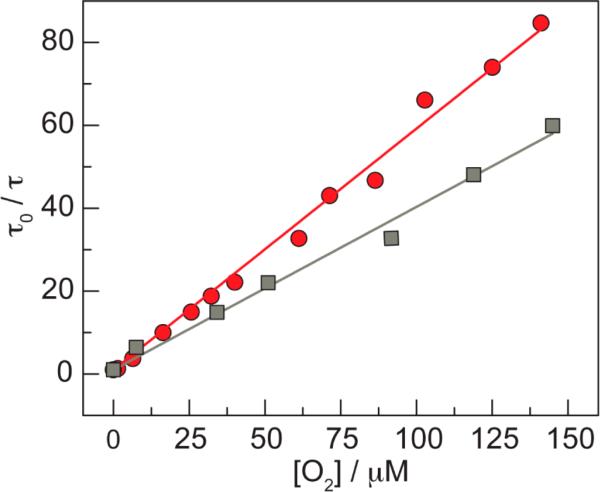
where τ_o is the natural radiative lifetime of the phosphor in the absence of quencher, τ is the lifetime of the phosphor at a given oxygen concentration [O₂], and k_q is the bimolecular quenching rate constant. Figure 5 illustrates representative examples of the long lifetime component at 25 and 37 °C. Values of the Stern–Volmer constant of K_SV (= k_q τ_o) = 0.371 ± 0.099 μM⁻¹ and 0.370 ± 0.169 μM⁻¹, for the long and short decay components, respectively, were obtained from five independent samples at 25 °C (Table S5). Similar results are obtained for measurements at 37 °C, which were performed for the purposes of calibrating in vivo lifetimes. At 37 °C, five independent samples (Table S6) furnished an average K_SV = 0.588 ± 0.064 μM⁻¹ and 1.065 ± 0.473 for the long and short components, respectively. As mentioned above, the long lifetime component is attributed to porphyrins associated with the QD. Using the natural lifetime of this population, an oxygen quenching rate constants of k_q = 9.02 ± 2.41 × 10⁸ M⁻¹ s⁻¹ at 25 °C and k_q = 1.36 ± 0.15 × 10⁹ M⁻¹ s⁻¹ at 37 °C are obtained. This increase in k_q at higher temperatures agrees with previously devised empirical relationships for the temperature dependence of k_q for Pd(II) porphyrins k_q = (6.4 + 0.21T)².⁹⁰ The rate constants at 37 °C should be faster than that at 25 °C by a factor of 1.5, which is exactly what we observe for both the long and short components.

Figure 5.

A representative Stern–Volmer plot of the long component of the biexponential decay for QD1-MC at 25 °C (gray square) and 37 °C (red circle) under 450 nm excitation. These two data sets yield k_q values of 9.57 × 10⁸ M⁻¹ s⁻¹ at 25 °C and 1.35 × 10⁹ M⁻¹ s⁻¹ at 37 °C.

In addition to collisional quenching, the formation of singlet oxygen (¹O₂) may also deactivate the excited triplet state of the porphyrin in QD1-MC. There have been several reports of FRET-based QD-photosensitizer conjugates that produce ¹O₂.^91–93 To test this possibility, a DPBF assay⁹⁴ was performed, monitoring the disappearance of the 410 nm absorption feature of this molecule as a function of time (Figure S17). It was found that the slope of this plot for QD1-MC is identical to the DPBF control in PBS, indicating that a negligible amount of ¹O₂ is formed. Singlet oxygen will decay back to the ground state before diffusing out of the micelle: τ(¹O₂) = 20 μs in toluene⁹⁵ (similar dielectric to the hydrophobic interior of the micelle) and 2 μs in H₂O.⁹⁶ If ¹O₂ were to form, it is likely to react before diffusing out of the micelle as ¹O₂ is known to react with electron-rich olefins, such as those found in the oleate groups of the micelle phospholipid, to form the corresponding ketone.⁹⁷

In Vivo Oxygen Sensing

Having established that QD1-MC exhibits oxygen sensitivity at 0–160 Torr, which completely covers the biologically relevant range, in vivo oxygen concentration profiles were constructed from two-photon lifetime measurements of QD1-MC. Experiments were conducted on SCID mice with a surgically implanted DSC or CW. Collected light was separated into three optical channels: green for QD emission using a 565 or 570 nm long pass dichroic mirror and a HQ535/40m-2p bandpass filter, yellow for Q(0,0) fluorescence of 1 using a 585 nm long pass dichroic mirror, and red for T(0,0) phosphorescence of 1 using a HQ690/90m-2p bandpass filter. Figure S18 provides a schematic of the optical detection configuration as well as an illustration of the spectral ranges captured by each channel. Under typical imaging conditions (400 mW of 850 nm excitation light), significant signal intensity was observed after systemic injection of the sensor; minimal background signal was observed prior to injection (Figure S19). We observed that QD1-MC remains in circulation for several hours, obviating the need for additional injection of the sensor. A post-mortem examination of a mouse injected with QD-MC by fluorescence imaging showed that the micelles were distributed throughout the body, but were particularly concentrated in the liver.

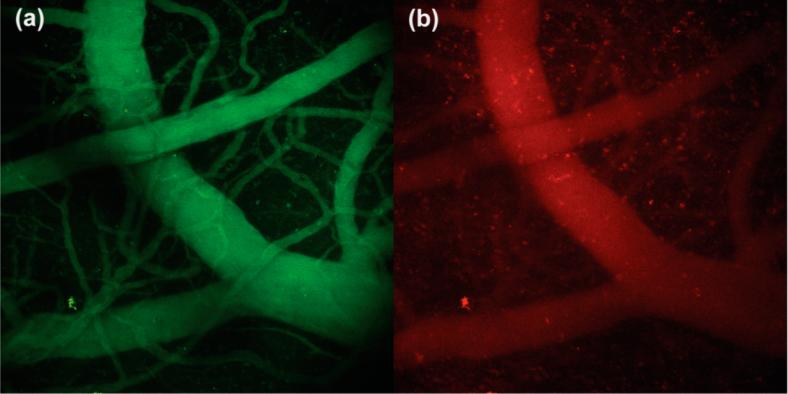
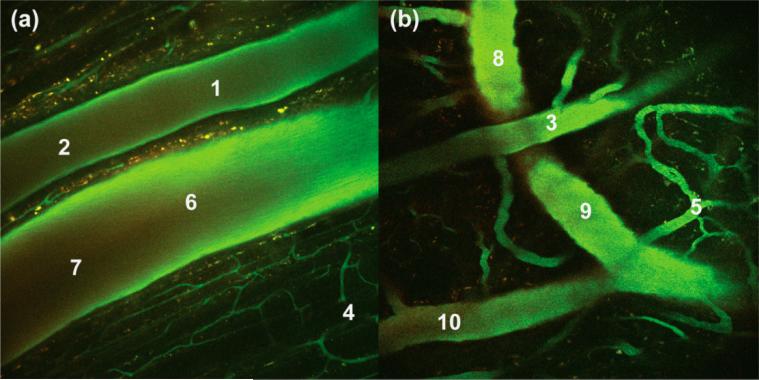
QD emission in the green channel served as a suitable means of tracking the sensor. Figure 6 shows 3-D depth projections of the brain vasculature, constructed from a series of images taken at 10 μm steps over a depth of 200 μm. As evidenced by the green channel, the sensor is evenly distributed throughout the vessels. Conversely, the intensity of the red channel is variable, illustrating differences in oxygen levels of arteries and veins. Figure 7 shows composite images of a DSC at a depth of 70 μm (a) and a CW at a depth of 115 μm (b). Lifetime measurements were made at the indicated points (1–10). Using the lifetime from the monoexponential fit, oxygen levels at these points were determined using eq 6 with τ_o = 233 μs (Table 1) and k_q = 1.36 × 10⁹ M⁻¹ s⁻¹. These data are summarized in Table 2.

Figure 6.

Three-dimensional projections of brain vasculature under two-photon excitation of a SCID mouse with a CW. Images were collected over a depth of 200 μm in 10 μm increments and combined into a projection using the ImageJ software package.

Figure 7.

Composite two-photon images of a SCID mouse with either (a) a DSC at a depth of 70 μm or (b) a CW at a depth of 115 μm. These images are an overlay of three optical channels. The indicated points (1–10) represent locations at which in vivo lifetimes were measured: arteries (1–3), capillaries (4 and 5), and veins (6–10).

Table 2.

In vivo Lifetime Measurements

point	τ (μs)a	[O2] (μM)b,c	pO2 (Torr)c,d
1	11.1 ± 0.4	63.3 ± 2.4	51.9 ± 2.0
2	8.0 ± 0.4	88.3 ± 4.6	72.3 ± 3.8
3	11.2 ± 0.5	62.5 ± 3.0	51.3 ± 2.5
4	24.9 ± 2.1	26.3 ± 2.5	21.6 ± 2.1
5	19.3 ± 1.0	34.9 ± 2.0	28.6 ± 1.7
6	26.4 ± 0.6	24.7 ± 0.6	20.2 ± 0.5
7	21.0 ± 1.5	31.8 ± 2.6	26.1 ± 2.2
8	18.3 ± 0.6	37.1 ± 1.4	30.4 ± 1.2
9	24.0 ± 0.1	27.4 ± 0.2	22.5 ± 0.2
10	27.0 ± 0.5	24.1 ± 0.5	19.7 ± 0.4

^aStandard deviation of three measurements at the same point.

^bCalculated using k_q = 1.36 × 10⁹ M^–1 s^–1 and τ_o = 233 μs in eq 6.

^cError estimated based on error of lifetime measurement.

^dPartial pressure of O₂ determined from O₂ concentration, see Experimental section.

In addition to lifetime measurements, we examined the red to green intensity ratios at each of these points in an effort to exploit the ratiometric nature of QD1-MC. Many of the points exhibit red/green ratios that fall outside of the in vitro calibration curve (Figure 4b). For points that fall on the curve, the intensity-based O₂ measurements deviate from the lifetime measurements. We have encountered similar problems when analyzing in vivo intensity data using a QD-SNARF-5F pH sensor in a colorectal adenocarcinoma model.²⁷ The primary reason for the disparity of in vivo data and the in vitro calibration is the difference in the scatter and absorption of photons as a function of wavelength,^98–100 thereby skewing the measured red:green ratio. As a result, the observed ratio will depend on both the depth at which the image was acquired as well as the optical properties of the tissue above the imaging plane. For these reasons, we preferred lifetime measurements for the quantification of oxygen.

Based on the size of the vessels in Figure 7a, the top vessel bearing points 1 and 2 is an artery, whereas the lower vessel with points 6 and 7 is a vein; the measured lifetimes and corresponding oxygen levels are consistent with this observation. Specifically, the artery (points 1 and 2) in Figure 7a has a diameter of 120 μm and exhibits O₂ pressures that fall within observed ranges for small mammals (50–70 Torr for ~100 μm arteries).^101,102 Owing to the lower O₂ levels in veins, the average intensity of red signal (see Figure S19f) in the vein is 1.25 times greater than it is in the artery. The vein (points 6 and 7) has a diameter of 185 μm, and the measured O₂ levels are consistent with those observed for veins (20–30 Torr for ~200 μm veins).¹⁰² It is further noteworthy that the partial pressure of oxygen increases by about 3 Torr when the smaller vein bearing point 10 joins the larger one with point 9; the observed increase is consistent with previously reported values for small veins flowing to larger ones.¹⁰² The capillaries (points 4 and 5) exhibit oxygen pressures that are consistent with literature reports (20–30 Torr).^102,103 Overall, the partial oxygen pressures in the CW and DSC models are similar for each vessel type, demonstrating that the sensor gives consistent oxygen readings, irrespective of the window model and the tissue that is imaged. Together, these results establish the viability of QD1-MC as an oxygen sensor in vivo and more generally the utility of the micelle approach for in vivo sensing.

CONCLUSIONS

We report the development of a micelle-encapsulated construct QD1-MC for in vivo oxygen sensing by microscopy. The synthesis of the sensors is rapid and scalable. Within the micelle, the porphyrin associates with the QD surface with a significant equilibrium constant such that cumbersome methods to conjugate the porphyrin covalently to the QD surface are circumvented. Moreover, sonication processing provides consistently sized particles without the need for chromatography. The porphyrin may be excited via FRET from the QD. Under one-photon excitation, the porphyrin may be directly excited, whether it is associated with the QD or free within the micelle. However, under two-photon excitation, only the porphyrin bound to the QD surface is selectively excited owing to the large two-photon absorption cross-section of QDs as compared to the porphyrin. The porphyrin excited state is quenched by molecular oxygen, and a quantitative measure of oxygen levels is provided by measurements of porphyrin lifetime, which fit a biexponential decay. The long component is attributed to the porphyrin bound to the surface of the QD, while the short component is due to free porphyrin dispersed in the lipids of the micelle. Stern–Volmer analysis indicates that the oxygen sensitivity of the porphyrin within the micelle occurs in a biologically relevant (0–160 Torr) range. Under two-photon excitation, the QD-bound porphyrin population is selectively excited via FRET, thereby eliminating background signal from free porphyrin. This is supported by the observation of monoexponential decay kinetics for oxygen quenching under two-photon irradiation both in vitro and in vivo. QD emission is unaffected by O₂, thereby serving as an intensity standard for ratiometric sensing.

The small size of the micelle permits the use of QD1-MC as a probe of biological microenvironments. QD1-MC provides sufficient signal to collect in vivo images and lifetime-based oxygen measurements that are consistent with known values. The cranial window image of Figure 5b demonstrates a known feature of oxygen levels in the vasculature: arteries exhibit higher levels of oxygen than veins, and moreover the partial pressure of oxygen decreases as the diameter of the vessel decreases.^101–103 Current work is directed to exploiting the ratiometric nature of this sensor by performing tissue phantom experiments to calibrate the red:green ratio as a function of depth. These experiments are performed in conjunction with Monte Carlo simulations and ex vivo tissue calibrations so that in vivo intensity data may be used quantitatively. This will enable faster data acquisition, thus affording greater fidelity in rapidly detecting real time changes in oxygen levels within living organisms.