ELASTIC MEMBRANE DEFORMATIONS GOVERN INTERLEAFLET COUPLING OF LIPID-ORDERED DOMAINS

Abstract

The mechanism responsible for domain registration in two membrane leaflets has thus far remained enigmatic. Using continuum elasticity theory, we show that minimum line tension is achieved along the rim between thicker (ordered) and thinner (disordered) domains by shifting the rims in opposing leaflets by a few nanometers relative to each other. Increasing surface tension yields an increase in line tension, resulting in larger domains. Because domain registration is driven by lipid deformation energy, it does not require special lipid components nor interactions at the membrane midplane.

Cell membranes accommodate domains with heterogeneous sizes ranging from 10–200 nm [1–3]. If enriched in cholesterol and saturated lipids with high melting temperature, such as N-(hexadecanoyl)-sphing-4-enine-1-phosphocholine (sphingomyelin), the domains may adopt a liquid-ordered (L_o) state which is referred to as a raft [4]. Since sphingomyelins bear a phosphate moiety, a choline headgoup and aliphatic chains like glycerophospholipids, their physicochemical properties closely resemble those of the major lipid family in the mammalian membrane. It has been hypothesized that rafts form independently in both leaflets of biological membranes and require transmembrane proteins for coupling [5]. However, coupling has also been observed between protein-free leaflets. The larger-sized L_o domains from monolayers of artificial membranes are always in register [6–9]. The spontaneous alignment suggests that rafts may be fundamental for the recruitment of proteins into signaling platforms [10–15], even though the driving force behind it has thus far remained enigmatic.

An early hypothesis suggested that dimerization of cholesterol from opposite monolayers drives registration [16,17]. However, it is not clear how this mechanism would result in highly dynamic entities required for cell signaling. However, domains can form in the absence of cholesterol [19–21]. Mechanistically, if lipid segregation into domains were induced by electrostatic interactions between charged proteins and polyanionic lipids [18], cholesterol recruitment into L_o phase would be a consequence of domain formation and not the cause. Since neither multivalent ligand binding to membranes, nor leaflet composition are symmetric, coupled phase separation in both monolayers was thought to be due to interlayer friction [22,23]. This idea seems questionable, since friction of the opposing leaflets cannot keep domains in register, even if the interlayer friction is tenfold larger than the in-layer friction [24]. The alternative idea is that stiff regions in both monolayers attract each other because their registration minimizes spatial restrains on membrane undulations (i.e., registration maximizes entropy [20]). If this mechanism were to act alone, phase modifications in one leaflet due to interactions with the opposing leaflet [19,22] would need to be explained in terms of coalescence of initially invisible small domains into visible ones. This agrees with observations of simple lipid systems where compositionally asymmetric bilayers remain phase asymmetric [25].

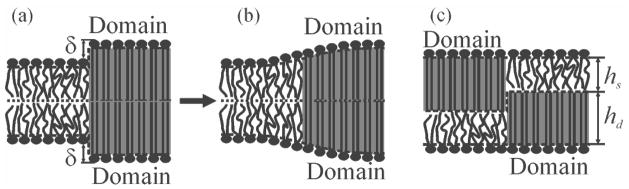
X-ray diffraction [26] experiments have proven that rafts are thicker than the surrounding liquid-disordered (L_d) membrane. If an abrupt “step-like” change in the monolayer’s thickness of ~0.5 nm were to exist at the domain boundary [Fig. 1(a)], and if the surface tension at the water/oil interface was about 50 mN/m ≈ 12.5 k_BT₀/nm² [27], the cost for exposing hydrophobic chains to water would be ~6 k_BT₀/nm ≈ 25 pN at room temperature T₀ = 300 K (k_B is Boltzmann constant). This line tension γ (the energy per unit length of domain boundary) is much larger than that experimentally measured for rafts [6,28,29]. Lipid deformations near the boundary act to prevent hydrophobic exposure, thereby reducing γ. The corresponding estimates have been made assuming mirror symmetrical membrane [Fig. 1(b)] [30–33]. However, the energetically most favorable configuration seems to be that found in silico: antisymmetric registration of equally sized L_o and L_d domains in which all “step-like” changes in monolayer’s thicknesses, and, consequently, γ vanishes [Fig. 1(c)] [34,35]. We show (i) why such an antisymmetric registration cannot be found in vitro or in vivo; (ii) why γ is sufficient to force symmetric registration with a small mismatch in domain boundaries.

FIG. 1.

Schematic representation of domain boundaries. The ordered domain (grey) is thicker than the surrounding membrane by δ = h_d − h_s. In a mirror symmetric configuration, the resulting exposure of hydrophobic lipid chains to water (a) may be prevented by membrane deformations at the boundary (b). Deformations are not required in an antisymmetric configuration of equally sized L_o and L_d domains (c).

For small deformations, zero spontaneous curvatures, and identical lateral tension σ for both leaflets, the deformation energy W can be calculated as [36]:

$$W=\int \left\{\frac{B}{2}{(\text{div}\mathbf{n})}^2+\frac{K_t}{2}{\mathbf{t}}^2+\sigma \right\}dS-\sigma A_0,$$ (1)

where A₀, S, B, K_t are the initial area, surface, splay and tilt modulus of the monolayer, respectively. The average orientation of lipids is given by the unit vector n called director. Divergence of n along the monolayer surface, divn, corresponds to splay deformation. n deviates from the normal N to the monolayer surface by the tilt-vector t. We utilize Eq. (1) for so-called neutral surface. Since K_t~40 mN/m is smaller than the compression/stretching modulus K_A~120 mN/m and the relative increment in area due to stretching σ/K_A < 5 % [37], we assume S to be non-stretching [compare Eqs. (S1)–(S3)]. If so, (i) an increment in A₀ can only occur when additional lipids are pulled from some reservoir, which requires additional work to be performed against σ [38]; (ii) any difference between monolayer thicknesses h₀ and h of the initial and the deformed monolayer, respectively, must be due to splay deformations [36]:

$$h=h_0-\frac{h_0^2}{2}\text{div}\mathbf{n},$$ (2)

Calculations were carried out for arbitrary domain radius [38]. However, for illustration, we now assume that domain radii are much larger than the characteristic deformation length, so the boundary may be considered a straight line. The system becomes translationally symmetric along the boundary, i.e. effectively one-dimensional. All vector variables may be substituted by their projections onto the Ox-axis: n→n_x = n, t→t_x = t and divn is roughly equal to dn/dx in a Cartesian coordinate system, where (i) plane Oxy aligns with the monolayer interface of the unperturbed membrane; (ii) Ox and Oy axes are perpendicular and parallel to the domain boundaries, respectively; (iii) Oz-axis is perpendicular to the membrane. Applying Eq. (2) to the individual monolayers yields:

$$\begin{array}{l}{H}_u(x)-M(x)=h_u-\frac{h_u^2}{2}{n}_u^{\prime },\\ M(x)-H_b(x)=h_b-\frac{h_b^2}{2}{n}_b^{\prime }.\end{array}$$ (3)

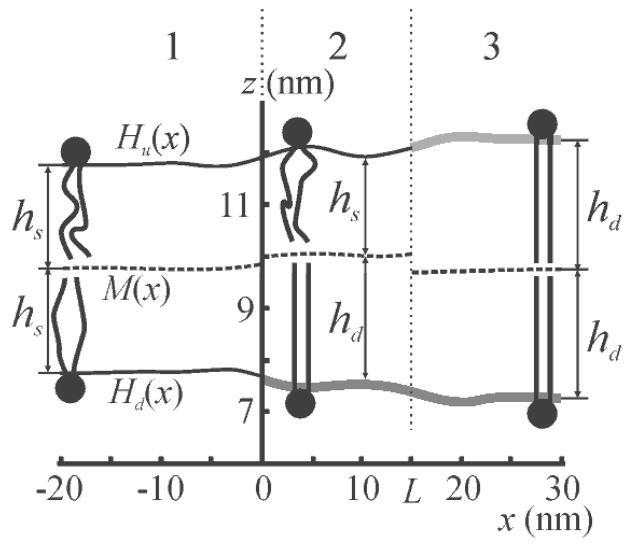
M(x), H_u(x), H_b(x) denote the shapes of the membrane midplane, upper, and bottom monolayer surfaces, respectively. The prime indicates derivative with respect to x. h_u and h_b are the thicknesses that upper and bottom monolayers would have in the absence of deformation, respectively. Letting h_d denote the thickness of the undeformed ordered domain monolayer, and h_s that of disordered monolayer of the surrounding membrane, we find for membrane zone #1: h_b = h_u = h_s; in zone #2: h_b = h_d, h_u = h_s; in zone #3: h_b = h_u = h_d (Fig. 2). The tilt vector projections adopt the form:

$$\begin{array}{l}{t}_u=n_u-N_u\approx n_u-H_u^{\prime }=n_u-M^{\prime }+\frac{h_u^2}{2}{h}_u^{″},\\ t_b=n_b-N_b\approx n_b+H_b^{\prime }=n_b+M^{\prime }+\frac{h_b^2}{2}{n}_b^{″}.\end{array}$$ (4)

FIG. 2.

Side view of membrane shape calculated for a distance L = 15 nm between the domain boundaries and a lateral tension in both monolayers σ = 5 mN/m. Membrane zones are denoted at the top. The thick grey lines correspond to surfaces of domain monolayers; the thin solid black lines correspond to surfaces of the surrounding membrane monolayers.

Expressing H_u′ and H_b′ from Eq. (3), inserting Eq. (4) into Eq. (1), and minimizing this functional with respect to n_u(x), n_b(x) and M(x) results in Euler-Lagrange equations [compare Eqs. (S1)–(S12)]:

$$\{\begin{array}{l}\frac{1}{4}{h}_u^4\left(K_t+{\sigma }_u\right)n_u^{(4)}+\left(K_t{h}_u^2-B\right)n_u^{″}+K_t{n}_u-\frac{1}{2}{h}_u^2\left(K_t+{\sigma }_u\right)M^{‴}-K_t{M}^{\prime }=0,\hfill \\ \frac{1}{4}{h}_b^4\left(K_t+{\sigma }_b\right)n_b^{(4)}+\left(K_t{h}_b^2-B\right)n_b^{″}+K_t{n}_b+\frac{1}{2}{h}_b^2\left(K_t+{\sigma }_b\right)M^{‴}+K_t{M}^{\prime }=0,\hfill \\ \frac{1}{2}{h}_u^2\left(K_t+{\sigma }_u\right)n_u^{‴}-\frac{1}{2}{h}_b^2\left(K_t+{\sigma }_b\right)n_b^{‴}+K_t{n}_u^{\prime }-K_t{n}_b^{\prime }-(2K_t+{\sigma }_u+{\sigma }_b)M^{″}=0.\hfill \end{array}$$ (5)

By positioning the membrane midplane to coincide with the Oxy plane for x → −∞, we find the boundary conditions

$$\{\begin{array}{l}{n}_{u,b}(\pm \infty )=0\hfill \\ M(-\infty )=0\hfill \\ M(+\infty )=\mathit{const}\hfill \end{array}$$ (6)

The solutions of Eqs. (5)–(6) are bulky; they contain exponentially increasing and decreasing oscillating functions, and polynomial functions [Eqs. (S31)–(S35)]. We joined the spatial distributions of the directors n_u, n_b, and the shape of monolayers surfaces H_u and H_b (Eq. 3) by imposing continuity onto each of the monolayers. We minimized the total energy W with respect to the remaining integration constants. Dividing W by the length of boundary along the Oy-axis yields γ [38].

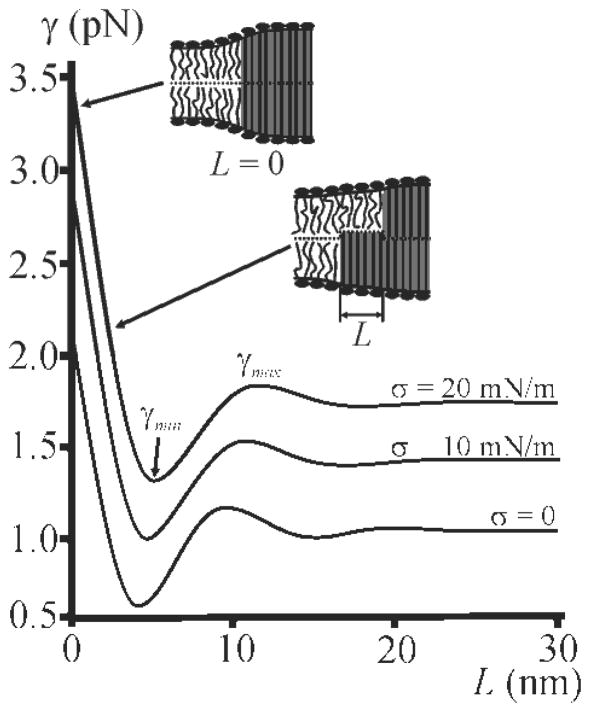
W is minimal when domain registration in the two monolayers remains incomplete, i.e. when the domain edges are shifted relative to each other by L~4 nm (Fig. 3). In the absence of an analytical expression for L we restrict our discussion to its main determinants: h_s, h_d, $l_t=\sqrt{B/K_t}$, and $l_{\sigma }=\sqrt{B/\sigma }$. From σ ≪ K_t it follows that l_σ ≫ l_t. Thus, σ is not the major determinant of L (Fig. S7). Since L does not depend on domain radius either (Fig. S10), the major determinants of L can only be h_s, δ, and l_t (Figs. S6, S13).

FIG. 3.

Dependence of line tension γ on the distance L between the boundaries of monolayer domains for different values of lateral tension σ. Lateral tension per monolayer, equal in both monolayers, is shown for each curve. The dependencies have global minima (γ_min) and local maxima (γ_max). Depictions illustrate the side views along the domain boundary for different L values; the ordered phase is filled by grey.

To calculate γ and L we used the following parameters: h_s = 2 nm, h_d = 2.5 nm, K_t = 40 mN/m = 10 k_BT₀/nm² [48], B = 10 k_BT₀ [37]. Accounting for different B in the ordered and disordered phases would change γ but would not significantly alter L (Sections III and IV in [38]). Our results do not imply that one monolayer will have a larger fraction of ordered lipids than the opposing monolayer. The L_o phase area disbalance in two monolayers of single bilayer domain would be balanced by one or several neighboring domains because the sign of L is arbitrary.

More accurate L values could be calculated if the sharp phase boundary were substituted by a gradual boundary, similar to the way amphiphilic additives can lower the free energy of membrane deformations around transmembrane proteins [49]. However, relinquishing the appeal of our simple model for a more detailed description is presently unjustified as experimental L values are not available, and estimates from simulation snapshots reveal satisfactory agreement: L amounted to 2.5 nm in [34,50,51]. We set δ~0.3–0.4 nm for h_s = 1.3 nm (as in [50]) within our formalism and obtained quantitative agreement with the results of molecular dynamics simulations (Figs. S4, S6, S8).

In silico domain registration of saturated phosphatidylcholine (PC), unsaturated PC, cholesterol mixtures was driven by localized curvature changes [50]. This is consistent with our conclusion that δ ≠ 0 determines registration, because δ ≠ 0 gives rise to both localized curvature changes and γ. δ and γ were found to guide monolayer domains together and to stabilize the registered state in molecular dynamics simulations [52]. Although the ordered domains were induced by counter-ions cross-linking charged lipids, a non-zero L was observed, confirming its dependence on δ.

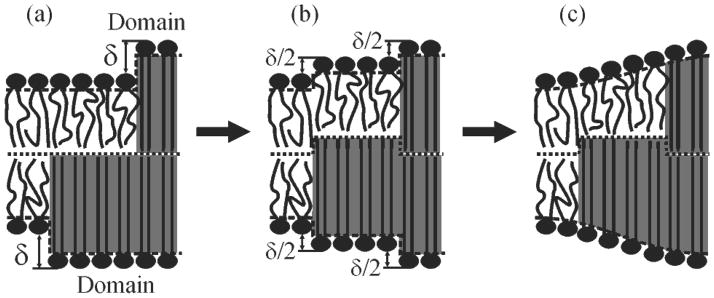
Simple considerations suggest that imperfect alignment must be energetically favorable compared to the mirror symmetric configuration [Fig. 1(b)]. For small deformations the elastic energy follows Hooke’s law, i.e. it is proportional to 2·δ²/2 = δ² [30–33]; the factor of 2 arises because there are two (upper and bottom) boundaries. In the imperfectly aligned configuration [Fig. 4(a)], the number of thickness jumps increases to four, but the height differences are halved [Fig. 4(b)]. Accordingly, the deformation energy [Fig. 4(c)] is halved since it is proportional to 4·(δ/2)²/2 = δ²/2. A non-monotonic interaction of the shifted boundaries results in an even greater energy gain for L~4 nm (compare values of γ_min and γ(L→∞) in Fig. 3).

FIG. 4.

Relative shift of monolayer domain boundaries allows decreasing in the energy of deformations by at least a factor of 2. (a) A hydrophobic mismatch of amplitude δ creates a large hydrophobic surface exposed to water. (b) Displacement of the transition zone by δ/2 results in an increase in the number of thickness jumps from two to four, but the step’s amplitude is decreased to δ/2. (c) Membrane deformations at the boundaries prevent the energetically costly exposure of hydrophobic surfaces to water.

Non-perfect alignment of domains has previously been noticed and addressed [53]. However, in the prior study, the displacement of the rims relative to each other was caused by thermal fluctuations and — in sharp contrast to our results — L was associated with a free-energy penalty for repelling ordered and disordered lipid tails [35,53]. We believe that the requirement of interdigidation for coupling [53] gave rise to the different result. In contrast, our model envisions a flat interface between the leaflets, as our analysis of friction at the membrane midplane does not support lipid interdigidation [24].

L = 0 yields maximum γ (Fig. 3). γ amounts to ~0.5 pN at zero σ, thickness mismatch of 0.5 nm, L = 4 nm. This is in line with the experimentally determined γ~1 pN [6,28]. The increase of L increases γ from γ_min to γ_max (Fig. 3). The energy, W_r = sγ, stored in the rim of the domain (s is the contour length) is minimal when γ = γ_min, i.e. when L~4 nm. Thus, the tendency to minimize γ drives an imperfect domain registration (see the example of circular domain registration in Figs. S9, S10). It provides the explanation as to why the antisymmetric registration [Fig. 1(c)] can only be observed in silico. W_r only vanishes when the sizes of all L_o domains exactly match the sizes of all L_d domains. Exact matching cannot generally be the case for real membranes. That is “antiregistration” in a real membrane is identical to the case of disentangled domains in which W_r is maximal, and thus energetically unfavorable.

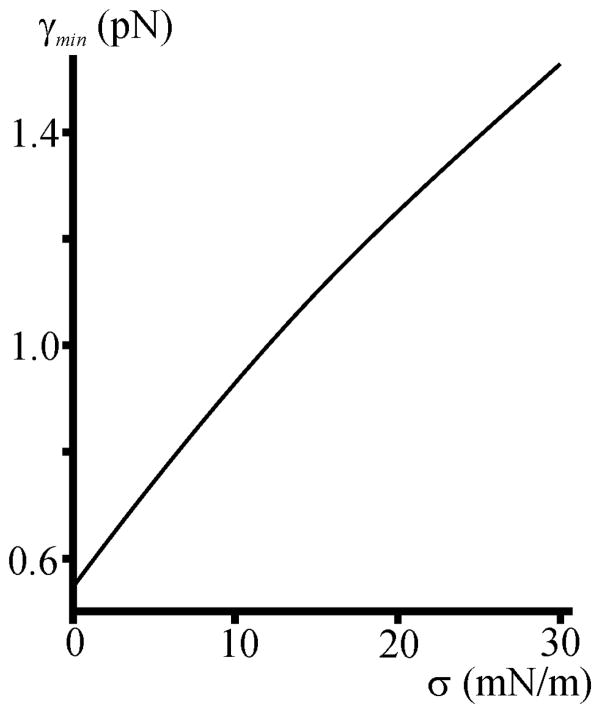
σ does not drive domain registration, but significantly affects the energetics of the process. Increasing σ induces greater γ values (Figs. 3, 5), as has been found experimentally [29,54]. γ depends on σ because there is always an increment Δa in surface area when an initially flat membrane is deformed. The work for pulling additional lipids from a reservoir is σΔa [38]. The increase in γ favors domain merger. That is, minimization of W_r is achieved via shortening of s, and domains size increases with σ. σ also accelerates the otherwise slow lipid redistribution in case of a slowly coalescing system [55]. Experimental data confirm our theoretical considerations: Increasing σ by osmotic swelling of liposomes, dramatically increases raft size [29,54], consistent with an increase of γ [32,55]. Our model correctly reflects the experimentally determined dependence [47] of γ_min on δ (Fig. S5). Considering variations in bending rigidity as well as the resultant “bulging” of domains [6, 57, 58] does not alter our conclusions (Section IV in [38]).

FIG. 5.

Dependence of γ_min on monolayer lateral tension σ. σ is assumed equal in both monolayers.

In summary, our theory identifies γ as the driving force for domain registration in two monolayers, and explains the effect of σ on domain size. In order to act, γ does not require a particular membrane constituent to be present. Consequently our theory should be applicable to domain registration in membranes of varied lipid composition.