Velocity computation in the primate visual system

Abstract

Computational neuroscience combines theory and experiment to shed light on the principles and mechanisms of neural computation. This approach has been highly fruitful in the ongoing effort to understand velocity computation by the primate visual system. This Review describes the success of spatiotemporal-energy models in representing local-velocity detection. It shows why local-velocity measurements tend to differ from the velocity of the object as a whole. Certain cells in the middle temporal area are thought to solve this problem by combining local-velocity estimates to compute the overall pattern velocity. The Review discusses different models for how this might occur and experiments that test these models. Although no model is yet firmly established, evidence suggests that computing pattern velocity from local-velocity estimates involves simple operations in the spatiotemporal frequency domain.

Vision, our intuition tells us, is about recognizing objects and colours. However, with a little more insight we realize that understanding spatial relationships is also crucial. In particular, the displacement of objects with time carries vital information. How difficult can it be to see an object move? The principle seems simple: an object is first in one location, and then a moment later it is in another. In reality, motion detection is fraught with difficulties, such as how to distinguish between image noise and actual motion, and how to deal with several movements in the same part of an image. But at the core of motion processing is the aperture problem, a computational obstacle that is as abstruse as it is inconvenient (Figure 1a). The aperture problem refers to the visual system's inability to sense the overall velocity of an object by sampling the velocity at just one location on the object's surface. Unless this problem is overcome, the velocity of objects cannot be computed. Therefore, a great deal of visual processing is dedicated to a problem that most of us have never heard of. This Review will cover the basic stages of velocity computation in the primate visual system, with emphasis on the mechanisms that create and solve the aperture problem. We aim to show how a combined theoretical and experimental approach can provide unique insights into computational neural systems.

Figure 1.

Even though the rectangle is moving directly to the right, it seems to be moving up and to the right when it is sampled through an aperture as shown (a). This is because object velocity can be decomposed into two orthogonal vectors (b), one perpendicular to the visible edge of the rectangle and one parallel to the edge. The parallel vector is invisible because one cannot detect the movement of an edge along its own length; thus, all we detect is the perpendicular vector. (c) The aperture problem, as incurred with a Reichardt detector. Each unfilled circle represents a detector that senses image contrast at a specific location and a specific time. The red and blue shapes represent moving objects. Motion is assumed to occur along the axis of the two detectors if they are activated in sequence with the appropriate timing. However, these conditions could be met for objects moving even orthogonally to the detector axis (as illustrated by the red object), depending on their speed and shape. Therefore a Reichardt detector does not signal object velocity.

Anatomy of the visual motion pathway

A number of recent reviews have discussed in detail the anatomy of the subcortical and cortical areas that are involved in motion processing [1–6]. Here, we relate computational models of motion processing to two cortical areas: area V1 (the primary visual cortex) and area MT (the middle temporal area). Both V1 [7] and MT [8] contain neurons that respond strongly to motion in a particular direction and weakly or not at all to motion in the opposite direction. The same neurons also typically respond best to a particular speed. Because direction and speed together define a single vector called velocity (speed is the magnitude), V1 and MT neurons are said to be velocity-tuned.

In V1, velocity-tuned neurons are concentrated in upper layer 4 [9]. There is an atypical, direct projection from this layer to MT [10]. Most MT neurons are velocity-tuned, compared with roughly a quarter in V1. Neurons in V1 project indirectly to MT through area V2 (the secondary visual cortex), but it is not clear whether this pathway is involved in velocity computation [11].

Pattern velocities and local velocities

Imagine a moving object with a considerable amount of structure — that is, not a bare sphere, but something similar to a branch or a hand. For simplicity we will discuss only rigid, non-rotating objects. The motion of the object is characterized at any instant by V_x and V_y, the horizontal and vertical components of velocity. The velocity vector's direction is arctan(V_y/V_x), and its magnitude (speed) is √(V_x² + V_y²). When referring to the velocity of the whole object we talk about the 'pattern', 'object' or 'global' velocity. However, we can also refer to the velocity measured at specific locations on the object: this is termed 'local', 'normal' or 'component' velocity. This distinction might seem odd — is the velocity not the same everywhere on the object?

The answer depends on whether we are talking about the true velocity of the sampled location or the velocity that the visual system detects (the apparent velocity). As we shall see, local-velocity measurements are not generally the same as the true object velocity. This discrepancy between local and global velocities is the aperture problem. What causes the discrepancy? The answer is rather complex, and it requires an understanding of both experimental results and theoretical concepts. The goal of this Review is to convey this understanding, beginning with the conventional view of the aperture problem.

The aperture problem

Figure 1a shows a rectangle that is moving to the right, seen through an aperture placed over its upper-right edge. Viewed through the aperture, this edge seems to be moving up and to the right, even though the rectangle is moving directly right. Thus, the local-velocity sample is different from the object velocity. This is because the rightward vector representing the object velocity is separable into one vector that is parallel to the edge and one vector that is normal (perpendicular) to it (Figure 1b). The parallel vector is invisible because there is no contrast (no intensity gradient) along the length of an edge; thus, one sees only the normal component. For this reason edges always seem to move perpendicularly to themselves, no matter which way they are really going.

This conventional depiction of the aperture problem is intuitive but incomplete. In reality the aperture problem takes different forms, depending on the model of velocity computation in question. In the following section we describe three approaches to local-velocity estimation and show how the aperture problem arises in each case.

Models of local-velocity detection

Most pattern-velocity models are based on two stages: one in which local velocities are estimated, and another in which local velocities are combined to compute the pattern velocity. Here we explain the basic operation of three models of local-velocity estimation. We first consider strictly theoretical ideas; in a later section we will discuss possible physiological counterparts.

Reichardt detectors

Arguably the most intuitive motion-detection model consists of two luminance (not motion) sensors that are offset in space [12]. The outputs of the two sensors are combined and multiplied to produce a response that is large when the sensors are triggered sequentially with a particular delay. The direction that the overall detector is tuned for depends on the alignment of the sensors in space, and the speed tuning is determined by the delay.

Let us imagine a moving object. If the object's direction happens to be aligned with the two sensors of the Reichardt model, then the leading edge of the object will trigger the sensors with a delay between the triggering of the first and the second sensor that depends only on the object's speed. However, if the object is moving in a different direction, the delay between the triggering of the two sensors will also depend on the object's shape (Figure 1c). Thus, as the only thing that is sensed by a Reichardt detector is the delay between the activation of its two sensors, Reichardt detectors cannot measure the direction or speed of an object. This is one manifestation of the aperture problem.

Gradient models

Gradient models were proposed as a fundamental basis for motion detection [13,14]. Let I(x, y, t) denote the measured image intensity at location x, y and time t. Let I_x, I_y and I_t be the partial derivatives of I with respect to x, y and t, respectively, and let V_x and V_y be the x and y components of the object's velocity. It can be shown that I_xV_x + I_yV_y = −I_t, which we can rewrite as (I_x, I_y)·(V_x, V_y) = −I_t. The intensity derivatives are measurable, but V_x and V_y are unknown. As there are two unknowns and a single equation, we cannot determine their separate values from just one sample. However, we can compute the component of the object's velocity in the direction of the gradient (I_x, I_y) using the following equation

$$\frac{(I_x,I_y)·(V_x,V_y)}{\sqrt{{I_x}^2+{I_y}^2}}=-\frac{I_t}{\sqrt{{I_x}^2+{I_y}^2}}$$ (1)

Thus, one cannot know object velocity from a single, local sample. Instead, we obtain an estimate of velocity in the direction of the gradient that is being sampled. This is the aperture problem in terms of the gradient model.

Spatiotemporal-energy models

Spatiotemporal energy (STE) models [15–19] (Figure 2) can account for a wide variety of data and are based on physiologically plausible mathematical operations. These models have three basic steps, known as linear filtering, motion energy and opponent energy. These steps are described below, first theoretically and then later in terms of cortical mechanisms. Understanding these models requires a basic understanding of frequency analysis, as outlined in Box 1.

Figure 2. Summary of the spatiotemporal energy (STE) model.

(a) A moving dot traces out a path in space–time. x and y correspond to horizontal and vertical axes, respectively, and t is time. The projection (shadow, shown in green) of the path on the x–y plane specifies an angle with the x axis; this angle is the direction of motion. The rate of ascent (slope, shown in red) in the t dimension corresponds to the speed of motion. (b) The movement of the dot (dashed red line) is shown by plotting x against t. The filled and unfilled ovals illustrate the orientation of the positive (unfilled) and negative (filled) lobes of a filter. If the filter is oriented in the same way as the dot's space–time path (top panel) it could be activated by this motion. A dot moving in the opposite direction (bottom panel) would always contact both positive and negative lobes of the filter and therefore could never produce a strong response. c | The complete model. Motion is first extracted with linear filters that are oriented in space and time. These are thought to correspond to the receptive fields of V1 (primary visual cortex) simple cells. For each direction to be detected (left and right in this example), two filters that are 90° out of phase are paired (a quadrature pair). Squaring the output of each of these filters and then summing them produces a phase-invariant response called the motion energy. This step is thought to take place in V1 complex cells. Finally, two opposite-direction energy detectors are opposed, either by subtraction as assumed here or by a nonlinear mechanism such as division in MT (middle temporal) cells.

Box 1. Basic introduction to frequency analysis.

Frequency analysis refers to the description of images in terms of their spectra and the description of neural transformations in terms of filter operations.

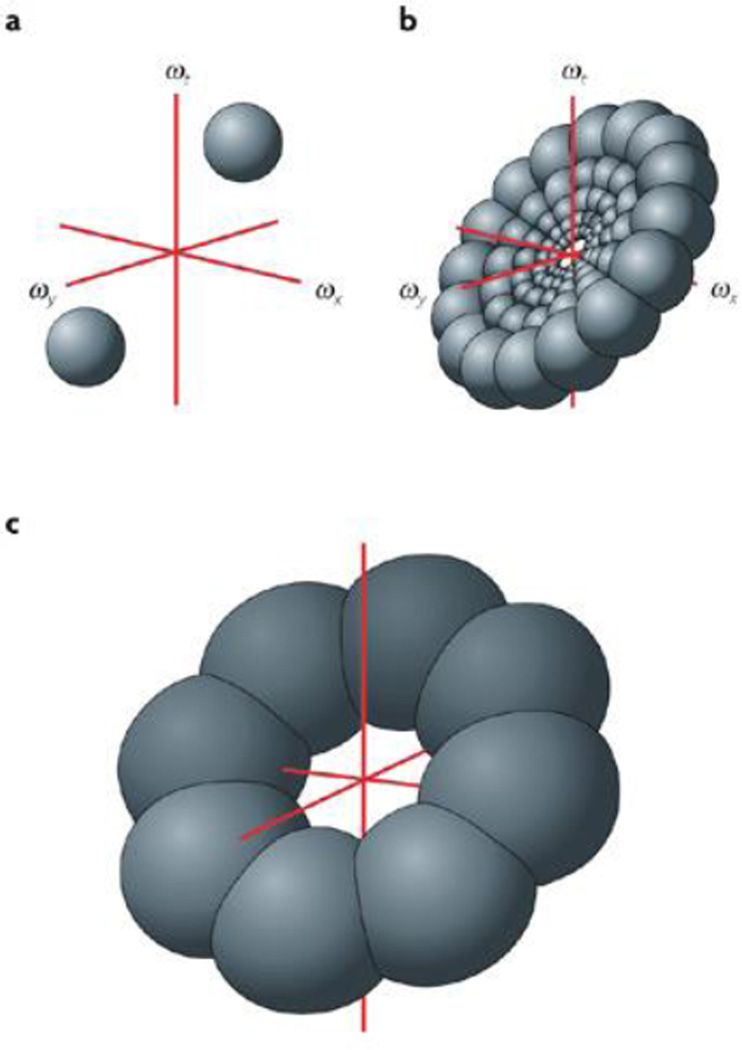
The spectrum of an image is computed with a Fourier transform, which sees the image as the sum of moving sinusoidal waves with different frequencies, amplitudes and phases. Each wave is called a frequency component and is three-dimensional (the three dimensions being ω_x, ω_y and ω_t) (see figure, part a). The amplitude spectrum depicts the amplitude of the waves as a function of their frequency, and its square is called the power spectrum. Both types of spectrum describe an image not in familiar space and time coordinates, but in the frequency, or Fourier, domain. For an image with spatial dimensions x and y and temporal dimension t, each frequency component can be depicted as a moving sinusoidal grating with a particular spatial frequency, direction and speed. The relationship between a grating's frequency vector and its velocity is given by: direction = arctan(ω_y/ω_x) and speed = ω_t/√(ω_x² + ω_y²).

A linear filter convolves its input with a specific kernel. Certain kernels give rise to band-pass filters, for which the amplitude of the output depends on the image intensity within a narrow range of frequencies that are characteristic of the filter. The centre of this range is called the centre frequency. Most simple cells behave like band-pass filters, with kernels that resemble Gabor functions. Part b of the figure shows a two-dimensional Gabor kernel. In the space–time domain, a Gabor function is a sinusoidal wave inside a Gaussian envelope. To describe a Gabor kernel in frequency space, we take the Fourier transform of the kernel to obtain the transfer function. The result is a fuzzy blob in frequency space, the density of which decreases with distance from the centre (see figure, part c). The location of the centre, (ω_x, ω_y, ω_t)^C, is the Gabor filter's centre frequency, which corresponds uniquely to a particular velocity according to the equations above.

Both the image and the kernel of a filter can thus be described in the frequency domain (that is, in terms of their spectra). For the image, the spectrum reflects image intensity at various frequencies. For the kernel, the spectrum reflects the weight of the kernel at various frequencies. The response of a filter to an image can be predicted by looking at how much the image spectrum and the transfer function overlap. More formally, the transform of the input multiplied point-wise by the transform of the kernel equals the transform of the convolution (the filter's output).

The spectrum of a rigid moving object is zero-valued except on a single plane in frequency space, the orientation of which corresponds to the object's velocity. Thus, a simple cell should respond well when the planar spectrum of the image passes through or near the centre of the blob that is the transfer function of the cell's Gabor kernel. (Because a complex cell is built from simple-cell inputs, its response region is determined in the same way.) However, any number of planes with different orientations can do this (see figure, part c); thus, a simple cell cannot sense the velocity of a moving object, it can only exclude object velocities for which the planar spectrum does not pass through its transfer function. This is a formal statement of the aperture problem in the context of a linear system, and it is important to realize that it has nothing to do with a spatial aperture.

In the linear filtering step, STE models detect motion using filters that are oriented in space and time. To understand this, we can plot the spatial coordinates x and y, and the time coordinate t, of a particle as it moves along a trajectory (Figure 2a). This shows that motion can be considered to be an orientation in space–time. It makes sense, therefore, that motion might be detected with a filter that is oriented in space–time (Figure 2b).

As described in Box 1, both images and filters can be described in the frequency domain. In the visual system, spatiotemporal-frequency filters are in fact band-pass filters, each responding to a narrow range of spatiotemporal frequencies. When an image passes through a filter, the filter's response depends on how much the spectrum of the image — its energy or intensity distribution in frequency space — and the spectrum of the filter overlap. V1 simple cells resemble filters with a small, spherical spectrum, whereas the spectrum of a moving object is a plane, the orientation of which specifies the object velocity. The filter responds best to planes that pass through the centre of its spectrum, but as planes with various orientations can do this (Box 1 figure, part c), the filter (the V1 neuron) cannot determine the object velocity. This is how the aperture problem is manifest in a system in which linear filters are used as the first step.

The role of the second step in the STE model, a motion-energy step, is mainly to remove phase-dependence from the output. As described in Box 1, the frequency components of an image can be depicted as moving sinusoidal gratings. The output of a band-pass filter that is convolving a moving sinusoidal grating is an oscillating scalar function of time. Because the output oscillates whereas the grating's motion is constant, the instantaneous output of the filter is not a useful indicator of motion. More useful information can be obtained from the amplitude of the filter's oscillating output. One way to compute this amplitude is to rectify the oscillating wave and then integrate over time. If this computation takes place in a neuron, rectification will occur automatically, because firing rates cannot be negative. For integration one could simply pass the rectified output through a low-pass temporal filter. But temporal integration is not strictly necessary. In particular, by squaring and then summing the outputs of two Gabor filters that are phase-shifted by 90° (a quadrature pair, see Figure 2c), one produces a quantity that does not vary with time [18].

The third step of STE models, called opponent energy, achieves noise reduction. Because motion signals fundamentally consist of space–time correlations of image contrast, random variations in image luminance tend to produce noisy motion signals. The visual system also has its own internal noise. Therefore, an opponent stage is introduced in which the output of each motion-energy detector that is tuned for a given direction is subtracted from that of a detector that is tuned for the opposite direction (Figure 2c). This relies on the principle that noise, because it tends to be omnidirectional, should activate oppositely-tuned detectors to similar extents. Thus, noise does not produce a net response.

Neurophysiological support for the STE model

The Reichardt, gradient and STE models are not really exclusive ideas; in fact, they are mathematically equivalent at certain stages (Box 2). However, the STE model is detailed and its steps map conveniently onto the known stages of neural motion processing. Therefore, in the following we discuss these neural stages and their relationship to elements of the STE model. We emphasize first that early formulations of the STE model were not meant to precisely represent neuronal properties but, rather, were intended to suggest basic types of algorithm that might be used in the visual system. One should not infer, for example, that the first step must be strictly linear, or that the opponent step is specifically subtractive. Nor should it be assumed that each step corresponds precisely to a particular cortical population. Nevertheless, there are important similarities between certain cortical neurons and the functions that are expressed by the STE model, along with some notable differences.

Box 2. Relationship of spatiotemporal energy (STE) models to gradient and Reichardt models.

Intensity gradients tend to be highly localized; that is, one tends to see 'edges', rather than large patches with a steady change in luminance. Therefore, gradient samples must take place on a very small scale. As a result they tend to be noisy, or uncertain. This noise can be minimized with a least-squares sampling approach that emphasizes regions with the steepest gradient, where uncertainty is at a minimum. Under such conditions the gradient model is formally equivalent to the STE model at the motion-energy step [16].

The basic idea of the Reichardt model was extended to include spatial filters (as a first step), subtractive opponency and other modifications [17]. This produces a model that is formally equivalent to STE models at the opponent-energy step.

Note that if different models produce the same output at certain stages, it need not follow that the models are equivalent. Nevertheless, the sequence of individual transformations that leads to that output can vary. Indeed, it is the nature of this sequence that interests us, because the different transformations can have correlates at different anatomical stages of neural processing.

The linear filtering step of the STE model strongly resembles the function of V1 simple cells. Following initial qualitative observations, various impulse-response [7,20] and linear-systems [21–26] techniques have supported the idea that the responses of simple cells are to a large extent linear in both space and time. Reverse-correlation studies have shown that the receptive fields of simple cells contain oriented, adjacent on and off regions, as predicted by the model. In fact, simple cells' receptive fields resemble Gabor kernels (Box 1), which are used in some STE models for the linear filtration stage.

Simple-cell responses are not entirely linear, however. As firing rates cannot be negative, they are rectified in some way, and this is a nonlinear effect. More nonlinearity results from response saturation and probably from gain normalization through recurrent inhibition [27]. In fact, linear and nonlinear mechanisms contribute approximately equally to direction selectivity in simple cells [22]. Therefore, although the basic tuning of simple cells is thought to derive from oriented, linear spatiotemporal filters, it should not be inferred that simple-cell responses are strictly linear transformations of the luminance input.

Substantial evidence links the motion-energy step of STE models to V1 complex cells. First, complex-cell but not simple-cell responses are largely phase-insensitive [28]. Second, a reverse-correlation technique was used to compute responses to single bars and two-bar interactions in cat complex cells [29]. The study also derived predictions from the STE model for the same stimuli, and found that the motion-energy output of the model corresponded closely to the responses of the complex cells. Finally, spike-triggered correlation [30] and covariance [31] were used to show that complex cells pool inputs from one or more quadrature pairs of linear kernels. These results suggest that, like the energy step of the STE model, complex cells pool input from simple cells with similar frequency tuning but phase-shifted receptive fields.

The opponent-energy stage predicts that there should be neurons that are inhibited by non-preferred directions. It was shown that MT neurons responding to their preferred direction were strongly (60%) suppressed by locally paired dots moving in the opposite direction [32]. The same tests in V1 neurons showed much weaker (20%) suppression. These findings suggest that the opponent stage could correspond to MT neurons, but they do not specifically imply that opponency occurs between motion-energy detectors. Also, the observed suppression in MT neurons was essentially divisive rather than subtractive. But the original STE model's assumption of subtractive opponency was not critical: what matters is that an opponent stage is needed for noise suppression and that this opponency has been observed in MT neurons.

Solving the aperture problem: concepts

In this section we discuss several theories about how the visual system deals with the ambiguity of local-velocity estimates. In some cases the approach is to pool local velocities in some fashion to derive the global (object) velocity. Another idea, called feature tracking, holds that by limiting local samples to specific features the ambiguity can be avoided altogether. The ideas in this section are strictly theoretical; in a later section we evaluate the evidence for and against each of them.

Vector summation

Perhaps the simplest way to estimate object velocity from local samples is with a vector average (VA), or vector sum. In the same way that the mean of multiple samples of a random variable can represent the variable's central tendency, one might expect the average of many local-velocity samples to reflect the overall velocity of an object. However, this does not really follow, because local velocities do not form a probability distribution but, rather, a deterministic distribution of speed versus direction.

Although the direction and speed of the VA tend to be roughly correlated with object direction and speed, the VA is in general a poor estimator of object velocity. For example, the VA speed is almost always less than the object speed. And although the VA speed scales with the object speed, it tends to vary from one object to the next — even if their speeds are the same — depending on the objects' shape (Figure 3). Also, there is no a priori reason for the directions of local-velocity samples to distribute symmetrically on either side of the object direction; thus, the VA is a biased estimator of object direction. Finally, the VA assumes that there is an input that consists of two-dimensional velocity vectors. But single-neuron firing rates are one-dimensional. Although one can imagine schemes in which multiple neurons are used to estimate the velocity vector at each location, followed by a VA of the local results, the simplicity of the VA approach — its only advantage — would be lost.

Figure 3. A vector average (or sum) of local velocities can grossly misrepresent speed.

The two circles represent objects moving slowly (left-hand circle) and quickly (right-hand circle). The black arrows symbolize two local-velocity samples. Even though the right-hand object is moving faster, the vector average for the right-hand object (represented by the green arrow) is actually smaller.

IOC solutions

Another approach to local-velocity detection is based on the intersection of constraints (IOC) principle. This principle recognizes that, for a given object velocity, the speed of every local sample is exactly determined by its direction. The relationship is

$$S_I=S_o\text{cos}({\theta }_I-{\theta }_o)$$ (2)

where S and θ are speed and direction, and the subscripts l and o indicate local and object properties. The local properties are measured, whereas the two object properties are unknown; thus, at least two equations (two samples) are required. This is the trigonometric expression of the IOC principle. The geometric expression is described in Figure 4.

Figure 4. A geometric expression of the intersection of constraints (IOC) principle.

The two-dimensional space that is shown is velocity space, whereV_x and V_y signify the horizontal and vertical components of velocity, respectively. Every local sample (black arrows) from a rigid moving object must terminate on the same circle in this space. The vector that bisects the circle (green arrow) corresponds to the object velocity. The two black lines show a more common depiction of the IOC: any local velocity has a perpendicular component that extends from its tip and crosses the tip of the object vector.

A third expression of the IOC principle involves frequency space. Essentially, the spectrum of a rigid, non-rotating moving object is zero everywhere except on a single plane, the orientation of which corresponds to the object velocity. As the orientation of a plane has two slope components and thus two unknowns, the frequency-space expression of the IOC, like the trigonometric and geometric expressions, in principle requires two (noise-free) local-velocity samples to obtain the object velocity.

The frequency-space version of the IOC principle is especially convenient because, unlike the trigonometric and geometric expressions (and the VA), the input is assumed to be a scalar that represents intensity somewhere in three-dimensional frequency space, rather than a velocity vector. As V1 neurons are not really velocity-tuned but rather are tuned for a three-dimensional frequency (their centre frequency), it is easy to see how the distribution of V1 responses over three-dimensional frequency space could in a simple fashion represent a plane, the orientation of which conveys the velocity of the object.

Simoncelli and Heeger developed a model along these lines (referred to here as the S and H model) [33,34]. It begins with linear simple cells that act as oriented space–time filters (Figure 5). These cells' responses are rectified and gain-normalized, and then they are spatially pooled by a complex cell to remove phase dependence. This part of the model is essentially an STE model. Next an MT cell, specifically a pattern-direction-selective (PDS) cell (see below), sums the inputs of complex cells that have centre frequencies that lie on a common plane in frequency space. The orientation of a PDS cell's pooling plane corresponds to its preferred velocity. The model's final stage rectifies and gain-normalizes the PDS-cell outputs.

Figure 5. The Simoncelli-Heeger (S and H) model.

In all three parts of the figure, the axes of the graph are horizontal frequency (ω_x), vertical frequency (ω_y) and temporal frequency (ω_t); the origin is zero. Thus, each panel depicts spatiotemporal frequency space. In each panel, the blobs depict the central region of a kernel that characterizes the image transformation that is effected by a V1 (primary visual cortex) simple or complex cell. The kernel can be thought of as the neuron's space–time receptive field, and its frequency-space representation (spectrum), shown here, is the transfer function. (a) The transfer function of a Gabor kernel that is commonly used to model V1 receptive fields (the S and H model uses the third derivative of a Gaussian function, which is very similar). For the purposes of the model, the V1 cell is a component-direction-selective (CDS) cell that serves as input to pattern-direction-selective (PDS) cells in the middle temporal area. (b) A PDS cell is created by summing the output of CDS cells (as in part a) with spectra centred on a common plane. (c) Frequency-space depiction of an 'inner tube' integration region for PDS cells. The inner tube is a variation of the S and H model that accommodates evidence for incompletely separable spatial-frequency and temporal-frequency tuning (for a given direction and speed). Each blob is flattened to reflect some inseparability that is inherited from V1 complex cells. According to this hypothesis, PDS cells would contribute inseparable speed and direction tuning but not spatial-frequency pooling beyond that which is accomplished in V1.

The S and H model was recently updated to include a specific kind of normalization: tuned normalization, which conveys a behaviour that is similar to surround inhibition [27]. The current model can therefore be understood as having a dynamic linear backbone — the V1 and MT selectivities for certain frequency ranges — with associated static nonlinearities. However, the IOC calculation is widely understood to be fundamentally nonlinear. This does not mean that the S and H model is not an IOC computation. The S and H model stops short of specifying the object velocity; instead it predicts a distribution of activity across PDS cells with different preferred velocities. Ultimately, the conversion of image contrast to a V_x, V_y coordinate pair has to be nonlinear, possibly a maximum-likelihood estimation over the MT population. The trigonometric and geometric expressions of the IOC give the illusion of obviating this problem because their inputs are already in the velocity domain.

Feature tracking

The third basic approach to pattern-velocity estimation involves feature tracking. The term 'feature tracking' is somewhat vague, but we will define it here as any algorithm that does not suffer the aperture problem. The idea is that the brain locates something — a feature — and tracks it over space and time. This feature could be, for example, a bright spot or a T-junction.

Feature tracking is deceptively intuitive. When we see a grating moving behind an aperture, we cannot detect in which direction the grating is really moving (Figure 1a). However, when a dot or a corner moves through the aperture, its two-dimensional velocity is unambiguous. In this context, the notion of feature tracking seems clear. But when it comes to postulating that individual neurons are feature trackers, we have to think of the problem in terms of these neurons' response properties. For example, a V1 simple or complex cell cannot signal where a dot really is: it can only signal that the dot is in its receptive field and, perhaps, a certain distance from the centre. Therefore, a V1 cell cannot by itself track a feature.

Feature-tracking mechanisms have been proposed in terms of non-Fourier motion detection [35]. Rather than delve into this rather complex theory, we use a model developed by Wilson and colleagues to illustrate it [36]. The model begins by squaring the spatial image to produce distortion products, which are then passed through a set of spatiotemporal filters, as in the STE model. But distortion products, unlike the raw image, do not have a local velocity distribution: instead, all velocity samples match the object velocity. Therefore, the aperture problem is obviated by stripping the input of ambiguous velocity signals.

A different idea involves a process termed endstopping in V1 [37–39]. Endstopping tends to suppress responses to contours and favour responses to features such as dots. One might thus expect endstopping to disambiguate motion signals. However, the motion that is detected by endstopped cells is no less ambiguous than it was in the first place, and so the cell still needs a way to sense the feature's velocity. The Wilson et al. model described above also has a mechanism for isolating features: a nonlinear transformation of the spatial image (although it is different from squaring, endstopping is also a nonlinear spatial transformation). The transformation that is used in the Wilson et al. model also limits these features to a specific velocity, however: that of the object. On the other hand, endstopping only isolates features, it does not restrict their velocity. Thus, although endstopping tends to remove one-dimensional signals (contours) from the input, it does not in itself provide a mechanism for tracking two-dimensional signals.

Endstopping could nevertheless still have a useful disambiguating effect. The difference between moving contours and moving dots is in their power spectra. In frequency space, a moving contour has energy that is distributed near a line that passes through the origin. A terminator has a point-like quality and therefore has energy that is spread out over a plane. So, as endstopping suppresses responses to contours and favours responses to dots, this shapes the input to MT and spreads it more evenly over a frequency plane. If MT neurons as a population are trying to find the orientation of the plane, this spreading effect should improve their accuracy.

Solving the aperture problem: evidence

Vector summation

We have already discussed the theoretical drawbacks of pooling local-velocity samples with a VA. Here we discuss a limited body of experimental evidence that concerns this mechanism. In short, we know of no substantial evidence that suggests that local velocities are combined with a VA in the visual system. Psychophysical experiments that have been carried out so far do not support the idea. For example, one study that used plaids (visual stimuli that are created by superimposing two moving sinusoidal gratings) showed that when the individual grating speeds were adjusted such that the directions that would be computed using the IOC and VA approaches were different, subjects briefly perceived the plaids' VA direction but quickly (in less than 100 ms) shifted to perceiving the IOC direction [40]. A physiological study in MT produced a similar result [41]. Nevertheless, there have been rather few experiments to directly test the VA hypothesis, so one cannot rule it out at this point.

The motion literature is somewhat confusing when it comes to VA mechanisms. In most cases the 'vector average' in question is not of the kind that we are discussing here. For example, some studies have looked at the VA of MT responses [36,42–46]. In such cases, the average in question is one of firing-rate-weighted preferred directions, not local-image velocity vectors. Others have suggested the vector sum as a way of combining Fourier and non-Fourier motion cues [36,43]. Here again the average in question does not operate on image velocities but, rather, on the output of velocity-tuned processing channels.

Finally, in a study that is sometimes misinterpreted as supporting a VA model, it was shown that the perceived direction of a pair of moving lines corresponded to the average of their directions [42]. Direction is a scalar, not a vector, so this study did not address the possibility of a VA.

IOC solutions

There is evidence that MT firing rates represent the velocity of moving objects using the IOC principle. First, a psychophysical study showed that the perception of moving plaids depends on conditions that specifically affect the detection of individual grating velocities [47]. This is consistent with a two-stage model in which component velocities are first detected and then pooled to compute pattern velocity. Second, plaids have been used to show that V1 neurons and some MT neurons (collectively termed component-direction-selective (CDS) cells) sensed the direction of the individual gratings of a plaid, whereas a subset of MT cells (PDS cells) responded to the overall direction of the plaid [48]. The properties of CDS and PDS cells are consistent with a two-stage computation. Finally, if MT is the seat of pattern-velocity computation, one would expect MT responses to correlate with our perception of velocity. Extensive studies used noisy dot patterns to demonstrate that monkeys' perception of direction or speed correlates in a predictable way with MT responses [49–58]. One would expect velocity percepts to be better linked to PDS- than CDS-cell responses, but tests of this prediction have yet to be published.

Note that although the above suggests a two-stage model, this does not by itself mean that the computation follows the IOC principle. There are two basic weaknesses of the plaid stimulus. First, the squaring (or other nonlinear transformation) of a plaid produces distortion products, or features. Therefore, an MT cell could calculate pattern velocity either with an IOC mechanism or by tracking features. Second, to establish an IOC mechanism one needs to create a stimulus for which the velocity which is defined by the IOC principle differs from that which is defined by other models.

The relationship in MT between direction tuning and the responses to static bars has been studied [59]. This revealed a subset of neurons for which the preferred direction of motion was parallel to the preferred bar orientation. This is fully consistent with the IOC rule: for an object that is moving upwards (for example), any samples from a vertical edge are expected to have zero speed. It was later shown that this subset of neurons coincides with the previously identified PDS cells [60]. This suggests that PDS cells gather local-velocity samples according to an IOC formulation, at least for low speeds.

PDS cells occasionally show bimodal tuning to slow-moving single gratings, a somewhat surprising and yet nevertheless firm prediction of the IOC principle [61]. Consider the trigonometric formulation of the IOC idea. Assuming that S_l < S_o then equation 2 is satisfied for two different values of θ_l. Therefore, the model predicts that a PDS cell will respond maximally to two different directions, which are symmetrically arranged on either side of the neuron's preferred direction, when the sample speed is below the preferred pattern speed. There is at least some evidence to suggest that this is the case [61].

The S and H model, which is a specific implementation of the IOC principle, is consistent with various experimental data, including speed tuning [62], responses to plaids [48,63], and inhibition by motion in non-preferred directions [64]. However, concordance between the predictions of a model and pre-existing data does not always validate a model, as one tends to consider the existing data when designing the model. Certain 'forward' predictions have been tested, however. In particular, an elaboration of the S and H model to include certain static nonlinearities was examined in the context of MT responses to complex moving plaids [27]. The model's predictions were close to the experimental results. Because the stimuli were distributed over a restricted range in frequency space, it was not possible to validate that PDS cells indeed integrate over a planar frequency range, as postulated by the core model.

Other, less direct tests have argued both for [62] and against [65] certain tenets of the S and H model. One such tenet concerns the inseparability of temporal-frequency tuning and spatial-frequency tuning (TF–SF tuning, sometimes called 'speed tuning') that is inherent in the model. The model predicts that as long as a stimulus moves at a given speed, the response to it should be the same regardless of its spatial and temporal frequencies. This is because the S and H model of a PDS cell assumes equal-weight integration over a plane in frequency space, and every line in this plane (assuming that it includes the origin) corresponds to a single speed: therefore the neuron should be speed-tuned. One study [62] found that some MT neurons are speed-tuned, at least over a certain range. However, others [65–67] found that speed tuning is no more prevalent in MT than in V1 complex cells, and that overall it is weak. One way to account for this, while recognizing that PDS cells and not complex cells have inseparable speed and direction tuning (as opposed to TF–SF tuning) [27,68], is to propose that PDS cells integrate responses from a frequency region that is shaped like a flattened inner tube (Figure 5c).

Another issue concerns the linearity of integration by PDS cells in frequency space. The S and H model assumes that each PDS cell takes a linear combination (sum) of activity over a frequency plane, but a recent study found that the integration of frequency components might instead be nonlinear [65]. For each stimulus, two gratings with the same velocity but with different spatial frequencies were superimposed. The responses of the neurons were not well predicted by adding the responses to the individual gratings. It remains to be seen whether integration is still nonlinear when the two gratings have the same spatial frequency but different velocities. In another study, psychophysical tests showed that speed percepts were not well predicted from the linear combination of single frequencies [69]. Thus, to the extent that PDS cells integrate motion energy over a frequency plane, they might do so with both linear and nonlinear components.

The S and H model is not yet complete, in that it does not attempt to predict the response dynamics that are observed in experimental studies. This will be an important adjustment. Studies [70,71] showed that PDS cells initially behave like CDS cells, and then over the course of approximately 80 ms acquire their own pattern property. This is consistent with psychophysical studies that suggested that humans initially perceive the vector-sum direction and then perceive the pattern direction [40]. The gain-normalization and tuned-normalization circuits of the current S and H model can be expected to create some response delay, but it is not yet clear how that delay would cause PDS cells to initially behave like CDS cells. It will be interesting to see what kinds of mechanism will have to be added or adjusted for the model to reproduce these dynamics.

Feature tracking

Evidence suggests that motion processing is coupled to some kind of feature-extraction mechanism [63,72–74]. However, although there is evidence for feature-based segmentation [63,72–74], there is comparatively little evidence for a feature-tracking mechanism in the visual cortex, because few studies have directly examined the issue.

Wilson et al. suggested that the mechanisms that are used for tracking feature motion might be in area V2 [36]. If so, V2 neurons should sense moving plaids in terms of their pattern direction, not in terms of their component direction, because gratings contain features that are produced by the regions where the peaks and troughs of the gratings coincide. However, tests in V2 failed to show an appreciable number of PDS cells [75].

Some studies have found PDS cells in V1, suggesting that a feature-tracking mechanism could operate there. One study observed PDS cells in animals under anaesthesia [76], whereas another found that PDS behaviour occurred in awake but not in anaesthetized animals [77]. Yet another study did not find any PDS behaviour in V1 [48]. Overall, the evidence for a substantive PDS mechanism (and thus feature-tracking) in V1 is weak.

Summary

Pattern-velocity computation is a difficult and fascinating problem. Ultimately it must be solved by examining signals that correlate with an object's velocity. Fundamentally these signals must be transformations of spatiotemporal image contrast¹. The various theories about velocity estimation differ in terms of how the correlated signals are extracted.

The IOC principle is based on the understanding that local velocities are collectively consistent with a single object velocity. Coincidence is a critical condition, as the local samples have to come from the same object at the same time to be meaningful. Feature-tracking approaches also rely on the superposition (coincidence) of frequency components: this creates distortion products, which can then be tracked in two dimensions.

Without tracking features, one is compelled to extract motion signals with linear mechanisms and then look at their correlation to derive the object velocity. Fortunately, velocity samples from rigid moving objects are heavily correlated; in fact, for a given object, the expected distribution of local samples is entirely specified by just two parameters corresponding to the object's direction and speed. The extraction of these parameters from a distribution of local velocities is one way of describing the IOC approach.

We expect several lines of experimental research to be important in the future. First, it will be useful to identify the system properties (the mechanisms and/or neural populations) that are responsible for the peculiar dynamics of PDS cells and the correlated delay in pattern-motion perception. Second, because MT neurons operate directly on V1 inputs, experimental methods are needed to sample sizeable V1 and MT populations simultaneously. The information that is yielded could be critical to our understanding of the transformations that are effected by MT. Third, there is currently no solid explanation for the large number of CDS cells in MT. How is the function of these CDS cells different from that of V1 CDS cells? Finally, it will be important to demonstrate that PDS cells signal pattern motion under conditions in which distortion products are not possible. Short of this, we cannot rule out the possibility that PDS cells draw input from neurons — wherever they might be — that circumvent the aperture problem with nonlinear spatial transformations.

Theoretical and experimental studies of velocity computation will need to increasingly interact in the coming years. Even what we currently know about the computational mechanisms of pattern velocity tends to be difficult to grasp. As our understanding of the problem deepens, mathematical models will be increasingly important for making sense of experimental observations and suggesting new experiments.