Tree-Based Models for Predicting Mortality in Gram-Negative Bacteremia: Avoid Putting the CART before the Horse

Abstract

Increasingly, infectious disease studies employ tree-based approaches, e.g., classification and regression tree modeling, to identify clinical thresholds. We present tree-based-model-derived thresholds along with their measures of uncertainty. We explored individual and pooled clinical cohorts of bacteremic patients to identify modified acute physiology and chronic health evaluation (II) (m-APACHE-II) score mortality thresholds using a tree-based approach. Predictive performance measures for each candidate threshold were calculated. Candidate thresholds were examined according to binary logistic regression probabilities of the primary outcome, correct classification predictive matrices, and receiver operating characteristic curves. Three individual cohorts comprising a total of 235 patients were studied. Within the pooled cohort, the mean (± standard deviation) m-APACHE-II score was 13.6 ± 5.3, with an in-hospital mortality of 16.6%. The probability of death was greater at higher m-APACHE II scores in only one of three cohorts (odds ratio for cohort 1 [OR₁] = 1.15, 95% confidence interval [CI] = 0.99 to 1.34; OR₂ = 1.04, 95% CI = 0.94 to 1.16; OR₃ = 1.18, 95% CI = 1.02 to 1.38) and was greater at higher scores within the pooled cohort (OR₄ = 1.11, 95% CI = 1.04 to 1.19). In contrast, tree-based models overcame power constraints and identified m-APACHE-II thresholds for mortality in two of three cohorts (P = 0.02, 0.1, and 0.008) and the pooled cohort (P = 0.001). Predictive performance at each threshold was highly variable among cohorts. The selection of any one predictive threshold value resulted in fixed sensitivity and specificity. Tree-based models increased power and identified threshold values from continuous predictor variables; however, sample size and data distributions influenced the identified thresholds. The provision of predictive matrices or graphical displays of predicted probabilities within infectious disease studies can improve the interpretation of tree-based model-derived thresholds.

INTRODUCTION

The use of tree-based modeling in clinical investigations has increased in recent years. Several common statistical packages employ these tools, including Classification and Regression Trees (CART; Salford Systems), Decision Trees add-on (SPSS), Enterprise Miner (SAS), Partition method (JMP/SAS), and several packages within the R environment such as “tree,” “rpart,” “party,” and “mvpart” (R Foundation for Statistical Computing). Tree-based modeling strategies are designed to find optimal splits (i.e., threshold values) between predictor and outcome variables and provide useful alternatives to traditional statistical models. Minimally, the predictor variable is continuous or ordinal in nature, while the outcome variable can be continuous, ordinal, or dichotomous (1). In the case of dichotomous outcomes, the methodology is often loosely termed binary recursive partitioning. In brief, individual analyses are completed at each incremental change of the predictor variable (2). After each analysis is completed, comparative statistics are utilized to generate post hoc classifications of the analyzed cohort (1–3). Optimal splits in outcome variables are derived from this iterative classification procedure wherein the fitted model minimizes misclassification within the tree (1, 2).

One potential reason for the increased use of tree-based models relates to the many advantages offered by this approach to data modeling. At its core, a tree-based model mimics human intuition in that it transforms a spread of data into discrete groups, and a fitted and pruned tree can reveal important predictors from a large set of candidate variables. Yet, the parsimony gained from pruned trees often results in a loss of information, as the pruning process is, by design, reductive in nature, yielding a minimal number of threshold values for a clinical outcome or effect and often a single split. A reductive approach can be a means to reveal clinically interesting interactions among complex variables (4). The ease of interpreting final trees, the flexibility of the model, and the ability to gain parsimony from a heterogeneous group of predictors together make the use of tree-based approaches attractive for many types of data.

In spite of the utility of tree-based modeling techniques, these approaches also have inherent drawbacks. Previous efforts have demonstrated that tree-fitting algorithms are highly sensitive to small sample sizes, and minor changes in effect size can significantly alter “optimal” data splits (4). Additionally, while the purpose of tree-based modeling is to simplify, trees can branch many times and result in nonsensical output. Therefore, pruning is often necessary to prevent overfitting of data. A less discussed limitation of utilizing model-derived threshold values, and the primary focus of our study, is the reductive nature of the analysis itself. The variability associated with the threshold criterion is lost when only the threshold value itself is presented. When confronted with a single threshold value, absent any measures of uncertainty, the clinician or researcher is deprived of the fullness of the data and may be led to incorrectly classify a given patient or case as positive or negative. Thus, tree-based models provide intuitive and understandable decision rules; yet, use of these methods alone does not allow clinicians and researchers to understand other candidate thresholds within the data, which may be more informative for decision making, depending on the actual clinical or research question posed.

Here, we propose that the truncation of information that occurs as a function of tree pruning may be remedied through construction of predictive matrices (sensitivity, specificity, percent correctly classified, and positive and negative predictive values [PPV and NPV]) across the range of observations. Further, generation of receiver operating characteristic (ROC) curves at every possible threshold value allows for quick visual analysis. To highlight the value of this approach, we draw comparisons between the tree-based modified acute physiology and chronic health evaluation (II) (m-APACHE-II) score thresholds identified using tree-based models to those thresholds identified using simple linear models (i.e., Student's t test) and log-linear probability fits (i.e., binary logistic regression). As morbidity indices (e.g., m-APACHE-II scores) are often among the most explanatory predictors of poor patient outcomes in the setting of acute sepsis (5–7), we explore the utility of tree-based modeling approaches to derive an m-APACHE-II threshold for in-hospital mortality across several cohorts. To elucidate the intricacies between predictor and outcome, we present the tree-based threshold values along with the attendant measures of uncertainty.

MATERIALS AND METHODS

Patient populations.

All patients were treated at Northwestern Memorial Hospital for Gram-negative (GN) bacteremia between the years 2005 and 2012. The patients evaluated made up three separate retrospective cohorts. To be included in the analysis, patients had to have received at least 24 h of treatment at the discretion of their primary medical team for their GN bacteremia. In the first cohort (cohort 1), patients received active antimicrobial treatment (n = 75) for infections due to Klebsiella pneumoniae (8). In the second cohort (cohort 2), patients were treated with cefepime (n = 91) for a GN bacteremia (9). The third cohort (cohort 3) was comprised of acutely ill (i.e., hospitalized) adult patients (n = 77) with a GN bacteremia who received active therapy (10). Therapy was considered to be active if the agent was rated as susceptible to the chosen therapy according to the Clinical and Laboratory Standards Institute susceptibility criteria in place at the time of the study. A pooled cohort of unique (i.e., nonduplicative) patients from all three cohorts was also assembled.

Variables.

All data elements were extracted from the electronic medical record by trained reviewers. The m-APACHE-II score on the day of the first positive blood culture was calculated for all patients (5, 6). This severity of illness score is a validated metric, which has been used to adjust mortality predictions among patients with bacteremia. Scoring accounted for whether patients were immunocompromised, were admitted primarily for a surgical indication, or had a primarily nonsurgical indication for admission. Other variables extracted for this analysis were patient demographics, including age, gender, and absolute neutrophil count (ANC) of <500 cells/mm² during the index admission.

Outcomes.

The primary outcome of the current analysis was identification of an in-hospital mortality threshold value for each cohort according to the m-APACHE-II score calculated on the day of infection (i.e., the first culture-positive day during the index admission). Outcomes for each cohort were determined individually, and patients were deduplicated as necessary for the pooled mortality analysis. Secondary outcomes included calculation of the sensitivity, specificity, and positive and negative predictive values at the tree-based-model-derived thresholds. Pooled and individual analyses were planned a priori to test the impact of sample size (vis-à-vis power) on the robustness of the tree-based-model-derived thresholds and the statistical significance observed in a sensitivity analysis. As we had previously analyzed these cohorts separately, a pooled analysis was considered, because mortality rates between groups were not significantly different. Only the severity of illness score was considered as a mortality predictor in this univariate analysis for simplicity.

Analyses.

Descriptive statistics were calculated for each of the cohorts using the “stats” package within R version 3.1.0 (11). Categorical variables were evaluated using chi-square or Fisher's exact tests as appropriate. Continuous data were evaluated using the Student t test or Wilcoxon rank-sum test as appropriate. Tree-based modeling was performed using data from three cohorts to predict in-hospital mortality thresholds from the morbidity indices collected. The binary recursive partitioning function within the classification and regression tree package “tree” (12) for R was utilized to determine threshold splits in m-APACHE-II score that predicted mortality. The minimum child node size was at least 10, with a maximum number of child node splits equal to 2. A default deviance of 0.01 was used for all models.

After identification of tree-based threshold values for each cohort and the pooled cohort, the impact of m-APACHE-II on mortality was calculated in several, more traditional ways, including (i) Student's t tests and (ii) binary logistic regressions with associated probabilities, with the latter calculations shown in equations 1 and 2:

$${\text{Odds}}_{\text{Death}}=e^{\text{Intercept}\hspace{0.17em}+\text{\hspace{0.17em}Beta}\hspace{0.17em}\times \hspace{0.17em}\mathit{m-}\text{APACHE}\hspace{0.17em}\text{II}\hspace{0.17em}\text{score}}\hspace{0.17em}$$ (1)

$$P_{\text{Death}}=\frac{{\text{Odds}}_{\text{Death}}}{1+{\text{Odds}}_{\text{Death}}}$$ (2)

Additionally, predictive matrices were generated using m-APACHE-II as a classifier of mortality. Identification of a threshold value that maximized the positive predictive value (PPV) (i.e., a threshold that minimized false-positive predictions of death among survivors) corresponded to maximized specificity. Likewise, identification of a threshold value that maximized negative predictive value (NPV) (i.e., a threshold that minimized false-negative predictions of survival among those who died) corresponded to maximized sensitivity. To test the robustness of the tree-based threshold predictions for mortality within the pooled cohort, bootstrap resampling was conducted to estimate the standard errors of the bivariate logistic regression of mortality according to the pooled threshold value using 1,000 replicates from the full sample size. Replicate size sufficiency was evaluated by resampling after setting at least two separate seeds and comparing the resulting differences in the coefficients and 95% confidence intervals between runs. Predictive matrices were created for sensitivity, specificity, and percent correctly classified using the “roctab” command. PPV and NPV were calculated using the “diagt” command. Except where otherwise specified, all statistical tests were performed using Intercooled Stata version 14.0 (Statacorp, College Station, TX).

RESULTS

A total of 243 patients were included from the three cohorts, comprising 235 unique patients for the pooled cohort (8–10). Within the pooled cohort, mean (SD) age was 59.4 (15.6) years, and males comprised 49.8% (n = 117/235) of the population. Neutropenia (i.e., an ANC of <500 mm²) was highly prevalent at 26.0% (n = 61/235). The mean (SD) m-APACHE-II score was 13.6 (5.3). As ANC was correlated with m-APACHE II scores (r = 0.5, P < 0.001), the m-APACHE-II score was evaluated as the primary predictor.

The characteristics of the three individual cohorts and the pooled cohort are shown in Tables 1 and 2 and are stratified by the outcome of in-hospital mortality. Overall, 16.6% (n = 39/235) of patients died within the pooled cohort while in hospital. The mean (SD) m-APACHE-II score was higher among those who died than among those who survived in hospital (16.1 [5.1] versus 13.1 [5.2]; P = 0.002). Mean age did not differ for those that survived and those that did not (61.7 versus 59.0, P = 0.31), and in-hospital mortality rates were not significantly different between male and female patients (15.4 versus 17.8%; P = 0.62). In-hospital mortality was more common among patients with concurrent neutropenia than among those without concurrent neutropenia (26.2% versus 13.2%; P = 0.02).

TABLE 1.

Outcomes by population characteristics within three individual cohorts and the pooled cohort of patients with bacteremia^a

Parameter	Cohort 1		Cohort 2		Cohort 3		Pooled cohort
	Survived	Died	Survived	Died	Survived	Died	Survived	Died	P value
No. of patients	n = 63	n = 12	n = 72	n = 19	n = 69	n = 8	n = 196	n = 39
No. of male patients (% of total)	31 (49.2%)	4 (33.3%)	39 (54.2%)	11 (57.9%)	33 (47.8%)	3 (37.5%)	99 (50.5%)	18 (46.2%)	0.62
No. with ANC <500 (% of total)	2 (3.2%)	0 (0.0%)	46 (63.9%)	15 (78.9%)	0 (0.0%)	1 (12.5%)	45 (23.0%)	16 (41.0%)	0.02
Mean age (SD)b	58.8 (16.6)	64.0 (11.7)	61.0 (14.7)	62.1 (10.6)	57.1 (17.2)	57.5 (16.8)	59.0 (16.2)	61.7 (12.3)	0.31
Mean m-APACHE II score (SD)	10.6 (4.3)	13.2 (4.9)	16.6 (4.8)	17.5 (4.2)	12.3 (5.2)	17.0 (6.0)	13.1 (5.2)	16.1 (5.1)	0.002

^aANC, absolute neutrophil count (in cells/square millimeter); m-APACHE II, modified APACHE II.

^bAge in years.

TABLE 2.

Outcomes by tree-based-model-derived morbidity threshold

m-APACHE II score	No. (%) of patients
	Cohort 1a		Cohort 2b		Cohort 3c		Pooled cohortd
	Survived (n = 63)	Died (n = 12)	Survived (n = 72)	Died (n = 19)	Survived (n = 69)	Died (n = 8)	Survived (n = 196)	Died (n = 39)
≥15.5	7 (11.1)	5 (41.7)
≥16.5			34 (47.2)	13 (68.4)
≥14.5					25 (36.2)	7 (87.5)	77 (39.3)	27 (69.2)

^aP = 0.019.

^bP = 0.10.

^cP = 0.008.

^dP = 0.001.

Linear and tree-based m-APACHE-II mortality splits for cohort 1.

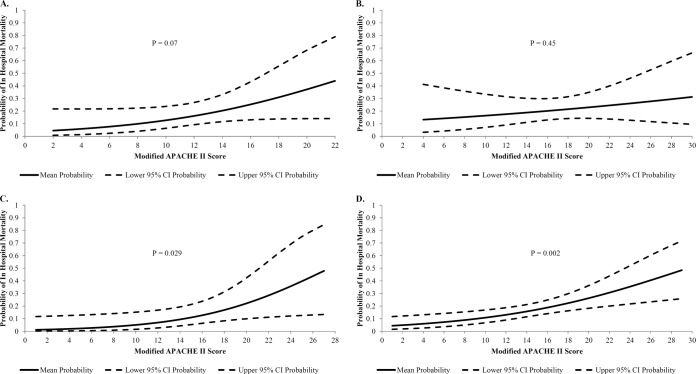
A total of 75 patients with Klebsiella pneumoniae bacteremia were included in cohort 1, of whom 12 (16%) died (8). When comparing m-APACHE-II scores as a linear variable, mean (SD) values did not statistically differ between those who survived and those who died (10.6 [4.31] versus 13.2 [4.86]; P = 0.07). Binary logistic regression identified a borderline significance for m-APACHE-II scores (odds ratio [OR], 1.15; 95% confidence interval [CI], 0.99 to 1.34; P = 0.07). That is, for each 1 unit increase in the m-APACHE-II score, the relative odds of in-hospital mortality increased 15%. Probabilities of in-hospital mortality are shown in Fig. 1A and increased steadily across the range of m-APACHE-II scores, though the log-linear trend failed to meet statistical significance. In order for the predicted mortality risk to double, the m-APACHE-II score would have needed to increase from a mean score of 11 to 14.3.

FIG 1.

Probabilities of in-hospital mortality according to m-APACHE-II score among patients with Gram-negative bacteremia. Unadjusted probabilities of death from a regression of predictors against the outcome of in-hospital mortality. (A) Probabilities of death according to increasing m-APACHE-II scores on the day of infection among 75 patients in cohort 1. (B) Probabilities of death according to increasing m-APACHE-II scores on the day of infection among 91 patients in cohort 2. (C) Probabilities of death according to increasing m-APACHE-II scores on the day of infection among 77 patients in cohort 3. (D) Probabilities of death according to increasing m-APACHE-II scores on the day of infection among 235 unique patients in the pooled cohort.

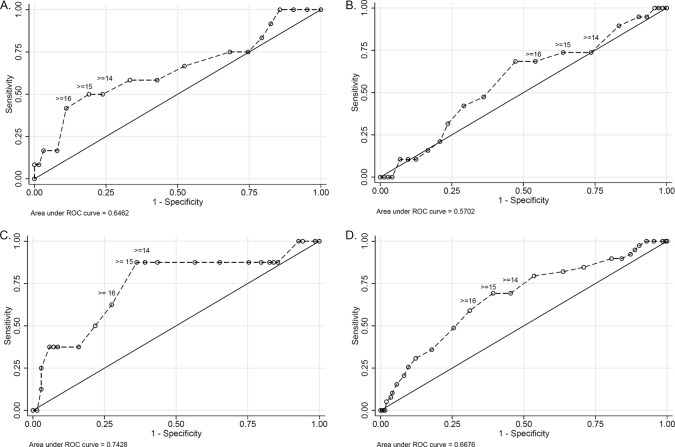
A tree-based model, alternatively, identified statistically significant mortality splits between m-APACHE-II scores of <15.5 and ≥15.5 (11.1% [n = 7/63] deaths and 41.7% [n = 5/12] deaths, respectively; P = 0.019) on day 0 of infection. However, the use of a tree-based approach provided an incomplete perspective on the role of increasing m-APACHE-II scores on mortality. The ROC curve (Fig. 2A) and each candidate threshold (e.g., values of 14, 15, and 16) demonstrated various levels of sensitivity and specificity (Table 3). By comparing crude mortality rates at each m-APACHE-II score in the cohort to the threshold identified by the tree-based model, one observes that sensitivity and specificity of the m-APACHE-II score (day 0) for death are most balanced around a value of 15 (Table 3). In this cohort, the tree-based-model threshold for an m-APACHE-II score of ≥15.5 for increased mortality was supported visually by the ROC curve and the associated predictive matrices.

FIG 2.

Receiver operating characteristic (ROC) curves for the predictive capacity of m-APACHE-II score (on day 0 of infection) for in-hospital mortality. Dashed lines, predictive capacity of the respective morbidity indices for the mortality; solid line, line of no-discrimination. m-APACHE-II score values of 14, 15, and 16 are labeled for visual interpretation. (A) ROC curve for m-APACHE-II score on the day of infection among 75 patients in cohort 1. (B) ROC curve for m-APACHE-II score on the day of infection among 91 patients in cohort 2. (C) ROC curve for m-APACHE-II score on the day of infection among 77 patients in cohort 3. (D) ROC curve for m-APACHE-II score on the day of infection among 235 unique patients in the pooled cohort.

TABLE 3.

Predictive performance of m-APACHE-II score for in-hospital mortality in cohort 1^a

m-APACHE-II score at day 0	Crude mortality rate (%)	Result for a threshold value ≥index value				% correctly classified
		Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)
2	0/3 (0.00)	100.0	0.0		100	16.0
3	0/3 (0.00)	100.0	4.8	16.7	100	20.0
4	0/3 (0.00)	100.0	9.5	17.4	100	24.0
6	1/3 (33.3)	100.0	14.3	18.2	100	28.0
7	1/3 (33.3)	91.7	17.5	17.5	91.7	29.3
8	1/4 (25.0)	83.3	20.6	16.7	86.7	30.7
9	0/4 (0.00)	75.0	25.4	16.1	84.2	33.3
10	1/11 (9.09)	75.0	31.8	17.3	87.0	38.7
11	1/7 (14.3)	66.7	47.6	19.5	88.2	50.7
12	0/6 (0.00)	58.3	57.1	20.6	87.8	57.3
13	1/7 (14.3)	58.3	66.7	25.0	89.4	65.3
14	0/3 (0.00)	50.0	76.2	28.6	88.9	72.0
15	1/6 (16.7)	50.0	81.0	33.3	89.5	76.0
16	3/5 (60.0)	41.7	88.9	41.7	88.9	81.3
17	0/3 (0.00)	16.7	92.1	28.6	85.3	80.0
18	1/2 (50.0)	16.7	96.8	50.0	85.9	84.0
21	0/1 (0.00)	8.3	98.4	50.0	84.9	84.0
22	1/1 (100.0)	8.3	100.0	100	85.1	85.3

^aCrude mortality rate is the ratio of the number of patients who died to the total number of patients. PPV, positive predictive value; NPV, negative predictive value.

Linear and tree-based m-APACHE-II mortality splits for cohort 2.

A total of 91 cefepime-treated GN bacteremia patients made up cohort 2, of whom 19 (20.9%) died in hospital (9). Mean (SD) values for m-APACHE-II did not significantly differ between those who survived and those who died in hospital (16.6 [4.79] versus 17.5 [4.19]; P = 0.45). Here, m-APACHE-II scores were not associated with in-hospital mortality in binary logistic regression (OR, 1.04; 95% CI, 0.94 to 1.1; P = 0.45) (Fig. 1B).

A tree-based model split mortality and lowered the P value compared to logistic regression, but failed to achieve significance, between m-APACHE-II scores of <16.5 and ≥16.5 (13.6% [n = 6/44] deaths versus 27.7% [n = 13/47] deaths; P = 0.10). Associated predictive matrices for crude mortality rates at each possible threshold m-APACHE-II (Table 4) demonstrated a relative balance of sensitivity and specificity around a score of 17. In this cohort, the tree-based model threshold for an m-APACHE-II score of ≥16.5 for increased mortality was supported visually by the ROC curve and the associated predictive matrices.

TABLE 4.

Predictive performance of m-APACHE-II score for in-hospital mortality in cohort 2^a

m-APACHE-II score at day 0	Crude mortality rate (%)	Result for a threshold value ≥index value				% correctly classified
		Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)
4	0/1 (0.00)	100	0.0		100	20.9
8	0/1 (0.00)	100	1.4	21.1	100	22.0
9	0/1 (0.00)	100	2.8	21.3	100	23.1
10	1/3 (33.3)	100	4.2	21.6	100	24.2
11	0/1 (0.00)	94.7	6.9	21.2	83.3	25.3
12	1/6 (16.7)	94.7	9.7	21.7	87.5	27.5
13	3/10 (30.0)	89.5	16.7	22.1	85.7	31.9
14	0/1 (0.00)	73.7	26.4	20.9	79.2	36.3
15	1/8 (12.5)	73.7	36.1	23.3	83.9	44.0
16	0/1 (0.00)	68.4	45.8	25.0	84.6	50.6
17	4/12 (33.3)	68.4	52.8	27.7	86.4	56.0
18	1/6 (16.7)	47.4	63.9	25.7	82.1	60.4
19	2/6 (33.3)	42.1	70.8	27.6	82.3	64.8
20	2/4 (50.0)	31.6	76.4	26.1	80.9	67.0
21	1/4 (25.0)	21.1	79.2	21.1	79.2	67.0
22	1/4 (25.0)	15.8	83.3	20.0	78.9	69.2
23	0/1 (0.00)	10.5	87.5	18.2	78.8	71.4
24	0/1 (0.00)	10.5	90.3	22.2	79.3	73.6
25	2/4 (50.0)	10.5	93.1	28.6	79.8	75.8
27	0/1 (0.00)	0.0	95.8	0.00	78.4	75.8
28	0/1 (0.00)	0.0	97.2	0.00	78.7	76.9
29	0/1 (0.00)	0.0	98.6	0.00	78.9	78.0

^aCrude mortality rate is the ratio of the number of patients who died to the total number of patients. PPV, positive predictive value; NPV, negative predictive value.

Linear and tree-based m-APACHE-II mortality splits for cohort 3.

Cohort 3 was comprised of 77 patients with GN bacteremia, of whom 8 (10.4%) died in hospital (10). Mean (SD) m-APACHE-II scores differed between those who survived and those who died in hospital (12.3 [5.2] versus 17.0 [6.0]; P = 0.02). Binary logistic regression also revealed that higher m-APACHE-II scores were significantly associated with higher odds of in-hospital mortality (OR, 1.18; 95% CI, 1.02 to 1.38; P = 0.029). That is, for each 1 unit increase in the m-APACHE-II score, there was a corresponding increase in the relative odds of in-hospital mortality of 18%, with associated probabilities displayed in Fig. 1C. Here, the m-APACHE-II score would have to increase from 12.8 to 15.6 before a relative doubling of mortality risk is observed.

A tree-based model further improved the P value and identified mortality splits between m-APACHE-II scores of <14.5 and ≥14.5 (2.2% [n = 1/45] deaths versus 21.9% [n = 7/32] deaths, respectively; P = 0.008). Sensitivity and specificity of m-APACHE-II were relatively balanced around a score of 15 (Table 5). In this cohort, the tree-based model threshold for an m-APACHE-II score of ≥14.5 for increased mortality was supported visually by the ROC curve and the associated predictive matrices.

TABLE 5.

Predictive performance of m-APACHE-II score for in-hospital mortality in cohort 3^a

m-APACHE-II score at day 0	Crude mortality rate (%)	Result (%) for a threshold value ≥index value				% correctly classified
		Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)
1	0/1 (0.00)	100.0	0.0		100	10.4
3	0/3 (0.00)	100.0	1.5	10.5	100.0	11.7
4	0/1 (0.00)	100.0	5.8	11.0	100.0	15.6
5	1/6 (16.7)	100.0	7.3	11.1	100.0	16.9
6	0/1 (0.00)	87.5	14.5	10.6	90.9	22.1
7	0/1 (0.00)	87.5	15.9	10.8	91.7	23.4
8	0/2 (0.00)	87.5	17.4	10.9	92.3	24.7
9	0/3 (0.00)	87.5	20.3	11.3	93.3	27.3
10	0/7 (0.00)	87.5	24.6	11.9	94.4	31.2
11	0/6 (0.00)	87.5	34.8	13.5	96.0	40.3
12	0/9 (0.00)	87.5	43.5	15.2	96.8	48.1
13	0/3 (0.00)	87.5	56.5	18.9	97.5	59.7
14	0/2 (0.00)	87.5	60.9	20.6	97.7	63.6
15	2/8 (25.0)	87.5	63.8	21.9	97.8	66.2
16	1/5 (20.0)	62.5	72.5	20.8	94.3	71.4
17	1/5 (20.0)	50.0	78.3	21.1	93.1	75.3
18	0/5 (0.00)	37.5	84.1	21.4	92.1	79.2
19	0/1 (0.00)	37.5	91.3	33.3	92.6	85.7
20	0/1 (0.00)	37.5	92.8	37.5	92.8	87.0
21	1/3 (33.3)	37.5	94.2	42.9	92.9	88.3
23	1/1 (100.0)	25.0	97.1	50.0	91.8	89.6
24	1/2 (50.0)	12.5	97.1	33.3	90.5	88.3
27	0/1 (0.00)	0.0	98.6	0.00	89.5	88.3

^aCrude mortality rate is the ratio of the number of patients who died to the total number of patients. PPV, positive predictive value; NPV, negative predictive value.

Linear and tree-based m-APACHE II mortality splits for the pooled cohort.

The pooled cohort revealed that mean (SD) m-APACHE-II scores differed significantly between those who died and those who survived (16.1 [5.1] versus 13.1 [5.2]; P = 0.002). Binary logistic regression revealed that higher m-APACHE-II scores were associated with a higher odds of in-hospital mortality (OR, 1.11; 95% CI, 1.04 to 1.19; P = 0.002). By comparing the pooled (Fig. 1D) and individual cohorts (Fig. 1A to C), the wide probability estimates seen in each subgroup became narrower in the pooled cohort and a lower P value was obtained.

Within the pooled cohort, a tree-based model identified a threshold of m-APACHE-II for death at a score of ≥14.5 compared to a score of <14.5 (26.0% [n = 27/104] versus 9.2% [n = 12/131]; P = 0.001). The ROC curve for the pooled m-APACHE-II score data is shown in Fig. 2D. When contrasted against the individual cohorts (Fig. 2A to C), the ROC curve for the pooled cohort has a slightly lower area under the curve and is slightly shallower than the ROC curve for the third cohort (Fig. 2C). Additionally, when the m-APACHE-II threshold score of ≥14.5 was regressed against the outcome of mortality using logistic regression, the bivariate analysis revealed 3.5-fold-higher mortality above the threshold value (OR, 3.48; 95% CI, 1.66 to 7.27; P = 0.001). The bootstrap resampled estimate for the same model produced similar estimates (OR, 3.48; 95% CI, 1.63 to 7.43; P = 0.001). A tree-based model threshold for an m-APACHE-II score of ≥14.5 for increased mortality was supported by the ROC curve (Fig. 2D) and the associated predictive matrices (Table 6).

TABLE 6.

Predictive performance of m-APACHE-II score for in-hospital mortality for pooled cohort of patients with Gram-negative bacteremia^a

m-APACHE-II score at day 0	Crude mortality rate (%)	Result for a threshold value ≥index value				% correctly classified
		Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)
1	0/1 (0.00)	100.0	0.0		100	16.6
2	0/2 (0.00)	100.0	0.5	16.7	100	17.0
3	0/6 (0.00)	100.0	1.5	16.8	100	17.9
4	0/5 (0.00)	100.0	4.6	17.3	100	20.4
5	1/6 (16.7)	100.0	7.1	17.6	100	22.6
6	1/4 (25.0)	97.4	9.7	17.7	95.0	24.3
7	1/4 (25.0)	94.9	11.2	17.5	91.7	25.1
8	1/7 (14.3)	92.3	12.8	17.4	89.3	26.0
9	0/7 (0.00)	89.7	15.8	17.5	88.6	28.1
10	2/21 (9.53)	89.7	19.4	18.1	90.5	31.1
11	1/15 (6.67)	84.6	29.1	19.2	90.5	38.3
12	1/21 (4.76)	82.1	36.2	20.4	91.0	43.8
13	4/20 (20.0)	79.5	46.4	22.8	91.9	51.9
14	0/12 (0.00)	69.2	54.6	23.3	89.9	57.0
15	4/20 (20.0)	69.2	60.7	26.0	90.8	62.1
16	4/15 (26.7)	59.0	68.9	27.4	89.4	67.2
17	5/20 (25.0)	48.7	74.5	27.5	88.0	70.2
18	2/13 (15.4)	35.9	82.1	28.6	86.6	74.5
19	2/7 (28.6)	30.8	87.8	33.3	86.4	78.3
20	2/5 (40.0)	25.6	90.3	34.5	85.9	79.6
21	2/7 (28.6)	20.5	91.8	33.3	85.3	80.0
22	2/5 (40.0)	15.4	94.4	35.3	84.9	81.3
23	1/2 (50.0)	10.3	95.9	33.3	84.3	81.7
24	1/4 (25.0)	7.7	96.4	30.0	84.0	81.7
25	2/3 (66.7)	5.1	98.0	33.3	83.8	82.6
27	0/1 (0.00)	0.0	98.5	0.00	83.2	82.1
28	0/1 (0.00)	0.0	99.0	0.00	83.3	82.6
29	0/1 (0.00)	0.0	99.5	0.00	83.3	83.0

^aCrude mortality rate is the ratio of the number of patients who died to the total number of patients. PPV, positive predictive value; NPV, negative predictive value.

DISCUSSION

We conducted individual analyses on three cohorts and a pooled analysis of all three in an attempt to predict mortality with morbidity surrogates (i.e., m-APACHE-II). Average differences in the means of morbidity indices did not predict mortality in two of the three individual cohorts but later became predictive of mortality in the pooled analysis when power was increased via sample size increase. Similarly, we evaluated the predictive value of m-APACHE-II on the binary outcome of death and observed identical findings; however, this methodology allowed for full visualization of the effect across m-APACHE-II. We noted that tree-based model fits resulted in increased statistical significance (i.e., improved P values) compared to that obtained with more traditional models (i.e., Student's t test and logistic regression) at the cost of a decrease in information as seen in the associated predictive matrices for each analysis (Tables 1 to 5).

The choice of whether or not to employ a tree-based model threshold depends on the intention of the end user. For example, the tree-based-model-derived threshold for the m-APACHE-II score in our pooled cohort was 14.5. Yet, if a clinician's intention is to triage care toward patients most likely to survive, a better approach would be to select an m-APACHE II threshold that minimizes false-negative classifications of death and thus raise the sensitivity (e.g., 90% sensitivity) threshold of the m-APACHE-II score for death. In other words, the negative predictive value (i.e., for no death) of m-APACHE II is greater when sensitivity is higher. Applying a 90% sensitivity threshold for mortality to our pooled cohort resulted in an m-APACHE II threshold score of ≥8 (i.e., those with an m-APACHE-II score of less than 8 have minimized false predictions of survival). Likewise, if a clinician wishes to predict patients most likely to die, a good approach would be to select an m-APACHE II threshold that minimizes false-positive classifications of death and thus raise the specificity (e.g., 90% specificity) of the m-APACHE-II threshold for death. In other words, the positive predictive value (i.e., for death) of m-APACHE II is greater when specificity is higher. Applying a 90% specificity threshold for mortality to our pooled cohort resulted in an m-APACHE II threshold score of ≥19. Thus, clinicians who routinely act on threshold values (e.g., critical electrolyte values, toxic drug levels, or pharmacokinetic/pharmacodynamic [PK/PD] safety and efficacy indices) would benefit from knowing the predictive matrices of individual thresholds in order to make the most informed decisions and avoid misclassifications.

Our examples utilizing 3 separate cohorts of GN bacteremia patients and a larger pooled analysis demonstrate that drawing inferences from tree-based modeling alone may overstate significance and be misleading when not paired with attendant measures of uncertainty (i.e., predictive matrices). Additionally, these three cohorts had patients with similar variance in their severity of illness (as measured by m-APACHE). The tree-based-model-derived threshold for in-hospital mortality according to m-APACHE-II score varied from 14.5 to 16.5 in the smaller cohorts and ultimately converged on 14.5 in the pooled analysis. Thus, both sample size and the underlying parameter distribution within a given cohort are critically important in identification of a threshold value in the larger population. Our examples utilized the m-APACHE-II score, yet the results are highly translatable and applicable to many infectious diseases applications. Thresholds derived from a single, less representative population may be less accurate than those from a larger, more representative population.

Our analysis has several limitations. First, we relied on data from three retrospective cohorts and a pooled analysis of all three. The retrospective nature of the data collection is subject to inherent biases and misclassification. However, trained reviewers collected data using standardized data collection instruments as previously described. Additionally, our retrospective measurement of outcomes was limited to in-hospital mortality, yet in-hospital mortality is also a clinically meaningful endpoint. Likewise, a univariate assessment of mortality differences is an oversimplification of reality, and our threshold values for m-APACHE II scores are inherently limited by the data from which they were derived. However, m-APACHE-II is explanatory as a mortality index, especially when analyzed early in the bacteremia course. In general, tree-based-model-derived thresholds are also subject to certain limitations. Multiple thresholds are possible depending on the partitioning goal. Selecting a single value is possible only if the intention is to (i) maximize either sensitivity or specificity or (ii) find the balance between the two (e.g., use tree-based modeling). Given the loss of information (i.e., the selection of a single value) when using the tree-based modeling approach, a fuller presentation of the proposed thresholds is necessary to adequately relay the variability of a proposed threshold value.

We have shown that multiple threshold values (e.g., thresholds observed from the data using ROC curves or predictive matrices) may exist for a given predictive variable in spite of observing a single “optimal” split using tree-based methodologies. Additionally, all tree-based models will ultimately fail to fully describe the observed data. Truncation of a model to a single number with heavily pruned trees can be potentially misleading. We suggest that future studies employing tree-based modeling approaches also report the above measures of uncertainty or provide graphical displays of adjusted probabilities from binary logistic regression to aid the reader in the best interpretation of data for their own specified purpose.

Funding Statement

Research reported in this publication was supported in part by the National Institute of Allergy and Infectious Diseases of the National Institutes of Health under award number R15-AI105742. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.