TRANSPOSABLE REGULARIZED COVARIANCE MODELS WITH AN APPLICATION TO MISSING DATA IMPUTATION

Abstract

Missing data estimation is an important challenge with high-dimensional data arranged in the form of a matrix. Typically this data matrix is transposable, meaning that either the rows, columns or both can be treated as features. To model transposable data, we present a modification of the matrix-variate normal, the mean-restricted matrix-variate normal, in which the rows and columns each have a separate mean vector and covariance matrix. By placing additive penalties on the inverse covariance matrices of the rows and columns, these so called transposable regularized covariance models allow for maximum likelihood estimation of the mean and non-singular covariance matrices. Using these models, we formulate EM-type algorithms for missing data imputation in both the multivariate and transposable frameworks. We present theoretical results exploiting the structure of our transposable models that allow these models and imputation methods to be applied to high-dimensional data. Simulations and results on microarray data and the Netflix data show that these imputation techniques often outperform existing methods and offer a greater degree of flexibility.

1. Introduction

As large datasets have become more common in biological and data mining applications, missing data imputation is a significant challenge. We motivate missing data estimation in matrix data with the example of the Netflix movie rating data [2]. This dataset has around 18,000 movies (columns) and several hundred thousand customers (rows). Customers have rated some of the movies, but the data matrix is very sparse with a only small percentage of the ratings present. The goal is to predict the ratings for unrated movies so as to better recommend movies to customers. The movies and customers, however, are very correlated and an imputation method should take advantage of these relationships. Customers who enjoy horror films, for example, are likely to rate movies similarly, in the same way that horror films are likely to have similar ratings from these customers. Modeling the ratings by the relationships between only the movies or only the customers as with multivariate methods and k-nearest neighbor methods, seems shortsighted. Customer A's rating of Movie 1, for example, is related to Customer B's rating of Movie 2 by more than simply the connection between Customer A and B or Movie 1 and 2. In addition, modeling ratings as a linear combination of the ratings of movies or a combination of customer ratings as with singular value decomposition (SVD) methods fails to capture a more sophisticated connection between the movies and customers [21]. Bell et. al, in their discussion of imputation for the Netflix data, call all of these methods either “movie-centric” or “user-centric” [1].

We propose to directly model the correlations among and between both the customers (rows) and the movies (columns). Thus, our model is transposable in the sense that it treats both the rows and columns as features of interest. The model is based on the matrix-variate normal distribution brought to our attention by Efron [8], which has separate covariance matrix parameters for both the rows and the columns. Thus, both the relationships between customers and between movies are incorporated in the model. If matrix-variate normal data is strung out in a long vector, then it is distributed as multivariate normal with the covariance related to the original row and column covariance matrices through their Kronecker product. This means that the relationship between Customer A's rating of Movie 1 and Customer B's rating of Movie 2 can be modeled directly as the interaction between Customers A and B and Movies 1 and 2.

In practice, however, transposable models based on the matrix-variate normal distribution have largely been of theoretical interest and have rarely applied to real datasets because of the computational burden of high-dimensional parameters [13]. In this paper, we introduce modifications of the matrix-variate normal distribution, specifically restrictions on the means and penalties on the inverse covariances, that allow us to fit this transposable model to a single matrix of data. The penalties we employ give us non-singular covariance estimates that have connections to the singular value decomposition and graphical models. With this theoretical foundation, we present computationally efficient Expectation Maximization-type (EM) algorithms for missing data imputation. We also develop a two-step process for calculating conditional distributions and an algorithm for calculating conditional expectations of scattered missing data that has the computational cost of comparable multivariate methods. These contributions allow one to fit this parametric transposable model to a single data matrix at reasonable computational cost, opening the door to numerous applications including user-ratings data.

We organize the paper beginning with a review of the multivariate regularized covariance models (RCM) and a new imputation method based on these models, Section 2. The RCMs form the foundation for the transposable regularized covariance models (TRCM) introduced in Section 3. We then present new EM-type imputation algorithms for transposable data, Section 4, along with a one-step approximation in Section 4.2. Simulations and results on microarray and the Netflix data are given in Section 5, and we conclude with a discussion of our methods in Section 6.

2. Regularized Covariance Models and Imputation with Multivariate Data

Several recent papers have presented algorithms and discussed applications of regularized covariance models (RCM) for the multivariate normal distribution [11, 22]. These models regularize the maximum likelihood estimate of the covariance matrix by placing an additive penalty on the inverse covariance or concentration matrix. The resulting estimates are nonsingular, thus enabling covariance estimation when the number of features is greater than the number of observations. In this section, we give a review of these models and briefly describe a new penalized EM algorithm for imputation of missing values using the regularized covariance model.

Let X_i ~ N(0, Δ) for i = 1 … n, i.i.d. observations and p features. Thus, our data matrix, X is n × p with covariance matrix Δ ∈ ℜ^{p × p}. The penalized log-likelihood of the regularized covariance model is then proportional to

$$\ell (\mathbf{\Delta })=\frac{n}{2}\text{log}|{\mathbf{\Delta }}^{-1}|-\frac{1}{2}\text{tr}({\mathbf{X}}^{\mathrm{T}}\mathbf{X}{\mathbf{\Delta }}^{-1})-\rho {\Vert {\mathbf{\Delta }}^{-1}\Vert }^q$$ (1)

where ${\Vert ·\Vert }^q={\sum }_{i=1}^{p^2}{|·|}^q$ and q is either 1 or 2, i.e. the sum of the absolute value or square of the elements of Δ⁻¹. The penalty parameter is ρ. With an L₂ penalty, we can write the penalty term as $\rho \text{tr}({\mathbf{\Delta }}^{-1}{\mathbf{\Delta }}^{-1})=\rho {\Vert {\mathbf{\Delta }}^{-1}\Vert }_{\mathrm{F}}^2$.

Maximizing ℓ(Δ) gives the penalized-maximum likelihood estimate (MLE) of Δ. Friedman et. al [11] present the graphical lasso algorithm to solve the problem with an L₁ penalty. The graphical lasso uses the lasso method iteratively on the rows of Δ̂⁻¹, and gives a sparse solution for Δ̂⁻¹. A zero in the ij^th component of Δ⁻¹ implies that variables i and j are conditionally independent given the other variables. Thus, these penalized-maximum likelihood models with L₁ penalties can be used to estimate sparse undirected graphs. With an L₂ penalty, the problem has an analytical solution [22]. If we take the singular value decomposition (SVD) of X, X = UDV^T, with d = diag(D), then

$$\hat{\mathbf{\Delta }}=\mathbf{V}\text{diag}(\theta ){\mathbf{V}}^{\mathrm{T}},{\theta }_i=\frac{d_i^2+\sqrt{d_i^4+16n\rho }}{2n}.$$ (2)

Thus, the inclusion of the L₂ penalty simply regularizes the eigenvalues of the covariance matrix. When p > n and letting r be the rank of X, the final n − r values of θ are constant and are equal to $2\sqrt{\rho /n}$. While a rank-k SVD approximation uses only the first k eigenvalues, the L₂ RCM gives a covariance estimate with all non-zero eigenvalues. Regularized covariance models provide an alternative method of estimating the covariance matrix with many desirable properties [18].

With this underlying model, we can form a new missing data imputation algorithm by maximizing the observed penalized log-likelihood of the regularized covariance model via the EM algorithm. Our method is the same as that of the EM algorithm for the multivariate normal described in Little and Rubin [16], except for an addition in the maximization step. In our M step, we find the MLE of the RCM covariance matrix instead of the multivariate normal MLE. Thus, our method fits into a class of penalized EM algorithms which give non-singular covariance estimates [12], thus enabling use of the EM framework when p > n. We give full details of the algorithm, which we call RCMimpute, in Supplementary Materials. As we will discuss later, this imputation algorithm is a special case of our algorithm for transposable data and forms an integral part of our one-step approximation algorithm presented in Section 4.2.

3. Transposable Regularized Covariance Models

As previously mentioned, we model the possible dependencies between and within the rows and columns using the matrix-variate normal distribution. In this section, we first present a modification of this model, the mean-restricted matrix-variate normal distribution. We confine the means to limit the total number of parameters and to provide interpretable marginal distributions. We then introduce our transposable regularized covariance models by applying penalties to the covariances of our matrix-variate distribution. Finally, we present the penalized-maximum likelihood parameter estimates and illustrate the connections between these estimates and those of multivariate models, the singular value decomposition and graphical models.

3.1. Mean-Restricted Matrix-variate Normal Distribution

We introduce the mean-restricted matrix-variate normal, a variation on the matrix-variate normal, presented by Gupta and Nagar [13]. A restriction on the means is needed because the matrix-variate normal has a mean matrix, M, of the same dimension as X, meaning that there are n × p mean parameters. Since the matrix-variate normal is mostly applied in instances where there are several independent samples of the random matrix X [7], this parameter formulation is appropriate. We propose, however, to use the model when we only have one matrix X from which to estimate the parameters. Also, we wish to parameterize our model so that the marginals are multivariate normal, thus easing computations and improving interpret-ability.

We denote the mean-restricted matrix-variate normal distribution by X ~ N_n,p (ν, μ, Σ, Δ) with X ∈ ℜ^{n × p}, the row mean ν ∈ ℜⁿ, the column mean μ ∈ ℜ^p, the row covariance Σ ∈ ℜ^{n × n} and the column covariance Δ ∈ ℜ^{p × p}. If we place the matrix X into a vector of length np, we have vec(X) ~ N (vec(M), Ω) where $\mathbf{M}=\nu {\mathbf{1}}_{(p)}^T+{\mathbf{1}}_{(n)}{\mu }^T$, and Ω = Δ ⊗ Σ. Thus, our mean-restricted matrix-variate normal model is a multivariate normal with a mean matrix composed of additive elements from the row and column mean vectors and a covariance matrix given by the Kronecker product between the row and column covariance matrices. This covariance structure can been seen as a tensor product Gaussian process on the rows and columns, an approach explored in [4, 23].

This distribution implies that a single element, X_ij has mean ν_i + μ_j along with variance Σ_ii Δ_jj, a mean and variance component from the row and column to which it belongs. As pointed out by a referee, this can be viewed as the following random effects model: X_ij = ν_i + μ_j + ε_ij, where ε_ij ~ N(0, Σ_ii Δ_jj), which has two additive fixed effects depending on the row and column means and a random effect whose variance depends on the product of the corresponding row and column covariances. This model shares the same first and second moments as elements from the mean-restricted matrix-variate normal. It does not, however, capture the Kronecker covariance structure between the elements of X unless both the row and column covariances, Σ and Δ are diagonal. This random effect model differs from the more common two-way random effects model with additive errors, which assumes that errors from the two sources are independent. Our model, however, assumes that the errors are related and models them as an interaction effect. A similar random effects approach was taken in [24], also using a Kronecker product covariance matrix.

To further illustrate the model, we note that the rows and columns are both marginally multivariate normal. The i^th row, denoted as X_ir, is distributed as, X_ir ~ N (ν_i + μ, Σ_ii Δ) and the j^th column denoted by X_cj, is distributed as X_cj ~ N (ν + μ_j, Δ_jj Σ). The familiar multivariate normal distribution is a special case of the mean-restricted matrix-variate normal as seen by the following two statements. If Σ = I and ν = 0 then, X ~ N (μ, Δ), and if Δ = I and μ = 0 then, X ~ N (ν, Σ). Also, two elements from different rows or columns are distributed as a bivariate normal, $(X_{ij},X_{i\prime j\prime })~N\left(\right(\begin{array}{c}\hfill {\nu }_i+{\mu }_j\hfill \\ \hfill {\nu }_{i\prime }+{\mu }_{j\prime }\hfill \end{array}),(\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{ii}{\mathbf{\Delta }}_{jj}\hfill & \hfill {\mathbf{\Sigma }}_{ii\prime }{\mathbf{\Delta }}_{jj\prime }\hfill \\ \hfill {\mathbf{\Sigma }}_{i\prime i}{\mathbf{\Delta }}_{j\prime j}\hfill & \hfill {\mathbf{\Sigma }}_{i\prime i\prime }{\mathbf{\Delta }}_{j\prime j\prime }\hfill \end{array}\left)\right)$. Thus, our model is more general than the multivariate normal, with the flexibility to encompass many different marginal multivariate models.

For completeness, the density function of this distribution is

$$p(\nu ,\mu ,\mathbf{\Sigma },\mathbf{\Delta })={(2\pi )}^{-\frac{np}{2}}{|\mathbf{\Sigma }|}^{-\frac{p}{2}}{|\mathbf{\Delta }|}^{-\frac{n}{2}}\text{etr}(-\frac{1}{2}(\mathbf{X}-\nu {\mathbf{1}}_{(p)}^T-{\mathbf{1}}_{(n)}{\mu }^T){\mathbf{\Delta }}^{-1}{(\mathbf{X}-\nu {\mathbf{1}}_{(p)}^T-{\mathbf{1}}_{(n)}{\mu }^T)}^T{\mathbf{\Sigma }}^{-1}),$$

where etr() is the exponential of the trace function. Hence, our formulation of the matrix-variate normal distribution adds restrictions on the means, giving the distribution desirable properties in terms of its marginals and easing computation of parameter estimates, discussed in the following section.

3.2. Transposable Regularized Covariance Model (TRCM)

In the previous section, we have reformulated the distribution to limit the mean parameters and in this section, we regularize the covariance parameters. This allows us to obtain non-singular covariance estimates which are important for use in any application, including missing data imputation.

As in the multivariate case, we seek to penalize the inverse covariance matrix. Instead of penalizing the overall covariance, Ω, we add two separate penalty terms, penalizing the inverse covariance of the rows and of the columns. The penalized log-likelihood is thus

$$\ell (\nu ,\mu ,\mathbf{\Sigma },\mathbf{\Delta })=\frac{p}{2}\text{log}|{\mathbf{\Sigma }}^{-1}|+\frac{n}{2}\text{log}|{\mathbf{\Delta }}^{-1}|-\frac{1}{2}\text{tr}({\mathbf{\Sigma }}^{-1}(\mathbf{X}-\nu {\mathbf{1}}_{(p)}^T-{\mathbf{1}}_{(n)}{\mu }^T){\mathbf{\Delta }}^{-1}{(\mathbf{X}-\nu {\mathbf{1}}_{(p)}^T-{\mathbf{1}}_{(n)}{\mu }^T)}^T)-{\rho }_r{\Vert {\mathbf{\Sigma }}^{-1}\Vert }^{q_r}-{\rho }_c{\Vert {\mathbf{\Delta }}^{-1}\Vert }^{q_c}.$$ (3)

where ${\Vert ·\Vert }^{q_r}={\sum }_{i=1}^{m^2}{|·|}^{q_r}$ and q_r and q_c are either 1 or 2, i.e. the sum of the absolute value of the matrix elements or squared elements. ρ_r and ρ_c are the two penalty parameters. Note that we will refer to the four possible types of penalties as L_qr : L_qc. Placing separate penalties on the two covariance matrices is not equivalent to placing a single penalty on the Kronecker product covariance matrix Ω. Using two separate penalties gives greater flexibility, as the covariance of the rows and columns can be modeled separately using differing penalties and penalty parameters. Also, having two penalty terms leads to simple parameter estimation strategies.

With transposable regularized covariance models, as with their multivariate counterpart, the penalties are placed on the inverse covariance matrix, or concentration matrix. Estimation of the concentration matrix has long been associated with graphical models, especially with an L₁ penalty which is useful to model sparse graphical models [11]. Here, a non-zero entry of the concentration matrix, Σ_ij ≠ 0, means that the i^th row conditional on all other rows is correlated with row j. Thus, a “link” is formed in the graph structure between nodes i and j. Conversely, zeros in the concentration matrix imply conditional independence. Hence, since we are estimating both a regularized row and column concentration matrix, our model can be interpreted as modeling both the rows and columns with a graphical model.

3.3. Parameter Estimation

We estimate the means and covariances via penalized maximum likelihood estimation. The estimates, however, are not unique, but the overall mean, M̂, and overall covariance Ω̂ are unique. Hence, ν̂ and μ̂ are unique up to an additive constant and Σ̂ and Δ̂ are unique up to a multiplicative constant. We first begin with the maximum likelihood estimation of the mean parameters.

Proposition 1

The MLE estimates for ν and μ are

$$\hat{\nu }=\sum _{j=1}^p\frac{(X_{cj}-{\hat{\mu }}_j)}{p},\hat{\mu }=\sum _{i=1}^n\frac{(X_{ir}-{\hat{\nu }}_i)}{n}.$$ (4)

where X_cj denotes the j^th column and X_ir the i^th row of X ∈ ℜ^{n × p}.

Proof

See Supplementary Materials.

The estimates for ν and μ are obtained by centering with respect to the rows and then the columns. Note that centering by the columns first will change μ̂ and ν̂, but will still give the same additive result. Thus, the order in which we center is unimportant.

Maximum likelihood estimation of the covariance matrices is more difficult. Here, we will assume that the data has been centered, M = 0. Then, the penalized log-likelihood, ℓ(Σ, Δ), is a bi-concave function of Σ⁻¹ and Δ⁻¹. In words, this means that for any fixed Σ^−1′, ℓ(Σ′, Δ) is a concave function of Δ⁻¹, and for any fixed Δ^−1′, ℓ(Σ, Δ′) is a concave function of Σ⁻¹. We exploit this structure to maximize the penalized likelihood by iteratively maximizing along each coordinate, either Σ⁻¹ or Δ⁻¹.

Proposition 2

Iterative block coordinate-wise maximization of ℓ(Σ, Δ) with respect to Σ⁻¹ and Δ⁻¹ converges to a stationary point of ℓ(Σ, Δ) for both L₁ and L₂ penalty types.

Proof

See Supplementary Materials.

While block coordinate-wise maximization (Proposition 2) reaches a stationary point of ℓ(Σ, Δ), it is not guaranteed to reach the global maximum. There are potentially many stationary points, especially with L₁ penalties, due to the high-dimensional nature of the parameter space. We also note a few straightforward properties of the coordinate-wise maximization procedure, namely that each iteration monotonically increases the penalized log-likelihood and the order of maximization is unimportant.

The coordinate-wise maximization is accomplished by setting the gradients with respect to Σ⁻¹ and Δ⁻¹ equal to zero and solving. We list the gradients with L₂ penalties. With L₁ penalties only the third term is changed and is given in parentheses.

$$\frac{\partial \ell }{\partial {\mathbf{\Sigma }}^{-1}}=\mathbf{\Sigma }-\mathbf{X}{\mathbf{\Delta }}^{-1}{\mathbf{X}}^{\mathrm{T}}/p-\frac{4{\rho }_r}{p}{\mathbf{\Sigma }}^{-1}(\frac{2{\rho }_r}{p}\text{sign}({\mathbf{\Sigma }}^{-1}))$$

$$\frac{\partial \ell }{\partial {\mathbf{\Delta }}^{-1}}=\mathbf{\Delta }-{\mathbf{X}}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\mathbf{X}/n-\frac{4{\rho }_c}{n}{\mathbf{\Delta }}^{-1}(\frac{2{\rho }_c}{n}\text{sign}({\mathbf{\Delta }}^{-1}))$$ (5)

Maximization with L₁ penalties can be achieved by applying the graphical lasso algorithm to the second term with the coefficient of the third term the as the penalty parameter. With L₂ penalties, we maximize by taking the eigenvalue decomposition of the second term and regularizing the eigenvalues as in the multivariate case, (2). Thus, coordinate-wise maximization leads to a simple iterative algorithm, but it comes at a cost since it does not necessarily converge to the global maximum. When both penalty terms are L₂ penalties, however, we can find the global maximum.

3.3.1. Covariance Estimation for L₂ Penalties

Covariance estimation when both penalties of the transposable regularized covariance model are L₂ penalties reduces to a minimization problem involving the eigenvalues of the covariance matrices. This problem has a unique analytical solution, and thus our estimates, Σ̂ and Δ̂, are globally optimal.

Theorem 1

The global unique solution maximizing ℓ(Σ, Δ) with L₂ penalties on both covariance parameters is given by the following: Denote the SVD of X as X = UDV^T with d = diag(D) and let r be the rank of X, then

$${\mathbf{\Sigma }}^{*}=\mathbf{U}\text{diag}({\beta }^{*}){\mathbf{U}}^{\mathrm{T}}\&{\mathbf{\Delta }}^{*}=\mathbf{V}\text{diag}({\theta }^{*}){\mathbf{V}}^{\mathrm{T}}$$ (6)

where β* ∈ ℜⁿ⁺ and θ* ∈ ℜ^p+ given by

$${\beta }_i^{*}=\{\begin{array}{cc}2\sqrt{\frac{{\rho }_r}{p}}\hfill & \mathit{\text{if}}i\ge r,\hfill \\ \sqrt{\frac{-c_2^{(i)}-\sqrt{{c_2^{(i)}}^2-4c_1^{(i)}{c}_3^{(i)}}}{2c_1^{(i)}}}\hfill & \mathit{\text{otherwise}}.\hfill \end{array}{\theta }_i^{*}=\{\begin{array}{cc}2\sqrt{\frac{{\rho }_c}{n}}\hfill & \mathit{\text{if}}i\ge r\hfill \\ \frac{d_i^2{\beta }_i^{*}}{p{{\beta }_i^{*}}^2-4{\rho }_r}\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

with coefficients

$$c_1^{(i)}=-4{\rho }_c{p}^2,c_2^{(i)}=32{\rho }_r{\rho }_{c}p+d_i^4(n-p),\&c_3^{(i)}=4{\rho }_r(d_i^4-16{\rho }_r{\rho }_c).$$

Proof

See Supplementary Materials.

With L₂ penalties, maximum likelihood covariance estimates Σ̂ and Δ̂ have eigenvectors given by the left and right singular vectors of X respectively. To reveal some intuition as to how these covariance estimates compare to other possible eigenvalue regularization methods, we present the two gradient equations in terms of the eigenvalues β and θ. (These are discussed fully in the proof of Theorem 1).

$$p{\theta }_i{\beta }_i^2-d_i^2{\beta }_i-4{\rho }_r{\theta }_i=0\&n{\beta }_i{\theta }_i^2-d_i^2{\theta }_i-4{\rho }_c{\beta }_i=0.$$

These are two quadratic functions in β and θ, so the quadratic formula gives us the eigenvalues in terms of each other. We see that the eigenvalues regularize the square of the singular values by a function of the dimensions, the penalty parameters and the eigenvalues of the other covariance estimate. From Theorem 1, L₂ : L₂ covariance estimation has a unique and globally optimal solution, which cannot be said of the other combinations of penalties. We give numerical results comparing our TRCM covariance estimates to other shrinkage covariance estimators in Supplementary Materials.

Here, we also pause to compare our TRCM model with L₂ penalties to the singular value decomposition model commonly employed with matrix data. If we include both row and column intercepts, we can write the rank-reduced SVD model as $X_{ij}={\nu }_i+{\mu }_j+{\mathbf{u}}_i^T{\mathbf{D}}_r{\mathbf{v}}_j+\epsilon$, where u_i and v_j are the i^th and j^th right and left singular vectors, D_r is the rank-reduced diagonal matrix of singular values and ε ~ N (0, σ²). Thus, the model appears similar to L₂ TRCM, which can be written as X_ij = ν_i + μ_j + ε_ij where ${\epsilon }_{ij}~N(0,{\mathbf{u}}_i^T\text{diag}(\beta ){\mathbf{u}}_i*{\mathbf{v}}_j^T\text{diag}(\theta ){\mathbf{v}}_j)$. There are important differences between the models, however. First, the left and right singular vectors are incorporated directly into the SVD model whereas they form the bases of the variance component of TRCM. Secondly, a rank-reduced SVD incorporates only the first r left and right singular vectors. Our model uses all the singular vectors as β and θ are of lengths n and p respectively. Finally, the SVD allows the covariances of the rows to vary with u_i, whereas with TRCM the rows share a common covariance matrix. Thus, while the SVD and TRCM share similarities, the models differ in structure and hence each offers a separate approach to matrix-data.

4. Imputation for Transposable Data

Imputation methods for transposable data are the main focus of this paper. We formulate methods based on the transposable regularized covariance models introduced in Section 3. Because computational costs have limited use of the matrix-variate normal in applications, we let computational considerations motivate the formulation of our imputation methods.

We propose a Multi-Cycle Expectation Conditional Maximization (MCECM) algorithm, given by Meng and Rubin [17], maximizing the observed penalized log-likelihood of the transposable regularized covariance models. The algorithm exploits the structure of our model by maximizing with respect to one block of coordinates at a time, saving considerable mathematical and computational time. First, we develop the algorithm mathematically, provide some rationale behind the structure of the algorithm via numerical examples, and then briefly discuss computational strategies and considerations.

In high dimensional data, however, the MCECM algorithm we propose for imputation is not computationally feasible. Hence, we suggest a computation-saving one-step approximation in Section 4.2. The foundation of our approximation lies in new methods, given in Theorems 2 and 3, for calculating conditional distributions with the mean-restricted matrix-variate normal. We also demonstrate the utility of this one-step procedure in numerical examples. A Bayesian variation of the one-step approximation using Gibbs sampling is given in Supplementary Materials.

Prior to formulating the imputation algorithm for transposable models, we pause to address a logical question: Why do we not use the multivariate imputation method based on regularized covariance models, given that the mean-restricted matrix normal distribution can be written as a multivariate normal with vec(X) ~ N(vec(M), Ω)? There are two reasons why this is inadvisable. First, notice that TRCMs place an additive penalty on both the inverse covariance matrices of the rows and the columns. The overall covariance matrix, Ω, however, is their Kronecker product. Thus, converting the TRCM into a multivariate form yields a messy penalty term leading to a difficult maximization step. The second reason to avoid multivariate methods is computational. Recall that Ω is a np × np matrix which is expensive to repeatedly invert. We will see that the mathematical form of the ECM imputation algorithm we propose leads to computational strategies that avoid the expensive inversion of Ω.

4.1. Multi-Cycle ECM Algorithm for Imputation

Before presenting the algorithm, we first review the notation used throughout the remainder of this paper. As previously mentioned, we use i to denote the row index and j the column index. The observed and missing parts of row i are o_i and m_i respectively, and o_j and m_j are the analogous parts of column j. We let m and o denote the totality of missing and observed elements respectively. Since with transposable data there is no natural orientation, we set n to always be the larger dimension of X and p the smaller.

4.1.1. Algorithm

We develop the ECM-type algorithm for imputation mathematically, beginning with the observed data log-likelihood which we seek to maximize. Letting $x_{o_j,j}^{*}={\mathbf{\Sigma }}_{o_j,o_j}^{-1/2}(x_{o_j,j}-{\nu }_{o_j})$,

$$\ell (\nu ,\mu ,\mathbf{\Sigma },\mathbf{\Delta })=\frac{1}{2}[\sum _{j=1}^p\text{log}|{{\mathbf{\Sigma }}^{-1}}_{o_j,o_j}|+\sum _{i=1}^n|{{\mathbf{\Delta }}^{-1}}_{o_i,o_i}|]-\frac{1}{2}\text{tr}(\sum _{i=1}^n{(x_{i,o_i}^{*}-{\mu }_{o_i})}^T(x_{i,o_i}^{*}-{\mu }_{o_i}){{\mathbf{\Delta }}^{-1}}_{o_i,o_i})-{\rho }_r{\Vert {\mathbf{\Sigma }}^{-1}\Vert }^{q_r}-{\rho }_c{\Vert {\mathbf{\Delta }}^{-1}\Vert }^{q_c}.$$ (7)

One can show that this is indeed the observed log-likelihood by starting with the multivariate observed log-likelihood and using vec(X) and the corresponding vec(M) and Ω. We maximize (7) via an EM-type algorithm which, similarly to the multivariate case, gives the imputed values as a part of the Expectation step.

We present two forms of the E step, one which leads to simple maximization with respect to Σ⁻¹ and the other with respect to Δ⁻¹. This is possible because of the structure of the matrix-variate model, specifically the trace term. Letting θ = {ν, μ, Σ, Δ}, the parameters of the mean-restricted matrix-variate normal, and letting o be the indices of the observed values, the E step, denoted by Q(θ|θ′, X_o), has the following form. Here, we assume that X is centered.

$$Q(\theta |\theta \prime ,X_o)=\mathrm{E}(\ell (\nu ,\mu ,\mathbf{\Sigma },\mathbf{\Delta })|X_o,\theta \prime )\propto \mathrm{E}[\text{tr}({\mathbf{X}}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\mathbf{X}{\mathbf{\Delta }}^{-1})|X_o,\theta \prime ]\propto \text{tr}[\mathrm{E}({\mathbf{X}}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\mathbf{X}|X_o,\theta \prime ){\mathbf{\Delta }}^{-1}]\propto \text{tr}[\mathrm{E}(\mathbf{X}{\mathbf{\Delta }}^{-1}{\mathbf{X}}^{\mathrm{T}}|X_o,\theta \prime ){\mathbf{\Sigma }}^{-1}].$$

Thus, we have two equivalent forms of the conditional expectation which we give below.

Proposition 3

The E step is proportional to the following form

$$\mathrm{E}[\text{tr}({\mathbf{X}}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\mathbf{X}{\mathbf{\Delta }}^{-1})|X_o,\theta \prime ]=\text{tr}[({\hat{\mathbf{X}}}^T{\mathbf{\Sigma }}^{-1}\hat{\mathbf{X}}+\mathbf{G}({\mathbf{\Sigma }}^{-1})){\mathbf{\Delta }}^{-1}]=\text{tr}[(\hat{\mathbf{X}}{\mathbf{\Delta }}^{-1}{\hat{\mathbf{X}}}^T+\mathbf{F}({\mathbf{\Delta }}^{-1})){\mathbf{\Sigma }}^{-1}],$$ (8)

where X̂ = E(X|X_o, θ′) and

$$\mathbf{G}({\mathbf{\Sigma }}^{-1})=\left(\begin{array}{ccc}\hfill \text{tr}({\mathbf{C}}^{(11)}{\mathbf{\Sigma }}^{-1})\hfill & \hfill \cdots \hfill & \hfill \text{tr}({\mathbf{C}}^{(1p)}{\mathbf{\Sigma }}^{-1})\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \text{tr}({\mathbf{C}}^{(p1)}{\mathbf{\Sigma }}^{-1})\hfill & \hfill \cdots \hfill & \hfill \text{tr}({\mathbf{C}}^{(pp)}{\mathbf{\Sigma }}^{-1})\hfill \end{array}\right),{\mathbf{C}}^{(jj\prime )=\text{Cov}(X_{cj},X_{cj\prime }|X_o,\theta \prime )},$$

$$\mathbf{F}({\mathbf{\Delta }}^{-1})=\left(\begin{array}{ccc}\hfill \text{tr}({\mathbf{D}}^{(11)}{\mathbf{\Delta }}^{-1})\hfill & \hfill \cdots \hfill & \hfill \text{tr}({\mathbf{D}}^{(1n)}{\mathbf{\Delta }}^{-1})\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \text{tr}({\mathbf{D}}^{(n1)}{\mathbf{\Delta }}^{-1})\hfill & \hfill \cdots \hfill & \hfill \text{tr}({\mathbf{D}}^{(nn)}{\mathbf{\Delta }}^{-1})\hfill \end{array}\right),{\mathbf{D}}^{(ii\prime )=\text{Cov}(X_{ir},X_{i\prime r}|X_o,\theta \prime )}.$$

Proof

See Supplementary Materials.

The E step in the matrix-variate normal framework has a similar structure to that of the multivariate normal (see Supplementary Materials) with an imputation step (X̂) and a covariance correction step (C^(jj′) and D^(ii′)). The matrices C^(jj′) ∈ ℜ^{n × n} and D^(ii′) ∈ ℜ^{p × p}, while G(Σ⁻¹) ∈ ℜ^{p × p} and F(Δ⁻¹) ∈ ℜ^{n × n}. Note that C^(jj′) is sparse and only non-zero at ${\mathbf{C}}_{ii\prime }^{(jj\prime )}$ when x_ij and x_i′j′ are both missing. C^(jj′) is not symmetric, but C^(jj′)T = C^(j′j), hence G(Σ⁻¹) is symmetric. The matrices D^(ii′) and F(Δ⁻¹) are structured analogously. Thus, we have two equivalent forms of the E step, which will be inserted between the two Conditional Maximization (CM) steps to form the MCECM algorithm.

The CM steps which maximize the conditional expectation functions, in Proposition 3, along either Σ⁻¹ or Δ⁻¹ are direct extensions of the MLE solvers for the multivariate RCMs. This is easily seen from the gradients. Note that we only show the gradients with an L₂ penalty, since an L₁ penalty differs only in the last term.

$$\frac{\partial Q}{\partial {\mathbf{\Sigma }}^{-1}}=\mathbf{\Sigma }-[\hat{\mathbf{X}}{\mathbf{\Delta }}^{-1}{\hat{\mathbf{X}}}^T+\mathbf{F}({\mathbf{\Delta }}^{-1})]/p-\frac{4{\rho }_r}{p}{\mathbf{\Sigma }}^{-1}.$$

$$\frac{\partial Q}{\partial {\mathbf{\Delta }}^{-1}}=\mathbf{\Delta }-[{\hat{\mathbf{X}}}^T{\mathbf{\Sigma }}^{-1}\hat{\mathbf{X}}+\mathbf{G}({\mathbf{\Sigma }}^{-1})]/n-\frac{4{\rho }_c}{n}{\mathbf{\Delta }}^{-1}.$$

With an L₂ penalty, the estimate is given by taking the eigenvalue decomposition of the second term and regularizing the eigenvalues as in (2). The graphical lasso algorithm applied to the second term gives the estimate in the case with an L₁ penalty.

We now put these steps together and present the Multi-Cycle ECM algorithm for imputation with transposable data, TRCMimpute, in Algorithm 1. A brief comment regarding the initialization of parameter estimates is needed. Estimating the mean parameters when missing values are present is not as simple as centering the rows and columns as in (4). Instead, we iterate centering by rows and columns, ignoring the missing values by summing over the observed values, until convergence. Secondly, the initial estimates of Σ̂⁻¹ and Δ̂⁻¹ must be non-singular in order to preform the needed computations in the E step. While any non-singular matrices will work, we find that the algorithm converges faster if we start with the MLE estimates with the missing values fixed and set to the estimated mean. Some properties and numerical comparisons of the MCECM algorithm are given in Supplementary Materials.

Algorithm 1.

Imputation with Transposable Regularized Covariance Models (TRCMimpute)

Initialization: Estimate ν̂ and μ̂ from the observed data. If xij is missing, set xij = ν̂i + μ̂j. Start with non-singular estimates Σ̂ and Δ̂. E Step (Δ): Calculate X̂T Σ̂−1X̂ + G(Σ̂−1). M Step (Δ): Update estimates of ν̂ and μ̂. Maximize Q with respect to Δ−1 to obtain Δ̂. E Step (Σ): Calculate X̂Δ̂−1X̂T + F(Δ̂−1), M Step (Σ): Update estimates of ν̂ and μ̂. Maximize Q with respect to Σ−1 to obtain Σ̂. Repeat Steps 2–5 until convergence.

4.1.2. Computational Considerations

We have presented our imputation algorithm for transposable data, TRCMimpute, but have not yet discussed the computations required. Calculation of the terms for the two E steps can be especially troublesome and thus we concentrate on these. Particularly, we need to find X̂ = E(X|X_o, θ′), and the covariance terms, C^(jj′) = Cov (X_cj, X_cj′|X_o, θ′) and D^(ii′) = Cov (X_ir, X_i′r|X_o, θ′). The simplest but not always the most efficient way to compute these is to use the multivariate normal conditional formulas with the Kronecker covariance matrix Ω, i.e. if we let m be the indices of the missing values of vec(X) and o be the observed,

$$\text{vec}{(\hat{\mathbf{X}})}_k=\{\begin{array}{cc}\text{vec}{(\mathbf{M})}_k+{\mathbf{\Omega }}_{ko}{\mathbf{\Omega }}_{oo}^{-1}(\text{vec}{(\mathbf{X})}_o-\text{vec}{(\mathbf{M})}_o)\hfill & \text{if}k\in m\hfill \\ \text{vec}{(X)}_k\hfill & \text{if}k\in o\hfill \end{array}$$ (9)

and, the non-zero elements of C and D corresponding to covariances between pairs of missing values come from

$$\text{Cov}(\text{vec}{(\mathbf{X})}_m,\text{vec}{(\mathbf{X})}_m|X_o\theta \prime )={\mathbf{\Omega }}_{mm}-{\mathbf{\Omega }}_{mo}{\mathbf{\Omega }}_{oo}^{-1}{\mathbf{\Omega }}_{om}.$$ (10)

This computational strategy may be appropriate for small data matrices, but even when n and p are medium-sized, this approach can be computationally expensive. Inverting Ω can be of order O(n³p³), depending on the amount of missing data. So, even if we have a relatively small matrix of dimension 100 × 50, this inversion costs around O (10¹⁰)! Using Gibbs sampling to approximate the calculations of the E steps in either a Stochastic or Stochastic Approximation EM-type algorithm [6] is one computational approach (we present Gibbs sampling as part of our Bayesian one-step approximation in Supplementary Materials). A stochastic approach, however, is still computationally expensive and thus, an approximation to our MCECM algorithm is needed.

4.2. One-Step Approximation to TRCMimpute

For high-dimensional transposable data, the imputation algorithm, TRCMimpute, can be computationally prohibitive. Thus, we propose a one-step approximation which has a computational costs comparable to multivariate imputation methods.

4.2.1. One-step Algorithm

The MCECM algorithm for imputation with transposable regularized covariance models iterates between the E step, taking conditional expectations, and the CM steps, maximizing with respect to the inverse covariances. Both of these steps are computationally intensive for high-dimensional data. While each iterate increases the observed log-likelihood, the first step usually produces the steepest increase in the objective. Thus, we propose an algorithm that instead of iterating between E and CM steps, approximates the solution of the MCECM algorithm by stopping after only one step.

Many have noted in other iterative maximum likelihood-type algorithms that a one-step algorithm from a good initial starting point often produces an efficient, if not comparable, approximation to the fully-iterated solution [15, 10]. Thus, for our one-step approximation we seek a good initial solution from which to start our CM and E steps. For this, we turn to the multivariate regularized covariance models. Recall that all marginals of the mean-restricted matrix-variate normal are multivariate normal, and hence, if one of the penalty parameters for the TRCM model is infinitely large, we obtain the RCM solution (i.e. if ρ_r = ∞, we get the RCM solution with penalized covariance among the columns). We propose to use the estimates from the two marginal distributions with penalized row covariances and penalized column covariances to obtain our initial starting point. This is similar to the COSSO one-step algorithm which uses a marginal solution as a good initial starting point, [15].

Since the final goal of our approximation algorithm is missing value imputation, and not parameter estimation, we then tailor our one-step algorithm to favor imputation. First, instead of using the marginal RCM covariance estimates as starting values for the subsequent TRCMimpute E and CM steps, we use the marginal estimates to obtain two sets of imputed missing values through applying the RCMimpute method to the rows and then the columns. We then average the two sets of missing value estimates and fix these to find the maximum likelihood parameter estimates for the TRCM model, completing the maximization step. In summary, our initial estimates are obtained by applying an EM-type method to the marginal models. Biernacki et al. [3] similarly use other EM-type algorithms to find good initial starting values for their EM mixture model algorithm. The final step of our algorithm is the Expectation step where we take the conditional expectation of the missing values given the observed values and the TRCM estimates. Note that the E step of the MCECM algorithm includes both an imputation part and a covariance correction part (see Proposition 3). For our one-step algorithm, however, the covariance correction part is unnecessary since our final goal is missing value imputation. We give the one-step approximation, called TRCMAimpute, in Algorithm 2.

Algorithm 2.

One-step algorithm approximating TRCMimpute (TRCMAimpute)

Initial imputation: Impute missing values with RCMimpute assuming Σ = I. Impute missing values with RCMimpute assuming Δ = I. Average the two estimates. Find the MLE’s of the transposable regularized covariance model, ν̂, μ̂, Σ̂ and Δ̂ with the imputed missing values fixed. Set the missing values to their conditional expectation given these parameters: X̂m = E (Xm | Xo, ν̂, μ̂, Σ̂, Δ̂).

Before discussing the calculations necessary in the final step of the algorithm, we pause to note a major advantage of our one-step method. If the sets of missing values from the marginal models using RCMimpute are saved in the first step, then TRCMAimpute can give three sets of missing value estimates. Since it is often unknown whether a given dataset may have independent rows or columns, cross validation, for example, can be used to determine whether penalizing the covariances of the rows, columns, or both is best for missing value imputation. This is discussed in detail in Supplementary Materials.

4.2.2. Conditional Expectations

We now discuss the final conditional expectation step of our one-step approximation algorithm. Recall that the conditional expectation can be computed via (9), but this requires inverting Ω and is therefore avoided. Instead, we exploit a property of the mean-restricted matrix-variate normal, namely that all marginals of our model are multivariate normal. This allows us to find the conditional distributions in a two step process given by Theorem 2.

Theorem 2

Let X ~ N_n,p (ν, μ, Σ, Δ), M = ν1^T + μ^T1 and partition X, M, Σ, Δ as

$$\mathbf{X}=\left(\begin{array}{cc}\hfill {\mathbf{X}}_{i,m_i}\hfill & \hfill {\mathbf{X}}_{i,o_i}\hfill \\ \hfill {\mathbf{X}}_{k,m_i}\hfill & \hfill {\mathbf{X}}_{k,o_i}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\mathbf{X}}_{m_j,j}\hfill & \hfill {\mathbf{X}}_{m_j,l}\hfill \\ \hfill {\mathbf{X}}_{o_j,j}\hfill & \hfill {\mathbf{X}}_{o_j,l}\hfill \end{array}\right),\mathbf{M}=\left(\begin{array}{c}\hfill {\mathbf{M}}_{i,r}\hfill \\ \hfill {\mathbf{M}}_{k,r}\hfill \end{array}\right)=({\mathbf{M}}_{c,j}{\mathbf{M}}_{c,l}),$$

$$\mathbf{\Sigma }=\left(\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{i,i}\hfill & \hfill {\mathbf{\Sigma }}_{i,k}\hfill \\ \hfill {\mathbf{\Sigma }}_{k,i}\hfill & \hfill {\mathbf{\Sigma }}_{k,k}\hfill \end{array}\right),\&\mathbf{\Delta }=\left(\begin{array}{cc}\hfill {\mathbf{\Delta }}_{j,j}\hfill & \hfill {\mathbf{\Delta }}_{j,l}\hfill \\ \hfill {\mathbf{\Delta }}_{l,j}\hfill & \hfill {\mathbf{\Delta }}_{l,l}\hfill \end{array}\right),$$

where i and j denote indices of a row and column respectively, k and l are vectors of indices of length n − 1 and p − 1 respectively, and m_i and o_i denote vectors of indices within row i and m_j and o_j indices within column j.

Define

$$\psi ={\mathbf{M}}_{i,r}+{\mathbf{\Sigma }}_{i,k}{\mathbf{\Sigma }}_{k,k}^{-1}({\mathbf{X}}_{k,r}-{\mathbf{M}}_{k,r}),\eta ={\mathbf{M}}_{c,j}+({\mathbf{X}}_{c,l}-{\mathbf{M}}_{c,l}){\mathbf{\Delta }}_{l,l}^{-1}{\mathbf{\Delta }}_{l,j},$$

$$\mathbf{\Gamma }=[{\mathbf{\Sigma }}_{i,i}-{\mathbf{\Sigma }}_{i,k}{\mathbf{\Sigma }}_{k,k}^{-1}{\mathbf{\Sigma }}_{k,i}]\otimes \mathbf{\Delta },\&\mathbf{\Phi }=\mathbf{\Sigma }\otimes [{\mathbf{\Delta }}_{j,j}-{\mathbf{\Delta }}_{j,l}{{\mathbf{\Delta }}^{-1}}_{l,l}{\mathbf{\Delta }}_{l,j}].$$

Partition ψ, η, Γ and Φ as $\psi =\left(\begin{array}{c}\hfill {\psi }_{m_i}\hfill \\ \hfill {\psi }_{o_i}\hfill \end{array}\right)$, η = (η_mj η_oj),

$$\mathbf{\Gamma }=\left(\begin{array}{cc}\hfill {\mathbf{\Gamma }}_{m_i,m_i}\hfill & \hfill {\mathbf{\Gamma }}_{m_i,o_i}\hfill \\ \hfill {\mathbf{\Gamma }}_{o_i,m_i}\hfill & \hfill {\mathbf{\Gamma }}_{o_i,o_i}\hfill \end{array}\right),\&\mathbf{\Phi }=\left(\begin{array}{cc}\hfill {\mathbf{\Phi }}_{m_j,m_j}\hfill & \hfill {\mathbf{\Phi }}_{m_j,o_j}\hfill \\ \hfill {\mathbf{\Phi }}_{o_j,m_j}\hfill & \hfill {\mathbf{\Phi }}_{o_j,o_j}\hfill \end{array}\right).$$

Then,

1. $$({\mathbf{X}}_{i,m_i}|{\mathbf{X}}_{i,o_i},{\mathbf{X}}_{k,r})~N({\psi }_{m_i}+{\mathbf{\Gamma }}_{m_i,o_i}{\mathbf{\Gamma }}_{o_i,o_i}^{-1}({\mathbf{X}}_{i,o_i}-{\psi }_{o_i}),{\mathbf{\Gamma }}_{m_{i,}{m}_i}-{\mathbf{\Gamma }}_{m_i,o_i}{\mathbf{\Gamma }}_{o_i,o_i}^{-1}{\mathbf{\Gamma }}_{o_i,m_i}).$$
2. $$({\mathbf{X}}_{m_j,j}|{\mathbf{X}}_{o_{j,j}},{\mathbf{X}}_{c,l})~N({\eta }_{m_j}+{\mathbf{\Phi }}_{m_j,o_j}{\mathbf{\Phi }}_{o_j,o_j}^{-1}({\mathbf{X}}_{o_j,j}-{\eta }_{o_j}),{\mathbf{\Phi }}_{m_j,m_j}-{\mathbf{\Phi }}_{m_j,o_j}{\mathbf{\Phi }}_{o_j,o_j}^{-1}{\mathbf{\Phi }}_{o_j,m_j}).$$

Proof

See Supplementary Materials.

Thus, from Theorem 2, the conditional distribution of values in a row or column given the rest of the matrix can be calculated in a two step process where each step takes at most the number of computations as required for calculating multivariate conditional distributions. The first step finds the distribution of an entire row or column conditional on the rest of the matrix, and the second step finds the conditional distribution of the values of interest within the row or column. By splitting the calculations in this manner, we avoid inverting the np × np Kronecker product covariance. This alternative form for the conditional distributions of elements in a row or column leads to an iterative algorithm for calculating the conditional expectation of the missing values given the observed values. We call this the Alternating Conditional Expectations Algorithm, given in Algorithm 3.

Algorithm 3.

Alternating Conditional Expectations Algorithm.

Initialize ${\hat{\mathbf{X}}}_{i,j}^{(0)}={\hat{\nu }}_i+{\hat{\mu }}_j$ for Xi,j ∈ Xm. For each row, i, with missing values: Set ${\hat{\mathbf{X}}}_{i,m_i}^{(k+1)}=\mathrm{E}({\mathbf{X}}_{i,m_i}|{\mathbf{X}}_{i,o_i}^{(k)},{\mathbf{X}}_{\ne i,r}^{(k)})$. For each column, j, with missing values: Set ${\hat{\mathbf{X}}}_{m_j,j}^{(k+1)}=\mathrm{E}({\mathbf{X}}_{m_j,j}|{\mathbf{X}}_{o_j,j}^{(k)},{\mathbf{X}}_{c,\ne j}^{(k)})$. Repeat Steps 1 and 2 until convergence.

Theorem 3

Let X ~ N_n,p (ν, μ, Σ, Δ) and partition vec(X) = (vec(X_m) vec(X_o)) where m and o are indices partitioned by rows, (m_i and o_i) and columns, (m_j and o_j), so that a row, X_i,r = (X_i,mi X_i,oi) and a column ${\mathbf{X}}_{c,j}=\left(\begin{array}{c}\hfill {\mathbf{X}}_{m_j,j}\hfill \\ \hfill {\mathbf{X}}_{o_j,j}\hfill \end{array}\right)$. Then, the Alternating Conditional Expectations Algorithm, Algorithm 3, converges to E(X_m |X_o).

Proof

See Supplementary Materials.

Theorem 3 shows that the conditional expectations needed in Step 3 of the one-step approximation algorithm can be calculated in an iterative manner from the conditional distributions of elements in a row and column, as in Algorithm 3. Thus, Theorems 2 and 3 mean that the conditional expectations can be calculated by separately inverting the row and column covariance matrices, instead of the overall Kronecker product covariance. This reduces the order of operations from around O(n³p³) to O(n³ + p³), a substantial savings. In addition, if both the covariance estimates and their inverses are known, then one can use the properties of the Schur complement to further speed computation. For extremely sparse matrices or data with few missing elements, the order of operations is nearly linear in n and p (See Supplementary Materials). We also note that the structure of the Alternating Conditional Expectations Algorithm often leads to a faster rate of convergence as discussed in the proof of Theorem 3. For high-dimensional data, these two results mean that matrix-variate models can be used in any application where multivariate models are computationally feasible, thus opening the door to applications of transposable models!

4.2.3. Numerical Comparisons

We now investigate the accuracy of the one-step approximation algorithm in terms of observed log-likelihood and imputation accuracy with a numerical example. Here, we simulate fifty datasets, 25 × 25, from the matrix-variate normal model with autoregressive covariance matrices.

• Autoregressive: Σ_ij = 0.8^|i−j| and Δ_ij = 0.6^|i−j|.

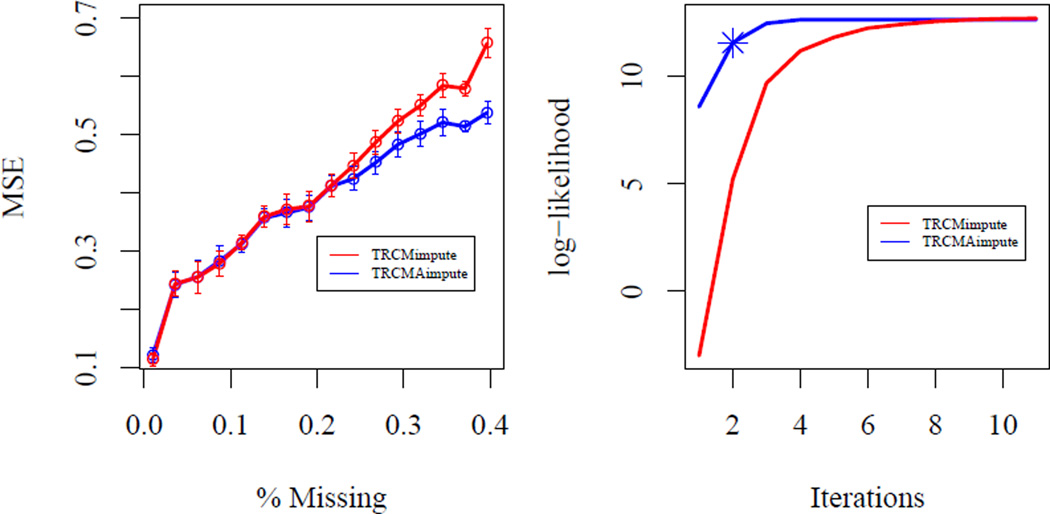
We delete values at random according to certain percentages and report the mean MSE for both the MCECM algorithm, TRCMimpute, and the one-step approximation, TRCMAimpute on the right in Figure 1. The one-step approximation performs comparably, or slightly better, in terms of imputation error to the MCECM algorithm for all percentages of missing values. We note that TRCMAimpute could give better missing value estimates if the MCECM algorithm converges to a sub-optimal stationary point of the observed log-likelihood. For a dataset with 25% missing values, we apply the MCECM algorithm and also apply our approximation extended beyond the first step, but denote the observed log-likelihood after the first step with a star on the right in Figure 1. This shows that using marginals to provide a good starting value, does indeed start the algorithm at a higher observed log-likelihood. Also, after the first step, the observed log-likelihood is very close to the fully-iterated maximum. Thus, the one-step approximation appears to be a comparable approximation to the TRCMimpute approximation which is feasible for use with high-dimensional datasets.

Fig 1.

Comparison of the mean MSE with standard errors (left) of the MCECM imputation algorithm (TRCMimpute) and the one-step approximation (TRCMAimpute) for transposable data of dimension 25 × 25 with various percentages of missing data. Fifty datasets were simulated from the matrix-variate normal distribution with autoregressive covariances as given in Section 4.2.3. Observed log-likelihood (right) verses iterations for TRCMimpute and TRCMAimpute with 25% missing values. The one-step approximation begins at the TRCM parameter estimates using the imputed values from RCMimpute. The observed log-likelihood of one-step approximation is given by a star after the first step. All methods use L₂ penalties with ρ_r = ρ_c = 1 for comparison purposes.

5. Results and Simulations

The following results indicate that imputation with transposable regularized covariance models is useful in a variety of situations and data types often giving much better error rates than existing methods. We first assess the performance of our one-step approximation, TRCMAimpute, under a variety of simulations with both full and sparse covariance matrices. Authors have suggested that microarrays and user-ratings data, such as the Netflix movie-rating data are transposable or matrix-distributed [9], [1], hence, we also assess the performance of our methods on these types of datasets. We compare performances to three commonly used single imputation methods - SVD methods (SVDimpute), k-nearest neighbors (KNNimpute), and local least squares (LLSimpute) [21], [14]. For the SVD method, we use a reduced rank model with a column mean effect. The rank of the SVD is determined by cross-validation; regularization is not used on the singular vectors so that only one parameter is needed for selection by cross-validation. For k-nearest neighbors and local least squares also, a column mean effect is used and the number of neighbors, k, is selected via cross-validation. If the number of observed elements is limited, the pairwise-complete correlation matrix is used to determine the closest neighbors.

5.1. Simulations

We test our imputation method for transposable data under a variety of simulated distributions, both multivariate and matrix-variate. All simulations use one of four covariance types given below. These are numbered as they appear in the simulation table.

1. Autoregressive: Σ_ij = 0.8^|i−j| and Δ_ij = 0.6^|i−j|.

2. Equal off-diagonals: Σ_ij = 0.5 and Δ_ij = 0.5 for i ≠ j, and Σ_ii = 1 and Δ_ii = 1.

3. Blocked diagonal: Σ_ii = 1 and Δ_ii = 1 with off-diagonal elements of 5 × 5 blocks of Σ are 0.8 and of Δ, 0.6.

4. Banded off-diagonals: Σ_ii = 1 and Δ_ii = 1 with

   $${\mathbf{\Sigma }}_{ij}=\{\begin{array}{cc}0.8\hfill & \text{if}|i-j|\text{divisible by}5.\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array},{\mathbf{\Delta }}_{ij}=\{\begin{array}{cc}0.6\hfill & \text{if}|i-j|\text{divisible by}5.\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}.$$

The first simulation, with results in Table 1, compares performances with both multivariate distributions, only Σ given, and matrix-variate distributions, both Σ and Δ given. In these simulations, the data is of dimension 50 × 50 with either 25% or 75% of the values missing at random. The simulation given in Table 2 gives results for matrix-variate distributions with one dimension much larger than the other, 100 × 10 and 10% of values missing at random. The final simulation, in Table 3, tests the performance of our method when the data has a transposable covariance structure, but is not normally distributed. Here, the data, of dimension 50 × 50 with 25% of values missing at random, is either distributed Chi-square with three degrees of freedom or Poisson with mean three. The Chi-square and Poisson distributions introduce large outliers and the Poisson distribution is discrete. All three sets of simulations are compared to SVD imputation and k-nearest neighbor imputation.

Table 1.

Mean MSE with standard error computed over 50 datasets of dimension 50 × 50 simulated under the matrix-variate normal distribution with covariances given in Section 5.1. In the upper portion of the table, 25% of values are missing and in the lower, 75% missing. The TRCM one-step approximation with L₁ : L₁, L₁ : L₂ and L₂ : L₂ penalties was used as well as the SVD and k-nearest neighbor imputation. Below the errors for TRCMAimpute, we give the number of simulations out of 50 in which a marginal, multivariate method (RCMimpute) was chosen over the matrix-variate method. Parameters were chosen for all methods via 5-fold cross validation. Best performing methods are given in bold.

	TRCMAimpute			Others
	L1 : L1	L1 : L2	L2 : L2	SVD	KNN
Σ1	0.8936 (0.01) 45/50	0.725 (0.0069) 0/50	0.5919 (0.0056) 50/50	0.634 (0.0081)	0.448 (0.005)
Σ1, Δ1	0.8255 (0.012) 0/50	0.6315 (0.0078) 0/50	0.5402 (0.0067) 0/50	0.4603 (0.0083)	0.8034 (0.016)
Σ2	0.895 (0.016) 43/50	0.7829 (0.013) 0/50	0.6392 (0.008) 48/50	0.993 (0.019)	0.9498 (0.017)
Σ2, Δ2	0.749 (0.044) 0/50	0.6867 (0.034) 0/50	0.4556 (0.0098) 48/50	0.6821 (0.051)	0.8273 (0.055)
Σ3	1.04 (0.017) 37/50	1.02 (0.017) 9/50	0.9348 (0.016) 49/50	0.7384 (0.012)	0.9115 (0.014)
Σ3, Δ3	1.012 (0.02) 5/50	0.9477 (0.019) 0/50	0.8585 (0.017) 37/50	0.7271 (0.016)	0.9886 (0.019)
Σ4	0.9986 (0.018) 37/50	0.9407 (0.017) 3/50	0.8067 (0.014) 48/50	0.4903 (0.0076)	0.9057 (0.014)
Σ4, Δ4	0.9726 (0.033) 6/50	0.855 (0.028) 0/50	0.6999 (0.022) 39/50	0.5282 (0.024)	0.9366 (0.031)
Σ1	0.9134 (0.0096) 21/50	0.9083 (0.0092) 18/50	0.8948 (0.009) 21/50	1.173 (0.013)	0.9349 (0.0092)
Σ1, Δ1	0.867 (0.011) 0/50	0.8569 (0.01) 0/50	0.845 (0.0096) 0/50	0.9535 (0.01)	0.9736 (0.013)
Σ3	1.053 (0.01) 7/50	1.052 (0.01) 7/50	1.048 (0.01) 7/50	1.22 (0.013)	1.03 (0.01)
Σ3, Δ3	1.001 (0.014) 0/50	0.9968 (0.014) 0/50	0.9945 (0.014) 1/50	1.11 (0.016)	1.006 (0.014)

Table 2.

Mean MSE with standard errors over 50 datasets of dimension 100 × 10 with 10% missing values simulated under the matrix-variate normal with covariances given in Section 5.1. The TRCM one-step approximation with L₂ : L₁ and L₂ : L₂ penalties was used as well as the SVD and k-nearest neighbor imputation. Parameters were chosen for all methods via 5-fold cross validation. Best performing methods are given in bold.

	TRCMAimpute		Others
	L2 : L1	L2 : L2	SVD	KNN
Σ1, Δ1	0.8227 (0.019)	0.7072 (0.016)	1.075 (0.024)	0.6971 (0.018)
Σ2, Δ2	1.019 (0.15)	0.9441 (0.13)	1.306 (0.23)	1.057 (0.17)
Σ3, Δ3	0.9372 (0.047)	0.841 (0.042)	1.121 (0.05)	0.9241 (0.042)
Σ4, Δ4	0.7044 (0.059)	0.6148 (0.049)	0.9751 (0.074)	1.118 (0.089)

Table 3.

Mean MSE with standard error computed over 50 datasets of dimension 50 × 50 with 25% missing values simulated under the Chi-square distribution with 3 degrees of freedom or the Poisson distribution with mean 3 with Kronecker product covariance structure given by the covariances in Section 5.1. The TRCM one-step approximation with L₂ : L₁ and L₂ : L₂ penalties was used as well as the SVD and k-nearest neighbor imputation. Parameters were chosen for all methods via 5-fold cross validation. Best performing methods are given in bold.

		TRCMAimpute		Others
		L2 : L1	L2 : L2	KNN	SVD
Chi-square	Σ1, Δ1	3.824 (0.065)	2.611 (0.044)	6.85 (0.34)	7.684 (0.15)
	Σ3, Δ3	5.525 (0.14)	5.068 (0.15)	29.41 (0.83)	50.16 (0.74)
Poisson	Σ1, Δ1	2.442 (0.05)	1.571 (0.021)	8.04 (0.34)	5.824 (0.11)
	Σ3, Δ3	3.045 (0.075)	2.813 (0.081)	29.13 (0.95)	49.2 (0.68)

These simulations show that TRCMAimpute is competitive with two of the most commonly used single imputation methods, SVD and k-nearest neighbor imputation. First, TRCM with L₂ penalties outperforms the other possible TRCM penalty types. This may be due to the fact that the covariance estimates with L₂ penalties has a globally unique solution, Theorem 1, while the estimation procedure for other penalty types only reaches a stationary point, Proposition 2. The one-step approximation permits the flexibility to choose either multivariate or transposable models. As seen with smaller percentages of missing values, cross-validation generally chooses the correct model for the L₁ : L₁ penalty-type, but seems to prefer the marginal multivariate models for the L₂ : L₂ penalties. However, with 75% of the values missing, the transposable model is often chosen even if the underlying distribution is multivariate. The additional structure of the TRCM covariances may allow for more information to be gleaned from the few observed values, perhaps explaining the better performance of the matrix-variate model. TRCMAimpute seems to perform best in comparison to SVD and k-nearest neighbor imputation for the full covariances with equal off-diagonal elements. Our TRCM-based imputation methods appear particularly robust to departures from normality and perform well even in the presence of large outliers, as shown in Table 3. Overall, imputation methods based on transposable covariance models compare favorably in these simulations.

5.2. Microarray Data

Microarrays are high-dimensional matrix-data that often contain missing values. Usually, one assumes that the genes are correlated while the arrays are independent. Efron questions this assumption, however, and suggests using a matrix-variate normal model [8]. Indeed, the matrix-variate framework, and more specifically the TRCM model seem appropriate models for microarray data for several reasons. First, one usually centers both the genes and the arrays before analysis, a structure which is built in to our model. Second, TRCMs have the ability to span many models which include a marginal model where the rows are distributed as a multivariate normal and the arrays are independent. Hence, if a microarray is truly multivariate, our model can accommodate this. But, if there are true correlations within the arrays, TRCM can appropriately measure this correlation and account for it when imputing missing values. Lastly, the graphical nature of our model can estimate the gene network and then use this information to more accurately estimate missing data.

For our analysis, we use a microarray dataset of kidney cancer tumor samples [25]. The dataset contains 14,814 genes and 178 samples. About 10% of the data is missing. For the following figures, all of the genes with no missing values were taken, totaling 1,031 genes. Missing values were then placed at random. Errors were assessed by comparing the imputed values to the true observed values.

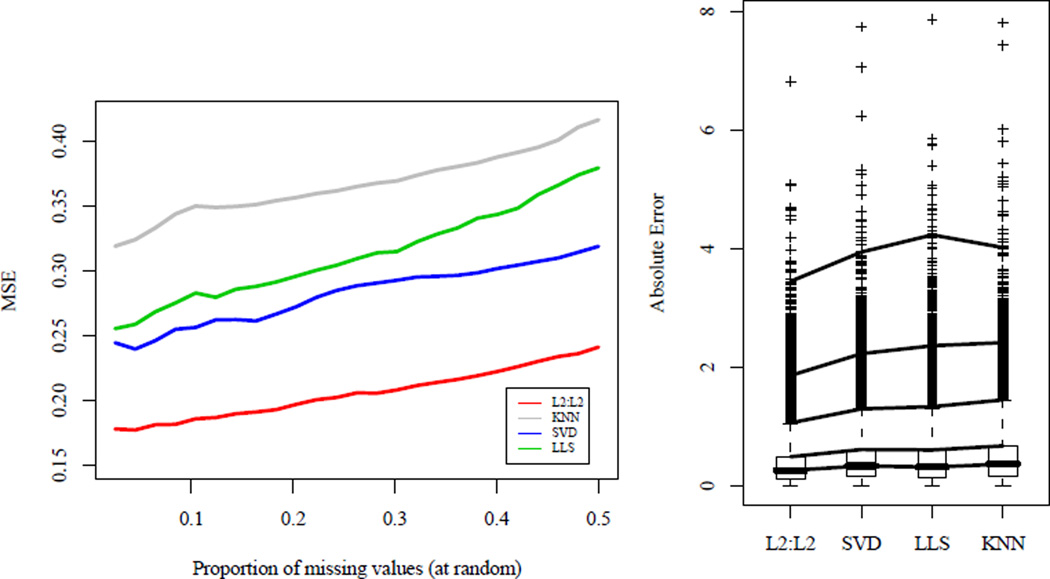
We assess the performance of TRCM imputation methods on this microarray data and compare them to existing methods for various percentages of missing values, deleted at random, on the right in Figure 2. Here, we use L₂ penalties since these are computationally less expensive for high-dimensional data. TRCMAimpute outperforms competing methods in terms of imputation error for all percentages of missing values. We note that cross-validation exclusively chose the marginal, multivariate model from the one-step approximation. This indicates that the arrays in this microarray dataset may indeed by independent.

Fig 2.

Left: Comparison of MSE for imputation methods on kidney cancer microarray data with different proportions of missing values. Genes in which all samples are observed are taken with values deleted at random. TRCMAimpute, L₂ : L₂ and common imputation methods KNNimpute, SVDimpute and LLSimpute are compared with all parameters chosen by 5-fold cross-validation. Cross-validation chose to penalize only the arrays for the one-step approximation algorithm, TRCMAimpute. Right: Boxplots of individual absolute errors for various imputation methods. Genes in which all samples are observed were taken and deleted in the same pattern as a random gene in the original dataset. Lines are drawn at the 50%, 75%, 95%, 99%, and 99.9% quantiles. TRCMAimpute, L₂ : L₂ has a mean absolute error of 0.37 and has lower errors at every quantile than its closest competitor, SVDimpute which has a mean absolute error of 0.46.

Often, microarray datasets are not missing randomly. Also, researchers are interested in not only the error in terms of MSE, but the individual errors made as well. To investigate these issues, we assess individual absolute errors of data that is missing in the same pattern as the original data. For each complete gene, values were set to missing in the same arrays as a randomly sampled gene from the original dataset. The right panel of Figure 2 displays the boxplots of the absolute imputation errors. Lines are drawn at quantiles to assess the relative performances of each method. Here, TRCMAimpute has lower absolute errors at each quantile. Also, the set of imputed values has far fewer outliers than competing methods. The mean absolute error for TRCMAimpute is 0.37, far below the next two methods, LLSimpute and SVDimpute which have a mean absolute error of 0.46. Altogether, our results illustrate the utility and flexibility of using TRCMs for missing value imputation in microarray data.

5.3. Netflix Data

We compare transposable regularized covariance models and existing methods on the Netflix movie rating data [2]. The TRCM framework seems well-suited to model this user-ratings data. As discussed in the introduction, our model allows for not only correlations among both the customers and movies, but between them as well. In addition, TRCM models the graph structure of the customers and the movies. Thus, we can fill in a customer's rating of a particular movie based on the customer's links with other customers and the movie's links with other movies. Also, many have noted that the unrated movies in the Netflix data are not simply missing at random and may contain meaningful information. A customer, for example, may not have rated a movie because the movie was not of interest and thus they never saw it. While it may appear that our method requires a missing at random assumption, this is not necessarily the case. When two customers have similar sets of unrated movies, after removing the means, our algorithm begins with the unrated movies set to zero. Thus, these two customers would exhibit high correlation simply due to the pattern of missing values. This correlation could yield an estimated “link” between the customers in the inverse covariance matrix. This would then be used to estimate the missing ratings. Hence, our method can find relationships between sets of missing values and use these to impute the missing values.

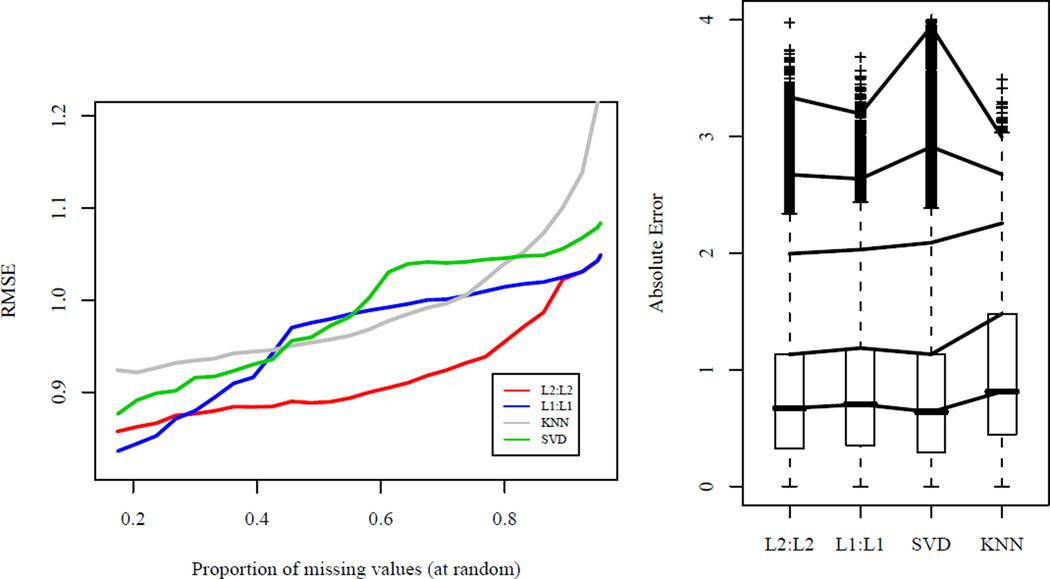
The Netflix dataset is extremely high-dimensional, with over 480,000 customers and over 17,000 movies, and is very sparse, with over 98% of the ratings missing. Hence, assessing the utility of our methods from this data as a whole is not currently feasible. Instead, we rank both the movies and the customers by the number of ratings and take as a subset, the top 250 customer's ratings of the top 250 movies. This subset has around 12% of the ratings missing. We then delete more data at random to evaluate the performance of the methods. In addition, for each customer in this subset ratings were deleted for movies corresponding to the unrated movies of a randomly selected customer with at least one rating out of the 250 movies. This leaves 74% of ratings missing. Figure 3 compares the performances of the TRCM methods to existing methods for both subset with both missing at random and missing in the pattern of the original values.

Fig 3.

Left: Comparison of the root MSE (RMSE) for a subset of the Netflix data for TRCMAimpute, L₂ : L₂ and L₁ : L₁, to KNNimpute and SVDimpute. A dense subset was obtained by ranking the movies and customers in terms of number of ratings and taking the top 250 movies and 250 customers. This subset has around 12% missing and additional values were deleted at random, up to 95%. With 95% missing, the RMSE of TRCMAimpute is 1.049 compared to 1.084 of the SVD and 1.354 using the movie averages. Right: Boxplots of absolute errors for the dense subset with missing entries in the pattern of the original data. Customers with at least one ranking out of the 250 movies were selected at random and entries were deleted according to these customers leaving 74% missing. Quantiles of the absolute errors are shown at 50%, 75%, 95%, 99%, and 99.9%. The RMSE of the methods are as follows L₂ : L₂: 1.005, L₁ : L₁: 1.029, SVD: 1.032, KNN: 1.184.

Before discussing these results, we first make a note about the comparability of our errors rates to those for the Netflix Prize [2]. Because we chose the subset of data based on the number of observed ratings, we can expect the RMSE to be higher here than applying these methods to the full dataset. This method of obtaining a subset leaves out potentially thousands of highly correlated customers or movies that would greatly increase a method's predictive ability. In fact, the RMSE of the SVD method on the entire Netflix data is 0.91 [20], much less than the observed RMSE of 1.084 for the SVD on our subset with 95% missing. Thus, we can conjecture, that all of the methods we present would do better in terms of RMSE using the entire dataset than the small subset on which we present results.

The results indicate that TRCM imputation methods, particularly with L₂ penalties, are competitive with existing methods on the missing at random data. At higher percentages of missing values, our methods perform notably well. With 95% missing values in our subset, TRCMAimpute has a RMSE of 1.049 compared to the SVD at 1.084 and 1.354 using the movie averages. This is of potentially great interest for missing data imputation on a larger scale where the percentage of missing data is greater than 98%. We note that at smaller percentages of missing values, marginal models penalizing the movies were often chosen by cross-validation, indicating that the movies may have more predictive power. Whereas, at larger percentages of missing values, cross-validation chose to penalize both the rows and the columns, indicating that possibly more information can be gleaned from few observed values using transposable methods.

Our methods also preform well when the data is missing in the same pattern as the original. The L₂ : L₂ method had the best results with a RMSE of 1.005 followed by L₁ : L1 with 1.029, SVD with 1.032 and k-nearest neighbors with 1.184. From the boxplots of absolute values Figure 3 (right), we see that the SVD has many large outliers in absolute value, while the L₁ penalties led to the fewest number of large errors. Since leading imputation methods for the Netflix Prize, are ensembles of many different methods [1], we do not believe that TRCM methods alone would outperform ensemble methods. If, however, our methods outperform other individual methods, they could prove to be beneficial additions to imputation ensembles.

6. Discussion

We have formulated a parametric model for matrix-data along with computational advances that allow this model to be applied to missing value estimation in high-dimensional datasets with possibly complex correlations between and among the rows and columns.

Our MCECM and one-step approximation imputation approaches are restricted to datasets where for each pair of rows, there is at least one column in which both entries are observed and vice versa for each pair of columns. A major drawback of TRCM imputation methods is computational cost. First, RCMimpute using the columns as features costs O (p³). This is roughly on the order of other common imputation methods such as the SVDimpute which costs O (np²). Our one-step approximation, TRCMAim-pute, using the computations for the Alternating Conditional Expectations algorithm given in Supplementary Materials, costs $O({\sum }_{i=1}^n\text{min}{\{|m_i|,|o_i|\}}^3+{\sum }_{j=1}^p\text{min}{\{|m_j|,|o_j|\}}^3+n^3+p^3)$, where |m_i| and |o_i| are the number of missing and observed elements of row i respectively.

The main application of this paper has been to missing value imputation. We note that this is separate from the matrix-completion methods via convex optimization of Candes and Recht [5], which focuses on matrix-reconstruction instead of imputation. Also, we have presented a single imputation procedure, but our techniques can easily be extended to incorporate multiple imputation. We present a repeated imputations approach by taking samples from the posterior distribution [19] with the Bayesian one-step approximation in the Supplementary Materials. In addition, we have not discussed ultimate use or analysis of the imputed data, which will often dictate the imputation approach. Our imputation methods form a foundation that can be extended to further address these issues.

We also pause to address the appropriateness of the Kronecker product covariance matrix to model the covariances observed in real data. While we do not assume that this particular structure is suitable for all data, we feel comfortable using the model because of its flexibility. Recall that all marginal distributions of the mean-restricted matrix-variate normal are multivariate normal. This includes the distribution of elements within a row or column, or the distribution of elements from different rows or columns. All of the marginals of a set of elements are given by the mean and covariance parameters of the elements' rows and columns. belong. Thus, our model says that the location of elements within a matrix determine their distribution, often a reasonable assumption. Also, if either the covariance matrix of the rows or the columns is the identity matrix, then we are back to the familiar multivariate normal model. This flexibility to fit numerous multivariate models and to adapt to structure within a matrix is an important advantage of our matrix-variate model.

Transposable regularized covariance models may be of potential mathematical and practical interest in numerous fields. TRCMs allow for non-singular estimation of the covariances of the rows and columns, which is essential for any application. Adding restrictions to the mean of the TRCM, allows one to estimate all parameters from a single observed data matrix. Also, introduction of efficient methods of calculating conditional distributions and expectations make this model computationally feasible for many applications. Hence, transposable regularized covariance models have many potential future uses in areas such as hypothesis testing, classification and prediction, and data mining.