Abstract
Water in its three ambient phases plays the central thermodynamic role in the terrestrial climate system. Clouds control Earth’s radiation balance, atmospheric water vapour is the strongest “greenhouse” gas, and non-equilibrium relative humidity at the air-sea interface drives evaporation and latent heat export from the ocean. In this paper, we examine the climatologically relevant atmospheric relative humidity, noting fundamental deficiencies in the definition of this key observable. The metrological history of this quantity is reviewed, problems with its current definition and measurement practice are analysed, and options for future improvements are discussed in conjunction with the recent seawater standard TEOS-10. It is concluded that the International Bureau of Weights and Measures, (BIPM), in cooperation with the International Association for the Properties of Water and Steam, IAPWS, along with other international organisations and institutions, can make significant contributions by developing and recommending state-of-the-art solutions for this long standing metrological problem, such as are suggested here.
1. Introduction
The term humidity indicates water vapour, normally admixed with air or other dry gas. Above liquid water and aqueous solutions, above ice, and in pore spaces lined with adsorbed water, water vapour will be found, often with an interface-crossing net flux of molecules. The irreversible net flux only ceases at equilibrium, at which point the chemical potential, μ, of each component is the same in all coexisting phases. The vapour-phase water mole fraction, x = nV/(nV + nA), where nV and nA, respectively, are the numbers of water and air molecules, at equilibrium depends primarily on the temperature, T, but also on the curvature of the interface between gas and liquid, the surface material, the gas mixture, the substances dissolved in the condensed phase and on the total pressure, p. If at equilibrium the condensed phase - either liquid water or ice - has a planar interface with the vapour phase, the vapour (or more loosely, the humid gas) is said to be saturated and the system at saturation.
In general, the relative humidity (RH), ψ, of humid air1 is the ratio of some non-negative humidity quantity, z, to the same quantity at saturation, zsat, at the same temperature, i.e.,
| (1) |
where the superscript ‘(s)’ indicates that the conditions at saturation need be specified as an additional relation imposed on the independent quantities xsat and psat. Choices for z have included the vapour mole fraction, x, the mixing ratio, r = MV/MA, the specific humidity, q = MV/(MV + MA), the saturation vapour pressure, esat, the water-vapour partial pressure, pV = xp, and the fugacity of water vapour, fV. Here, MV and MA represent the mass of water and air molecules, respectively, in a unit volume. A preferred choice for s has been p = psat, i.e., saturation is established via an isobaric process in contrast to, say, isothermal compression or vapour injection at constant volume. The subscript V is used here to distinguish fugacity from the common symbol f for the water-vapour enhancement factor. When expressing RH in percent, the unit symbol %rh will be used in this paper.
Note, however, that eq. (1) requires the specification of a saturated gas phase in order to calculate z(xsat, T, psat); this condition is not trivially obeyed under any practical circumstances. To date, the most important definition has set z = x, which with s: p = psat is equivalent to z = pV. This de facto standard definition (as it will be referred to in this paper) has been authorised by the WMO2 since 1950 and by many other organisations (see Section 3.2). However, the standard definition is valid only over a limited range, and attempts to create full-range definitions have lacked both clear theoretical basis and official sanction. Finally, a variety of other non-standard definitions (e.g., with z = q and z = r) continue to propagate in particular in climatological and meteorological textbooks or research articles.
We present in Section 2 a brief review of the importance of relative humidity in climate dynamics, and emphasise the related need for its unambiguous definition and consistent measurement, traceable to the International System of Units, the SI. Apparently self-evident, this requirement is by no means a metrologically well-settled subject, as is evident from the history reviewed in Section 3. In Sections 4 and 5, the core of this paper provides an analysis of the various inconsistent definitions in use for relative humidity, especially in geophysical and climate research (Katsaros, 2001), which neither cover the complete range of reasonable applicability (Böse and Mitter, 2004; Lovell-Smith and Pearson, 2006) nor represent physically rigorous measures of the thermodynamic driving force to equilibrium. To provide a consistent solution to these long-standing problems, we suggest in Section 6 an axiomatic approach based on equations of state for humid air, liquid water and ice that are parts of TEOS-10, the Thermodynamic Equation of Seawater 2010 (IOC et al., 2010). This approach is supported by an explicit example specified in Appendix D in the supplement of the Part 1 companion paper (Feistel et al., 2015b).
2. Climatological relevance
Hypothetically, our early ancestors developed sweating for effective cooling in the hot but arid African savannah, likely more than a million years ago (Rantala, 2007). At least since then, the spatially and temporally widely varying amounts of water vapour in the air of the terrestrial climate zones from deserts to jungles have influenced our social evolution, our living conditions, agriculture, technology, ways of life and even our spoken language (Everett et al., 2015). As a result of this variety, humidity problems are investigated today in various branches of science and engineering, from air conditioning to weather forecast.
Water is a key player in terrestrial climate dynamics; Heinrich Hertz in 1885 was perhaps the first who painted the physical picture of climate as a “gigantic steam engine” (Mulligan and Hertz, 1997, p. 41). Related knowledge is still insufficient because processes involving water in the atmosphere are very complex, theoretically and observationally demanding, and subject to significant uncertainties (Chahine, 1992; Schneider et al., 2010; Randal, 2012; Gimeno, 2013; Josey et al., 2013). In contrast to the greenhouse effect, the hydrological cycle has received only marginal attention in the recent public debates on global warming related to carbon dioxide emissions. For example, the observed seasonal cycle of ocean temperatures cannot be explained by merely the radiation balance without latent heat export which, similar to that of the sweaty human skin, is controlled by ambient RH (Kraus, 1972; Pierce et al., 2011; Feistel and Ebeling, 2011).
2.1 Greenhouse feedback of water-vapour amount
Water vapour is the Earth’s main greenhouse gas - and usefully so. Without it, average temperatures would be uncomfortably colder (Le Treut et al., 2007). But unlike man-made CO2 emissions, water-vapour emissions generally cannot be controlled: surface water evaporates everywhere, in amounts governed mostly by temperature, wind and humidity. Atmospheric water vapour forms clouds and falls as rain, when temperature, pressure and air movements dictate. To the terrestrial greenhouse effect, i.e., to the atmospheric absorption of outgoing thermal radiation, CO2 actually contributes only one quarter while the major part comes mainly from water vapour and from clouds (Abbot and Fowle, 1908; Emden, 1913; Trenberth et al., 2007; Lacis et al., 2010; Schmidt et al., 2010).
On average per surface area, liquid water in clouds amounts to about 0.11 kg m−2 (Greenwald and Stephens, 1995), a fraction slightly less than 0.5 % of the total water mass of about 25 kg m−2 contained in the vertically integrated air column. About twice as much water as in clouds resides in the stratosphere above the “cold trap” tropopause (Seidel, 2002), while about 98 % constitutes moisture confined to the troposphere below where it strongly absorbs and emits infrared radiation (Sugiyama et al., 2005). The increasing amount of tropospheric water, which is assumed to result from global warming, in turn amplifies the temperature rise via a positive feedback loop (Komabayasi, 1967; Ingersoll, 1969, 2013; Dessler et al., 2008; Dessler, 2010; Ingram, 2010; Soares, 2010, Pierrehumbert, 2010). About 80 to 90 % of global evaporation originates from the ocean (Reid and Valdés, 2011; Durack et al., 2013). The moisture content of the air column over the ocean has increased by 0.41 kg m−2 or 1.6 % per decade since 1988 (Santer et al., 2007), in accord with a mean warming rate of 13 mK yr−1 of the marine atmosphere (Trenberth et al., 2007). Along with the increase in precipitable water, atmospheric circulation seems to be slowing down (Laliberté et al., 2015; Coumou et al., 2015).
2.2 Relative fugacity driving the hydrological cycle
On the annual average, 72 % of the Earth’s cross section exposed to sunlight is covered by the ocean (Feistel, 2013) where about 60 % of the solar energy is absorbed (Macdonald and Baringer, 2013) and subsequently exported to the atmosphere by radiation, by sensible heat flux and by latent heat of evaporation controlled by RH. Largely unaffected by tropospheric CO2 levels, latent heat energy is carried by water vapour across the dense layers of the atmosphere before it is released in clouds and radiated to the cold cosmic background. The dominant role of this transport route in the global energy balance is not always clearly emphasised in climatological literature; the following estimates regarding the three ways of oceanic heat loss may underpin this role and in turn that of RH.
Estimates for the latent-heat fraction of ocean-atmosphere energy exchange vary between 45 % (Emery et al., 2006) and 90 % (Wells, 2012). The mean oceanic evaporation of about 1200 mm yr−1 (Baumgartner and Reichel, 1975; Peixoto and Oort, 1992) corresponds to a latent heat export rate of approximately 100 W m−2, or to roughly 2/3 of the solar irradiation absorbed in the water column (Pierce et al., 2011; Feistel and Ebeling, 2011). On land, the latent heat flux is dominated by transpiration that amounts to 33 W m−2 (Jasechko et al., 2013), or to about 1/2 of the irradiation absorbed there (Trenberth et al., 2009). Thus, driven by atmospheric subsaturation measured in terms of RH, evaporation is the dominant process of oceanic energy export (Pierrehumbert, 1996). In contrast, even if any greenhouse effect is ignored, black-body radiation from the ocean surface is too slow to explain the observed oceanic thermal relaxation time of only 2–3 months (Prescott and Collins, 1951; Schwartz, 2007; Feistel and Ebeling, 2011) and may not dominate ocean cooling. Finally, sensible heat flow is driven by the sea-air temperature difference such as from the warm water to the colder air above. However, this difference is generally small (Kara et al., 2007), and in addition, when a turbulent isentropic greenhouse atmosphere is in radiation balance with the ocean, the air temperature at the sea surface appears even slightly higher than that of the emitting water underneath, as a result of the adiabatic vertical temperature gradient (Feistel, 2011a), which suggests that the average sensible heat transfer in such a conceptual model is instead downward from the air to the sea. Also, the cool oceanic skin caused by evaporation (Saunders, 1967; Schluessel et al., 1990) counteracts sensible heat export. Compared to the former two processes, sensible heat exchange plays only a minor role in sea-air interaction.
In irreversible thermodynamics, fluxes of heat and matter result from Onsager forces which are combinations of gradients of temperature and chemical potentials (de Groot and Mazur, 1962; Glansdorff and Prigogine, 1971; Falkenhagen et al., 1971; Landau and Lifschitz, 1974). Climate processes are driven by such gradients that are built up by uneven absorption of solar energy and its subsequent conversion and self-organised redistribution by radiation, phase transitions and global circulation. The most relevant differences of chemical potentials are those of water between ocean, ice cover and humid air, at the boundary of and within the atmosphere. These differences can be exactly expressed in terms of the relative fugacity (see Appendix C in the Digital Supplement of Part 1 of this series) of water vapour in the atmosphere, which is one of the options for defining RH. To a reasonable approximation, see Sec. 5, the spatial distribution of the relative fugacity of water vapour can be described by that of the RH in the standard definition (Erikson, 1965; Kraus, 1972; Hansen and Takahashi, 1984; IOC et al., 2010; Feistel et al., 2010a; Feistel and Ebeling, 2011; Li and Chylek, 2012; Li et al., 2014). At the sea surface, the thermodynamic driving force for evaporation is the difference between the chemical potentials of water in the ocean and in the atmosphere (Kraus and Businger, 1994; IOC et al., 2010). Thus, RH immediately above the sea surface essentially controls the latent heat export from the ocean. Similar to the variety of empirical equations in use for estimating RH, the driving forces for the mass transfer of water across phase boundaries are parameterised by differences of various alternative humidity quantities (Kusuda, 1965; Erikson, 1965; Liu and Niiler, 1990; Katsaros, 2001; Schneider et al., 2010), motivated mainly by practical convenience rather than by physical rigor.
After averaging over diurnal cycles and weather fluctuations, RH over the oceans is rather constant at values of about 80 %rh, almost independent of region, season, or atmospheric warming (Albrecht, 1940; Gill, 1982; Mitchell, 1989; Peixoto and Oort, 1996; Allen and Ingram, 2002; Dai, 2006; Pierrehumbert, 2010), in contrast to RH in the upper troposphere (Paltridge et al., 2009; Fasullo and Trenberth, 2012). Mean sea-surface RH is slightly higher (up to 85 %rh) in the tropics and slightly lower (down to 75 %rh) in the trade-wind belt. A global climatological atlas of ocean-surface RH was published by Wright (1988). A spurious “decline in marine relative humidity around 1982” in climate data was caused by “a change in reporting practice for dew-point temperature” (IPCC, 2013, p. 206). While the approximate constancy of RH is well-known from observations and models, its fundamental physical causes remain elusive (Ingram, 2010; Pierrehumbert, 2010; Held and Shell, 2012). A simple hypothesis is that slightly deviating values of RH may drive the global energy fluxes out of balance and the resulting deviations of ocean temperature, hydrological cycle and cloudiness will quickly return RH to its observed value (Feistel, 2013).
Climatological sensitivity, planetary albedo and changes in cloudiness are closely linked to changes of RH (Smagorinsky, 1960; Hansen and Takahashi, 1984; Fasullo and Trenberth, 2012; Quaas, 2012; Feistel, 2013; Lea, 2015; Martínez-Botí et al., 2015). No significant trend for the land-ocean average of the total cloud cover was found for the period 1971–96 (Warren et al., 2007). Also, no significant change in cloud albedo has yet been detected (Wielicki et al., 2005); certain trends found in remotely sensed cloudiness may suffer from monitoring inadequacies (Dai et al., 2006). While surface RH drives the ocean’s cooling, clouds and albedo control its heating by sunlight in such a way that on the global average, gain and loss are almost perfectly balanced by a stable feedback loop. Thus, small long-term trends possibly observed in surface RH are key indicators for fundamental changes in the climate system and may offer insights in, for example, the effects of volcanic eruptions or solar activity, in the variability of the global albedo or cloudiness, and in regional acceleration of the water cycle (Held and Shell, 2012; Durack et al., 2012; Fasullo and Trenberth, 2012; Josey et al., 2013; Gimeno, 2013; Yu and Luo, 2014; Bintanja and Selten, 2014). Cloud-climate interaction is poorly understood in general, in particular how humid air is lifted into the atmosphere and drives cloud formation and rainfall (Bony et al., 2015; Schiermeier, 2015). Solar dimming measures of “geo-engineering” occasionally discussed to counteract global warming may substantially modify the atmospheric RH as a risky side-effect (Schmidt et al., 2012).
All the above estimates suffer from considerable uncertainties; monitoring and modelling the latent heat flux and the related evaporative cooling still poses a challenge (Kleeman and Power, 1995; Pierrehumbert, 1996, 2010; Josey et al., 1999, 2013; Worley et al., 2005; van Hooidonk and Huber, 2009). Based on the best measurements, closing the global ocean energy budget still fails by as much as about 20 %, or 30 W m−2, likely due to poor knowledge of the latent heat flux (Chahine, 1992; Katsaros, 2001; Stephens et al., 2012; Josey et al., 2013). For comparison, natural albedo fluctuations typically change solar irradiation by only about 1 % (Wielicki et al., 2005), while a tiny systematic imbalance on the order of 0.003 %, or 0.005 W m−2, of the terrestrial heat flux is large enough to raise the atmospheric temperature at the observed rate of 2 K per century (Hansen et al., 2006). Theoretically, under otherwise unaltered conditions, a minor systematic offset of 1 %rh (an uncertainty typical for meteorological observation, see Section 4.3) in mean sea-surface RH would suffice to cause a significant oceanic latent heat-flux difference of almost 6 W m−2 (Feistel and Ebeling, 2011). Thus, the heat-flux deviation to be monitored for global warming is about three orders of magnitude less than the uncertainty of oceanic latent-heat export estimates.
The recent pause (“hiatus”) in global surface warming (Kosaka and Xie, 2013; Li et al., 2013; Tollefsen, 2014; Clement and DiNezio, 2014; Chen and Tung, 2014) indicates that heat-flux fluctuations of a magnitude typical for global warming, likely caused by ocean-atmosphere interaction, may well occur on climatic time scales. Possibly related global fluctuations of RH are unclear. Perhaps, the disputed hiatus may be just an insignificant spurious effect within data uncertainty and natural fluctuations (Cowtan and Way, 2014; Kintisch, 2014; Curry, 2014; Marotzke and Forster, 2015; Steinman et al., 2015).
2.3 Importance of atmospheric humidity to salinity and climate variability
Local and temporal changes of atmospheric humidity significantly influence the sea-surface salinity, the hydrological cycle and the climatic variability (Dai, 2006; Santer et al., 2007; Durack and Wijffels, 2010; Durack et al., 2012; Pierce et al., 2012), see also the Part 2 companion paper. As an example, after the closing of the Isthmus of Panama about 3.5 million years ago (Coates, 1997), the increasing humidity over the North Atlantic is considered responsible for the subsequent Arctic glaciation (Haug and Tiedemann, 1998; Haug et al., 2005). The somewhat later polar warming of between 8 K and 19 K cannot be explained by the CO2 levels that were similar to the present ones, however, uncertain additional feedbacks, in particular related to water vapour, may grow stronger in warmer climates (Lea, 2015; Martínez-Botí et al., 2015). Moisture dynamics also governs, e.g., the anomalies of rainy seasons in the African Sahel zone (Poan et al., 2013), the yields in the US Corn Belt (Ort and Long, 2014), and the climate sensitivity to CO2 (Wang et al., 2014). Also, atmospheric water vapour affects almost any radiation-based measurements from space. Measurement and numerical simulation of global atmospheric humidity distributions and their changes on the long-term scale are therefore fundamental for understanding and monitoring climatic change. The global water cycle is expected to become a major focus for climate research in the coming years (Sherwood et al., 2010; Reid and Valdés, 2011; Tollefsen, 2012; Fasullo and Trenberth, 2012; Stevens and Bony, 2013; IPCC, 2013).
3. Brief history
The scientific concept of relative humidity arose with the development of instruments (hygrometers) to measure humidity (Molyneux, 1685; Arderon, 1746; Gatley, 2013). De Luc provided what is possibly the first formal definition of relative humidity and recognition of an underlying physical reality, noting that many natural fibre-based materials, including hygrometer sensing fibres, were observed to respond to the “degree of saturation” (i.e., to the ratio of the actual quantity of “steam” to the maximum possible at that temperature) rather than to the absolute quantity of water vapour, (de Luc, 1792, pp. 412–413). Gilbert (1803) is credited with the first use of the term “relative humidity” although a variety of ratios (e.g., density and vapour tension) and terms (e.g., “fraction of saturation”, “degrees of saturation”, “relative degree of humidity”, “degree of moisture” and “percentage humidity”) were used throughout the 19th century (Regnault, 1845; Miller, 1851; Guyot, 1859; Shaw, 1889).
Detailed reviews of the history of atmospheric humidity measurements were published by Sonntag (1966), Möller (2008), Holland and Stöhr (2011) and Gatley (2013). The beginning of quasi-regular meteorological measurements of RH can be dated to 1873, when OMI/IMO3 was established to coordinate the collection and international exchange of meteorological data and information4. Since its invention in 1887 (Sprung, 1888), Assmann’s psychrometer has proven to be a robust instrument for practical meteorological observations of RH (WMO, 2008). Diurnal and seasonal cycles as well as spatial variability of RH were already known at certain locations before 1873 (Brewster, 1832; Forbes and Mahlmann, 1836). For example, records between 1849 and 1868 of dry-bulb and wet-bulb thermometers at the Royal Observatory at Greenwich were analysed by Ellis (1878), and at the German weather station Hohenpeissenberg, where continuous RH records began in 1879 (DWD, 2012), different hygrometers and a psychrometer (in 1841) had been used since 17815. Nevertheless, long-term series of RH comparable in length and quality to historical records of temperature and precipitation are “almost not available” (Hocke et al., 2013) for modern climate research.
3.1 Vapour pressure, partial pressure, fugacity and the enhancement factor
Relative-humidity definitions based on vapour pressure are not equivalent to those based on vapour density since, as was noted by Regnault (1845), the partial density of saturated water vapour in moist air is greater than the density of pure saturated vapour at the same temperature. In other words, the saturation partial pressure of water vapour in humid air, , is greater than the pressure of pure saturated water vapour, esat, at the same temperature. By the end of the 19th century, this enhancement of the partial pressure above esat was recognised to be a combination of three thermodynamic phenomena, whereby the “effective” water vapour pressure (and hence evaporative flux), associated with the condensed phase, increases due to the applied pressure (Poynting effect) and decreases due to dissolved gas (colligative or Raoult effect), and whereby the “effective” water-vapour pressure (and hence condensing flux) in the gas phase is reduced due to interactions among air and water molecules (Van der Waals, 1873; Maxwell, 1874; Poynting, 1881; Lewis, 1901a,b; McDonald, 1963; Hyland, 1975; Wisniak, 2001).
Consequently, for humid air the “effective” vapour pressure driving water transport toward equilibrium is identified with neither esat nor but with the fugacity, fV, of water vapour relative to the fugacity of water in the other phases. The concept of fugacity, which is related to the free energy and chemical potential, was introduced in 1901 by Lewis as the tendency of a molecular species to escape from the phase it is in, such that at equilibrium the fugacities (and chemical potentials) of the species in each phase are equal. With units of pressure, the value of fV is smaller than pV but approaches pV in the ideal-gas limit (Lewis, 1901a, p. 48; Lewis, 1901b, p. 54, and see Appendices A–C in the Digital Supplement of Part 1 of this series). The ratio fV / pV is known as the fugacity coefficient, φV (x,T,p).
The ratio is known as the water-vapour enhancement factor, f(T, p). Thermodynamically-based equations for the enhancement factor in air were developed by Goff and Gratch (1945) for ASHVE6 and revised by Wexler and Hyland (1983) whose work for ASHRAE was most recently updated by Herrmann et al. (2009) using the latest virial coefficients and the IAPWS equations for esat(T) over water and ice (IAPWS, 1992, 2011; Wagner and Pruss, 1993; Wagner et al., 2011).
The expression for the enhancement factor is based on the equality at equilibrium of the chemical potential of water in the gas and condensed phases (and hence of the respective fugacities) and consists of a product of terms accounting for the Raoult, Poynting and (non-ideal) gas-phase molecular interaction effects (Hyland, 1975) in the general form (Feistel et al., 2015a; see also Part 1 of this series and eq. C.19 in Appendix C of its Digital Supplement),
| (2) |
This equation is equivalent to the complex formula given by Herrmann et al. (2009) if the mole fraction of liquid water, xW, is expressed by Henry’s law for dissolved air, the Poynting factor of liquid water, π(T,p), is estimated by assuming a linear pressure dependence of specific volume, and a virial approximation of the fugacity coefficient (Feistel et al., 2015a) is used.
Figure 1 shows how the partial pressure, xp (solid black curve), would increase, were dry air to be added to a system at T = 300 K initially containing saturated vapour above a pool of water in a sealed box, for which the fugacities of the liquid water, fW, and the saturated water vapour, , are equal. The green ‘△’, blue ‘+’ and blue ‘□’, curves represent the results of multiplying the Raoult, Poynting and gas-phase interaction factors by the pure vapour pressure, esat (solid green line). Initially, the total pressure, p, in the container is due to the water vapour, so that the partial pressure xp = esat, since x = 1. At this stage, is slightly less than esat because of interactions between vapour-phase water molecules. As dry air is added, the small amount of air dissolving causes a slight decrease in fW. At the same time, the increase in total pressure exerted on the liquid causes a substantial increase in fW. These phenomena, respectively, contribute a slight decrease and increase in partial pressure. The dominant contributor to the increase in partial pressure is the gas-phase interaction amongst water and air molecules, which acts to lower the fugacity of water in the vapour phase and thus increase the net evaporation until .
Figure 1.
This chart shows, for saturated humid air at 300 K, the theoretical water-vapour partial pressures as functions of pressure, p, that would arise were each of the Raoult, Poynting or interaction contributions to act alone in the enhancement of the full partial pressure (thick black line) above the pure saturation vapour pressure (dashed green line). The theoretical partial pressures shown are calculated using the enhancement-factor equation from Herrmann et al. (2009) modified to highlight the Raoult (green ‘△’), Poynting (blue ‘+’) and gas-phase interaction (blue ‘□’) effects individually. Also shown for comparison is the water-vapour fugacity (red ‘●’), which was calculated using TEOS-10 functions (Feistel et al., 2010b; Wright et al., 2010). Note that for pure saturated vapour at 300 K (black ‘■’), p sat = e sat = 3.537kPa and because of water-water gas-phase interaction. See text for details.
3.2 Formal definition by the WMO
In 1953, the newly formed WMO adopted the definition that had been proposed in the first of two resolutions issued earlier by the International Joint Committee on Psychrometric Data (IJCPD) (List, 1959), which in turn followed a dominant historic practice in the meteorological community of defining relative humidity as the ratio of vapour pressures. The WMO definition sets z = x in eq. (1) which, with the condition that saturation is defined at the same pressure, i.e., s: psat = p, is equivalent to also setting z = pV, so that in this paper’s notation,
| (3) |
(WMO, 2008, p. 1.4–27). Note that to indicate saturation with respect to liquid water or hexagonal ice I, subscripts ‘W’ and ‘Ih’, respectively, will be used where relevant and omitted otherwise. Also, superscript ‘s’ will be omitted for simplicity. The WMO has continued to recommend this definition through seven editions of “The WMO Guide to Meteorological Instruments and Methods of Observation (CIMO Guide)” from 1954 to 20087 (WMO, 2008). The definition is also promoted by many other influential organisations8 and standards publications (ASHRAE, 1994; NF X 15–110, 1994; IMC, 1996; BS 1339-1, 2002; ASTM, 2006, 2014) and as the de facto standard is referred to here also as the standard definition. It is widely accepted, extremely useful and can be accurately calculated from other humidity quantities using reference equations for pure-water saturation vapour pressure, esat(T), and for the humid-air water-vapour enhancement factor, f(T, p).
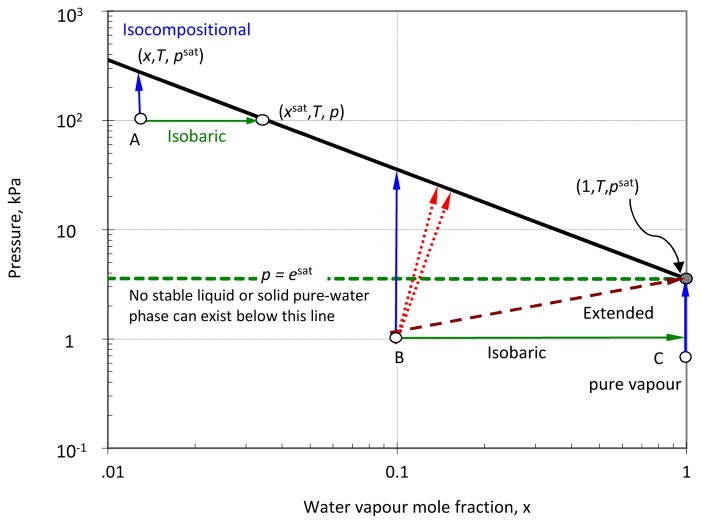
The WMO definition does “not apply to moist air when the pressure p is less than the saturation water vapour pressure [esat(T)] … at temperature T” (WMO, 2008, p. 1.4–27). To illustrate, the range of possible states of humid air defined by the triple, (x, T, p), for T = 300 K is shown in Fig 2. The thick solid curve represents the pressure at which the humid gas becomes saturated as a function of x. While from any point below the curve (e.g., A, B or C), saturation is possible, the WMO definition was only intended to cover that part above the horizontal dashed green line, p ≥ esat, of the range where, as in most meteorological conditions, saturation could be achieved at constant pressure (i.e., isobaric saturation s: psat = p) represented by a horizontal green arrow from A to the state (xsat, T, p) on the saturation curve.
Figure 2.
The saturation-pressure curve, p = psat(x, T), and unsaturated states for humid air at 300 K at pressure p, as a function of x. The saturation curve is found from x = esat(T) f(T, p) / p, and is represented by the thick solid line. Humid air can exist at 300 K at any state represented by a point below the saturation curve. The horizontal dashed green line indicates the saturation vapour pressure for pure water at 300 K. Circles represent particular humid-air or vapour states and the arrows indicate potential paths to saturation including isobaric (from A and B) and isocompositional (from A, B and C). See text for details.
The second resolution issued by the IJCPD (1950) defined an extended form of eq. (3) to the effect that when “barometric pressure and temperature … [conditions were] … such that saturation was impossible, relative humidity is the ratio of the partial pressure of water vapor in the mixture or sample to the saturation pressure of pure water [esat] at the given temperature” (List, 1959; Goff, 1960). In the notation used here, the extension is
| (4) |
and is indicated by the dashed brown arrow from B in Fig. 2. The resolution was issued subject to verification, but no further action was taken. Worrall (1965) proposed the same definition, emphasising that here esat is used “as a reference only”. In his definitive work, Harrison (1965) published a definition for unsaturated pure vapour,
| (5) |
which is a special case of ψext for which x = 1 so that pV = p (vertical blue arrow from C), but omitted an extended-range definition. The issue was further addressed by Böse and Mitter (2004), who called psat the “virtual” saturation pressure, and by Lovell-Smith and Pearson (2006), and in 2007, an extended -range definition was included in the German Standard VDI/VDE 3514 (2007), where saturation occurs at a “hypothetical” system pressure equal to esat.
3.3 Relative fugacity and water activity
Lewis (1901a, p. 55) wrote that the “great utility of this new quantity [fugacity] … [lies] in the fact that the approximate equations containing the vapor pressure and developed rigorously except for the assumption that the vapor pressure obeys the [ideal] gas law, may be replaced by exact equations of the same form or of equal simplicity containing the fugacity instead of the vapor pressure” (see also Gavroglu and Simões, 2012). While the fugacity of water is equilibrated across phases at saturation, the relative fugacity of water, ψf, (also known as the water activity, aW, see Appendix B and C in the supplement of the Part 1 companion paper) has been defined with reference to pure water under pressure p at the same temperature rather than to water containing some dissolved air when p > esat (Lewis and Randall, 1923, p. 349, 1961, p. 243). However, in practice difficulties in measurement of fV, and the close approximation of fV to pV over much of the range, have meant that the water activity aW has usually been approximated by the ratio of vapour pressures ψe measured directly (Robinson and Sinclair, 1934; Scott, 1958) or by ψx determined using RH sensors (Schiraldi et al., 2012).
4. Current definition and measurement practice
4.1 Current definitions
We can identify four major usages of RH definitions in contemporary publications.
-
The WMO or standard definition, eq. (3),
(6) is valid over most (but not all) of the range addressed by industry and by the meteorological, domestic and commercial air-conditioning communities. Over the valid range, the metrological community provides traceability to the SI for standard RH via calibration (see Section 4.2).
-
Full-range definition: In the absence of official sanction (apart from the comparatively recent standard VDI/VDE 3514 (2007)), those who need to calculate, measure or calibrate in the subsaturation pressure region have generally developed a pragmatic solution based on z = pv rather than z = x. Since f(T, p) = 1 when p = esat, the “pragmatic” full-range definition is
(7) Nevertheless, with many major manufacturers of RH sensors extending the range well above 100 °C and as high as 180 °C, the need for widespread sanction of a definition covering the full range is clear. For example, this definition is recommended by a major manufacturer of humidity sensors and instruments9,10.
-
Other non-standard definitions: Beside the predominant standard definition, several other RH definitions such as ψr and ψq continue to be used and to propagate on-line and in print. For example, the OMI (1951) definition ψr
(8) is occasionally mistakenly referred to as the WMO definition. The mistake possibly originated in a WMO training manual (Retallack, 1973) and continues to propagate (Gill, 1982; Rogers and Yau, 1989; Pruppacher and Klett, 1997; Katsaros, 2001; Jacobson, 2005; Dai, 2006; Pierrehumbert, 2010), including in some background articles of TEOS-10 (Feistel et al., 2010a, 2010b) and online11. On the other hand, ASHRAE (1994) and BS 1339-1 (2002) identify the ratio of mixing ratios, r / rsat, as the “degree of saturation” and “percentage saturation”, respectively, thus clearly distinguishing it from the standard definition. Again, several papers define RH in terms of specific humidity as(9) (e.g., Sundqvist, 1978; Peixoto and Oort, 1992; Katsaros, 2001; Tompkins et al., 2007; Lamquin et al., 2009; Quaas, 2012; Wells, 2012). In the category of other non-standard definitions we note that IUPAC’s online “Goldbook” (IUPAC, 2006) defines RH as(10) which is problematic because it does not yield exactly 100 %rh at saturation of humid air.
-
Water-vapour relative fugacity (see Appendix C in the supplement of the Part 1 companion paper):
-
For unsaturated humid air specified by (x, T, p) in the presence of a bulk condensed phase, the thermodynamic driving force for net flux of water molecules is the difference between the (mass-based) chemical potentials and μW(T, p) of water in the gas and condensed phases, respectively. This difference can be expressed in terms of the ratio of the fugacity, fV (or equivalently the absolute activity, λV, see Appendix B and C in the supplement of the Part 1 companion paper), of water in the gas phase to that in the condensed phase, i.e, in terms of the relative fugacity, ψf, or water activity, aW, of the unsaturated air,
(11) where RW is the specific gas constant of water (see Appendix D in the supplement of the Part 1 companion paper). This ratio characterises unsaturated humid air with reference to a theoretical bulk condensed phase, and also arises in thermodynamic derivations of the Kelvin equation for non-planar interfaces and of the vapour-pressure modifications associated with solutions (see also IOC et al., 2010; Feistel, 2012). This thermodynamic definition is widely referred to in food and solution chemistry, but its use in practice is limited, see entry (b) below. Consistent with TEOS-10, a virial equation for the calculation of the fugacity of water vapour in humid air has recently been published (Feistel et al., 2015a; IAPWS, 2015). Note that the definition (11) is preliminary as it refers to pure liquid water as the condensed phase rather than to air-saturated water, i.e., the Raoult effect is neglected (see Appendix C in the supplement of the Part 1 companion paper for more details).
-
For many physical chemists, climate modelers and chemical and food engineers, the water-vapour partial pressure is viewed as a convenient ideal-gas approximation to the fugacity, and the standard definition (3) used as a convenient approximation to the relative fugacity, i.e.,
(12) (Loncin et al., 1968; Hamer and Wu, 1972; Kraus, 1972; Greenspan, 1977; Mathlouthi, 2001; Blandamer et al., 2005; Choosri et al., 2009; Björklund and Wadsö, 2011; Feistel and Ebeling, 2011; Schiraldi et al., 2012; Li and Chylek, 2012).
-
4.2 Measurement practice, use and calculation of relative humidity
Whilst there are many methods of measuring individual quantities from which the RH could be calculated when T and p are known, metrology-type applications favour chilled-mirror dew-point meters, since these offer the most reliability and precision over the greatest range, and because dew-point temperature Td is often the quantity realised at the primary standard level.
For most industrial applications and for ground-based meteorology, RH is measured using the electrical response of thin-film humidity sensors and, less frequently, using wet and dry-bulb psychrometers, and chilled-mirror hygrometers. Satellite and airborne remote-sensing applications tend to use electromagnetic absorption methods yielding a volumetric concentration. Good overviews of current and historical meteorological practice including calibration are given in WMO (2008) and Kämpfer (2013). Although all humidity sensors require calibration, those measuring RH require more frequent calibration because of processes associated with drift, aging and contamination of the sensitive material.
Calibration implies comparison against a traceable reference and assumes appropriate propagation of the associated measurement uncertainty (VIM, 2012). SI-traceability is disseminated through a chain of calibrations via a primary humidity standard. Currently, the primary humidity generator12 (HG) is the most common ultimate source of traceability in humidity measurements, and a typical traceability chain for RH is presented in Fig. 3. In most such generators, a continuously flowing gas is brought to saturation at a known temperature, T1, and pressure, p1. In so-called two-pressure and two-temperature humidity generators, the saturated gas passes through an expansion valve and/or heater to flow as an unsaturated humid gas without changing its vapour mole fraction, x, provided no condensation or evaporation takes place. This, now unsaturated mole fraction, x, can be calculated as
Figure 3.
Typical traceability chains for RH based on a primary humidity generator (HG) conditioning air to a known water-vapour mole fraction x which is calculated as a function of the saturation temperature and pressure (T1 and p1, respectively, see eq. (13)) and the humidity reference functions for the vapour pressure esat(T) and enhancement factor f(T, p). The quantity x can be used to calibrate a cavity-ring-down spectrometer (CRDS), for example. A further pressure and temperature measurement allows Td(x, p2) using eq. (16) and ψ(x, p2, T2) using eqs. (3) and (14) to be calculated for calibration of chilled-mirror hygrometers (CMH) and RH hygrometers as secondary standards, respectively. When using a generator as a non-traceable stable source, the secondary standards can be used to measure x, Td or ψ of conditioned air for calibration of a “device under calibration” (DUC), including, as illustrated, a RH hygrometer.
| (13) |
Here, Fe(T1;a) and Ff(T1,p1;b) represent reference functions that allow the calculation at T1 of the saturation water vapour pressure esat and at T1 and p1 of the water vapour enhancement factor f respectively, and a and b are vectors of fitted parameters for the respective reference functions (see Lovell-Smith, 2009; 2012). In other generators the input gas may be humidified directly to a non-saturated level - using partial saturation, diffusion or blending approaches - that is, definitively characterised in terms of mass, volume or amount of component substances, and that enables the mole fraction to be calculated (Hasegawa and Little, 1977; Stevens and Bell, 1992; Heinonen, 2002, Lovell-Smith, 2009; Mackrodt, 2012; Meyer et al., 2012).
Once the mole fraction, x, is known, by whatever method, the measurement of other parameters at the device under calibration (DUC) such as the gas temperature, T2, and pressure, p2, enable calculation of other unknown quanities such as dew-point temperature, RH or others. The standard RH at the DUC is, from eqs. (3) and (13),
| (14) |
in general, and for the two-pressure humidity generator,
| (15) |
Where RH traceability is required using a generator as a stable source, the reference hygrometer is usually a chilled-mirror hygrometer calibrated for dew-point temperature, Td, which is found by solving
| (16) |
in general, and for the two-pressure humidity generator, by solving
| (17) |
The output from a saturator may be fed directly to a hygrometer with minimal reduction in pressure, such that p2 ≈ p1 and Td ≈ T1. This is the principle of the single-pressure humidity generator. In practice, for greater accuracy, the pressure difference Δp = p1 − p2 is measured and a correction added (Lovell-Smith, 2009).
Note the necessity to calculate esat(T) and f(T, p) in (14) and (16) above, and in most calculations. The most up-to-date versions of esat reference equations are reported by IAPWS (1992, 2011), and the most up-to-date version of the f(T, p) reference function is given in Herrmann et al. (2009). However, a wide variety of reference functions continue to be used. For example, the WMO CIMO Guide (WMO, 2008) recommends the so-called Magnus equations (IMC, 1996) for calculating esat above ice and water for meteorological conditions, and a simple equation to calculate f(T, p) as a function of p only when the pressure is around 100 kPa. For values of f(T, p) over a wider pressure and temperature range, WMO recommends International Meteorological Tables of 1966 (WMO, 1966), which were calculated using the original Goff and Gratch equations (Goff, 1949).
Under the axiomatic framework of TEOS-10, the calculation of the standard RH requires solving for x and xsat, respectively, the implicit equations
| (18) |
which replace eqs. (13) and (14). Eq. (18) may equivalently be expressed in terms of fugacities substituting the corresponding chemical potentials, see eq. (C.1) in the Digital Supplement of the Part 1 companion paper. Similarly, the equation
| (19) |
must be solved to find the dew-point temperature Td. Note that including the dissolution of air in liquid water will require a future extension of TEOS-10.
4.3 Meteorological uncertainty requirements
The spatiotemporal pattern of atmospheric water vapour fields result from the superposition of contributions from microscopic to macroscopic length and time scales. The length, period and amplitude of the smallest scales that need to be resolved depend on the question of interest and may strongly differ between uses in
applied meteorology (e.g., agriculture and forest meteorology, hydrology, environmental and technical meteorology),
numerical meteorology (e.g., numerical weather prediction, general circulation and climate modeling), and
monitoring tasks (e.g., regional and global climate monitoring).
Atmospheric water vapour observation is based on both in-situ and remote-sensing measurement techniques with different measurement uncertainties, collocation and representativeness errors (Peixoto and Oort, 1996; Randal et al., 1996; Miloshevich et al., 2006; Kämpfer, 2013). For applications in synoptic, aeronautical, agricultural and marine meteorology, hydrology and climatology, the WMO CIMO Guide recommends target uncertainties13 for surface humidity of 1 %rh and 5 %rh at high-range and mid-range RH, respectively, with a reporting resolution of 1 %rh (WMO, 2008, Table 4.1, p. I.4-2 and Annex 1.B), whilst recognizing that these can be difficult to achieve in practice. The monitoring of the current increase in stratospheric water14 by approximately 0.5 μmol mol−1 per decade (Kley et al., 2000; Rosenlof et al., 2001; Leiterer et al., 2005), as well as the quantification of the water vapour transport from the troposphere to the stratosphere (Hintsa et al., 1999) requires very high accuracies of humidity measurements in the upper troposphere/lower stratosphere and at the hygropause (Kley et al., 1979). The latter is characterised by joint occurrences of low temperatures down to 190 K and low water-vapour mole ratios15 (see Section 2) down to (2 ± 1) μmol mol−1 at an altitude of 17 km in the tropics (Teitelbaum et al., 2000). Best performing state-of-the-art radiosondes with application of sophisticated correction schemes were demonstrated to achieve a mean relative uncertainty, u(ψ)/ψ, of about 1 % in the lower and middle troposphere (where RH >10 %rh) and of about 2 % in the upper troposphere under mostly nighttime conditions (Miloshevich et al., 2006, Table 3 therein). By application of the method of standardised frequencies to a research radiosonde, Nagel et al. (2001) and Leiterer et al. (2005) exceptionally reported an achievable repeatability of 0.01 %rh and a standard uncertainty of 1 %rh for RH determination in the temperature region down to −70 °C. This accuracy is comparable with the accuracy of the traditional aspiration method of meteorology and close to the uncertainty requirement of better than 1 %rh for climatological research (Leiterer et al., 2005). However, in view of the multitude of different radiosonde types and correction schemes in use, the required accuracy for climate research is still very difficult to realise in the operational radiosounding service (Miloshevich et al., 2001; Antikainen et al., 2002; Ovarlez et al., 2002; Tompkins et al., 2007). Forward simulation of atmospheric dynamics from an initial state, such as boundary-layer turbulence-forced moist convection, also poses very high requirements on the observation (and initialization) of humidity fields (Crook, 1996). The very high sensitivity of predicted convective rainwater to the initial specific humidity at the surface suggests a required uncertainty below 1 %rh for surface RH in order to fulfill hydrological demands with respect to flood prediction in the course of severe weather events.
Given that RH is a nonlinear function of temperature, pressure and vapour mole fraction, the current fixed meteorological uncertainty requirement of 1 %rh for RH measurements is already demanding at both high relative humidities and low temperatures, yet might still be too large a tolerance with respect to error propagation in the derivation of climatological long-term statistics including higher-order statistical moments and cross correlations. The consideration of uncertainties in the analysis of meteorological time series is beginning (Willett et al, 2013), but is not yet common practice as can be seen from the comparatively small number of dedicated studies on uncertainty analysis. Continued dialog and collaboration between the meteorological and metrological communities will enable the best use of resources to maintain and improve (i) strict and unified metrological requirements for RH in the operational observation service and for data processing (inclusive protocol standards), and (ii) SI-traceability of humidity measurements.
5. Problems and deficiencies
For a number of reasons, the definition of RH requires attention. A good definition should have a firm thermodynamic foundation, it should be unambiguous, complete and internally consistent, and tailored subset definitions should be derivable to meet more limited applications. While meeting these requirements, it must also be possible to relate any definition to achievable practical realisations, so that the definition can be connected with disseminated traceable measurements.
(1) The de facto standard definition of RH is incomplete and other non-standard definitions compete
While the standard definition, ψx, given by eq. (6) has widespread official sanction and use, it is defined over only part of the full range over which other humidity quantities are defined, where the concept of RH is meaningful and useful, and where RH sensors respond sensibly. The definition is restricted to humid-air states where p ≥ esat(T) and isobaric saturation is possible.
Two non-standard definitions, ψr, given by eq. (8), and ψq, given by eq. (9), share the limited range of the standard definition and continue to appear in the literature. A third non-standard definition, eq. (10) sanctioned by IUPAC, defines the saturated state with reference to pure water, but is inconsistent since it yields RH of 100 %rh before saturation is reached. Differences between the standard and non-standard definitions including also the relative fugacity eq. (11) are shown in Fig. 4. Most traceable RH calibrations will be based on the standard definition ψx, and the incorrect assumption by some users that the hygrometer instead reports ψr, ψq or ψIUPAC (or has been calibrated with respect to these) could lead to significant error.
Figure 4.
Differences between the standard definition ψx and four non-standard definitions at 40 °C (hollow symbols) and 80 °C (filled symbols) for pressures p = 0.1 MPa, panel (a), and p = 1 MPa, panel (b). Three non-standard definitions are of the form ψz, where the humidity quantity z is the the mixing ratio, r (squares), the specific humidity q (triangles), and the fugacity fV (diamonds). The fourth non-standard definition is ψIUPAC (circles).
The differences between different RH measures are often significant, and to prevent invisible propagation of non-standard definitions, the definition used should always be documented to allow conversion to ψx as in
| (20) |
Here, ω is the ratio of the molar masses of water and dry air and φV is the fugacity coefficient of water in the gas phase (see Appendix C and D in the supplement of the Part 1 companion paper).
(2) The “full-range” definition lacks official sanction and theoretical justification
The full-range definition ψfull, eq. (7), has been a common-sense but informal choice by those needing to measure outside the standard range. Although proposed by the IJCPD in 1949, until the publication of the German Standard VDI/VDE 3514 (2007), the full definition had no official sanction, and to date no other authorities have provided recognition. Note that to achieve saturation, in Fig. 2 any number of paths could be chosen from an unsaturated state such as B to the saturation curve. The definition of a “theoretical” saturation state such that psat = esat provides continuity and consistency with the standard definition, yet theoretical justification is lacking. Nor is it clear in what sense the saturation state for the pure-vapour definition is “theoretical”.
(3) The reference saturation phase is not fully specified
The key to a definition of the relative humidity of unsaturated humid air (or water vapour) at T and p is the specification of the nature of the reference condensed phase. Under the standard definition, the reference phase is fully specified over the limited range p ≥ esat, through the isobaric condition defining the total pressure (s: psat = p), and through the water-vapour enhancement-factor reference function that implicitly defines the associated dissolution of air in the condensed phase. For a full definition, the saturation phase cannot be so defined. From a typical unsaturated state in the extended range (e.g., state B in Fig. 2), saturation is not possible unless psat > p and here the isobaric condition must be replaced by another constraint such as on xsat (e.g., xsat = 1) or psat (e.g., psat = esat) in order to specify a unique condensed-phase state.
(4) Standard approaches are lacking for gas compositions different from standard air
The water-vapour enhancement factor for humid air (e.g., Herrmann et al., 2009) is specified for air of a standard composition. However, the composition of air is neither uniform nor invariable. Under ambient conditions of air-conditioning or meteorology, such nonuniformity and variability is irrelevant for practical purposes, but for industrial applications (such as for flue gases, carbon sequestration, or fuel cells) the conditions and composition may be sufficiently different as to require a new or modified enhancement-factor reference function (or at least allowance for differing composition in the uncertainty budget). For example, the enhancement factor of H2O in CO2 differs greatly from that in air (Meyer and Harvey, 2015). From equation (2), the requirements for modification of the enhancement factor to allow for variation in composition are evident. While the Poynting factor and the fugacity coefficient for pure saturated water vapour are independent of dry-gas species, the fugacity coefficient describing nonideality due to interactions in the gas-phase mixture will strongly depend on gas composition. The equilibrium mole fraction of liquid water will also change due to different solubility of the gas compared to standard air, but for sparingly soluble gases at pressures near atmospheric this difference will be negligible. For high concentrations of dissolved gases, the ideal-solution approximation used in eq. (2) may also require correction.
(5) Most RH definitions do not directly represent thermodynamic driving forces
The main relative-humidity definitions reported here, i.e., eqs. (6)–(11), can be calculated and realised with equal traceability to the SI. But not one of the quantities xsat, rsat, qsat and esat has a related quantity in the condensed phase to which it may become equilibrated. Rather, these quantities represent gas-phase properties at the outcome of a saturation process. The saturated state itself occurs at equilibrium when the chemical potentials of species existing in two or more phases are equilibrated, and the fugacity of water can be used to quantify the saturated state. Significantly, the driving force toward the saturated state of any particular unsaturated humid-air or pure-vapour state is the difference in chemical potential of water in each phase, and this difference can be expressed equivalently as the relative fugacity of water, which seems, therefore, to provide a suitable thermodynamic basis for the definition of RH.
Against this, it might be argued that the usefulness of the partial-pressure and mole-fraction RH definitions will outweigh consideration of relative fugacity in the near future. After all, in those fields such as food chemistry where water activity is used, the reference saturation state is most often defined with respect to pure water (or ice), and esat is almost inevitably used as a suitable approximation to . The problem of developing relative fugacity as the thermodynamic basis for a relative-humidity definition is tied to the problem of providing a firm thermodynamic basis for defining the reference state.
(6) There is no internationally agreed unit symbol for RH, nor an agreed method for scaling of the dimensionless unit
By its definition, eq. (1), RH is a non-negative quantity of dimension one (commonly referred to as “dimensionless”) with values ranging from 0 for dry gas to 1 for saturated gas and higher for supersaturated states common in upper-air meteorology (Peter et al., 2006) or in transient states of technical processes. According to the SI (BIPM, 2006), the expressions ψ = 0.5 and ψ = 50 % are equivalent. The SI suggests that dimensionless numbers should be specified in terms of the entities, so that the vapour mole fraction x = 2.5 × 10−3 may also be written as x = 2.5 mmol mol−1. For example, for mixing ratio the correct wording is “water in air at a mass fraction of 0.05” or “water in air at a mass fraction of 50 g kg−1”. However, widespread preferred usage is to express relative humidity as a percentage, usually with an associated text qualifier giving for example “%rh” rather than %. The qualifier allows a clear distinction to be made between RH “percentage units” and intervals expressed as “percent of value”, in particular when different values of RH are compared or uncertainties reported. The unit symbol %rh is in some cases standardised nationally (BS 1339-1, 2002) but not universally, and some language variations exist. Although the SI Brochure stipulates that ‘Phrases such as “percentage by mass”, “percentage by volume”, or “percentage by amount of substance” should not be used’, the use of the symbol %rh is consistent with the recommendation that ‘extra information on the quantity should instead be conveyed in the description of the measurand and the name and symbol for the unit’ (BIPM, 2006, p.134).
As a rule, the form (1) of the various RH definitions ensures that at saturation, ψ = 100 %rh, however, where a different form is used, such as for relative fugacity, saturation should occur at 100 %rh. This should be spelled out, since at least one relatively authoritative definition ψIUPAC is a ratio of two different humidity quantities: vapour partial pressure and pure-water saturation vapour pressure. This definition does apply over the extended range; however, within the standard range, where esat < p and hold, eq. (10) will always give ψIUPAC >100 %rh at saturation (e.g., see Fig. 4).
(7) Reference-equation uncertainty is incompletely specified
Currently, in meteorological articles and manuals, equations and data used for the evaluation of the RH are often not accompanied by reasonable uncertainty estimates. Similarly, approximations such as using ψe for ψx are sometimes given, but uncertainty associated with the approximation is not. While usual uncertainty propagation rules sum over all positive contributions, a procedure that ignores uncertainty covariance’s may produce estimated uncertainties that are much too large for the case of eq. (16). To account for this effect, covariance coefficients need to be included appropriately (Lovell-Smith, 2006, 2012; BIPM et al., 2008; Feistel, 2011b).
6. Suggested tasks
A number of problems and deficiencies in or associated with the definition of RH have been raised. The immediate task seems to be to provide a framework within which existing definitions fit (or are excluded) and from there to explore the thermodynamic basis and the potential usefulness of the different definitions, and hence also to provide means to calculate and compare the definitions.
(1) Framework
The framework is straightforward: the standard definition, where p ≥ esat and x < 1, and the pure-vapour definition, where p = esat and x = 1, are each a special case of the full-range definition. Saturation is attained isobarically and isocompositionally, respectively.
The full-range definition with its “hypothetical” saturation can be viewed as an approximation to a relative-fugacity definition in the same way that the ITS-90 temperature scale acts as a useful, consistent and SI-traceable approximation to the thermodynamic temperature.
The relative-fugacity definition can, at least initially, take on the same extended range and justification as the full-range RH definition, as the starting point to explore the underlying theoretical basis. The relative-fugacity definition will need some qualifier to distinguish it from the more general term of relative humidity. Steps will need to be taken to determine the status of water activity and (relative) activity within the framework.
The ratios r/rsat and q/qsat as RH definitions will be deprecated but will retain their other assigned names of the “degree of saturation” and the “relative specific humidity”, respectively.
(2) Thermodynamic basis
For a given sample of unsaturated humid air, what are the advantages of having a definition of relative humidity directly linked to the sample’s mass-based chemical potential and fugacity, as opposed to a definition directly linked to the sample’s vapour mole fraction or water vapour partial pressure? Given that it is straightforward to calculate one from the other, the advantages will probably lie in understanding and developing not only the thermodynamic basis of saturation but also the thermodynamic basis of non-saturated equilibrium such as might be found between humidity sensors and the adjacent humid air, or between industrial surfaces and conditioning gases. For example, it will be useful to derive the Kelvin equation for curved interfaces (and extensions for electric field, aqueous solutions, etc.) in terms of fugacity and relative fugacity without resorting to the ideal-gas limit.
Such investigation should also explore the nature of the equilibrium when the pressure is too low to support a bulk condensed phase, i.e., under conditions where the extended-range part of the relative-fugacity definition applies. To what extent does the clear thermodynamic basis of relative fugacity over the standard range support a single unified definition over the full range?
(3) Means to calculate
The relationship between the fugacity and partial pressure of water vapour in humid air was sketched in Section 3. TEOS-10 and the work of Feistel et al. (2015a) provide new means to calculate the fugacity and relative fugacity of water in humid air. Additional corrections for dissolved air in liquid water are required. Further work is needed to enable propagation of uncertainty from the large amount of data input to the Helmholtz and Gibbs energy equations forming the basis of TEOS-10 into those equations through to the many calculable quantities including the fugacity. Again, stand-alone virial equations for the fugacity (Feistel et al., 2015a) and for the enhancement factor (Herrmann et al., 2009) should also have associated uncertainty presented in a way that allows correct accounting for covariance’s.
On the basis of the framework, thermodynamic basis and the means to calculate we can identify further main tasks:
Investigate the need to account for departure from standard air composition including isotopic and chemical variation and chemical reactions associated with the gas and condensed phases.
Encourage official sanction of the framework and associated thermodynamic basis. Encourage the reporting of applied RH definition in calibration reports and in journal articles.
Identify non-standard definitions and publicise alternative names. Identify incorrect attribution to WMO or other sources. Provide documentation of terms and definitions on websites such as WMO (where it already exists) and IAPWS, AMS16, IUPAC, etc., and also Wikipedia.
Develop reference equations (such as for the virial expression for fugacity, the enhancement factor and vapour-pressure reference functions, and for larger systems such as TEOS-10) with uncertainty expressed in the form of fitted parameter covariance.
Develop a mise en pratique (BIPM, 2006) for RH to provide guidance for practitioners to realise RH according to its definition, as well as guidance for calculating the quantities and their associated uncertainties. The mise en pratique will be informed by the definition hierarchy, and will link to similar mises en pratique for other humidity quantities and also to TEOS-10 or some subset as outlined in Appendix D of the Digital Supplement to Part 1 of this series.
Develop an “axiomatic” approach to humidity. TEOS-10 has demonstrated the possibility and value of a rigorous axiomatic foundation of the description of seawater-ice-air thermodynamic properties. Using the same approach, development of a consistent axiomatic definition and nomenclature of humidity quantities as derived from a small set of empirical fundamental equations will help provide clarity and consistency within the wider humidity community. One such axiomatic approach to humidity, which uses an enhanced subset of TEOS-10, is outlined in Appendix D of the Digital Supplement to Part 1 of this series. The enhanced subset of TEOS-10-based functions will also include tailored standalone functions (such as for saturation vapour pressure, the enhancement factor and fugacity, Feistel et al., 2015a) where less computational complexity is desired, while maintaining consistency with TEOS-10 within a specified tolerance.
Develop standardised nomenclature and units. This activity would be integrated with (e). Note that the definition of a physical quantity is independent of the particular unit in which the measured values may be expressed.
Consider other humid gases besides standard air for which real-gas properties are available to derive corresponding fugacity equations.
Continue to dialogue with organisations representative of users of the alternative definitions of RH, to increase the level of harmonisation, where possible.
7. Conclusion
A thermodynamically founded definition of relative humidity could be formulated in terms of water-vapour fugacity. Other definitions currently in widespread use, such as the relative partial pressure, can be understood as practical proxies to the fugacity definition, consistent within the uncertainty of routine measurements in industry or meteorology. As a preferred SI-traceable surrogate measurand, dew-point temperature is adopted for its realisability and low measurement uncertainty. Calculation of relative fugacity from dew-point temperature, and conversion between alternative RH definitions, is possible using TEOS-10 equations, with an extension to dissolved air to be specified in the future. Consistently covering also the low-pressure range where saturated humid air does not stably exist seems possible, but will require future studies. Unambiguous nomenclature may be developed and recommended by the international committees governing the SI.
Acknowledgments
The authors express their gratitude to Prof. Michael Kühne, who as the Director of the BIPM organised the meetings with IAPWS representatives at the BIPM in August 2011 and February 2012 and inspired the writing of this review article. Valuable suggestions were provided by our colleagues Richard Davis, Don Gatley, Sebastian Herrmann, Joachim Pelkowski, Rod White and Christoph Zülicke. The authors also thank the journal editor and the anonymous referees for encouraging comments and constructive suggestions. Organisations financially supporting this work include the Scientific Committee on Oceanic Research (SCOR), with funding from national SCOR committees, and the International Association for the Properties of Water and Steam (IAPWS), with funding from IAPWS National Committees. Part of this work was funded by the New Zealand Government as part of a contract for the provision of national measurement standards. Partial contribution of the National Institute of Standards and Technology (NIST) is not subject to copyright in the US. The contribution of NPL was funded by the UK National Measurement System Programme for Engineering and Flow Metrology, and by the EMRP Joint Research Project ENV 58 MeteoMet2. The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union. This paper contributes to the tasks of the Joint SCOR/IAPWS/IAPSO Committee on the Properties of Seawater (JCS).
Footnotes
Although this section primarily concerns humid air and water vapour, much of the discussion can be generalised to apply to any humid gas or to different samples of humid air of varied composition.
WMO: World Meteorological Organization, http://www.wmo.int
OMI: Organisation Météorologique Internationale, IMO: International Meteorological Organisation (1873–1951), a forerunner of WMO (founded in 1950)
Donald P. Gatley, personal communication (2012)
Wikipedia: Meteorologisches Observatorium Hohenpeißenberg http://de.wikipedia.org/wiki/Meteorologisches_Observatorium_Hohenpei%C3%9Fenberg#Literatur, retrieved 18 Jan. 2015
ASHVE: American Society of Heating and Ventilation Engineers, a forerunner of ASHRAE
Although the 1953 definition included a note that relative humidity at temperatures less than 0 °C is to be evaluated with respect to liquid water, it now allows evaluation with respect to ice and requires appropriate identification to avoid ambiguity.
For example, ASHRAE: American Society of Heating, Refrigeration and Air-conditioning Engineers; AFNOR: Association Française de Normalisation; IMC: Institute of Measurement and Control; VDI/VDE: Verein Deutscher Ingenieure/Verband der Elektrotechnik, Elektronik und Informationstechnik; BSI: British Standards Institute; ASTM: American Society for Testing and Materials
Vaisala Humidity Calculator, http://www.vaisala.com/en/services/technicalsupport/downloads/HumidityCalculator/Pages/default.aspx, retrieved 17 April 2015
Certain commercial products are identified in this paper, but only in order to foster understanding. Such identification neither constitutes nor implies recommendation or endorsement by any of the organisations represented by the authors..
For example, the on-line “Glossary of Meteorology” of the American Meteorological Society (AMS) incorrectly states that relative humidity “is alternatively defined by the World Meteorological Organization as the ratio of the mixing ratio to the saturation mixing ratio.” (http://glossary.ametsoc.org/wiki/Relative_humidity, retrieved 17 April 2015
Occasionally gravimetric hygrometers are used as additional confirmation of generator performance; however, it is rare for this to be the main route of traceability to the SI.
This uncertainty is equal to the width of the interval in which the true value lies with a probability level of 95 %, corresponding to the 2σ level for a Gaussian distribution of the variable (WMO, 2008, Annex 1.B).
Water vapour significantly contributes to the total hydrogen budget of the stratosphere (Dessler et al., 1994; Hurst et al., 1999) and plays an important role in stratospheric chemistry such as in formation of polar stratospheric clouds, the ozone hole, and photochemically reactive radicals (Brasseur and Solomon, 2005; Farman et al., 1985; Solomon, 1988; Spivakovsky et al., 2000). It may also serve as a tracer to study atmospheric circulation and the hydrological budget (Brewer, 1949; Dobson, 1956; Johnston and Solomon, 1979; Newell and Gould-Stewart, 1981; Danielsen, 1982; Hintsa et al., 1994; Webster et al., 1994; Crook, 1996; Mote et al., 1996; Dethof et al., 1999; Romps and Kuang, 2010).
In order to be consistent with WMO (2008) and other authorities, for the quantity nv/na (see Section 1) we use the term mole ratio rather than mixing ratio, which is the term used by Teitelbaum et al. (2000).
AMS: American Meteorological Society, http://www.ametsoc.org/
List of symbols used in the article
| Symbol | Quantity | Remarks | |
|---|---|---|---|
| a | Vector of fitted parameters | (13) | |
| aW | Relative activity of water | ||
| b | Vector of fitted parameters | (13) | |
| esat | Water-vapour pressure at saturation | Pure water | |
| Fe, Ff | Saturation reference functions | (13) | |
| f | Water-vapour enhancement factor | ||
| fV | Fugacity of water in vapour phase | ||
|
|
Fugacity of water in vapour phase at saturation | ||
| fW | Fugacity of water in liquid phase | ||
| k | Uncertainty coverage factor | ||
| MA | Molar mass of dry air | MA = 0.028 965 46 kg mol−1 | |
| MA | Mass of dry-air molecules | ||
| MW | Molar mass of water | MW = 0.018 015 268 kg mol−1 | |
| MV | Mass of water-vapour molecules | ||
| p | Absolute pressure | ||
| psat | Pressure at saturation | ||
| pV | Water-vapour partial pressure | ||
|
|
Reference partial pressure of water vapour | ||
|
|
Saturation partial pressure of water vapour | ||
| q | Specific humidity | ||
| qsat | Specific humidity at saturation | ||
| R | Molar gas constant | R = 8.314 4621 J K−1 mol−1 | |
| RW | Specific gas constant of water | RW = R/MW | |
| r | Mixing ratio | ||
| rsat | Mixing ratio at saturation | ||
| s | Saturation condition | ||
| T | Absolute temperature, ITS-90 | ||
| Td | Dew-point temperature | ||
| x | Mole fraction of water vapour | ||
| xsat | Mole fraction at saturation | ||
| xW | Mole fraction of liquid water | ||
| z | Humidity quantity (with superscripts) | ||
| φV | Fugacity coefficient of water vapour | ||
| λ | Absolute activity | ||
| μ | Chemical potential (with super/subscripts) | ||
| π | Poynting correction factor of liquid water | ||
| ω | Ratio of molar masses of water and dry air | ||
| ψ | Relative humidity (with super/subscripts) | ||
| ψfull | Relative humidity in the extended range, esat > p |
References
- Abbot CG, Fowle FE., Jr . Annals of the Astrophysical Observatory. Vol. 2. Smithsonian Institution; Washington DC: 1908. Income and Outgo of Heat from the Earth, and the Dependence of Its Temperature Thereon; pp. 159–176. [Google Scholar]
- Albrecht F. Untersuchungen über den Wärmehaushalt der Erdoberfläche in verschiedenen Klimagebieten. Julius Springer; Berlin: 1940. [Google Scholar]
- Allen MR, Ingram WJ. Constraints on future changes in climate and the hydrologic cycle. Nature. 2002;419:224–232. doi: 10.1038/nature01092. [DOI] [PubMed] [Google Scholar]
- Antikainen V, Paukkunen A, Jauhiainen H. Measurement Accuracy and Repeatability of Vaisala RS90 Radiosonde. Vaisala News. 2002;159:11–13. http://www.vaisala.com/Vaisala%20Documents/Vaisala%20News%20Articles/VN159/VN159_Measurement_Accuracy_and_Repeatability_of_Vaisala_RS90_Radiosonde.pdf. [Google Scholar]
- Arderon W. Philosophical Transactions. Vol. 44. The Royal Society; 1746. Extract of a Letter from Mr. William Arderon F. R. S. to Mr. Henry Baker, F. R. S. with the Description of an Improved Hygroscope; pp. 95–96. http://www.jstor.org/stable/104787. [Google Scholar]
- ASHRAE. Standard 41.6-1994 Method for Measurement of Moist Air Properties. American Society of Heating, Refrigerating and Air-Conditioning Engineers; 1994. [Google Scholar]
- ASTM. D1356-05: Standard Terminology Relating to Sampling and Analysis of Atmospheres. American Society for Testing and Materials, ASTM International; West Conshohocken, PA: 2006. 2003. www.astm.org. [DOI] [Google Scholar]
- ASTM. D1356-14: Standard Terminology Relating to Sampling and Analysis of Atmospheres. American Society for Testing and Materials, ASTM International; West Conshohocken, PA: 2014. 2003 www.astm.org. [DOI] [Google Scholar]
- Baumgartner A, Reichel E. The World Water Balance. R. Oldenbourg Verlag; München: 1975. [Google Scholar]
- BIPM. The International System of Units (SI) 8. Organisation Intergouvernementale de la Convention du Mètre, Bureau International des Poids et Mesures; Sevres: 2006. http://www.bipm.org/en/si/si_brochure/ [Google Scholar]
- BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, OIML. Evaluation of Measurement Data - Supplement 1 to the ‘Guide to the Expression of Uncertainty in Measurement’ - Propagation of distributions using a Monte Carlo method. Joint Committee for Guides in Metrology, JCGM 101. 2008 http://www.bipm.org/utils/common/documents/jcgm/JCGM 101 2008 E.pdf.
- Bintanja R, Selten FM. Future increases in Arctic precipitation linked to local evaporation and sea-ice retreat. Nature. 2014;509:479–482. doi: 10.1038/nature13259. [DOI] [PubMed] [Google Scholar]
- Björklund S, Wadsö L. A calorimetric method to determine water activity. Review of Scientific Instruments. 2011;82:114903. doi: 10.1063/1.3660815. http://dx.doi.org/10.1063/1.3660815. [DOI] [PubMed] [Google Scholar]
- Blandamer MJ, Engberts JBFN, Gleeson PT, Reis JCR. Activity of water in aqueous systems; a frequently neglected property. Chemical Society Reviews. 2005;34:440–458. doi: 10.1039/b400473f. [DOI] [PubMed] [Google Scholar]
- Böse N, Mitter H. Calculation and Measurement of Humidity at Temperatures higher than 100 °C. Proceedings of TEMPMEKO; 2004; Cavtat-Dubrovnik, Croatia. 2004. pp. 689–693. [Google Scholar]
- Bony S, Stevens B, Frierson DMW, Jakob C, Kageyama M, Pincus R, Shepherd TG, Sherwood SC, Siebesma AP, Sobel AH, Watanabe M, Webb MJ. Clouds, circulation and climate sensitivity. Nature Geoscience. 2015;8:261–268. doi: 10.1038/ngeo2398. [DOI] [Google Scholar]
- Brasseur GP, Solomon S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere. Springer Dordrecht; The Netherlands: 2005. [Google Scholar]
- Brewer AW. Evidence for a world circulation provided by the measurements of helium and water vapour distribution in the stratosphere. Quarterly Journal of the Royal Meteorological Society. 1949;75:351–363. [Google Scholar]
- Brewster P, editor. The American Edition of the New Edinburgh Encyclopaedia. Joseph and Edward Parker; Philadelphia: 1832. Hygrometry. [Google Scholar]
- BS 1339-1. Humidity Terms, definitions and formulae. British Standards Institution; 2002. [Google Scholar]
- Chahine MT. The hydrological cycle and its influence on climate. Nature. 1992;359:373–380. doi: 10.1038/359373a0. [DOI] [Google Scholar]
- Chen X, Tung KK. Varying planetary heat sink led to global-warming slowdown and acceleration. Science. 2014;345:897–903. doi: 10.1126/science.1254937. [DOI] [PubMed] [Google Scholar]
- Choosri T, Koglbauer G, Wendland M. A new method for the measurement of the water activity or relative humidity by Fourier transform infrared spectroscopy. Journal of Chemical & Engineering Data. 2009;54:1179–1182. [Google Scholar]
- Clement A, DiNezio P. The Tropical Pacific Ocean—Back in the Driver’s Seat? Science. 2014;343:976–978. doi: 10.1126/science.1248115. [DOI] [PubMed] [Google Scholar]
- Coates AG, editor. A Natural and Cultural History. Yale University Press; New Haven and London: 1997. Central America. [Google Scholar]
- Coumou D, Lehmann J, Beckmann J. The weakening summer circulation in the Northern Hemisphere mid-latitudes. Sciencexpress. 2015 Mar 13; doi: 10.1126/science.1261768. [DOI] [PubMed] [Google Scholar]
- Cowtan K, Way RG. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Quarterly Journal of the Royal Meteorological Society. 2014 doi: 10.1002/qj.2297. [DOI] [Google Scholar]
- Crook NA. Sensitivity of moist convection forced by boundary layer processes to low-level thermodynamic fields. Monthly Weather Review. 1996;8:1767–1785. [Google Scholar]
- Curry J. Uncertain temperature trend. Nature Geoscience. 2014;7:83–84. [Google Scholar]
- Dai A. Recent Climatology, Variability, and Trends in Global Surface Humidity. Journal of Climate. 2006;19:3589–3605. [Google Scholar]
- Dai A, Karl TR, Sun B, Trenberth KE. Recent Trends in Cloudiness over the United States: A Tale of Monitoring Inadequacies. Bulletin of the American Meteorological Society. 2006;87:597–606. doi: 10.1175/BAMS-87-5-597. [DOI] [Google Scholar]
- Danielsen E. A dehydration mechanism for the stratosphere. Geophysical Research Letters. 1982;9:605–608. [Google Scholar]
- De Groot SR, Mazur P. Non-equilibrium thermodynamics. North Holland Publishing Company; Amsterdam: Dover Publications; New York: 1962. [Google Scholar]
- de Luc JA. On Evaporation. Philosophical Transactions of the Royal Society of London. 1792;82:400–424. doi: 10.1098/rstl.1792.0025. [DOI] [Google Scholar]
- Dessler AE. A Determination of the Cloud Feedback from Climate Variations over the Past Decade. Science. 2010;330:1523–1527. doi: 10.1126/science.1192546. [DOI] [PubMed] [Google Scholar]
- Dessler AE, Weinstock EM, Hintsa EJ, Anderson JG, Webster CR, May RD, Elkins JW, Dutton GS. An examination of the total hydrogen budget of the lower stratosphere. Geophysical Research Letters. 1994;21:2563–2566. [Google Scholar]
- Dessler AE, Zhang Z, Yang P. Water-vapor climate feedback inferred from climate fluctuations, 2003–2008. Geophysical Research Letters. 2008;35:L20704. doi: 10.1029/2008GL035333. [DOI] [Google Scholar]
- Dethof A, O’Neill A, Slingo JM, Smit HGJ. A mechanism for moistening the lower stratosphere involving the Asian summer monsoon. Quarterly Journal of the Royal Meteorological Society. 1999;125:1079–1106. [Google Scholar]
- Dobson GMB. Origin and distribution of polyatomic molecules in the atmosphere. Proceedings of the Royal Society London A. 1956;236:187–193. [Google Scholar]
- Durack PJ, Wijffels SE. Fifty-year trends in global ocean salinities and their relationship to broad-scale warming. Journal of Climate. 2010;23:4342–4362. [Google Scholar]
- Durack PJ, Wijffels SE, Matear RJ. Ocean Salinities Reveal Strong Global Water Cycle Intensification During 1950 to 2000. Science. 2012;336:455–458. doi: 10.1126/science.1212222. [DOI] [PubMed] [Google Scholar]
- Durack PJ, Wijffels SE, Boyer TP. Long-term Salinity Changes and Implications for the Global Water Cycle. In: Siedler G, Griffies SM, Gould J, Church JA, editors. Ocean Circulation and Climate. A 21st Century Perspective. Elsevier; Amsterdam: 2013. pp. 727–757. [Google Scholar]
- DWD. Geschichte des Observatoriums Hohenpeissenberg. 2012 Feb; http://www.dwd.de. 2012.
- Ellis W. Note on the mean relative humidity at the royal observatory, Greenwich. Quarterly Journal of the Royal Meteorological Society. 1878;4:194–198. [Google Scholar]
- Emden R. Über Strahlungsgleichgewicht und atmosphärische Strahlung. Ein Beitrag zur Theorie der oberen Inversion. Sitzungsberichte der mathematisch-physikalischen Klasse der Königlich Bayerischen Akademie der Wissenschaften zu München. Jahrgang. 1913;1913:55–142. [Google Scholar]
- Emery WJ, Talley LD, Pickard GL. Descriptive Physical Oceanography. Elsevier; Amsterdam: 2006. [Google Scholar]
- Erikson TA. Forced Vaporization of Water. In: Wexler A, Wildhack WA, editors. Humidity and Moisture, Vol. III, Fundamentals and Standards. Reinhold Publishing Corporation; New York: 1965. pp. 351–354. [Google Scholar]
- Everett C, Blasi DE, Roberts SA. Climate, vocal folds, and tonal languages: Connecting the physiological and geographic dots. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:1322–1327. doi: 10.1073/pnas.1417413112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falkenhagen H, Ebeling W, Hertz HG. Theorie der Elektrolyte. S. Hirzel Verlag; Leipzig: 1971. [Google Scholar]
- Farman JC, Gardiner BG, Shanklin JD. Large losses of total ozone in Antarctica reveal seasonal ClOx/NOx interaction. Nature. 1985;315:207–210. [Google Scholar]
- Fasullo JT, Trenberth KE. A Less Cloudy Future: The Role of Subtropical Subsidence in Climate Sensitivity. Science. 2012;338:792–794. doi: 10.1126/science.1227465. [DOI] [PubMed] [Google Scholar]
- Feistel R. Radiative Entropy Balance and Vertical Stability of a Gray Atmosphere. European Physical Journal B. 2011a;82:197–206. [Google Scholar]
- Feistel R. Stochastic ensembles of thermodynamic potentials. Accreditation and Quality Assurance. 2011b;16:225–235. [Google Scholar]
- Feistel R. TEOS-10: A New International Oceanographic Standard for Seawater, Ice, Fluid Water and Humid Air. International Journal of Thermophysics. 2012;33:1335–1351. [Google Scholar]
- Feistel R. Water, Steam and Climate. Proceedings of the 16th International Conference on the Properties of Water and Steam; Greenwich, UK. 1 – 5 September 2013; 2013. [DOI] [Google Scholar]
- Feistel R, Ebeling W. Physics of Self-Organization and Evolution. Wiley-VCH; Weinheim: 2011. [Google Scholar]
- Feistel R, Lovell-Smith J, Hellmuth O. Virial Approximation of the TEOS-10 Equation for the Fugacity of Water in Humid Air. International Journal of Thermophysics. 2015a;36:44–68. Erratum: 36, 204. [Google Scholar]
- Feistel R, Wielgosz R, Bell SA, Camões MF, Cooper JR, Dexter P, Dickson AG, Fisicaro P, Harvey AH, Heinonen M, Hellmuth O, Kretzschmar H-J, Lovell-Smith JW, McDougall TJ, Pawlowicz R, Ridout P, Seitz S, Spitzer P, Stoica D, Wolf H. Metrological challenges for measurements of key climatological observables: Oceanic salinity and pH, and atmospheric humidity. Part 1: Overview. Metrologia. 2015b doi: 10.1088/0026-1394/53/1/R1. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feistel R, Wright DG, Jackett DR, Miyagawa K, Reissmann JH, Wagner W, Overhoff U, Guder C, Feistel A, Marion GM. Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 1: Background and equations. Ocean Science. 2010b;6:633–677. http://www.oceansci.net/6/633/2010/ [Google Scholar]
- Feistel R, Wright DG, Kretzschmar HJ, Hagen E, Herrmann S, Span R. Thermodynamic Properties of Sea Air. Ocean Science. 2010a;6:91–141. http://www.oceansci.net/6/91/2010/ [Google Scholar]
- Forbes J, Mahlmann W. Abriss einer Geschichte der neueren Fortschritte und des gegenwärtigen Zustandes der Meteorologie. C.G. Lüderitz; Berlin: 1836. https://books.google.de/books?id=dSEzAQAAMAAJ&printsec=frontcover&hl=de#v=onepage&q&f=false. [Google Scholar]
- Gatley DP. Understanding Psychrometrics. 3. The American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc; Atlanta, Georgia, USA: 2013. [Google Scholar]
- Gavroglu K, Simões A. From Physical Chemistry to Quantum Chemistry: How Chemists Dealt with Mathematics. HYLE--International Journal for Philosophy of Chemistry. 2012;18:45–69. http://www.hyle.org/journal/issues/18-1/gavroglu-simoes.htm. [Google Scholar]
- Gilbert LW. Einige Bemerkungen zu Dalton’s Untersuchungen über die Verdünstung. Annalen der Physik (Gilbert) 1803;15:144–168. [Google Scholar]
- Gill AE. Atmosphere Ocean Dynamics. Academic Press; San Diego: 1982. [Google Scholar]
- Gimeno L. Grand challenges in atmospheric science. Frontiers in Earth Science. 2013;1:1–5. doi: 10.3389/feart.2013.00001. [DOI] [Google Scholar]
- Glansdorff P, Prigogine I. Thermodynamic Theory of Structure, Stability and Fluctuations. Wiley-Interscience; New York: 1971. [Google Scholar]
- Goff JA. Final Report of the Working Subcommittee of the International Joint Committee on Psychrometric Data. ASME Trans. 1949;71:903–913. [Google Scholar]
- Goff JA. There Should Be Thermodynamic Consistency in the Construction and Use of Psychrometric Charts. ASHRAE Journal. 1960 May;:70–75. [Google Scholar]
- Goff JA, Gratch S. Thermodynamic Properties of Moist Air. The American Society of Heating and Ventilating Engineers Transactions. 1945;51:125–164. [Google Scholar]
- Greenspan L. Humidity fixed points of binary saturated aqueous solutions. Journal of Research of the National Bureau of Standards. 1977;81A:89–96. [Google Scholar]
- Greenwald TJ, Stephens GL. Atmospheric Science Paper No. 572. Department of Atmospheric Science, Colorado State University; Fort Collins, CO: 1995. Satellite Microwave Sensing of Oceanic Cloud Liquid Water: Application to the Earth Radiation Budget and Climate. [Google Scholar]
- Guyot A. Tables, meteorological and physical prepared for the Smithsonian Institution. 3. Smithsonian Institution; Washington: 1859. [Google Scholar]
- Hamer WJ, Wu YC. Osmotic Coefficients and Mean Activity Coefficients of Uni-univalent Electrolytes in Water at 25 °C. Journal of Physical and Chemical Reference Data. 1972;1:1047–1099. [Google Scholar]
- Hansen J, Sato M, Ruedy R, Lo K, Lea DW, Medina-Elizade M. Global temperature change. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:14288–14293. doi: 10.1073/pnas.0606291103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen JE, Takahashi T, editors. Geophysical Monograph Series. Vol. 29. American Geophysical Union; Washington D.C: 1984. Climate Processes and Climate Sensitivity; p. 368. [Google Scholar]
- Harrison LP. In: Humidity and Moisture, Volume 3 – Fundamentals and standards. Wexler A, editor. Reinhold; New York: 1965. pp. 3–256. [Google Scholar]
- Hasegawa S, Little JW. The NBS two-pressure humidity generator, mark 2. Journal of Research of the National Bureau of Standards–A Physics and Chemistry. 1977;81:81–88. [Google Scholar]
- Haug GH, Ganopolski A, Sigman DM, Rosell-Mele A, Swann GEA, Tiedemann R, Jaccard SL, Bollmann J, Maslin MA, Leng MJ, Eglinton G. North Pacific seasonality and the glaciation of North America 2.7 million years ago. Nature. 2005;433:821–825. doi: 10.1038/nature03332. [DOI] [PubMed] [Google Scholar]
- Haug GH, Tiedemann R. Effect of the formation of the Isthmus of Panama on Atlantic Ocean thermohaline circulation. Nature. 1998;393:673–676. [Google Scholar]
- Heinonen M. A comparison of humidity standards at seven European national standards laboratories. Metrologia. 2002;39:303–308. [Google Scholar]
- Held IM, Shell KM. Using Relative Humidity as a State Variable in Climate Feedback Analysis. Journal of Climate. 2012;25:2578–2582. http://dx.doi.org/10.1175/JCLI-D-11-00721.1. [Google Scholar]
- Herrmann S, Kretzschmar H-J, Gatley DP. Thermodynamic Properties of Real Moist Air, Dry Air, Steam, Water, and Ice. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc; Atlanta: 2009. ASHRAE RP-1485. [Google Scholar]
- Hintsa EJ, Weinstock EM, Anderson JG, May RD, Hurst DF. On the accuracy of in situ vapor measurements in the troposphere and lower stratosphere with the Harvard Lyman-α hygrometer. Journal of Geophysical Research. 1999;104(D7):8183–8189. [Google Scholar]
- Hintsa EJ, Weinstock EM, Dessler AE, Anderson JG, Loewenstein M, Podolske JR. SPADE H2O measurements and the seasonal cycle of stratospheric water vapor. Geophysical Research Letters. 1994;21:2559–2562. [Google Scholar]
- Hocke K, Martin L, Kämpfer N. Survey of Intercomparisons of Water Vapour Measurements. In: Kämpfer N, editor. Monitoring Atmospheric Water Vapour. Springer; New York Dordrecht Heidelberg London: 2013. pp. 243–288. [Google Scholar]
- Holland RG, Stöhr G. Eine Zeitreise durch die Jahrhunderte. Schirmerdruck; Rieslingen: 2011. Geschichte der Hygrometer. [Google Scholar]
- Hurst DF, Dutton GS, Romashkin PA, Wamsley PR, Moore FL, Elkins JW, Hintsa EJ, Weinstock EM, Herman RL, Moyer EJ, Scott DC, May RD, Webster CR. Closure of the total hydrogen budget of the northern extratropical lower stratosphere. Journal of Geophysical Research. 1999;104(D7):8191–8200. [Google Scholar]
- Hyland RW. A correlation for the second interaction (cross) virial coefficients and enhancement factors for moist air. J Res Natl Bur Stand A. 1975;79:551–560. doi: 10.6028/jres.079A.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IAPWS. Revised Supplementary Release on Saturation Properties of Ordinary Water Substance. The International Association for the Properties of Water and Steam, Revision 2012. 1992 http://www.iapws.org.
- IAPWS. Revised Release on the Pressure along the Melting and Sublimation Curves of Ordinary Water Substance. The International Association for the Properties of Water and Steam. 2011 http://www.iapws.org.
- IAPWS. Guideline on a Virial Equation for the Fugacity of H2O in Humid Air. The International Association for the Properties of Water and Steam. 2015 http://www.iapws.org, to be adopted.
- IJCPD. In: List RJ, editor. Smithsonian Meteorological Tables; Definition of relative humidity issued by The International Joint Committee on Psychrometric Data (IJCPD) at its May 5, 1950 meeting; Philadelphia. 1950. Sixth Revised Edition, First Reprint, 1958. [Google Scholar]
- IMC. A Guide to the Measurement of Humidity. The Institute of Measurement and Control; London: 1996. [Google Scholar]
- Ingersoll AP. The Runaway Greenhouse: A History of Water on Venus. Journal of the Atmospheric Sciences. 1969;26:1191–1198. [Google Scholar]
- Ingersoll AP. Planetary Climates. Princeton University Press; Princeton & Oxford: 2013. [Google Scholar]
- Ingram W. A very simple model for the water vapour feedback on climate change. Quarterly Journal of the Royal Meteorological Society. 2010;136:30–40. [Google Scholar]
- IOC, SCOR, IAPSO. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English) Paris: 2010. The international thermodynamic equation of seawater - 2010: Calculation and use of thermodynamic properties; p. 196. http://www.TEOS-10.org. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM, editors. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge, United Kingdom and New York, NY, USA: 2013. p. 1535. http://www.ipcc.ch/report/ar5/wg1/ [Google Scholar]
- McNaught AD, Wilkinson A, compilers. IUPAC. In: Compendium of Chemical Terminology. 2. Blackwell Scientific Publications; Oxford: 2006. the “Gold Book”. (1997). XML on-line corrected version: http://goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. [DOI] [Google Scholar]
- Jacobson MZ. Fundamentals of Atmospheric Modeling. 2. University Press; Cambridge: 2005. [Google Scholar]
- Jasechko S, Sharp ZD, Gibson JJ, Birks SJ, Yi Y, Fawcett PJ. Terrestrial water fluxes dominated by transpiration. Nature. 2013;496:347–350. doi: 10.1038/nature11983. [DOI] [PubMed] [Google Scholar]
- Johnston HS, Solomon S. Thunderstorms as possible micrometeorological sinks of stratospheric water. Journal of Geophysical Research. 1979;84:3155–3158. [Google Scholar]
- Josey SA, Gulev S, Yu L. Exchanges Through the Ocean Surface. In: Siedler G, Griffies SM, Gould J, Church JA, editors. Ocean Circulation and Climate. A 21st Century Perspective. Elsevier; Amsterdam: 2013. pp. 115–140. [Google Scholar]
- Josey SA, Kent EC, Taylor PK. New Insights into the Ocean Heat Budget Closure Problem from Analysis of the SOC Air–Sea Flux Climatology. Journal of Climate. 1999;12:2856–2880. [Google Scholar]
- Kämpfer N, editor. Ground-based Remote Sensing and In-situ Methods. Vol. 10. Springer; New York: 2013. Monitoring Atmospheric Water Vapour; p. 326. ISSI Scientific Report Series. [Google Scholar]
- Kara AB, Hurlburt HE, Loh WY. Which near-surface atmospheric variable drives air-sea temperature differences over the global ocean? Journal of Geophysical Research. 2007;112:C05020. [Google Scholar]
- Katsaros K. Encyclopedia of Ocean Sciences. Vol. 2. Elsevier Ltd; 2001. Evaporation and Humidity; pp. 870–877. [Google Scholar]
- Kintisch E. Climate Outsider Finds Missing Global Warming. Science. 2014;344:348. doi: 10.1126/science.344.6182.348. [DOI] [PubMed] [Google Scholar]
- Kleeman R, Power SB. A Simple Atmospheric Model of Surface Heat Flux for Use in Ocean Modeling Studies. Journal of Physical Oceanography. 1995;25:92–105. [Google Scholar]
- Kley D, Russell JM III, Phillips C, editors. SPARC assessment of upper tropospheric and stratospheric water vapour. Paris: 2000. p. 312. WCRP-No. 113, WMO/TD-No. 1043, SPARC Rep. No. 2. [Google Scholar]
- Kley D, Stone EJ, Henderson WR, Drummond JW, Harrop WJ, Schmeltekopf AL, Thompson TL, Winkler RH. In situ measurements of the mixing ratio of water vapor in the stratosphere. Journal of the Atmospheric Sciences. 1979;36:2513–2524. [Google Scholar]
- Komabayasi M. Discrete equilibrium temperatures of a hypothetical planet with the atmosphere and the hydrosphere of one component-two phase system under constant solar radiation. Journal of the Meteorological Society of Japan. 1967;45:137–138. [Google Scholar]
- Kosaka Y, Xie SP. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature. 2013;501:403–407. doi: 10.1038/nature12534. [DOI] [PubMed] [Google Scholar]
- Kraus EB. Atmosphere-Ocean Interaction. Clarendon Press; Oxford: 1972. [Google Scholar]
- Kraus EB, Businger JA. Atmosphere-Ocean Interaction. Oxford University Press; New York: Clarendon Press; Oxford: 1994. [Google Scholar]
- Kusuda T. Calculation of the Temperature of a Flat-plate Wet Surface under Adiabatic Conditions with Respect to the Lewis Relation. In: Ruskin RE, editor. Humidity and Moisture, Vol. I, Principles and Methods of Measuring Humidity in Gases. Reinhold Publishing Corporation; New York: 1965. pp. 16–32. [Google Scholar]
- Lacis AA, Schmidt GA, Rind D, Ruedy RA. Atmospheric CO2: Principal Control Knob Governing Earth’s Temperature. Science. 2010;330:356–359. doi: 10.1126/science.1190653. [DOI] [PubMed] [Google Scholar]
- Laliberté F, Zika J, Mudryk L, Kushner PJ, Kjellsson J, Döös K. Constrained work output of the moist atmospheric heat engine in a warming climate. Science. 2015;347:540–543. doi: 10.1126/science.1257103. [DOI] [PubMed] [Google Scholar]
- Lamquin N, Gierens K, Stubenrauch CJ, Chatterjee R. Evaluation of upper tropospheric humidity forecasts from ECMWF using AIRS and CALIPSO data. Atmospheric Chemistry and Physics. 2009;9:1779–1793. [Google Scholar]
- Landau LD, Lifschitz EM. Hydrodynamik. Akademie-Verlag; Berlin: 1974. [Google Scholar]
- Lea DW. Climate sensitivity in a warmer world. Nature. 2015;518:46–47. doi: 10.1038/518046b. [DOI] [PubMed] [Google Scholar]
- Leiterer U, Dier H, Nagel D, Naebert T. Correction method for RS80-A Humicap humidity profiles and their validation by lidar backscattering profiles in tropical cirrus clouds. Journal of Atmospheric and Oceanic Technology. 2005;22:18–29. [Google Scholar]
- Le Treut H, Somerville R, Cubasch U, Ding Y, Mauritzen C, Mokssit A, Peterson T, Prather M. Historical Overview of Climate Change. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL, editors. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge, United Kingdom and New York, NY, USA: 2007. http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-chapter1.pdf. [Google Scholar]
- Lewis GN. The Law of Physico-chemical Change. Proceedings of the American Academy of Arts and Sciences 37, 49–69; Das Gesetz physiko-chemischer Vorgänge. Zeitschrift für Physikalische Chemie (Leipzig) 1901a;38:205–226. http://www.biodiversitylibrary.org/bibliography/3934. [Google Scholar]
- Lewis GN. A New Conception of Thermal Pressure and a Theory of Solutions. Proceedings of the American Academy of Arts and Sciences. 1901b Oct;36(9):145–168. Stable http://www.jstor.org/stable/20020988. [Google Scholar]
- Lewis GN, Randall M. Thermodynamics and the Free Energy of Chemical Substances. MacGraw-Hill Book Company; New York: 1923. [Google Scholar]
- Lewis GN, Randall M. Thermodynamics. McGraw-Hill Book Company; New York, Toronto, London: 1961. [Google Scholar]
- Li J, Chylek P. Atmospheric Entropy. Part I: Climate Dissipation Structure. Journal of Climate. 2012;25:3173–3190. [Google Scholar]
- Li J, Sun C, Jin FF. NAO implicated as a predictor of Northern Hemisphere mean temperature multidecadal variability. Geophysical Research Letters. 2013;40:1–6. [Google Scholar]
- Li Y, Gu W, Chao J, Li L, Liu C, Xu Y, Chang Z, Wu L, Chen J. Atmospheric parameters affecting sea ice losses in the context of gravity desalination. Theoretical and Applied Climatology. 2014 Sep; doi: 10.1007/s00704-014-1264-2. 2014. [DOI] [Google Scholar]
- List RJ. Meteorologist. U.S. Weather Bureau, Smithsonian Institution; 1959. Smithsonian Meteorological Tables, Sixth Revised Edition, Publication 4014, Prepared by Robert J. List; pp. 348–349. [Google Scholar]
- Liu WT, Niiler PP. The Sensitivity of Latent Heat Flux to the Air Humidity Approximations Used in Ocean Circulation Models. Journal of Geophysical Research. 1990;95:9745–9753. [Google Scholar]
- Loncin M, Bimbenet JJ, Lenges J. Influence of the activity of water on the spoilage of foodstuffs. International Journal of Food Science & Technology. 1968;3:131–142. [Google Scholar]
- Lovell-Smith JW. On correlation in the water vapour pressure formulations. Metrologia. 2006;43:556–560. [Google Scholar]
- Lovell-Smith JW. The propagation of uncertainty for humidity calculations. Metrologia. 2009;46:607–615. [Google Scholar]
- Lovell-Smith JW. Modification of vapor-pressure reference functions to include parameter covariance. International Journal of Thermophysics. 2012;33:1390–1407. [Google Scholar]
- Lovell-Smith JW, Pearson H. On the concept of relative humidity. Metrologia. 2006;43:129–134. [Google Scholar]
- Macdonald AM, Baringer MO. Ocean Heat Transport. In: Siedler G, Griffies SM, Gould J, Church JA, editors. Ocean Circulation and Climate. A 21st Century Perspective. Elsevier; Amsterdam: 2013. pp. 759–785. [Google Scholar]
- Mackrodt P. A new attempt on a coulometric trace humidity generator. International Journal of Thermophysics. 2012;33:1520–1535. [Google Scholar]
- Marotzke J, Forster PM. Forcing, feedback and internal variability in global temperature trends. Nature. 2015;517:565–570. doi: 10.1038/nature14117. [DOI] [PubMed] [Google Scholar]
- Martínez-Botí MA, Foster GL, Chalk TB, Rohling EJ, Sexton PF, Lunt DJ, Pancost RD, Badger MPS, Schmidt DN. Plio-Pleistocene climate sensitivity evaluated using high-resolution CO2 records. Nature. 2015;518:49–54. doi: 10.1038/nature14145. [DOI] [PubMed] [Google Scholar]
- Mathlouthi M. Water content, water activity, water structure and the stability of foodstuffs. Food control. 2001;12:409–417. [Google Scholar]
- Maxwell JC. Van der Waals on the continuity of the gaseous and liquid states. Nature. 1874;10:477–480. http://www.nature.com/nature/journal/v10/n259/pdf/010477a0.pdf. [Google Scholar]
- McDonald JE. Intermolecular Attractions and Saturation Vapor Pressure. Journal of the Atmospheric Sciences. 1963;20:178–180. [Google Scholar]
- Meyer CW, Harvey AH. Dew-Point Measurements for Water in Compressed Carbon Dioxide. AIChE Journal. 2015 doi: 10.1002/aic.14818. in press. [DOI] [Google Scholar]
- Meyer CW, Miller WW, Ripple DC, Scace GE. Uncertainty Budget for the NIST Hybrid Humidity Generator. International Journal of Thermophysics. 2012;33:1488–1499. [Google Scholar]
- Miller JF. On the Relation of the Air and Evaporation Temperatures to the Temperature of the Dew-Point, as Determined by Mr. Glaisher’s Hygrometrical Tables, Founded on the Factors Deduced from the Six-Hourly Observations Made at the Royal Observatory, Greenwich. Philosophical Transactions of the Royal Society of London. 1851;141:141–148. http://www.jstor.org/stable/108392. [Google Scholar]
- Miloshevich LM, Vömel H, Paukkunen A, Heymsfield AJ, Oltmans SJ. Characterization and correction of relative humidity measurements from Vaisala RS80-A radiosondes at cold temperatures. Journal of Atmospheric and Oceanic Technology. 2001;18:135–156. [Google Scholar]
- Miloshevich LM, Vömel H, Whiteman DN, Lesht BM, Schmidlin FJ, Russo F. Absolute accuracy of water vapor measurements from six operational radiosonde types launched during AWEX-G and implications for AIRS validation. Journal of Geophysical Research. 2006;111:D09S10. doi: 10.1029/2005JD006083. [DOI] [Google Scholar]
- Mitchell JFB. The “Greenhouse” Effect and Climate Change. Reviews of Geophysics. 1989;27:115–139. [Google Scholar]
- Möller D. On the history of the scientific exploration of fog, dew, rain and other atmospheric water. Special Issue: Fog Research. DIE ERDE. 2008;139:11–44. [Google Scholar]
- Molyneux W. Philosophical Transactions. Vol. 15. The Royal Society; 1685. To One of the S. of the R. S. concerning a New Hygroscope, Invented by Him; pp. 1032–1035. http://www.jstor.org/stable/102152. [Google Scholar]
- Mote PW, Rosenlof KH, McIntyre ME, Carr ES, Gille JC, Holton JR, Kinnersley JS, Pumphrey HC, Russel JM, III, Waters JW. An atmospheric tape recorder: The imprint of tropical tropopause temperatures on stratospheric water vapour. Journal of Geophysical Research. 1996;101:3989–4006. [Google Scholar]
- Mulligan JF, Hertz HG. An unpublished lecture by Heinrich Hertz: “On the energy balance of the Earth”. American Journal of Physics. 1997;65:36–45. [Google Scholar]
- Nagel D, Leiterer U, Dier H, Kats A, Reichardt J, Behrendt A. High accuracy humidity measurements using the standardized frequency method with a research upper-air sounding system. Meteorologische Zeitschrift. 2001;10:395–405. [Google Scholar]
- Newell RE, Gould-Stewart S. A stratospheric fountain? Journal of the Atmospheric Sciences. 1981;38:2789–2796. [Google Scholar]
- NF X 15-110. Measurement of air moisture. Hydrometric parameters. - Mesure de l’humidité de l’air – Parametres hygrométriques. 1994 Jul; http://www.boutique.afnor.org/standard/nf-x15-110/measurement-of-air-moisture-hydrometric-parameters/article/771320/fa037684.
- OMI. Definitions and Specifications of Water Vapour in the Atmosphere. Organisation Météorologique Internationale; Lausanne: 1951. Values of some Physical Functions and Constants Used in Meteorology. Publication 79. [Google Scholar]
- Ort DR, Long SP. Limits on Yields in the Corn Belt. Science. 2014;344:484–485. doi: 10.1126/science.1253884. [DOI] [PubMed] [Google Scholar]
- Ovarlez J, Gayet JF, Gierens K, Ström J, Ovarlez H, Auriol F, Busen R, Schumann U. Water vapour measurements inside cirrus clouds on Northern and Southern hemispheres during INCA. Geophysical Research Letters. 2002;29(16):601–60-4. [Google Scholar]
- Paltridge G, Arking A, Pook M. Trends in middle- and upper-level tropospheric humidity from NCEP reanalysis data. Theoretical and Applied Climatology. 2009;98:351–359. [Google Scholar]
- Peixoto JP, Oort AH. Physics of Climate. American Institute of Physics; New York: 1992. [Google Scholar]
- Peixoto JP, Oort AH. The Climatology of Relative Humidity in the Atmosphere. Journal of Climate. 1996;9:3443–3463. [Google Scholar]
- Peter T, Marcolli C, Spichtinger P, Corti T, Baker MB, Koop T. When dry air is too humid. Science. 2006;314:1399–1402. doi: 10.1126/science.1135199. [DOI] [PubMed] [Google Scholar]
- Pierce DW, Barnett TP, Gleckler PJ. Ocean Circulations, Heat Budgets, and Future Commitment to Climate Change. Annual Review of Environment and Resources. 2011;36:27–43. doi: 10.1146/annurev-environ-022610-112928. [DOI] [Google Scholar]
- Pierce DW, Gleckler PJ, Barnett TP, Santer BD, Durack PJ. The fingerprint of human-induced changes in the ocean’s salinity and temperature fields. Geophysical Research Letters. 2012;39:L21704. doi: 10.1029/2012GL053389. [DOI] [Google Scholar]
- Pierrehumbert RT. Some remarks on mechanisms for the regulation of tropical sea surface temperature. In: Cutzen PJ, editor. Clouds, Chemistry and Climate. Vol. 35. Springer; Berlin: 1996. pp. 153–172. NATO ASI Ser., Ser. I. http://geosci.uchicago.edu/~rtp1/papers/NATO_SST/NATO_SST.pdf. [Google Scholar]
- Pierrehumbert RT. Principles of Planetary Climate. Cambridge University Press; Cambridge: 2010. [Google Scholar]
- Poan DE, Roehrig R, Couvreux F, Lafore JP. West African Monsoon Intraseasonal Variability: A Precipitable Water Perspective. Journal of the Atmospheric Sciences. 2013;70:1035–1052. [Google Scholar]
- Poynting JH. Change of state: solid-liquid. Philosophical Magazine. 1881;12:32. http://www.archive.org/download/londonedinburg5121881lond/londonedinburg5121881lond.pdf. [Google Scholar]
- Prescott JA, Collins JA. The lag of temperature behind solar radiation. Quarterly Journal of the Royal Meteorological Society. 1951;77:121–126. [Google Scholar]
- Pruppacher HR, Klett JD. Second Revised and Enlarged Edition with an Introduction to Cloud Chemistry and Cloud Electricity. Kluwer Academic Publishers; Dordrecht/Boston/London: 1997. Microphysics of Clouds and Precipitation. [Google Scholar]
- Quaas J. Evaluating the “critical relative humidity” as a measure of subgrid-scale variability of humidity in general circulation model cloud cover parameterizations using satellite data. Journal of Geophysical Research. 2012;117:D09208. doi: 10.1029/2012JD017495. [DOI] [Google Scholar]
- Randal DL, Vonder Haar TH, Ringerud MA, Stephens GL, Greenwald TL, Combs CL. A new global water vapor dataset. Bulletin of the American Meteorological Society. 1996;77:1233–1246. [Google Scholar]
- Randal D. Atmosphere, Clouds, and Climate. Princeton University Press; Princeton: 2012. [Google Scholar]
- Rantala MJ. Evolution of nakedness in Homo sapiens. Journal of Zoology. 2007;273:1–7. doi: 10.1111/j.1469-7998.2007.00295.x. [DOI] [Google Scholar]
- Regnault V. Hygrometrical Researches. In: Taylor R, editor. Scientific Memoirs selected from the transactions of foreign academies of science and learned academies and from foreign journals. V4. London: 1845. pp. 606–660. 1846. [Google Scholar]
- Reid PC, Valdés L. ICES Cooperative Research Report. Vol. 310. ICES; Copenhagen: 2011. ICES status report on climate change in the North Atlantic. [Google Scholar]
- Retallack BJ. Compendium of Meteorology; For Use by Class I and II Meteorological Personnel. 1973. Physical Meteorology Training Manual Series WMO N°364 Vol. I-Part 2. [Google Scholar]
- Robinson RA, Sinclair DA. The activity coefficients of the alkali chlorides and of lithium iodide in aqueous solution from vapor pressure measurements. Journal of the American Chemical Society. 1934;56:1830–1835. [Google Scholar]
- Rogers RR, Yau MK. Short Course in Cloud Physics. 3. Butterworth-Heinemann; Oxford: 1989. [Google Scholar]
- Romps DM, Kuang Z. Do undiluted convective plumes exist in the upper tropical troposphere? Journal of the Atmospheric Sciences. 2010;67:468–484. [Google Scholar]
- Rosenlof KH, Oltmans SJ, Kley D, Russell JM, III, Chiou EW, Chu WP, Johnson DG, Kelly KK, Michelsen HA, Nedoluha GE, Remsberg EE, Toon GC, McCormick MP. Stratospheric water vapor increases over the past half-century. Geophysical Research Letters. 2001;28:1195–1198. [Google Scholar]
- Santer BD, Mears C, Wentz FJ, Taylor KE, Gleckler PJ, Wigley TML, Barnett TP, Boyle JS, Brüggemann W, Gillett NP, Klein SA, Meehl GA, Nozawa T, Pierce DW, Stott PA, Washington WM, Wehner MF. Identification of human-induced changes in atmospheric moisture content. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:15248–15253. doi: 10.1073/pnas.0702872104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders PM. The Temperature at the Ocean-Air Interface. Journal of the Atmospheric Sciences. 1967;24:269–273. [Google Scholar]
- Schiermeier Q. Climatologists to physicists: your planet needs you. Nature. 2015;520:140–141. doi: 10.1038/520140a. [DOI] [PubMed] [Google Scholar]
- Schiraldi A, Fessas D, Signorelli M. Water Activity in Biological Systems - A Review. Polish journal of food and nutrition sciences. 2012;62:5–13. [Google Scholar]
- Schluessel P, Emery WJ, Grassl H, Mammen T. On the Bulk-Skin Temperature Difference and Its Impact on Satellite Remote Sensing of Sea Surface Temperature. Journal of Geophysical Research. 1990;95(C8):13341–13356. [Google Scholar]
- Schmidt GA, Ruedy RA, Miller RL, Lacis AA. The attribution of the present-day total greenhouse effect. Journal of Geophysical Research. 2010;115:D20106. doi: 10.1029/2010JD014287. [DOI] [Google Scholar]
- Schmidt H, Alterskjær K, Bou Karam D, Boucher O, Jones A, Kristjánsson JE, Niemeier U, Schulz M, Aaheim A, Benduhn F, Lawrence M, Timmreck C. Solar irradiance reduction to counteract radiative forcing from a quadrupling of CO2: climate responses simulated by four earth system models. Earth System Dynamics. 2012;3:63–78. www.earth-syst-dynam.net/3/63/2012/ [Google Scholar]
- Schneider T, O’Gorman PA, Levine XJ. Water vapor and the dynamics of climate changes. Reviews of Geophysics. 2010;48:RG3001. doi: 10.1029/2009RG000302. [DOI] [Google Scholar]
- Schwartz SE. Heat capacity, time constant, and sensitivity of Earth’s climate system. Journal of Geophysical Research. 2007;112:D24S05. doi: 10.1029/2007JD008746. [DOI] [Google Scholar]
- Scott WJ. The effect of residual water on the survival of dried bacteria during storage. Journal of general microbiology. 1958;19:624–633. doi: 10.1099/00221287-19-3-624. [DOI] [PubMed] [Google Scholar]
- Seidel DJ. Encyclopedia of Global Environmental Change. Wiley; 2002. Water Vapor: Distribution and Trends. http://eu.wiley.com/legacy/wileychi/egec/pdf/GB085-W.PDF. [Google Scholar]
- Shaw N. Philosophical transactions, Series A: Mathematical and Physical Sciences. Vol. 179. London: 1889. Report on Hygrometric Methods, First part, Including the Saturation Method, and Chemical Method and Dew point instruments; pp. 73–149. [Google Scholar]
- Sherwood SC, Ingram W, Tsushima Y, Satoh M, Roberts M, Vidale PL, O’Gorman PA. Relative humidity changes in a warmer climate. Journal of Geophysical Research. 2010;115:D09104. doi: 10.1029/2009JD012585. [DOI] [Google Scholar]
- Smagorinsky J. On the Dynamical Prediction of Large-Scale Condensation by Numerical Methods. Geophysical Monograph. 1960;5:71–78. [Google Scholar]
- Soares PC. Warming Power of CO2 and H2O: Correlations with Temperature Changes. International Journal of Geosciences. 2010;1:102–112. [Google Scholar]
- Solomon S. The mystery of the Antarctic ozone hole. Reviews of Geophysics. 1988;26:131–148. [Google Scholar]
- Sonntag D. Hygrometrie. Akademie-Verlag; Berlin: 1966. [Google Scholar]
- Spivakovsky CM, Logan JA, Montzka SA, Balkanski YJ, Foreman-Fowler M, Jones DBA, Horowitz LW, Fusco AC, Brenninkmeijer CAM, Prather MJ, Wofsy SC, McElroy MB. Three-dimensional climatological distribution of tropospheric OH: update and evaluation. Journal of Geophysical Research. 2000;105:8931–8980. [Google Scholar]
- Sprung A. Über die Bestimmung der Luftfeuchtigkeit mit Hilfe des Assmannschen Aspirationspsychrometers. Das Wetter. 1888;5:105–108. [Google Scholar]
- Steinman BA, Mann ME, Miller SK. Atlantic and Pacific multidecadal oscillations and Northern Hemisphere temperatures. Science. 2015;347:988–990. doi: 10.1126/science.1257856. [DOI] [PubMed] [Google Scholar]
- Stephens GL, Li J, Wild M, Clayson CA, Loeb N, Kato S, L’Ecuyer T, Stackhouse PW, Lebsock M, Andrews T. An update on Earth’s energy balance in light of the latest global observations. Nature Geoscience. 2012;5:691–696. doi: 10.1038/NGEO1580. [DOI] [Google Scholar]
- Stevens B, Bony S. What Are Climate Models Missing? Science. 2013;340:1053–1054. doi: 10.1126/science.1237554. [DOI] [PubMed] [Google Scholar]
- Stevens M, Bell SA. The NPL standard humidity generator: an analysis of uncertainty by validation of individual component performance. Measurement Science and Technology. 1992;3:943–952. [Google Scholar]
- Sundqvist H. A parameterization scheme for non-convective condensation including prediction of cloud water content. Quarterly Journal of the Royal Meteorological Society. 1978;104:677– 690. doi: 10.1002/qj.49710444110. [DOI] [Google Scholar]
- Sugiyama M, Stone PH, Emanuel KA. The Role of Relative Humidity in Radiative–Convective Equilibrium. Journal of the Atmospheric Sciences. 2005;62:2001–2011. [Google Scholar]
- Teitelbaum H, Moustaoui M, Basdevant C, Holton JR. An alternative mechanism explaining the hygropause formation in tropical regions. Geophysical Research Letters. 2000;27:221–224. [Google Scholar]
- Tollefsen J. A break in the clouds. Nature. 2012;485:164–166. doi: 10.1038/485164a. [DOI] [PubMed] [Google Scholar]
- Tollefsen J. Climate change: The case of the missing heat. Nature. 2014;505:276–278. doi: 10.1038/505276a. [DOI] [PubMed] [Google Scholar]
- Tompkins AM, Gierens K, Rädel G. Ice supersaturation in the ECMWF integrated forecast system. Quarterly Journal of the Royal Meteorological Society. 2007;133:53–63. [Google Scholar]
- Trenberth KE, Fasullo JT, Kiehl J. Earth’s global energy budget. Bulletin of the American Meteorological Society. 2009;90:311–323. [Google Scholar]
- Trenberth KE, Jones PD, Ambenje P, Bojariu R, Easterling D, Klein Tank A, Parker D, Rahimzadeh F, Renwick JA, Rusticucci M, Soden B, Zhai P. Observations: Surface and Atmospheric Climate Change. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL, editors. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge, United Kingdom and New York, NY, USA: 2007. http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-chapter3-supp-material.pdf. [Google Scholar]
- Van der Waals JD. PhD thesis. Leiden University; The Netherlands: 1873. Over de Continuiteit van den Gas- en Vloeistoftoestand. [Google Scholar]
- van Hooidonk R, Huber M. Equivocal evidence for a thermostat and unusually low levels of coral bleaching in the Western Pacific Warm Pool. Geophysical Research Letters. 2009;36:L06705. doi: 10.1029/2008GL036288. [DOI] [Google Scholar]
- VDI/VDE 3514. VDI VDE-Gesellschaft Mess- und Automatisierungstechnik (GMA) Fachausschuss Gasfeuchtemessung; 2007. Measurement of humidity - Characteristics and symbols. [Google Scholar]
- VIM. International vocabulary of metrology – Basic and general concepts and associated terms (VIM), 3rd edition. JCGM. 2012;200:2012. http://www.bipm.org/en/publications/guides/vim.html. [Google Scholar]
- Wang X, Piao S, Ciais P, Friedlingstein P, Myneni RB, Cox P, Heimann M, Miller J, Peng S, Wang T, Yang H, Chen A. A two-fold increase of carbon cycle sensitivity to tropical temperature variations. Nature. 2014;506:212–215. doi: 10.1038/nature12915. [DOI] [PubMed] [Google Scholar]
- Wagner W, Pruss A. International equations for the saturation properties of ordinary water substance – Revised according to the International Temperature Scale of 1990. Addendum to J. Phys. Chem. Ref. Data 16, 893 (1987) Journal of Physical and Chemical Reference Data. 1993;22:783–787. [Google Scholar]
- Wagner W, Riethmann T, Feistel R, Harvey AH. New Equations for the Sublimation Pressure and Melting Pressure of H2O Ice Ih. Journal of Physical and Chemical Reference Data. 2011;40:043103. doi: 10.1063/1.3657937. [DOI] [Google Scholar]
- Warren SG, Eastman RM, Hahn CJ. A Survey of Changes in Cloud Cover and Cloud Types over Land from Surface Observations, 1971–96. Journal of Climate. 2007;20:717–738. [Google Scholar]
- Webster CR, May RD, Trimble CA, Chave RG, Kendall J. Aircraft (ER-2) Laser Infrared Absorption Spectrometer (ALIAS) for in situ stratospheric measurements of HCl, N2O, CH4, NO2 and HNO3. Applied Optics. 1994;33:454–472. doi: 10.1364/AO.33.000454. [DOI] [PubMed] [Google Scholar]
- Wells NC. The Atmosphere and Ocean. Wiley-Blackwell; Oxford: 2012. [Google Scholar]
- Wexler A, Hyland RW. Thermodynamic properties of dry air, moist air and water and SI psychrometric charts. In: Wexler A, Hyland RW, Stewart R, editors. ASHRAE (Project 216-RP) 1983. pp. 150–303. [Google Scholar]
- Wielicki BA, Wong T, Loeb N, Minnis P, Priestley K, Kandel R. Changes in Earth’s Albedo Measured by Satellite. Science. 2005;308:825. doi: 10.1126/science.1106484. [DOI] [PubMed] [Google Scholar]
- Willett KM, Williams CN, Jr, Dunn RJH, Thorne PW, Bell S, de Podesta M, Jones PD, Parker DE. HadISDH: an updateable land surface specific humidity product for climate monitoring, Clim. Past. 2013;9:657–677. doi: 10.5194/cp-9-657-2013. [DOI] [Google Scholar]
- Wisniak J. Historical development of the vapor pressure equation from Dalton to Antoine. Journal of Phase Equilibria. 2001;22:622–630. [Google Scholar]
- Letestu S, editor. WMO. International Meteorological Tables. 1966. WMO-No. 188.TP.94. [Google Scholar]
- WMO. Guide to meteorological instruments and methods of observation. 7. World Meteorological Organisation; Geneva: 2008. http://www.wmo.int/pages/prog/gcos/documents/gruanmanuals/CIMO/CIMO_Guide-7th_Edition-2008.pdf. [Google Scholar]
- Worley SJ, Woodruff SD, Reynolds RW, Lubker SJ, Lott N. ICOADS Release 2.1 Data and Products. International Journal of Climatology. 2005;25:823–842. [Google Scholar]
- Worrall RW. Psychrometric determination of relative humidities in air with dry-bulb temperatures exceeding 212°F. In: Ruskin RE, editor. Humidity and Moisture, Volume 1 – Principles and methods of measuring humidity in gases. Reinhold; New York: 1965. pp. 105–109. [Google Scholar]
- Wright DG, Feistel R, Reissmann JH, Miyagawa K, Jackett DR, Wagner W, Overhoff U, Guder C, Feistel A, Marion GM. Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 2: The library routines. Ocean Science. 2010;6:695–718. http://www.ocean-sci.net/6/695/2010/ [Google Scholar]
- Wright PW. An Atlas Based on the ‘COADS’ Data Set: Fields of Mean Wind, Cloudiness and Humidity at the Surface of the Global Ocean. Max-Planck-Institute for Meteorology; Hamburg: 1988. Report No. 14. [Google Scholar]
- Yu F, Luo G. Effect of solar variations on particle formation and cloud condensation nuclei. Environmental Research Letters. 2014;9:045004. doi: 10.1088/1748-9326/9/4/045004. [DOI] [Google Scholar]