DIFFUSED SOLUTE-SOLVENT INTERFACE WITH POISSON–BOLTZMANN ELECTROSTATICS: FREE-ENERGY VARIATION AND SHARP-INTERFACE LIMIT

Abstract

A phase-field free-energy functional for the solvation of charged molecules (e.g., proteins) in aqueous solvent (i.e., water or salted water) is constructed. The functional consists of the solute volumetric and solute-solvent interfacial energies, the solute-solvent van der Waals interaction energy, and the continuum electrostatic free energy described by the Poisson–Boltzmann theory. All these are expressed in terms of phase fields that, for low free-energy conformations, are close to one value in the solute phase and another in the solvent phase. A key property of the model is that the phase-field interpolation of dielectric coefficient has the vanishing derivative at both solute and solvent phases. The first variation of such an effective free-energy functional is derived. Matched asymptotic analysis is carried out for the resulting relaxation dynamics of the diffused solute-solvent interface. It is shown that the sharp-interface limit is exactly the variational implicit-solvent model that has successfully captured capillary evaporation in hydrophobic confinement and corresponding multiple equilibrium states of underlying biomolecular systems as found in experiment and molecular dynamics simulations. Our phase-field approach and analysis can be used to possibly couple the description of interfacial fluctuations for efficient numerical computations of biomolecular interactions.

1. Introduction

The solvation of charged molecules such as DNAs and proteins in aqueous solvent (i.e., water or salted water) is a fundamental biological process. Implicit-solvent models provide efficient predictions of the solvation free energies and equilibrium conformations of underlying molecular systems [35]. In such a model, the solvent molecules and ions are treated implicitly and their effects are coarse-grained. In a large class of implicit-solvent models, the solute-solvent interface that separates the solvent region from solutes is used to calculate the surface energy and electrostatic energy. The later is often done by solving Poisson’s or the Poisson–Boltzmann equation with the dielectric coefficient close to 1 and 80 in the solute and solvent regions, respectively [7,16,27,38]. In a variational implicit-solvent model (VISM) [19,20,44], one determines the solvation free energies and stable equilibrium conformations by minimizing a macroscopic free-energy functional of all possible solute-solvent interfaces, i.e., dielectric boundaries.

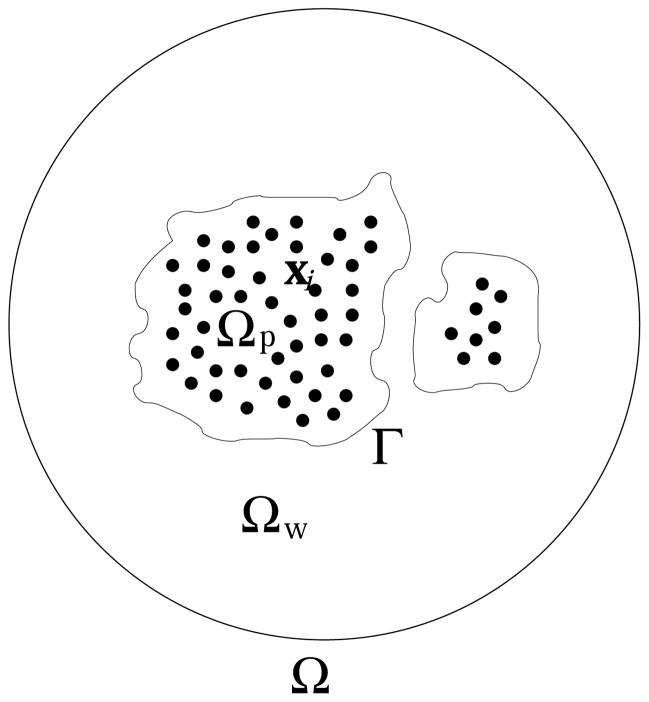
Let us denote by Ω ⊂ ℝ³ the region of an underlying solvation system; cf. Figure 1.1. Assume that there are total N solute atoms located at x₁, …, x_N inside Ω and carrying partial charges Q₁, …, Q_N, respectively. Assume also that there are M ionic species in the solvent, and denote by $c_j^{\infty }$ and q_j = z_je the bulk concentration and charge for the jth ionic species, respectively, where z_j is the valence and e elementary charge. Let Γ be a closed and smooth surface, a possible solute-solvent interface, that encloses all x₁, …, x_N and that divides Ω into two regions: the solute region Ω_p (p stands for protein) and the solvent region Ω_w (w stands for water). The VISM solvation free-energy functional is then defined for all such solute-solvent interface Γ by

Fig. 1.1.

A schematic view of a solvation system with an implicit solvent. A solute-solvent interface Γ separates the solute region Ω_P (p stands for protein) from the solvent region Ω_W (w stands for water). Dots represent solute atoms located at x_i carrying partial charges Q_i(i = 1, …, N).

$$F[\mathrm{\Gamma }]=P\text{Vol}({\mathrm{\Omega }}_{\mathrm{p}})+{\gamma }_0\text{Area}(\mathrm{\Gamma })+{\rho }_{\mathrm{w}}{\int }_{{\mathrm{\Omega }}_{\mathrm{w}}}U(x)dx+{\int }_{\mathrm{\Omega }}\left[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}{\mid \nabla \psi \mid }^2+{\rho }_{\mathrm{f}}\psi -{\chi }_{\mathrm{w}}V(\psi )\right]dx.$$ (1.1)

The first term here is the energy of creating a solute cavity in the solvent against the pressure difference P between the solvent liquid and solute vapor. The second term is the surface energy with γ₀ being the constant surface tension. For simplicity, we neglect the Tolman correction to the surface tension [40]. The third term is the energy of the van der Waals (vdW) type interaction between the solute atoms x_i (1 ≤ i ≤ N) and continuum solvent, where ρ_w is the constant bulk solvent density. The interaction potential U is often defined by

$$U(x)=\sum _{i=1}^N{U}_{\text{LJ}}^{(i)}(\mid x-x_i\mid ),$$

where each

$$U_{\text{LJ}}^{(i)}(r)=4{\epsilon }_i\left[{\left(\frac{{\sigma }_i}{r}\right)}^{12}-{\left(\frac{{\sigma }_i}{r}\right)}^6\right]$$

is a Lennard-Jones potential, and all the parameters ε_i of energy and σ_i of length are given.

The last term is the electrostatic free energy, where ψ is the electrostatic potential, ε_Γ is the coefficient of permittivity, ρ_f is a fixed charge density approximating the solute point charges ${\sum }_{i=1}^N{Q}_i{\delta }_{x_i}$ with δ_xi being the Dirac delta function at x_i, χ_w is the characteristic function of the solvent region Ω_w, and V(ψ) describes the ionic contribution to the electrostatic interaction. Here, ions are assumed to be in an equilibrium macroscopically; and the equilibrium ionic concentrations are given by the Boltzmann distributions through the electrostatic potential ψ [7, 27]. The potential ψ is the solution to a boundary-value problem of the dielectric-boundary Poisson–Boltzmann equation

$$\nabla ·{\epsilon }_{\mathrm{\Gamma }}\nabla \psi -{\chi }_{\mathrm{w}}{V}^{\prime }(\psi )=-{\rho }_{\mathrm{f}}\text{in}\mathrm{\Omega },$$ (1.2)

$$\psi ={\psi }_{\infty }\text{on}\partial \mathrm{\Omega },$$ (1.3)

where ψ_∞ is a given function on the boundary ∂Ω. The coefficient ε_Γ is defined by

$${\epsilon }_{\mathrm{\Gamma }}(x)=\{\begin{array}{ll}{\epsilon }_{\mathrm{p}}{\epsilon }_0\hfill & \text{if}x\in {\mathrm{\Omega }}_{\mathrm{p}},\hfill \\ {\epsilon }_{\mathrm{w}}{\epsilon }_0\hfill & \text{if}x\in {\mathrm{\Omega }}_{\mathrm{w}},\hfill \end{array}$$ (1.4)

where ε_p and ε_w are the dielectric coefficients (relative permitivities) of the solute and solvent regions, respectively, and ε₀ is the vacuum permittivity. In general, ε_p ≈ 1 and ε_w ≈ 80. In the classical Poisson–Boltzmann theory,

$$V(\psi )={\beta }^{-1}\sum _{j=1}^M{c}_j^{\infty }(e^{-\beta q_j\psi }-1),$$

where β = 1/(k_BT) is the inverse thermal energy with k_B the Boltzmann constant and T absolute temperature. Different forms of V (ψ) can be used for the linearized or size-modified Poisson–Boltzmann equation [26, 45]. More complicated forms V = V(ψ, ∇ψ) involving both ψ and ∇ψ can be used to model effects such as the ionic concentration dependent dielectric response but can also be more complicated for implementation [2,23,29].

Cheng et al. [9,10,12,41,44] developed a highly accurate, compact coupling interface method for solving the dielectric-boundary Poisson–Boltzmann equation and a robust level-set method to minimize the VISM functional (1.1). The normal velocity in the level-set formulation is the (normal component of) effective boundary force defined to be the negative variational derivative −δ_ΓF [Γ] : Γ → ℝ of the free-energy functional F[Γ] with respect to the location change of interface Γ. Let n denote the unit normal to the interface Γ pointing from the solvent region Ω_w to solute region Ω_p. We have [5,9–11,28,44]

$$-{\delta }_{\mathrm{\Gamma }}F[\mathrm{\Gamma }]=P+2{\gamma }_{0}H-{\rho }_{\mathrm{w}}U+\frac{1}{2}\left(\frac{1}{{\epsilon }_{\mathrm{p}}{\epsilon }_0}-\frac{1}{{\epsilon }_{\mathrm{w}}{\epsilon }_0}\right){\left({\epsilon }_{\mathrm{\Gamma }}\frac{\partial \psi }{\partial n}\right)}^2+\frac{1}{2}({\epsilon }_{\mathrm{w}}{\epsilon }_0-{\epsilon }_{\mathrm{p}}{\epsilon }_0){\mid {\nabla }_{\mathrm{\Gamma }}\psi \mid }^2+V(\psi )\text{on}\mathrm{\Gamma },$$ (1.5)

where H is the mean curvature that is positive if Ω_p is a sphere and ∇_Γ = (I − n ⊗ n) ∇, with I the identity matrix, is the surface gradient along Γ.

While successful initially [9, 12, 22, 41, 44], the sharp-interface VISM needs to be improved in several aspects. The most critical one is to include the description of fluctuations, both around the solute-solvent interface and in the bulk solvent. Such fluctuations are particularly crucial in the transition of one equilibrium conformation to another and in sampling different states to accurately predict the free energies of underlying biomolecular systems. It is certainly possible to describe interfacial fluctuations within a sharp-interface framework. But several implementational difficulties can arise. For instance, the extension of normal velocity in the level-set method can be hard for a moving fluctuating interface. Moreover, fluctuations can nucleate and coalesce small bubbles (water regions) inside solutes, making it hard to solve the dielectric boundary Poisson–Boltzmann equation in a sharp-interface formulation. In seeking for an alternative approach, we notice that initial theoretical and computational studies of interfacial fluctuations using a diffused-interface approach seem promising [3,17,24]. We therefore propose in this work a diffused-interface approach to the solvation of charged molecules. In a slight different language, this is a phase-field approach as it is well appreciated that the solvent-solute interface in a biomolecular system resembles a liquid-vapor interface, and the solvent and solute can be regarded as two different phases [6,42]. The phase-field approach has been widely used in studying interface problems arising in many scientific areas, such as materials physics, complex fluids, biomembranes, and cell motility, cf. e.g., [1, 13, 18, 25, 31, 37] and the references therein.

Our phase-field model is governed by the free-energy functional

$$F_{\xi }[\varphi ]=P{\int }_{\mathrm{\Omega }}{\varphi }^2\mathrm{d}x+{\gamma }_0{\int }_{\mathrm{\Omega }}\left[\frac{\xi }{2}{\mid \nabla \varphi \mid }^2+\frac{1}{\xi }W(\varphi )\right]\mathrm{d}x+{\rho }_{\mathrm{w}}{\int }_{\mathrm{\Omega }}{(\varphi -1)}^{2}U\mathrm{d}x+{\int }_{\mathrm{\Omega }}\left[-\frac{\epsilon (\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2+{\rho }_{\mathrm{f}}{\psi }_{\varphi }-{(\varphi -1)}^{2}V({\psi }_{\varphi })\right]\mathrm{d}x$$ (1.6)

for all phase fields ϕ : Ω → ℝ, where the electrostatic potential ψ_ϕ is the solution to the boundary-value problem of Poisson–Boltzmann equation with a diffused dielectric boundary

$$\nabla ·\epsilon (\varphi )\nabla {\psi }_{\varphi }-{(\varphi -1)}^2{V}^{\prime }({\psi }_{\varphi })=-{\rho }_{\mathrm{f}}\text{in}\mathrm{\Omega },$$ (1.7)

$${\psi }_{\varphi }={\psi }_{\infty }\text{on}\partial \mathrm{\Omega }.$$ (1.8)

Here ξ > 0 is a small number. With a low free energy, a phase field ϕ should be close to two values, say, 0 and 1, respectively, in the solvation region Ω, except a thin transition layer that represents the dielectric boundary. The sets {ϕ ≈ 0} and {ϕ ≈ 1} represent the solvent and solute regions, respectively. With such a convention, the first term in (1.6) corresponds to that in (1.1), describing the volumetric energy. The second term in (1.6), in which,

$$W(\varphi )=18{\varphi }^2{(1-\varphi )}^2,$$

approximates the surface energy [30, 33, 39]. The third term in (1.6) corresponds to that in (1.1), describing the energy of solute-solvent interaction. Finally, the last term in (1.6) corresponds to that in (1.1), describing the electrostatic free energy. In this term, ε(ϕ) is defined to be a smooth function of ϕ that interpolates the piecewise constant dielectric coefficient: ε(0) = ε_wε₀ and ε(1) = ε_pε₀. We shall require that ε′(0) = ε′(1) = 0. Note that the electrostatic potential ψ_ϕ depends on ϕ.

We study our proposed phase-field solvation free-energy functional (1.6), and the corresponding relaxation dynamics. Our main results are as follows:

1. We prove the well-posedness of the boundary-value problem of Poisson–Boltzmann equation (1.7) and (1.8), and obtain some bounds for the electrostatic potential; cf. Theorem 2.1;

2. We derive, first intuitively and then rigorously, the first variation of the phase-field free-energy functional (1.6)

   $${\delta }_{\varphi }F[\varphi ]=2P\varphi -{\gamma }_0\left[\xi \mathrm{\Delta }\varphi -\frac{1}{\xi }{W}^{\prime }(\varphi )\right]+2{\rho }_{\mathrm{w}}(\varphi -1)U-\frac{1}{2}{\epsilon }^{\prime }(\varphi ){\mid \nabla \psi \mid }^2-2(\varphi -1)V(\psi );$$

   cf. Theorem 3.1;

3. We consider the relaxation dynamics ∂_tϕ = −δ_ϕF[ϕ] for ϕ = ϕ (x, t) with t denoting the time variable. Using the method of matched asymptotic analysis [4, 14, 15, 34, 36], we show that, in the sharp-interface limit, the normal velocity of the solute-solvent interface is exactly the boundary force (1.5) in the original sharp-interface variational approach; cf. Theorem 5.1.

Several remarks are in order. First, our diffuse-interface model (1.6) differs from our previous one [30,43] significantly in that we use the Poisson–Boltzmann equation, rather than the Coulomb-field approximation [8, 41] which requires no solution of partial differential equations, to describe the electrostatic interaction. Second, our relaxation dynamics ∂_tϕ = −δ_ϕF[ϕ] is a non-conservative dynamics with respect to the phase-field function ϕ. In fact, the relaxation process can change the volume of solute region {ϕ ≈ 1}. The amount of ions, however, are controlled through their bulk concentrations $c_j^{\infty }(j=1,\dots ,M)$ that are input parameters. Third, the surface energy term described by the gradient-square and double-well terms in our phase-field energy functional (1.6) coincides with the part in an effective Hamiltonian for the large-scale solvent density in the Lum–Chandler–Weeks theory of solvation [32].

The rest of the paper is organized as follows: In Section 2, we prove the existence and uniqueness of, and provide bounds for, the solution to the Poisson–Boltzmann equation with a diffused dielectric boundary that is given by a phase field. In Section 3, we derive the first variation of the phase-field free-energy functional. In Section 4, we use the matched asymptotic analysis to study the relaxation dynamics in a fast and the regular time scales. In Section 5, we continue our matched asymptotic analysis for a slow time scale to show that the sharp-interface limit of the relaxation dynamics is exactly the same as in the original sharp-interface variational model.

2. Poisson–Boltzmann Electrostatics with a Diffused Dielectric Boundary

We make the following assumptions:

• (A1)The solvation region Ω is a bounded, connected, open set with a sufficiently smooth boundary ∂Ω. All x₁, …, x_N are given points in Ω. All P, γ₀, ρ_w, ε_p, and ε_w are positive constants with ε_p < ε_w. The function ρ_f ∈ L^∞(Ω). The function ψ_∞ ∈ W^1,∞ (Ω);
• (A2)The function U : ℝ³ \ {x₁, …, x_N} → ℝ is continuously differentiable and bounded below. Moreover, lim_x→xiU(x) = +∞ for each i (1 ≤ i ≤ N) and lim_x→∞ U(x) = 0;
• (A3)The function ε ∈ C¹(ℝ). There exist positive numbers ε_min, ε_max, and ${\epsilon }_{max}^{\prime }$ such that ε_min ≤ ε(ϕ) ≤ ε_max and $\mid {\epsilon }^{\prime }(\varphi )\mid \le {\epsilon }_{max}^{\prime }$ for all ϕ ∈ ℝ. Moreover, ε(0) = ε_wε₀, ε(1) = ε_pε₀, ε′(0) = ε′(1) = 0, and ε′(ϕ) ≠ 0 if 0 < ϕ < 1;
• (A4)The function V ∈ C²(ℝ). It is strictly convex. Moreover, V (0) = min_s∈ℝ V(s) < V(s) for any s ≠ 0, V(±∞) = +∞, and V′(±∞) = ±∞.

Here are two examples of the function ε = ε(ϕ) with all the desired properties.

Example 1.

$$\epsilon (\varphi )=\{\begin{array}{ll}{\epsilon }_{\mathrm{w}}{\epsilon }_0\hfill & \text{if}\varphi \le 0,\hfill \\ \frac{{\epsilon }_{\mathrm{p}}{\epsilon }_0{\mathrm{e}}^{tan(\pi (\varphi -1/2))}+{\epsilon }_{\mathrm{w}}{\epsilon }_0{e}^{-tan(\pi (\varphi -1/2))}}{e^{tan(\pi (\varphi -1/2))}+e^{-tan(\pi (\varphi -1/2))}}\hfill & \text{if}0<\varphi <1,\hfill \\ {\epsilon }_{\mathrm{p}}{\epsilon }_0\hfill & \text{if}\varphi \ge 1.\hfill \end{array}$$

In fact, this is a C^∞-function. Moreover, for any integer m ≥ 1, ε^(m)(ϕ) = 0 for all ϕ ∉ (0, 1) and ε^(m)(ϕ) ≠ 0 for all ϕ ∈ (0, 1).

Example 2.

$$\epsilon (\varphi )=\{\begin{array}{ll}{\epsilon }_{\mathrm{w}}{\epsilon }_0\hfill & \text{if}\varphi \le 0,\hfill \\ \frac{1}{2}({\epsilon }_{\mathrm{w}}{\epsilon }_0-{\epsilon }_{\mathrm{p}}{\epsilon }_0)cos\pi \varphi +\frac{1}{2}({\epsilon }_{\mathrm{w}}{\epsilon }_0+{\epsilon }_{\mathrm{p}}{\epsilon }_0)\hfill & \text{if}0<\varphi <1,\hfill \\ {\epsilon }_{\mathrm{p}}{\epsilon }_0\hfill & \text{if}\varphi \ge 1.\hfill \end{array}$$

In what follows, we shall denote by C a generic constant that may depend on Ω, ρ_f, ψ_∞, and ε but is independent of $\varphi \in H_0^1(\mathrm{\Omega })$. We shall also denote by C(ϕ) a generic constant that can depend on ϕ in addition to Ω, ρ_f, ψ_∞, and ε. The following theorem is our main result in this section:

Theorem 2.1

For any $\varphi \in H_0^1(\mathrm{\Omega })$ there exists a unique weak solution ψ_ϕ ∈ H¹(Ω) to the boundary-value problem (1.7) and (1.8), i.e., ψ_ϕ = ψ_∞ on ∂Ω in the sense of trace and

$${\int }_{\mathrm{\Omega }}[\epsilon (\varphi )\nabla {\psi }_{\varphi }·\nabla \eta +{(\varphi -1)}^2{V}^{\prime }({\psi }_{\varphi })\eta ]dx={\int }_{\mathrm{\Omega }}{\rho }_{\mathrm{f}}\eta dx\forall \eta \in H_0^1(\mathrm{\Omega }).$$ (2.1)

Moreover, ψ_ϕ ∈ L^∞(Ω) and

$${\Vert {\psi }_{\varphi }\Vert }_{H^1(\mathrm{\Omega })}\le C(1+{\Vert \varphi \Vert }_{L^2(\mathrm{\Omega })}),$$ (2.2)

$${\Vert {\chi }_{\{\varphi \ne 1\}}{\psi }_{\varphi }\Vert }_{L^{\infty }(\mathrm{\Omega })}\le C,$$ (2.3)

$${\Vert {\psi }_{\varphi }\Vert }_{L^{\infty }(\mathrm{\Omega })}\le C\left(1+{\Vert \varphi \Vert }_{H^1(\mathrm{\Omega })}^2\right).$$ (2.4)

Proof

We divide our proof in three steps.

Step 1

Let ψ̂_ϕ ∈ H¹(Ω) be the unique weak solution to the boundary-value problem −∇ · ε(ϕ)∇ψ̂_ϕ = ρ_f in Ω and ψ̂_ϕ = ψ_∞ on ∂Ω. This means that ψ̂_ϕ is the unique function in H¹(Ω) such that ψ̂_ϕ = ψ_∞ on ∂Ω and

$${\int }_{\mathrm{\Omega }}\epsilon (\varphi )\nabla {\widehat{\psi }}_{\varphi }·\nabla \eta dx={\int }_{\mathrm{\Omega }}{\rho }_{\mathrm{f}}\eta dx\forall \eta \in H_0^1(\mathrm{\Omega }).$$ (2.5)

Since 0 < ε_min ≤ ε(ϕ) ≤ ε_max for all ϕ ∈ ℝ, we have by the standard elliptic theory (cf. Theorem 8.3 and Theorem 8.16 in [21]) that ψ̂_ϕ ∈ H¹(Ω) ∩ L^∞(Ω), and

$${\Vert {\widehat{\psi }}_{\varphi }\Vert }_{H^1(\mathrm{\Omega })}+{\Vert {\widehat{\psi }}_{\varphi }\Vert }_{L^{\infty }(\mathrm{\Omega })}\le C.$$ (2.6)

Step 2

We define I: $H_0^1(\mathrm{\Omega })\to ℝ\cup \{+\infty \}$ by

$$I[u]={\int }_{\mathrm{\Omega }}\left[\frac{\epsilon (\varphi )}{2}{\mid \nabla u\mid }^2+{(\varphi -1)}^{2}V(u+{\widehat{\psi }}_{\varphi })\right]\mathrm{d}x\forall u\in H_0^1(\mathrm{\Omega }).$$

It is easy to see that ${inf}_{u\in H_0^1(\mathrm{\Omega })}I[u]$ is finite. By the direct method in the calculus of variations, there exists a unique minimizer $u\in H_0^1(\mathrm{\Omega })$ of I over $H_0^1(\mathrm{\Omega })$.

By our assumption (A4) on the function V and by (2.6), there exists λ > 0, independent of ϕ, such that V′ (λ + ψ̂_ϕ) > 1 and V′(−λ + ψ̂_ϕ) < −1 a.e. on Ω. We prove that

$$\mid u\mid \le \lambda \text{a.e.}\text{on}\{\varphi \ne 1\}.$$ (2.7)

Define u_λ : Ω → ℝ by

$$u_{\lambda }(x)=\{\begin{array}{ll}-\lambda \hfill & \text{if}u(x)<-\lambda ,\hfill \\ u(x)\hfill & \text{if}-\lambda \le u(x)\le \lambda ,\hfill \\ \lambda \hfill & \text{if}u(x)>\lambda .\hfill \end{array}$$

Since I[u_λ] ≥ I[u] and |∇u_λ| ≤ |∇u| a.e. Ω, we have

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}{(\varphi -1)}^{2}V(u+{\widehat{\psi }}_0)\mathrm{d}x=I[u]-{\int }_{\mathrm{\Omega }}\frac{\epsilon (\varphi )}{2}{\mid \nabla u\mid }^{2}dx\\ \le I[u_{\lambda }]-{\int }_{\mathrm{\Omega }}\frac{\epsilon (\varphi )}{2}{\mid \nabla u_{\lambda }\mid }^{2}dx\\ ={\int }_{\mathrm{\Omega }}{(\varphi -1)}^{2}V(u_{\lambda }+{\widehat{\psi }}_{\varphi })\mathrm{d}x.\end{array}$$

Consequently, it follows from the convexity of V and our choice of λ that

$$\begin{array}{l}0\ge {\int }_{\mathrm{\Omega }}{(\varphi -1)}^{2}V(u+{\widehat{\psi }}_{\varphi })\mathrm{d}x-{\int }_{\mathrm{\Omega }}{(\varphi -1)}^{2}V(u_{\lambda }+{\widehat{\psi }}_{\varphi })\mathrm{d}x\\ ={\int }_{\mathrm{\Omega }}{\chi }_{\{u>\lambda \}}{(\varphi -1)}^2\left[V(u+{\widehat{\psi }}_{\varphi })-V(\lambda +{\widehat{\psi }}_{\varphi })\right]\mathrm{d}x+{\int }_{\mathrm{\Omega }}{\chi }_{\{u<-\lambda \}}{(\varphi -1)}^2\left[V(u+{\widehat{\psi }}_{\varphi })-V(-\lambda +{\widehat{\psi }}_{\varphi })\right]\mathrm{d}x\\ \ge {\int }_{\mathrm{\Omega }}{\chi }_{\{u>\lambda \}}{(\varphi -1)}^2{V}^{\prime }(\lambda +{\widehat{\psi }}_{\varphi })(u-\lambda )\mathrm{d}x+{\int }_{\mathrm{\Omega }}{\chi }_{\{u<-\lambda \}}{(\varphi -1)}^2{V}^{\prime }(-\lambda +{\widehat{\psi }}_{\varphi })(u+\lambda )\mathrm{d}x\\ \ge {\int }_{\mathrm{\Omega }}{\chi }_{\{u>\lambda \}}{(\varphi -1)}^2(u-\lambda )\mathrm{d}x+{\int }_{\mathrm{\Omega }}{\chi }_{\{u<-\lambda \}}{(\varphi -1)}^2(-u-\lambda )\mathrm{d}x\\ ={\int }_{\mathrm{\Omega }}{\chi }_{\{\mid u\mid >\lambda \}}{(\varphi -1)}^2\mid \mid u\mid -\lambda \mid \mathrm{d}x\\ \ge 0.\end{array}$$

This leads to (2.7).

The minimizer u of I: $H_0^1(\mathrm{\Omega })\to ℝ\cup \{+\infty \}$ is the weak solution to the Euler–Lagrange equation

$$\nabla ·\epsilon (\varphi )\nabla u-{(\varphi -1)}^2{V}^{\prime }(u+{\widehat{\psi }}_{\varphi })=0\text{in}\mathrm{\Omega },$$

i.e.,

$${\int }_{\mathrm{\Omega }}\left[\epsilon (\varphi )\nabla u·\nabla \eta +{(\varphi -1)}^2{V}^{\prime }(u+{\widehat{\psi }}_{\varphi })\eta \right]\mathrm{d}x=0\forall \eta \in H_0^1(\mathrm{\Omega }).$$ (2.8)

This is true by (2.7) and the Lebesgue Dominated Convergence Theorem if $\eta \in H_0^1(\mathrm{\Omega })\cap L^{\infty }(\mathrm{\Omega })$. For a general $\eta \in H_0^1(\mathrm{\Omega })$, this is also true, since (ϕ − 1)²V′(u+ψ̂_ϕ) ∈ L⁴(Ω) by (2.7) and since $H_0^1(\mathrm{\Omega })\cap L^{\infty }(\mathrm{\Omega })$ is dense in $H_0^1(\mathrm{\Omega })$. The convexity of V implies that the weak solution $u\in H_0^1(\mathrm{\Omega })$ defined by (2.8) is unique.

If we choose η = u in the equation of (2.8), we obtain by (2.6), (2.7), and Poincaré’s inequality that

$${\Vert u\Vert }_{H^1(\mathrm{\Omega })}^2\le C{\int }_{\{\varphi \ne 1\}}\left|{(\varphi -1)}^2{V}^{\prime }(u+{\widehat{\psi }}_{\varphi })u\right|\mathrm{d}x\le C{\int }_{\mathrm{\Omega }}(1+{\varphi }^2)\mathrm{d}x,$$

leading to

$${\Vert u\Vert }_{H^1(\mathrm{\Omega })}\le C(1+{\Vert \varphi \Vert }_{L^2(\mathrm{\Omega })}).$$ (2.9)

It now follows from the regularity theory (cf. Theorem 8.16 in [21]), (2.6), (2.7), and the imbedding H¹(Ω) ↪ L⁴(Ω) that

$${\Vert u\Vert }_{L^{\infty }(\mathrm{\Omega })}\le C{\Vert {(\varphi -1)}^2{V}^{\prime }(u+{\widehat{\psi }}_{\varphi })\Vert }_{L^2(\mathrm{\Omega })}\le C\left(1+{\Vert \varphi \Vert }_{L^4(\mathrm{\Omega })}^2\right)\le C\left(1+{\Vert \varphi \Vert }_{H^1(\mathrm{\Omega })}^2\right).$$ (2.10)

Step 3

Let ψ_ϕ = u + ψ̂_ϕ. Then ψ_ϕ = ψ_∞ on ∂Ω. Moreover, (2.5) and (2.8) imply (2.1). The uniqueness of ψ_ϕ follows from the convexity of V and a usual argument. The estimates (2.2)–(2.4) follow from (2.6), (2.9), (2.7), and (2.10).

3. First Variation of Free-Energy Functional

We calculate the first variation of the free-energy functional F_ξ defined by (1.6). The first variation of each of the first three parts in the functional F_ξ can be obtained by routine calculations. So, we focus on the electrostatic part

$$F_{\text{ele},\xi }[\varphi ]:={\int }_{\mathrm{\Omega }}\left[-\frac{\epsilon (\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2+{\rho }_{\mathrm{f}}{\psi }_{\varphi }-{(\varphi -1)}^{2}V({\psi }_{\varphi })\right]\mathrm{d}x,$$ (3.1)

where ψ_ϕ is the unique solution to the boundary-value problem (1.7) and (1.8). Heuristically, if we denote by δ_ϕ the “derivative” with respect to ϕ and δϕ the variation of ϕ, and “differentiate” both sides of the above equation, then we obtain by the chain rule and product rule for differentiation that

$$\begin{array}{l}{\delta }_{\varphi }{F}_{\text{ele},\xi }[\varphi ]\delta \varphi ={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }^{\prime }(\varphi )}{2}\delta \varphi {\mid \nabla {\psi }_{\varphi }\mid }^2-\epsilon (\varphi )\nabla {\psi }_{\varphi }·\nabla {\delta }_{\varphi }{\psi }_{\varphi }+{\rho }_{\mathrm{f}}{\delta }_{\varphi }{\psi }_{\varphi }-2(\varphi -1)\delta \varphi V({\psi }_{\varphi })-{(\varphi -1)}^2{V}^{\prime }({\psi }_{\varphi }){\delta }_{\varphi }{\psi }_{\varphi }]\mathrm{d}x\\ ={\int }_{\mathrm{\Omega }}\left[-\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2-2(\varphi -1)V({\psi }_{\varphi })\right]\delta \varphi \mathrm{d}x+{\int }_{\mathrm{\Omega }}{\rho }_{\mathrm{f}}{\delta }_{\varphi }{\psi }_{\varphi }\mathrm{d}x-{\int }_{\mathrm{\Omega }}[\epsilon (\varphi )\nabla {\psi }_{\varphi }·\nabla {\delta }_{\varphi }{\psi }_{\varphi }+{(\varphi -1)}^2{V}^{\prime }({\psi }_{\varphi }){\delta }_{\varphi }{\psi }_{\varphi }]\mathrm{d}x\\ ={\int }_{\mathrm{\Omega }}\left[-\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2-2(\varphi -1)V({\psi }_{\varphi })\right]\delta \varphi \mathrm{d}x,\end{array}$$

where in the last step we used the weak form (2.1) of the Poisson–Boltzmann equation with η = δ_ϕψ_ϕ. We then identify δ_ϕF_ele,ξ[ϕ] as

$${\delta }_{\varphi }{F}_{\text{ele},\xi }[\varphi ]=-\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2-2(\varphi -1)V({\psi }_{\varphi }).$$

We remark that −δ_ϕF_ele,ξ [ϕ] is an approximation of the electrostatic part of the boundary force −δ_ΓF [Γ] in (1.5) if ϕ ≈ 0 in the solvent region and ϕ ≈ 1 in the solute region. In fact, the V-terms are similar, since the perturbation δϕ is localized at the interface. With our notation, the unit normal n ≈ −∇ϕ/|∇ϕ|. Moreover, ε(ϕ) ≈ ε_Γ. Therefore,

$$\begin{array}{l}\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2=\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }·n\mid }^2+\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid {\nabla }_{\mathrm{\Gamma }}{\psi }_{\varphi }\mid }^2\\ =-\frac{1}{2}\frac{d}{d\varphi }\left[\frac{1}{\epsilon (\varphi )}\right]{\mid \epsilon (\varphi )\nabla {\psi }_{\varphi }·n\mid }^2+\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid {\nabla }_{\mathrm{\Gamma }}{\psi }_{\varphi }\mid }^2\\ \approx -\frac{1}{2}\left(\frac{1}{{\epsilon }_{\mathrm{p}}{\epsilon }_0}-\frac{1}{{\epsilon }_{\mathrm{w}}{\epsilon }_0}\right){\mid {\epsilon }_{\mathrm{\Gamma }}\nabla {\psi }_{\varphi }·n\mid }^2+\frac{1}{2}({\epsilon }_{\mathrm{p}}{\epsilon }_0-{\epsilon }_{\mathrm{w}}{\epsilon }_0){\mid {\nabla }_{\mathrm{\Gamma }}{\psi }_0\mid }^2.\end{array}$$

The final result is exactly the corresponding part in (1.5).

We now give a rigorous justification of our derivation. We recall that if $G:H_0^1(\mathrm{\Omega })\to ℝ$ is a functional and if ϕ, $\eta \in H_0^1(\mathrm{\Omega })$, then the first variation of G at ϕ in the “direction” η is defined to be

$${\delta }_{\varphi }G[\varphi ][\eta ]=\underset{t\to 0}{lim}\frac{G[\varphi +t\eta ]-G[\varphi ]}{t}={\frac{d}{dt}|}_{t=0}G[\varphi +t\eta ],$$

if the limit exists.

Theorem 3.1

Let $\varphi \in H_0^1(\mathrm{\Omega })$. Let ψ_ϕ ∈ H¹(Ω) be the weak solution of the corresponding boundary-value problem (1.7) and (1.8). Let $\eta \in L^{\infty }(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })$. Then

$${\delta }_{\varphi }{F}_{\text{ele},\xi }[\varphi ][\eta ]={\int }_{\mathrm{\Omega }}\left[-\frac{1}{2}{\epsilon }^{\prime }(\varphi ){\mid \nabla {\psi }_{\varphi }\mid }^2-2(\varphi -1)V({\psi }_{\varphi })\right]\eta dx.$$ (3.2)

To prove the theorem, we need the following lemma:

Lemma 3.2

Let $\varphi \in H_0^1(\mathrm{\Omega })$ and $\eta \in L^{\infty }(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })$. Let t ∈ ℝ with |t| ≤ 1. Let ψ_ϕ and ψ_ϕ+tη be the weak solutions to the boundary-value problems of Poisson–Boltzmann equation (1.7) and (1.8) corresponding to ϕ and ϕ + tη, respectively. Then there exists a constant C = C(ϕ, η) > 0 that may depend on both ϕ and η such that

$${\Vert {\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\Vert }_{H^1(\mathrm{\Omega })}\le C(\varphi ,\eta )\mid t\mid \text{if}\mid t\mid \le 1.$$

Proof

By the weak form for ψ_ϕ and that for ψ_ϕ+tη, cf. (2.1), we have for any $\zeta \in H_0^1(\mathrm{\Omega })$ that

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}[\epsilon (\varphi )\nabla {\psi }_{\varphi }·\nabla \zeta +{(\varphi -1)}^2{V}^{\prime }({\psi }_{\varphi })\zeta ]dx={\int }_{\mathrm{\Omega }}{\rho }_{\mathrm{f}}\zeta \mathrm{d}x,\\ {\int }_{\mathrm{\Omega }}[\epsilon (\varphi +t\eta )\nabla {\psi }_{\varphi +t\eta }·\nabla \zeta +{(\varphi +t\eta -1)}^2{V}^{\prime }({\psi }_{\varphi +t\eta })\zeta ]dx={\int }_{\mathrm{\Omega }}{\rho }_{\mathrm{f}}\zeta dx.\end{array}$$

It follows from these two equations with ζ = ψ_ϕ+tη − ψ_ϕ, the property of ε, and the convexity of V that

$$\begin{array}{l}{\epsilon }_{min}{\Vert \nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\Vert }_{L^2(\mathrm{\Omega })}^2\\ \le {\int }_{\mathrm{\Omega }}\epsilon (\varphi )\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ ={\int }_{\mathrm{\Omega }}\epsilon (\varphi )\nabla {\psi }_{\varphi +t\eta }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx-{\int }_{\mathrm{\Omega }}\epsilon (\varphi )\nabla {\psi }_{\varphi }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ =-{\int }_{\mathrm{\Omega }}[(\epsilon (\varphi +t\eta )-\epsilon (\varphi ))]\nabla {\psi }_{\varphi +t\eta }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ +{\int }_{\mathrm{\Omega }}\epsilon (\varphi +t\eta )\nabla {\psi }_{\varphi +t\eta }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx-{\int }_{\mathrm{\Omega }}\epsilon (\varphi )\nabla {\psi }_{\varphi }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ =-{\int }_{\mathrm{\Omega }}[(\epsilon (\varphi +t\eta )-\epsilon (\varphi )]\nabla {\psi }_{\varphi +t\eta }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ -{\int }_{\mathrm{\Omega }}[{(\varphi +t\eta -1)}^2-{(\varphi -1)}^2]V^{\prime }({\psi }_{\varphi +t\eta })({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ -{\int }_{\mathrm{\Omega }}{(\varphi -1)}^2[V^{\prime }({\psi }_{\varphi +t\eta })-V^{\prime }({\psi }_{\varphi })]({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ \le -{\int }_{\mathrm{\Omega }}[(\epsilon (\varphi +t\eta )-\epsilon (\varphi ))]\nabla {\psi }_{\varphi +t\eta }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ -{\int }_{\mathrm{\Omega }}[{(\varphi +t\eta -1)}^2-{(\varphi -1)}^2]V^{\prime }({\psi }_{\varphi +t\eta })({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })dx\\ \le {\epsilon }_{max}^{\prime }\mid t\mid {\Vert \eta \Vert }_{L^{\infty }(\mathrm{\Omega })}{\Vert \nabla {\psi }_{\varphi +t\eta }\Vert }_{L^2(\mathrm{\Omega })}{\Vert \nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\Vert }_{L^2(\mathrm{\Omega })}\\ +(2\mid t\mid {\Vert \eta (\varphi -1)\Vert }_{L^2(\mathrm{\Omega })}+t^2{\Vert {\eta }^2\Vert }_{L^2(\mathrm{\Omega })}){\Vert V^{\prime }({\psi }_{\varphi +t\eta })\Vert }_{L^{\infty }(\mathrm{\Omega })}{\Vert {\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\Vert }_{L^2(\mathrm{\Omega })}.\end{array}$$

Since |t| ≤ 1, we have by (2.2) and (2.4) that both ||ψ_ϕ+tη||_H¹(Ω) and ||V′(ψ_ϕ + tη)||_L^∞(Ω) are bounded by some constants that can depend on ϕ and η. An application of Poincaré’s inequality then implies the desired inequality.

Proof of Theorem 3.1

For any t with |t| ≪ 1, we denote by ψ_ϕ+tη the weak solution to the boundary-value problem (1.7) and (1.8) with ϕ + tη replacing ϕ. Setting ${\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\in H_0^1(\mathrm{\Omega })$ as the test function in the corresponding weak formulation for ψ_ϕ+tη, we obtain

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}{\rho }_{\mathrm{f}}({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\mathrm{d}x={\int }_{\mathrm{\Omega }}\epsilon (\varphi +t\eta )\nabla {\psi }_{\varphi +t\eta }·\nabla ({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\mathrm{d}x+{\int }_{\mathrm{\Omega }}{(\varphi +t\eta -1)}^2{V}^{\prime }({\psi }_{\varphi +t\eta })({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\mathrm{d}x\\ =\frac{1}{2}{\int }_{\mathrm{\Omega }}\epsilon (\varphi +t\eta )({\mid \nabla {\psi }_{\varphi +t\eta }\mid }^2+{\mid \nabla {\psi }_{\varphi +t\eta }-\nabla {\psi }_{\varphi }\mid }^2-{\mid \nabla {\psi }_{\varphi }\mid }^2)\mathrm{d}x+{\int }_{\mathrm{\Omega }}{(\varphi +t\eta -1)}^2{V}^{\prime }({\psi }_{\varphi +t\eta })({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\mathrm{d}x.\end{array}$$

Consequently, by the definition of the functional F_ele,ξ (cf. (3.1)), we have

$$\begin{array}{l}{F}_{\text{ele},\xi }[\varphi +t\eta ]-F_{\text{ele},\xi }[\varphi ]\\ ={\int }_{\mathrm{\Omega }}[-\frac{\epsilon (\varphi +t\eta )}{2}{\mid \nabla {\psi }_{\varphi +t\eta }\mid }^2+\frac{\epsilon (\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2+{\rho }_{\mathrm{f}}({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })\\ -{(\varphi +t\eta -1)}^{2}V({\psi }_{\varphi +t\eta })+{(\varphi -1)}^{2}V({\psi }_{\varphi })]dx\\ ={\int }_{\mathrm{\Omega }}\frac{1}{2}\epsilon (\varphi +t\eta ){\mid \nabla {\psi }_{\varphi +t\eta }-\nabla {\psi }_{\varphi }\mid }^{2}dx\\ -{\int }_{\mathrm{\Omega }}\frac{1}{2}[\epsilon (\varphi +t\eta )-\epsilon (\varphi )]{\mid \nabla {\psi }_{\varphi }\mid }^{2}dx\\ -{\int }_{\mathrm{\Omega }}[{(\varphi +t\eta -1)}^2-{(\varphi -1)}^2]V({\psi }_{\varphi })dx\\ -{\int }_{\mathrm{\Omega }}{(\varphi +t\eta -1)}^2[V({\psi }_{\varphi +t\eta })-V({\psi }_{\varphi })-V^{\prime }({\psi }_{\varphi +t\eta })({\psi }_{\varphi +t\eta }-{\psi }_{\varphi })]dx\\ =:{\mathrm{\Lambda }}_1(t)-{\mathrm{\Lambda }}_2(t)-{\mathrm{\Lambda }}_3(t)-{\mathrm{\Lambda }}_4(t),\end{array}$$ (3.3)

where Λ_i(t) (i = 1, …, 4) denote the corresponding integrals.

By Lemma 3.2, we have

$$\left|\frac{{\mathrm{\Lambda }}_1(t)}{t}\right|\le \frac{{\epsilon }_{max}}{2\mid t\mid }{\Vert {\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\Vert }_{H^1(\mathrm{\Omega })}^2\le C(\varphi ,\eta )t\to 0\text{as}t\to 0.$$ (3.4)

Since η ∈ L^∞(Ω), we have for a.e. x ∈ Ω that

$$\frac{1}{t}[\epsilon (\varphi +t\eta )-\epsilon (\varphi )]={\epsilon }^{\prime }(\varphi +\theta t\eta )\eta \to {\epsilon }^{\prime }(\varphi )\eta \text{as}t\to 0,$$

where θ = θ(x) ∈ [0, 1]. The Lebesgue Dominated Convergence Theorem then implies that

$$\underset{t\to 0}{lim}\frac{{\mathrm{\Lambda }}_2(t)}{t}={\int }_{\mathrm{\Omega }}\frac{1}{2}{\epsilon }^{\prime }(\varphi ){\mid \nabla {\psi }_{\varphi }\mid }^2\eta dx.$$ (3.5)

Similarly, since ψ_ϕ ∈ L^∞(Ω) by Theorem 2.1,

$$\underset{t\to 0}{lim}\frac{{\mathrm{\Lambda }}_3(t)}{t}={\int }_{\mathrm{\Omega }}2(\varphi -1)V({\psi }_{\varphi })\eta dx.$$ (3.6)

Let a ∈ ℝ and define g(b) = V (b) − V (a) − V′(b)(b − a) for all b ∈ ℝ. Note that g(a) = 0 and g′(b) = −V″(b)(b − a). By Taylor’s expansion,

$$g(b)=g(a)+g^{\prime }(a+\mu (b-a))(b-a)=-\mu V^{″}(a+\mu (b-a)){(b-a)}^2,$$

where μ = μ(b) ∈ [0, 1]. With a = ψ_ϕ and b = ψ_ϕ+tη, we obtain by (2.4), the Cauchy–Schwarz inequality, the imbedding H¹(Ω) ↪ L⁴(Ω), and Lemma 3.2 that

$$\begin{array}{l}\left|\frac{{\mathrm{\Lambda }}_4(t)}{t}\right|\le \frac{C(\varphi ,\eta )}{t}{\int }_{\mathrm{\Omega }}{(\varphi +t\eta -1)}^2{\mid {\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\mid }^{2}dx\\ \le \frac{C(\varphi ,\eta )}{t}{\Vert {(\varphi +t\eta -1)}^2\Vert }_{L^2(\mathrm{\Omega })}{\Vert {\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\Vert }_{L^4(\mathrm{\Omega })}^2\\ \le \frac{C(\varphi ,\eta )}{t}{\Vert {(\varphi +t\eta -1)}^2\Vert }_{L^2(\mathrm{\Omega })}{\Vert {\psi }_{\varphi +t\eta }-{\psi }_{\varphi }\Vert }_{H^1(\mathrm{\Omega })}^2\\ \to 0\text{as}t\to 0.\end{array}$$ (3.7)

Now (3.2) follows from (3.3)–(3.7).

The next theorem provides the formula of first variation of the solvation free-energy functional F_ξ defined in (1.6). It follows from Theorem 3.1 and routine calculations. We thus omit the proof.

Theorem 3.3

Let $\varphi \in H_0^1(\mathrm{\Omega })$ and $\eta \in L^{\infty }(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })$ be such that

$${\int }_{\mathrm{\Omega }}{(\varphi -1)}^{2}Udx<\infty \mathit{and}{\int }_{\mathrm{\Omega }}{\eta }^{2}Udx<\infty .$$

Let ψ_ϕ ∈ H¹(Ω) be the unique weak solution to the boundary-value problem (1.7) and (1.8) corresponding to ϕ. Then

$${\delta }_{\varphi }{F}_{\xi }[\varphi ][\eta ]={\int }_{\mathrm{\Omega }}\left\{{\gamma }_0\xi \nabla \varphi ·\nabla \eta +\left[2P\varphi +\frac{{\gamma }_0}{\xi }{W}^{\prime }(\varphi )+2{\rho }_w(\varphi -1)U-\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2-2(\varphi -1)V({\psi }_{\varphi })\right]\eta \right\}dx.$$

If in addition ϕ ∈ H²(Ω) then the integral of ∇ϕ · ∇η becomes that of −Δϕη. Therefore, we shall denote

$${\delta }_{\varphi }{F}_{\xi }[\varphi ]=2P\varphi -{\gamma }_0\left[\xi \mathrm{\Delta }\varphi -\frac{1}{\xi }{W}^{\prime }(\varphi )\right]+2{\rho }_{\mathrm{w}}(\varphi -1)U-\frac{{\epsilon }^{\prime }(\varphi )}{2}{\mid \nabla {\psi }_{\varphi }\mid }^2-2(\varphi -1)V({\psi }_{\varphi }),$$ (3.8)

and call it the first variation of F_ξ at ϕ.

4. Relaxation Dynamics: Fast and Regular Time Scales

We now consider the relaxation dynamics ∂_tϕ = −δ_ϕF_ξ[ϕ]. By Theorem 3.3, this dynamics is described by the following initial-boundary-value problem for the phase field ϕ = ϕ(x, t) and the corresponding electrostatic potential ψ = ψ(x, t):

$${\partial }_t\varphi =-2P\varphi +{\gamma }_0\left[\xi \mathrm{\Delta }\varphi -\frac{1}{\xi }{W}^{\prime }(\varphi )\right]-2{\rho }_{\mathrm{w}}(\varphi -1)U+\frac{1}{2}{\epsilon }^{\prime }(\varphi ){\mid \nabla \psi \mid }^2+2(\varphi -1)V(\psi ),$$ (4.1)

$$\nabla ·\epsilon (\varphi )\nabla \psi -{(\varphi -1)}^2{V}^{\prime }(\psi )=-{\rho }_{\mathrm{f}},$$ (4.2)

$$\varphi =0\text{on}\partial \mathrm{\Omega },$$ (4.3)

$$\psi ={\psi }_{\infty }\text{on}\partial \mathrm{\Omega },$$ (4.4)

together with some initial condition for ϕ. If the solution ϕ = ϕ(x, t) and ψ = ψ(x, t) are smooth, then we have by (1.6), (3.8), the chain rule, and integration by parts that

$$\begin{array}{l}\frac{d}{dt}{F}_{\xi }[\varphi (·,t)]={\int }_{\mathrm{\Omega }}{\partial }_t\varphi {\delta }_{\varphi }{F}_{\xi }[\varphi ]dx-{\int }_{\mathrm{\Omega }}[\epsilon (\varphi )\nabla \psi ·\nabla {\partial }_t\psi -{\rho }_{\mathrm{f}}{\partial }_t\psi +{(\varphi -1)}^2{V}^{\prime }(\psi ){\partial }_t\psi ]dx\\ =-{\int }_{\mathrm{\Omega }}{({\partial }_t\varphi )}^{2}dx\le 0,\end{array}$$

where the vanish of the second integral follows from the weak formulation for (4.2) with the test function ∂_tψ. Therefore, the energy decays, explaining the terminology “relaxation dynamics”.

Assume 0 < ξ ≪ 1. We expect that, after a short time period, the solution ϕ will take the value close to 0 or 1 in most of the region Ω, due to the fast reaction described by the term −(1/ξ)W′(ϕ). Moreover, in the regions {ϕ ≈ 0} and {ϕ ≈ 1}, the leading-order term of the electrostatic potential should solve the boundary-value problem (4.2) and (4.4), as the electrostatic relaxation is instantaneous: there is no ∂_tψ term. In the subsequent long time period, the relaxation dynamics is mainly the motion of the interface that separates the two regions {ϕ ≈ 0} and {ϕ ≈ 1}. It is reasonable to assume that the early fast time scale is determined by the basic reaction-diffusion equation

$${\partial }_t\varphi =\xi \mathrm{\Delta }\varphi -\frac{1}{\xi }{W}^{\prime }(\varphi ),$$

as again the electrostatic relaxation is instantaneous. Perturbing the unstable constant equilibrium solution ϕ₀(x) = 1/2 by δ exp (ik · x + ωt) with |δ| ≪ 1, we find the most unstable mode k_c = 0 and the corresponding fastest growth rate ω(k_c) = O(1/ξ). Therefore, the fast time scale is t/ξ. The next time scales are the regular time scale t, a slow time scale ξt, and so on.

Let us first consider the fast time scale T = t/ξ. We assume that

$$\varphi (x,t)={\varphi }_0(x,T)+\xi {\varphi }_1(x,T)+{\xi }^2{\varphi }_2(x,T)+\cdots ,$$ (4.5)

$$\psi (x,t)={\psi }_0(x,T)+\xi {\psi }_1(x,T)+{\xi }^2{\psi }_2(x,T)+\cdots ,$$ (4.6)

where ϕ_i = ϕ_i(x, T) and ψ_i = ψ_i(x, T) (i = 0, 1, …) are smooth and bounded functions satisfying the boundary conditions

$${\varphi }_i=0(i\ge 0),{\psi }_0={\psi }_{\infty },\text{and}{\psi }_i=0(i\ge 1)\text{on}\partial \mathrm{\Omega }.$$ (4.7)

Substitute ϕ and ψ in (4.1) by these expansions and match terms with the same orders of ξ. At the leading order O(ξ⁻¹), we obtain ∂_T ϕ₀ = −γ₀W′(ϕ₀). This equation has two stable fixed points 0 and 1. So,

$$\text{for}\text{any}x\in \mathrm{\Omega },{\varphi }_0(x,T)\to 0\text{or}1\text{exponentially}\text{as}T\to \infty .$$ (4.8)

Similarly, placing our expansions into (4.2), we obtain the leading-order O(1)-equation

$$\nabla ·\epsilon ({\varphi }_0)\nabla {\psi }_0-{({\varphi }_0-1)}^2{V}^{\prime }({\psi }_0)=-{\rho }_{\mathrm{f}}.$$ (4.9)

This is exactly (4.2), as expected. More equations corresponding to other higher powers of ξ can be obtained but they provide less useful information. We therefore need to examine the next time scale, the regular time scale.

We assume that, at the regular time scale, the solution ϕ and ψ have the expansions

$$\begin{array}{l}\varphi (x,t)={\varphi }_0(x,t)+\xi {\varphi }_1(x,t)+{\xi }^2{\varphi }_2(x,t)+\cdots ,\\ \psi (x,t)={\psi }_0(x,t)+\xi {\psi }_1(x,t)+{\xi }^2{\psi }_2(x,t)+\cdots ,\end{array}$$

where ϕ_i = ϕ_i(x, t) and ψ_i = ψ_i(x, t) (i = 0, 1, …) are smooth and bounded functions that satisfy the boundary conditions (4.7). Note that these are functions of (x, t), different from those of (x, T) in (4.5) and (4.6). Substituting ϕ and ψ in (4.1) by these expansions and matching the terms with the same orders of ξ, we obtain the first two equations

$$\begin{array}{ll}O({\xi }^{-1}):\hfill & W^{\prime }({\varphi }_0)=0,\hfill \\ O(1):\hfill & {\partial }_t{\varphi }_0=-2P{\varphi }_0-{\gamma }_0{W}^{″}({\varphi }_0){\varphi }_1-2{\rho }_{\mathrm{w}}({\varphi }_0-1)U\hfill \end{array}$$ (4.10)

$$+\frac{1}{2}{\epsilon }^{\prime }({\varphi }_0){\mid \nabla {\psi }_0\mid }^2+2({\varphi }_0-1)V({\psi }_0).$$ (4.11)

Note that Eq. (4.2) does not involve any time derivatives. Thus, substituting ϕ and ψ in (4.2) by their expansions, we obtain the same equation (4.9) in the leading order.

Eq. (4.10) implies that ϕ₀ = 0, 1, or 1/2. By (4.8), we must have ϕ₀ = 0 or 1. Since ϕ₀ = 0 on ∂Ω, we have ϕ₀ = 0 near ∂Ω. By the assumption (A2) on the function U in Section 2 and (4.11), ϕ₀ cannot be identically 0 in Ω. Thus, both {ϕ₀ = 0} and {ϕ₀ = 1} are nonempty. But ϕ₀ is a continuous function. This means that our above expansions for ϕ and ψ are valid only in the outer region, i.e., the union of ${\mathrm{\Omega }}_{\xi }^{+}(t):=\{x\in \mathrm{\Omega }:\varphi (x,t)\approx 1\}$ and ${\mathrm{\Omega }}_{\xi }^{-}(t):=\{x\in \mathrm{\Omega }:\varphi (x,t)\approx 0\}$. The region ${\mathrm{\Omega }}_{\xi }^{+}(t)$ contains all the points x_i (1 ≤ i ≤ N). The boundary of the region ${\mathrm{\Omega }}_{\xi }^{-}(t)$ contains the boundary of Ω.

We assume the inner region, a thin transition layer of width O(ξ) that is complement to the outer region, centers around the closed and smooth interface Γ_ξ(t) = {x ∈ Ω : ϕ(x, t) = 1/2} enclosing ${\mathrm{\Omega }}_{\xi }^{+}(t)$. This interface is the perturbation of a closed and smooth interface Γ(t) that is also inside the inner region and that does not depend on ξ. We assume that all the principal curvatures of these interfaces are O(1) with respect to ξ → 0. For a given point x in the inner region, we denote by s(x, t) the signed distance from x to Γ_ξ(t), positive interior and negative exterior of the interface. This is a smooth function depending on ξ such that |∇s(x, t)| = 1. Let P_tx ∈ Γ_ξ(t) be the projection of x onto Γ_ξ(t), defined by |s(x, t)| = ||x − P_tx||. (We use the Euclidean norm and distance.) The projection P_t depends on ξ. For ξ > 0 small enough, one can expect that the projection P_tx ∈ Γ_ξ(t) is unique. We shall assume so. Consequently, the vector x − P_t(x) is normal to Γ_ξ(t) at P_tx.

We shall show that, to the leading order with respect to ξ → 0, the interface Γ(t), or equivalently the interface Γ_ξ(t), does not move at this time scale. To this end, let us introduce a local coordinate system for the inner region [14, 15]. Consider an open neighborhood D(t) in ℝ³ that covers an O(ξ)-neighborhood of a part of Γ_ξ(t). Let Q(t) ⊂ ℝ² be a smooth domain and Φ(·, t) : Q(t) → D(t) ∩ Γ_ξ(t) a smooth parameterization of the patch of interface D(t) ∩ Γ_ξ(t) such that the coordinate lines y_i = 0 (i = 1, 2) are exactly the lines of principal curvature and the coordinates y₁ and y₂ of y = (y₁, y₂) ∈ Q(t) are the corresponding arc lengths of these lines on Γ_ξ(t). Then any point x ∈ D(t) of the inner region can be expressed uniquely as

$$x=\mathrm{\Phi }(y,t)+\xi z(t)n(y,t),$$ (4.12)

where Φ(y, t) is exactly the projection of x onto Γ_ξ(t), z(t) = s(x, t)/ξ, and n(y, t) = ∇_xs(x, t) is the unit normal to the interface Γ_ξ(t) at the projection Φ(y, t), pointing from the exterior to interior of the interface Γ_ξ(t). We shall denote by J = J (y, t) the Jacobian matrix of the mapping Φ(·, t) : Q(t) → D(t) ∩ Γ_ξ(t). This is a 3 × 2 matrix at each point y = (y₁, y₂) with the jth column being the vector ∂_yj Φ(y, t) (j = 1, 2). These columns are orthonormal vectors and are tangent to the surface Γ_ξ(t). Note that all D(t), Φ(y, t), J (y, t), z(t), and n(y, t) can depend on ξ. Both Φ(y, t) and J(y, t) are O(1) with respect to ξ → 0. Note also that the z component of the (z, y) coordinate is a global variable, independent of the parameterization Φ(·, t) of the patch of interface D(t) ∩ Γ_ξ(t).

The relation (4.12) determines locally y = y(x, t) and z = z(x, t) as smooth functions of x and t. In particular, z(x, t) = s(x, t)/ξ. Let v = v(y, t) and H = H(y, t) be the normal velocity and mean curvature of the point Φ(y, t) ∈ Γ_ξ(t) defined by v(y, t) = ∂_tΦ(y, t) · n(y, t) and H(y, t) = ∇_y · n(y, t)/2, respectively. We have for any x related to (z, y) by (4.12) that

$${\nabla }_{x}z(x,t)={\xi }^{-1}n(y,t),$$ (4.13)

$${\mathrm{\Delta }}_{x}z(x,t)=2{\xi }^{-1}H(y,t)+O(1),$$ (4.14)

$${\partial }_{t}z(x,t)=-{\xi }^{-1}v(y,t),$$ (4.15)

$${\nabla }_{x}y(x,t)=J(y,t)+O(\xi ).$$ (4.16)

Eq. (4.13) follows from n(y, t) = ∇_xs(x, t) and ξz(x, t) = s(x, t). Eq. (4.14) follows from the fact that ∂_yjn is the jth column of J multiplied by the jth principal curvature; cf. (2.3) in [15]. Fixing x and replacing z(t) by s(x, t) in (4.12), differentiating both sides of this equation with respect to t, and then dotting with the unit vector n = n(y, t), we then obtain (4.15). Finally, Eq. (4.16) follows from a formula for ∇_xy in Lemma 2.1 of [15]. With these, we further obtain by a series of calculations that, for any smooth functions f = f(x, t) and f̃ = f̃(z, y, t) that satisfy f(x, t) = f̃(z, y, t) with x and (z, y) related by (4.12),

$${\nabla }_{x}f=(J{\nabla }_y+{\xi }^{-1}n{\partial }_z)\stackrel{\sim }{f}+O(\xi ),$$ (4.17)

$${\mathrm{\Delta }}_{x}f=({\xi }^{-1}2H{\partial }_z+{\xi }^{-2}{\partial }_{zz}^2)\stackrel{\sim }{f}+O(1),$$ (4.18)

$${\partial }_{t}f=({\partial }_t-{\xi }^{-1}v{\partial }_z)\stackrel{\sim }{f}.$$ (4.19)

We now assume that the solutions ϕ = ϕ(x, t) and ψ = ψ(x, t) have the following expansions in the intersection of D(t) and the inner region [4, 34, 36]:

$$\begin{array}{l}\varphi (x,t)={\stackrel{\sim }{\varphi }}_0(z,y,t)+\xi {\stackrel{\sim }{\varphi }}_1(z,y,t)+{\xi }^2{\stackrel{\sim }{\varphi }}_2(z,y,t)+\cdots ,\\ \psi (x,t)={\stackrel{\sim }{\psi }}_0(z,y,t)+\xi {\stackrel{\sim }{\psi }}_1(z,y,t)+{\xi }^2{\stackrel{\sim }{\psi }}_2(z,y,t)+\cdots ,\end{array}$$

where x and (z, y) are related by (4.12), and all ϕ̃_i = ϕ̃_i(z, y, t) and ψ̃_i = ψ̃_i(z, y, t) (i = 0, 1, …) are smooth and bounded functions. Substitute ϕ and ψ in (4.1) with these inner expansions, apply (4.17)–(4.19), and group terms of the same orders in terms of powers of ξ.

Equating the terms of the order O(ξ⁻²), we get ε′(ϕ̃₀)(∂_z ψ̃₀)² = 0. Since ϕ₀ = 0 or 1 in the outer region, we can assume that the set of points in the inner region at which ϕ̃ = 0 or 1 has the Lebesgue measure zero. Thus, by our assumption (A3) in Section 2, ε′(ϕ̃₀) ≠ 0 almost everywhere in the inner region. Consequently, ∂_z ψ̃₀ = 0 in the inner region. With this, we obtain at the next order O(ξ⁻¹) that

$$-v{\partial }_z{\stackrel{\sim }{\varphi }}_0={\gamma }_0\left[{\partial }_{zz}^2{\stackrel{\sim }{\varphi }}_0-W^{\prime }({\stackrel{\sim }{\varphi }}_0)\right].$$ (4.20)

By matching the inner and outer solutions, we have ϕ̃₀(z, y, t) → 0 if z → −∞ and ϕ̃₀(z, y, t) → 1 if z → +∞. Moreover, since ϕ̃₀ is smooth and bounded, we have also that ∂_z ϕ̃₀ → 0 as z → −∞ or ∞. Therefore, multiplying both sides of (4.20) by ∂_z ϕ̃₀ and integrating over z from −∞ and ∞, we obtain

$$-v{\int }_{-\infty }^{\infty }{\left({\partial }_z{\stackrel{\sim }{\varphi }}_0\right)}^{2}dz={{\gamma }_0\left[\frac{1}{2}{({\partial }_z{\stackrel{\sim }{\varphi }}_0)}^2-W({\stackrel{\sim }{\varphi }}_0)\right]|}_{z=-\infty }^{z=\infty }=0.$$

Hence v = v(y, t) = 0. Therefore, at the leading order of ξ, the interface does not move at the regular time scale. However, in the next long time period measured by a slow time scale, the interface still moves. Note that all these results depend only on the global variable z but not on the local variable y, i.e., not on the parametrization Φ(·, t) : Q(t) → D(t) ∩ Γ_ξ(t).

5. Relaxation Dynamics: Slow Time Scale and Sharp-Interface Limit

We now consider the slow time scale τ = ξt and obtain the leading order of the normal velocity for this interface motion. Based on the previous analysis, we assume at each τ the system region Ω is divided by a closed and smooth interface Γ(τ) into two regions Ω⁻(τ) and Ω⁺(τ), outside and inside of Γ(τ), respectively. We assume the principal curvatures at any point of Γ(τ) are of order O(1) with respect to ξ → 0. We have ϕ ≈ 0 in Ω⁻(τ) and ϕ ≈ 1 in Ω⁺(τ). Moreover, all x_i ∈ Ω⁺(τ) (1 ≤ i ≤ N). Hence Ω⁺(τ) approximates the solute region Ω_p and Ω⁻(τ) approximates the solvent region Ω_w.

We assume that in the outer region—the region outside an O(ξ) neighborhood of Γ(τ)—the solutions ϕ and ψ have the expansions

$$\begin{array}{l}\varphi (x,t)={\varphi }_0(x,\tau )+\xi {\varphi }_1(x,\tau )+{\xi }^2{\varphi }_2(x,\tau )+\cdots ,\\ \psi (x,t)={\psi }_0(x,\tau )+\xi {\psi }_1(x,\tau )+{\xi }^2{\psi }_2(x,\tau )+\cdots ,\end{array}$$

where ϕ_i = ϕ_i(x, τ) and ψ_i = ψ_i(x, τ) with τ = ξt are smooth and bounded functions that satisfy the boundary conditions (4.7). Plugging these into (4.1) and comparing the terms of the same orders of ξ, we obtain

$$O({\xi }^{-1}):0=W^{\prime }({\varphi }_0),$$ (5.1)

Similarly, we have by (4.2) that

$$O(1):\nabla ·\epsilon ({\varphi }_0)\nabla {\psi }_0-{({\varphi }_0-1)}^2{V}^{\prime }({\psi }_0)=-{\rho }_{\mathrm{f}}.$$ (5.2)

By (5.1) and the boundary condition for ϕ₀, we get ϕ₀ = 0 in the Ω⁻(τ) part of the outer region and ϕ₀ = 1 in the Ω⁺(τ) part of the outer region. In particular, as ξ → 0, ϕ₀ converges to 1 and 0, inside and outside Γ(τ), respectively.

We now consider the solutions ϕ and ψ in the inner region, an O(ξ)-neighborhood of Γ(τ). As before, we introduce a local coordinate system for the inner region. Let s(x, τ), P_τ(x), D(τ), Q(τ), Φ = Φ(y, τ), J = J(y, τ), z = z(τ), n = n(y, τ), H = H(y, τ), and v = v(y, τ) be all the same as those in Section 4 with τ replacing t and Γ(τ) replacing Γ_ξ(t), respectively. We relate a point x ∈ D(τ) in the inner region to the local coordinates (z, y) by

$$x=\mathrm{\Phi }(y,\tau )+\xi z(\tau )n(y,\tau ).$$ (5.3)

We still have (4.13), (4.14), and (4.16) with t replaced by τ. Eq. (4.15) is changed now to ∂_tz(x, τ) = −v(x, τ). If f(x, τ) and f̃(z, y, τ) are two smooth functions and f(x, τ) = f̃(z, y, τ) with x and (z, y) related by (5.3), then (4.17) and (4.18) still hold true; but (4.19) is changed to ∂_tf = (ξ∂_τ − v∂_z) f̃.

We assume now the following local expansions in the inner region:

$$\begin{array}{l}\varphi (x,t)={\stackrel{\sim }{\varphi }}_0(z,y,\tau )+\xi {\stackrel{\sim }{\varphi }}_1(z,y,\tau )+{\xi }^2{\stackrel{\sim }{\varphi }}_2(z,y,\tau )+\cdots ,\\ \psi (x,t)={\stackrel{\sim }{\psi }}_0(z,y,\tau )+\xi {\stackrel{\sim }{\psi }}_1(z,y,\tau )+{\xi }^2{\stackrel{\sim }{\psi }}_2(z,y,\tau )+\cdots ,\end{array}$$

where ϕ̃_i = ϕ̃_i(z, y, τ) and ψ̃_i = ψ̃_i(z, y, τ) (i = 0, 1, …) are smooth and bounded functions, and x and (z, y) are related by (5.3). We also have by (5.3) that

$$U(x)=U(\mathrm{\Phi }(y,\tau )+\xi z(\tau )n(y,\tau ))={\stackrel{\sim }{U}}_0(y,\tau )+O(\xi ).$$

where Ũ₀(y, τ) = U(Φ(y, τ)). If x = Φ(y, τ) ∈ Γ(τ) then Ũ₀(y, τ) = U(x).

Plug these expansions into (4.1) and equate the terms with the same power of ξ to obtain

$$O({\xi }^{-2}):0={\partial }_z{\stackrel{\sim }{\psi }}_0,$$ (5.4)

$$\begin{array}{ll}O({\xi }^{-1}):& 0={\partial }_{zz}^2{\stackrel{\sim }{\varphi }}_0-W^{\prime }({\stackrel{\sim }{\varphi }}_0).\\ O(1):& -v{\partial }_z{\stackrel{\sim }{\varphi }}_0=-2P{\stackrel{\sim }{\varphi }}_0+{\gamma }_0\left[2H{\stackrel{\sim }{\varphi }}_0+{\partial }_{zz}^2{\stackrel{\sim }{\varphi }}_1-W^{″}({\stackrel{\sim }{\varphi }}_0){\stackrel{\sim }{\varphi }}_1\right]-2{\rho }_{\mathrm{w}}({\stackrel{\sim }{\varphi }}_0-1){\stackrel{\sim }{U}}_0\end{array}$$ (5.5)

$$+\frac{1}{2}{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0)\left[{\mid {\nabla }_{\mathrm{\Gamma }(\tau )}{\stackrel{\sim }{\psi }}_0\mid }^2+{({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2\right]+2({\stackrel{\sim }{\varphi }}_0-1)V({\stackrel{\sim }{\psi }}_0).$$ (5.6)

In obtaining (5.4), we use the fact that ϕ₀ = 0 or 1 in the outer region to assume that ϕ̃₀ ∈ (0, 1) and hence ε′(ϕ̃₀) ≠ 0 almost everywhere in the inner region. Eq. (5.4) is used to obtain (5.5) and (5.6). By (5.4), ψ̃₀(z, y, τ) = ψ̃₀(0, y, τ) is the value of ψ̃₀ at the point Φ(y, τ) ∈ Γ(τ). Note that the surface graident term ∇_Γ(τ)ψ̃₀ in (5.6) is an O(ξ)-approximation of J∇_yψ̃₀ by (4.16) and the fact that columns of J are orthogonal to n:

$$\begin{array}{l}{\nabla }_{\mathrm{\Gamma }(\tau )}{\stackrel{\sim }{\psi }}_0=(I-n\otimes n){\nabla }_x{\stackrel{\sim }{\psi }}_0=(I-n\otimes n)D_{x}y{\nabla }_y{\stackrel{\sim }{\psi }}_0\\ =(I-n\otimes n)J{\nabla }_y{\stackrel{\sim }{\psi }}_0+O(\xi )=J{\nabla }_y{\stackrel{\sim }{\psi }}_0+O(\xi ).\end{array}$$

Similarly, plugging the inner expansions of ϕ and ψ into (4.2), we obtain by (5.4) and the fact that columns of J = J(y, τ) are orthogonal to the normal n = n(y, τ) that

$$O({\xi }^{-1}):{\partial }_z\left[\epsilon ({\stackrel{\sim }{\varphi }}_0){\partial }_z{\stackrel{\sim }{\psi }}_1\right]=0.$$ (5.7)

Fix x = Φ(y, τ) ∈ Γ(τ). Let us employ the following matching conditions [4, 34, 36]:

$$\underset{z\to \pm \infty }{lim}{\stackrel{\sim }{\varphi }}_0(z,y,\tau )={\varphi }_0^{\pm }(x,\tau ),$$ (5.8)

$$\underset{z\to \pm \infty }{lim}{\stackrel{\sim }{\psi }}_0(z,y,\tau )={\psi }_0^{\pm }(x,\tau ),$$ (5.9)

$${\stackrel{\sim }{\psi }}_1(z,y,\tau )=({\psi }_1^{\pm }+z\nabla {\psi }_0^{\pm }·\nabla s)(x,\tau )+o(1)\text{as}z\to \pm \infty ,$$ (5.10)

where ${\varphi }_0^{\pm }(x,\tau )={lim}_{\alpha \to 0^{\pm }}{\varphi }_0(x+\alpha \nabla s(x,\tau ))$ and ${\psi }_i^{\pm }(x,\tau )={lim}_{\alpha \to 0^{\pm }}{\psi }_i(x+\alpha \nabla s(x,\tau ))$. Since ϕ₀ = 0 in Ω⁻(τ) and ϕ₀ = 1 in Ω⁺(τ), we have by (5.5) and (5.8) that

$${\stackrel{\sim }{\varphi }}_0(z,y,\tau )={\stackrel{\sim }{\varphi }}_0(z)=\frac{1}{2}+\frac{e^{3z}-e^{-3z}}{2(e^{3z}+e^{-3z})}.$$ (5.11)

We now derive the following matching condition that will be used later:

$${\partial }_z{\stackrel{\sim }{\psi }}_1(z,y,\tau )=\nabla {\psi }_0^{\pm }(x,\tau )·\nabla s(x,\tau )+o(1)\text{as}z\to \pm \infty .$$ (5.12)

Let us rewrite the matching condition (5.10) as

$${\stackrel{\sim }{\psi }}_1(z,y,\tau )={\psi }_1^{\pm }(x,\tau )+z\nabla {\psi }_0^{\pm }(x,\tau )·\nabla s(x,\tau )+g^{\pm }(z,y,\tau )$$

for some smooth functions g⁺ = g⁺(z, y, τ) (z > 0) and g⁻ = g⁻(z, y, τ) (z < 0) such that g^±(z, y, τ) = o(1) as z → ±∞, respectively. Thus

$${\partial }_z{\stackrel{\sim }{\psi }}_1(z,y,\tau )=\nabla {\psi }_0^{\pm }(x,\tau )·\nabla s(x,\tau )+{\partial }_z{g}^{\pm }(z,y,\tau ).$$ (5.13)

By (5.7), we have ∂_zψ̃₁(z, y, τ) = h(y, τ)/ε(ϕ̃₀(z)) for some smooth and bounded function h = h(y, τ) independent of z. This and (5.13) imply that ∂_zg^± are bounded as z → ±∞. Moreover, with these two equations and (5.11), we obtain

$$\mid {\partial }_{zz}^2{g}^{\pm }(z,y,\tau )\mid =|{\partial }_{zz}^2{\stackrel{\sim }{\psi }}_1(z,y,\tau )|=\left|{\partial }_z\left[\frac{h(y,\tau )}{\epsilon ({\stackrel{\sim }{\psi }}_0(z))}\right]\right|\le \frac{6{\epsilon }_{max}^{\prime }\mid h(y,\tau )\mid }{{\epsilon }_{max}^2}{e}^{-6z}.$$

Consequently, for any A₂ > A₁ > 0,

$$|{[{\partial }_z{g}^{+}(A_2)]}^2-{[{\partial }_z{g}^{+}(A_1)]}^2|=\left|{\int }_{A_1}^{A_2}{\partial }_z\left[{({\partial }_z{g}^{+})}^2\right]dz\right|\le 2{\int }_{A_1}^{A_2}\mid {\partial }_z{g}^{+}\mid \mid {\partial }_{zz}{g}^{+}\mid dz\to 0$$

as A₁, A₂ → ∞. Therefore, (∂_zg⁺)² → a⁺ as z → ∞ for some a⁺ ≥ 0. We must have a⁺ = 0, since g⁺ → 0 as z → ∞. Therefore ∂_zg⁺ → 0 as z → ∞. Similarly ∂_zg⁻ → 0 as z → −∞. Hence (5.12) follows from (5.13).

We now show that ψ₀ solves the Poisson–Boltzmann equation with the dielectric boundary Γ(τ). By (5.4), ψ̃₀ is independent of z. Therefore, (5.2), the matching condition (5.9), and the boundary condition ψ₀ = ψ_∞ on ∂Ω allow us to determine ψ₀ in the outer region. Moreover, the matching condition (5.9) implies that ${\stackrel{\sim }{\psi }}_0={\psi }_0^{+}={\psi }_0^{-}$ on Γ(τ). Integrating both sides of Eq. (5.7) over z from −∞ to ∞, we obtain by (5.12) that ${\epsilon }_{\mathrm{w}}{\epsilon }_0\nabla {\psi }_0^{-}·n={\epsilon }_{\mathrm{p}}{\epsilon }_0\nabla {\psi }_0^{+}·n$ on Γ(τ). These, together with (5.2) and (4.7), imply that ψ₀ is the solution to the elliptic interface problem

$$\{\begin{array}{ll}{\epsilon }_{\mathrm{w}}{\epsilon }_0\mathrm{\Delta }{\psi }_0-V^{\prime }({\psi }_0)=-{\rho }_{\mathrm{f}}\hfill & \text{in}{\mathrm{\Omega }}^{-}(\tau ),\hfill \\ {\epsilon }_{\mathrm{p}}{\epsilon }_0\mathrm{\Delta }{\psi }_0=-{\rho }_{\mathrm{f}}\hfill & \text{in}{\mathrm{\Omega }}^{+}(\tau ),\hfill \\ {\psi }_0^{-}={\psi }_0^{+}\hfill & \text{on}\mathrm{\Gamma }(\tau ),\hfill \\ {\epsilon }_{\mathrm{w}}{\epsilon }_0\nabla {\psi }_0^{-}·n={\epsilon }_{\mathrm{p}}{\epsilon }_0\nabla {\psi }_0^{+}·n\hfill & \text{on}\mathrm{\Gamma }(\tau ),\hfill \\ {\psi }_0={\psi }_{\infty }\hfill & \text{on}\partial \mathrm{\Omega }.\hfill \end{array}$$ (5.14)

This is equivalent to the boundary-value problem of the Poisson–Boltzmann equation (1.2) and (1.3) with ψ replaced by ψ₀ [27].

We finally derive the motion law for the interface Γ(τ). For notational simplicity, let us skip writing the variables y and τ for a moment. Multiplying both sides of (5.6) by ${\stackrel{\sim }{\varphi }}_0^{\prime }$ and integrating over z from −∞ to ∞, we obtain that

$$-vS={\int }_{-\infty }^{\infty }{R}_1(z){\stackrel{\sim }{\varphi }}_0^{\prime }(z)\mathrm{d}z+{\int }_{-\infty }^{\infty }{R}_2(z){\stackrel{\sim }{\varphi }}_0^{\prime }(z)\mathrm{d}z+{\int }_{-\infty }^{\infty }{R}_3(z){\stackrel{\sim }{\varphi }}_0^{\prime }(z)\mathrm{d}z,$$ (5.15)

where by (5.11)

$$\begin{array}{l}S:={\int }_{-\infty }^{\infty }{\left[{\stackrel{\sim }{\varphi }}_0^{\prime }(z)\right]}^2\mathrm{d}z={\int }_{-\infty }^{\infty }\frac{36e^{12z}}{{(e^{6z}+1)}^4}\mathrm{d}z={\int }_0^{\infty }\frac{6x}{{(x+1)}^4}\mathrm{d}x=1,\\ R_1(z):=-2P{\stackrel{\sim }{\varphi }}_0-2{\rho }_{\mathrm{w}}({\stackrel{\sim }{\varphi }}_0-1){\stackrel{\sim }{U}}_0+2({\stackrel{\sim }{\varphi }}_0-1)V({\stackrel{\sim }{\psi }}_0),\\ R_2(z):={\gamma }_0\left[2H{\partial }_z{\stackrel{\sim }{\varphi }}_0+{\partial }_{zz}^2{\stackrel{\sim }{\varphi }}_1-W^{″}({\stackrel{\sim }{\varphi }}_0){\stackrel{\sim }{\varphi }}_1\right],\\ R_3(z):=\frac{1}{2}{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0)\left[{\mid {\nabla }_{\mathrm{\Gamma }(\tau )}{\stackrel{\sim }{\psi }}_0\mid }^2+{({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2\right].\end{array}$$ (5.16)

Since Ũ₀ and V(ψ̃₀) are independent of z, we have

$$\begin{array}{l}{\int }_{-\infty }^{\infty }{R}_1(z){\stackrel{\sim }{\varphi }}_0^{\prime }(z)\mathrm{d}z=-2P{\int }_{-\infty }^{\infty }{\stackrel{\sim }{\varphi }}_0{\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z+2\left[V({\stackrel{\sim }{\psi }}_0)-{\rho }_{\mathrm{w}}{\stackrel{\sim }{U}}_0\right]{\int }_{-\infty }^{\infty }\left({\stackrel{\sim }{\varphi }}_0-1\right){\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z\\ ={-P{\stackrel{\sim }{\varphi }}_0^2|}_{z=-\infty }^{z=\infty }+{\left[V({\stackrel{\sim }{\psi }}_0)-{\rho }_{\mathrm{w}}{\stackrel{\sim }{U}}_0\right]{\left({\stackrel{\sim }{\varphi }}_0-1\right)}^2|}_{z=-\infty }^{z=\infty }\\ =-P+{\rho }_{\mathrm{w}}U-V({\psi }_0),\end{array}$$ (5.17)

where we have on Γ(τ) that Ũ₀ = U, and that ψ̃₀ = ψ₀ by (5.4) and (5.9).

By integration by parts and the fact that ${\stackrel{\sim }{\varphi }}_0^{\prime }(\pm \infty )={\stackrel{\sim }{\varphi }}_0^{″}(\pm \infty )=0$, we have

$${\int }_{-\infty }^{\infty }{\partial }_{zz}^2{\stackrel{\sim }{\varphi }}_1{\stackrel{\sim }{\varphi }}_0^{\prime }dz={\int }_{-\infty }^{\infty }{\stackrel{\sim }{\varphi }}_0^{‴}{\stackrel{\sim }{\varphi }}_{1}dz.$$

Therefore, by (5.16) and (5.5), we have

$${\int }_{-\infty }^{\infty }{R}_2(z){\stackrel{\sim }{\varphi }}_0^{\prime }(z)\mathrm{d}z=2{\gamma }_{0}H{+}_0{\int }_{-\infty }^{\infty }{\partial }_z\left[{\stackrel{\sim }{\varphi }}_0^{″}-W^{\prime }({\stackrel{\sim }{\varphi }}_0)\right]{\stackrel{\sim }{\varphi }}_1\mathrm{d}z=2{\gamma }_{0}H.$$ (5.18)

Now, since ${\stackrel{\sim }{\psi }}_0={\psi }_0^{-}={\psi }_0^{+}$ on Γ(τ), we have ${\nabla }_{\mathrm{\Gamma }(\tau )}{\stackrel{\sim }{\psi }}_0={\nabla }_{\mathrm{\Gamma }(\tau )}{\psi }_0^{-}={\nabla }_{\mathrm{\Gamma }(\tau )}{\psi }_0^{+}={\nabla }_{\mathrm{\Gamma }(\tau )}{\psi }_0$. Consequently,

$$\begin{array}{l}{\int }_{-\infty }^{\infty }{R}_3(z){\stackrel{\sim }{\varphi }}_0^{\prime }(z)\mathrm{d}z=\frac{1}{2}{\int }_{-\infty }^{\infty }{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0)\left[{\mid {\nabla }_{\mathrm{\Gamma }(\tau )}{\stackrel{\sim }{\psi }}_0\mid }^2+{({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2\right]{\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z\\ =\frac{1}{2}({\epsilon }_{\mathrm{p}}{\epsilon }_0-{\epsilon }_{\mathrm{w}}{\epsilon }_0){\mid {\nabla }_{\mathrm{\Gamma }(\tau )}{\psi }_0\mid }^2+\frac{1}{2}{\int }_{-\infty }^{\infty }{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0){({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2{\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z.\end{array}$$ (5.19)

Rewrite (5.7) as $\epsilon ({\stackrel{\sim }{\varphi }}_0){\partial }_{zz}^2{\stackrel{\sim }{\psi }}_1=-{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0){\stackrel{\sim }{\varphi }}_0^{\prime }{\partial }_z{\stackrel{\sim }{\psi }}_1$. With this and (5.12), we have

$$\begin{array}{l}\frac{1}{2}{\int }_{-\infty }^{\infty }{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0){({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2{\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z={\frac{1}{2}\epsilon ({\stackrel{\sim }{\varphi }}_0){({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2|}_{z=-\infty }^{z=\infty }-{\int }_{-\infty }^{\infty }\epsilon ({\stackrel{\sim }{\varphi }}_0){\partial }_z{\stackrel{\sim }{\psi }}_1{\partial }_{zz}^2{\stackrel{\sim }{\psi }}_1\mathrm{d}z\\ =\frac{1}{2}{\epsilon }_{\mathrm{p}}{\epsilon }_0{\mid \nabla {\psi }_0^{+}·n\mid }^2-\frac{1}{2}{\epsilon }_{\mathrm{w}}{\epsilon }_0{\mid \nabla {\psi }_0^{-}·n\mid }^2+{\int }_{-\infty }^{\infty }{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0){({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2{\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z.\end{array}$$

Note that the last term on the right-hand side doubles the term on the left-hand side. This and the third equation in (5.14) then lead to

$$\begin{array}{l}\frac{1}{2}{\int }_{-\infty }^{\infty }{\epsilon }^{\prime }({\stackrel{\sim }{\varphi }}_0){({\partial }_z{\stackrel{\sim }{\psi }}_1)}^2{\stackrel{\sim }{\varphi }}_0^{\prime }\mathrm{d}z=\frac{1}{2}{\epsilon }_{\mathrm{w}}{\epsilon }_0{\mid \nabla {\psi }_0^{-}·n\mid }^2-\frac{1}{2}{\epsilon }_{\mathrm{p}}{\epsilon }_0{\mid \nabla {\psi }_0^{+}·n\mid }^2\\ =\frac{1}{2}\left(\frac{1}{{\epsilon }_{\mathrm{w}}{\epsilon }_0}-\frac{1}{{\epsilon }_{\mathrm{p}}{\epsilon }_0}\right){\mid {\epsilon }_{\mathrm{\Gamma }(\tau )}\nabla {\psi }_0·n\mid }^2,\end{array}$$ (5.20)

where ε_Γ(τ) is defined in (1.4) with Γ(τ) replacing Γ.

Finally, it follows from (5.15)–(5.20) that

$$v=P-2{\gamma }_{0}H-{\rho }_{\mathrm{w}}U+\frac{1}{2}\left(\frac{1}{{\epsilon }_{\mathrm{p}}{\epsilon }_0}-\frac{1}{{\epsilon }_{\mathrm{w}}{\epsilon }_0}\right){\mid {\epsilon }_{\mathrm{\Gamma }(\tau )}\nabla {\psi }_0·n\mid }^2+\frac{1}{2}({\epsilon }_{\mathrm{w}}{\epsilon }_0-{\epsilon }_{\mathrm{p}}{\epsilon }_0){\mid {\nabla }_{\mathrm{\Gamma }(\gamma )}{\psi }_0\mid }^2+V({\psi }_0).$$

Since our normal n points from the interior to exterior and mean curvature H = ∇ · n/2, opposite to that in the sharp-interface model (cf. the description above Eq. (1.5)), this is exactly the normal velocity v_n = −δ_ΓF[Γ] in the sharp-interface model (cf. (1.5)).

We summarize our analysis in the following:

Theorem 5.1

Assume as above the existence of a closed and smooth interface Γ(τ), the outer and inner expansions for the solutions ϕ and ψ to the initial-boundary-value problem (4.1)–(4.4), and the corresponding matching conditions. Then the following are true:

1. As ξ → 0, the leading order of the phase-field function ϕ converges to 1 in Ω⁺(τ) and 0 in Ω⁻(τ), respectively;

2. The leading-order of the electrostatic potential is the unique solution to the boundary-value problem of the Poisson–Boltzmann equation (1.2) and (1.3);

3. As ξ → 0, the normal velocity of the interface Γ(τ) converges to the boundary force −δ_ΓF[Γ] in (1.5), with Γ(τ) replacing Γ, as in the sharp-interface model.