Optimal-mass-transfer-based estimation of glymphatic transport in living brain

Abstract

It was recently shown that the brain-wide cerebrospinal fluid (CSF) and interstitial fluid exchange system designated the ‘glymphatic pathway’ plays a key role in removing waste products from the brain, similarly to the lymphatic system in other body organs^1,2. It is therefore important to study the flow patterns of glymphatic transport through the live brain in order to better understand its functionality in normal and pathological states. Unlike blood, the CSF does not flow rapidly through a network of dedicated vessels, but rather through para-vascular channels and brain parenchyma in a slower time-domain, and thus conventional fMRI or other blood-flow sensitive MRI sequences do not provide much useful information about the desired flow patterns. We have accordingly analyzed a series of MRI images, taken at different times, of the brain of a live rat, which was injected with a paramagnetic tracer into the CSF via the lumbar intrathecal space of the spine. Our goal is twofold: (a) find glymphatic (tracer) flow directions in the live rodent brain; and (b) provide a model of a (healthy) brain that will allow the prediction of tracer concentrations given initial conditions. We model the liquid flow through the brain by the diffusion equation. We then use the Optimal Mass Transfer (OMT) approach³ to derive the glymphatic flow vector field, and estimate the diffusion tensors by analyzing the (changes in the) flow. Simulations show that the resulting model successfully reproduces the dominant features of the experimental data.

1. Introduction

Clearance of interstitial waste products is essential to normal brain function. Hence, disturbances in waste removal of toxic products such as amyloid beta (Aβ) and tau proteins are implicated in the pathogenesis of Alzheimer's disease⁹. In most organs lymphatic vessels provide for the drainage of waste proteins, antibodies and solutes, however, the brain is unique in this regard because it lacks a conventional lymphatic drainage system¹⁰. In the central nervous system (CNS), clearance and/or transport of protein and excess solutes from the interstitial fluid (ISF) space is less well understood but is thought to be governed in part by cerebrospinal fluid (CSF) exchanging with ISF via para-arterial conduits (Virkow-Robin spaces)¹. In recent studies using optical imaging in combination with fluorescently tagged tracers injected into the intrathecal space, this CSF-ISF exchange system was further characterized in the live rodent brain². Specifically, it was demonstrated that small molecular weight (MW) tracers injected into the subarachnoid CSF move rapidly into the brain along both penetrating cortical and basal arteries (but not veins) to reach the capillary beds and associated interstitial compartments ² (Fig.1). It is confirmed that the fluorescently tagged tracers administered into CSF are cleared from the brain along the same pathways as intra-parenchymally injected tracers, accumulating primarily along large draining veins. It was also discovered that astrocytes play a pivotal role in linking the para-arterial inflow and the para-venous efflux pathways². In mice harboring the deletion of the astroglial aquaporin 4 (AQP4) water channels, tracer influx along para-arterial routes and through the brain interstitium was sharply reduced suggesting that fluid is mass transported through the astrocytic network. Together, the paravascular influx and clearance routes, coupled by trans-astroglial fluid mass transport, constitute a brain-wide waste clearance pathway, which is designated the ‘glymphatic system’².

Figure 1.

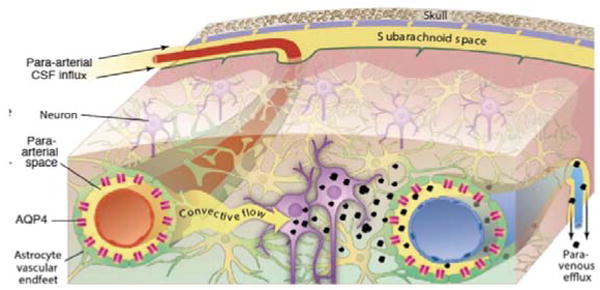
Schematic of the glymphatic pathway in rodent brain. Para-arterial inflow of cerebrospinal fluid (CSF) enters the brain tissue faciliated by astrocytic AQP4 water channels. The CSF mixes with the interstitial fluid (ISF) and propels the waste products of neuronal metabolism into the para-venous space, from which they are directed into cervical lymphatic vessels and ultimately returned to the general circulation for clearance by the liver.

To translate the glymphatic pathway findings observed with fluorescently tagged tracers and optical imaging towards a relevant preclinical test-bed, intrathecal injection of paramagnetic contrast molecules was combined with dynamic T1-weighted 3D brain MRI on a 9.4TmicroMRI instrument in rodents¹¹.

In the rodent brain, the primary, most rapid glymphatic inflow (defined as total normalized uptake >100) occurs at the level of the hypothalamus, olfactory, retrosplenial cortex, pons, amygdala, cerebellum and the hippocampus. Slower influx and clearance of Gd-DTPA is observed in the entorhinal cortex, insula and more remote brain regions such as caudate putamen, midbrain and thalamus. Importantly, the contrast-enhanced MRI technique for quantifying glymphatic pathway function was validated using conventional ex vivo optical imaging and fluorescently tagged tracers of same molecular weight¹¹. These studies show that we can quantify and capture both influx and efflux components of glymphatic transport the live rodent brain using contrast-enhanced MRI¹¹.

Driven by the initial image data of flow in the glymphatic system, use optimal mass transport to try to estimate the velocity vector field, and in turn use this to derive better computational fluid models, especially modelling the diffusion and advection fluxes at various point in the brain. Having a mathematical model would give us a better physical understanding of what occurs in the glymphatic systems, will allow us to propose further experiments, and allow us to predict how changes in the parameters (e.g., cell volume, pulsatility, AQP4 channels, and supine/prone positions) effect the overall flow.

The purpose of this research is to derive an analytic model of the transport through the glymphatic system of the brain, based upon a dynamic series of contrast-enhanced MRI images.

2. Algorithmic Details

2.1 Assumptions about the Data

The data is collected as a time series of T1-weighted MRI images taken after administration of paramagnetic contrast (Gd-DTPA, molecular weight 938 Da) into the lumbar intrathecal space of an anesthetized rat. The dynamic acquisition of data depicts a gradual propagation of the tracer into the brain. Based on anatomical mapping of signal changes induced by Gd-DTPA on the MRI images over time we assume (assumption 1) that the tracer is transported via the glymphatic pathway. We further assume (assumption 2) that brain-wide glymphatic transport can be described by the diffusion equation with anisotropic tensor coefficients that do not change with time (or change very slowly). The problem of flow estimation and modeling is then translated into the inverse problem of estimating the diffusion coefficients from concentration data. The model estimation process consists of two steps: an optical flow computation and diffusion tensor estimation; each of which are described below.

We finally assume (assumption 3) that the total mass of the tracer agent in the brain is almost constant (mass preservation) between consecutive time points. This assumption was made in order to simplify the optical flow estimation (and because modeling the tracer inflow and decay is not an easy task). A new model that takes tracer mass changes into account is currently being developed.

2.2 Optical Flow

At first, optical flow is computed between each pair of consecutive MRI images^4,5. One of the simplest flow models is based on optimal mass transport (OMT) also known as the Monge-Kantorovich problem^3,6. It is based on an energy minimization principle with a mass conservation constraint. Let Ω₀ and Ω₁ denote two subdomains of R^d, having smooth boundaries, each with a positive density function, μ₀ and μ₁, respectively. We assume ∫_Ω0 μ₀ = ∫_Ω1 μ₁ = 1 so that the same total mass is associated with Ω₀ and Ω₁ (assumption 3). We consider diffeomorphisms ϕ from (Ω₀, μ₀) to (Ω₁, μ₁), which map one density to the other in the sense that

$${\mu }_0=|\nabla \varphi |{\mu }_1\circ \varphi$$ (1)

(Jacobian equation). A mapping ϕ that satisfies the Jacobian equation is said to have the mass preservation (MP) property, written as ϕ ∈ MP. Here |∇ϕ| denotes the determinant of the Jacobian map ∇ϕ. A mapping ϕ that satisfies this property may be considered as a redistribution of the mass of material from one distribution μ₀ to another distribution μ₁. There may be many such mappings, and we want to pick out an optimal one. Accordingly, the optimization in the L^p Kantorovich – Wasserstein metric

$$d_p{({\mu }_0,{\mu }_1)}^p:=\underset{\varphi \in \mathit{\text{MP}}}{inf}{\int \Vert \varphi (x)-x\Vert }^p{\mu }_0(x)dx,$$ (2)

seeks an optimal MP map which, when it exists, minimizes a cost functional. This functional is seen to place a penalty on the distance the map ϕ moves each bit of material, weighted by the material's mass. The cases p = 1, 2 has been extensively studied. For p = 2, a fundamental result is that there is a unique optimal ϕ ∈ MP transporting μ₀ to μ₁, and that this ϕ is the gradient of a convex function u, i.e., ϕ = ∇u. Thus, the Kantorovich-Wasserstein metric defines as distance between two mass densities the cheapest way to transport one mass distribution to the other. The optimal transport map, denoted by ϕ_MK in the p = 2 case, can be computed by solving a PDE³.

2.3 Diffusion and the Analytical Model of the Brain

Let μ(t, x) be a nonnegative function describing the density of the tracer over the 3D brain domain, in time. We assume that tracer propagation through the brain tissue can be described by the diffusion equation (assumption 2):

$$\frac{\partial }{\partial t}\mu -\nabla ·(D(x,y,z)\nabla \mu )=0,$$ (3)

where ∇ · and ∇ denote divergence and gradient with respect to spatial coordinates, respectively, and D is a (spatially varying) symmetric 3×3 matrix (diffusion tensor). The eigenvectors of D point in the main diffusion directions, with the eigenvalues denoting the diffusivity (diffusion strength) in those directions. Our goal is to find D, given the transfer speeds defined for each MRI time sample by the mass transport maps ϕ_MK. Once D is known, we can compute tracer concentration at any point in time and space given any initial (and boundary) conditions.

Given a single transport map, we can only find the strength, k, of diffusion in the direction of the transport vector, w, in each voxel as follows:

$$k=\frac{\mu \Vert w\Vert }{\Vert \nabla \mu \Vert }.$$ (4)

This single direction-value combination does not provide sufficient information about the diffusion tensor. An analysis of all such combinations, however, reveals a more complete picture. At first, we construct a set Σ for each pixel, composed of vectors whose directions are those of the transport vectors (w) originating from that pixel at different times, and their magnitudes – the corresponding scalar diffusivities (k). For every v ∈ Σ, we also add −v ∈ Σ, since the diffusion direction is unsigned (i.e. diffusivity in one direction is the same as that in the opposite direction). The principal components of Σ are therefore parallel to the eigenvectors of the (approximated) diffusion tensor D, and their variances are the corresponding eigenvalues.

3. Results

We performed two experiments on the existing datasets. Firstly, we computed the CSF flow using OMT. We evaluated the results with the help of a medical expert; we also checked if the computed flow can accurately predict the behavior of the real system, by deriving an estimate of an image at a given time using the image at a previous time-frame and the computed flow (Fig. 2). Secondly, we estimated the diffusion tensors, and simulated the diffusion process using the first time slice of the real data as the initial conditions (Fig. 4).

Figure 2.

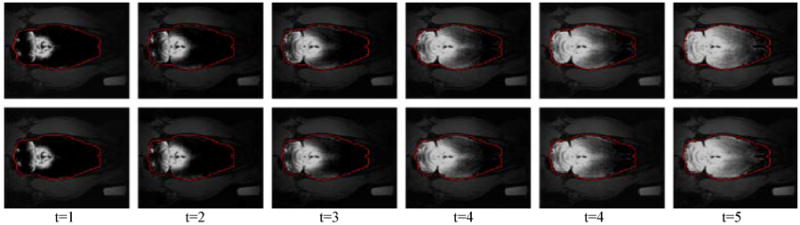
Modeling brain-wide glymphatic transport of Gd-DTPA using optimal mass transport (OMT). Comparison of the original locally enhanced T1-weighted MRI images (top row), and optimal mass transport reconstruction results (bottom row) from a rat receiving Gd-DTPA into the CSF at time-frames 1-5. The enhanced brain regions are enclosed by red contours. The brightness corresponds to the amount of Gd-DTPA induced signal change in the current cross-section. The reconstruction uses the previous timeframe of the real data and the computed flow between current and previous time-frames to estimate data at the current time-frame. As we see, the reconstructed images are very close to the originals.

Figure 4.

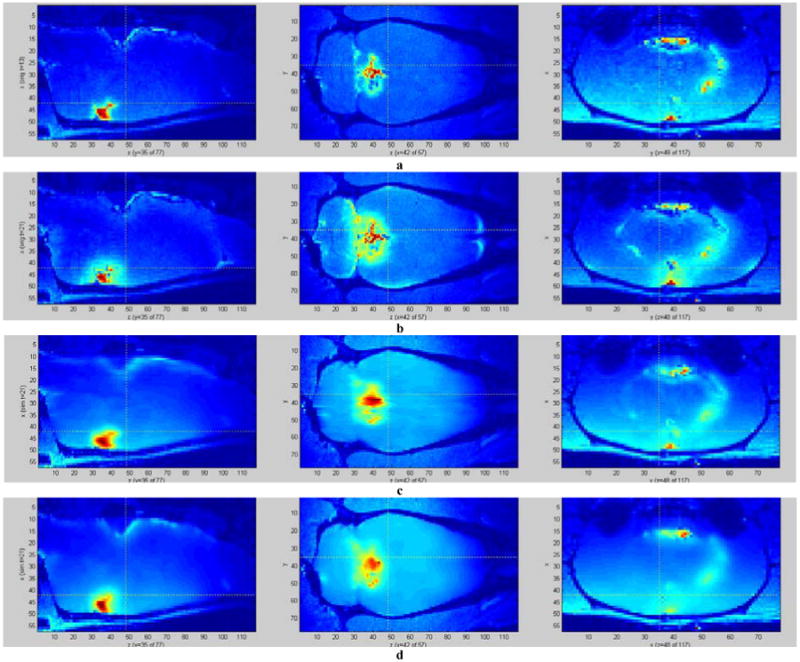
Simulation of tracer propagation through the brain using computed diffusion tensors. a – initial tracer concentration (time point 13), used as the initial conditions for the diffusion simulation; b – final (real) tracer concentration (time point 21); c – final tracer concentration simulated by a diffusion equation with the proposed tensor calculation scheme (PCA-based); d – final tracer concentration simulated by diffusion in the direction of the mean transport (over time) at each pixel. While the proposed method yields a somewhat smoothened estimate, it manages to capture many of the features of the real data, compared to the more primitive estimate (d).

The computed flow field (Fig. 3) is consistent with the current understanding of the glymphatic system². Furthermore, using the flow to warp data from previous time frames yields a very good approximation of the real data in the current time-frame (Fig. 2). The diffusion model derived from the flow field yields a reasonable approximation of the real data (Fig. 4). The approximation is smoother than the original, however it contains most of the original features.

Figure 3.

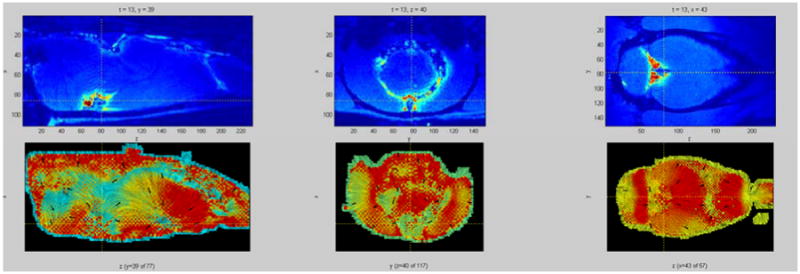
Top row: y, z, and x slices of a rat brain at a given time with color showing the concentration of a tracer (red – high concentration, blue – low concentration). Bottom row: Tracer flow through the respective slices depicted in the top row, presented as a LIC (Line Integral Convolution) image. Intensity lines are tangential to the computed flow direction over the slice, with arrows pointing in the actual flow direction. The color information depicts the strength of the flow component that is tangential to the slice plane (red – strong tangential component, i.e. the flow vector mostly lies within the slice plane; blue – weak tangential component, i.e. the flow vector is orthogonal to the slice plane). Most of the flow estimate agrees with the current understanding of the brain-wide glymphatic transport patterns (i.e. validated by optical imaging experiments). In some areas the estimate failed because the tracer has not reached them during the simulation time, therefore, the computation was mostly affected by the regularization (smoothness term) and not by the data.

4. Discussion

A number of other researchers have modeled liquid propagation by diffusion equations including those in hydrogeology and brain research^7,8. Most of these studies attempt to solve the estimation problem for a domain with constant, or locally constant coefficients. In the present work, we present the first attempt (to our knowledge) to fully solve the inverse problem of dense estimation of coefficients that are either anisotropic or spatially-varying or both, from concentration measurements. Also, none of the previous attempts to solve the inverse problem (assuming simpler, homogeneous models) utilized OMT.

OMT provides a good estimate of the actual glymphatic flow. Despite its simplicity, the proposed model mimics the real data closely, with some errors arising from the difficulty of the inverse problem. Some refinement of the diffusion model, such as including additional terms in the diffusion equation and compensating for the mass source (and loss of mass) while computing the OMT flow, should improve its accuracy.