Constrained optimization of gradient waveforms for generalized diffusion encoding

Abstract

Diffusion MRI is a useful probe of tissue microstructure. The conventional diffusion encoding sequence, the single pulsed field gradient, has recently been challenged as more general gradient waveforms have been introduced. Out of these, we focus on q-space trajectory imaging, which generalizes the scalar b-value to a tensor valued entity. To take full advantage of its capabilities, it is imperative to respect the constraints imposed by the hardware, while at the same time maximizing the diffusion encoding strength. We provide a tool that achieves this by solving a constrained optimization problem that accommodates constraints on maximum gradient amplitude, slew rate, coil heating and positioning of radio frequency pulses. The method's efficacy and flexibility is demonstrated both experimentally and by comparison with previous work on optimization of isotropic diffusion sequences.

Graphical Abstract

1. Introduction

Diffusion MRI probes the structure of biological tissue structure on a microscopic scale using the random translational motion of water molecules [1, 2, 3]. In the brain, tissue components—such as cell membranes, nerve fibers and macromolecules—impede the diffusion, making its characteristics different from that of freely diffusing water. In particular, the organization of white matter tracts into fiber bundles with preferential directions makes the diffusion anisotropic [4]. In diffusion tensor imaging (DTI), the diffusion in a voxel is described by a tensor with six degrees of freedom [5, 6]. Consequently, it requires the acquisition of at least six diffusion-weighted images. The trace of the diffusion tensor, which relates to the mean diffusivity (MD), is a useful biomarker e.g. when studying tumor cellularity [7] or diagnosing stroke [8]. In fact, the mean diffusivity can be determined by single-shot isotropic diffusion weighting [9], i.e. without doing full DTI. Although a good idea this has rarely been done in practice—until recently. The recent revival has been spurred by advancements on both the methodological and the technical sides. On the methodological side, isotropic diffusion weighting has been shown useful when studying microscopic diffusion anisotropy [10] and, in combination with directional diffusion weighting, it can be used to distinguish between microscopic anisotropy and orientational order [11, 12]. On the technical side, the limited gradient amplitudes achievable in clinical scanners have made it challenging to obtain sufficient diffusion weighting when using isotropic encoding. Rapid progress is being made on the hardware side [13, 14] but in the numerical optimization of gradient waveforms there is still room for improvement, although there has been some promising research in this direction [15, 16]. A gradient waveform that yields isotropic diffusion encoding can—in theory—easily be remapped to achieve a general diffusion encoding [17], which can be tuned to maximize sensitivity to the microstructure parameters of interest [18, 19].

In some of the earlier work [15, 16] the numerical optimization was strongly model driven, with constraints implicitly incorporated into a parametrization of the pulse sequence which was then optimized with respect to the parameters. This makes the obtained optimization less transparent and less adaptable to a new setting. Remapping a waveform with isotropic diffusion encoding into a generalized diffusion measurement [17] does not take the inherent constraints into account. Subsequently adjusting the remapped gradient waveform to make it feasible comes at the cost of efficiency.

In this work, we propose a new optimization framework for these gradient waveforms that makes far less modeling assumptions than previous work while it is at the same time easily adaptable to hardware constraints on maximum gradient amplitude, slew rate, heating and positioning of RF pulses. Taking gradient heating into account is of particular interest for diffusion imaging where the power dissipation can otherwise hinder operation at a high duty cycle [13, 14]. A further generalization of our approach is that it allows arbitrary positioning of time intervals with zero gradients (or slice-selective gradients), during which an RF pulse can be applied, and not requiring a mirror-symmetric gradient waveform.

2. Optimization

The most common pulse sequence in diffusion MRI is single diffusion encoding (SDE) by a pair of short gradient pulses separated by a diffusion time [20]. Each repetition of such a measurement probes the diffusion in one direction. In this work we consider more general scenarios with time-varying gradients that probe trajectories in so-called q-space [17]. The q-space trajectory is determined by gradient waveforms g(t) = (g_x(t),g_y(t),g_z(t))^T according to

$$\mathbf{q}\left(t\right)=\gamma {\int }_0^t\mathbf{g}\left(t^{\prime }\right)d{t}^{\prime }$$ (1)

where γ is the gyromagnetic ratio. It is the q-space trajectories q(t) that constitute the degrees of freedom that we consider in the optimization.

Restricted diffusion does not follow the Gaussian behavior that is characteristic of free diffusion [1]. Nevertheless, the model of diffusion—on the voxel scale—as a mixture of Gaussians has found widespread use [21, 22, 23] and captures relevant information about the tissue microstructure [2].

Under the Gaussian approximation, the geometry of the diffusion encoding is captured by the measurement tensor [1, 17]

$$\mathbf{B}={\int }_0^{\tau }\mathbf{q}\left(t\right)\mathbf{q}{\left(t\right)}^{T}dt,$$ (2)

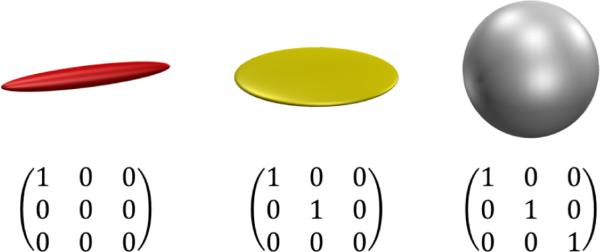
where τ is the echo time. The measurement tensor extends the conventional b -value to a matrix-valued entity (the conventional b -value is given by the trace of B). The rank of the measurement tensor depends on the q-space trajectory: it is one in the case of SDE, two for double diffusion encoding (DDE) [24], and three in the isotropic encoding case. Figure 1 shows the correspondence between the graphical- and the matrix representations of measurement tensors used in this work.

Figure 1.

Measurement tensors: the top row is the graphical representation of the corresponding matrix representations in the bottom row. In the graphical representation, the magnitudes of the eigenvalues are mapped to red-green-blue. Note that in this case the b -value of the rightmost tensor is three times as high as that of the leftmost one.

By definition, isotropic diffusion encoding corresponds to a measurement tensor

$${\mathbf{B}}_{\mathrm{iso}}=b\left(\begin{array}{ccc}\hfill 1∕3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1∕3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1∕3\hfill \end{array}\right).$$ (3)

There is a direct link between the diffusion tensor in a voxel,

$$\mathbf{D}=\left(\begin{array}{ccc}\hfill D_{xx}\hfill & \hfill D_{xy}\hfill & \hfill D_{xz}\hfill \\ \hfill D_{yx}\hfill & \hfill D_{yy}\hfill & \hfill D_{yz}\hfill \\ \hfill D_{zx}\hfill & \hfill D_{zy}\hfill & \hfill D_{zz}\hfill \end{array}\right)$$ (4)

and the measurement tensor B; the normalized echo amplitude E(q) in a diffusion experiment is [1]

$$\begin{array}{cc}\hfill -\log \left(E\left(\mathbf{q}\right)\right)=& {\int }_0^{\tau }\mathbf{q}{\left(t^{\prime }\right)}^T\mathbf{D}\mathbf{q}\left(t^{\prime }\right)d{t}^{\prime }\hfill \\ \hfill =& \sum _{\alpha ,\beta }{D}_{\alpha \beta }{\int }_0^{\tau }{q}_{\alpha }\left(t^{\prime }\right)q_{\beta }\left(t^{\prime }\right)d{t}^{\prime }\hfill \\ \hfill =& \mathrm{Tr}\left(\mathbf{DB}\right),\hfill \end{array}$$ (5)

where α, β ∈ {x, y, z}. From the basics of the trace operator it follows that the attenuation is directly related to the sum of the eigenvalues of the matrix product DB. In particular B = B_iso gives Tr(DB) = b(λ₁ + λ₂ + λ₃)/3 = bD̄, where D̄ is usually referred to as the mean diffusivity.

It is convenient to define a general measurement tensor as B = bB̂, where Tr(B̂) = 1, because then b is the conventional b -value and Tr(DB) = b·Tr(DB̂). Combining this with equation (5) it is evident that—independent of the choice of B̂—maximizing the diffusion weighting amounts to maximizing b. However, the hardware imposes a multitude of constraints that prevents a universally optimal formula. It might seem a bit backwards to optimize b for a given echo time, instead of the converse, but in practice it is not an issue: using bisection the minimum echo time for a given b can be found in a small number of optimization runs. In return, the problem can be formulated as a constrained optimization problem in a more natural way.

2.1. Constraints

A pulse sequence optimization needs to respect a number of hardware dependent and sequence dependent constraints. We will describe these constraints in an idealized, continuous, scenario; implementation details can be found in appendix Appendix A. To facilitate the numerical treatment, we phrase the optimization problem in terms of q(t), rather than working directly with the gradient waveforms g(t). Converting in between is straightforward: it follows from eq. (1) that $\mathbf{g}\left(t\right)=\frac{1}{\gamma }\frac{d\mathbf{q}}{dt}$.

2.1.1. Sequence dependent constraints

There are three constraints specific to the sequence desired. First, we want to achieve a given diffusion encoding as described by a (normalized) measurement tensor B̂, i.e.

$${\int }_0^{\tau }\mathbf{q}\left(t\right)\mathbf{q}{\left(t\right)}^{T}dt=b\widehat{\mathbf{B}}.$$ (6)

Second, in order for the sequence to produce an echo at the desired echo time, τ, it must hold that

$$\mathbf{q}\left(0\right)=\mathbf{q}\left(\tau \right)=0.$$ (7)

Third, it may be desirable to enforce the gradients to be zero (or active only in the slice encoding direction) during certain time intervals, I_t, to allow for RF pulses. Since the gradients are found by differentiating q(t) this is to say

$${\phantom{\mid }\frac{d\mathbf{q}}{dt}\mid }_{t\in I_t}=0.$$ (8)

In particular, we will impose throughout that the gradients are zero at the start and end of the pulse sequence.

2.1.2. Hardware constraints

The hardware constraints considered are the maximum gradient strength, slew rate and heating. The gradient amplitude, G_max, is one of the most severe factors limiting the diffusion encoding strength [2, 14] and it is therefore important to account for it explicitly in the optimization. This is done through the constraint

$$\Vert \frac{d\mathbf{q}}{dt}\Vert \le \gamma G_{\max },$$ (9)

where the norm is either the max-norm, ∥(x₁, x₂, x₃)∥_∞ = max(|x₁|, |x₂|, |x₃|), or the Euclidean norm, ${\Vert (x_1,x_2,x_3)\Vert }_2=\sqrt{x_1^2+x_2^2+x_3^2}$. The first corresponds to actual scanner constraints whereas the latter can be used to obtain a rotationally invariant waveform (more on that in section 4.1).

A similar, but often not as severe, constraint is the maximum slew rate (rate of change), R_max, of the gradients, which translates into

$${\Vert \frac{d^2\mathbf{q}}{d{t}^2}\Vert }_{\infty }\le \gamma R_{\max }.$$ (10)

An additional—at times overlooked—part of an efficient pulse sequence is the ability to perform at a high duty-cycle without inactive cool-down periods. An intense diffusion encoding block often requires a rather long idle time, which reduces the number of samples per unit of time and thereby the effective signal-to-noise ratio. This means that there is much to gain by accounting for the heat dissipation when optimizing the pulse sequence. Assuming resistive heating [13], the heat dissipation in gradient coil α is proportional to the time integral of g_α(t)². This can be captured by the constraint

$${\int }_0^{\tau }{\left(\frac{d{q}_{\alpha }}{dt}\right)}^{2}dt\le \eta {\gamma }^2{G}_{\max }^2\tau ,\alpha =x,y,z,$$ (11)

where η ∈ [0, 1] is a dimensionless scalar. Varying the parameter η allows us to balance heat dissipation against diffusion encoding.

2.2. The optimization problem

Taken together, we arrive at the optimization problem

$$\begin{array}{cc}\underset{\mathbf{q},b}{\text{maximize}}\hfill & b\hfill \\ \text{subject to}\hfill & {\int }_0^{\tau }\mathbf{q}\left(t\right)\mathbf{q}{\left(t\right)}^{T}dt=b\widehat{\mathbf{B}}\hfill \\ \hfill & \mathbf{q}\left(0\right)=\mathbf{q}\left(\tau \right)=0\hfill \\ \hfill & {\phantom{\mid }\frac{d\mathbf{q}}{dt}\mid }_{t\in I_t}=0\hfill \\ \hfill & \Vert \frac{d\mathbf{q}}{dt}\Vert \le \gamma G_{\max },\hfill \\ \hfill & {\Vert \frac{d^2\mathbf{q}}{d{t}^2}\Vert }_{\infty }\le \gamma R_{\max }\hfill \\ \hfill & {\int }_0^{\tau }{\left(\frac{d{q}_{\alpha }}{dt}\right)}^{2}dt\le \eta {\gamma }^2{G}_{\max }^2\tau ,\alpha =x,y,z.\hfill \end{array}$$ (12)

To solve this problem we discretize q(t) and replace the derivatives and integrals with finite difference approximations (see Appendix A). To achieve better convergence, we also relax the equality in the measurement tensor constraint by allowing a small violation ε in Frobenius norm. These steps turn the problem into a form in which it can be solved efficiently using sequential quadratic programming. This is a deterministic algorithm, meaning that it always returns the same solution for a given initial guess. Our experience is that a random initialization works best and, with large¹ probability, results in one out of a number of different but equally good (same objective function value) solutions. To further increase this probability, it is of course possible to run the optimization multiple times, with different initial guesses, and choose the best solution. The numerical results presented in sections 4.1 and 4.2 all use the same random initial guess, i.e. a single starting configuration.

Incidentally, note that this optimization problem does not impose any particular shape on q(t), only that its diffusion encoding matches the desired measurement tensor. The shape can be important when considering restricted diffusion. However, if a particular shape is desired it is straightforward to check which constraint will be the limiting one and set the magnitude accordingly.

2.3. Evaluation

The performance of the different gradient waveforms can be compared with respect to their diffusion weighting and the amount of dissipated heat. In general, the b -value of any gradient waveform can be expressed as

$$b=\kappa \frac{{\gamma }^2{G}_{\max }^2{\tau }^3}{4},$$ (13)

where κ is a dimensionless efficiency factor that depends on the gradient waveform. For a single coil, the maximum efficiency, κ = 1/3, results from applying maximum gradient in one direction for half the echo time and in the opposite direction for the other half of the time. It thus requires an infinite slew rate. Only by applying this gradient sequence in the three coils simultaneously is it possible to attain κ = 1.

To capture the slew rate limitation we introduce another dimensionless parameter, ξ ∈ [0, 1], as

$$\xi =\frac{G_{\max }}{R_{\max }\tau }.$$ (14)

In other words, ξ is the fraction of the echo time it takes to increase the gradient amplitude from zero to max.

2.4. Heat dissipation and repetition times

The signal-to-noise ratio (SNR) of a measurement can be increased by repeating the measurement n times and averaging the results. A short repetition time T_R allows more repetitions in a given time. A short and intense gradient sequence suffers less from transverse relaxation but dissipates more heat—and may therefore require longer T_R—than a more gentle gradient sequence. A relevant question is therefore: provided a set amount of time, how to choose τ and T_R to maximize the SNR?

We will answer this question by considering two gradient sequences referred to as A and B. Gradient sequence A, with corresponding τ_A and η_A, is held fixed while we change gradient sequence B and record the ratio of their SNRs. In general, for a repeated spin echo experiment

$$\mathrm{SNR}\propto \sqrt{n}\exp (-\tau ∕T_2)\left(1-\exp \left(-\frac{T_R-\tau ∕2}{T_1}\right)\right).$$ (15)

To proceed we make the following two assumptions: first, that equation (13), with κ = κ(η) (as will be shown in figure 5), holds as τ and η are varied. This is a reasonable approximation as long as the slew rate is not a major limitation (ξ small). Second, that the average heat dissipation per unit time is sufficient to represent the thermal dynamics and that the system adjusts $T_R^{\left(A\right)}$ so that the average heat dissipation is precisely as high as acceptable. If this is not the case, it is best to simply use the most intense gradient sequence possible. As shown in Appendix B, the resulting ratio of the pulse sequences SNRs is

$$\begin{array}{cc}\hfill \frac{{\mathrm{SNR}}_B}{{\mathrm{SNR}}_A}=& {\left(\frac{{\eta }_A}{{\eta }_B}\right)}^{1∕2}{\Psi }^{-1∕2}\exp \left((1-\Psi )\frac{{\tau }_A}{T_2}\right).\hfill \\ \hfill & \frac{1-\exp \left(\Psi \frac{{\tau }_A}{2T_1}\right)\exp \left(-\Psi \frac{{\eta }_B}{{\eta }_A}\frac{T_R^{\left(A\right)}}{T_1}\right)}{1-\exp \left(\frac{{\tau }_A}{2T_1}\right)\exp \left(-\frac{T_R^{\left(A\right)}}{T_1}\right)},\hfill \end{array}$$ (16)

where Ψ = (κ(η_A)/κ(η_B))^1/3. The highest SNR can be found by maximizing the ratio with respect to η_B, which in turn yields τ_B and $T_R^{\left(A\right)}$.

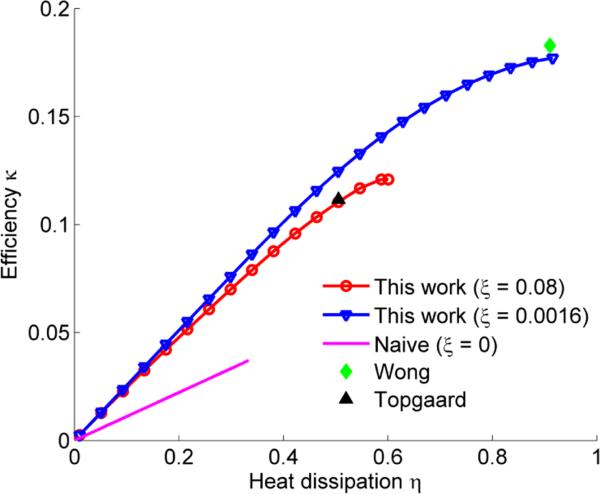
Figure 5.

Sequence efficiency factor κ and relative heat dissipation η for isotropically encoding sequences optimized in this work and in previous work. The larger η is the more heat is generated by the sequence. Two sets of optimizations were done using different slew rates, as specified by the dimensionless constant ξ.

3. Experiments

We performed two types of experiments: the first, detailed in Appendix C, aimed to verify that optimized waveforms achieve isotropic diffusion encoding when intended to; the second, detailed below, considers the implementation of optimized waveforms on a clinical MRI scanner.

3.1. In vivo experiments

To demonstrate that the optimized waveforms could be implemented on a clinical scanner system, MRI data was acquired in 10 healthy volunteers (all male, mean age (standard deviation) was 30 (4) y, interval [24, 34] y), using a Siemens Skyra 3 T system, equipped with 43 mT/m gradients with a maximum slew rate of 200 mT/m/ms, and a 20-channel receiver head coil. Written consent was received from all volunteers prior to scanning. The diffusion experiments were based on those reported by Szczepankiewicz et al. [12], although using another sequence implementation. Briefly, the experiment combines equal amounts of images acquired with directional and isotropic diffusion encoding at b -values 100, 500, 1000, 1500 and 2000 s/mm². The directional encoding in each shell was performed in 6, 6, 12, 20 and 48 directions, respectively, and the isotropic encoding was repeated the same number of times for each shell. The directions were optimized across all b -shells simultaneously using a charged container model [25]. All images were acquired in 11 contiguous axial slices using an echo time (τ) of 130 ms, repetition time (T_R) of 2500 ms, 128 × 128 acquisition matrix, spatial resolution of 2 × 2 × 4 mm³ partial Fourier factor of 6/8, bandwidth of 1500 Hz/voxel, and a GRAPPA factor of 2. The diffusion encoding was performed during 55.44 ms and 48.16 ms before and after the refocusing pulse, respectively; the duration of the refocusing pulse and slice-selection gradients was 7.76 ms. The waveform was optimized to this timing using 2-norm, η = 0.6, G_max = 43 mT/m, R_max = 130 T/m/s and N = 200 discretization points. The maximum slew rate was limited to avoid peripheral nerve stimulation. Total scan time for the isotropic and anisotropic encoding sequences was 8:00 min. All data was smoothed with a 3D Gaussian kernel (FWHM 2 mm) to mitigate Gibbs ringing artefacts [26], and corrected for motion and eddy-current distortions using ElastiX [27] with extrapolated references [28]. Parameter maps of the mean diffusivity (MD) and microscopic fractional anisotropy (μFA), were calculated according to the framework suggested by Lasič et al. [11, 12]. The conventional fractional anisotropy (FA) was calculated from the directionally encoded data, using standard diffusion tensor analysis [29, 12]. The potential benefit of using optimized waveforms was evaluated by comparing the maximal b -values that could be achieved by the qMAS waveforms, used in Szczepankiewicz et al. [12], to the optimized waveforms.

In addition to this, a separate investigation of the SNR was performed in a single volunteer where optimized waveforms were compared to qMAS. To this end, the in vivo protocol was modified to contain only isotropic encoding at a single b -value of 2000 s/mm². The echo time was minimized and the repetition time was set to 4000 ms to not incur restrictions on the maximal echo time. This measurement was repeated 20 times and the SNR was calculated in each voxel as the mean signal divided by the signal's standard deviation across all repetitions.

4. Results

We first present results from numerical studies and then experimental results. The numerical studies consider, in turn, varying the measurement tensor, varying the heat dissipation and the heat dissipation's effect on the total SNR. Then, the results of the in vivo experiments follow. The result of the experiment aimed to verify the isotropic encoding of an optimized waveform is presented in Appendix C.

4.1. Optimization of axisymmetric measurement tensors

Axially symmetric tensors are of particular interest since they can be used to distinguish between prolate and oblate microscopic diffusion tensors with unknown orientation distribution [30].

Often, it is desirable to use a pulse sequence that can be rotated to achieve arbitrary directional encoding. This means that the total gradient magnitude can never exceed what a single gradient coil can generate, i.e. ∥g(t)∥₂ ≤ G_max. Geometrically, the gradient trajectory is then constrained to lie inside a sphere of radius G_max. In what follows we will only consider diagonal measurement tensors; provided that the rotational dependence of the slew rate constraint can be neglected, this assumption incurs no loss of generality.

For comparison we consider a naïve approach: consecutive application of a conventional SDE sequence in each gradient direction as shown in figure 2. Assuming infinite slew rate and τ_x = ατ, τ_y = τ_z = (1 – α)/τ/2, where α ∈ [0, 1], this gives ${\lambda }_{\text{axial}}=\left({\alpha }^3{\gamma }^2{G}_{\max }^2{\tau }^3\right)∕12$ and a resulting efficiency

$${\kappa }_{\mathrm{na}\ddot{\mathrm{i}}\mathrm{ve}}=\frac{1}{3}\left({\alpha }^3+\frac{{(1-\alpha )}^3}{4}\right).$$ (17)

Figure 3 compares the efficiency of this approach compared to an optimization, as proposed in this work, for axially symmetric measurement tensors

$$\widehat{\mathbf{B}}\left({\lambda }_{\text{axial}}\right)=\mathrm{diag}\left({\lambda }_{\text{axial}},\frac{1-{\lambda }_{\text{axial}}}{2},\frac{1-{\lambda }_{\text{axial}}}{2}\right)$$ (18)

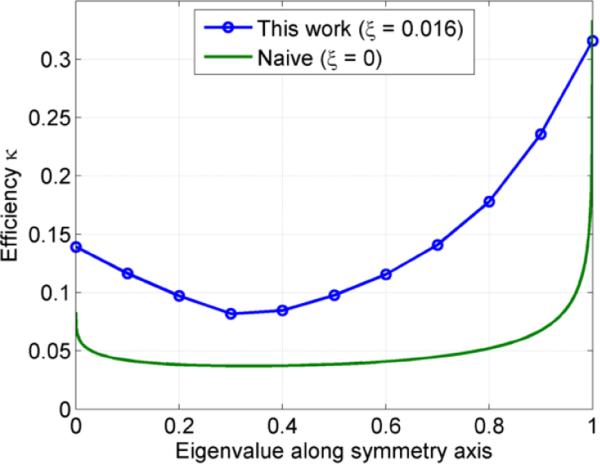
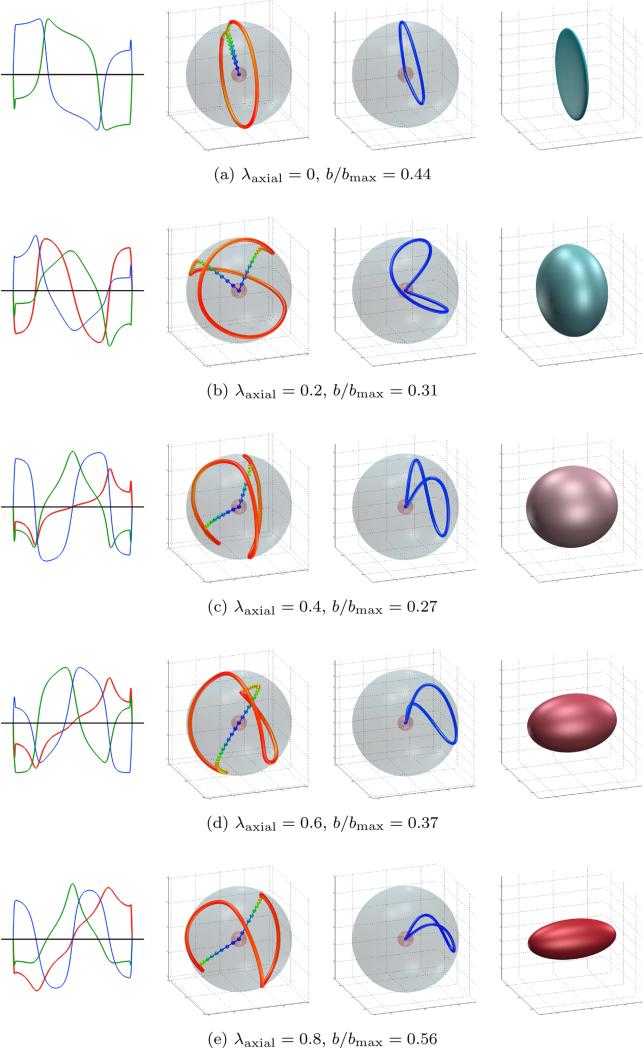
where λ_axial ∈ [0, 1]. These optimizations were done using G_max = 80 mT/m, R_max = 100 T/m/s (ξ = 0.016), η = 1, τ = 50 ms, ε = 10⁻⁴ and N = 100 discretization points. Figure 4 shows five of the optimized trajectories. To achieve the same b -value, it follows from equation (13) that the optimized waveforms allow reductions in echo time by 16% and 22% in the double diffusion encoding (λ_axial = 0) and triple diffusion encoding (λ_axial = 1/3) cases, respectively.

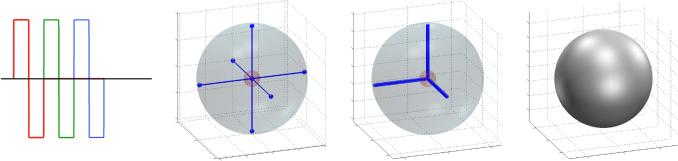
Figure 2.

An example of a naïve gradient waveform used for comparison throughout this work. From left to right: the x-y-z gradients in red-green-blue; gradient trajectory; q-space trajectory and the resulting measurement tensor (isotropic in case).

Figure 3.

Efficiency κ for sequences with diagonal, axially symmetric, measurement tensors as the eigenvalue along the symmetry axis is varied.

Figure 4.

Optimized gradient waveforms and trajectories. Columns from left to right: gradients, gradient trajectory, q-space trajectory and measurement tensor. The trajectories are color coded according to rate of change: from slow (red), through intermediate (green) to fast (blue). The fourth column shows the resulting measurement tensor; the magnitudes of the eigenvalues are mapped to red-green-blue.

4.2. The trade-off between heat dissipation and efficiency

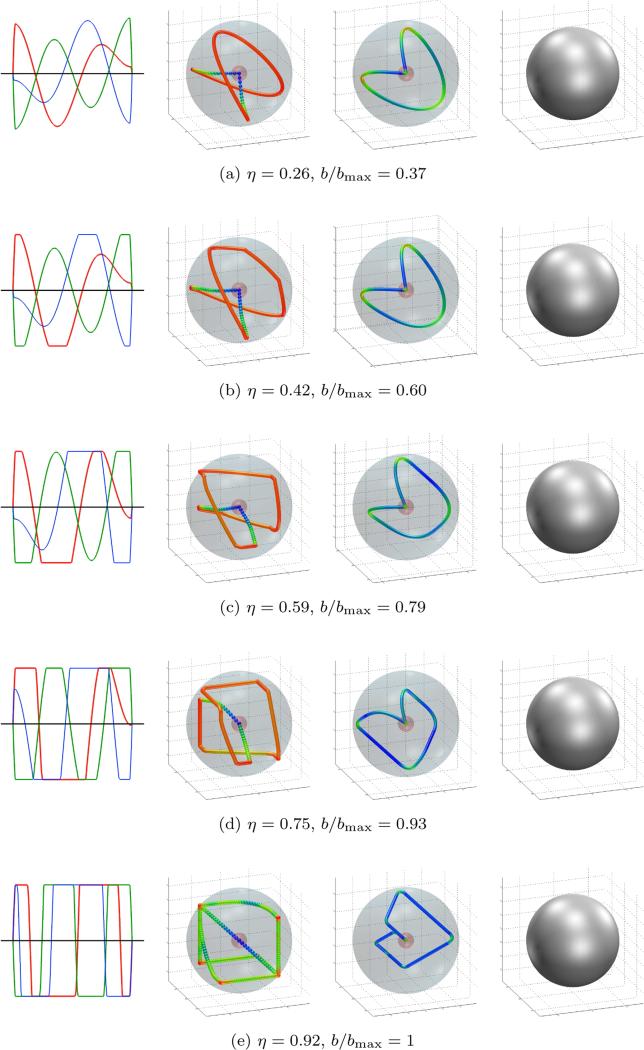
We explored the trade-off between heat dissipation and efficiency by fixing the measurement tensor to be isotropic and varying the heat dissipation η. Again, we used the settings G_max = 80 mT/m, τ = 50 ms, ε = 10⁻⁴ and N = 100. However, to investigate the influence of the slew rate, we repeated the experiment twice: first with R_max = 100 T/m/s (ξ = 0.016) and then with R_max = 20 T/m/s (ξ = 0.08). The resulting efficiencies as a function of the heat dissipation are shown in figure 5, which also shows the results from previous work and compares with a naïve sequence defined as in section 4.1 but with the gradient magnitudes scaled to meet the heat dissipation requirement. Figure 6 shows five trajectories optimized with ξ = 0.016 and different values of η. As the allowable heat dissipation is varied from low to high, the gradient waveforms transition from smooth, almost sinusoidal, to rectangular.

Figure 6.

Gradient waveforms optimized with ξ = 0.016 and different values of η. Columns from left to right: gradients, gradient trajectory, q-space trajectory and measurement tensor. Color coding as in figure 4.

The fact that the gradient amplitude and slew rate apply to each coil separately means that the gradients are constrained by a cube with its sides at ±G_max. The strongest diffusion encoding is achieved in the corners of this cube (recall that the b -value scales quadratically with the gradient). So, whenever heat dissipation can be neglected, this is where we expect to find the gradients. The slew rate then limits how fast the gradient trajectory transitions between corners. This behavior is clearly visible in figure 6e.

4.3. Heat dissipation and repetition times

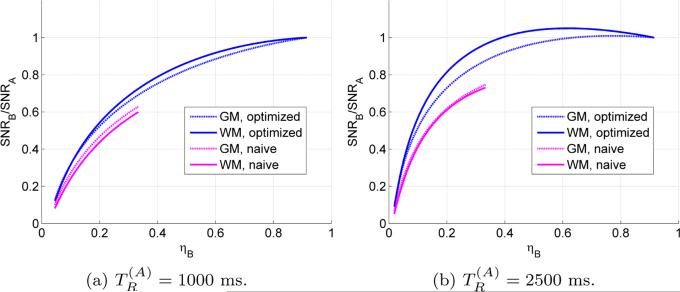
To illustrate the heat dissipation's effect on SNR, as described in section 2.4, we consider the optimized sequences from section 4.2 with ξ = 0.016 that are shown in figure 5 and the corresponding naïve sequences. Figure 7 shows the ratio of SNRs, for $T_R^{\left(A\right)}\in \{1000\mathrm{ms},2500\mathrm{ms}\}$, when gradient sequence A is taken to be the most intense one. Here, we used T₁ = 1331 ms and T₂ = 110 ms for gray matter (GM); T₁ = 832 ms and T₂ = 80 ms for white matter (WM) [31].

Figure 7.

Comparison of signal-to-noise ratio in gray matter (GM) and white matter (WM) as the heat dissipation of the gradient sequences from section 4.2 is varied. The baseline, gradient sequence A, is the most intense gradient sequence and is assumed to require a repetition time $T_R^{\left(A\right)}$ to reach a sustainable average heat dissipation. The naïve gradient sequence consists of consecutive SDE sequences in each gradient direction and the resulting heat dissipation can thus be at most η_B = 1/3.

4.4. In vivo experiments

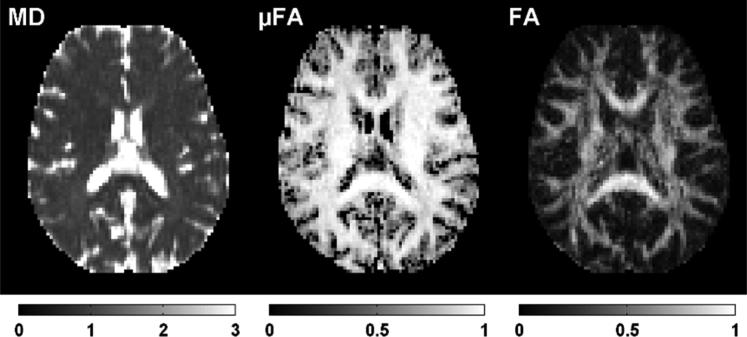
All volunteers were successfully scanned. A qualitative examination of the diffusion weighted images showed that the image quality was good, and that no prominent artefacts were introduced by the optimized waveforms. Parameter maps of a subject are shown in figure 8.

Figure 8.

Parameter maps in axial slice through the corpus callosum in a healthy volunteer. Data quality for all volunteers was qualitatively good, and no additional artefacts were observed as a result of employing the optimized waveforms. As previously reported by Szczepankiewicz et al. [12], the μFA map is homogeneous in regions of white matter, and the difference between the μFA and FA maps is most prominent in regions where complex white matter architecture is expected, such as in crossing white matter pathways.

The maximal b -value achievable for isotropic encoding with τ = 130 ms (see section 3.1) was 3000 s/mm² for the optimized waveforms, and 1050 s/mm² for the qMAS waveforms, respectively. Thus, to achieve a b -value of 3000 s/mm² the echo time could be reduced from 180 ms to 130 ms when employing the optimized waveforms.

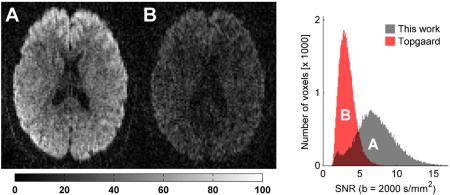
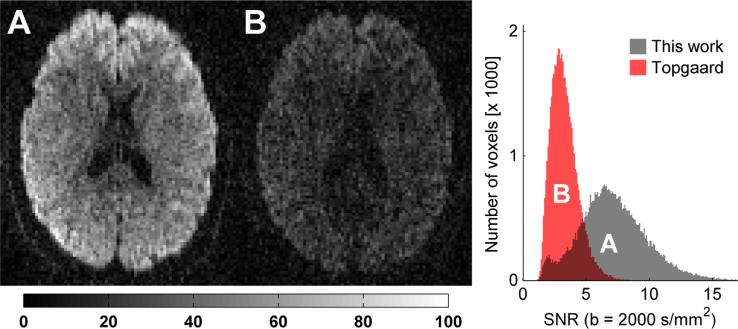
A b -value of 2000 s/mm² was achievable with an echo time of 116 and 170 ms for the optimized waveform and qMAS waveforms, respectively. Due to transverse relaxation effects, the signal at b = 2000 s/mm² is thus expected to increase by 63 % and 96 % for gray matter (T₂ = 110 ms) and white matter (T₂ = 80 ms), respectively. To make these statements more tangible, figure 9 shows an example of raw diffusion weighted images acquired with the different methods together with a histogram of the voxelwise SNR. As expected, the shorter echo time, facilitated by the optimized waveform, rendered a markedly higher SNR in the images.

Figure 9.

Raw diffusion weighted images in an axial slice through the corpus callosum in a healthy volunteer. The encoding strength is b = 2000 s/mm² in both images. The measured signal is markedly higher in the images encoded with the optimized waveform (A, echo time 116 ms) compared to the qMAS waveform (B, echo time 170 ms) suggested by Topgaard et al. [15]. The histogram shows the distribution of voxelwise SNR from brain tissue located within the imaging slab. There is a clear tendency towards higher SNR for the optimized waveform, due to the shorter echo time.

5. Discussion

In optimization, a good practice is to formulate a problem that is a caricature of the real problem—capturing all the essential characteristics and ignoring the rest. This often makes solving the problem more reliable, thereby producing a better end result than a too detailed model. In addition, the problem formulation will be easier to adapt to a different setting.

An example of this is the model of the signal as a mixture of Gaussians, from which our objective function derives. This is not a physically well-founded model for restricted diffusion but it has found widespread use. With this work, we do not attempt to answer whether this is the most appropriate way of modeling the signal; instead our hope is to provide a tool that researchers in the field will find useful. Consequently, we have assumed that the object of interest is the measurement tensor, but we have left its application undetermined. On the other hand, we have placed virtually no other restrictions on the shape of the gradient waveforms other than those imposed by the hardware. This makes the model much more flexible than if deciding upon particular basis functions or similar. This means our formulation can, witout modifications, be used for a range of experiments—be it in NMR or in vivo diffusion MRI. Another example of this flexibility is the possibility to impose zero-gradient intervals, or intervals with specified slice encoding gradients, at arbitrary points in time, i.e. not requiring the gradient waveform to be symmetric. This was taken advantage of in our in vivo experiments and was one of the reasons why it was possible to reduce the echo time from 180 ms to 130 ms. It can, however, be expected that the slice selection gradient will perturb the obtained measurement tensor, but only by a little.

The importance of explicitly taking the hardware constraints into account can be appreciated from the q-space trajectories in figure 4, where the total gradient magnitude is limited by what a single gradient coil can generate (in order to allow arbitrary rotation of the resulting waveforms). The lack of dynamics in the color coding reflects that this constraint is active throughout almost the entire trajectory—an indication of the solutions high quality and a feat that would otherwise be very difficult to accomplish.

As another example, a more intense gradient sequence may reduce the echo time at the cost of prolonging the repetition time (to allow for cooling). A general procedure to maximize the SNR using the methods we have presented would be as follows. First, given a desired b -value, use bisection to find— with no concern for heat dissipation (η = 1)—the shortest echo time possible. Then, test what the minimum repetition time allowed by the scanner is. If it appears that cooling is not a limitation then stop, else maximize equation (16) with respect to η_B either numerically or graphically. Figure 7 suggests that beyond a certain value of the repetition time it becomes more efficient to decrease the pulse's heat dissipation than to use the most intense one. Incidentally, the figure also shows that compared with a naïve sequence for isotropic diffusion encoding, the optimized sequences can increase the SNR by about 60%.

Our experiments have shown that the optimized waveforms can achieve the expected isotropic encoding and that it is possible to implement optimized waveforms on a clinical MRI scanner with a drastically reduced echo time yet no prominent artefacts. The latter finding is in line with our theoretical comparison with naïve double diffusion encoding (DDE) and triple diffusion encoding (TDE), that showed that reductions in echo time by 16 % and 22 %, respectively, are possible.

6. Conclusions

We have proposed a new framework for optimization of gradient waveforms that maximizes the b -value for a given measurement tensor and echo time. From this it is straightforward to obtain gradient waveforms that minimize the echo time for a given b. The formulation as a constrained optimization problem allows explicit control of hardware requirements, including maximum gradient amplitude, slew rate, heating and positioning of RF pulses.

Based on two reasonable assumptions, we have derived an expression for the signal-to-noise ratio's dependence on the heat dissipation and outlined how this can be used to strike a balance between gradient intensity and heat dissipation that maximizes the signal-to-noise ratio.

We have verified by experiments on a water/surfactant mixture that the method can achieve the desired diffusion encoding. By in vivo experiments and numerical comparisons with previous work, we have shown that substantial gains in terms of reduced echo times and better signal-to-noise ratio's can be achieved, in particular as compared with naïve double diffusion encoding (DDE) and triple diffusion encoding (TDE).

Highlights.

• We describe a framework for optimization of gradient waveforms for diffusion MR.

• To maximize diffusion encoding it is imperative to respect hardware constraints.

• Our framework accommodates constraints on gradient magnitude and coil heating.

• We provide both experimental results and numerical comparisons with previous work.

Appendix A. Explicit problem formulation

In summary, we strive to find the q-space trajectory q(t) that maximizes b, everything else is considered fixed parameters. This is done by discretizing q(t) into N time steps of length Δt = τ/N, forming the N × 3 matrix

$$\mathbf{Q}=\left(\begin{array}{ccc}\hfill q_{x,1}\hfill & \hfill q_{y,1}\hfill & \hfill q_{z,1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill q_{x,N}\hfill & \hfill q_{y,N}\hfill & \hfill q_{z,N}\hfill \end{array}\right).$$ (A.1)

where we have used the notation q_α,k = q_α((k – 1/2)Δt). To discretize the measurement tensor constraint in equation (6), we first introduce a diagonal “integration matrix” corresponding to the trapezoid rule

$$ϴ=\Delta t\left(\begin{array}{ccccc}\hfill 1∕2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1∕2\hfill \end{array}\right),$$ (A.2)

so that the discretized version of equation (6) reads

$${\mathbf{Q}}^Tϴ\mathbf{Q}=b\widehat{\mathbf{B}}.$$ (A.3)

However, because nonlinear equality constraints should be avoided, we relax this and instead require

$${\Vert {\mathbf{Q}}^Tϴ\mathbf{Q}-b\widehat{\mathbf{B}}\Vert }_{\mathrm{F}}^2\le {\left(bϵ\right)}^2,$$ (A.4)

where we have introduced a tolerance ε on the isotropy violation.

Many of the remaining constraints involve the gradients; these are easily implemented through a finite difference scheme. We used a central difference scheme shifted by half a time step,

$${\phantom{\mid }\frac{d{\mathbf{q}}_{\alpha }}{dt}\mid }_{k+1∕2}\approx \frac{q_{\alpha ,k+1}-q_{\alpha ,k}}{\Delta t},$$ (A.5)

which can also be interpreted as the average value over the bin centered at kΔt. The boundary constraints on the gradients, which are of Dirichlet type, were implemented using ghost points. The (N – 1) internal derivatives were thus approximated using the (N – 1) × N-matrix

$${\mathbf{A}}_1=\frac{1}{\Delta t}\left(\begin{array}{cccc}\hfill -1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right).$$ (A.6)

Similarly, the second derivatives were approximated using the N × N-matrix

$${\mathbf{A}}_2=\frac{1}{{\left(\Delta t\right)}^2}\left(\begin{array}{ccccc}\hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill \end{array}\right).$$ (A.7)

In Euclidean norm, a constraint on the gradient amplitude can thus be written as the nonlinear inequality constraints (interpreted componentwise)

$${\left({\mathbf{A}}_1{\mathbf{q}}_x\right)}^2+{\left({\mathbf{A}}_1{\mathbf{q}}_y\right)}^2+{\left({\mathbf{A}}_1{\mathbf{q}}_z\right)}^2\le {\gamma }^2{G}_{\max }^2.$$ (A.8)

In contrast, max-norm constraints on the gradient amplitude and slew rate can be translated into linear inequality constraints

$$-\gamma G_{\max }\le {\mathbf{A}}_1{\mathbf{q}}_{\alpha }\le \gamma G_{\max },\alpha =x,y,z$$ (A.9)

$$-\gamma R_{\max }\le {\mathbf{A}}_2{\mathbf{q}}_{\alpha }\le \gamma R_{\max },\alpha =x,y,z.$$ (A.10)

Similarly, a constraint on the gradients being zero during an interval I_t can be written

$${\mathbf{A}}_1{q}_{\alpha ,k}=0\text{if}k\Delta t\in I_t,\alpha =x,y,z.$$ (A.11)

The heat dissipation constraint, equation (11), can be approximated as

$${\int }_0^{\tau }{\left(\frac{d{q}_{\alpha }}{dt}\right)}^{2}dt\approx \Delta t\cdot {\mathbf{q}}_{\alpha }^T{\mathbf{A}}_1^T{\mathbf{A}}_1{\mathbf{q}}_{\alpha },\alpha =x,y,z.$$ (A.12)

In conclusion, following the discretization scheme above, the explicit formulation of the constrained optimization problem in equation (12) is:

$$\begin{array}{cc}\underset{\mathbf{Q},b}{\text{minimize}}\hfill & -b\hfill \\ \text{subject to}\hfill & {\Vert {\mathbf{Q}}^Tϴ\mathbf{Q}-b\widehat{\mathbf{B}}\Vert }_{\mathrm{F}}^2\le {\left(bϵ\right)}^2\hfill \\ \hfill & {\mathbf{A}}_1{q}_{\alpha ,k}=0\text{if}k\Delta t\in I_t\hfill \\ \hfill & q_{\alpha ,1}=q_{\alpha ,N}=0\hfill \\ \hfill & -\gamma G_{\max }\le {\mathbf{A}}_1{\mathbf{q}}_{\alpha }\le \gamma G_{\max }\hfill \\ \hfill & -\gamma R_{\max }\le {\mathbf{A}}_2{\mathbf{q}}_{\alpha }\le \gamma R_{\max }\hfill \\ \hfill & {\mathbf{q}}_{\alpha }^T{\mathbf{A}}_1^T{\mathbf{A}}_1{\mathbf{q}}_{\alpha }\le \eta G_{\max }^2\tau ∕\Delta t,\hfill \end{array}$$ (A.13)

where the constraints are understood to apply to each coil separately (α = x, y, z). If the Euclidean version of the gradient constraint is desired, one just has to replace the corresponding max-norm expression with that in equation (A.8). In addition to that nonlinear inequality, there are two more: the measurement tensor constraint, equation (A.4), and the heat dissipation constraint, equation (A.12). The cross-terms in the measurement tensor constraint make the problem non-convex. Nevertheless, Sequential Quadratic Programming (SQP) [32] seems to produce a good local optimum reasonably fast—typical computation times on a modern laptop are about 30 s for N = 100 and 15 min for N = 200.

Appendix B. Derivation of the ratio of SNRs

Here we will show how the assumptions in section 2.4 lead to equation (16) for the ratio of the SNRs of pulse sequences A and B.

Requiring equal b -values and using the first assumption gives

$${\tau }_B={\tau }_A{\left(\frac{\kappa \left({\eta }_A\right)}{\kappa \left({\eta }_B\right)}\right)}^{1∕3}\triangleq {\tau }_A\Psi ,$$ (B.1)

where we for convenience have introduced the function Ψ = (κ(η_A)/κ(η_B))^1/3.

From the second assumption and equation (11) it follows that the maximum heat dissipation per unit time is

$$w=\frac{{\eta }_A{\gamma }^2{G}_{\max }^2{\tau }_A}{T_R^{\left(A\right)}}.$$ (B.2)

For gradient sequence B to have the same heat dissipation per unit time it must hold that

$$\frac{{\eta }_B{\tau }_B}{T_R^{\left(B\right)}}=\frac{{\eta }_A{\tau }_A}{T_R^{\left(A\right)}}.$$ (B.3)

Of course, $T_R^{\left(B\right)}\ge {\tau }_B$, which means that

$$\frac{{\eta }_B}{{\eta }_A}\ge \frac{{\tau }_A}{T_R^{\left(A\right)}}.$$ (B.4)

The number of repetitions n (neglecting round-off) is

$$n_A=\frac{T_{\text{total}}}{T_R^{\left(A\right)}},n_B=\frac{T_{\text{total}}}{T_R^{\left(B\right)}}=\frac{{\eta }_A{\tau }_A}{{\eta }_B{\tau }_B}\frac{T_{\text{total}}}{T_R^{\left(A\right)}},$$ (B.5)

where we used equation (B.3) in the second expression. The ratio is

$$\frac{n_B}{n_A}=\frac{{\eta }_A{\tau }_A}{{\eta }_B{\tau }_B}=\frac{{\eta }_A}{{\eta }_B}{\Psi }^{-1}.$$ (B.6)

From equation (15) it follows that

$$\frac{{\mathrm{SNR}}_B}{{\mathrm{SNR}}_A}=\sqrt{\frac{n_B}{n_A}}\exp \left(-\frac{({\tau }_B-{\tau }_A)}{T_2}\right)\frac{1-\exp \left(\frac{{\tau }_B}{2T_1}\right)\exp \left(-\frac{T_R^{\left(B\right)}}{T_1}\right)}{1-\exp \left(\frac{{\tau }_A}{2T_1}\right)\exp \left(-\frac{T_R^{\left(A\right)}}{T_1}\right)}$$ (B.7)

$$={\left(\frac{{\eta }_A}{{\eta }_B}\right)}^{1∕2}{\Psi }^{-1∕2}\exp \left((1-\Psi )\frac{{\tau }_A}{T_2}\right).$$ (B.8)

$$\frac{1-\exp \left(\Psi \frac{{\tau }_A}{2T_1}\right)\exp \left(-\Psi \frac{{\eta }_B}{{\eta }_A}\frac{T_R^{\left(A\right)}}{T_1}\right)}{1-\exp \left(\frac{{\tau }_A}{2T_1}\right)\exp \left(-\frac{T_R^{\left(A\right)}}{T_1}\right)}.$$ (B.9)

Appendix C. Experimental verification of isotropic encoding

To experimentally verify that the optimization produces a waveform that achieves isotropic diffusion encoding we prepared a sample consisting of a non-ionic surfactant mixed with water, as in [33]. This sample is characterized by the formation of concentric cylindrical layers throughout the test tube, which in this case had an inner diameter of 4 mm. The mean diffusivity in each domain is expected to be the same, but the orientations different.

In section 2 we saw that, under the assumption of Gaussian diffusion, the normalized echo amplitude E(q) = Tr(BD). Consequently, an isotropically encoding pulse results in log (E_iso(b)) = −bD̄, where D̄ is the mean diffusivity. A conventional SDE sequence applied in the direction n̂ corresponds to a measurement tensor B_n̂ = bn̂n̂^T. So, it gives rise to a normalized echo amplitude

$$\log \left(E_{\widehat{\mathbf{n}}}\left(b\right)\right)=\mathrm{Tr}\left(b\widehat{\mathbf{n}}{\widehat{\mathbf{n}}}^T\mathbf{D}\right)=-b\mathrm{Tr}\left({\widehat{\mathbf{n}}}^T\mathbf{D}\widehat{\mathbf{n}}\right)=-b{\widehat{\mathbf{n}}}^T\mathbf{D}\widehat{\mathbf{n}}.$$ (C.1)

For a system consisting of multiple non-interacting compartments, the total signal is the sum of the signals from each compartment. Assuming that the experimental conditions are such that the diffusion in each compartment can be approximated as Gaussian, the resulting echo amplitudes using SDE and an isotropically encoding pulse are,

$$E_{\widehat{\mathbf{n}}}\left(b\right)=\sum _{i=1}^N{p}_i{e}^{-b{\widehat{\mathbf{n}}}^T{\mathbf{D}}_i\widehat{\mathbf{n}}},E_{\mathrm{iso}}=\sum _{i=1}^N{p}_i{e}^{-b{\stackrel{‒}{\mathbf{D}}}_{\mathrm{i}}},$$ (C.2)

where p_i is the fraction of protons in compartment i. If the mean diffusivity in every compartment is the same, then $E_{\mathrm{iso}}=e^{-b\stackrel{‒}{\mathbf{D}}}{\sum }_{i=1}^N{p}_i=e^{-b\stackrel{‒}{\mathbf{D}}}$. To derive a rotationally invariant quantity from SDE measurements one may average the signal over all directions. This is sometimes referred to as the powder average and can be approximated as [11]

$$\log E\left(b\right)=-\frac{3}{\stackrel{‒}{K}}\log \left(1+\frac{\stackrel{‒}{K}}{3}b\stackrel{‒}{\mathbf{D}}\right)$$ (C.3)

$$\approx -b\stackrel{‒}{\mathbf{D}}+\frac{\stackrel{‒}{K}}{6}{\left(b\stackrel{‒}{\mathbf{D}}\right)}^2$$ (C.4)

where K̄ is the kurtosis of the powder-averaged data [34]. The approximation (C.4), which coincides with the cumulant expansion [35], follows from a Taylor expansion of the logarithm.

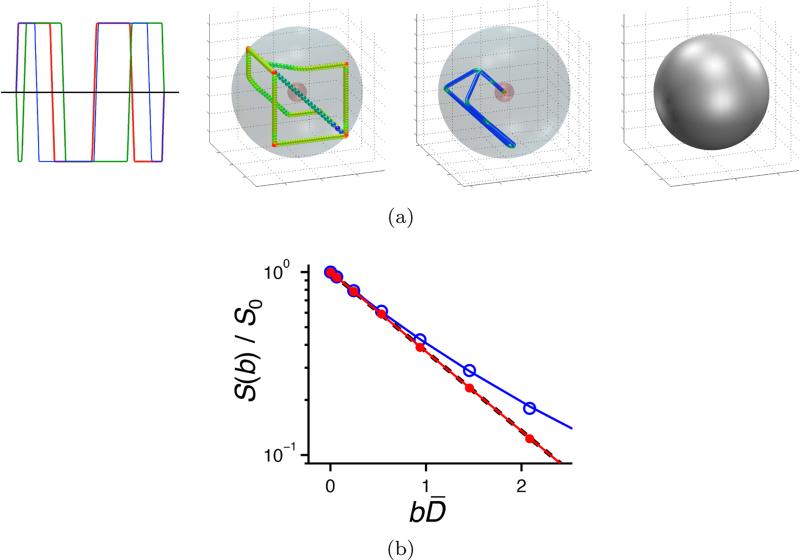
Experiments were performed on a 11.74 T Bruker AVII-500 spectrometer equipped with a MIC-5 probe capable of delivering 3 T/m gradients in three orthogonal directions. We optimized an isotropically encoding waveform with G_max = 0.3 T/m, R_max = 1000 T/m/s, echo time τ = 20 ms, no heating constraint (η = 1), max norm constraint on the gradients and used N = 200 discretization points. The pulse sequence was the same as in figure 4 of [11], i.e. spin-echo diffusion encoding with RARE image read-out, wherein the optimized gradient waveform was inserted before and after the first 180° RF pulse. The directional measurements were done with a waveform for which the magnitude of q(t) was the same as for the isotropic waveform [10]. The optimized waveform and resulting measurements, in a representative pixel, are shown in figure C.10 together with powder averaged measurements. The expected behavior is clearly visible: a straight line for the optimized isotropic waveform (E_iso = e^−bD̄) and a curved line for the powder average, corresponding to equation (C.3).

Figure C.10.

(a) Waveform optimized to achieve isotropic diffusion encoding for an NMR experiment. See caption of figure 4 for figure details. (b) Normalized signal E(b) = S(b)/S₀ vs. normalized diffusion weighting bD̄ for a representative pixel in an NMR experiment on a water/surfactant mixture. Powder-averaged measurements are shown with open blue circles, the measurements using the optimized waveform are shown with solid red circles. The blue and red lines show the corresponding fits of equation (C.3). The dashed black line is the single-exponential E(b) = e^−bD̄. The overlapping of the solid red and dashed black lines shows that the optimized waveform achieves the expected encoding.