The importance of decision onset

Abstract

The neural mechanisms of decision making are thought to require the integration of evidence over time until a response threshold is reached. Much work suggests that response threshold can be adjusted via top-down control as a function of speed or accuracy requirements. In contrast, the time of integration onset has received less attention and is believed to be determined mostly by afferent or preprocessing delays. However, a number of influential studies over the past decade challenge this assumption and begin to paint a multifaceted view of the phenomenology of decision onset. This review highlights the challenges involved in initiating the integration of evidence at the optimal time and the potential benefits of adjusting integration onset to task demands. The review outlines behavioral and electrophysiolgical studies suggesting that the onset of the integration process may depend on properties of the stimulus, the task, attention, and response strategy. Most importantly, the aggregate findings in the literature suggest that integration onset may be amenable to top-down regulation, and may be adjusted much like response threshold to exert cognitive control and strategically optimize the decision process to fit immediate behavioral requirements.

a great deal of work in perceptual decision making has focused on describing the “stopping rules” that terminate a decision process when integration of further evidence provides little added benefit. It is often neglected that understanding when and how the decision process is initiated may be equally important. In line with sequential sampling models of decision making reviewed below, the decision process can be defined as the integration of evidence over time. Within this framework, decision onset is the time at which evidence integration begins. If integration is initiated too early, i.e., before relevant information is available, it may be hampered by noise or irrelevant information (Laming 1979). Conversely, important information may be lost and/or the decision process may be prolonged unnecessarily if the integration is initiated too late. These issues are further complicated by the fact that the encoding of a stimulus and extraction of task-relevant features take variable amounts of time depending on task demands and stimulus properties. Hence, the optimal time for integration onset may be hard to predict and may vary on a trial-by-trial basis.

This review argues that not only is a detailed understanding of the neural mechanisms governing decision onset necessary to provide a comprehensive description of evidence-based decision making but decision onset can have a profound impact on decision outcomes in everyday life. Over the past decade numerous articles have reviewed diverse aspects of decision making (Churchland and Ditterich 2012; Drugowitsch and Pouget 2012; Heekeren et al. 2008; Heitz and Schall 2013; Kepecs and Mainen 2012; Kurniawan et al. 2011; Mulder et al. 2014; Nienborg et al. 2012; Ratcliff 2006; Ratcliff and Smith 2004; Romo et al. 2012; Shadlen and Kiani 2013; Siegel et al. 2011; Standage et al. 2014; Zhang 2012). However, so far, there is no review of the growing body of work that relates to issues of decision onset. The present article aims to provide such a comprehensive review of the decision making literature in order to deepen our understanding of the mechanisms that mediate decision onset.

The review focuses on two main questions: 1) Is the integration process initiated automatically by the appearance of a sensory stimulus, or does its onset vary as a function of stimulus properties or task demands? If the latter, 2) are the changes of decision onset adaptive, and can they be used strategically to optimize decision making? The review highlights the complexity of decision onset and presents converging evidence from different investigators, species, and methodological approaches suggesting that decision onset can depend on stimulus properties and is to some degree under cognitive control. Furthermore, we suggest that changes of decision onset can be adaptive and used to effectively increase decision accuracy. Theoretical Framework outlines several theoretical considerations that help frame the question of decision onset. Psychophysical Findings focuses on recent psychophysical findings that shed light on the phenomenology of decision onset. In particular, it focuses on studies that question the notion that decisions are initiated automatically by the appearance of suitable (sensory) information. Neural Correlates reviews potential electrophysiological correlates of decision onset. While important progress has been made, the lack of clearly defined neural correlates poses a significant challenge and opportunity for the field.

Theoretical Framework

This part introduces the reader to important theoretical concepts that help frame the question of decision onset and the mechanisms that may mediate decision onset. It covers 1) sequential sampling models and bounded integration, 2) two different theoretical frameworks about the flow of information between different processing stages, 3) a formal definition and practical measures of decision onset, and finally 4) two theoretical challenges that integration onset poses to sequential sampling models.

Models of decision making.

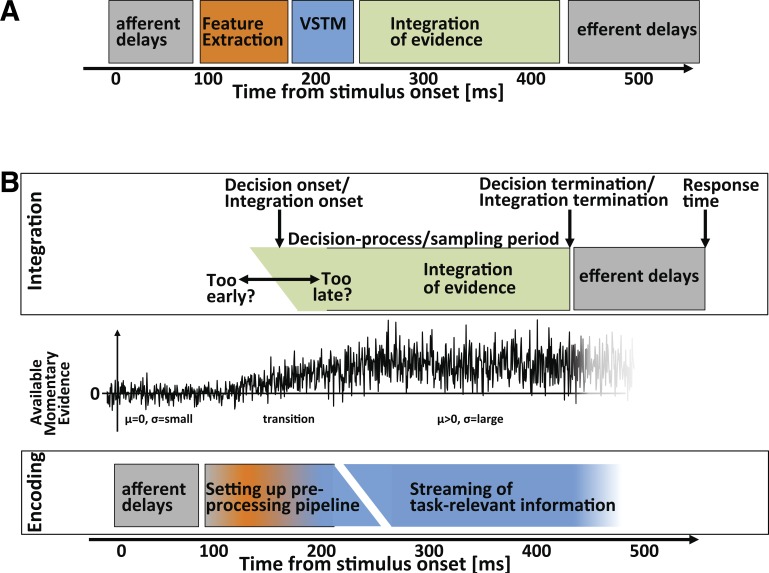
The concept of decision onset is intimately linked to a class of mathematical models known as sequential sampling models (Smith and Ratcliff 2004) that are based on sequential probability ratio tests (Wald 1947). Sequential sampling models view decision making as the bounded integration of noisy (sensory) information over an extended period of time until a criterion indicates that sufficient information has been collected (bounded integration). The integration process sums independent estimates of sensory evidence to average out noise that can be present in the stimulus or its neural representation (Rothenstein and Tsotsos 2014; Smith et al. 2004). Sequential sampling models are closely related to signal detection theory (Rothenstein and Tsotsos 2014). However, in contrast to signal detection theory, they treat decision making as a process that extends over time, rather than as a single discrete event. Hence, the decision process is limited by two distinct points in time that mark its beginning (decision onset or integration onset) and its end (decision point or integration termination).

Sequential sampling models have been instrumental in providing a theoretical framework for understanding decision making as well as capturing a large body of experimental results. Their main focus is on single-stage decision processes that generally last no longer than 1–1.5 s (Ratcliff and Rouder 2000). Sequential sampling models can be grouped into different categories according to certain core features: 1) time-discrete vs. time-continuous sampling and integration of evidence, 2) absolute vs. relative stopping rules, and 3) leaky vs. perfect integration of evidence (Smith and Ratcliff 2004). Models that use absolute stopping rules maintain information for different alternatives in separate integrator units. A decision is made if evidence for one of the alternatives exceeds a preset threshold. Models that use a relative stopping rule combine the differential information of two competing alternatives in a single integrator. A decision is made as soon as the differential evidence favors one alternative over the other by a predefined amount. Of particular interest for the question of decision onset is the dichotomy between perfect and leaky integration (see The challenge of decision onset). A leaky integrator retains information for a limited amount of time, and in the absence of external drive its activity decays exponentially to zero. In contrast, the activity of a perfect integrator will remain at a constant level, and information is retained indefinitely. Hence, leaky integration ameliorates the problem of integrating noise prior to stimulus onset that could create bias in a perfect integrator.

In the following we briefly review one sequential sampling model, the drift-diffusion model (Laming 1968; Ratcliff 1978; Ratcliff and Murdock 1976), in more detail. We focus on the diffusion model because it is commonly used in the literature and many of the studies reviewed below are based on the diffusion model or variants thereof. However, the core concepts of interest to our questions apply equally to other sequential sampling models such as the race model (Vickers 1970), the feedforward inhibition model (Shadlen and Newsome 2001), or the leaky competing accumulator model (Usher and McClelland 2001).

The diffusion model, as all sequential sampling models, treats decision making as the integration of noisy evidence over time (Fig. 1). For small time increments, dt, noisy sensory evidence, x, is modeled as a Gaussian random variable with mean μ × dt and variance s² × dt. The variable μ is typically referred to as drift rate and corresponds to the average value of the evidence integrated during a time interval of unit duration. The variable s describes the standard deviation of the evidence integrated during a time interval of unit duration. The noisy evidence is integrated over time, and the result of this integration process is referred to as the decision variable y(s) = ∫₀^sx(t)dt. The decision process ends as soon as the decision variable exceeds or falls below certain predefined bounds at ±B, where each bound is associated with a particular response option. The so-called starting point, z, is a value between −B and +B that describes the value of the integrator at time 0, when the integration is initiated, z = y(0). If z is equal to 0, both bounds have the same a priori likelihood of being reached. If z is positive (or negative), the upper (or lower) bound is more likely to be reached. The time from integration onset to the time at which the bound is reached corresponds to the duration of the decision/integration process. Overall reaction time (RT) corresponds to the duration of the integration process plus afferent and efferent delays in the system that are not related to the decision process (non-decision time, t_nd).

Fig. 1.

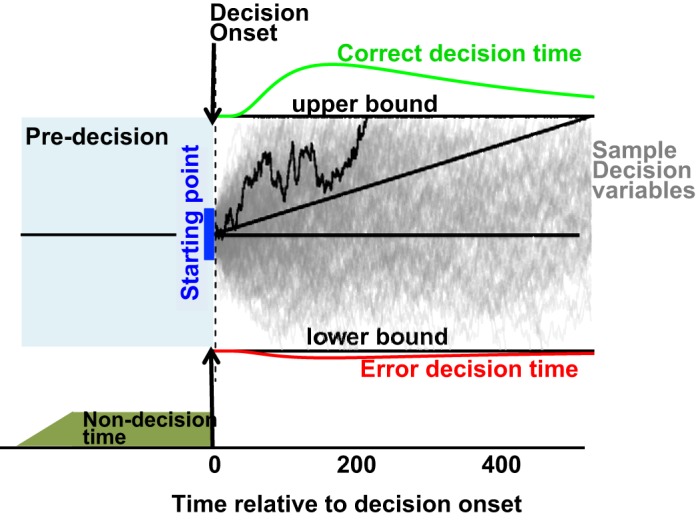
Drift-diffusion model. The drift-diffusion model views decision making as the integration of differential evidence to 1 of 2 response bounds. Thin gray lines represent sample traces of the decision variable in different simulated trials. A decision process ends as soon as the decision variable reaches 1 of the 2 bounds. Thin black line highlights 1 example trace that reaches the correct (upper) boundary ∼220 ms after integration onset. Green and red curves above and below the upper and lower bound represent the distribution of decision times for the correct and wrong choices. The total reaction time is defined as the sum of decision time and non-decision time. Solid blue vertical bar at time 0 represents the distribution of the decision variable at the time of integration onset. Straight black line emerging from the origin represents mean path of the decision variable in the absence of absorbing boundaries.

Allowing all the parameters, s, μ, z, and B, to vary leads to families of redundant models that all predict identical RT distributions and choices. To resolve this redundancy, one of the variables—most commonly s—is set to a prespecified value, typically either 1 or 0.1 (Ratcliff 2001; Ratcliff and Tuerlinckx 2002; Smith et al. 2004). As a result, the remaining variables B, μ, and z are reported as multiples of s. Additional parameters have been incorporated into the diffusion model to capture more subtle details of the behavioral data. For example, σ_t describes the trial-by-trial variability of non-decision time (Ratcliff and Tuerlinckx 2002) and σ_z describes the trial-by-trial variability of the starting point z. Finally, σ_μ describes the trial-by-trial variability of drift rate. Most recent variants of the diffusion model also include the option to allow the value of the decision threshold, B, to vary as a function of time (Zhang et al. 2014).

Cascade vs. stage models of processing.

In its most abstract form, decision onset is a question about the flow of information between different stages of processing (Woodman et al. 2008). Most models of cognitive function assume that a single task can be broken down into individual processing stages (McClelland 1979; Sternberg 1969). For example, deciding whether a group of dots is moving to the left or right may be broken down into the encoding of local visual features, the extraction of motion information, the decision, and motor response. There are two different notions about the flow of information between different stages of processing. So-called stage or discrete-flow models (Sternberg 1969) are based on the insertion principle by Donders (Donders 1868) and assume that processing occurs serially: information is passed from one stage to the next only after processing at the earlier stage is complete. Thus only one process is active at any one time. In contrast, cascade or continuous-flow models (McClelland 1979) are based on the principle of parallel contingent processing and assume that information is continuously transmitted from one stage to the next, even if processing at the earlier stage is not yet complete (Miller and Hackley 1992). As a result, processing in different stages can occur in parallel.

Bounded integration models of decision making such as the diffusion model include aspects of both discrete and continuous-stage models. The presumed relation between the decision and motor stages is a textbook example for “stagelike” information processing: the decision stage finishes as soon as a threshold is reached, and no information is passed to the motor stage until then. In contrast, the information flow between the sensory encoding stage and the integration stage shares properties of both concepts. On the one hand, it is known that the integration stage remains sensitive to changes in dynamic stimulus displays (Kiani et al. 2008) until the decision threshold is reached. This indicates a continuous flow of information from the stimulus representation to the integration stage. On the other hand, most models implicitly assume that integration begins only after all preprocessing steps, including the encoding of relevant stimulus information, have been completed. This view has been made explicit, for example, by Ratcliff and Rouder (2000), who found that information flow (drift rate) remained constant even after the stimulus had been replaced with a mask on the screen. This finding suggests that the integrator does not receive input directly from sensory units but rather from a stable visual short-term memory (VSTM) trace (Reeves and Sperling 1986; Shih and Sperling 2002; Sperling 1960). Later, Ratcliff, Smith, and colleagues (Ratcliff and Smith 2010; Smith et al. 2004; Smith and Ratcliff 2009) suggested that the VSTM stage is not an optional stage that can provide backup information in case the actual visual input is no longer visible. Rather, they suggest that VSTM is the only stage that provides direct information to the integrator units. This yields the following hierarchy of serial processing stages: information from early visual processing is encoded into VSTM, which in turn provides the input to the decision stage (see also Decision onset and encoding of relevant information and Fig. 2A).

Fig. 2.

The challenge of decision onset. Figure outlines the challenges of decision onset within the context of a serial (A) and a hybrid serial/parallel (B) model of decision making. Transitions between stages are indicated by rectangular blocks and black lines if the stages occur in series or by slanted unbounded polygons if the stages occur in parallel. A: the serial model is largely consistent with the diffusion model elaborated in Decision onset and encoding of relevant information. Following afferent delays, relevant information is extracted and encoded in visual short-term memory (VSTM). Integration begins only after the VSTM memory trace has been established. Consequently, drift rate is constant over the entire integration period. B: the hybrid serial/parallel model of decision making is divided into 2 layers (encoding and integration) that are typically believed to occur in different cortical areas or distinct neural populations within a layer. Middle: cartoon of momentary sensory information that is provided to the integration stage at each point in time. Prior to stimulus onset the momentary evidence fluctuates around a mean μ of 0. Once sensory-evoked activity reaches the relevant cortical areas both the mean and the variance σ of the momentary evidence increase toward a steady state until the preprocessing has isolated the relevant stream of information. We conceptualize preprocessing as the process of setting up a pipeline to stream task-relevant information to the integrator (see Cascade vs. stage models of processing). The parallel nature of the preprocessing reflects the fact that a sensory area will encode certain aspects of a stimulus even before the task-relevant stream of information has been isolated. The key challenge of decision onset is to balance the need to use all task-related information with the need to prevent the integration of noise or misleading information.

One potential way to consolidate these two views is to reconceptualize the idea of the preprocessing stage. Typically, preprocessing refers to the idea of refining the neural representation of a stimulus before it is passed on to downstream stages. Alternatively, preprocessing may not operate on the neural representation of a stimulus but rather represents the process of bringing neural circuits into a state of readiness for the processing of a particular stimulus. Hence, preprocessing may be viewed as the process of setting up a pipeline that will eventually route a stream of task-relevant information to the integrator unit (Fig. 2B). This view can consolidate a potentially serial preprocessing stage with the concept of continuous flow of information from the stimulus representation to the integrator. We argue below that in certain conditions that involve simple stimulus features and intuitive stimulus-response mapping (e.g., rightward motion = right button press) such a pipeline is available by default and can be engaged immediately by the appearance of a suitable stimulus. In other instances, engaging the pipeline will involve time-consuming steps such as feature binding, short-term memory encoding, the activation of specific stimulus-response mapping, or the engagement of selective attention to isolate the relevant stream of information.

In Psychophysical Findings we review several lines of evidence to describe the relationship between preprocessing and the integration stage. In some situations decision onset is contingent on the completion of preprocessing; in others integration can begin before the processing pipeline provides task-relevant information. Most importantly, we review several studies that show that the onset of the integration process is to some degree under cognitive control and can be adjusted to stimulus properties, task demands, or personal preferences.

Defining and measuring integration onset.

Following Laming's “epoch of sampling onset” (Laming 1979), we define decision onset as the onset of the integration process. This section elaborates on the limitations of this definition and provides different mechanisms of “effective integration onset” that are general enough to apply to different sequential sampling models and potential neural mechanisms.

Within the context of sequential sampling models, the activity of the integrator unit is often defined in the form of a stochastic differential equation:

$$\text{dy}=(x+\nu )\mathrm{d}t$$

In this simple form, the change of activity of the accumulator, y, is defined as the sum of a deterministic input, x, and a stochastic noise process, v, defined as the derivative of the Wiener process, W. Without further restriction, this equation is valid for any point in time. Hence, the value of the integrator at a particular time, s, is defined as the integration of x + v from −∞ to s:

$$y(s)=\underset{-\infty }{\overset{s}{\int }}x(t)+\nu (t)\mathrm{d}t$$

In this general case, decision onset is equal to −∞, and hence not defined in a meaningful way. In most experimental settings, it is assumed that the integration process is initiated at some point, t₀, typically some time after the onset of a task-relevant stimulus_.

$$y(s)=\underset{t_0}{\overset{s}{\int }}x(t)+\nu (t)\mathrm{d}t$$

In most cases it makes sense to define time of integration onset, t₀, relative to stimulus onset, although in principle integration can start before the stimulus is turned on, in which case t₀ would be negative. In most cases, however, decision onset will likely occur some time after stimulus onset. It is very important to stress the fundamental difference between decision onset and non-decision time, t_nd. Within the framework of the diffusion model, non-decision time represents the sum of durations of all processes that are not related to the decision process, mostly afferent and efferent delays. Decision onset, in contrast, is a single point in time that determines when integration starts. In the ideal case, integration starts immediately after afferent delays are over and stimulus information is available. However, as outlined in Decoupling stimulus onset and decision onset and Decision onset in interference tasks, decision onset has been suggested to occur either before or after afferent delays are completed. In certain situations, however, non-decision time and decision onset can be related. For example, many studies argue that delaying decision onset by a fixed amount increases non-decision time by the same amount (see Potential psychophysical correlates of changes in decision onset).

Integration onset is an abstract concept that is based on the potential of a (neural) system to integrate incoming information. An integrator can be “on” even if there is no input or integrated evidence to prove it. Because the abstract concept is extremely difficult to measure in complex neural systems, we need practical measures that provide a proxy of whether an integrator is on or not. We first discuss potential measures in the mathematical framework of stochastic integration. These considerations will later help us define the concept of effective integration onset in sequential sampling models and neural networks.

In certain situations, integration onset can be approximated as the point in time t when over many trials the average activity of the integrator, E[y(t)], begins to change, where y(t) is the value of the integrator at time t. This approximation is valid as long as we know that the deterministic input component, x, is not equal to 0. If x is equal to 0, as may be the case prior to stimulus onset, E[y(t)] remains at baseline, no matter how long the integration process lasts. Consequently, E[y(t)] can remain constant even if the integrator is “on.”

A second proxy for integration onset uses the stochastic input component. In a noisy system like the brain, stochastic background activity is likely to be present continuously. Hence, a measure that quantifies integration onset based on the stochastic component will be more robust than a measure that depends on a nonzero deterministic component. By definition, the mean of the stochastic component is zero, so it will not change the mean of the integrator. However, integration of zero-mean noise can be inferred by changes in the variance of the integrator Var[y(t)]. If the integration time constant is infinite, variance increases linearly over time when the integration is ongoing and remains constant otherwise. For leaky integration the increase is not linear and eventually saturates. In both cases, integration onset can be indicated as the point in time when Var[y(t)] starts increasing (Churchland et al. 2011; Kiani et al. 2008). This estimate is a valid indication of integration onset as long as the stochastic component is not equal to zero and, in case of leaky integration, the integration of noise has not already saturated. Note that both E[y(t)] and Var[y(t)] need to be assessed across many trials with presumably similar time of integration onset.

We have presented a mathematical definition of decision onset that is based on the ability of an integrator unit to store its input. Furthermore, we outlined two measurable quantities that can mark integration onset given that the potential integrator unit receives nonzero input. Both measures are merely indirect probes of whether or not the integrator is “on.” These considerations will be helpful below for generating practical definitions of decision onset in the context of complex neural models or actual physiological data.

The mechanism that most closely resembles the mathematical definition of decision onset in a neural network involves a change of the integration time constant. A network with a short time constant computes a moving average of only the most recent input (strong leakage). In contrast, a network with a long time constant will retain information for a long time, enabling integration over a meaningful timescale (no/weak leakage). Hence, it is possible to define effective integration onset as a point in time when an abrupt change of network properties leads to a substantial increase of the integration time constant. Changes in real neural networks are probably less extreme and less abrupt than those implied by the mathematical definition. Nevertheless, the mechanism of increasing integration time constant comes closest to the abstract concept of the mathematical definition.

A second possible mechanism to mediate effective integration onset can be based on the gating of the flow of information to the network. The formal definition of integration onset implies that input prior to integration onset is forgotten while input occurring after integration onset is retained. This effect can be achieved by simply preventing any input to the integrator prior to a particular point in time. In this case, the integrator may have been “on” for the entire time, even though it did not receive any input and thus did not integrate any information. Importantly, it is necessary to prevent all input, including the stochastic component. A more realistic requirement may be a very substantial, but not necessarily complete, attenuation of input.

A third mechanism of effective integration onset can be based on top-down inhibitory input that suppresses the ramping of activity that might otherwise result from the integration process. This mechanism would require neither the input to the integrator to be gated nor the integration constant to be changed. Nevertheless, it would have a very similar overall effect of preventing the integration of information up until the point when the top-down inhibition is removed.

Finally, a closely related concept may mediate effective integration onset by simply resetting the integrator at a specific point in time. The reset could be mediated by a top-down control signal and wipe out all the accumulated information in the network. Thus integration could start from scratch.

The mechanisms of effective integration onset outlined above were derived based on the theoretical properties of a perfect integrator. However, integration circuits in the brain are most likely not perfect, despite the fact that time constants can be long enough to enable almost perfect integration over the time course of short perceptual decisions. Furthermore, many sequential sampling models explicitly assume integrator leakage to account for the problem of integrating noise prior to stimulus onset. For these types of leaky integrators, it is necessary to elaborate a special case of effective decision onset. In theory, leaky integrators are designed so they can be “on” continuously without reaching a response threshold and triggering an unwanted response in the absence of a stimulus. Nevertheless, it is possible to define effective integration onset for these leaky units. If input is constant over time, they reach a steady state that depends on internal network dynamics as well as the amplitudes of the deterministic and stochastic components of the input. However, as soon as the deterministic and/or stochastic input changes, mean or variance of the leaky integrator will start converging to a new steady state. Effective integration onset can be defined as the onset of these changes that depend on the properties of the integrator input. In other words, effective integration onset will correspond to the point in time at which the input to the integrator changes. This time may depend, for example, on afferent delays or preprocessing.

In summary, we have provided one formal mathematical definition of integration onset and several potential mechanisms (effective integration onset) that capture the spirit of the formal definition within the domain of more complex neural networks. For the remainder of this article we will use the term “integration onset” rather than “effective integration onset” for simplicity. Oftentimes we will use “decision onset” and “integration onset” interchangeably, but we try to use the former when highlighting the concept and the latter when highlighting the mechanism.

The challenge of decision onset.

Task-relevant information is believed to be represented in sensory neurons such as the motion-sensitive neurons in the middle temporal area (MT) or visual neurons in the frontal eye fields (FEFs) (see Neural Correlates). Prior to stimulus onset these neurons have low firing rates. Nevertheless, their activity is subject to random fluctuations due to internal network dynamics (Fig. 2B, middle). After stimulus onset, their activity increases in response to the stimulus onset before settling into a period of sustained activity. Depending on task and/or brain region, the very first transient pulse of evoked activity may (Ferrera et al. 1994; Mendoza-Halliday et al. 2014) or may not (Schall et al. 1995) be selective for the feature in question. It has been shown that sequential sampling models provide the best performance (the highest accuracy for a given mean RT) if all available information is integrated and maintained without loss in the integrator units (perfect integration) (Wald 1947). However, if the integrator starts accumulating before the stimulus is presented, it will sample noise from the empty stimulus display (Laming 1968). Furthermore, the extraction of task-relevant information can take a certain amount of time that may differ depending on the signal-to-noise ratio of the stimulus (see Decision onset and encoding of relevant information), spatial attention (see Decision onset and spatial attention), and the presence of salient but irrelevant features (Desimone 1998). The integration of noise and task-irrelevant information may lead to a reduction of accuracy or introduce a bias.

Here we outline two closely related main challenges for mechanisms that mediate decision onset: 1) delaying decision onset until after stimulus onset to avoid the integration of noise prior to stimulus onset and 2) delaying decision onset until task-relevant information has been extracted to avoid the integration of task-irrelevant information. A mechanism that can solve challenge 2 will automatically solve challenge 1, but not vice versa. Solutions for challenge 1 tend to be simpler and do not require an active mechanism; for example, integrator leakage may provide a satisfactory solution. In contrast, mechanisms that address challenge 2 tend to be more complex, involving active mechanisms such as top-down initiation of integration.

AVOIDING INTEGRATION OF NOISE.

While loss-free retention of information is the ideal behavior for an integrator during the decision process, it causes problems before and after the integration process. In particular, a perfect integrator will 1) retain information even if the information is no longer relevant and 2) accumulate and retain noise even in the absence of a stimulus or a choice to be made. Noise may arise from processing the empty stimulus display or from task-unrelated internal neural dynamics. While some models assume that noise is weaker in the absence of a stimulus, it is important to note that even small amounts of noise will eventually, within a finite amount of time, drive a perfect integrator beyond any arbitrary response threshold (±B). Even when the integrator has not reached threshold, the accumulated noise may perturb the starting point, z, of the integrator from its optimal value for the next decision (i.e., z = 0 in case of an unbiased decision without prior information). Hence, noise accumulated at an earlier point in time may decrease the accuracy of an upcoming decision.

In contrast to perfect integrators, leaky integrators are better behaved in the time between decisions: leaky integrators naturally decay back to zero after the flow of sensory information stops. Hence, information from the last decision naturally fades, eliminating the need for an active reset (Larsen and Bogacz 2010). Furthermore, the integration of noise between decisions is less of a concern because leaky integrators will reach a point when, on average, the amount of noise integrated per unit time is canceled out by the amount of activity lost to integrator leakage. Based on this steady state it is possible to set the response thresholds at a level that is not exceeded by random fluctuations. Purcell and colleagues provide a practical example of the effect of prestimulus noise on perfect and leaky accumulators (Purcell et al. 2010).

Integrator leakage provides a simple and physiologically plausible solution for the problem of integrating noise prior to stimulus onset, and models with leaky integrators have been quite successful at explaining many aspects of behavioral data. However, the notion of integrator leakage has also been criticized, and there is a long-standing debate as to whether models with or without leakage are best suited to explain behavioral data (Ratcliff and Smith 2004; Usher and McClelland 2001;). It is not our intention to review this literature or to take sides in the debate. Rather, we argue below that even if we assume that integrator leakage addresses the problem of noise integration prior to stimulus onset, it cannot contribute to the second challenge, i.e., delaying the integration until task-relevant information has been extracted from the stimulus. As we outline in Psychophysical Findings, integrator leakage alone cannot account for many behavioral phenomena that suggest an explicit control of decision onset.

AVOIDING INTEGRATION OF TASK-IRRELEVANT INFORMATION.

The encoding of a stimulus and the extraction of task-relevant information takes time. The amount of time can depend on the type of stimulus and the nature of the task. Thus, while in some cases integration should start 120 ms after stimulus onset, other cases may require the integration to begin 180 ms after stimulus onset. As a result, there is no hard and fast rule that relates the time of stimulus onset to the optimal time of integration onset. In principle, it is possible that a “metachoice” control process monitors the stream of information to the integrator and initiates or resets it as soon as task-relevant stimulus information becomes available. The main task achieved by such a control process would be to determine the time at which the integration of evidence for the decision in question effectively begins (decision onset). Following the nomenclature proposed by Purcell and colleagues, we refer to the process of mediating decision onset as gating (Purcell et al. 2010). While the term “gating” suggests that the effective decision onset is mediated by controlling the flow of information to the integrator, we do not exclude other potential mechanisms such as integrator reset.

Gating can be very effective and can maintain the positive aspects of perfect integration while avoiding the unwanted integration and retention of noise. However, it has been pointed out that any gating process would be time-consuming and require a significant amount of computational overhead (Larsen and Bogacz 2010). In particular, the task of determining when to initiate the decision process on a case-by-case basis might be almost as complex as the decision itself. However, Purcell and colleagues recently proposed an alternative way to dynamically adjust integration onset that is computationally almost as simple as a leak yet is more flexible at adjusting integration onset to different stimulus properties and task demands (Purcell et al. 2010, 2012). Rather than using integrator leak, they propose a gate that prevents the flow of information to the integrator until it exceeds a certain predefined threshold (activity-dependent gating).

Another suggestion to reduce computational complexity was made by Teichert et al. (2014). They argued that there are two fundamentally different ways in which decision onset can be controlled that differ with respect to the amount of computational overhead they require: 1) online, on a case-by-case basis (interference-dependent gating), or 2) in a stimulus-independent way that can modify decision onset for certain task demands (task set-dependent gating). Both mechanisms have been put forward in the context of a Stroop-like response interference task, hence the term “interference-dependent gating.” Here we use the more general term “stimulus-dependent gating,” which captures the same idea but remains agnostic about which features of a stimulus may be used to adjust decision onset.

Stimulus-dependent gating would delay decision onset in trials where the extraction of task-relevant stimulus information takes longer than usual. It would be very effective in delaying decision onset only if necessary. However, it requires a significant amount of computational overhead. Task set-dependent gating, in contrast, would be less computationally demanding. In principle it could be adjusted in a similar way as decision bounds are believed to be adjusted, i.e., prior to decision onset in order to account for certain speed or accuracy demands. However, it would delay decision onset regardless of whether a specific stimulus actually requires longer non-decision times or not.

Psychophysical Findings

Over the past decade, numerous psychophysical studies have contributed to the emergence of a complex and intriguing picture of the phenomenology of decision onset. Evidence for changes in decision onset has been found in a range of different tasks and contexts. Decision onset was reported to vary over a range of up to 400 ms, though in most cases more modest effects in the range of 100 ms were reported. Changes in decision onset were proposed to arise through differences in stimulus encoding duration (Decision onset and encoding of relevant information), allocation of spatial attention (Decision onset and spatial attention), top-down strategic adjustments (Decoupling stimulus onset and decision onset, Decision onset in interference tasks, Decision onset in Stop-signal tasks), and task set reconfiguration (Decision onset and task switching). In the following we review several psychophysical studies that provide important insights about decision onset.

Potential psychophysical correlates of changes in decision onset.

Because the time of decision onset cannot be observed directly, we first describe several behavioral indicators that have been used to infer the time of decision onset: 1) a change in non-decision time, t_nd, that leads to a shift in the RT distribution (the “leading edge effect”), 2) error rate, and 3) proportion of fast errors.

CHANGE IN NON-DECISION TIME.

The most commonly reported indicator of a change in decision onset is a change in non-decision time of diffusion model fits. It is important to note that equating changes of non-decision time with changes in decision onset is only valid under the additional assumptions that 1) drift rate and other decision-relevant parameters are not affected by delaying decision onset and 2) the changes in non-decision time do not map onto changes in efferent (non-decision) delays. If these assumptions are true, then delaying decision onset by a certain amount will lead to a uniform shift of the entire RT distribution. This is in contrast to other parameters such as drift rate, starting point, or bound that can also prolong RTs but only in conjunction with changes to the shape of the RT distribution and error rate.

Ratcliff has argued that a change in non-decision time can be inferred from the leading edge of the RT distribution (“leading edge effect,” see Decision onset and encoding of relevant information), defined as the 10% RT quantile (Ratcliff and Smith 2010). The 10% quantile denotes the time within which the earliest 10% of responses have occurred. Ratcliff has shown that within the framework of the diffusion model the leading edge of the RT distribution mostly reflects non-decision-related processing stages such as afferent and efferent delays. In contrast, the right tail of the RT distribution is more strongly affected by properties of the decision process such as task difficulty (drift rate) and emphasis on speed or accuracy (decision bound). In summary, it has been suggested that changes of the 10% quantile may be a good proxy for changes of non-decision time, which in turn may map onto a corresponding change of decision onset if certain restrictions are met.

ERROR RATE.

In addition to changes of non-decision time, a delay in decision onset may also have an effect on error rate, for example, if the available sensory information changes systematically during the decision process (Smith et al. 2004; Smith and Ratcliff 2009; Teichert et al. 2014). If the first piece of sensory information supports the wrong choice, then initiating the integration process earlier should result in higher error rates. Such changes in error rate would be associated with a corresponding change in the leading edge of the RT distribution as outlined in change in non-decision time.

PROPORTION OF FAST ERRORS.

The first behavioral correlate of changes of decision onset was described by Laming (1968). Laming considered the case in which subjects can anticipate the time of appearance of an informative stimulus. He argues that in order to sample the entire stimulus presentation, subjects would initiate the decision process slightly ahead of stimulus onset. On average, the integrator would accumulate a small amount of noise prior to stimulus onset. He referred to this as starting point variability. It has been shown in theory that increased starting point variability increases the proportion of fast errors. Hence, an increase in the proportion of fast errors may be an indication of earlier decision onset.

While all of these measures can indicate a change of decision onset time, it is important to note that none is a direct measure. In all three cases, there are alternative accounts that do not involve changes in decision onset. Changes of non-decision time may also be explained by longer efferent delays, and changes in error rate can also be caused by changes of decision bound or drift rate. Finally, starting point variability (and hence the presence of fast errors) may also reflect the steady state of a leaky integrator. In some cases, the alternative explanations make different predictions about other aspects of the behavioral data. For example, changes in threshold predict very different effects on RT distributions than changes of decision onset. It is thus important to keep in mind that all three indicators can be evaluated only within the context of certain model assumptions and depend on the precise fit of mathematical models to all aspects of the observed behavioral data. Consequently, convergent findings from different approaches will provide an additional layer of confidence that cannot be achieved from a single dependent variable. The inherent limitations of behavioral indicators highlight the need for reliable neural correlates of decision onset (see Neural Correlates).

Decision onset and encoding of relevant information.

We start our review of the psychophysics literature with a series of experiments by Ratcliff and Smith that test whether integration onset is contingent on the extraction of task-relevant information. They concluded that decision onset is delayed when noise slows the process of forming a perceptual representation of the stimulus features needed to perform the task (Ratcliff and Smith 2010). These studies provide an ideal starting point for several reasons. First, they provide a rationale for the strictly serial processing hierarchy (Fig. 2A) that forms the, often implicit, basis of most studies of decision making. Second, they show that decision onset is a carefully controlled process that can successfully be adjusted to different task demands and stimulus properties. Finally, the studies use the simplest proxy of decision onset: a change in non-decision time that does not require detailed understanding of some of the more complex computational models of later sections.

In these studies, subjects performed a two-alternative forced-choice letter discrimination task. Letter stimuli were degraded by randomly changing contrast polarity in some proportion of pixels in the stimulus display. The leading edge of the RT distribution (see change in non-decision time) was delayed by as much as 140 ms when the proportion of inverted pixels approached 50% (complete degradation of the stimulus). With a drift-diffusion model, the leading edge effect could not be explained by lower drift rates alone. Rather, the leading edge effect required a systematic increase in non-decision time with noise level. Interestingly, a similar brightness discrimination task did not reveal a leading edge effect. This difference between letter and brightness discrimination was replicated even after the two tasks were modified to use identical stimuli. This finding rules out the possibility that the degraded stimuli themselves or an increase in task difficulty is responsible for changes in non-decision time. Similarly, non-decision time remained unaffected if stimulus information was instead degraded by a backward mask. In summary, the observed pattern of data suggests that non-decision time was selectively increased when static or dynamic noise delayed the formation of a perceptual representation of the relevant stimulus features. In the letter task, the noise slowed down the extraction of the relevant features; in the brightness task, the noise was the relevant feature.

In follow-up experiments, the authors tested the hypothesis that the leading edge is determined by a burst of uninformative stimulus energy that accompanies stimulus onset (see Decision onset and spatial attention). To that aim, they increased contrast energy by placing the stimulus on top of various types of pedestals. However, none of the manipulations removed the leading edge effect. Similarly, they increased stimulus energy by brightening the pixels in part of the letter. The brightened part was chosen so that it was common to both alternatives and hence would not provide any discriminative information. Rather, the brightened element would merely support the notion that some letter is present in the noise. This burst of stimulus energy might then drive decision onset and remove the leading edge effect. However, this was also not the case.

A final experiment tested the leading edge hypothesis by using a different way of manipulating the time needed to extract task-relevant information. The binary letter discrimination task used in the earlier experiments can be performed based on simple visual features present in one but not the other letter. Consequently, the extraction of such a feature is relatively easy. As an alternative, subjects were asked to perform a letter-digit discrimination task. Letters and digits are made up of identical features, and the letter-digit discrimination depends on a complete encoding of the stimulus. Thus the letter-digit task should yield a strong leading edge effect. Indeed, the leading edge effect was stronger than in the letter discrimination task (up to 160 ms for correct and 200 ms for error RTs).

In summary, the foregoing experiments suggest that decision onset, measured as non-decision time, is delayed until task-relevant features have been encoded into VSTM. These findings are consistent with previously proposed “stage models” (McClelland 1979; Sternberg 1969), which require a representation of the stimulus to be formed before integration can be initiated.

One of the critical features of the interpretation put forward above is the lack of a leading edge effect for the brightness discrimination task. Ratcliff and Smith argued that the relevant information for the brightness discrimination task is immediately apparent and does not require detailed extraction. A recent study by Coallier and Kalaska can be used to further test this hypothesis (Coallier and Kalaska 2014). In their task, subjects viewed a fine-grained checkerboard pattern with randomly distributed red, blue, and yellow squares. The subjects were asked to judge whether the checkerboard contained more yellow or blue squares while ignoring the red squares that made up about half of all squares. In different trials, the ratio of blue to yellow squares varied from 100/0 to 52/48. On the surface, this task is similar to the brightness discrimination task that did not elicit a leading edge effect (Ratcliff and Smith 2010), the main difference being the presence of task-irrelevant stimuli (red squares). However, the color-discrimination task yielded a substantial leading edge effect between 300 and 400 ms. We suggest that the difference between the two experiments may have been caused by the presence of the task-irrelevant red squares. Following the logic outlined by Ratcliff and Smith, one could argue that the distractor squares may have prolonged the encoding of task-relevant information into VSTM. An alternative explanation is offered by the authors, who suggest that decision onset was adjusted on a trial-by-trial basis as a function of response conflict. Note, however, that this argument by itself would predict the same leading edge effect in the brightness discrimination task by Ratcliff and Smith that failed to find such an effect. We further explore the notion that task-irrelevant information plays an important role for decision onset in Decision onset in interference tasks.

Decision onset and spatial attention.

The next set of studies explores potential mechanisms and additional factors that determine the speed of encoding into VSTM and hence decision onset. In contrast to the studies in Decision onset and encoding of relevant information, the authors relaxed the assumption of strictly serial processing of VSTM and the integration stage. Rather, they analyzed the data with a series of models that explicitly allow the two processes to occur in parallel (Fig. 2B). As a result, drift rate gradually increases until encoding into VSTM is complete. These studies suggest that top-down attention as well as overall stimulus contrast facilitate the encoding of stimulus information into VSTM and hence advance decision onset. In particular, they outline two mechanisms that may affect how quickly the VSTM trace is formed: 1) a spatial cue may accelerate the deployment of spatial attention to the stimulus location, and 2) the total stimulus contrast energy may determine the rate of encoding of information into VSTM.

In a study by Smith and colleagues (Smith et al. 2004), subjects classified a near-threshold grating patch of 60-ms duration as either horizontal or vertical. Location of the grating patches was unambiguous because they were presented on top of a luminance pedestal. On 50% of the trials a spatial cue correctly predicted the position of the upcoming stimulus. If the cue was valid, RT was reduced in a manner consistent with a 10- to 20-ms reduction of non-decision time. This decrease suggests either an earlier onset of the decision process or reduced motor delays. The authors speculated that the cue allowed spatial attention to move to the target location more quickly and accelerated the encoding of the stimulus into VSTM, so that the decision process could be initiated earlier. In this model, spatial attention is the limiting factor that ultimately advances or delays the integration process. Smith and Ratcliff subsequently estimated that the valid spatial cue reduced spatial orienting time by ∼50 ms (Smith and Ratcliff 2009).

A follow-up study by Gould and colleagues (Gould et al. 2007) used a variant of this orientation discrimination task. Rather than the gratings being presented on a luminance pedestal, stimuli were presented directly on the gray background. On half the trials, the grating's position was indicated by a simultaneously appearing high-contrast fiducial cross. Smith and Ratcliff reanalyzed the data of this experiment and pointed out that non-decision time varied as a function of the contrast of the grating (Ratcliff and Smith 2010; Smith and Ratcliff 2009). Interestingly, such a “leading edge effect” was not found when the stimuli were presented on top of luminance pedestals in the experiment by Smith and colleagues (Smith et al. 2004). In light of these differences, Smith and Ratcliff suggested that the speed of encoding into VSTM depends not only on top-down spatial attention but also on the total contrast power of the stimulus. Stimuli on a pedestal have high total contrast energy independent of the contrast of the grating, preventing a leading edge effect. However, for stimuli that were presented directly on the background, total contrast energy, and hence rate of encoding into VSTM, depended exclusively on the contrast of the grating.

In summary, these studies suggest that the onset of the decision process is determined by the speed of stimulus encoding into VSTM. The encoding into VSTM in turn depends on the top-down allocation of spatial attention to the relevant region in space and the total contrast energy of the compound stimulus. Of particular interest for the present review is that the authors derive two distinct models of how attention and stimulus contrast can facilitate the formation of the VSTM trace: a switching model that assumes that attention needs to be aligned with the stimulus location before any information can be transferred into VSTM and a gain model that assumes that spatial attention at a particular location speeds up the rate of encoding of information into VSTM. Strictly speaking, only the former model assumes a change in decision onset. The gain model just predicts different rates of increase of drift rate. Interestingly, the two models make almost indistinguishable predictions. This inability of behavioral data to decide between clearly distinct models highlights the importance of electrophysiological studies (Neural Correlates).

Decoupling stimulus onset and decision onset.

The previous two sections reviewed situations in which decision onset can be modulated by attention, task demands, and stimulus properties. In the following we review two studies that argue in favor of an even stronger dissociation of decision onset from the stimulus. In 1979, Laming suggested that in certain conditions decision onset is under the subject's control and can be decoupled from the time of stimulus onset (Laming 1979). In his study a warning signal allowed subjects to anticipate the onset of the task-relevant stimulus. Diffusion models predict faster responses and higher error rates if the integration process is initiated too early, i.e., before the onset of the task-relevant stimulus. Initiating the decision process too late will lead to unnecessarily long RTs. Laming argued that the common finding of longer RTs and higher accuracy after an error is consistent with the assumption that subjects delay integration onset after an error. His arguments are further strengthened by studies in which the duration of the foreperiod varied as an experimental manipulation. Trials in which the stimulus was presented a bit earlier (later) had higher (lower) accuracy and longer (shorter) RTs. This mimics the results when subjects presumably vary integration onset on their own account.

A recent study by Stanford and colleagues (Stanford et al. 2010) suggests that macaque monkeys can also initiate a decision process independent of the time of appearance of relevant sensory information. In their task, monkeys were instructed to make a left- or rightward saccade to a green (red) target while ignoring an otherwise identical red (green) target. However, at the time of the Go-signal (the disappearance of the fixation point) both targets were still yellow, and the animal did not know the location of the rewarded target. The relevant color information appeared between 50 and 250 ms after the Go-signal. The RTs were approximately constant across all color-cue delays. However, accuracy declined to chance levels as color-cue delay increased, and animals had less time to incorporate color information into their motor plan. In separate experiments, one of the saccade directions was associated with a larger reward and animals were more likely to make a saccade in this direction. This effect was especially pronounced if the color-cue delay was long.

The authors elaborate a sequential sampling model that fits all aspects of the behavioral data. The model suggests that the Go-cue initiates the integration process in two competing accumulators. Drift rate is driven initially by internal preference or reward-induced bias and only later by the relevant color information. It is fair to assume that the internal preference and/or the reward-induced bias are present before the Go-signal. Nevertheless, the accumulation of evidence was found to begin only once the disappearance of the fixation point instructed animals to initiate their decision process. Hence, decision onset was linked to neither the appearance of the task-relevant color information nor the presence of an internal bias signal that determined choice in the absence of relevant sensory information. Rather, decision onset was instead initiated by the Go-signal, which provided no relevant information at all. In this particular case, the presence of the fixation point may have activated fixation neurons in the saccadic system and thus prevented ramping activity in neurons representing the two potential saccade targets (see Onset of ramping for a neural model implementation of such a mechanism). These findings suggest that decision onset can be decoupled from the appearance or presence of task-relevant information. Additional unpublished analyses confirmed that the internal reward bias did in fact exert its effect by changing drift rate after the Go-cue appeared, rather than by changing the starting point (E. Salinas, personal communication). Additional support for the behavioral model was provided by concurrently recorded FEF movement neurons.

Decision onset in interference tasks.

Interference tasks such as the Eriksen flanker task (Eriksen 1974) have been used to gain important insights into the properties of decision onset. Interference tasks are particularly useful because incomplete extraction of task-relevant information may actually invert the sign of drift rate if the distractors are incongruent with the target. Negative drift rate provides a strong signal that can be measured more easily than a gradual increase of drift rate. In a groundbreaking study, Gratton and colleagues (Gratton et al. 1988) argued that processing in interference tasks can be broken down into two stages: a parallel processing phase in which targets and distractors are represented in parallel and a focused processing phase when only the target is represented. During the parallel processing stage information from the distractor automatically activates the corresponding response channel in parallel with information from the target stimulus. They found a higher error rate for incongruent trials only when responses were based on the parallel representation stage. Based on this finding, influential models of decision making in interference tasks such as the conflict monitoring model (Botvinick et al. 2001) assume continuous flow and predict that integration starts automatically with stimulus onset (the parallel stage), not after the extraction of task-relevant information.

Recent findings by Teichert and colleagues (Teichert et al. 2014) have provided a more detailed view of this issue. In particular, their findings suggest that even in interference tasks subjects have some control over decision onset. However, the control does not operate on a case-by-case basis but reflects strategic changes that adjust decision onset as a function of speed-accuracy demands. Teichert et al. used an interference paradigm in which subjects were asked to report the direction of motion of a set of target dots while ignoring the direction of motion of a set of distractor dots that moved in the same (congruent condition), opposite (incongruent condition), or orthogonal (neutral condition) direction as the target dots. The distractor dots had higher luminance contrast to engage bottom-up attention and dominate the motion energy in the parallel processing phase. Subjects performed the task under instructions that favored either speed or accuracy.

A second experiment used a response signal task to measure the information that was available to the integrator as a function of time from stimulus onset and distractor congruency. This estimate of time-dependent drift rate was then fed into a variable-drift rate diffusion model to fit RT and error rate in the speed and accuracy blocks. Contrary to the common finding in tasks without interference, the speed-accuracy trade-off could not be explained by an increase in response threshold alone. To explain the substantial reduction of error rate that was achieved with a rather modest increase in RT, it was necessary to allow decision onset to vary as a function of speed-accuracy instruction. These findings suggest that subjects were able to strategically, though not necessarily consciously, delay decision onset to increase response accuracy. Teichert and colleagues further compared the efficacy of the two speed-accuracy mechanisms. They concluded that in this particular task, adjusting decision onset provides a much more effective way to trade speed for accuracy than changes in response threshold. Nevertheless, the subjects did not use the optimal strategy (defined as highest rate of information transfer in bits/s), which would have required an even lower threshold and later decision onset. However, the subjects' speed-accuracy adjustments moved in the right direction and made extensive use of the more effective decision onset mechanism rather than relying exclusively on suboptimal threshold adjustments. It is important to note that this mechanism is particularly useful under the specific conditions of the paradigm such as a high fraction of salient and incongruent distractors and implicit knowledge that quality of the momentary information will increase over the time course of the trial.

Most studies reviewed thus far use changes in non-decision time as a proxy for decision onset. This is based on the assumption that efferent processing remains unchanged and that instead non-decision time maps onto a delay of the decision stage. However, in the biased competition model of decision making put forward by Teichert and colleagues, non-decision time and decision onset are two clearly distinct parameters with distinct effects on error rate and RT. While stimulus encoding is typically subsumed into the non-decision parameter, the biased competition model takes a different approach. Stimulus (pre-)processing is its own stage that occurs in parallel with and independent of the decision stage. While the decision stage receives input from the stimulus processing stage, integration can be initiated at any point in time (Fig. 1). A change in non-decision time will shift both processing stages equally and lead to a uniform shift of the entire RT distribution while leaving error rate unaffected. However, changes in decision onset act to delay or advance the integration stage relative to the stimulus processing stage. Because relevant target information is gradually extracted over a period of ∼120 ms, delaying decision onset relative to this extraction process increases accuracy, in addition to a complex effect on RT distributions. In summary, the observed changes in the decision onset parameter cannot easily be explained by processes such as efferent delays that can confound the interpretation in other tasks.

These findings suggest that humans delay decision onset in interference tasks to trade speed for accuracy. However, another recent study using an Eriksen flanker task did not report a similar effect (White et al. 2011). There are no obvious differences in methodology that would explain the discrepant findings. However, two points may be worth mentioning: 1) while White and colleagues used a spatial attention task, Teichert and colleagues used a feature-based attention task; 2) while both paradigms allowed subjects to predict the time of stimulus onset, the timing may have been more obvious in the motion direction discrimination task because the cue always appeared 500 ms prior to stimulus onset. To our knowledge the two studies by White et al. and Teichert et al. are the only ones that have fit a variable-drift rate diffusion model to data from an interference task with speed-accuracy instructions. Most other studies of response interference have used sequential sampling models that involve mutually inhibitory accumulators such as the conflict monitoring model (Botvinick et al. 2001; Yeung et al. 2004). While the complexity of the conflict monitoring model makes it harder to fit behavioral data with the same rigor as the diffusion model, the proposed mechanisms for speed-accuracy trade-off may nevertheless be of interest. For example, Yeung and colleagues (Yeung et al. 2004) suggested that subjects use a higher response criterion and a stronger top-down attentional signal to increase response accuracy. While this mechanism differs from those proposed by Teichert et al. and White et al., it is worth pointing out that the stronger top-down attention signal has an effect very similar to delaying decision onset—it helps solve the problem that a modest increase in decision bound that can explain the observed increase in RT is not sufficient to account for the substantial increase in accuracy.

In The challenge of decision onset, we mentioned that models with leaky accumulators may be less prone to the problems associated with decision onset. This may be particularly true for interference tasks, where integrator leak can provide a natural way to clear out information from the distractor that was accumulated during the parallel stage. Unfortunately, neither White nor Teichert incorporated a model with integrator leak in their analysis. In addition to conventional leaky models, the data from interference tasks may be amenable to other models that have been developed to explain decision making in situations where drift rate changes over the course of a trial. In particular, the urgency model by Cisek (Thura et al. 2012) combines the concept of strong integrator leakage with a multiplicative urgency signal that increases over the time of a decision. When sensory information remains constant, the model mimics the standard diffusion model. However, when sensory information changes at random points during a decision process, Cisek's model can easily “forget” information that is no longer valid. This model may provide an alternative fit to the data in interference tasks. Interestingly, for the urgency gating model the question about decision onset would be replaced with the question about the onset of the ramping of the urgency signal. Does the urgency signal start ramping immediately after stimulus onset, or does it start only after task-relevant information has been extracted?

The results reviewed so far indicate that subjects may be able to adjust decision onset in interference tasks in the form of a speed-accuracy trade-off. However, other studies have suggested that subjects may also be able to adjust decision onset on the fly as a function of response conflict in a particular trial. In an experiment by Ratcliff and Frank (2012) subjects chose between two letters each with a different probability of leading to positive feedback if selected. Trials were grouped into three categories: win-win (2 options with high likelihood of reward), win-lose, and lose-lose. The win-win and lose-lose conditions can both be considered high conflict. Fitting a diffusion model to the data revealed that non-decision times in the lose-lose condition were 100 ms longer than in the other two conditions. This increase in non-decision time may be interpreted as a delay in decision onset. However, Ratcliff and Frank also provide a more detailed analysis of the potential underlying mechanisms based on the basal ganglia (BG) model by Frank (2006). The model assumes that response conflict increases activity in the subthalamic nucleus (STN). The STN provides diffuse excitation to the external part of the globus pallidus (GPe), which in turn prevents the disinhibition of thalamus and the execution of a response. Based on the BG model, Ratcliff and Frank develop two variants of the diffusion model that can capture the effect of conflict on both STN and action selection. They suggest that the effect of increased activity in the STN can be modeled either as a temporary increase in bound or as a delay in decision onset. Furthermore, they argue that STN activity should be especially high on lose-lose trials because, in addition to conflict, the STN gets disinhibited via a branch of the indirect pathway that is very active on lose-lose trials and projects from the striatum via GPe to STN. The link between STN activity in the BG model and decision onset in the diffusion model provides an interesting and physiologically plausible mechanism that can explain the finding of delayed decision onset.

In contrast to the studies by Teichert et al. and White et al., these findings suggest that decision onset (or response threshold) is a function of conflict that is computed instantaneously at each point in the trial. This is an interpretation similar to that put forward by Coallier and Kalaska for the findings in their color discrimination task that was discussed in Decision onset and encoding of relevant information. It is possible that different neural mechanisms are at work in sensory interference tasks such as the Eriksen flanker task and a probabilistic value-based decision task or a color discrimination task. In particular, the learned and arbitrary association between a symbol/color and a response may not be as fast as the natural association between a rightward arrow and a right button press. This extra delay may provide sufficient time for a trial-by-trial adjustment of decision onset (or response threshold) in the presence of conflict.

Decision onset in Stop-signal tasks.

Stop-signal tasks provide an unexpected but informative window onto decision onset. In Stop-signal tasks, subjects are required to respond as quickly as possible to a discriminative stimulus such as a right- or leftward arrow by pressing a button with their right or left index finger. On a fraction of trials, a Stop-signal instructs them to withhold this response. Contrary to the instruction to always respond as quickly as possible, subjects will slow their RTs in certain conditions to increase their chances of correctly inhibiting a response on stop trials (Verbruggen and Logan 2009). This slowdown provides a unique opportunity to test whether subjects can strategically delay decision onset. The observed delay in RT can map onto a reduction in drift rate, an increase of response threshold, or an increase in non-decision time. Verbruggen and colleagues examined RT slowdown in a number of conditions that encourage proactive adjustments in response strategy to enhance the likelihood of correctly inhibiting a response (Verbruggen and Logan 2009). In all experiments, they found that the observed proactive RT slowdown was explained by an increase in non-decision time as well as an increase in response threshold (Verbruggen and Logan 2009).

Supporting evidence comes from a study by Leotti and colleagues (Leotti and Wager 2010) in which subjects performed Stop-signal tasks with different reward structures that either stressed fast Go responses or correct cancellations. In line with the incentives, subjects responded faster/slower to the Go-cue when the task rewarded fast responses/correct cancellations. Shenoy and Yu fit a race model to this data set and found that increased RT was explained by increased non-decision time rather than slower drift rate or higher bound (Shenoy and Yu 2011). Similar effects were present in a data set by White and colleagues (White et al. 2014). When analyzing the cause for the commonly observed RT slowdown between the first vs. the second half of the experiment, they found an increase in non-decision time (C. White, personal communication).

These findings can be interpreted in two ways: 1) either subjects delayed the onset of the decision process or 2) they delayed motor execution. In the strict sense of the horse race model that forms the foundation of the analysis of stop signal reaction time (SSRT) data (Logan 1981), the latter alternative is not adaptive, because the decision reaches a point of no return as soon as the response threshold is attained. Hence, a delay that occurs after reaching threshold would not change the subjects' ability to inhibit the response but rather increase SSRT. However, it is possible that the assumptions of the horse race model are not met in this particular circumstance. If so, it seems possible that subjects first identify the correct response and then delay the execution of the response for a certain amount of time, depending on how much weight they place on fast RTs. Finally, it is also possible that this delay in response execution is not intentional but arises from increased STN activity as stated in the response suppression hypothesis (Verbruggen and Logan 2009).

In summary, the psychophysical data do not allow us to distinguish whether subjects strategically delay decision onset or delay response execution. However, responses of single neurons recorded from the FEFs during an oculomotor Stop-signal task provide support for the assumption of delayed decision onset (see Onset of ramping).

Decision onset and task switching.

The preceding sections examined non-decision time/decision onset in situations where subjects repeatedly performed the same task. Hence, while subjects did not know which stimulus to expect, they had enough time to prepare for the task per se, for example, by activating the adequate stimulus-response associations. However, flexibility is one of the hallmarks of human behavior, and depending on context we can classify the same stimulus according to very different task requirements. Different tasks require different task sets, e.g., the activation of different stimulus-response associations. Task set configuration or reconfiguration is believed to take time and may lead to switch costs that arise if a decision is requested before the configuration is complete. Switch costs can be measured as longer RTs and higher error rate.

Task switch costs allow us to take a different look at the question of whether a decision process is initiated automatically by the presence of a sensory stimulus. In particular, it is possible that decision onset is postponed until the correct task set has been activated. Alternatively, the decision process may be activated automatically by the presence of the stimulus, even if the correct task set has not been activated. In the former case, we would expect longer non-decision times in combination with a uniform shift of the RT distribution. Drift rate and error rate should not be affected. In the latter case, we expect to see less effective use of stimulus information (lower drift rate), which goes along with higher error rate and longer RTs.

The actual findings suggest that both mechanisms contribute to the switch costs. Three studies have made an effort to map the observed switch costs onto parameters of the diffusion model (Karayanidis et al. 2009; Madden et al. 2009; Schmitz and Voss 2012). All three studies come to similar conclusions. We will briefly review the most recent study by Schmitz and Voss (2012). In their study, subjects viewed a stimulus that comprised a digit and a letter. The stimulus could be classified according to two different task rules. In one task subjects were required to classify the digit as odd or even while ignoring the letter. In the second task subjects were asked to classify the letter as a vowel or a consonant while ignoring the digit. Different types of cues (the position of the stimulus pair on the monitor or the background color) instructed subjects which task to perform. In a series of experiments, Schmitz and Voss showed that non-decision time was longer if subjects did not receive information about an upcoming change in the task early enough. If the task-cue preceded stimulus onset by 400 ms, non-decision times were at the same level seen in the single-task condition. However, if subjects had 100 ms or less to prepare for a new task, non-decision times increased from ∼350 ms to ∼500 ms.

In addition to the effects of task switching on non-decision time, trials after a task switch also had lower drift rates. Interestingly, lower drift rates were also found when subjects had 400 ms to prepare for the new task. Note that the 400-ms preparation time was sufficient to eliminate task switch effects from non-decision time. In addition, the authors could show that while non-decision time was mostly determined by how much time subjects had to prepare for the new task, drift rate depended on the time between trials, i.e., how long ago subjects had last used the task set of the previous task. Hence, Schmitz and Voss suggest that different mechanisms may be responsible for the effects of task switching on non-decision time and drift rate, respectively. Non-decision time effects may reflect an active mechanism, possibly the need to wait for the activation of the new task set (task set reconfiguration), and drift rate effects may reflect a passive decay of the old task set (task set inertia) that interferes with the execution of the new task.

In summary, these findings suggest that task switching affects both non-decision time and drift rate via independent mechanisms. Task set reconfiguration is a fast process (<400 ms), and decision onset is delayed until this process is complete. Task set inertia has a longer-lasting effect on drift rate, but decision onset is not delayed until task set inertia has decayed completely. This interpretation of the data suggests distinct mechanisms for the effect of task switching (task set reconfiguration) and the effects of task difficulty discussed in Decision onset and spatial attention (slower extraction of task-relevant information into VSTM). However, the task-switching paradigm not only requires subjects to activate different stimulus-response associations but also requires them to extract different stimulus features for the different tasks. Hence, it is possible to explain both phenomena with a similar mechanism: a delay of encoding information into VSTM due to the need to refocus attention to the task-relevant aspect of the stimulus.

Cautionary note.

Most sequential sampling models decompose RT into two components that presumably represent two distinct functional processes related to the integration process on the one hand and non-decision-related processes on the other. However, RT can be decomposed in many different, but not necessarily functionally meaningful, ways. For example, the convolution of a Gaussian and exponential distribution provides good fits to empirical RT distributions. Nevertheless, the implied decomposition does not seem to map onto any functionally relevant distinction (Matzke and Wagenmakers 2009). One of the strong points of sequential sampling models is that non-decision time is typically not affected by components of the decision task. Rather, task-relevant manipulations typically affect the duration (and accuracy) of the decision-related components. These findings provide strong face validity to the decomposition into decision- and non-decision-related components. However, much of the work cited here challenges this straightforward separation. For example, non-decision time in the study by Ratcliff and colleagues depends on the signal-to-noise ratio of the stimulus display, a parameter that seems to be more related to the decision process than non-decision-related afferent and efferent delays. All the studies reviewed above provide very good arguments in support of the notion that their findings are simply beginning to map the more subtle determinants of non-decision time. In the case of Ratcliff's study, for example, the idea is that lower signal-to-noise prolongs the encoding of relevant sensory information into VSTM, a process that corresponds to neither a simple afferent delay nor a decision-related component. However, despite these arguments, the concern remains that these studies are pushing past the scope where sequential sampling models provide a functionally valid segregation of RT into decision- and non-decision-related components. The strongest arguments to refute this notion will necessarily come in the form of neural correlates that support (or refute) the psychophysics and modeling findings.

Neural Correlates

The psychophysical studies outlined above suggest that the time between stimulus onset and the onset of the integration process may depend on various factors including spatial attention, stimulus contrast, extraction of task-relevant information, and strategic adjustments. Primate electrophysiology studies over the past two decades have identified neural correlates of different aspects of the decision process. Momentary sensory information is believed to be represented in relevant sensory neurons, for example, motion-sensitive neurons in the MT (Mazurek et al. 2003) or visual neurons in the FEF (Purcell et al. 2012). This information is then believed to be integrated over time in visuo-movement neurons, for example, in the lateral intraparietal area (Roitman and Shadlen 2002) or the FEF (Purcell et al. 2012). These neurons in posterior parietal and prefrontal cortex have been shown to behave much like the integrator units in the proposed mathematical models. Their firing rate ramps up gradually over time as more information is accumulated, and a response is triggered if the firing rate exceeds a specific threshold (Boucher et al. 2007; Hanes and Schall 1996; Roitman and Shadlen 2002; Shadlen and Newsome 2001; Woodman et al. 2008). In this part, we outline potential neural correlates of decision onset in these presumed integrator neurons and whether or not these correlates exhibit a similar dependence on the factors that affect non-decision time and integration onset in psychophysical studies. We will not review several interesting findings in the EEG literature but refer the interested reader to the discussion section of our recent paper (Teichert et al. 2014).

Preexcitatory pause or “the dip.”

Studies of decision-related activity in FEF, lateral intraparietal cortex (LIP), and superior colliculus (SC) of monkeys have revealed a dip in firing rate (preexcitatory pause, PEP) that reaches a minimum between 80 and 150 ms after stimulus onset (Churchland et al. 2008; Kiani et al. 2008; Kiani and Shadlen 2009; Ratcliff et al. 2003, 2007; Roitman and Shadlen 2002; Sato and Schall 2001; Shadlen and Newsome 2001). The dip may be due to local inhibition that is activated either by feedforward inputs (e.g., the discriminative stimulus might impinge on the inhibitory surround of the visual receptive field) or by top-down input from executive control regions. In the latter case, the PEP may mark the top-down initiation of the integration process (Roitman and Shadlen 2002). The timing and other properties of this dip have received little systematic study. However, it is noteworthy that the time of the PEP varies substantially between experiments. For data recorded in LIP during the standard motion discrimination task, times of the dip vary between 80 and 150 ms. It is possible that some of this variability reflects different analysis routines. However, it is also possible that they reflect different decision strategies that may be triggered by subtle differences in the task or training of the animals. Interestingly, all of the studies show that the timing of the PEP is independent of the signal-to-noise ratio of the stimulus. Under the assumption that the PEP indeed marks integration onset, it provides no indication that decision onset depends on stimulus properties or task requirements such as speed-accuracy instructions (Hanks et al. 2014). However, it is important to note that the PEP has mostly been studied in motion discrimination or similar tasks. In light of the behavioral data, one would not expect decision onset to vary as a function of stimulus contrast in these tasks (see Decision onset and encoding of relevant information). It would be interesting to examine the PEP, for example, in near-threshold orientation discrimination tasks, which in humans lead to changes of non-decision time as a function of stimulus contrast (Gould et al. 2007). Similarly, based on the findings of Laming (Laming 1979) and Teichert (Teichert et al. 2014) we might have expected PEP and hence decision onset to vary as a function of speed-accuracy instructions. The lack of such findings in the study of Hanks et al. may be related to task differences. In contrast to Laming's task, the animals in the Hanks et al. study could not anticipate the appearance of the task-relevant stimuli. In contrast to the Teichert et al. study, the task did not require animals to extract task-relevant from irrelevant information.

It is important to mention that, at this point in time, it has not been established that the PEP indeed reflects decision onset. There are at least two alternative interpretations. 1) The PEP may result from the onset of the motion stimulus that draws attention away from the targets. 2) Similarly, the PEP may reflect the appearance of the motion stimulus in the inhibitory surround of the LIP neurons' receptive field (Falkner et al. 2010).

Onset of ramping.

While the PEP may be a marker of decision onset, it may also obscure a different marker: the onset of ramping. If the PEP is caused by a sharp increase of inhibition, then the subsequent increase in firing rate may at least partially reflect a gradual release from this inhibition rather than ramping due to integration (Ratcliff et al. 2007). In FEF movement neurons, the PEP is less pronounced and its absence makes it easier to determine the onset of ramping activity. In a series of papers, Schall and colleagues provided important insights into the onset of the accumulation process in FEF movement neurons (Heitz and Schall 2012; Pouget et al. 2011; Purcell et al. 2010, 2012). The papers are built around the assumption that visual FEF neurons represent salience in visual search tasks while FEF movement neurons mediate response preparation, possibly based on integrating the information provided by FEF visual neurons (Purcell et al. 2012).

In two recent papers Purcell and colleagues (Purcell et al. 2010, 2012) used spike trains recorded from visual neurons in a visual search task as input to different sequential sampling models to test their ability to predict behavior as well as activity in FEF movement neurons recorded in the same task. The models provided several interesting results. First, models without integration failed to fit the data, ruling out the assumption that all the necessary integration already happened in the visual neurons. Second, perfect integrator models failed to predict behavior and FEF movement neuron activity, because of integration of FEF baseline activity. Third, models with leaky integrators predicted the behavior well but failed to predict FEF movement neuron activity. Finally, gated models accurately captured both behavior and FEF movement neuron activity. In the gated model, the input to each accumulator was computed by subtracting a constant gating value, g, from the FEF visual neuron activity and setting ensuing negative values to zero. This gating procedure operates on the input to the integrator, rather than on the activity of the integrator directly, and thereby postpones ramping activity until activity of visual neurons believed to encode salience is strong enough to exceed the gating threshold. A related set of ideas and models has recently been reviewed under the umbrella of robust integration (Cain et al. 2013).

A similar gating mechanism may also play a role in other situations. Pouget et al. (2011) measured single-cell responses in FEF and SC during a saccade countermanding task. Longer RTs after successful response inhibition were associated with a delayed onset of ramping in FEF and SC movement cells. Because FEF movement neurons receive input from FEF visual neurons, it is feasible that the delayed ramping in the movement cells is inherited from visual cells. However, no such delay in visual neuron activity was found. In general, these findings are consistent with longer response times in human studies that were found to be mediated by increased non-decision time (see Decision onset in Stop-signal tasks). The FEF data provide additional evidence for the assumption that the increase in non-decision time indeed reflects delayed integration onset rather than delayed response execution.

Delayed integration onset in the countermanding task provides compelling single-cell evidence that primates can strategically delay decision onset. The delayed onset of ramping could be due to competition between neurons that initiate the motor response (“go” cells) and neurons that inhibit the response (“no-go” or fixation cells). Lo and colleagues elaborated an attractor model of FEF activity and behavior in the countermanding task based on the assumption that the fixation neurons, in addition to being driven by the Stop-signal, also receive input from a pool of “control” neurons in frontal cortex (Lo et al. 2009). These control neurons remain active for a variable amount of time after the fixation point is extinguished, thus delaying the onset of ramping activity in motor neurons. It is feasible that control neuron activity is systematically prolonged after successful response inhibition trials, thus causing the observed delay of ramping and longer RTs in these trials.

Heitz and Schall investigated speed-accuracy trade-offs in visual search (Heitz and Schall 2012). Animals were trained to make a saccade to a shape oddball. A color cue instructed them to perform the task at one of three different speed requirements: fast, medium, or slow. In light of the strategic delay of decision onset of human subjects in the dot-motion interference task (Teichert et al. 2014) and the delayed integration onset in the countermanding task (Pouget et al. 2011), we might expect the onset of the ramping activity of FEF motor neurons to be delayed in the accuracy condition. However, there was no evidence of such slowing. FEF motor neuron activity started ramping ∼120 ms after stimulus onset, regardless of speed instruction. Similar results were found in LIP (Hanks et al. 2014). Rather than delaying ramping onset, slower RTs in the accuracy condition were achieved by reducing the rate of growth in FEF and a lower baseline firing rate in LIP. As discussed in the case of the PEP (Preexcitatory pause or “the dip”), we believe that task differences are the most likely explanation for this discrepancy.

Point of divergence of firing rate in different conditions.

In principle, the time at which task-relevant evidence is integrated should go along with a divergence of firing rates in conditions with different stimulus strength. As with the timing of the PEP, there is considerable variability in time of divergence between studies, but we are not aware of a systematic analysis of the differences. It is noteworthy that the point of divergence is typically observed rather late in the trial, up to 200 ms after stimulus onset. In contrast, neurons in MT signal motion direction much earlier in the trial, reaching asymptotic levels around 80 ms after stimulus onset (Raiguel et al. 1999). While there is certainly some delay to relay information from MT to LIP, it is unlikely to be on the order of up to 120 ms. Thus the question arises: what happens to motion-sensitive information from MT before it is being accumulated in LIP? It is feasible that information arrives at LIP integrator neurons but they are being actively suppressed or the circuit is not set up to accumulate and store the information. Alternatively, it is possible that the information is not relayed directly to LIP. The computational models reviewed in Decision onset and encoding of relevant information and Decision onset and spatial attention assume that the information first needs to be encoded in VSTM. Such an additional processing stage might account for the additional delay. In theory, the short-term memory store could be located in the medial superior temporal area (MST), which receives input from MT and has been shown to exhibit feature-selective delay activity (Mendoza-Halliday et al. 2014).

In addition, it is worth mentioning that, typically, the point of divergence is observed later in time than the PEP (Preexcitatory pause or “the dip”). This could be taken to suggest that, as predicted by Laming, the integration process is initiated a small amount of time before task-relevant information is available (Potential psychophysical correlates of changes in decision onset and Decoupling stimulus onset and decision onset). Alternatively, this may suggest that the PEP does not mark the time of integration onset. It is also noteworthy that the time between the PEP and the divergence point varies between experiments. In the study by Kiani and Shadlen the point of divergence almost coincides with the dip at ∼150 ms (Kiani and Shadlen 2009), while in the study by Roitman and Shadlen (2002), the point of divergence is at ∼200 ms, ∼70 ms after the PEP.

Trial-to-trial spike count variability (Fano factor, variance of conditional expectation).

In addition to changes in firing rate, it was recently pointed out that changes in trial-to-trial variability in spike count can be used to infer the time at which the integration process starts (Churchland et al. 2011; Kiani et al. 2008). The between-trial spike count variability is the sum of two independent factors that are related to 1) the stochasticity of the Poisson-like spike process and 2) the underlying variance of the true firing rate. Estimates of the variance of the underlying rate have been referred to as either input variance (Kiani et al. 2008) or variance of the conditional expectation (VarCE) (Churchland et al. 2011). Under the assumption of identical and stationary input, the between-trial variance of a perfect integrator increases linearly as a function of time from integration onset. This should lead to a linear increase in VarCE of neurons that act as integrators. Indeed, VarCE has been used to infer the time of integration onset (Kiani et al. 2008) and distinguish ramping activity of an integrator from a “simple” increase of firing rate prior to saccade onset that is not expected to change VarCE (Churchland et al. 2011).

In addition to the linear increase of VarCE, it is also possible to make a second prediction regarding integration onset of a perfect integrator. As pointed out earlier, a perfect integrator may need to be reset prior to integration onset, and the dip in firing rate described in Preexcitatory pause or “the dip” may provide such a reset signal. If this is indeed the case, we would expect to see a reduction in VarCE around the time of the dip. In contrast, if decision onset is mediated by a change in the leakiness of the integrator, we would not expect to see a decrease in VarCE. The data show a decrease in VarCE around the time of the dip (Churchland et al. 2011; Kiani et al. 2008) and hence favor the first assumption. However, the reduction in VarCE is neither specific to potential integrator units nor linked to decision tasks. Rather, a reduction of VarCE, i.e., a quenching of internally driven spike rate variability, seems to be a natural response to stimulus onset in a wide range of cortical areas and behavioral paradigms (Churchland et al. 2010). In summary, the dip in VarCE prior to decision onset is probably not a correlate of the resetting of the integrator.

Competitive networks.

The problem of sorting out multiple sources of evidence prior to initiating integration may involve competitive interactions of the sort that have been proposed in studies of selective attention and oculomotor target selection (Desimone and Duncan 1995; Ferrera and Lisberger 1995; Koch and Ullman 1985). Physiological and behavioral studies have identified neural correlates of competition such as a shift from averaging to winner-take-all responses (Ferrera 2000; Reynolds et al. 1999). When eye movements are initiated in the presence of multiple targets, early responses tend to average information across targets while later responses tend to selectively follow a single target (Ferrera 2000; Ottes et al. 1985). The degree of target selectivity is subject to voluntary control and correlates with the delay in movement onset (Ferrera 2000).

One physiological correlate of competition is that neuronal responses in the presence of multiple stimuli tend to be weaker than responses to a single stimulus (Churchland et al. 2008; Schall et al. 1995). The degree of response reduction may scale with the number of targets and could be due to recurrent inhibition among neurons that respond to the individual targets. Such set size effects have been documented in several structures involved in the selection of eye movements, including the SC (Basso and Wurtz 1997), area LIP (Balan et al. 2008), and the FEF (Cohen et al. 2009). The response reduction implies that the starting point for evidence accumulation might depend on the number of alternatives (Churchland and Ditterich 2012; Cohen et al. 2009). In particular, more targets might cause the accumulator to start at a lower value and therefore take a longer time to reach threshold. This is consistent with the well-known observation that response time tends to be longer with increasing alternatives (Hick 1952; Hyman 1953).

Visual search is a well-studied paradigm in which behavioral response latencies may depend on the number of display items (Treisman and Gelade 1980). Combined physiology and modeling studies of visual search in the FEF have shown that the activity of visual neurons scales inversely with the number of distractors (Purcell et al. 2010, 2012). This is similar to results in SC (Basso and Wurtz 1997) and LIP (Churchland et al. 2008)—although the response amplitude of visual neurons decreased with the number of distractors, response latency was constant.

Models that integrate sequential sampling into networks with recurrent inhibition and excitation (Deco and Rolls 2005; Goldman et al. 2003; Lo and Wang 2006; Wang 2002; Wong and Wang 2006) will likely be needed to fully explain single-neuron, population, and behavioral dynamics. Any proposed mechanism of decision onset should be specific enough to be implemented in a spiking model. Such models should make clear predictions about firing statistics as well as behavioral correlates such as RT and error rate. More developed models should take into account network effects due to recurrent excitation and inhibition, as well as making more biophysically plausible assumptions regarding things like evidence to spike rate conversion. These predictions should be tested simultaneously in subjects where both behavior and physiological correlates can be measured.

Conclusions

In this review we have surveyed the recent decision making literature to answer two questions about decision onset, defined as the starting time of the integration process: Is the integration process initiated automatically by the appearance of a sensory stimulus, or does its onset vary as a function of stimulus properties and task demands? If the latter, are the changes of decision onset adaptive and can they be used strategically to optimize decision making? Our review of the literature revealed a complex and multifaceted picture of the phenomenology of decision onset. The literature suggests that 1) decision onset can vary as a function of several experimental manipulations in numerous behavioral tasks, thus arguing against the assumption that decision onset is simply triggered by the appearance of a suitable stimulus, and 2) decision onset is amenable to top-down control and can be used to optimize processing to specific strategic demands such as speed and accuracy.

Stimulus contrast vs. extraction of task-relevant information.

In most real-life situations and many experimental tasks, decision-relevant information is contained in suprathreshold sensory stimuli. In the visual system, for example, the appearance of these stimuli is associated with a strong pulse of contrast energy. It is possible that this pulse of energy initiates the integration process, regardless of whether or not relevant information has been extracted. In general the reviewed studies do not support this view, although under certain conditions stimulus contrast may be coupled to decision onset.

In a series of studies, Ratcliff, Smith, and colleagues argue that the flow of information to the integrator unit is contingent on the formation of a stable trace in VSTM. The speed of encoding into VSTM, and hence the onset of the decision process, was argued to depend on total stimulus contrast. If total stimulus contrast was low, near-threshold amounts of task-relevant information determined non-decision time. If stimuli contained large amounts of task-irrelevant contrast, non-decision time no longer depended on task-relevant contrast. In summary, it was suggested that total stimulus energy determines the speed of encoding into VSTM and hence decision onset, whereas task-relevant information determines the content of VSTM and hence the speed and accuracy of the integration process (Smith and Ratcliff 2009).

Other studies provide support for the notion that stimulus contrast is not the only determinant of decision onset. One of the most illustrative examples derives from the observation that identical stimuli can lead to substantially different non-decision times when different aspects of the stimuli are relevant for the task (Ratcliff and Smith 2010). If the decision required the extraction of form information from a noisy display, the non-decision time increased as a function of noise. In contrast, when the task required a decision about the overall luminance of the exact same stimulus, non-decision time was independent of the noise level. These data suggest that decision onset can vary as a function of task demands. Consequently, the time of decision onset cannot simply be determined by the properties of the stimulus. Further studies will need to clarify under which conditions decision onset will depend on extraction of task-relevant information and when it will depend on a pulse of contrast energy that accompanies the onset of suprathreshold stimuli.

According to the contrast-energy hypothesis, decision onset should be approximately constant in tasks that use suprathreshold stimuli. However, as discussed in the previous paragraph, several studies using high-contrast stimuli found longer non-decision times when different aspects of the stimulus were relevant for the task or when the stimuli were more ambiguous (Coallier and Kalaska 2014; Ratcliff and Frank 2012; Ratcliff and Smith 2010).

Changes of decision onset are adaptive.

Several of the studies reviewed above suggest that the changes of decision onset are adaptive in the sense that they help improve decision accuracy. In situations where the duration of task-relevant information is limited by a mask, allocation of spatial attention may speed up the encoding into VSTM and hence advance decision onset. This faster extraction of task-relevant information increases decision accuracy (Smith et al. 2004). More commonly, however, an increase of accuracy was associated with delayed integration onset (Pouget et al. 2011; Purcell et al. 2012; Ratcliff and Frank 2012; Schmitz and Voss 2012; Teichert et al. 2014). For example, delayed decision onset may allow feature-based attention more time to extract task-relevant information in a Stroop-like interference task (Teichert et al. 2014). Similarly, delayed integration onset may provide the visually responsive neurons in FEF more time to identify the location of a visual search target if it is embedded in a larger stimulus array (Purcell et al. 2012).

Decision onset is amenable to top-down control.

One of the most exciting developments is the converging evidence from different labs and methodologies that decision onset is to some degree under cognitive control and may be used to adjust the decision process to certain strategic demands. To date, the main candidate mechanism to exert control was the (time-dependent) setting of the response thresholds, and the closely related concept of an urgency signal. The finding that decision onset may be an independent mechanism with different properties, limitations, and opportunities may enable more efficient and flexible ways to adjust the properties of the decision process. In interference tasks, for example, response accuracy may be increased via two independent mechanisms: an increase of response thresholds and a delay of decision onset. While the former prolongs the decision process with only a moderate improvement in accuracy, the latter is much more effective, as it addresses the root cause of response errors, namely, a premature onset of the decision process that leads to the integration of task-irrelevant information from the empty stimulus display (Laming 1979) or from a stream of information dominated by the distractor (Teichert et al. 2014). Similarly, a strategic delay of integration onset may give subjects a better chance at inhibiting a response in a Stop-signal task (Pouget et al. 2011).

Future directions—opportunities and challenges.

This review has identified exciting developments in the emerging field of decision onset. It has also identified several areas of opportunity for future studies. For example, while hundreds of studies have estimated non-decision time in a large number of diverse tasks, we are not aware of a meta-analysis to identify systematic differences in non-decision time between different types of tasks. Non-decision times typically range from 200 to 400 ms in different studies. This variability may in part be random or reflect different instructions. However, it is very likely that some of the variability can be traced back to task differences, and some of these differences may actually map onto changes in decision onset rather than changes in motor delay. Hence, such a meta-analysis may provide the basis to develop additional hypotheses about the determinants of decision onset.

A second opportunity in the field relates to the relatively low number of behavioral phenomena that have been combined with single-cell recordings. Studies examining single-cell correlates of decision onset are rare, and the field would benefit from more studies like the ones by Schall and colleagues (see Onset of ramping). For example, to date there is no neural correlate for the task-dependent variation of non-decision time that was reported for identical stimuli in the letter but not the contrast discrimination task (Ratcliff and Smith 2010). Similarly, there are no neural data that speak to whether or not encoding into VSTM is an obligatory step prior to evidence accumulation or address the question of whether the time of integration onset is indeed tied to the encoding of a VSTM trace.

Finally, it is important to mention a significant challenge to the study of decision onset using psychophysics and modeling approaches. Changes of decision onset are often inferred from changes in non-decision time alone. However, non-decision time may also be affected by factors other than decision onset. Hence, while changes in non-decision time can indeed signal changes in decision onset, they should not be considered sufficient evidence. In addition, while changes of decision onset may exclusively map onto non-decision time in certain scenarios, it is clear that in other conditions changes of decision onset will also affect error rate and/or the ratio of fast and slow errors. We have observed three potential safeguards for this problem in the literature: 1) detailed experimentation and testing of alternative accounts (Ratcliff and Smith 2010), 2) validation by verifying RT-unrelated additional predictions (Smith et al. 2004; Smith and Ratcliff 2009; Teichert et al. 2014), and 3) validation via electrophysiological correlates (Pouget et al. 2011).

We want to encourage one additional control to rule out the most likely alternative explanation: changes in duration of motor execution. The vigor and speed of motor output can depend on properties of the decision, in particular when the response is given via finger press or arm movement. While easy to rule out, for example, by measuring movement onset rather than movement offset (Coallier and Kalaska 2014), this is not common practice in the field. In addition, it might also be highly useful to routinely measure EMG of the relevant muscle groups (Gratton et al. 1988).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: T.T. prepared figures; T.T. and V.P.F. drafted manuscript; T.T., J.G., and V.P.F. edited and revised manuscript; T.T., J.G., and V.P.F. approved final version of manuscript.