A Computational Cognitive Biomarker for Early-Stage Huntington’s Disease

Abstract

Huntington’s disease (HD) is genetically determined but with variability in symptom onset, leading to uncertainty as to when pharmacological intervention should be initiated. Here we take a computational approach based on neurocognitive phenotyping, computational modeling, and classification, in an effort to provide quantitative predictors of HD before symptom onset. A large sample of subjects—consisting of both pre-manifest individuals carrying the HD mutation (pre-HD), and early symptomatic—as well as healthy controls performed the antisaccade conflict task, which requires executive control and response inhibition. While symptomatic HD subjects differed substantially from controls in behavioral measures [reaction time (RT) and error rates], there was no such clear behavioral differences in pre-HD. RT distributions and error rates were fit with an accumulator-based model which summarizes the computational processes involved and which are related to identified mechanisms in more detailed neural models of prefrontal cortex and basal ganglia. Classification based on fitted model parameters revealed a key parameter related to executive control differentiated pre-HD from controls, whereas the response inhibition parameter declined only after symptom onset. These findings demonstrate the utility of computational approaches for classification and prediction of brain disorders, and provide clues as to the underlying neural mechanisms.

Introduction

Huntington’s disease (HD) is a debilitating neurodegenerative disease with progressive degradation of motor and cognitive function. From a neurocognitive perspective, HD is a highly interesting disorder as it has a clearly defined, single genetic mutation in the form of an expanded CAG repeat in the HTT gene, which predicts with certainty that the disease will develop in an individual. The effects of this mutation on neurobiology have been the subject of intense study with notable progress, although many questions still remain. Indeed, no clinical phase 3 trial to date has been successful for a drug that slows or reverses progression of HD, raising the question of whether the most efficient drug development methods are being leveraged [1]. A central requirement for success in clinical trials are objective and quantitative outcome measures that are sensitive to early-stage changes in presymptomatic individuals (pre-HD) as well as early stage manifest HD. Better clinical markers of disease progression could inform when to initiate treatment: too early would increase accumulation of negative side-effects, whereas too late could prevent successful therapeutic intervention.

TRACK-HD was a large multi-site longitudinal study to evaluate various behavioral and imaging measures for their appropriateness in tracking HD progression [2]. While many measures were sensitive to changes in early symptomatic HD, a key conclusion was that “these measures are insensitive to change in pre-HD over timescales realistic for clinical trials [3] and more sensitive measures are required to capture subtle changes that might be taking place before symptom onset.” [4]. In sum, there is a current lack of clinical markers sensitive to the cognitive changes that occur during the pre-HD stages.

Oculomotor abnormalities have been investigated, both at very early stages and even during the premanifest period by a number of studies [5–7]. The antisaccade conflict task has been widely used to study executive control and response inhibition of eye movements that has well-studied and dissociable neural mechanisms associated with (i) the prepotency of a pro-saccade response, (ii) the inhibition of that response, and (iii) the executive control needed to dictate the alternative response given the instructed task rule [8, 9]. Notably, several studies have found reliable antisaccade performance deficits in HD subjects well before full onset of HD symptoms [10–12].

Traditional studies with this task mostly analysed and interpreted behavioral summary statistics such as mean reaction time and accuracy. However, despite the apparent task simplicity, its successful completion involves an intricate interaction within a complex network of brain areas including the frontal cortex and basal ganglia. Indeed, neural circuit modeling and empirical studies suggest that a deficit in any of the involved areas can lead to increased error rates and reaction times, leading to ambiguity in interpretation of observed deficits [8]. The emerging field of computational psychiatry [13, 14] approaches this problem with the help of computational models that can deconstruct behavioral and neural data into separable generative processes, and to identify whether any of these processes is preferentially altered in mental illness [15].

At a mechanistic level, the classical view is that HD arises from selective neurodegeneration within the indirect pathway of the basal ganglia that normally acts to suppress unwanted movements [2, 16–20]. In addition to this clearly defined atrophy, there is also more widespread degeneration in frontal cortex [10, 11, 21], which could act to impair executive control over action selection [8, 22–24].

The aim of the current study was to apply quantitative computational modeling to the TRACK-HD behavioral data set (specifically, the antisaccade conflict task) to separate processes thought to relate to selective response inhibition and executive control. We then use machine learning classification to demonstrate that the executive control parameter is predictive of HD prior to symptom onset, whereas response inhibition processes are impaired only after motor symptoms are observed.

Methods

This was a novel analysis of a multinational longitudinal observational study approved across sites as described in [2].

371 subjects performed an antisaccade task as part of the TRACK-HD study [2]. This task requires subjects to look away from an appearing stimulus on a screen. The data set consists of 123 healthy controls (mean age 46±10 years), 122 presymptomatic gene carriers (pre-HD; mean age 41±8.7 years) that will develop HD later in life, and 125 subjects diagnosed with HD (mean age 49.3±9.8 years). Pre-HD subjects were further subdivided into pre-HD-A and pre-HD-B, where pre-HD-B were estimated to be closer than pre-HD-A to progression to HD based on CAG repeat length and age [25]. Specifically, this group was split at the median predicted years to onset (10.8 years) into preHD-A (≤10.8 years from predicted onset) and preHD-B (<10.8 years). HD subjects were similarly divided using UHDRS total functional capacity (TFC) score. Participants with early HD were designated either HD-1 (TFC 11–13) or HD-2 (TFC 7–10), with HD-2 group having more advanced symptoms [26].

Several clinical measures were collected. The Unified Huntington’s Disease Rating Scale (UHDRS) is the standard assessment tool for HD symptom severity and has two relevant subscores: Total functional capacity (TFC), tracking ability to perform daily events, and the total motor score (TMS) tracking motor abilities specifically [27].

Mean and standard-deviaton (SD) of prosaccade RTs, mean and SD of correct and error antisaccade RTs, as well as accuracy on antisaccade trials were computed as summary statistics.

Behavioral testing

Oculomotor testing was carried out using a “saccadometer advanced” (Ober consulting)—a head mounted oculometer using a miniaturized infra-red 1kHz camera to track eye movements [28]. Since it is head mounted, it sits comfortably on the patients’ nose and there is no need for head restraint. This methodology has been previously used successfully with Huntington’s patients [7].

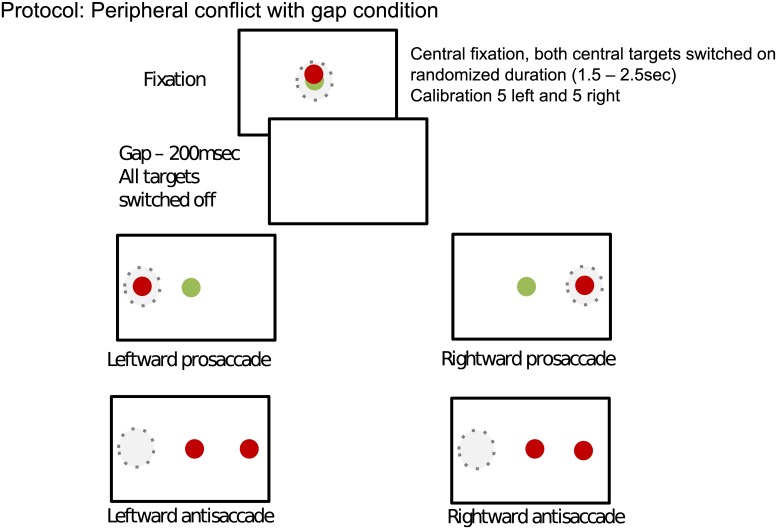
The test starts with a pair of red and green lights presented in the center of a computer screen. The participants were directed to look at these lights to get ready. Next, the pair of lights turned off. Participants then would see the single colored light in the center and the red target off to the side. The participants were instructed that the color of the central cue would inform them to make a pro (i.e. green cue) or antisaccade (i.e. red cue) to or away from a target, respectively. Target location was randomly on the left or right side of the target (see Fig 1). Pro and antisaccades were randomly interleaved. Prosaccade errors were very rare (<1% of all trials) and not analyzed further.

Fig 1. Structure of the antisaccade task.

Participants first fixated on the center of the screen. Afterwards, a blank screen was presented followed by either a green or red central cue instructing participants to either make a pro or antisaccade, respectively.

Distributional analysis

Summary statistics are a useful and easy measure to compute. But while mean and variance can describe a Gaussian distribution perfectly, RT distributions are well known to be quite skewed and non-normal. Thus, summary statistics often fail to capture more nuanced aspects of conflict resolution that are present in the full RT distributions of correct and error trials. Indeed, distributional analysis can help tease apart different processes that can lead to various changes in the RT distributions (due to conflict or other factors), such as a shift in the entire distribution, or preferential changes to the leading edge or the tails of the distribution, and how any such changes are related to increased or decreased accuracy [29–31]. Distributional analysis typically involves dividing the RT distribution into quantiles, e.g., the mean of the first 20% of the RT distribution, the second 20%, and so on.

In order to better capture differences in the RT distribution between congruent and incongruent trials, [29] suggested the use of delta-plots. For each subject, RT is split into 6 quantile ranges (0–10, 10–30, 30–50, 50–70, 70–90, 90–100) for pro and antisaccade trials separately (only correct antisaccade trials are used). Mean RTs of each range are then averaged across pro and antisaccade trials and plotted along the x-axis. To capture conflict-induced slowing, mean RT in each antisaccade range is subtracted from mean RT of the corresponding prosaccade range and plotted along the y-axis. Thus, the relative slowing for antisaccades compared to prosaccades is captured by a positive y-value in the delta plot. The commonly observed effect is that conflict effects are observed to a greater degree on early RTs, as captured by a decreasing slope of the delta-plot.

Computational modeling

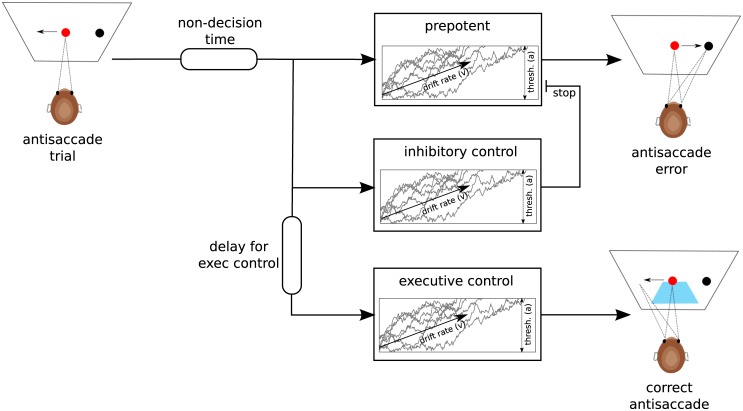
While the delta-plot can reveal behavioral signatures of conflict resolution it does not provide a process level description of how such signatures arise. To this end, we fit a computational model summarizing the three major components to the behavior in the task and which approximate those embedded in more detailed neural models. The model is an extension of a sequential sampling model typically used in two-alternative forced-choice decision making tasks, in which sensory evidence is accumulated up to a response threshold used to initiate motor activity, and where the speed of evidence accumulation is reflected by a “drift rate”. The extended model used here takes into account the dynamics and interactions of prepotent responses, response inhibition, and executive control. As such, the model comprises three single-boundary Wald accumulators: a prepotent (pre), an inhibitory (inhib) and an executive control (exec) accumulator (see Fig 2). These accumulators race against and interact with each other. Each accumulator is associated with an individual drift-rate (v_pre, v_inhib and v_exec) that determines the speed of integration towards its threshold a. To take into account additional time unrelated to decision processes but summarizing sensory perception and motor execution, we also incorporate a non-decision time parameter t. If the prepotent accumulator reaches its threshold first during an antisaccade trial an error is commited. If the inhibitory accumulator reaches the threshold before the prepotent one, it stops the prepotent accumulator from reaching its threshold. In addition, the executive control accumulator is delayed by a fixed time (t_exec) to capture additional time required for rule-retrieval, vector inversion etc. Once it reaches threshold a correct antisaccade is performed. While parameters of the prepotent accumulator (i.e. v_pre, a and t) are identified by fitting across both pro and antisaccade trials, all other parameters are fit using only antisaccade trials (as they are irrelevant in prosaccade trials). This model was chosen from various configurations by performing model comparison (see the appendix).

Fig 2. Computational process model of the antisaccade task.

The architecture of accumulators during an antisaccade trial is depicted. During prosaccade trials, only the prepotent process is used. See the main text for a description of the model.

As a closed-form solution to this likelihood is difficult to compute, we used probability density approximation (PDA) introduced by [32]. This likelihood-free method only requires simulation of data from a generative process and approximates a likelihood function using kernel density estimation. We can then easily evaluate the data on the approximated likelihood to compute the summed log probability and find the best fitting parameters using Powell optimization [33] with basin-hopping [34] to avoid getting stuck in local maxima. While ideally we would use hierarchical Bayesian estimation of the model parameters [35] the small randomness along with the large number of simulations required for a single evaluation of the PDA likelihood function lead to convergence issues and prohibitively long running times.

Machine Learning

In order to assess the viability of using these methods to classify subjects, we used machine learning classifiers based on summary behavioral statistics and computational model parameters. The goal was to train classifiers based on behavioral and model parameters in a sample of subjects, and test whether the classifier could discriminate between novel groups of subjects. For two-class classification we used logistic regression with L2-regularization. To optimize the strength of the regularization parameter we ran 10-fold stratified cross-validation, which keeps the distribution of labels constant across every split. During cross-validation, the classifier is trained to differentiate 90% of the subjects but tested and evaluated based on its classification accuracy of the previously unseen 10% of subjects. This splitting procedure is repeated 10 times so that all data has been used once to test the classifier. To evaluate the performance of this classifier we ran this cross-validation procedure 200 times on training data and tested the best-performing classifier on held-out test data in a shuffle-split cross-validation with 20% of the data used for testing each time. Classifier performance was then compared using the Area Under the Receiver-Operator-Characteristic Curve (AUC), a measure robust to unequal class sizes. Intuitively, it can be interpreted as the probability of correctly classifying two samples randomly drawn from each of the classes. For multiclass classification we used a Random Forest classifier [36] that was trained in the same manner. We have experimented with various other more advanced ML classification algorithms including Support Vector Machines and Elastic Nets but had almost identical results and thus present the results using a simpler classifier.

Results

Behavior

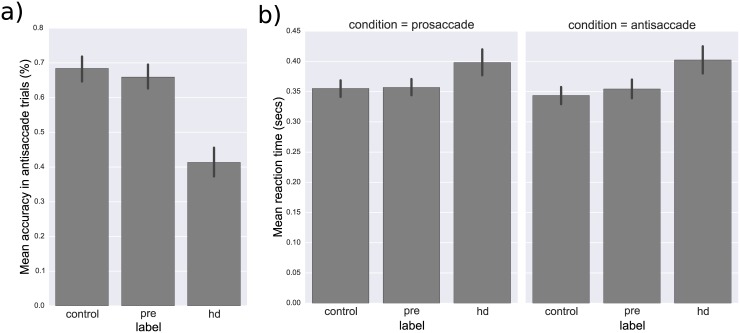
Standard measures of behavior were more than sufficient to discriminate HD subjects from both controls and pre-HD. Specifically, for prosaccade trials, control subjects t(246) = -3.25, p = 0.001) as well as pre-HD subjects (t(245) = -3.13, p = 0.002) were significantly faster (0.344±0.0806 secs and 0.357±0.0799 secs, respectively) than HD subjects (0.398±0.1226 secs; see Fig 3a). A similar pattern emerged in antisaccade trials where control subjects t(246) = -4.25, p < 0.001 as well as pre-HD subjects t(245) = -3.39, p = 0.001 were significantly faster (0.344±0.0806 secs and 0.355±0.0866 secs, respectively) than HD subjects (0.402±0.1308; see Fig 3a). Control subjects t(246) = 9.68, p < 0.001 as well as pre-HD subjects t(245) = 8.85, p < 0.001 were also more accurate (68.4±19.77% and 65.9±19.31%, respectively) than HD subjects (41.3±24.06%) on antisaccade trials.

Fig 3.

a) Bar-plots of mean reaction time (in seconds) across different groups. b) Bar-plots of mean percent accuracy during antisaccade trials across different groups. Error-bars depict 95% confidence intervals.

Notably, there was no significant difference between control and pre-HD subjects in mean RT in either prosaccade t(243) = 0.15, p = 0.879 or antisaccade t(243) = 1.01, p = 0.315 trials, nor in antisaccade accuracy t(243) = -1.00, p = 0.318 (see Fig 3b). There was, however, a trend for pre-HD to demonstrate increase antisaccade RT variability (standard deviation) between pre-HD (0.139±0.0756 secs) and controls (0.122±0.0615 secs), t(243) = 1.95, p = 0.052.

Distributional analysis

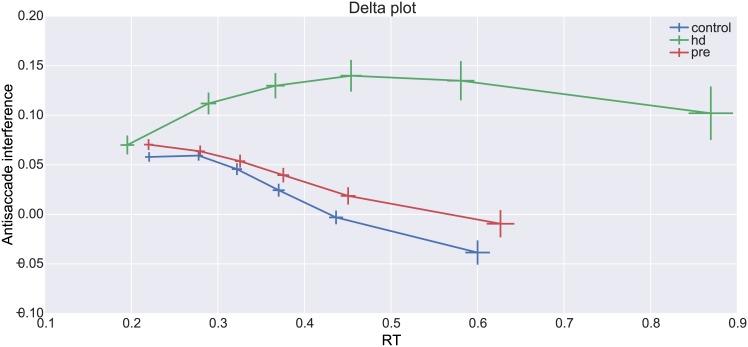
Delta-plots subtract pro from antisaccade RTs for each quantile along the distribution and show the conflict interference effect (positive deflections) and how it gets resolved over time. The delta-plots for the three different subject groups are shown in Fig 4. The common pattern of a negative slope [37] is strongly visible in all groups and suggests that conflict is successfully resolved as time progresses. While there are striking differences in the last 3 quantiles between control and HD as well as pre-HD and HD (all p-values < 0.001) there were no differences between controls and pre-HD (all p-values >.05).

Fig 4. Delta-plot showing conflict resolution (negative slope) across time in different groups.

Error-bars represent standard errors. See text for details.

Computational modeling

Separable effects of response inhibition and executive control

Before describing group differences, it is important to highlight that the model comprises multiple mechanisms by which a correct or incorrect antisaccade is executed. High values of v_pre lead to faster prosaccades but also fast antisaccade errors. Both the response inhibition parameter v_stop, which allows a prepotent saccade to be suppressed, and the executive control parameter v_exec, which provides evidence for the controlled antisaccade response, contribute to successful performance (decreased errors). However, high values of v_exec lead not only to higher accuracy but faster and less skewed correct antisaccade RTs. In contrast, high values of v_stop do not affect antisaccade RTs but rather right-censor the antisaccade error RT distribution (i.e., erroneous pro-saccades will only occur with very fast RTs). Finally, longer t_exec time will allow for more time for the prepotent process to reach threshold, and thus will also increase antisaccade errors, but does so by causing a constant shift forward of the whole RT distribution, accounting for the commonly observed pattern of relatively fast errors and delayed correct antisaccade RTs. Thus, each of the model parameters quantify separately identifiable cognitive processes (and putative underlying neural mechanisms). We verified through generative simulations and parameter recovery that indeed these parameters are separately identifiable.

Model fit

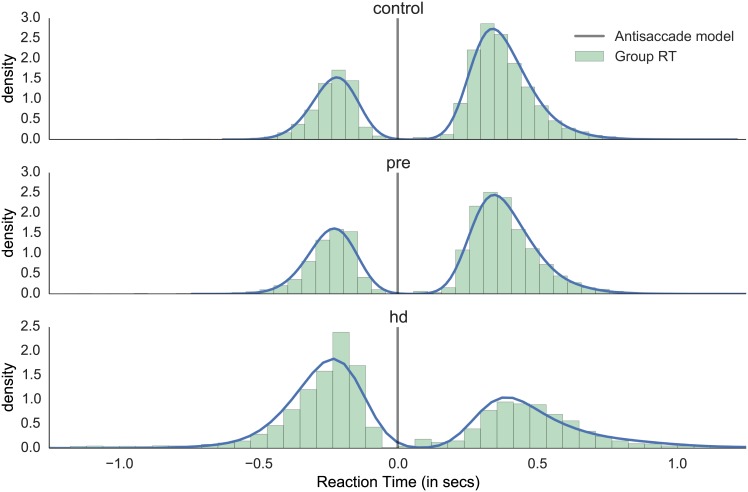
Visual inspection of model fit to aggregate RT data shows that the model is able to capture the overall shape of correct and incorrect antisaccade trials across the three different groups (Fig 5). Note that the results reported elsewhere in this study rely on fits to individual subjects, the group fit is done for visualization purposes only (i.e. to assess how well the model captures the mean behavioral patterns).

Fig 5. Model fit for antisaccade trials.

Aggregate RT histograms were generated from the model with fitted parameters for each group, overlaid on top of empirical normalized aggregate RT histogram. Errors are mirrored along the y-axis and appear on the negative side.

For more analyses of model fit and model comparison we refer to the supplement.

Group differences

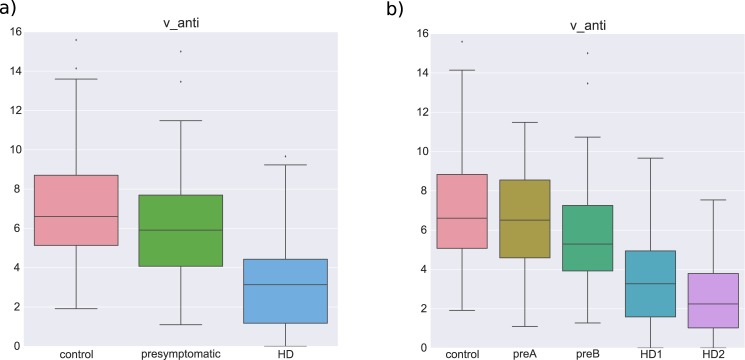
Unsurprisingly, given the large behavioral differences between symptomatic HD subjects and both controls and pre-HD, all model parameters significantly differed between controls and HD as well as between pre-HD and HD (all p-values < 0.01). The more interesting question is whether the refined modeling could help to differentiate pre-HD from controls given that most traditional behavioral analyses revealed no clear differences. Notably, we found that the executive control drift-rate (v_exec) was significantly lower t(243) = -2.66, p = 0.008 in pre-HD subjects (6.218±2.6506) compared to controls (7.101±2.5423; see Fig 6a). This finding suggests subtle executive control deficits in premanifest HD gene carriers. Moreover, visual analysis of changes in executive control drift-rate across subgroups of HD (Fig 6b) suggests a linear relationship between progression of HD and this parameter, as we assess next.

Fig 6.

a) Box-plots of v_exec in different groups. b) Box-plots of v_exec in different subgroups.

Correlations

A multiple linear regression between all model parameters and a linear coding of HD stage (controls = 0, pre-HD-A = 1, pre-HD-B = 2, HD-1 = 3, HD-2 = 4) revealed strong correlations between v_exec, t_exec, v_inhib and HD stage. Overall, the model parameters explained 39% of the variance F(4,353) = 54.81, p < 0.001 (see Table 1).

Table 1. Results of multiple linear regression of model parameters on disease stage, where disease stage was coded linearly (controls = 0, pre-HD-A = 1, pre-HD-B = 2, HD-1 = 3, HD-2 = 4).

Dep. Variable:	stage	R-squared:	0.393
Model:	OLS	Adj. R-squared:	0.383
Method:	Least Squares	F-statistic:	38.08
No. Observations:	360	AIC:	1116.
Df Residuals:	353	BIC:	1143.

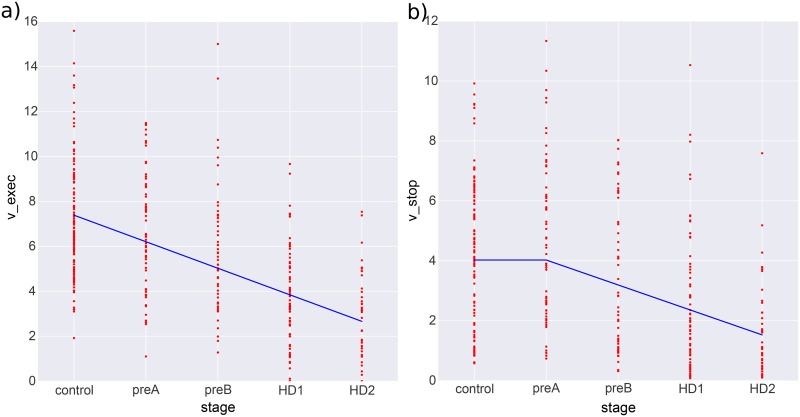
While some parameters might show an impairment only after symptoms are evident (e.g., if the mechanisms of motor symptoms are related to the mechanisms producing the reduced model parameter), other parameters might show a more progressive signal even in the stages of pre-HD. We thus assessed for a piecewise linear relationship between parameters and disease stage using a Multivariate Adaptive Regression Spline (MARS) [38] regression. This iterative algorithm can detect break points in the linear relationship and model them explicitly. The results can be appreciated in Fig 7. While v_exec shows a directly linear relationship, declining from early stages of pre-HD, v_inhib seems to only change in later stages once motor symptoms are present. This fits with our group difference results that showed a significant difference between controls and pre-HD in v_exec, but not in v_inhib. Interestingly, these results suggest that executive control deficits occur before inhibitory control degradation that are only noticable after full HD onset.

Fig 7. Multivariate Adaptive Regression Splines (MARS) estimation of a piece-wise linear relationship between v_stop (a) and v_exec (b).

See text for more details.

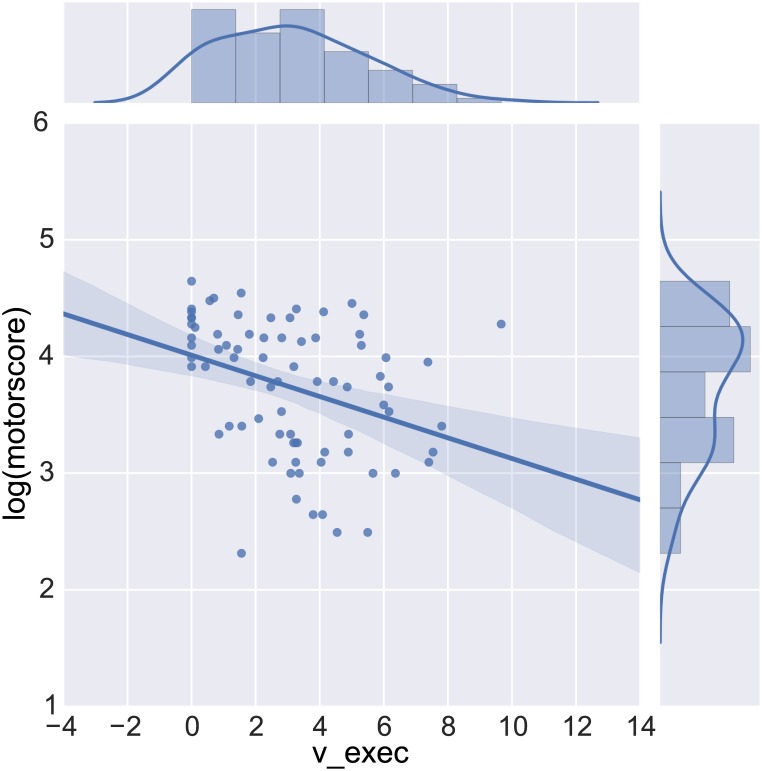
Deficits in both v_exec and v_inhib were also strongly related to subjects’ TMS motor scores p < 0.001 (see Fig 8 and Table 2 for a multiple linear regression analysis). Moreover, model parameters were significantly correlated with TFC F(363, 6) = 19.74 and explained 24% of the variance (see Table 3 for details).

Fig 8. Best fitting linear regression line between v_exec and log-transformed total motoro score (TMS) on top of raw subject scores.

Table 2. Results of multiple linear regression of model parameters on total motor score (TMS)—higher scores indicate worse motor problems.

Dep. Variable:	TMS	R-squared:	0.399
Model:	OLS	Adj. R-squared:	0.389
Method:	Least Squares	F-statistic:	40.14
No. Observations:	370	AIC:	2714.
Df Residuals:	363	BIC:	2742.

Table 3. Results of multiple linear regression of model parameters on total functional capacity (TFC).

Higher TFC indicates better functioning than lower scores.

Dep. Variable:	tfc	R-squared:	0.246
Model:	OLS	Adj. R-squared:	0.234
Method:	Least Squares	F-statistic:	19.74
No. Observations:	370	AIC:	1268.
Df Residuals:	363	BIC:	1296.

There was no correlation between any of the model parameters and the CAG repeat length in a multlinear regression R² = 0.02, F(240, 6) = 0.8, p = 0.57.

Machine Learning

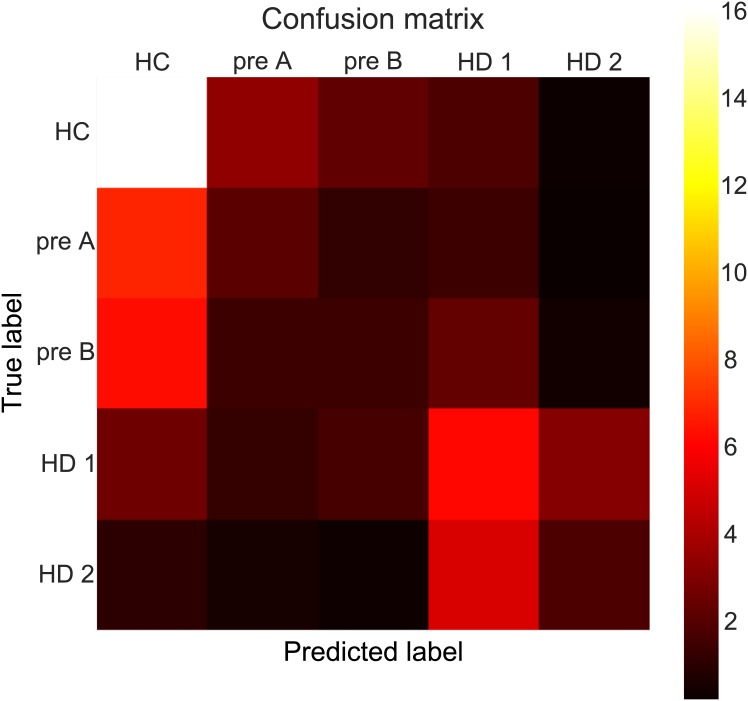
We next asked if disease state could be predicted using the model parameters alone. First, we wanted to assess how well each subgroup could be identified given only the model parameters. The confusion matrix in Fig 9 shows the results of training a random forest and testing its multiclass predictions on held-out data (i.e, predicting patient group status in subjects for whom the training procedure had not seen). The classifier achieves an accuracy of 40% which is modestly above chance (i.e. 33% due to class imbalances).

Fig 9. Confusion matrix showing true class labels as well as class labels predicted.

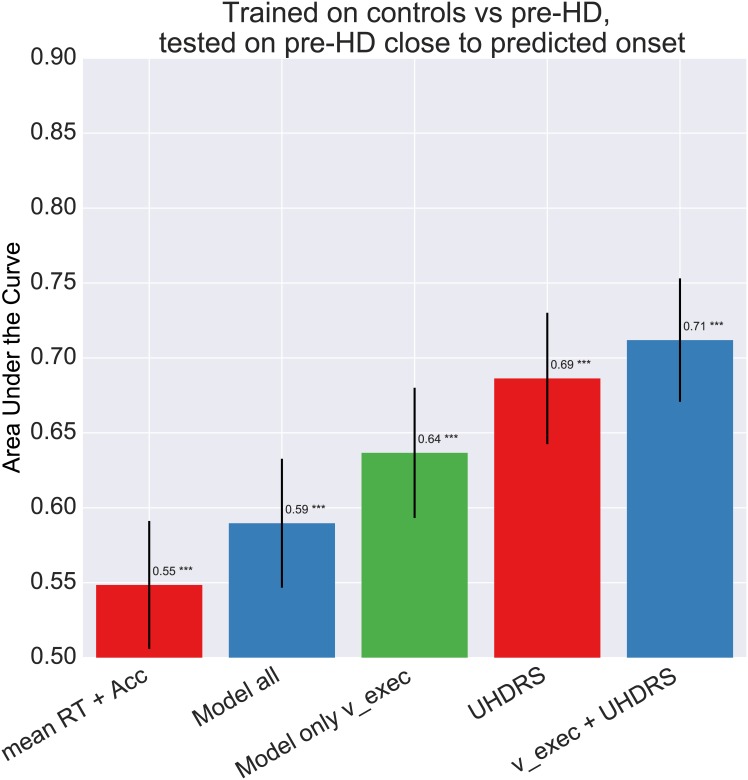
Next we evaluated how well the above classifer was able to discriminate pre-HD-B subjects—those presymptomatic patients closer to converting—from controls. As can be seen in Fig 10, the success of the classifer was improved when considering pre-HD-B subjects, particularily when the classifiers were trained on both model parameters and UHDRS scores. Summary statistics were not sensitive to this pattern and had significantly lower AUC than all other classifiers (all p-values < 0.0001). Interestingly, combining v_exec with UHDRS scores also leads to higher accuracy than using UHDRS alone.

Fig 10. Bar-plot comparing Area under the ROC Curve (AUC) of a logistic regression classifier trained to differentiate pre-HD subjects from controls, evaluated specifically here on its performance predicting pre-HD-B.

Error-bars represent standard deviation.

The next clinical setting we consider is whether a classifier can discriminate between controls and non-symptomatic subjects carrying the CAG repeat mutation. This application could be of interest if any signal picked up by the classifier could help identify pre-HD subjects that might be closer to converting to symptom onset. We compare classifier performance when trained on behavioral summary data (mean and SD RT in pro and antisaccade trials as well as accuracy in antisaccade trials), versus when it is trained on the discriminative model parametes v_exec, versus when it is trained on the standard UHDRS assessment score consisting of TMS and TFC. The AUC of the classifiers on held-out data can be appreciated in Figure A in S1 File. All classifiers were significantly better than chance (all p-values < 0.05). As can be seen, UHDRS provides the highest level accuracy (p < 0.001) followed by v_exec, followed by all model parameters, and finally the summary scores (p < 0.001) which operate close to chance.

In the case where we know if a patient has the CAG repeat mutation it is relevant to classify how close a pre-HD individual is to progressing to manifest HD. We thus trained a classifier to predict subgroups pre-HD-A and pre-HD-B. As can be seen in Figure B in S1 File, our previously identified parameter v_exec results in the highest accuracy. However, significance testing only relevealed a trend (p = 0.089) when comparing v_exec to UHDRS scores and no significant difference when comparing accuracy using all model parameters to UHDRS (p = 0.28). All parameters, v_exec and UHDRS significantly outperformed RT summary measures (all p-values < 0.001). All classifiers were significantly different from chance (all p-values < 0.001). While the combination of v_exec and UHDRS scores suggest a slight improvement, this difference was not significant (p = 0.12).

Discussion

We demonstrated that computational methods based on the antisaccade behavioral data are useful in detecting subtle differences between non-symptomatic HD subjects and controls, and between different stages of pre-HD. As in earlier reports, manifest HD subjects had longer, more variable RTs as well as increased error rates in antisaccade trials [10–12]. This result was echoed by our analysis using delta-plots. We then fit a computational model inspired by [30] that decomposes the behavior on the antisaccade task into cognitive processes that quantify prepotent response tendencies, speed of inhibitory control to stop the prepotent response when it is maladaptive, and speed and onset time of executive control to initiate volitional saccades. The HD group was associated with differences in every model parameter, suggesting wide-spread neurodegeneration in this group. In contrast, the pre-HD group was selectively associated with deficits in executive control parameter, accompanied by skewed correct antisaccade trials

The pre-HD stage has mostly been in association with response inhibition deficits assumed to result from indirect pathway degeneration [2, 16–20, 39]. The indirect pathway of the BG has been suggested to provide a selective NoGo signal that suppresses maladaptive response tendencies [40–42]. Only in later stages, once motor-symptoms set in, other areas become impacted, such as other BG nuclei (subthalamic nucleus and substantia nigra), the thalamus, as well as cerebellum, cortex, and brainstem [43–45]. Contrary to this theory, our modeling results suggest that the early deficits observed in selective response inhibition tasks such as the antisaccade task result from executive control deficits rather than reduced response inhibition per-se. This result could suggest that it might not be indirect pathway degeneration that occurs in the early, pre-HD stages but rather frontal or fronto-striatal degradation. Our elaborated neural model of these tasks identify a pathway from prefrontal cortex to striatum that is involved in executive control to facilitate an adaptive rule-based response [8]. This theory is corroborated by a diffusion tensor imaging study that found reductions in white matter fibers projecting from the FEF to the caudate body of the BG in pre-HD individuals [10]. The amount of this degradation, as well as the UHDRS motor score [11], are associated with increased RT variability in voluntarily guided saccades, consistent with our findings and with a reduction in drift-rate [31, 46]. Furthermore, some evidence suggests that pre-HD is actually associated with increased indirect pathway activity [47], perhaps needed to counteract prepotent response tendencies when executive control is weakened. A recent study [21] also suggests that deficits in inhibitory control tasks like the stop-signal task are related to reduced activation of frontal areas such as the pre-supplementary motor cortex (pre-SMA) and dorsal anterior cingulate cortex (dACC). Note, however, that this theory rests on a link between the executive drift-rate parameter and frontal function which has theoretical linking in neural simulations [8], but has not been firmly established. Nevertheless, some recent data provides some supporting evidence from fMRI that the SMA is related to alterations in drift rate during executive control [48].

A second explanation of our finding is that it is indeed caused by indirect pathway degradation but in parts of the BG responsible for executive control which could in principle be affected in earlier disease stages than parts of the BG responsible for motor control. The BG has traditionally been associated with gating motor commands [49]. However, more recently it was shown that it also is involved in higher cognitive processing such as working memory updating [50–53]. Anatomically, the BG is known to form loops that originate in cortex, innervate the BG, and connect back up to the cortex via the thalamus in highly structured circuits [54]. Dorso-lateral PFC (DLPFC) is associated with executive control [22, 55] and consistently activated in antisaccade trials [56–58]. Notably, DLPFC innervates anatomical regions of the BG distinct from certain motor areas relevant for saccade generation (including FEF [59], SEF [60] and pre-SMA [61–63]). This alternative account thus suggests that indirect pathway degradations first happen in the BG areas innervated by DLPFC and only later progresses to areas innervated by motor cortex. However at this time, no clear mechanism is known which would lead to this progression within the BG.

These results might also be relevant for clinical and pharmaceutical research. Currently, there are no clinically proven therapies that could reverse the cognitive decline associated with the symptomatic stages of this disease. Thus, as with other neuronal disorders like Alzheimer’s disease, focus in the clinic has shifted towards early intervention to slow the progression which requires detection of subtle cognitive changes before the symptoms become visible neurologically.

Unfortunately, neither summary statistics nor delta-plots showed significant differences between control subjects and pre-HD individuals. Strikingly, however, our computational modeling analysis did show a significant difference in the drift-rate parameter for executive control (v_exec). Moreover, when splitting subjects into subgroups a linear relationship between v_exec and the progressive stages from early pre-HD to late HD emerged. Other model parameters associated with inhibitory control v_inhib, delay of executive control, prepotent response bias, response caution and motor execution were only affected in HD subjects suggesting non-linear degradation of the various cognitive processes involved in the antisaccade task.

The computational approach provided several advantages. The model allowed us to detect an effect between controls and pre-HD. Moreover, the affected parameter allows for a more cognitive interpretation of the results. Our classification results show that the model parameters, specifically the above identified v_exec parameter can provide higher classification accuracy than RT summary statistics, albeit not by a huge margin. The accuracies overall were not higher than the current clinical standard UHDRS. Moreover, the classifier was more successful in specifically discriminating pre-HD-B subjects from controls, suggesting that it could potentially detect subjects that are closer to reaching motor symptom onset. This hope awaits further data after more subjects have converted to be tested. Moreover, in a clinical setting we would likely use a battery of various cognitive tasks that could increase classification accuracy. The fact that data from a single task is competitive with UHDRS in certain circumstances is thus encouraging.

Ultimately, the hope is to identify measures that are more sensitive than TFC and TMS which are of limited clinical use to track disease progression in pre-HD [3]. As v_exec showed correlations with these measures it could be such a clinical marker but it would require more validation and further analysis on longitudinal data to establish it as such.

Limitations

A limiting factor of our computational analysis is that it assesses model parameters that guide inhibitory control without regard for sequential effects. A large body of literature shows that such effects do impact performance in conflict and inhibition tasks, such that conflict, errors or inhibitory demands on the previous trial all influence performance on the next trial [64–67]. However, our computational model is already somewhat complex, in that it contains multiple free parameters, and investigating how sequential effects further modulate these parameters poses an additional challenge for quantitative fitting, given that these parameters are somewhat collinear with each other. Future research should develop hierarchical Bayesian parameter estimation methods [35] which improve the ability to infer model parameters and to deal with such collinearity, but such methods benefit strongly from a closed form analytic solution to the likelihood of observations given the model. This solution is available for simpler sequential sampling models like the drift diffusion model used in other studies, but the model we used here to simulate the temporally evolving dynamics of inhibitory control does not benefit from that luxury. Addressing such limitations to assess the degree to which trial-to-trial behavioral adjustments are altered as a function of disease stage may be able to further improve classification performance.

Supporting Information

S1 File. Supporting information.

Algorithm A, Algorithm to draw a single antisaccade trial. InvGaussian(μ, λ) is the first-passage-time distribution for a Wiener diffusion process with drift μ and a single upper threshold λ. t is a constant corresponding to non-decision time. t_exec is a second constant that captures the time needed to implement additional processing on antisaccade versus prosaccade trials. By running this algorithm 10000 times for each parameter setting and using kernel density estimation on the simulated RTs, we approximated a likelihood function. Prosaccade trials were fit using only the prepotent accumulator for which a closed-form solution is available. The parameters a, t and v_pre are thus constrained by prosaccade as well as antisaccade trials while the parameters v_stop, v_exec, and t_exec are only constrained by the latter. Figure A, Bar-plots of behavioral mean reaction time in seconds across different groups in the antisaccade condition. Ellipses in grey represent mean RT of trials simulated from models fit to each individual subject. Height of the ellipses represents standard-deviation. Figure B, Bar-plot comparing Area under the ROC Curve (AUC) of a logistic regression classifier trained on different data to predict HC and pre-HD. Error-bars represent standard deviation. Figure C, Bar-plot comparing Area under the ROC Curve (AUC) of a logistic regression classifier trained on different data to predict pre-HD-A and pre-HD-B. Error-bars represent standard deviation. Table A, AIC values of different model configurations. Lower AIC values represent a better trade-off between parsimony and model fit. Table B, Multiple Comparison of Means of t parameter—Tukey HSD. Table C, Multiple Comparison of Means of v_pro parameter—Tukey HSD. Table D, Multiple Comparison of Means of v_stop parameter—Tukey HSD. Table E, Multiple Comparison of Means of v_exec parameter—Tukey HSD. Table F, Multiple Comparison of Means of t_exec parameter—Tukey HSD. Table G, Multiple Comparison of Means of a_mean parameter—Tukey HSD. Table H, Multiple Comparison of Means of a_diff parameter—Tukey HSD.

(PDF)

Data Availability

All the raw behavioral data, clinical measures, model fits, and analysis scripts are available via Figshare at the following links: https://figshare.com/articles/RT_accuracy_and_clinical_measures/2008407https://figshare.com/articles/Parameter_fits/2008404https://figshare.com/articles/Notebook_file_containing_all_analyses_to_reproduce_plots_and_statistics/2008401.

Funding Statement

This work was supported by CHDI/High Q Foundation. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.