Molecular features in complex environment: Cooperative team players during excited state bond cleavage

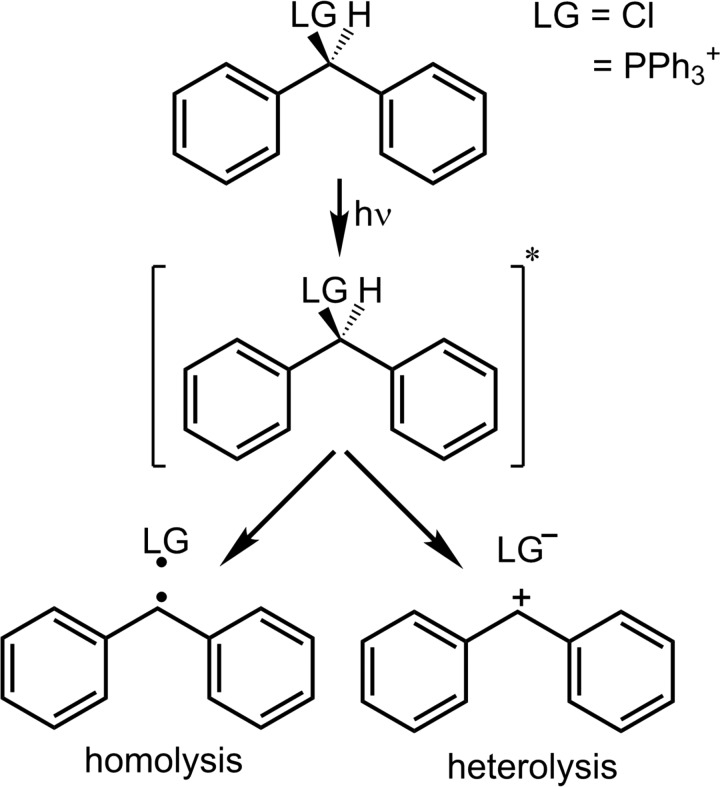
Abstract

Photoinduced bond cleavage is often employed for the generation of highly reactive carbocations in solution and to study their reactivity. Diphenylmethyl derivatives are prominent precursors in polar and moderately polar solvents like acetonitrile or dichloromethane. Depending on the leaving group, the photoinduced bond cleavage occurs on a femtosecond to picosecond time scale and typically leads to two distinguishable products, the desired diphenylmethyl cations (Ph₂CH⁺) and as competing by-product the diphenylmethyl radicals (${\text{Ph}}_2{\text{CH}}^{•}$). Conical intersections are the chief suspects for such ultrafast branching processes. We show for two typical examples, the neutral diphenylmethylchloride (Ph₂CH–Cl) and the charged diphenylmethyltriphenylphosphonium ions (${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$) that the role of the conical intersections depends not only on the molecular features but also on the interplay with the environment. It turns out to differ significantly for both precursors. Our analysis is based on quantum chemical and quantum dynamical calculations. For comparison, we use ultrafast transient absorption measurements. In case of Ph₂CH–Cl, we can directly connect the observed signals to two early three-state and two-state conical intersections, both close to the Franck-Condon region. In case of the ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, dynamic solvent effects are needed to activate a two-state conical intersection at larger distances along the reaction coordinate.

I. INTRODUCTION

Photoinduced bond cleavage constitutes a common way to generate highly reactive species like carbocations in situ.^1–6 In particular, in the case of diarylmethyl (Ar₂CH) compounds, the in situ generated carbocations are used to study their reactions with nucleophiles.^6,7 Ph₂CH⁺ and its various derivatives serve as reference electrophiles for one of the most extensive reactivity scales covering 40 orders of magnitude which is being developed by Mayr and coworkers.^7–10 Different leaving groups (LGs) are used depending on the conditions under which the reactive species are generated.^4–6 In the case of polar solvents like acetonitrile, Ph₂CH–Cl is a suitable precursor. But for less polar solvents like dichloromethane or chloroform, the Ph₂CH⁺ cation yield is extremely small on the nanosecond time scale.^5,6 Using these solvents, ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ constitutes a much better precursor for the Ph₂CH⁺ generation.^4,6 From a chemists point of view, this seems to be reasonable as the ${\text{PPh}}_3^{+}$ LG carries already a positive charge, and thus the generation of cations should be electrostatically preferred because no charge separation is necessary during bond cleavage.

Ultrafast broadband transient absorption measurements show that the Ph₂CH⁺ generation differs for both LGs. In the case of Cl, initially homolytic bond cleavage occurs on the hundreds of femtoseconds time scale followed by an electron transfer, which finally results in the ion pairs Ph₂CH⁺+ Cl⁻.⁵ The smaller driving force of the electron transfer in less polar solvents is the reason why the Cl LG is not suited for moderately polar solvents. In the case of ${\text{PPh}}_3^{+}$, the measurements reveal a direct formation of Ph₂CH⁺ for polar as well as moderately polar solvents.⁴ These observations already indicate that the underlying bond cleavage mechanisms might be different.

In the present work, we theoretically investigate the photoinduced bond cleavage of Ph₂CH–Cl and ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ (see Fig. 1) by means of state-of-the-art quantum chemical and quantum dynamical methods. We will discuss the individual molecular features introduced by the LG including two- and three-state conical intersections (CoIns) optimized at the complete active space self consistent field (CASSCF) level of theory. Three-state CoIns have already been shown to be important for photochemistry.^11–13 To perform quantum dynamics (QD), we calculated potential energy surfaces (PESs) for both precursors in reduced dimensionality at the “our own n-layered integrated molecular orbital and molecular mechanics” (ONIOM) level of theory.^14–17 In the case of Ph₂CH–Cl, the PESs have been diabatized to describe the coupling through the three-state CoIn properly. For the first time to our knowledge, we present QD simulations including a three-state CoIn seam. Moreover in the case of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, the solvent environment comes into play during the bond cleavage and has a decisive influence on the reaction process.^18,19

FIG. 1.

Reaction scheme for the photoinduced bond cleavage of diphenylmethyl derivatives. Note that in the case of ${\text{PPh}}_3^{+}$ being the leaving group (LG), homolysis (${\text{Ph}}_2{\text{CH}}^{•}+{\text{PPh}}_3^{•+}$) as well as heterolysis (Ph₂CH⁺+ PPh₃) result in one positively charged and one neutral fragment.

The article is structured as follows: In Sec. II A, we discuss the quantum chemical results for Ph₂CH–Cl. Subsequently, the QD simulations are presented (Sec. II B). Then, the results for ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ are compared therewith. Again they are split into a quantum chemical (Sec. III A) and a quantum dynamical part (Sec. III B). Finally, we conclude in Section IV.

II. BOND CLEAVAGE OF Ph₂CH–Cl

This section discusses the dissociation process of Ph₂CH–Cl that has been extensively studied experimentally.^1,5,20,21 The initial bond cleavage is found to be mainly homolytic on the sub-hundred femtosecond time scale, while a small heterolytic fraction is slightly delayed.²¹ In a previous theoretical study, a S₁/S₀ CoIn was identified connecting the heterolytic and homolytic product channel, but two-dimensional QD simulations revealed that the wave packet does not reach the CoIn.²² Thus, the exclusive product of the initial bond cleavage was—in contradiction to the experimental results—the ion pair of Ph₂CH⁺ and Cl⁻. In this previous study, the calculations have been performed at the CASSCF level of theory with an active space built up from all π-orbitals of one phenyl ring and the σ- and σ*-orbitals of the carbon chlorine bond.²² Later, the importance of the Cl lone pairs has been shown by quantum chemical calculations.²¹

In the present work, we take both Cl lone pairs into account and employ an active space of 12 electrons in 10 orbitals, i.e., CASSCF(12,10). In addition, we use the ONIOM method.^14–16 The angle between the phenyl moieties of Ph₂CH–Cl at the Franck-Condon (FC) point is 77°, which is comparable to triarylmethyl derivatives for which it is reported in the literature that the π-systems of the phenyl rings are uncoupled.^23,24 In previous CASSCF calculations for the whole molecule, it was demonstrated that the π- and π*-orbitals of the phenyl rings can be separated.²² Furthermore, CASSCF calculations including the π-orbitals of both phenyl rings in the active space have shown that only one phenyl ring can interact with the σ*-orbital of the C1-Cl bond.²¹ Therefore, it is possible that the high-level system treated at the CASSCF level of theory contains only one phenyl ring. This significantly reduces the computational cost. The second phenyl ring of the diphenylmethyl (Ph₂CH) moiety is replaced by a H atom in the high-level system and is solely included in the low-level system. It is evaluated at the UB3LYP level using Gaussian.²⁵ Fig. 2(a) displays the partitioning of the molecule with the thicker drawn part representing the high-level or model system. The constrained low-level state (CLS) approximation for ONIOM is used throughout the whole work.¹⁷ The basis set employed in all calculations is 6-31G(d).

FIG. 2.

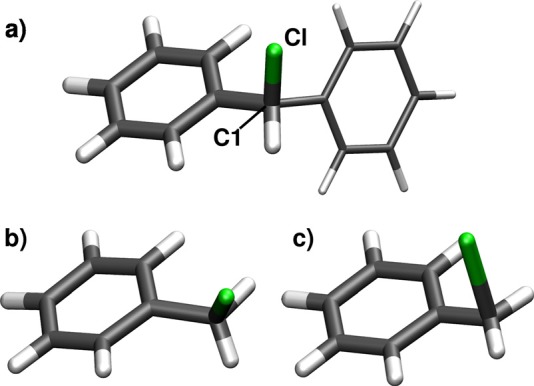
(a) Optimized geometry of the S₀ minimum and visualization of the ONIOM partitioning for Ph₂CH–Cl: The thicker drawn part represents the high-level system treated with CASSCF(12,10). The second phenyl ring is only included in the low-level calculations with UB3LYP. (b) Optimized geometry of the three-state CoIn for the model system with a C1-Cl distance of 2.15 Å. (c) Optimized geometry of the two-state CoIn for the model system with a C1-Cl distance of 2.58 Å.

A. Potential energy surfaces and the influence of the chlorine lone pairs

We optimized two CoIns for the model system which are shown in Figs. 2(b) and 2(c). A three-state CoIn could be located between the ππ* S₁ state and both lone pair states exhibiting nπ* character with the program package COLUMBUS^26–29 (see Fig. 2(b)). The C1-Cl distance is 2.15 Å, the maximum energy gap between each pair of states is 0.017 eV. A second CoIn—this time a two-state CoIn—between the S₄ state of mixed ππ* and πσ* character and the ππ* state S₁ is located at a C1-Cl distance of 2.58 Å with the program package Molpro^30–33 (see Fig. 2(c)). Here, the energy gap is 2.4 × 10⁻⁴eV.

First, we calculated PESs along the dissociation coordinate, the C1-Cl distance r_C1Cl. Fig. 3 illustrates them in the diabatic representation as used in the QD calculations which will be discussed in Sec. II B. The bound S₀ state (black) correlates with the homolytic bond cleavage leading to radical pairs. The reaction starts with a π-π* excitation to the S₁ state (red). The excitation energy is 4.88 eV (254 nm), which is in good agreement with the experimental value of 4.66 eV (266 nm).²⁰ At 2.12 Å, the lone pair states (green) cross the S₁ forming a three-state CoIn and are more and more stabilized with increasing C1-Cl distance, while their character changes from nπ* to nσ*. Finally, they become degenerate with the ground state S₀. Therefore, the lone pair states constitute a direct connection between the optically accessed S₁ state and the homolytic product channel. After the three-state CoIn, the S₁ energy increases slightly to reach the S₄/S₁ CoIn at 2.60 Å. The S₄ state (blue) is identified as the heterolytic reaction channel for large C1-Cl distances. The S₁ state finally correlates with the first excited radical channel. Altogether, two consecutive CoIns are accountable for the product splitting, and the lone pair states are the key elements here.

FIG. 3.

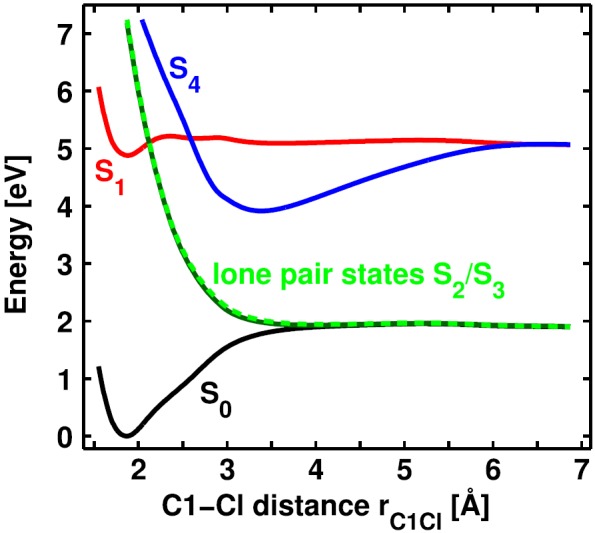
Diabatic PESs of Ph₂CH–Cl calculated at the ONIOM level of theory along the C1-Cl distance r_C1Cl. The S₀ state (black) and the lone pair states (green) form the homolytic product channel, the S₄ state (blue) forms the heterolytic product channel. The S₁ state (red) leads to excited radical pairs.

To demonstrate the crucial influence of the Cl lone pairs, we performed CASSCF calculations without the Cl lone pairs being in the active space, i.e., CASSCF(8,8). At this level of theory, we optimized an additional S₁/S₀ CoIn for the model system which is the analog to the one identified previously,²² showing the Cl atom above an allylic subunit. We linearly interpolated the structure between the optimized S₁/S₀ CoIn and the S₀ minimum of the model system. Based on the obtained geometries, Fig. 4 compares the resulting PESs at the CASSCF(8,8) (dashed lines) and the CASSCF(12,10) level of theory (solid lines). Around the FC region, both methods yield similar results. But as soon as the lone pair states (green solid lines) cross the S₁ state (red solid line), the PESs begin to differ. In the case of CASSCF(8,8), the S₁/S₀ CoIn is clearly visible at r_C1Cl = 3.11 Å with an energy gap of 4.96 × 10⁻⁵eV. In contrast thereto, the S₁/S₀ energy gap increases to 1.59 eV at the CASSCF(12,10) level of theory because the lone pair states intrude. Nevertheless, the character of S₀ and S₁ is remarkably similar. Obviously, the Cl lone pairs prevent the S₁/S₀ CoIn observed at the CASSCF(8,8) level of theory. Instead, they open up a completely new and direct connection between S₁ and S₀ already in the FC region, resulting in the formation of radical pairs.

FIG. 4.

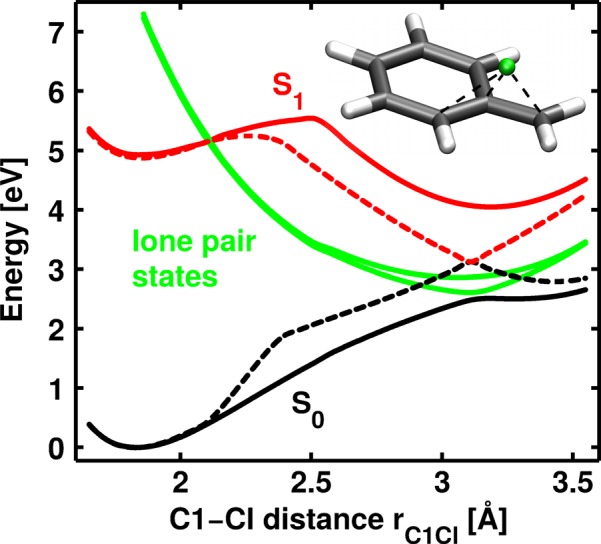
PESs for the model system of Ph₂CH–Cl using two different active spaces. The dashed lines show the results for the active space containing only the π-system and the C1-Cl bond (CASSCF(8,8)). The solid lines are obtained if the Cl lone pairs are additionally included in the active space (CASSCF(12,10)). The geometries are interpolated between the S₀ minimum and a S₁/S₀ CoIn located using CASSCF(8,8). This CoIn connects S₁ (red) and S₀ (black) at r_C1Cl = 3.11 Å. Its geometry is depicted in the right upper corner as inlay. The lone pair states (green) which are shown as diabatic states separate S₁ and S₀ by 1.59 eV at the former CoIn.

B. Quantum dynamics in the presence of a three-state conical intersection

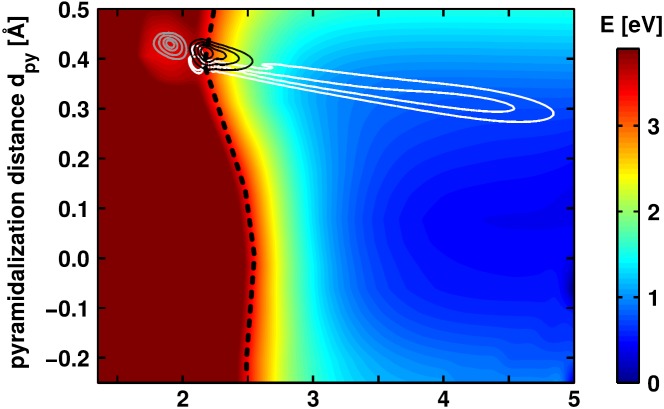
As a full dimensional quantum dynamical treatment is not feasible, we use a two-dimensional subspace to describe the reaction. The chosen coordinates are the C1-Cl distance and a coordinate accounting for the relaxation occurring in the carbon backbone during the bond cleavage. Most important is the hybridization of the central carbon atom C1 which changes from sp³ to sp². Thus, the C1 environment gets more and more planar during the reaction. We use the pyramidalization distance d_py to measure the distance of C1 above the plane formed by its three remaining neighboring atoms as coordinate. It includes additional relevant changes during re-hybridization like adaptations of bond lengths and ring positioning. As the lone pair states are rather independent of the carbon backbone relaxation, the three-state CoIn forms a seam along the pyramidalization distance d_py (see Fig. 5).

FIG. 5.

PES of the adiabatic S₁ state of Ph₂CH–Cl calculated at the ONIOM level of theory. Three wave packet snapshots taken from the diabatic propagation at different time points are also plotted. The first snapshot (gray isolines) is taken after 19 fs, the second (black isolines) after 36 fs, and the third (white isolines) after 82 fs. The three-state CoIn seam (black dashed line) is visible around the energy range of 3.3 eV (bright red).

Since the quantum dynamical study should include population transfer between electronic states, the calculation of coupling elements is necessary. As the two lone pair states are always nearly degenerate, there will be significant coupling throughout the whole coordinate space that is not relevant for the product formation. To avoid this omnipresent coupling, we switch to the diabatic picture where the electronic states maintain their specific character while passing a CoIn. In this picture, the coupling between the lone pair states can easily be set to zero. To transform the PESs, we solely employ ab initio molecular properties, namely, dipole ${\mu }_{\mathit{i}\mathit{i}}^{\mathit{a}\mathit{d}}$ and transition dipole moments ${\mu }_{\mathit{i}\mathit{j}}^{\mathit{a}\mathit{d}}$ forming the matrix μ^ad. The matrix elements are functions depending on the electronic structure and thus show the same behavior at the CoIn as the electronic energy. We will briefly discuss the procedure which is based on transformations for two-state CoIns.^34–36 Due to the three-state CoIn, the matrix dimension is 3 × 3.

Because the population transfer only occurs if two states come very close, it is useful to neglect the coupling far from the CoIn. Therefore, the off-diagonal terms ${\mu }_{\mathit{i}\mathit{j}}^{\mathit{a}\mathit{d}}$ between the states i and j are damped according to the following equation:³⁴

$${\tilde{\mu }}_{\mathit{i}\mathit{j}}^{\mathit{a}\mathit{d}}={\mu }_{\mathit{i}\mathit{j}}^{\mathit{a}\mathit{d}}·e^{-f\Delta E_{\mathit{i}\mathit{j}}^2}.$$ (1)

Here, ${\mu }_{\mathit{i}\mathit{j}}^{\mathit{a}\mathit{d}}$ is multiplied by an exponential function depending on a damping factor f and the squared energy difference ΔE_ij. The damping factor f has to be chosen carefully with respect to a smooth behavior in the resulting PESs. In the present work, f = 500 for the three-state CoIn and f = 5000 to 10 000 for the two-state CoIn. The modified matrix ${\tilde{\mu }}^{\mathit{a}\mathit{d}}$ is then diagonalized

$${\mu }^{\mathit{d}\mathit{i}\mathit{a}}={\mathbf{U}}^{†}{\tilde{\mu }}^{\mathit{a}\mathit{d}}\mathbf{U},$$ (2)

and the resulting transformation matrix U is applied to obtain the diabatic energies $H_{\mathit{i}\mathit{i}}^{\mathit{d}\mathit{i}\mathit{a}}$ and couplings $H_{\mathit{i}\mathit{j}}^{\mathit{d}\mathit{i}\mathit{a}}$ of the matrix H (Eq. (3))

$$H_{\mathit{i}\mathit{j}}^{\mathit{d}\mathit{i}\mathit{a}}=\stackrel{3}{\sum _{k=1}}{U}_{\mathit{k}\mathit{i}}{E}_k{U}_{\mathit{k}\mathit{j}}.$$ (3)

E_k represents the adiabatic energies.

Fig. S1 in the supplementary material³⁷ shows the resulting two-dimensional diabatic PESs. The QD simulations were performed using the Chebychev propagation scheme³⁸ and the Wilson G-matrix formalism^39–41 (for details, see supplementary material³⁷). The ground state vibrational eigenfunction was transferred to the S₁ PES and slightly shifted to a smaller C1-Cl distance and a higher pyramidalization distance d_py to account for the minimal barrier being not contained in the ONIOM PES. Fig. 5 depicts snapshots of the wave packet at three points in time. Although the propagation is performed in the diabatic presentation, the adiabatic S₁ PES is shown. This allows to place the three wave packets in the respective potential, which they experience during the propagation. The three-state CoIn seam (black dashed line) is very prominent in this representation. It is present for all values of d_py in the range of r_C1Cl = 2.1 Å to r_C1Cl = 2.5 Å at an energy of approximately 3.3 eV (bright red).

The first snapshot (gray isolines) is taken 19 fs after the propagation has been started and shows the wave packet at the S₁ minimum in the FC region. After 36 fs (black isolines), the wave packet has already coupled through the three-state CoIn seam and starts to follow the steep gradient of the lone pair state PES toward larger r_C1Cl. As there is also a small gradient in d_py toward planarization, the wave packet is slightly asymmetric in the direction of d_py. After 82 fs (white isolines), the wave packet is stretched from the three-state CoIn seam at r_C1Cl = 2.1 Å to r_C1Cl = 4.9 Å which results from the ongoing coupling through the three-state CoIn seam, while the first parts of the wave packet evolve very fast. It reaches a maximum C1-Cl distance of r_C1Cl = 5 Å, which means that the bond cleavage is fully performed. But there still maintains a considerably large pyramidalization of d_py= 0.3 Å. This observation is in agreement with experimental observations and on-the-fly simulations which reveal that the formation of the full absorption signal of the Ph₂CH⁺ cation occurs with a time constant of 300 fs, which is attributed to planarization and solvation effects.⁴²

Fig. 6 illustrates the product formation obtained by the QD simulations. Therefore, the population of each state is collected at r_C1Cl = 4.0 Å. It is clearly visible that the radical pairs are the main product of the initial bond cleavage. In the course of the propagation, 82% of the initial population reach the dissociation limit in the lone pair states or in the excited radical channel. At 67 fs, the radical yield starts to grow very rapidly as more and more parts of the wave packet couple through the three-state CoIn seam. This delay time is in very good agreement with the experimentally observed 76 fs.²¹ The delay time of 143 fs for the ion pairs is only slightly longer than the measured one of 124 fs (Ref. 21) and in excellent agreement with previous QD calculations where the lone pair states have not been considered.²² The simulated product yields deviate more from the experimental observations.⁵ The experimental radical yield of 40% is approximately half of the simulated yield of 82%. This may be attributed to recombination which is not considered in the simulation. On the other hand, the cation yield is underestimated with 0.2% here compared to 2% in the experiment. This might be due to the fact that the minimal barrier in the S₁ state before the S₄/S₁ CoIn is not included in the PES. Thus, the fraction of the wave packet reaching the S₄/S₁ CoIn is underestimated. All in all, it is possible to successfully model the initial bond cleavage of Ph₂CH–Cl with radical pairs as the main product by the sequential passage through the CoIns in the FC region and to reproduce the observed delay times very well.

FIG. 6.

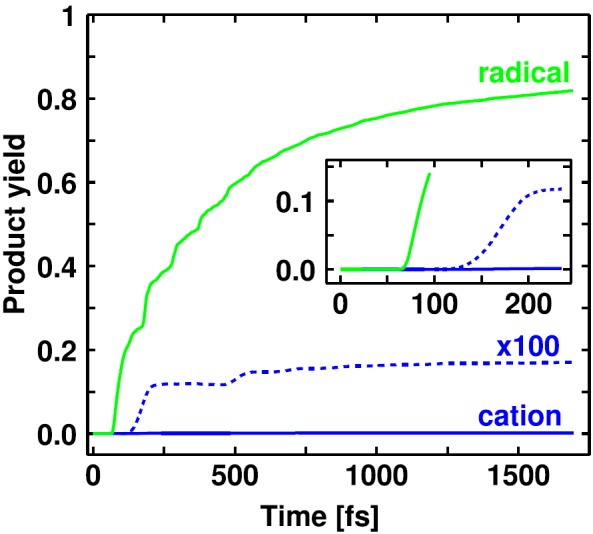
Product yield progress for the propagation of Ph₂CH–Cl up to 1700 fs. The ion pair yield is additionally plotted enlarged by the factor 100 with dashed lines. The inset especially depicts the onset of the rise of the product yield curves for the first 250 fs.

The subsequent processes—in particular, electron transfer, diffusional separation, and geminate recombination—can be treated with a combined Marcus-Smoluchowski model.⁵ Thereto, a pair of coupled differential equations can be set up and solved numerically (for details, see Ref. 5). The secondary processes typically take place on a time scale ranging from a few picoseconds up to several nanoseconds. They determine the chemically relevant cation yield which is available for subsequent, mostly bimolecular reactions.^6–8,10

III. BOND CLEAVAGE OF Ph₂CH−PPh₃⁺

In this section, we will focus on the bond cleavage of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, which contains ${\text{PPh}}_3^{+}$ as LG in contrast to the previously investigated Ph₂CH–Cl. At first sight, the exchange of the LG introduces four major modifications: First, the ${\text{PPh}}_3^{+}$ moiety is considerably larger than the Cl atom. Second, it carries a positive charge. Third, the additional phenyl rings on the LG can be excited at a similar energy as the Ph₂CH moiety and thus are competing chromophores. And fourth, in contrast to the Cl, the P atom does not posses any lone pairs which have shown to be of great importance for the bond cleavage of Ph₂CH–Cl. Altogether, these changes coming along with the exchange of the Cl atom with the ${\text{PPh}}_3^{+}$ moiety already indicate changes of the key features during the bond cleavage.

A. Potential energy surfaces and a second chromophore carrying a positive charge

Initially, we take a look at the optical excitation process. As already mentioned, the phenyl rings of the ${\text{PPh}}_3^{+}$ moiety constitute additional chromophores, which absorb in the same spectral region as the phenyl rings of the Ph₂CH moiety. This results in an increased excited state manifold. The full system ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ exhibits five locally excited states which are energetically quite close—two on the Ph₂CH moiety and three on the LG.⁴³ In addition, charge transfer excitations between both moieties are present. They are energetically well separated from the locally excited states and higher in energy.⁴³ Like in the case of Ph₂CH–Cl, the PESs for the QD calculations are evaluated at the ONIOM level of theory. The characteristics of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ in the FC region—in particular, the charge transfer states—already reveal that the high-level system has to contain not only one phenyl ring of the Ph₂CH moiety but also one of the ${\text{PPh}}_3^{+}$ moiety. Thus, the interplay between locally excited and charge transfer states can be described. Fig. 7(a) shows the ground state minimum structure of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$. The thick part of the molecule is the high-level system phenylmethylphenylphosphonium ion (PhCH₂–PH₂Ph⁺), while the thinner phenyl rings are only contained in the low-level system. The high-level system is calculated at the CASSCF(10,10) level of theory. The active space contains two π- and two π*-orbitals of each phenyl ring as well as the σ- and σ*-orbitals of the C1-P bond.⁴³ The low-level system is evaluated at the density functional theory (DFT) level of theory (functional M06-2X⁴⁴).

FIG. 7.

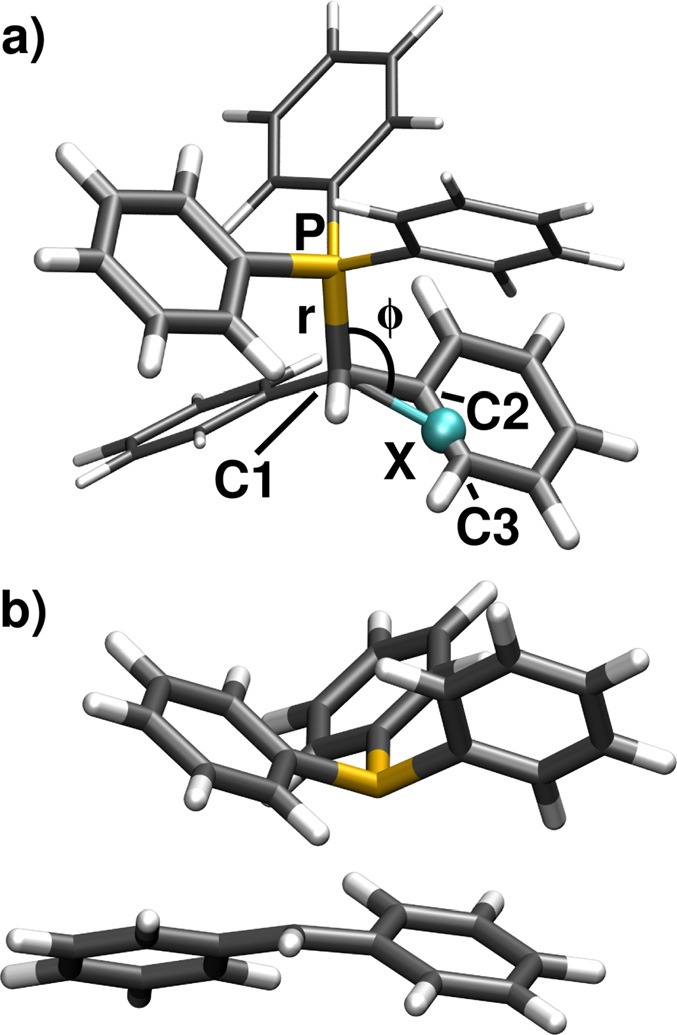
(a) Ground state minimum geometry of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ optimized at the DFT level of theory (functional B3LYP). The thicker drawn part of the molecule constitutes the high-level system of the ONIOM calculations, while the thinner drawn phenyl rings are only contained in the low-level system. (b) Geometry of the S₁/S₀ CoIn of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ calculated at the ONIOM level of theory.

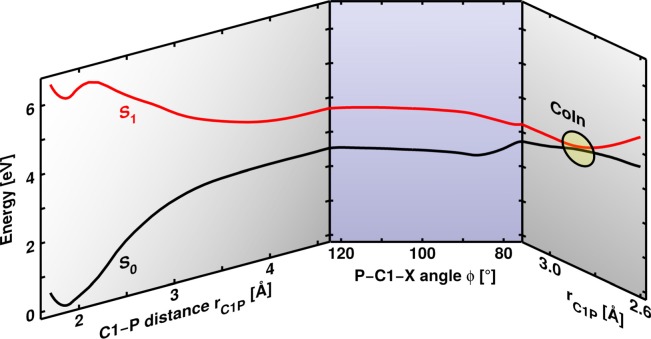
Fig. 8 illustrates the PES of the four lowest singlet states along the C1-P distance r_C1P for a constant P-C1-X angle $\varphi =125°$ (see Fig. 7). A local π-π* excitation on ${\text{PPh}}_3^{+}$ leads to the S₁ state (red line), while the S₂ (blue line) is characterized by a local π-π* excitation on the Ph₂CH moiety. The S₃ state (orange line) has charge transfer character in the FC region. To observe bond cleavage experimentally, the system is excited to the locally excited states.⁴ The S₁ state opens the preferred reaction path compared to the S₂ as first it has the lower barrier, and second the S₂ population can immediately relax to the S₁ via a S₂/S₁ CoIn.⁴³ Therefore, we will focus on the S₁ state from now on. At a C1-P distance of r_C1P = 2.1 Å, the S₁ state exhibits a barrier of 0.3 eV. Here, the S₁ character changes to πσ* followed by a change to a σσ* character. This is in clear contrast to the excited state bond cleavage of Ph₂CH–Cl, where the Cl lone pairs induce the strong energetic stabilization of the adiabatic S₁ state after the three-state CoIn. In the dissociation limit, the ground state S₀ of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ has heterolytic character leading to Ph₂CH⁺ + PPh₃, whereas the first and second excited state—S₁ and S₂—have homolytic character. They result in the formation of radical pairs: diphenylmethyl radicals ${\text{Ph}}_2{\text{CH}}^{•}+{\text{PPh}}_3^{•+}$. This is the second major difference with respect to the Cl leaving group, where the S₀ has homolytic and the S₁ heterolytic character. The difference can be traced back to the initial positive charge of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, which leads to one positively charged and one neutral fragment in both (homolytic and heterolytic) dissociation channels. Thus, no charge separation occurs during the bond cleavage, which is the major reason for the destabilization of the heterolytic channel in Ph₂CH–Cl.

FIG. 8.

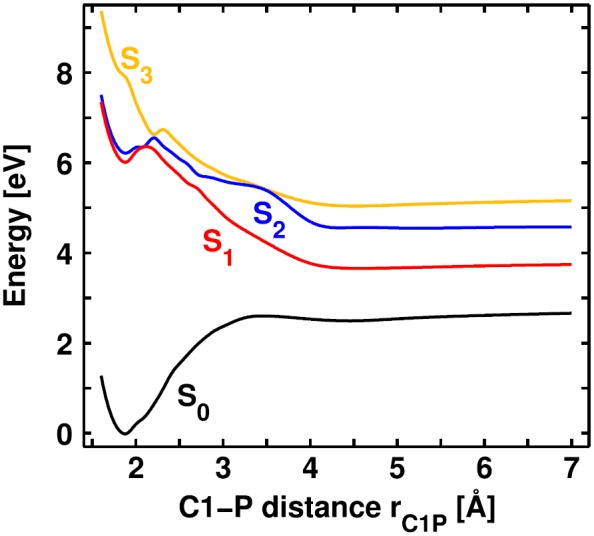
Potential energy surface of the four lowest singlet states of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ along the C1-P distance r_C1P calculated at the ONIOM level of theory. The P-C1-X angle is kept constant at $\varphi =125°$.

Due to the lack of lone pairs at the P atom, the three-state CoIn which is present in the FC region of Ph₂CH–Cl disappears completely in ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ as mentioned above. But at the same time, an energetically low lying two-state CoIn between S₁ and S₀ can be optimized in the high-level system PhCH₂–PH₂Ph⁺, which is located at a larger C1-P distance.⁴³ The P atom is located above an allylic C₃ subunit containing C1, C2, and C3 showing a related geometry to the S₁/S₀ CoIn of Ph₂CH–Cl calculated at the CASSCF(8,8) level of theory. For the full system ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, this S₁/S₀ CoIn is depicted in Fig. 7(b). The C1-P distance is r_C1P = 2.9 Å; the P-C1-X angle is $\varphi =75°$. The energy difference between S₁ and S₀ is 0.085 eV at the ONIOM level of theory. In the case of Ph₂CH–Cl, the CoIn was prevented by the Cl lone pairs (cf. Fig. 4). After the photoexcitation of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, the experimentally observed main products are Ph₂CH⁺ and PPh₃.⁴ Hence, the system has to relax to the ground state during the bond cleavage process because only there the Ph₂CH⁺ are formed. The localized S₁/S₀ CoIn offers a fast way for the system to reach the S₀.

In order to test the efficiency of the S₁/S₀ CoIn by QD simulations, like in Ph₂CH–Cl, a two-dimensional subspace is chosen in such a way that the CoIn can be described.^18,19 Besides the C1-P distance r_C1P, an angular motion of the LG is necessary to reach the structure of the CoIn.⁴³ Thus, the P-C1-X angle $\varphi$ shown in Fig. 7(a) is introduced as the second coordinate. The dummy atom X is placed in such a way in the allylic plane at the optimized CoIn of PhCH₂–PH₂Ph⁺ that the angle $\varphi$ optimally leads to the CoIn.⁴⁵ The relaxation of the carbon backbone of the Ph₂CH moiety which is the second coordinate in the case of Ph₂CH–Cl is embedded into the r_C1P coordinate.⁴⁵ As a result, the CoIn shown in Fig. 7(b) is contained in the ONIOM PES.

Fig. 9 shows a one-dimensional representation of the minimum energy path (MEP) in the S₁ state in the two-dimensional subspace at the ONIOM level of theory. The first part on the left side starts in the FC region and is depicted depending on r_C1P. After crossing the barrier, the system moves mainly along r_C1P gaining about 2.6 eV of potential energy. Simultaneously, the energy of the ground state rises by 2.5 eV. In the second part (middle), where the primary motion is along $\varphi$, the energy of both electronic states remains almost constant. Only from $\varphi =90°$ to $\varphi =76°$, the S₁ energy lowers by approximately 0.36 eV. The last part of the MEP (right) is depicted again depending on r_C1P. A shortening of the C1-P distance to r_C1P = 2.9 Å finally leads to the S₁/S₀ CoIn, where in principle the S₁ population can be transferred to the ground state to generate Ph₂CH⁺. The S₁ MEP emphasizes the fact that the system has to move considerably along $\varphi$. The key question is whether the motion from the FC region toward the CoIn is possible despite the large initial gradient along r_C1P.

FIG. 9.

Minimum energy path in the first excited state S₁ (red line) for the bond cleavage of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ in the two-dimensional coordinate space $\{r_{\mathrm{C}1\mathrm{P}},\varphi \}$. The ground state S₀ is depicted in black. The PES is displayed in three parts along the respective mainly changing coordinate. The first and the third part primarily involve changes in r_C1P, while in the second part the major motion is along $\varphi$.

B. Quantum dynamics influenced by the solvent cage

We could show that the molecular PES does not allow for the change of momentum from the r_C1P to the $\varphi$ coordinate necessary to reach the CoIn.¹⁸ As the experiments are performed in solution, the solvent has to be considered in the simulation. In the case of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, both dissociation channels lead to one positively charged and one neutral fragment. Therefore, electrostatic solvent effects are insignificant.⁴³ Only dynamic solvent effects can come into play.^18,19

Thereby, the solvent cage prevents the free dissociation of the fragments and decelerates the motion along r_C1P. These dynamic solvent effects can be accounted for in QD calculations by means of an additional potential term ${\widehat{V}}_{\text{solv}}$ in the Hamiltonian ${\widehat{H}}_{\text{tot}}$,^18,19

$${\widehat{H}}_{\text{tot}}=\widehat{T}+{\widehat{V}}_{\text{mol}}+{\widehat{V}}_{\text{solv}},$$ (4)

with the kinetic energy operator $\widehat{T}$ and the molecular potential ${\widehat{V}}_{\text{mol}}$. Recently, we developed two different approaches with increasing complexity to calculate the solvent potential ${\widehat{V}}_{\text{solv}}$. The first method includes the solvent effects in a continuum-like fashion,¹⁸ the second treats the solvent environment explicitly.¹⁹ We will give a brief overview of both methods in the following.

In the dynamic continuum ansatz, Stokes' law is employed to calculate a decelerating force which acts on the wave packet. Thereto, the dynamic viscosity of the solvent η together with the expectation value of velocity $⟨v(t)⟩$ of the wave packet and an effective radius R_eff are needed

$$F_0(t)=-6\pi \eta R_{\text{eff}}⟨v(t)⟩.$$ (5)

R_eff takes into account the different masses and radii of the generated fragments. To guarantee a deceleration of the wave packet only in an area where the solvent cavity is deformed, the actual decelerating force F_dec(r, t) is obtained by multiplication of F₀(t) with a sigmoid shape function. It was fitted to the course of the cavity surface area along the major bond cleavage coordinate r_C1P. Finally, an integration of F_dec(r_C1P, t) over r_C1P yields the solvent potential V_solv,

$$V_{\text{solv}}(r_{\mathrm{C}1\mathrm{P}},t)={\int }_0^{r_{\mathrm{C}1\mathrm{P}}}{F}_{\text{dec}}(r_{\mathrm{C}1\mathrm{P}}^{\prime },t)d{r}_{\mathrm{C}1\mathrm{P}}^{\prime }.$$ (6)

In addition to the usual spatial dependence of a potential, V_solv(r_C1P, t) is time-dependent. This is due to the time-dependence of the expectation value of velocity $⟨v(t)⟩$ and describes the deceleration decrease with reducing velocity. For a more detailed description, see Ref. 18.

The second method, the QD/MD approach, combines QD calculations with molecular dynamics (MD) simulations of the solvent environment.¹⁹ Randomly selected snapshots from the MD trajectories give an averaged picture of the atomistic solvent surrounding of the reactant. The solvent potential V_solv is calculated for each snapshot individually. It contains the quantum chemically calculated interaction energy E_sf between each of the two fragments and each solvent molecule

$$V_{\text{solv}}(r_{\mathrm{C}1\mathrm{P}},\varphi )=\sum _{i=1}^{N_{\text{solv}}}\sum _{j=1}^{N_{\text{frag}}}{E}_{\text{sf}}(q_1^{\mathit{i}\mathit{j}},q_2^{\mathit{i}\mathit{j}},q_3^{\mathit{i}\mathit{j}},\dots ,q_6^{\mathit{i}\mathit{j}}),$$ (7)

with N_frag and N_solv being the number of fragments and solvent molecules, respectively. For each thus obtained V_solv, a QD simulation is conducted. The average of all wave packet propagations describes the effect of the solvent environment. More details to the QD/MD approach can be found in Ref. 19.

Here, we want to focus on the results obtained with the dynamic continuum ansatz. Acetonitrile is used as solvent with its dynamic viscosity of η = 0.343 mPas at 25 °C. But first of all, let us take a look at the bond cleavage process in the molecular potential without taking the solvent into account. Fig. 10(a) shows the S₁ PES together with snapshots from different QD simulations. The snapshots depicted by the dark gray and the black isolines are obtained by a QD simulation using only the molecular potential. They are taken 170 fs (dark gray) and 290 fs (black) after the wave packet started in the FC region. Obviously, the wave packet misses the CoIn as the initial gain of momentum in the r_C1P direction is too large to be compensated by the comparably small gradient toward the CoIn. Thus, the system dissociates in the first excited state, and radical pairs are generated.¹⁸ This is in clear contrast to the experimental observations in solution where Ph₂CH⁺ cations are the main product.⁴

FIG. 10.

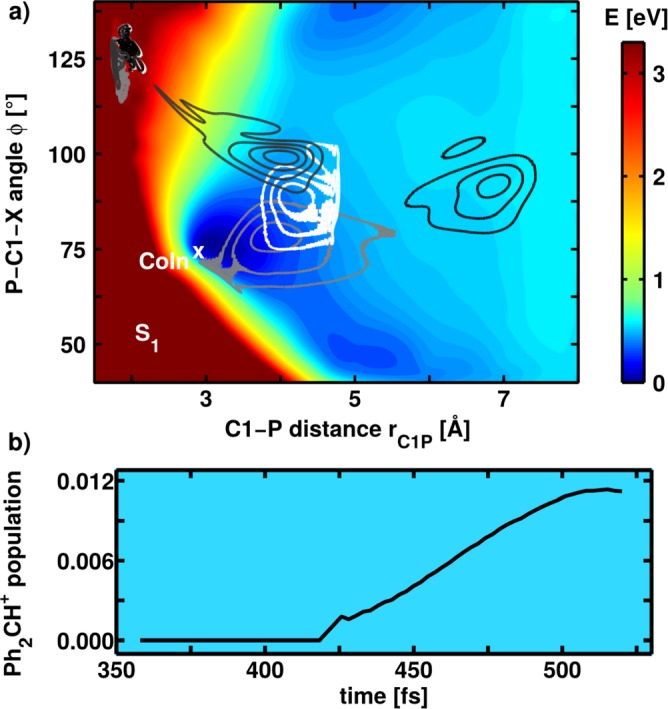
(a) Potential energy surface of the S₁ state of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ calculated at the ONIOM level of theory. The S₀ minimum is located at r_C1P = 1.87 Å and $\varphi =125°$. In addition, snapshots from two different wave packet propagations are shown: The dark gray and black isolines depict wave packets from a normal propagation taken at 170 fs (dark gray) and 290 fs (black) after starting in the FC region. The white and light gray isolines display wave packets from a QD simulation with the dynamic continuum ansatz. They are taken at 290 fs (white) and 390 fs (light gray) after starting in the FC region. (b) Population of the S₀ state which evolves toward larger r_C1P values after coupling through the CoIn finally leading to Ph₂CH⁺ cation generation.

Fig. 10(a) displays two additional wave packet snapshots obtained from a propagation with the dynamic continuum ansatz. The snapshots are taken at 290 fs (white isolines) and 390 fs (light gray isolines) after starting in the FC region. The white isolines show the wave packet after the same propagation time as the black isolines for the QD simulation without the solvent potential. It is clearly visible that the motion along r_C1P is decelerated due to the solvent surrounding. Thus, the wave packet can experience the small gradient toward the CoIn and approaches it after approximately 390 fs. Here, the S₁ population can relax to the ground state where finally the formation of the experimentally observed Ph₂CH⁺ cations takes place. Fig. 10(b) shows the rise of the Ph₂CH⁺ cation population in the ground state after transfer through the S₁/S₀ CoIn calculated in the adiabatic picture.¹⁸ The population rise between 400 and 500 fs compares well with the experimentally observed initial rise of the cation absorption signal.⁴

IV. SUMMARY

We theoretically investigated the initial bond cleavage process in two Ph₂CH derivatives, namely, Ph₂CH–Cl and ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$. By means of quantum chemical calculations, we first identified the individual molecular features of both precursors, which are clearly depending on the LG. Based on the knowledge of the important stationary points, we calculated PESs at the ONIOM level of theory and performed two-dimensional QD simulations.

The lowest excited state of both molecules is characterized by a local π-π* excitation on one phenyl ring. In the case of Ph₂CH–Cl, it is located on the Ph₂CH moiety; in the case of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$ on the LG. These local ππ* S₁ states initiate the bond cleavage. We showed that for Ph₂CH–Cl the Cl lone pairs have a decisive impact on the molecular features in the FC region. Two successive CoIns determine the product formation at a very early stage of the bond cleavage. The first CoIn is a three-state CoIn which includes the lone pair states and opens the homolytic reaction channel, resulting in the formation of ${\text{Ph}}_2{\text{CH}}^{•}+{\text{Cl}}^{•}$. The second CoIn—this time a two-state CoIn—occurs at a slightly elongated C1-Cl distance and leads to the heterolytic channel with Ph₂CH⁺+ Cl⁻. QD simulations on the diabatic PESs reveal an extremely fast and efficient formation of ${\text{Ph}}_2{\text{CH}}^{•}+{\text{Cl}}^{•}$ within 67 fs. This delay time is in very good agreement with the observed 76 fs.²¹ The ion pair formation takes place on a slightly longer time scale of 143 fs compared to the experimental value of 124 fs and is like in the experiment the minor product channel. Our QD simulation shows the key role of the three-state CoIn seam during the photoinduced bond cleavage of Ph₂CH–Cl and compares well with the experiment.

Changing the LG to ${\text{PPh}}_3^{+}$ results in significantly different molecular features. As the LG does not possess any lone pairs, the corresponding states being decisive in Ph₂CH–Cl do not exist. Instead, we localized a two-state CoIn at longer C1-P distance far beyond the FC-region which connects both reaction channels. QD simulations for the isolated molecule show that the wave packet misses the CoIn and dissociates in the S₁ state which has homolytic character. Thus, radical pairs are generated which is in contrast to the experimentally observed formation of Ph₂CH⁺ cations.⁴ Only if the dynamic solvent effects are taken into account which lead to a deceleration of the wave packet during dissociation, the molecular system can follow the slight gradient toward the CoIn and reaches it after approximately 390 fs. Here, the S₁ population can relax to the ground state which has heterolytic character in the dissociation limit. The simulated onset of the Ph₂CH⁺ population is in accordance with the initial rise of the Ph₂CH⁺ absorption signal in the experiment.⁴

In a simplistic concept of photoinduced bond cleavage, the LG has just the function to leave the precursor and form a fragment, which is as stable as possible in the desired product channel. Our results impressively demonstrate that changing the LG may introduce far more extensive changes of the molecular features which set the stage for the bond cleavage process. In the presented cases of Ph₂CH–Cl and ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, the LG controls the position of the CoIns which decide the branching for the product formation. Furthermore, the delay time until the products are formed also depends on the spatial and energetic position of the CoIns. In addition, the LG influences the environmental impact on the reaction. In the case of ${\text{Ph}}_2\text{CH}-{\text{PPh}}_3^{+}$, the solvent cage decelerates the wave packet on the sub-picosecond time scale, and only thus enables a coupling through the CoIn to form the Ph₂CH⁺ cations. The influence of the solvent environment occurs on a longer time scale for Ph₂CH–Cl. Here, an electron transfer subsequent to the initial bond cleavage described in the present work leads to Ph₂CH⁺ generation. This electron transfer is strongly depending on the polarity of the solvent. Changing the LG of Ph₂CH derivatives from neutral to charged does not only modify the stability of the isolated fragments after bond cleavage, it also alters the molecular response and reaction outcome on the femtosecond time scale. Thus, a minor chemical change leads to a substantial change in the femtochemistry of the system.