Multiscale modeling and simulation of brain blood flow

Abstract

The aim of this work is to present an overview of recent advances in multi-scale modeling of brain blood flow. In particular, we present some approaches that enable the in silico study of multi-scale and multi-physics phenomena in the cerebral vasculature. We discuss the formulation of continuum and atomistic modeling approaches, present a consistent framework for their concurrent coupling, and list some of the challenges that one needs to overcome in achieving a seamless and scalable integration of heterogeneous numerical solvers. The effectiveness of the proposed framework is demonstrated in a realistic case involving modeling the thrombus formation process taking place on the wall of a patient-specific cerebral aneurysm. This highlights the ability of multi-scale algorithms to resolve important biophysical processes that span several spatial and temporal scales, potentially yielding new insight into the key aspects of brain blood flow in health and disease. Finally, we discuss open questions in multi-scale modeling and emerging topics of future research.

I. INTRODUCTION

As outlined in the BRAIN 2025 initiative,¹ “the human brain is the source of our thoughts, emotions, perceptions, actions, and memories; it confers on us the abilities that make us human, while simultaneously making each one of us unique.” Although it weights less than 2% of a humans body weight, it receives about 20% of the resting cardiac output of blood and 25% of the body’s oxygen supply. While many biological aspects have been studied systematically, surprisingly less effort has been put into studying blood flow patterns within the brain, let alone their interaction with key biophysical mechanisms (e.g., coupling to astrocytes and neurons — the so-called neuro-vascular coupling — or the formation of thrombus in cerebral aneurysms).

Interactions of blood flow in the human brain occur between different scales, determined by flow features in the large arteries of the macrovascular network (MaN, diameter of 0.5 mm or larger), the smaller arteries and arterioles of the mesovascular network (MeN, 500 μm to 10 μm), and the capillaries of the microvasculature (MiN, mean diameter of 5 μm), all being coupled to cellular and sub-cellular biological processes. Understanding such multi-scale phenomena is a matter of critical relevance to the clinical evolution of life threatening conditions such as cerebral aneurysms, sickle cell anemia, and malaria.^2–4 Such pathologies are affected by the global blood circulation as well as by the local microrheology. For instance, the blood flow may be Newtonian or non-Newtonian depending on the scale.⁵ In addition to the multi-scale nature of the underlying physics, the complexity in geometry also plays an important role, thus necessitating a patient-specific modeling approach. For example, Fig. 1 illustrates the complex geometry including possible anatomical abnormalities in the human Circle of Willis (CoW) — a mechanism that can potentially supply oxygen to any area of the brain if one or more of the supply trunks are interrupted.⁶ Such abnormalities are not uncommon, affecting up to 50% of the population according to Lippert and Pabst.⁷ Although generic/consensus geometries⁸ representing healthy or pathological configurations can be very useful in practice for performing systematic studies and understanding the main characteristics of a pathology, for certain cases, such as the cerebral aneurysms considered in this work, using a patient-specific geometry is of crucial importance. In such cases, the complex geometry (curvature, tortuosity, etc.) is known to directly affect the flow patterns, the resulting wall shear stresses and displacements, and, consequently, the onset and evolution of the pathology. Several studies^8–10 have demonstrated this high sensitivity of the flow field on geometry, and in the particular case of cerebral aneurysms, this can lead to developments of inherently different nature (e.g., fusiform vs saccular aneurysms¹⁰).

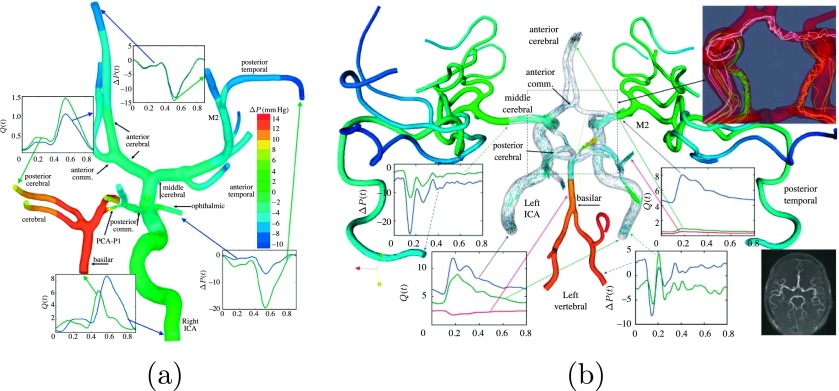
FIG. 1.

Simulation of the human intracranial arterial tree: (a) Brain blood flow simulation in an incomplete CoW of a patient with hydrocephalus: geometrical model of 23 cranial arteries.⁶ (b) Brain blood flow simulation in complete CoW: geometrical model of 65 cranial arteries.⁶ Colors represent pressure, arrows represent velocity fields, plots depict the flow rate in ml/s and pressure drop in mm Hg, where the reference pressure is the average pressure at the internal carotid artery (inlet). Top right: instantaneous streamlines showing complex swirling flow in communicating arteries. Bottom right: MRA image of the cranial arterial system. Reprinted with permission from Grinberg et al., “Simulation of the human intracranial arterial tree,” Philos. Trans. R. Soc., A 367, 2371–2386 (2009). Copyright 2009 Royal Society Publishing.

Putting it all together, the development of physiologically accurate computational models in complex geometries requires the coupling of disparate spatial and temporal scales often governed by diverse mathematical descriptions, e.g., deterministic partial differential equations (PDEs) for continuum mechanics and stochastic ordinary differential equations for discrete particle dynamics (see Fig. 2). Consequently, modeling blood flow as a patient-specific multi-scale phenomenon using coupled continuum-atomistic models is essential to better understand key biophysical and biochemical processes in health and disease (e.g., thrombus formation in aneurysms¹¹ and vaso-occlusion in sickle cell anemia³).

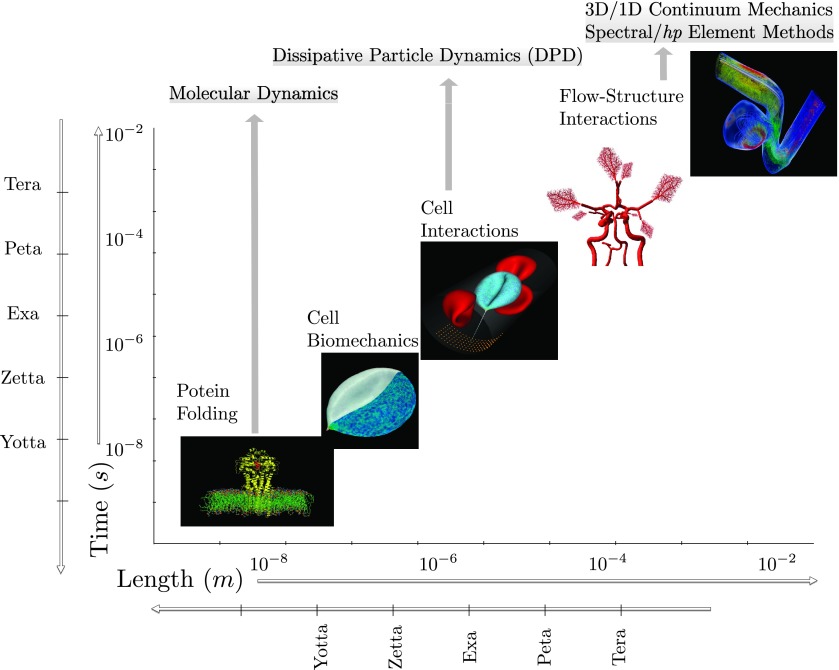
FIG. 2.

Multi-scale modeling of the brain vasculature: A cascade of spatial and temporal scales governing key biophysical mechanisms in brain blood flow requires effective multi-scale modeling and simulation techniques. A suggestive, yet non-exhaustive, list of modeling approaches is provided for each spatial/temporal regime, showing how an increase in computational demands is inevitable as one pursues an integrated resolution of interactions in finer and finer scales.

Multi-scale modeling and simulation of blood flow give rise to several challenges. First, it requires the derivation of mathematical models which are able to accurately predict physiological processes. Second, it demands the design of robust interface conditions required to integrate the continuum and atomistic simulations. Third, it inherently involves the processing of non-stationary data from atomistic simulations. The fourth challenge is a computational one. In particular, billions of degrees of freedom are required to accurately resolve the micro-scale and also the interaction between the blood cells and endothelial cells in a volume as small as 1 mm³. Simulating effects of small scales on the larger scales requires increased local resolution in the discretization of computational domain within the continuum description. For example, clot formation starts from aggregation of individual platelets and the clot must grow to a certain size before affecting the large scale flow dynamics. However, to accurately capture the clot geometry and its shedding off thrombi, very high local resolution is required. Moreover, to follow the detached clot segments, an adaptive local mesh refinement must be used.

In what follows, we present an overview of some multi-scale methods that aim to address the aforementioned challenges. Specifically, first we discuss modeling approaches focusing on resolving blood flow dynamics at the macro-vascular, meso-vascular, and micro-vascular regimes. Then, we will present coupling strategies for constructing multi-scale models in patient-specific geometries and set the foundations towards establishing an integrated framework for seamlessly modeling blood flow and arterial wall mechanics at different scales. Finally, we conclude with a discussion on open questions in multi-scale modeling and outline some emerging topics of future research.

II. METHODS

A. Macro-scale models

1. MaN — Computational aspects

The MaN hemodynamics and fluid-structure interactions (FSIs) are governed by the 3D, unsteady, incompressible Navier-Stokes equations, coupled to the 3D elastodynamic equations.¹² Given proper initial conditions and boundary conditions, we can compute the velocity and pressure fields of the fluid domain along with the structural displacements and corresponding stresses in the arterial wall. At the macro-scale regime, blood predominately behaves as a Newtonian fluid, while the arterial wall constitutive law may be represented by linear elastic, hyper-elastic, or Mooney-Rivlin materials.¹³ More recent developments have included anisotropic constitutive laws¹⁴ and fractional-order viscoelasticity.¹⁵ The fluid and solid domains are coupled through kinematic and dynamics boundary condition at the interface under the arbitrary Lagrangian-Eulerian (ALE) framework,¹² ensuring continuity of velocity and traction forces at the fluid-solid interface.

Over the years, a multitude of different numerical schemes for FSI problems have been proposed.^{12,14,16–20} They can be generally classified as either monolithic or partitioned approaches. In monolithic solvers, the fluid and structure equations are solved simultaneously as a large nonlinear system. This approach features favorable numerical stability properties since it automatically ensures energy balance between the fluid and structure at each time step.¹⁶ On the other hand, in partitioned FSI approaches, the governing system of equations is split into separate fluid and structure solves, thus promoting software modularity and scalability to large-scale parallel computing environments.^19–21 Moreover, numerical stability issues can be overcome by strategies based on fixed-point iterations and Aitken relaxation, leading to stable coupling schemes even for small mass ratios — a common problem in FSI simulations.^19,20

Simulations presented in this work have been performed using our research spectral/hp-element solver NekTar.^13,19–24 For a detailed exposition to the numerical methods and implementational aspects of this work, the reader is referred to the bibliography. Finally, we note that one way to scale macro-scale methods to extremely large problems results by applying the multi-patch domain decomposition introduced by Grinberg and Karniadakis,²⁵ where a large domain is divided into a series of loosely coupled overlapping subdomains (patches) of manageable size. In this setting, the continuum solver is employed within each sub-domain independently over non-overlapping processor groups (sub-communicators). Solution continuity at the sub-domain interfaces is obtained via properly formulated inter-patch conditions.²⁵ This non-intrusive approach is general and results in parallel efficiency of more than 90%.²⁶

2. MaN — Physical aspects

Geometrical complexity in conjunction with physiological aspects (e.g., atherosclerotic plaques) not only can give rise to complex swirling flow patterns but may also trigger flow instabilities and transition to turbulence. This, in turn, may cause significant variations in the magnitude and distribution of wall shear stresses, arterial wall displacements, and eventually help trigger or suppress the evolution of certain pathologies. To this end, 3D-FSI simulations can help elucidate key physical aspects of blood circulation in the larger brain arteries. Examples of such computational studies include analyzing transition to turbulence in stenosed carotid arteries^27,28 and flow instabilities in cerebral aneurysms.²

Figure 3 illustrates the complexity of flow patterns encountered in cranial arterial networks as revealed by high-fidelity 3D-FSI simulations. In particular, Fig. 3(a) shows the computed flow field in a patient-specific circle of Willis topology. It is evident that the complexity of the geometry leads to complex vortical flows. A detailed resolution of the flow is critical for accurately predicting derived quantities such as the wall shear stress distribution on the arterial wall. The latter is known to play a key role in the onset and subsequent evolution of certain brain pathologies, such as cerebral aneurysms.² Figure 3(b) reveals the intricate interplay between blood flow and the induced stresses inside the tissue of a saccular aneurysm, shedding light on the factors that may contribute to an eventual rupture.^20,29

FIG. 3.

Complexity of flow patterns and stresses in cranial arterial trees: (a) Illustration of the highly vortical flow patterns predicted by high-fidelity Navier-Stokes simulations in a patient-specific circle of Willis topology.⁶ (b) Flow patterns and resulting mechanical stresses inside a compliant patient-specific cerebral aneurysm resulting from 3D-FSI simulations.^20,29 Reprinted with permission from Grinberg et al., “Simulation of the human intracranial arterial tree,” Philos. Trans. R. Soc., A 367, 2371–2386 (2009). Copyright 2009 Royal Society Publishing and Perdikaris et al., “Visualizing multiphysics, fluid-structure interaction phenomena in intracranial aneuryms,” Parallel Comput. (published online). Copyright 2015 Elsevier B.V.

B. Meso-scale models

1. MeN — Computational aspects

Advances in macro-scale blood flow modeling have enabled detailed, high-fidelity, patient-specific 3D-FSI simulations in large arterial topologies, consisting of tens to hundreds of arterial segments obtained by medical imaging.^6,30,31 However, any attempt to model the entire brain circulation ($\mathcal{O}\left(10^6\right)$ arteries and arterioles) using such approach is prohibited by the enormous number of degrees of freedom to be resolved ($\mathcal{O}\left(10^9\right)$ per variable). To bridge this gap one may employ reduced-order representations of the so-called sub-pixel vasculature, accounting for flow dynamics using 1D blood flow models.

1D blood flow models have been used extensively in recent years due to their low computational cost and ability to accurately capture the most significant features of pulse wave propagation in the systemic arterial system. Their predictions have been successfully validated against clinical measurements,³² as well as high-fidelity 3D-FSI simulations.^33,34 Deriving such models can be achieved by reducing the dimensionality of the full Navier-Stokes system under the assumptions of axial symmetry, negligible longitudinal displacements, constant pressure along each section, absence of external body forces and dominance of the axial velocity component.^12,35 This results in a nonlinear system of hyperbolic PDEs that governs the time-evolution of the unknown axial velocity and cross-sectional area displacements in each compliant arterial segment.^12,35 This system can be accurately and efficiently solved using numerical schemes for hyperbolic conservation laws, such as discontinuous Galerkin discretizations.^12,35 Moreover, the 1D formulation can easily accommodate complex constitutive laws, allowing one to account for non-Newtonian flow effects,³⁶ viscoelastic energy dissipation in the arterial wall,¹⁵ as well as oxygen transport phenomena.³⁷

Despite their simplifications, 1D models have provided a robust tool for estimating flow properties and studying problems that either cannot be addressed in vivo or are too computationally expensive to be resolved in three dimensions. In the context of this study, we exploit their low cost and scalability to simulate blood flow in massive arterial trees of the meso-vascular regime (radii 500 μm to 10 μm, see Fig. 5).³⁶ Due to their size and complexity, the topology of such meso-vascular 1D networks cannot be patient-specific. However, the findings of Zamir³⁸ suggest that arteries and arterioles in this regime exhibit a self-similar structure, and certain fractal laws have been proposed to mimic the arterial branching patterns, thus allowing the generation of such trees in silico. As we will describe in Sec. II D 1, this construction can be used as a closure model for truncated 3D arterial domains, leading to coupled, geometrically heterogeneous blood flow solvers that can simulate dynamics throughout the entire systemic circulation at scales where the continuum hypothesis still holds. To account for the effect of smaller scales, one needs to switch to a different modeling approach and employing the micro-scale models described in Sec. II C.

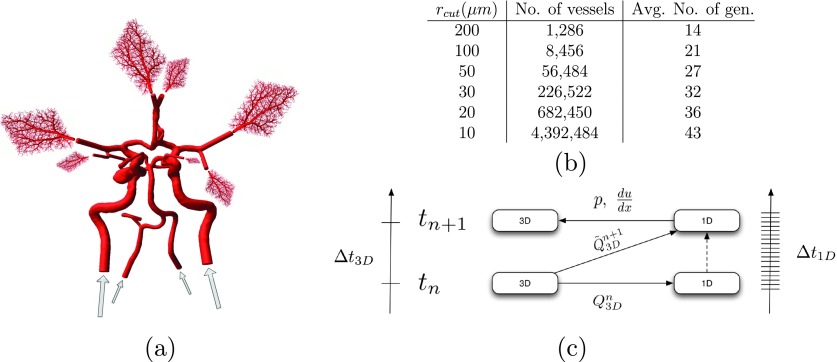
FIG. 5.

MaN-MeN coupling: (a) Flow dynamics in the meso-vascular regime are modeled using nonlinear 1D blood flow models in fractal arterial trees attached to each of the terminal vessels of the parent, patient-specific 3D domain.³⁶ (b) Total number of arteries in the resulting MaN-MeN topology as a function of the cut-off radius r_cut of the fractal trees.³⁶ (c) Exchanged quantities at the MaN-MeN interface and asynchronous time-stepping communication (Δt_3D: time step size of the 3D-FSI solver, Δt_1D: time step size of the 1D-FSI solver, $Q_{3D}^n$: flow-rate at the 3D outlet at time step n, ${\tilde{Q}}_{3D}^{n+1}$: extrapolated flow-rate at the 3D outlet, p: total pressure at the 1D inlet at time step n + 1, $\frac{du}{dx}$: velocity gradient at the 1D inlet at time step n + 1). Reprinted with permission from P. Perdikaris, L. Grinberg, and G. E. Karniadakis, “An effective fractal-tree closure model for simulating blood flow in large arterial networks,” Ann. Biomed. Eng. 43, 1432–1442 (2014). Copyright 2014 Springer.

2. MeN — Physical aspects

So far, we have introduced 1D models in the context of multi-scale modeling as a computationally efficient tool that helps us bridge the spatial gap and resolve blood flow from large arteries to small arterioles and capillaries. However, we must stress that 1D models can provide a robust stand-alone predictive tool for pulse wave propagation in arterial trees. This is of significant value in physiological situations and pathologies of major clinical interest for which local details in flow are not important. An example of such cases is isolated systolic hypertension, which results from the interaction between the pumping heart and the arterial system (load) and in which augmented pressure wave reflections due to arterial stiffening with age are thought to be important determinants.³⁹ In general, 1D models offer an inexpensive and relatively accurate way of computing pressure and flow distributions across the arterial tree, thus creating an effective tool for diagnostics and planning of treatment.

C. Micro-scale models

1. MiN — Computational aspects

Modeling of blood flow dynamics at the atomistic/mesoscopic scale is commonly addressed using Lagrangian particle methods. At the microscopic level, stochastic molecular dynamics models⁵ are employed, while for mesoscopic simulations one needs to introduce a proper coarse-graining strategy.^5,40 Here, we present a brief overview of the dissipative particle dynamics (DPD) method, aiming to highlight the key features of this modeling approach. For a detailed presentation, the reader is referred to the related references.^5,40–43

In general, a DPD system is represented by N particles, each one of them representing a collection of molecules, with particle interactions being enabled through pairwise conservative, dissipative, and random forces. The random and dissipative forces form a thermostat and must satisfy the fluctuation-dissipation theorem.⁵ The motion of DPD particles is governed by Newton’s law in fixed non-periodic domains, where the fluid is represented by a collection of solvent particles with a number of suspended particles, such as platelets, red blood cells (RBCs), and proteins. The domain boundaries are endowed with appropriate boundary conditions that represent no-slip solid walls and inflow/outflow particle fluxes through imposing effective boundary forces.^44,45 Leveraging the capacity of modern GPU accelerators, DPD codes have been recently scaled to problems involving hundreds of millions of particles.⁴⁶

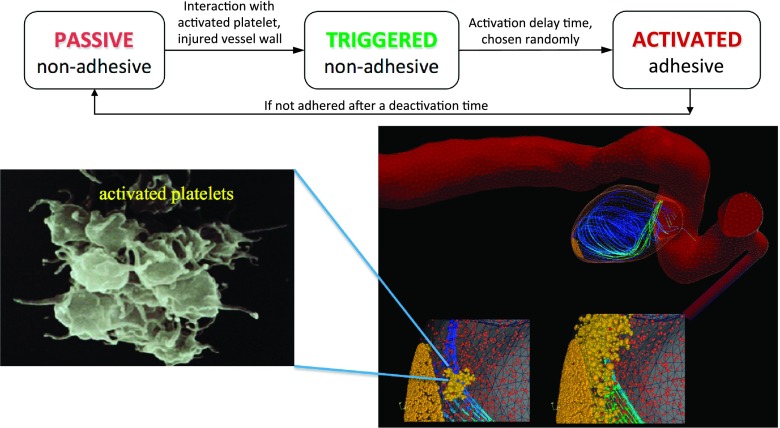
Of particular interest to our presentation is the work of Pivkin et al.⁴⁷ that elaborates on modeling platelet activation during the formation and growth of thrombi. The authors propose a model involving three different biological states in platelet behavior: passive, triggered, and activated (see Fig. 4). In the passive state, platelets are not adhesive, which is a normal state of the platelets in blood. If a passive platelet interacts with an injured wall or an activated platelet, it becomes triggered and after an activation delay time it becomes activated and adhesive. The activation delay time is chosen uniformly at random from a specified range. If after a finite recovery time an activated platelet does not adhere to anything it returns back to a passive state.⁴⁷ In Sec. II D 2, we will describe how such misco-scale models can be coupled to continuum formulations and provide a demonstration of multi-scale simulations of thrombi formation in a patient-specific brain aneurysm.

FIG. 4.

DPD simulations of thrombus formation and growth. Top: Schematic representation of the platelet activation model put forth by Pivkin et al.⁴⁷ Bottom: DPD simulation of platelet deposition and aggregation on an aneurysm wall. Reprinted with permission from I. V. Pivkin, P. D. Richardson, and G. E. Karniadakis, “Blood flow velocity effects and role of activation delay time on growth and form of platelet thrombi,” Proc. Natl. Acad. Sci. U. S. A. 103, 17164–17169 (2006). Copyright 2006 National Academy of Sciences.

2. MiN — Physical aspects

DPD provides a computational tool that is based on first principles and enables modeling of fluids and soft matter at regimes where the continuum hypothesis fails. Particular applications include the modeling of proteins, RBCs, plasma, and, more recently, the micro-structure of arterial walls.⁴⁸ DPD models essentially provide a platform for integrating single cell behavior and cross-cell interactions into a predictive tool for bulk rheology and micro-scale biomechanics. The physical insights gained by employing such models have proven to be very diverse, with recent research highlights including the in silico prediction of human blood viscosity,⁴⁹ the unveiling of the flow mechanics triggering vaso-occlusion in sickle cell anemia,³ and the quantification of the biophysical characteristics of red blood cell microcirculation in malaria.⁴

D. Multi-scale coupling

Scales are integrated through designing appropriate interface conditions between the heterogeneous solvers. The interface conditions are derived to respect the physical conservation constraints and the requirements of each solver. Specifically, mass conservation is of primary importance, while momentum and energy conservation are desirable but present several challenges, with the latter being nearly impossible in practice. Interface conditions are concurrently enforced by constructing appropriate projection, interpolation, de-noising, and statistical moment matching techniques that aim to transfer information across the different domains in a compatible way with the requirements and data format of each solver. In particular, domain decomposition is performed either using overlapping interfaces or embedded sub-domains. While the former choice is preferable, it is practically intractable as the resources required to resolve the full aneurysm sac using mesoscopic DPD simulations were beyond our computing capabilities. To alleviate this limitation, in this study, we have adopted the approach of simulating the full geometry using continuum 3D solvers, while embedding small atomistic sub-domains in areas of increased interest (e.g., inside the sac of a cerebral aneurysm). In what follows, we provide an outline of this multi-scale “message passing” between each one of MaN-MeN, MaN-MiN, and MeN-MiN interfaces.

1. MaN-MeN

As described in Sec. II B, we aim to use nonlinear 1D blood flow solvers in fractal mesovascular arterial trees as closure models for truncated patient-specific 3D domains.³⁶ A schematic representation of this construction is given in Fig. 5(a) where generated 1D fractal trees are coupled to each one of the terminal outlets of a patient-specific cranial arterial network obtained by medical imaging. The topology of the fractal trees is controlled by the parametrization of the self-similarity laws that govern their branching patterns, while their size is predominately controlled by a cut-off threshold for the radius of their terminal branches. The table of Fig. 5(b) gives an indication of the total size of the resulting MaN-MeN topology once the fractal trees have been attached to each of the 21 outlets of the parent, patient-specific domain shown in Fig. 5(a). Fast 1D blood flow simulations in such massive fractal trees are enabled by scaling up 1D solvers to modern parallel computer architectures.³⁶

The goal of the MaN-MeN coupling is three-fold. First, it aims to provide physiologically correct outflow boundary conditions to the truncated 3D continuum domain. Second, it aims to model oxygen transport and diffusion in the brain tissue. Finally, it provides a way to bridge the gap in spatial scales between blood flow in patient-specific 3D networks of large cerebral arteries and the microcirculation in small arterioles and the capillary network.

The coupling of 3D and 1D continuum domains requires interface conditions ensuring the continuity of mass flow and total pressure. A detailed discussion on such interface conditions, including the well-posedness and stability of the resulting system, has been given in Refs. 50–54. Since 1D dynamics are governed by a hyperbolic system of PDEs, the 1D-FSI solver of each fractal tree can only admit a single boundary constraint, which is typically the averaged mass flow computed at the outlet of the parent 3D domain (see Fig. 5(c)). In return, each 1D-FSI solver provides the pressure, velocity flux, and cross area displacement at the inlet of its fractal tree, to be inscribed as outflow boundary conditions at the corresponding outlet of the parent 3D domain. The wave propagation nature of the 1D solver typically leads to a more pronounced Courant-Friedrichs-Lewy stability restriction²² in time-stepping size compared to the one corresponding to the 3D solver. Since this mandates each solver to march in time with a different time step, we need to devise an asynchronous communication pattern that synchronizes the solution between the two solvers accordingly (see Fig. 5(c)). Finally, we note that strong coupling between the 3D and 1D domains may result either from an implicit monolithic solving approach⁵⁵ or by explicitly coupling different modular solvers by means of sub-iterations.⁵³

2. MaN-MiN

Coupling of atomistic and continuum solvers requires the calculation and communication of averaged properties, such as fluid velocity and density, across heterogeneous solver interfaces. First, one needs to perform a proper non-dimensionalization of the corresponding time and length scales of each solver to ensure consistency in the non-dimensional numbers that characterize the flow (e.g., the Reynolds number). Then, interface conditions should be derived to respect the requirements of each solver. For example, atomistic solvers require a local velocity flux to be imposed at each cell of the atomistic domain. This is achieved though constructing appropriate interpolation and projection operators that are capable of mapping the continuum velocity field onto the atomistic domain (see continuum to atomistic, C2A, operators in Figure 7). Specifically, to enforce mass conservation, the continuum solver computes the fluxes through the surface interfaces with the DPD domains, and particles as inserted in the DPD domain in such a way that these fluxes are preserved, and the velocity vector of the DPD particles corresponds to the velocity sampled in the continuum solver.

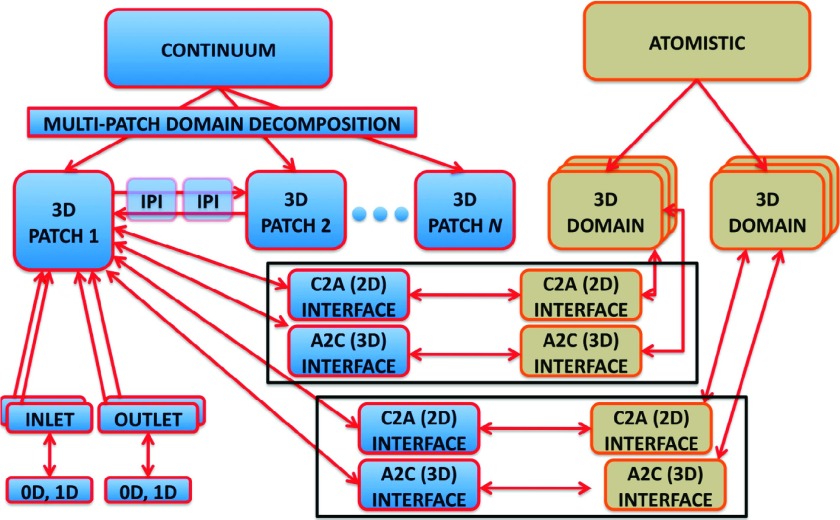
FIG. 7.

Multi-scale coupling of continuum and atomistic solvers: Functional task decomposition between the tightly coupled continuum and atomistic solvers.¹¹ The continuum domain is partitioned into overlapping patches and the patches exchange data via inter-patch communicators. Each patch may have multiple inlets and outlets and may be connected to 1D fractal tree models in order to model boundary conditions for inlets/outlets. Atomistic domains are embedded inside the continuum. Each can be replicated several times to reduce statistical error. Communication between the continuum and atomistic domains is performed consistently through appropriate projection, interpolation, and filtering routines in the continuum to atomistic (C2A) and atomistic to continuum (A2C) operators.¹¹ Reprinted with permission from L. Grinberg, D. A. Fedosov, and G. E. Karniadakis, “Parallel multiscale simulations of a brain aneurysm,” J. Comput. Phys. 244, 131–147 (2013). Copyright 2013 Elsevier B.V.

Similarly, the continuum solver requires the geometrical representation of moving boundaries and flow “obstacles” arising due to aggregation of atomistic particles (e.g., thrombus formation)¹¹ (see Fig. 6). Calculating flow around a growing thrombus presents new challenges. The obstacle is defined by thresholding the activated platelets density, volumes with relatively high density represent the blood clot. Moreover, the clot geometry and speed vary over time. To avoid forming new body fitted grid, the “smooth profile method” (SPM)⁵⁶ has been employed to model moving surfaces within a fixed computational grid. This immersive-type boundary technique is appropriate for spectral methods and uses a scalar “indicator function” that equals 1 inside the moving domain and 0 outside.

FIG. 6.

Multi-scale coupling of continuum and atomistic solvers. Top left: Sketch of a continuum arterial domain with an embedded atomistic domain. Top right: Asynchronous time-matching and synchronization of the continuum and atomistic solvers. Bottom: Coupled continuum-atomistic simulation of flow in an arterial segment for Re = 350. A clot is formed by platelet aggregation on the artery wall.¹¹ Reprinted with permission from L. Grinberg, D. A. Fedosov, and G. E. Karniadakis, “Parallel multiscale simulations of a brain aneurysm,” J. Comput. Phys. 244, 131–147 (2013). Copyright 2013 Elsevier B.V.

Accurate computing of averaged fields through processing of non-stationary atomistic data presents several challenges including geometrical complexity of the atomistic domains, thermal fluctuations, and flow unsteadiness. This renders the need of effective averaging and filtering techniques before the data are transmitted to the continuum domains^57,58 (see atomistic to continuum, A2C, operators in Figure 7). In particular, to filter out the stochastic component (thermal fluctuations) at all interfaces with the continuum domain, the Window Proper Orthogonal Decomposition (WPOD) has been employed.^57,58

From the parallel computing perspective, handling coupled simulations at the continuum and atomistic levels requires coupling two parallel solvers, each running on its own set of processors (task decomposition). In Figure 7, we present an overview of the functional and task decomposition strategy employed in the multi-scale scheme put forth by Grinberg et al.¹¹ The scheme combines the multi-patch domain decomposition to enable scaling to extremely large continuum problems,²⁵ with a communication interface for the concurrent coupling of the continuum and atomistic solvers. The operators C2A and A2C take care of all necessary data exchanges between the two solvers at the continuum-atomistic interfaces.

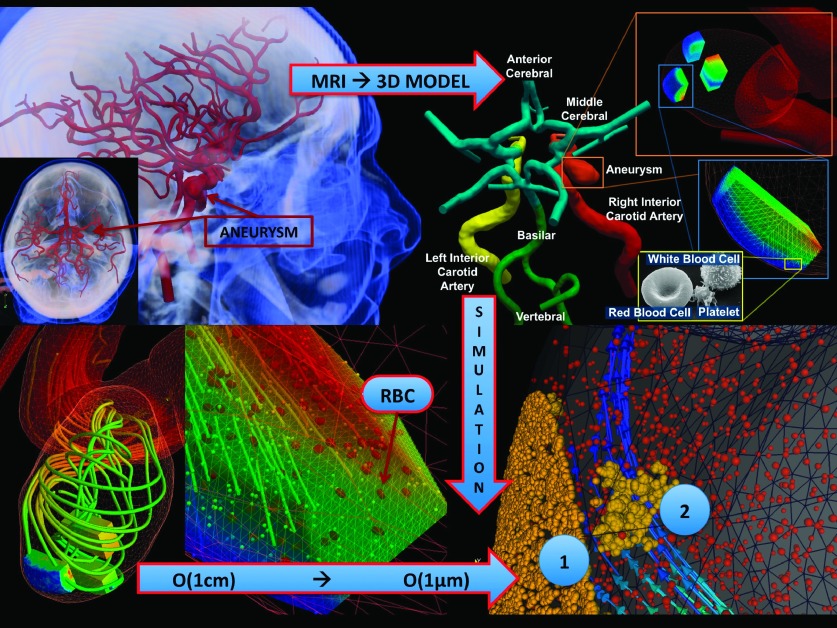
Figure 8 shows a realistic application of multi-scale modeling where a continuum solver is used to accurately compute the flow patterns in a patient-specific intracranial network, whereas the concurrent coupling to embedded atomistic domains aims to resolve local platelet aggregation and possible clot formation inside a cerebral aneurysm.²⁶ The multi-scale simulation of blood clot formation was performed on 32 K nodes of BlueGene/P supercomputer, capable of simulating one cardiac cycle in about 24 h. Each BlueGene/P node was composed of 4 cores, had 2 GB of memory, and was capable to perform 13.6 GFLOPS. The need for such large allocation of computer resources was not due to memory demands, but it was rather targeting to perform a compelling simulation for the purpose of competing for the Gordon Bell award in supercomputing (2011 finalist). Although the BlueGene/P was one of the flagship supercomputers just a few years ago, the next generation of supercomputers available for open-science research⁵⁹ will be $\mathcal{O}\left(100\right)$ times more powerful and will be able to perform similar simulations in just a few minutes.

FIG. 8.

Multi-scale simulation of brain blood flow: Continuum-atomistic simulation of platelet aggregation at the wall of an aneurysm at Re = 394 obtained by coupling NekTar with the atomistic code DPD-LAMMPS.¹¹ The patient-specific geometry was constructed from MRI imaging and contains 3 embedded atomistic domains to resolve the microrheology. Continuum blood flow is computed with O(0.1 mm) resolution and clot formation with O(1 μm) resolution. Yellow dots correspond to active platelets and red dots to inactive platelets. Streamlines depict the instantaneous velocity field. Notice the predicted detachment of small platelet clusters due to shear-flow as the clot formation process progresses in time and space. Reprinted with permission from L. Grinberg, D. A. Fedosov, and G. E. Karniadakis, “Parallel multiscale simulations of a brain aneurysm,” J. Comput. Phys. 244, 131–147 (2013). Copyright 2013 Elsevier B.V.

Before concluding this section, we would like to underline that given the algorithmic complexity of concurrently coupling heterogeneous solvers, most efforts in the literature have been limited to highly specialized, hand-engineered coupling algorithms. To this end, we should highlight the recent efforts by Tang and Karniadakis⁴⁶ to develop solver/scheme-agnostic coupling approaches, allowing for a simple programming interface that can accommodate a large class of heterogeneous solvers in a highly intuitive and scalable fashion.

3. MeN-MiN

The last connecting link towards a full MaN-MeN-MiN multi-scale coupling is the development of proper interface conditions for coupling nonlinear 1D blood flow models to atomistic and mesoscopic particle domains. In the context of this study, the MeN-MiN coupling would serve for connecting the terminal arterioles of the fractal 1D networks to vessels of the capillary bed. This would enable one to study several important biophysical processes in health and disease, such as oxygen transport in the brain tissue⁶⁰ and vaso-occlusion due to sickle cells³ in an integrated manner.

Although to our knowledge no effort to establish a MeN-MiN interface has been reported in the literature, here we underline that such coupling is conceptually much simpler than the MaN-MiN interface described in Sec. II D 2. In particular, the 1D solver can readily pass an averaged axial velocity flux at every terminal outlet, which, given a chosen velocity profile, can be prescribed as an inflow boundary condition to the atomistic arterial domain. Similarly, the averaged pressure at the inlet of the atomistic domain can be computed given the particle velocity and force fields, and be inscribed as a pressure outflow boundary condition at the corresponding terminal vessels of the 1D domain. One question that remains open is the type of boundary conditions to be imposed at the outflow of the atomistic domains, although the recent works of Lykov et al.⁴⁴ and Lei et al.⁴⁵ provide some options.

III. DISCUSSION

Over the last decade, the everlasting growth in computational resources in conjunction with modeling and algorithmic advances has opened new frontiers in the study of multi-scale and multi-physics phenomena. The specific area of modeling blood flow in the human circulation has undergone great growth itself, moving way beyond simulating flow in simple arterial bifurcations, as now we have tackled challenges such as complex patient-specific geometries, fluid-structure interactions, scaling to extremely large problems, as well as modeling multi-physics and multi-scale phenomena. In this paper, we have outlined a number of available methodologies that have been successfully used to study multi-scale interactions for several cases pertaining to pathologies related to brain blood flow. However, despite the tremendous progress, there still exists a number of important open questions to be addressed.

From an application viewpoint, modern multi-scale simulations produce terabytes of high-dimensional and heterogeneous data-sets, yielding the need for scalable data analysis and visualization tools.^29,61 To this end, leveraging progress in statistical learning,⁶² multi-fidelity modeling,⁶³ and bioinformatics techniques⁶⁴ will enable us to meaningfully explore multi-scale cross-correlations and causality in the data. This is essential towards disseminating the insight gained from our simulations and further engaging the medical community in this interdisciplinary effort of bringing multi-scale modeling to the bedside.

As solvers are integrated with more multi-physics/multi-scale capabilities, they inevitably become more algorithmically complex, thus necessitating the design of consistent benchmarking tools to assess model validity, model inadequacy, as well as to quantify the uncertainty associated with our predictions. Although the individual components described in Sec. II (3D-FSI, 1D-FSI, and DPD models) have been thoroughly studied and validated against clinical and experimental data, no similar procedure is known for assessing validity in the multi-scale setting. To our knowledge, this is an open question that has to be addressed in the future. In vitro measurement techniques are not yet capable to offer a multi-scale resolution, and in vivo model validation is currently almost impossible. Moreover, the development of such validation procedures is an inherently interdisciplinary task due to the multi-physics/multi-scale character of the problem. Here, we highlight that recent advances in clinical measurement techniques, such as two-photon microscopy,^65,66 can help extract flow velocity profiles in vivo and potentially provide accurate means of validating the simulated flow predictions at different spatial scales (see Fig. 9).

FIG. 9.

In vivo two-photon excited fluorescence imaging of vascular topology and cerebral blood flow during the cardiac cycle: (a) and (c) Low-magnification image of the fluorescently labeled brain vasculature in an anesthetized mouse. (b) Three-dimensional rendering of the vasculature with the brain surface at the top of the image. (d) Pulsatile red blood cell flow speed across the spatial profile of an arteriole over the cardiac cycle. Reprinted with permission from Santisakultarm et al., “In vivo two-photon excited fluorescence microscopy reveals cardiac-and respiration-dependent pulsatile blood flow in cortical blood vessels in mice,” Am. J. Physiol.: Heart Circ. Physiol. 302, H1367–H1377 (2012). Copyright 2012 American Journal of Physiology — Heart and Circulatory Physiology.

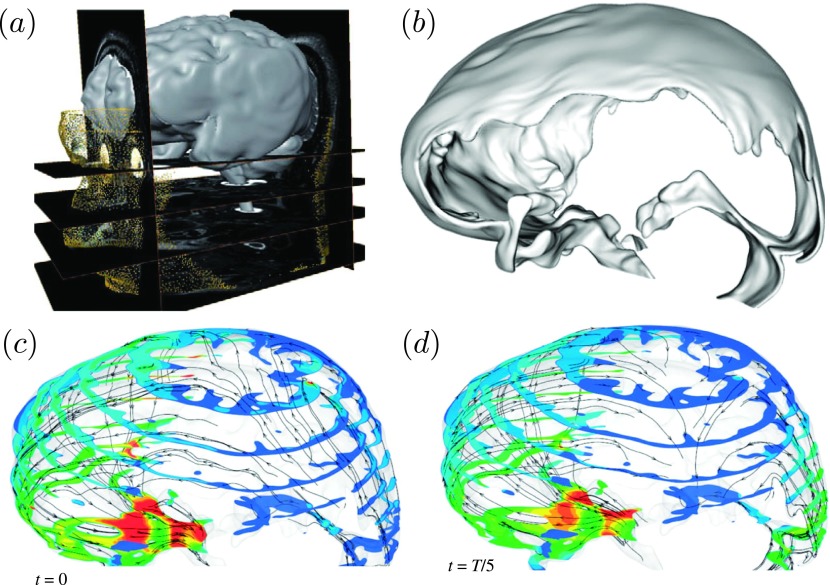
From a modeling viewpoint, several extensions can be pursued to enhance our understanding of different brain pathologies. For example, it is hypothesized that the disruption of cerebrospinal fluid (CSF) flow may be linked to neurodegenerative diseases such as Alzheimer’s disease through disturbed regulation of intracranial pressure, accumulation of toxic metabolites, or through a combination of both.⁶⁷ Computational models have been used to analyze CSF flow in patient-specific topologies of the cranial subarachnoid space (SAS), providing a comparison tool for the transport of metabolites and neuroendocrine substances in healthy and diseased brains^68–71 (see Fig. 10). A multi-scale/multi-physics approach to this problem can offer new insight on the interplay between cranial blood flow and CSF flow, as well as to study the microrheology of CSF absorption through the arachnoid granulations and extra-cranial lymphatic pathways.

FIG. 10.

Cerebrospinal fluid dynamics in the human cranial subarachnoid space: (a) Anatomic MRI images of the cranial space. (b) Rendering of a reconstructed patient-specific cranial SAS. (c) and (d) Computed CSF velocity magnitude contours at cross sections of the cranial SAS at selected points in time within one cardiac cycle. Reprinted with permission from Gupta et al., “Cerebrospinal fluid dynamics in the human cranial subarachnoid space: An overlooked mediator of cerebral disease. I. Computational model,” J. R. Soc., Interface 7, 1195–1204 (2010). Copyright 2010 Royal Society Publishing.

Another exciting direction for future research is aligned with the fact that the cerebral vasculature has been considered not as an isolated system, but as being integrated with the brain system of neurons, astrocytes, and microvessels in a coordinated, interactional, and autoregulating fashion.^71–74 This hypothesis is supported by recent experimental evidence⁷⁵ suggesting the intriguing possibility that information processing in this vast network of $\mathcal{O}\left(10^{11}\right)$ neurons is not limited to neural activity, but could also be influenced by slight modulation in the brain blood flow. Extending our multi-scale modeling capabilities to account for bidirectional neuro-vascular coupling could bring us one step closer to understanding the awe-inspiring functionality of the human brain,¹ as well as to study inherently multi-scale pathologies such as Parkinson’s disease.