Marker-free motion correction in weight-bearing cone-beam CT of the knee joint

Abstract

Purpose:

To allow for a purely image-based motion estimation and compensation in weight-bearing cone-beam computed tomography of the knee joint.

Methods:

Weight-bearing imaging of the knee joint in a standing position poses additional requirements for the image reconstruction algorithm. In contrast to supine scans, patient motion needs to be estimated and compensated. The authors propose a method that is based on 2D/3D registration of left and right femur and tibia segmented from a prior, motion-free reconstruction acquired in supine position. Each segmented bone is first roughly aligned to the motion-corrupted reconstruction of a scan in standing or squatting position. Subsequently, a rigid 2D/3D registration is performed for each bone to each of K projection images, estimating 6 × 4 × K motion parameters. The motion of individual bones is combined into global motion fields using thin-plate-spline extrapolation. These can be incorporated into a motion-compensated reconstruction in the backprojection step. The authors performed visual and quantitative comparisons between a state-of-the-art marker-based (MB) method and two variants of the proposed method using gradient correlation (GC) and normalized gradient information (NGI) as similarity measure for the 2D/3D registration.

Results:

The authors evaluated their method on four acquisitions under different squatting positions of the same patient. All methods showed substantial improvement in image quality compared to the uncorrected reconstructions. Compared to NGI and MB, the GC method showed increased streaking artifacts due to misregistrations in lateral projection images. NGI and MB showed comparable image quality at the bone regions. Because the markers are attached to the skin, the MB method performed better at the surface of the legs where the authors observed slight streaking of the NGI and GC methods. For a quantitative evaluation, the authors computed the universal quality index (UQI) for all bone regions with respect to the motion-free reconstruction. The authors quantitative evaluation over regions around the bones yielded a mean UQI of 18.4 for no correction, 53.3 and 56.1 for the proposed method using GC and NGI, respectively, and 53.7 for the MB reference approach. In contrast to the authors registration-based corrections, the MB reference method caused slight nonrigid deformations at bone outlines when compared to a motion-free reference scan.

Conclusions:

The authors showed that their method based on the NGI similarity measure yields reconstruction quality close to the MB reference method. In contrast to the MB method, the proposed method does not require any preparation prior to the examination which will improve the clinical workflow and patient comfort. Further, the authors found that the MB method causes small, nonrigid deformations at the bone outline which indicates that markers may not accurately reflect the internal motion close to the knee joint. Therefore, the authors believe that the proposed method is a promising alternative to MB motion management.

1. INTRODUCTION

Recently we proposed a method that allows for weight-bearing imaging of the knee joint using a C-arm cone-beam CT (CBCT) that is usually operated in the interventional suite.^1,2 The CBCT is mounted on a robotic arm and acquires volumetric images with high-spatial resolution and a relatively large field-of-view (FOV), using a horizontal trajectory around a standing patient.³ Such weight-bearing scans pose a challenging reconstruction problem, as the patients’ unsupported standing or squatting position induces involuntary motion of the knee joint. Initially, we used externally attached metallic markers that can be tracked in the projection images to estimate the motion.^1,4 The markers yielded accurate reconstruction results and were able to remove most of the motion artifacts. However, in clinical routine, the attachment of the markers will be bothersome as they need to be placed carefully to avoid overlaps in the projection images. Also, the internal motion of the joint might not be accurately reflected as the markers are attached to the skin. Finally, the markers cause metallic artifacts in the reconstruction which degrade image quality.⁵ Therefore, a motion correction method which performs similarly well as the marker-based (MB) method but works directly on the acquired projection images is desirable. This could substantially reduce the preparation time for weight-bearing CT and increase patient comfort.

One method to estimate motion from projection images is 2D/2D registration. Here, the acquired projections are usually registered in 2D to digitally rendered radiographs (DRRs). The DRR can be computed from an initial gated reconstruction^6,7 or alternatively from previously acquired images. The estimated 2D deformations can be directly incorporated into a motion-compensated reconstruction.

Alternatively, the motion can be estimated directly in the volume domain using 2D/3D registration with a similarity measure that is defined over the projection images. Prior work for the knee joint was done by Tsai et al. where they introduced a new similarity measure called weighted edge matching score (WEMS).⁸ WEMS matches edges extracted by a Canny edge detector incorporating increased weights for long edges. WEMS has also been used by Lin et al. to register a prior 3D MRI to a real-time 2D MRI slice during exercise using a custom weight-bearing apparatus.⁹ A slightly different method for 2D/3D registration of bones in the knee and shoulder joints was presented by Zhu et al.^10,11 They first computed the outline of the forward projected vertices of a 3D mesh originating from a prior segmentation. The outline is then registered to the 2D outline of the bone which was segmented in the 2D projection image.

In skeletal 2D/3D registration, Wang et al. proposed a differential approach for registration of a prior thorax CT to fluoroscopic images.¹² Their method is also based on 2D contour segmentation, where they report increased accuracy in estimating longitudinal off-plane motion. Bifulco et al. used the normalized cross correlation (NCC) to register prior 3D CT volumes of vertebrae to 2D fluoroscopic images.^13,14 Otake et al. used normalized gradient information (NGI) for registration of vertebra to a single projection image.¹⁵ NGI compares the 2D gradient directions and weighs them with the minimum gradient magnitude. Yet, in more recent work,¹⁶ they decided to use the well known gradient correlation (GC) measure as described by Penney et al.¹⁷ Only very little work has been done in 2D/3D registration using a full set (>100) of projection images from a CBCT scan. Recently, Ouadah et al.¹⁸ presented a method for image-based geometric calibration of mobile C-arm systems using the NGI similarity measure and a statistical optimization. Overall, 9 parameters were estimated for each of the 360 projection images yielding a total of 3240 parameters.

In weight-bearing knee-joint imaging, we neither have access to surrogate signals such as ECG in cardiac imaging nor can we rely on motion periodicity. Thus, many 2D/2D and 2D/3D registration methods known in the literature are not applicable. Furthermore, methods based on implicit segmentations in the projection domain, such as WEMS or the work by Zhu et al.,^10,11 work only on single- or pairs of projection images which can usually be positioned such that there is only little overlap with background structures. We scan both knees using a horizontal trajectory, i.e., overlap of tibia, femur, fibula, patella, and the skin boundary is inevitable which make these methods hardly applicable.

In a first attempt of image-based motion estimation, we used a simple 2D/2D registration for marker-free weight-bearing CBCT projection images of the knee joint.¹⁹ The DRR was calculated by maximum intensity projections (MIPs) of an initial, motion-corrupted reconstruction. In the context of this work, we estimated 2D translations for each pair of projection images using a similarity measure based on mutual information (MI) and a gradient-descent optimizer. The approach did not require any additional or prior data and improved the image quality compared to a reconstruction without correction. However, we still observed large discrepancies from the image quality achieved with the MB approach.

To further improve our marker-free motion compensation, we now make use of an already existent, motion-free CBCT reconstruction of the knee joints acquired in supine position. This enables rigid 2D/3D registration of the segmented left and right tibia and femur from the motion-free scan. All four segmentations are rigidly registered to each of the K motion-corrupted projection images, for example, for K = 248 yielding a total of 4 × 6 × 248 = 5952 parameters. The estimated motion between the acquired projection images and the static 3D reference is then incorporated into a motion-compensated FDK-type reconstruction to obtain a corrected 3D volume. A first version of the proposed method has already shown promising results when evaluated on a numerically simulated dataset as shown in Berger et al.²⁰

2. METHODS AND MATERIALS

2.A. Reference method using metallic fiducial markers

To thoroughly evaluate the proposed method, we compare it with the motion-compensated reconstruction that is based on externally attached fiducial markers. In the following, we briefly summarize the MB motion estimation method. For details, we refer to the work of Müller et al.,⁴ which combines the MB motion estimation presented by Choi et al.¹ with the automatic marker detection and removal presented by Berger et al.⁵ The optimization problem for K projection images and M markers is given by

$${\displaystyle \underset{\alpha }{\arg \hspace{0.17em}\min }f\left(\mathit{\alpha }\right)=\underset{\alpha }{\arg \hspace{0.17em}\min }\hspace{0.17em}\hspace{0.17em}\frac{1}{2}\sum _{k=1}^K\sum _{i=1}^M\underset{2}{\overset{2}{∥h\left(\mathit{n}\right)-{\mathit{u}}_{ik}∥}}}$$

$${\displaystyle \mathit{n}={\left(\begin{array}{ccc}\hfill n_1\hfill & \hfill n_2\hfill & \hfill n_3\hfill \end{array}\right)}^{\mathit{T}}={\mathit{P}}_k\cdot {\mathit{T}}_k\left(\mathit{\alpha }\right)\cdot {\left(\begin{array}{cc}\hfill {\mathit{x}}_i\hfill & \hfill 1\hfill \end{array}\right)}^{\mathit{T}},}$$ (1)

where α ∈ ℝ^6K is a vector containing three rotation and translation parameters per projection, P_k ∈ ℝ^3×4 is the kth projection matrix as given by the system’s calibration, T_k(α) ∈ ℝ^4×4 applies the rigid motion for projection k given the parameters in α, x_i ∈ ℝ³ is the 3D reference position of the ith marker and u_ik the ith marker’s measured 2D position in projection k. Further, n is the homogeneous representation of the motion-compensated and projected 3D reference position x_i. The function h : ℝ³ → ℝ² describes the mapping of n to 2D pixel coordinates. It is defined by $h\left(\mathit{n}\right)={\left(\begin{array}{cc}\hfill n_1/n_3\hfill & \hfill n_2/n_3\hfill \end{array}\right)}^{\mathit{T}}$. Thus, by adjusting the motion parameters, we minimize the distance between forward projected 3D reference positions and measured 2D marker positions over all detected markers and all projections. Marker detection in the projection-domain is done by applying the fast-radial-symmetry-transform (FRST)²¹ with subsequent thresholding and center-point detection. The 3D reference positions for each marker are obtained automatically. First, we apply a Gaussian filter to the 2D FRST result yielding bloblike structures at marker locations. These images are then backprojected to 3D, resulting in high-intensity 3D blobs where the backprojected 2D blobs overlap. These blobs are then segmented using a maximum entropy thresholding. Finally, the 3D reference positions are extracted from the blobs’ centroids using a 3D connected-components analysis. The assignment of 2D detections to 3D reference positions is given by the smallest Euclidean distance of forward projected 3D reference and 2D detection. For more details on 2D marker detection and 3D reference point extraction, we refer to our previous work.⁵

As a new feature, we introduce an analytic gradient computation of the cost-function which reduced the algorithm’s run-time drastically compared to a forward-differences type gradient estimation used in Müller et al.⁴ and Choi et al.¹ Using the chain rule for multivariate functions the partial derivatives of Eq. (1) with respect to the individual parameters is given by

$${\displaystyle \frac{\partial f\left(\mathit{\alpha }\right)}{\partial {\alpha }_j}=\sum _k\sum _i\hspace{0.17em}\hspace{0.17em}{\left(h\left(\mathit{n}\right)-{\mathit{u}}_{ik}\right)}^{\mathit{T}}\cdot J_h\left(\mathit{n}\right)\cdot {\mathit{P}}_k\hspace{0.17em}\hspace{0.17em}\frac{\partial {\mathit{T}}_k}{\partial {\alpha }_j}\left(\begin{array}{c}\hfill {\mathit{x}}_i\hfill \\ \hfill 1\hfill \end{array}\right),}$$ (2)

where J_h(n) denotes the Jacobian of function h,

$${\displaystyle J_h\left(\mathit{n}\right)=\left(\begin{array}{ccc}\hfill \frac{1}{n_3}\hfill & \hfill 0\hfill & \hfill -\frac{n_1}{{n_3}^2}\hfill \\ \hfill 0\hfill & \hfill \frac{1}{n_3}\hfill & \hfill -\frac{n_2}{{n_3}^2}\hfill \end{array}\right).}$$ (3)

For outlier detection and removal, we applied an iterative removal of worst contributions. After optimization, we find those u_ik that belong to the 0.5% highest 2D distances with respect to their forward-projected reference point. They were then removed from the measurements using the following rules: (1) only remove one detection per projection and (2) only remove if at least M_min detections are left for this projection. This process is repeated iteratively for J times.

2.B. Motion compensation using 2D/3D registration

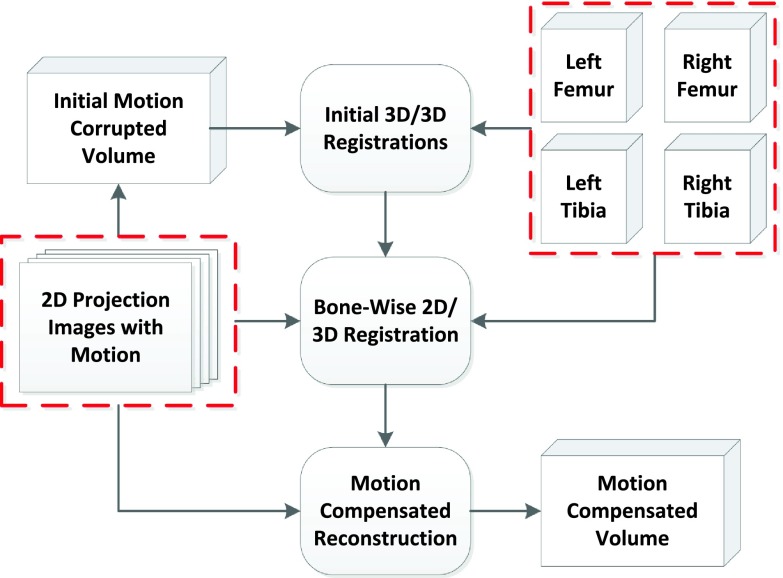
Our method is based on 2D/3D registration of segmentations from a prior, motion-free reconstruction acquired in supine position. To limit complexity of the optimization problem, we focus on four bones that represent both knee joints, i.e., left and right femur and tibia. An overview of the proposed method is given in Fig. 1. As input we have a stack of projection images acquired under weight-bearing conditions along with the segmented femur and tibia volumes, both emphasized by a dashed box. First we perform a motion-corrupted reconstruction of the acquired projections. Then, a 3D/3D registration of each segmented bone volume to the motion-corrupted reconstruction to align the standing and supine coordinate system and to account for different positions of the bones among one another. Note, that this global 3D/3D alignment does not include any estimation for intrascan patient motion. Subsequently, the initial 3D/3D registration results are used as initialization for the 2D/3D registration. 2D/3D registration is performed between each bone and every acquired projection image using a rigid motion model. The result of the 2D/3D registration is the individual bone motion over the acquisition time. To perform a motion-compensated backprojection, we also need to extrapolate the motion that occurs in between bones, e.g., at muscle or skin tissue. We use a thin-plate-spline (TPS) extrapolation method as explained in Müller et al.²²

FIG. 1.

Overview of the proposed motion compensation approach. The inputs are the femur and tibia volumes and the 2D projection images, both marked by a dashed frame.

The accuracy of the 2D/3D registration is the important step for a successful motion compensation. A crucial component is the similarity measure used to compare DRR images with the acquired projections. In this work, we assess the influence of two different similarity measures on the reconstructed image quality. First, we apply the GC that computes the NCC between vertical and horizontal gradient images. Further, we use the NGI measure that is also gradient-based but has been reported to be more stable against outlier intensities and thus more performant in presence of overlapping structures.¹⁵ To avoid convolution-based gradient computation for every DRR we create gradient DRRs directly by ray-tracing through the precomputed 3D volume gradients.^23,24

2.B.1. GC

GC is a state-of-the-art similarity measure and has been widely used to register bones to their projection images. For the initial formulation of GC, we refer to Penney et al.¹⁷ Let ∇p_k(u; γ) : ℝ² → ℝ² be the DRR’s gradient and u ∈ ℝ² a 2D pixel location. Further, ∇b_k(u) : ℝ² → ℝ² is the gradient of the kth acquired projection image computed using the Sobel operator. In contrast to the MB approach, the parameter vector is now γ ∈ ℝ^6KL, containing six rigid parameters for each of the K projections and each of the L segmented bone volumes. The GC can be formulated as

$${\displaystyle \mathrm{GC}(p,b;\mathit{\gamma })=\frac{1}{2}\sum _{k=1}^K\sum _{\mathit{u}\in \underset{k}{\mathrm{\Omega }}}\left(\nabla p_k{(\mathit{u};\mathit{\gamma })}^{\mathit{T}}\hspace{0.17em}\hspace{0.17em}{\mathit{W}}^{-1}\hspace{0.17em}\hspace{0.17em}\nabla b_k\left(\mathit{u}\right)\right).}$$ (4)

In our formulation, the normalization, i.e., a division by the standard deviations, is incorporated into the weighting matrix W ∈ ℝ^2×2 given in Eq. (5), where diag(⋅) represents a matrix with the vector argument being on the diagonal.

$${\displaystyle \mathit{W}=\mathrm{diag}{\left(\left(\begin{array}{c}\hfill \sum _{\mathit{u}}{\left(\frac{\partial p_k(\mathit{u};\hspace{0.17em}\mathit{\gamma })}{\partial u_1}\right)}^2\times \sum _{\mathit{u}}{\left(\frac{\partial b_k\left(\mathit{u}\right)}{\partial u_1}\right)}^2\hfill \\ \hfill \sum _{\mathit{u}}{\left(\frac{\partial p_k(\mathit{u};\hspace{0.17em}\mathit{\gamma })}{\partial u_2}\right)}^2\times \sum _{\mathit{u}}{\left(\frac{\partial b_k\left(\mathit{u}\right)}{\partial u_2}\right)}^2\hfill \end{array}\right)\right)}^{\frac{1}{2}}.}$$ (5)

The set Ω_k defines the image region used for the computation of the GC measure, which may vary for each projection image as indicated by the subscript k. The normalization W is used to adjust intensity differences and depends on the region Ω_k. During our experiments, we set Ω_k such that it contains every nonzero gradient value of the DRR image, i.e., ${\mathrm{\Omega }}_k=\left\{\mathit{u}\mid {∥\nabla p_k(\mathit{u};\mathit{\gamma })∥}_2>0\right\}$.

2.B.2. NGI

The idea behind NGI is to compare the similarity of gradient directions at each pixel position. This is done by computing the cosine of the angle between the gradient directions, followed by a weighting with the pixel’s gradient magnitude. To improve robustness against outliers, at each pixel, the minimum gradient magnitude of DRR and acquired image is used as a weighting factor for that pixel location. This scheme was described to be more robust against intensity outliers and thus overlapping structures.¹⁵ In contrast to GC, the NGI does not perform an intensity normalization and therefore intensities of the DRR image need to be adjusted heuristically. For more information, we refer to Otake et al.¹⁵ The NGI can be formulated as

$${\displaystyle \mathrm{NGI}(p,b;\mathit{\gamma })=\frac{\mathrm{GI}(p,b;\mathit{\gamma })}{\mathrm{GI}(b,b)},}$$ (6)

with the variable measure

$${\displaystyle \mathrm{GI}(p,b;\mathit{\gamma })=\sum _{k=1}^K\sum _{\mathit{u}\in \underset{k}{\mathrm{\Omega }}}\left(\frac{1}{2}\frac{\nabla p_k{(\mathit{u};\mathit{\gamma })}^{\mathit{T}}\hspace{0.17em}\hspace{0.17em}\nabla b_k\left(\mathit{u}\right)}{{∥\nabla p_k(\mathit{u};\mathit{\gamma })∥}_2\hspace{0.17em}\hspace{0.17em}{∥\nabla b_k\left(\mathit{u}\right)∥}_2}+\frac{1}{2}\right)\times min\left({∥\nabla p_k(\mathit{u};\mathit{\gamma })∥}_2,{∥\nabla b_k\left(\mathit{u}\right)∥}_2\right)}$$ (7)

and the constant normalization

$${\displaystyle \mathrm{GI}(b,b)=\sum _{k=1}^K\sum _{\mathit{u}\in \underset{k}{\mathrm{\Omega }}}{∥\nabla b_k\left(\mathit{u}\right)∥}_2.}$$ (8)

Because the gradient magnitude of the DRR equals zero outside the projected bone volume, we can set the region Ω_k such that it covers the full image domain for all k.

2.B.3. Regularization, cost-function, and optimization

We assume that the variation of all six motion parameters is physically limited given the knee-joint anatomy. Therefore, we add a temporal smoothness regularizer to our cost-function. We minimize the energy of the difference of the estimated parameters and their Gaussian filtered parameters. This can be understood as a minimization of energies present in high temporal frequencies,

$${\displaystyle \mathit{\gamma }={\left(\begin{array}{c}\hfill {\mathit{\zeta }}_{11}^{\mathit{T}},\dots ,{\mathit{\zeta }}_{1K}^{\mathit{T}},{\mathit{\zeta }}_{21}^{\mathit{T}},\dots ,{\mathit{\zeta }}_{LK}^{\mathit{T}}\hfill \end{array}\right)}^{\mathit{T}},}$$ (9)

$${\displaystyle {\mathit{\zeta }}_{lk}={\left(\begin{array}{c}\hfill {\varphi }_x,{\varphi }_y,{\varphi }_z,t_x,t_y,t_z\hfill \end{array}\right)}_{lk}^{\mathit{T}},}$$

$${\displaystyle r\left(\mathit{\gamma }\right)=\sum _{l=1}^L\sum _{k=1}^K\underset{2}{\overset{2}{∥{\mathit{\zeta }}_{lk}-{\left(\mathit{\zeta }*g^{\sigma }\right)}_{lk}∥}}.}$$ (10)

In Eq. (9), we outline the structure of the parameter vector γ, where ζ_lk ∈ ℝ⁶ holds the Euler angles ϕ_x, ϕ_y, ϕ_z and the translations t_x, t_y, t_z for the lth bone and the kth projection. Equation (10) shows the smoothness regularizer, where g^σ are Gaussian filter coefficients for standard deviation σ and $\left(\mathit{\zeta }*g^{\sigma }\right)$ denotes the convolution filtering over the temporal direction k.

The overall optimization problem is then given by

$${\displaystyle \underset{\mathit{\gamma }}{\arg \hspace{0.17em}\min }\hspace{0.17em}\hspace{0.17em}-c(p,b;\mathit{\gamma })+\lambda \hspace{0.17em}r\left(\mathit{\gamma }\right),}$$ (11)

where c(p, b; γ) can be either GC(p, b; γ) or NGI(p, b; γ).

Both GC and NGI need to be maximized. This is achieved by minimization of the negative cost-function value. We use a nonconstrained gradient-based minimization method for optimization. The gradient is estimated by forward-differences and the Hessian is approximated using BFGS. The step-direction is then computed by attempting a Newton step using the approximated Hessian. The step-size is calculated by a line-search method. We optimize the rotational parameters in degrees instead of radians to ensure that rotation and translation parameters are in a similar range. For more information, we refer to the optimizers documentation.²⁵

2.B.4. Noise reduction in DRRs

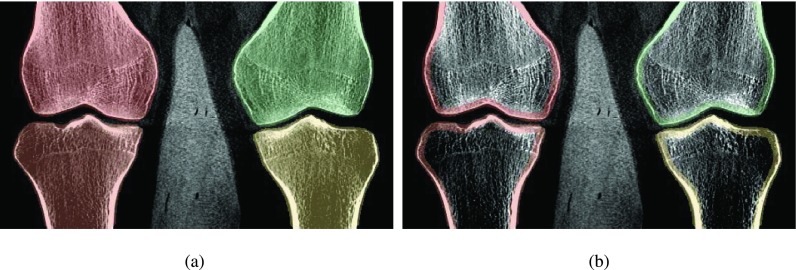
We observed a high amount of noise in the forward projected gradient images which led to unsatisfactory registration results. As the noise originates from the segmented volume, we applied a 3D edge-preserving bilateral filter as described by Lorch et al.²⁶ before calculation of the 3D gradient volumes. Additionally, we observed that the trabecular bone and the bone marrow show rather homogeneous intensities and hence contain only little structural information that is useful for 2D/3D registration. Therefore, the segmentation masks were adjusted such that they focus on cortical bone, i.e., the outline of the bone. This was done by first applying a 3D erosion to the segmentation masks and in another step a 3D dilation. Subtracting the eroded from the dilated mask results in a mask which contains the bone outline only. This process is illustrated in Fig. 2.

FIG. 2.

Adjustment of 3D segmentation masks to reduce the noise level in DRRs. (a) Original masks, (b) adjusted masks for DRR generation.

2.B.5. Unified coordinate system, TPS estimation, and reconstruction

After 2D/3D registration, we know the individual bone motion over time. As a next step, we extrapolate a global nonrigid motion field d(x, k) : ℝ⁴ → ℝ³ based on the rigid bone motion using a TPS model.²² We use the vertices of the segmented surface meshes as known TPS control points. The deformation field is estimated for each projection image separately. I_l ∈ ℝ^4×4 contains the rigid motion that was estimated by initial manual 3D/3D registration between supine and motion-corrupted scan. Further, ${\hat{\mathit{T}}}_{lk}\in {\mathbb{R}}^{4\times 4}$ are the final rigid motion matrices obtained from the 2D/3D registration. After selection of a reference time point $\hat{k}$, we can express the rigid alignment to a common coordinate system by ${\mathit{R}}_l={\hat{\mathit{T}}}_{l\hat{k}}$. We choose $\hat{k}$ to correspond to an anterior–posterior viewing direction, where no overlapping bones are present. First, we adjust all rigid transformations such that they operate in the reference coordinate system, i.e.,

$${\displaystyle {\mathit{T}}_{lk}={\hat{\mathit{T}}}_{lk}\hspace{0.17em}{\mathit{R}}_l^{\mathrm{-1}}.}$$ (12)

Subsequently, all supine mesh vertices are propagated to the standing reference coordinate system. Let ${\hat{\mathit{v}}}_l^n={\hat{\mathit{v}}}_l\in {\mathbb{R}}^3$ be the nth vertex of the lth bone in the supine coordinate system. In the following we omit the superscript n assigned to each vertex to improve clarity. Then, its static reference position v_l ∈ ℝ³ for the reference time point $\hat{k}$ can be calculated as is given by

$${\displaystyle \underset{¯}{{\mathit{v}}_l}=\left({\mathit{R}}_l\hspace{0.17em}{\mathit{I}}_l\right)\hspace{0.17em}\underset{¯}{\widehat{{\mathit{v}}_l}},}$$ (13)

where $\underset{¯}{\mathit{v}}\in {\mathbb{R}}^4$ represents a 3D point in homogeneous coordinates. Finally, we apply the updated matrices T_lk to the standing reference positions

$${\displaystyle \underset{¯}{{\mathit{v}}_{lk}}=T_{lk}\hspace{0.17em}\underset{¯}{{\mathit{v}}_l}.}$$ (14)

According to Davis et al.,²⁷ the TPS deformation at a point x ∈ ℝ³ can be formulated by

$${\displaystyle \mathit{d}(\mathit{x},k)=\sum _{n=1}^N\sum _{l=1}^L\mathit{G}(\mathit{x}-{\mathit{v}}_{lk}){\mathit{c}}_{lk}+{\mathit{A}}_k\hspace{0.17em}\mathit{x}+{\mathit{b}}_k,}$$ (15)

where c_lk ∈ ℝ³ are the unknown spline coefficients and the matrix A_k ∈ ℝ^3×3 and vector b_k ∈ ℝ³ are additional rigid motion parameters. The kernel matrix $\mathit{G}\left(\tilde{\mathit{x}}\right):{\mathbb{R}}^3\to {\mathbb{R}}^{3\times 3}$ for a 3D deformation is given by

$${\displaystyle \mathit{G}\left(\tilde{\mathit{x}}\right)=\Vert \tilde{\mathit{x}}{\Vert }_2\cdot \mathit{I},}$$ (16)

where I ∈ ℝ^3×3 denotes the identity matrix. To train the TPS model, we need to determine the unknown coefficients c_lk, A_k, and b_k. As they have a linear relationship within Eq. (15), they can be estimated in a straightforward manner. Inserting the known 2D/3D motion vectors of the vertices, i.e., u_lk = v_lk − v_l, for x in Eq. (15) yields a system of linear equations which can be solved by singular value decomposition. To constrain the spline deformation at the periphery of the reconstruction, we also added the eight bounding box corners as control points for each volume. As displacement vector, we assigned the motion generated by the geometrically closest bone, e.g., for the upper-left corners we applied the estimated left femur motion. For more details on solving the TPS equations we refer to Davis et al.²⁷

The reconstruction pipeline includes the following steps: (1) a simplified beam-scatter-kernel scatter estimation²⁸ assuming that the object consists only of water and that the water-equivalent-thickness is uniform, (2) cosine weighting, (3) Parker redundancy weighting,²⁹ (4) a simple truncation correction,³⁰ ramp filtering with a smooth Shepp–Logan kernel,³¹ and a motion-compensated GPU backprojector.³² The deformation field d(x, k) was incorporated into the GPU-based backprojection step as described by Schäfer et al.³³ That means, we evaluate the TPS model in Eq. (15) for each voxel coordinate and use the updated instead of the original coordinate to compute the 2D detector location. It should be noted that this type of reconstruction algorithm is approximate as it cannot guarantee a correct filtering and weighting of the projection images.³³

2.C. Evaluation procedure

In this work, we compare the state-of-the-art MB approach and two versions of the proposed motion correction based on 2D/3D registration. We chose to focus on the reconstruction image quality, as this includes all possible steps and parameters of the individual approaches and also validates clinical applicability. To improve early diagnosis of osteoarthritis, we want to investigate the change in joint space under weight-bearing conditions. The joint space in the knee is defined between the femoral and tibial bone surfaces.³⁴ As the bones will be directly involved in the measurement process, we are especially interested in correcting motion at the distal femur and the proximal tibia. We tailor our evaluation pipeline accordingly and focus on the improvement of bone structure when applying our motion correction methods.

2.C.1. Data acquisition and parameter selection

We evaluated our method on four acquisitions of the same patient, where large motion was present in two standing scans. The study included (1) one motion-free scan in supine position with high angular resolution, (2) a standing scan with an upright stand, (3) a standing scan with 35^∘ knee flexion, and (4) a standing scan with 60^∘ knee flexion. The motion severity increased with the flexion angle. Supine scanning took 20 s acquiring 496 projection images over 200^∘, whereas the standing scans took 10 s with 248 projection images over the same angular range. The detector size was 1240 × 960 pixels with an isotropic pixel size of 0.308 mm. For the supine and initial motion-corrupted data, we reconstructed a 512 × 512 × 256 volume with isotropic resolution of 0.5 mm, using the same preprocessing steps as described for the motion-compensated reconstruction. A total of 12 metallic beads were attached to the skin at both knees. We set the minimum number of beads to be detected per projection to M_min = 6 and repeated the optimization for J = 4 times. The 2D/3D registration was applied using a two-fold multiresolution, where only the resolution of the projection images was adjusted. For the first optimization, we used a projection image size of 310 × 240. In the second step, we initialized the parameters with the results from the first optimization and used a size of 620 × 480. The weighting factor λ = 5 × 10³ as well as the standard deviation of the Gaussian smoothing σ = 2 has been determined heuristically and was kept constant for all experiments. Further, we ensured that the initial cost-function values for GC and NGI are within the same range by incorporating a normalization factor.

The 2D/3D registration and the marker-based approach have been implemented using conrad, a dedicated and open-source software platform for CBCT reconstruction.³⁵ Function evaluations for the 2D/3D registration are entirely done on the GPU using OpenCL. The segmentation was done using itk-snap,³⁶ and initial 3D/3D registration was done manually using 3D Slicer.³⁷ To reduce artifacts due to detector saturation, the patient’s legs were wrapped in a layer of plasticine which can be seen clearly in the reconstructed volumes (see Choi et al.¹ for more information).

2.C.2. Quantitative evaluation

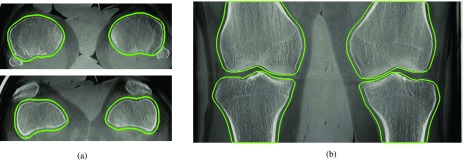
We conducted an image-based quantitative comparison between the supine, motion-free and the standing, motion-corrected reconstructions by computing the universal image quality index (UQI).³⁸ A key problem for quantitative evaluation is that there is no unified coordinate system for the motion-corrected reconstruction. Depending on which reference projection index $\hat{k}$ is chosen in Eq. (12), the final reconstruction will represent a different motion state. Assuming that the motion parameters for 2D/3D registration are estimated perfectly, the alignment between corrected and supine reconstruction should still work accurately. However, small errors in the 2D/3D registration for the reference projection $\hat{k}$ lead to a piecewise rigid motion that is based on only 6 × 4 = 24 parameters of the 6 × 4 × 248 = 5952 estimated parameters. This misalignment would dominate the image-based measures. Our main interest, however, is the improvement in the actual image quality. To become independent of this offset, we applied an automated 3D/3D rigid registration for each bone to the reference reconstruction using 3D Slicer³⁷ and evaluated the image quality for each bone region separately. For the rigid 3D/3D registration, we used a MI-based similarity measure that ensured proper alignment even in presence of motion artifacts. For registration and UQI computation, we used bonewise region-of-interests (ROIs) as depicted in Fig. 3. We made sure that the ROIs include a soft tissue margin around the bone. This was done by dilating the segmentation masks in x and y direction with a circular structuring element of radius 2.5 mm. We excluded the z-direction from the dilation as this would have caused an overlap of different bones in the ROIs. Details are given in Algorithm I.

ALGORITHM I.

Quantitative evaluation pipeline.

1: Corrected reconstruction with respect to reference projection $\hat{k}$

2: Extraction of bonewise ROI using dilated segmentation masks

3: for each ROI do

4: 3D/3D registration of ROI to supine volume

5: New reconstruction including the registration result to avoid additional interpolation

6: Computation of the UQI for each bone ROI

7: end for

8: Construction of mean and standard deviation of bonewise measures

FIG. 3.

Axial and coronal slices of the motion-free supine data. The green line corresponds to the regions used for the numerical evaluation in Sec. 3.B. The images show a clear reconstruction of the bones without any apparent motion artifacts. (a) Supine—axial, (b) supine—coronal. (See online version.)

2.C.3. Target registration error (TRE)

To evaluate how accurate the TPS extrapolation can model the motion in a certain distance to the bone we calculated the TRE using the attached metallic beads. To do so, we first detect the 3D bead locations in the corrected reconstructions using the same automatic detection approach as for the MB method, except that the backprojection now involves the estimated TPS motion fields. Then we apply the TPS motion field to the detected 3D point locations and project the resulting point to the individual projection images. The TRE can now be computed by the mean distance between the detected bead locations in 2D and the reprojections of the 3D bead locations. To avoid wrong assignments of 2D and 3D points, we used the correspondences as determined after the outlier detection of the MB method.

2.C.4. Relative bone motion

To assess the amount of nonrigidity, we measured the relative bone motion during a scan, i.e., how much the rigid motions of the bones deviate from each other. All estimated rigid motion matrices T_lk of the 2D/3D registration are relative to their individual manual initialization I_l, thus, a direct comparison of motion parameters will be difficult. As a first step, we remove the mean rigid transform $\overline{{\mathit{T}}_l}$ over all time steps k, from all T_lk, yielding the temporal, mean-free rigid transforms ${\mathbf{\Psi }}_{lk}={\mathit{T}}_{lk}\hspace{0.17em}{\overline{\mathit{T}}}_l^{\mathrm{-1}}$.

In case that all bones move with the same rigid transform, their deviation to the mean rigid transform over the bones, i.e., $\overline{{\mathbf{\Psi }}_k}$, is the identity matrix. To visualize the relative motion between the bones, we decided to compute the differences to their mean rigid transform ${\mathbf{\Delta \Psi }}_{lk}={\mathbf{\Psi }}_{lk}\hspace{0.17em}{\overline{{\mathbf{\Psi }}_k}}^{\mathrm{-1}}$. Finally, we extract all angles ${\left(\begin{array}{ccc}\hfill \mathrm{\Delta }{\varphi }_x\hfill & \hfill \mathrm{\Delta }{\varphi }_y\hfill & \hfill \mathrm{\Delta }{\varphi }_z\hfill \end{array}\right)}_{lk}$ and translations ${\left(\begin{array}{ccc}\hfill \mathrm{\Delta }{t}_x\hfill & \hfill \mathrm{\Delta }{t}_y\hfill & \hfill \mathrm{\Delta }{t}_z\hfill \end{array}\right)}_{lk}$ from ΔΨ_lk.

3. RESULTS

3.A. Visual comparison

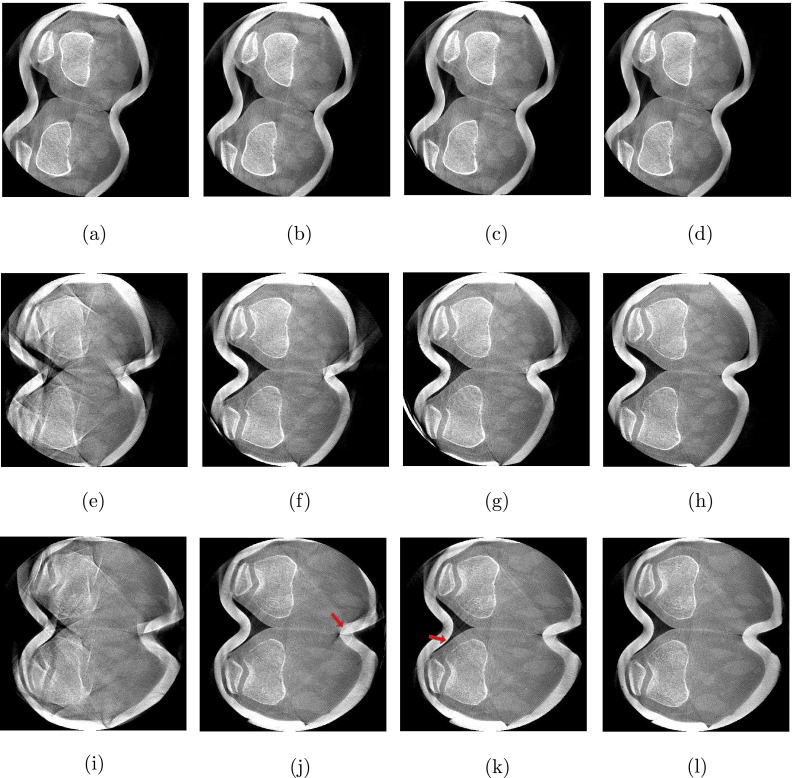
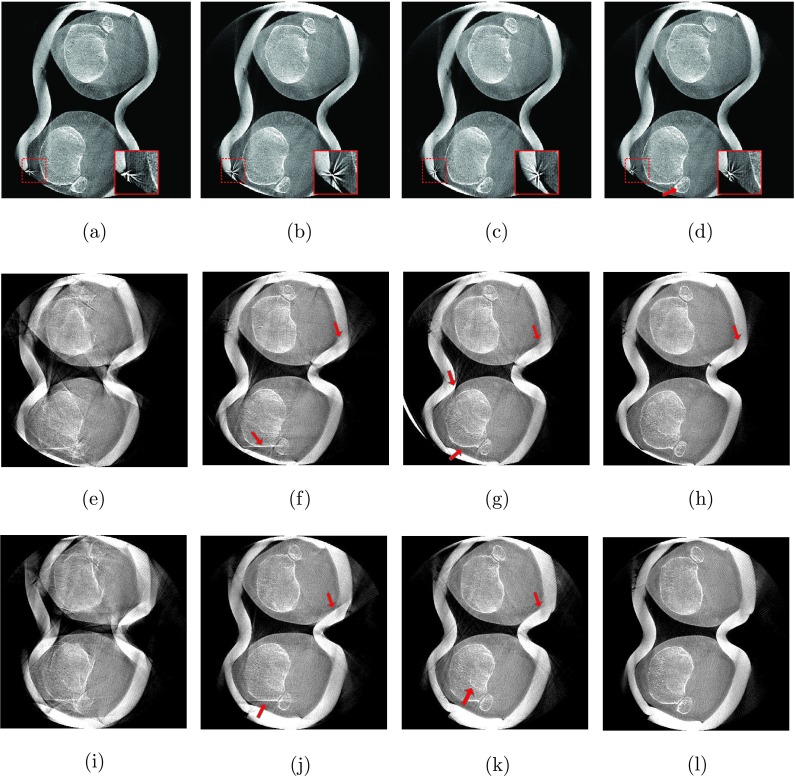
For the 0^∘ flexion angle, we observed only little motion artifacts. Slight streaking is present at the outline of femur and patella [Fig. 4(a)] but also at tibia and fibula [Fig. 5(a)]. All three methods were able to restore the bone outlines, yielding similar visual results, shown in Figs. 4(b)–4(d) and Figs. 5(b)–5(d). Yet, the MB approach shows a slightly sharper correction of the fibula’s interior compared to GC and NGI as indicated by the arrow in Fig. 5(d). Note the zoomed version of the reconstructed marker shown in the embedded box in the lower, right corner of the images. As expected the marker was accurately reconstructed using the MB method but also the NGI method did not substantially distort the marker’s appearance, indicating a good estimation of the motion at the skin boundary. A little more distortion (i.e., starlike appearance) can be seen at the marker for the GC case.

FIG. 4.

Axial slices through the femur. From left to right: Reconstructions without motion correction (NoCorr), the proposed method using GC, the proposed method using NGI and the MB reference method. The rows correspond to the three different weight-bearing scans from 0^∘ flexion angle at the top to 60^∘ flexion angle at the bottom (W: 2025 HU, C: 145 HU). (a) NoCorr-0°, (b) GC-0°, (c) NGI-0°, (d) MB-0°, (e) NoCorr-35°, (f) GC-35°, (g) NGI-35°, (h) MB-35°, (i) NoCorr-60°, (j) GC-60°, (k) NGI-60°, and (l) MB-60°.

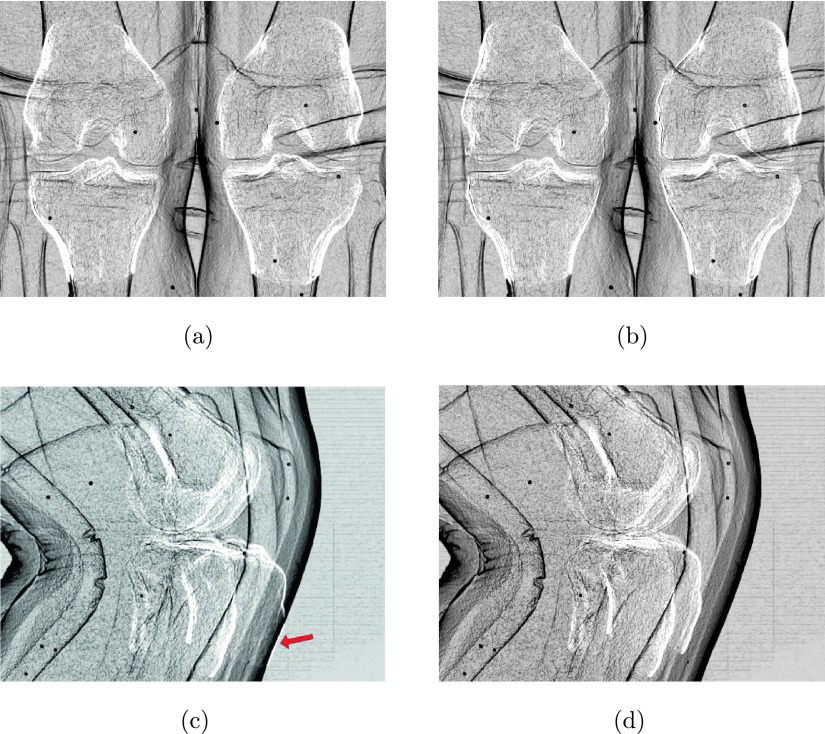
FIG. 5.

Axial slices through the tibia and fibula. From left to right: Reconstructions without motion correction (NoCorr), the proposed method using GC, the proposed method using NGI and the MB reference method. The rows correspond to the three different weight-bearing scans from 0^∘ flexion angle at the top to 60^∘ flexion angle at the bottom (W: 2025 HU, C: 145 HU). (a) NoCorr-0°, (b) GC-0°, (c) NGI-0°, (d) MB-0°, (e) NoCorr-35°, (f) GC-35°, (g) NGI-35°, (h) MB-35°, (i) NoCorr-60°, (j) GC-60°, (k) NGI-60°, and (l) MB-60°.

All methods could substantially reduce the large amount of motion artifacts for the 35^∘ case. Not many differences are seen at bone outlines between the results for the femur slices in Figs. 4(f)–4(h). As expected, the MB method shows a better result at the skin boundary and was able to restore the shape of the plasticine wrap. The slight streaking at the anterior skin boundary in NGI and GC originates from the plasticine wrap and is not related to the image quality of the bones. A clearer difference can be seen at the tibia. Again, all methods clearly improved image quality, yet, the GC could not fully correct the bones’ outlines, especially in case of the left tibia [see Fig. 5(f)]. The MB and NGI images are of similar image quality with slightly more residual streaking in the NGI case [see Figs. 5(g) and 5(h)]. The reduced image quality of the GC case is due to misregistrations of the 2D/3D alignment as illustrated in Fig. 6.

FIG. 6.

Difference of gradient magnitudes between DRR and acquired projections after registration. Top row: Projections used for extracting the reference coordinate system. Bottom row: Projections with large occlusions led to incorrect registration of the left tibia using the GC method. (a) GC-60°—Ref. projection, (b) NGI-60°—Ref. projection, (c) GC-60°—First projection, (d) NGI-60°—First projection.

The highest amount of motion was observed in the scan with a 60^∘ flexion angle, as can be seen in the uncorrected reconstructions in Figs. 4(i) and 5(i). Both GC and NGI successfully estimated the patient’s femoral motion, yielding comparable reconstructions of the femur with substantially improved image quality compared to an uncorrected reconstruction. More streaking is present in the left tibia for GC, whereas NGI shows a good tibial reconstruction. Similar to the scan at 35^∘ flexion angle, the skin boundaries are better corrected when using the MB approach with slight streaking in the 2D/3D registration-based approaches. Apart from that, the visual results are comparable.

3.B. Image quality measures

The qualitative measures yielded a UQI value for each combination of bone, flexion angle, and correction method. Table I shows the mean values over all four bone regions together with the standard deviation. Note that the UQI has been scaled by a factor of 100 throughout the paper for better visualization. Each weight-bearing scan showed moderate intensity variations due to different detector saturation and truncation artifacts. The UQI is known to be robust against intensity variations,³⁸ which allows for a fair differentiation between the methods as well as the individual weight-bearing scans.

TABLE I.

Mean and standard deviation of the UQI over four bone regions. All correction methods lead to an increased UQI compared to an uncompensated reconstruction. The bold font emphasizes the method with the highest UQI for each dataset.

UQI (×102)
Dataset (deg)	NoCorr	GC	NGI	MB
0	34.9 ± 2.3	62.6 ± 3.6	63.5 ± 4.3	57.2 ± 6.4
35	11.2 ± 3.5	47.2 ± 6.7	53.1 ± 3.7	50.0 ± 7.1
60	9.0 ± 4.1	49.9 ± 5.7	51.7 ± 5.0	52.9 ± 7.4

3.B.1. Interscan comparison

A reduction of the UQI value in case of noncorrected reconstructions from 34.9 to less than 9.0 is in line with the amount of motion observed visually. This is supported by the maximum achieved UQI values when applying correction methods. All methods showed the highest values for the 0^∘ flexion with an average UQI of 61.1. The best achieved UQI values for flexion angles 35^∘ and 60^∘ have been substantially lower with a maximum UQI of 53.1. UQI values between 35^∘ and 60^∘ flexion did not show a substantial difference.

3.B.2. Method comparison

We notice a large improvement of the UQI values from no correction to any of the correction methods. The relative improvement for each dataset is well supported by the visual impression in Figs. 4 and 5. The GC showed the lowest improvement for all flexion angles and also high interbone variations which may originate from the misregistration-based streaking artifacts seen in Figs. 5(j) and 5(f). Even though the MB method yields better reconstructions with less streaking, the NGI method shows higher UQI values for the 0^∘ and 35^∘ dataset. This discrepancy is analyzed in more detail in Sec. 3.C.

3.C. Deformation of bone outline for MB method

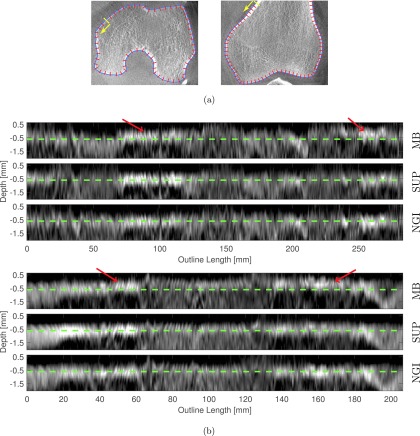
In contrast to the visual results, the highest UQI values were achieved by the NGI method with a mean distance to the MB correction of 6.3 in the 0^∘ dataset, 3.1 in the 35^∘ dataset, and comparable results for the 60^∘ dataset. This could be explained by a small deformation of the reconstructed bones in case of the MB approach. To analyze this deformation, we extracted line profiles equidistantly and orthogonal to the femur’s outline. The semiautomatic segmentation generally yielded an outline that slightly extended outside the visually determined bone outline. Therefore, we manually refined the segmentation results for a selected axial and coronal slice of the supine acquisition, such that the bone’s outline is covered exactly. The refinement was performed using the manual segmentation functionality of itk-snap.³⁶ Then, 2D spline models of the refined segmentation mesh were obtained for the selected axial and coronal slice. We also extracted the corresponding image slices for NGI, MB, and the supine data. Finally, we sampled line profiles perpendicular to the fitted spline, equidistantly along the whole spline curve.

Figure 7(a) shows the axial and coronal slice of the motion free reconstruction with an overlay of the extracted spline curves and a subset of the line profiles. In Fig. 7(b), the extracted profiles are shown. We incorporated a dashed reference line at 0.5 mm distance to the spline, which corresponds roughly to the center of the femur’s cortical bone edge in the supine scan.

FIG. 7.

Edge profiles along the outline of the right femur for NGI-0^∘, MB-0^∘, and the supine, motion-free reference (SUP). The depth axis points from the bone outward. The starting point and direction of the x-axis is indicated by arrows in (a). Compared to the NGI method the edge shifts upward for the MB method indicating a scaling effect. (a) Line profile measurement in an axial and coronal slice, (b) edge profiles along the right femur’s outline in an axial (top) and coronal (bottom) slice.

The resulting profiles show that for the MB approach, the edge intensities shift upward at multiple locations with respect to the reference line. This is not the case for the NGI approach. Shifting “upward” corresponds to a deformation perpendicular to the bone’s surface. It can be interpreted as scaling or distortion if it occurs uniformly along the spline. In addition to the distortion, we can observe that the edge of the NGI approach is more similar to the motion-free scan, than the edge of the MB method.

3.D. Target registration error

As expected, for all datasets, the MB method yielded the smallest TRE values and also the smallest deviations. Table II shows that the maximum TRE of the GC method amounts to 1.55 mm, whereas all TRE values were no larger than 0.92 mm for the NGI method. Compared to the MB approach, the standard deviations for NGI and GC increased substantially. Yet, for the NGI method, the highest standard deviation (1.07 mm) is still considerably smaller than for the GC case (2.46 mm).

TABLE II.

Mean and standard deviations for the 2D TRE of reprojected marker locations. 3D marker detection was done in the motion corrected reconstructions for GC and GI. For MB, the existing 3D estimates have been used.

TRE (mm)
Dataset (deg)	GC	NGI	MB
0	0.45 ± 0.29	0.37 ± 0.24	0.15 ± 0.08
35	1.45 ± 1.32	0.92 ± 0.86	0.35 ± 0.17
60	1.55 ± 2.46	0.75 ± 1.07	0.29 ± 0.16

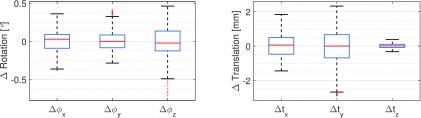
3.E. Relative bone motion

In Fig. 8, we show boxplots based on all relative motion parameters over all bones and all projections. We limited the analysis to the NGI method using the 60^∘ case, as this corresponded to the highest amount of motion estimated with the best performing registration approach. The boxes depict the 25th and the 75th percentiles and the whiskers cover ≈99% of the samples in case of a normal distribution. The red line shows the median of the samples. Almost all rotation angles lie within a range of 1^∘, which corresponds to the maximum rotational deviation between the bones. The translations in vertical direction, i.e., Δt_z show only little difference with a maximum range below 1 mm. In contrast, translations in x- and y-axis are in the range of [ − 1.44 mm, 1.84 mm] and [ − 2.89 mm, 2.32 mm], respectively.

FIG. 8.

Relative bone motion during the 60^∘ scan estimated by the NGI approach. The motion parameters show the deviation to the average rigid transform over all four bones.

4. DISCUSSION

CBCT scanning of knees under weight-bearing conditions poses a difficult motion estimation and compensation problem. In previous work on image-based motion correction, we tried to correct for involuntary patient motion without markers using 2D/2D registration of projection images and maximum intensity DRRs of a motion-corrupted reconstruction.¹⁹ However, the improvement in image quality was limited due to the amount of motion artifacts present in the initial reconstruction. All of our weight-bearing studies include a nonweight bearing scan in supine position, which serves as a reference for the investigation of functional parameters, such as joint space analysis.

A non-weight-bearing scan in a supine patient position is part in all our weight-bearing studies to obtain a reference for further investigation, e.g., a joint space analysis. Therefore, we propose a marker-free motion correction method based on piecewise-rigid 2D/3D registration of a motion-free reference volume to all projection images acquired in a weight-bearing scan. The proposed method builds on previous work by Berger et al.,²⁰ where a proof-of-concept for the GC approach is presented and evaluated on a noise-free numerical phantom. We developed the method further to allow its application to real patient acquisitions. Our main contributions are an improved similarity measure (NGI), a noise reduction approach for the forward projected gradient images and a more sophisticated estimation of a global motion field using nonrigid TPS extrapolation. Further, we extended the MB motion estimation as shown in Müller et al.⁴ by an analytic gradient computation and an improved outlier detection scheme. Moreover, this work gives a complete overview of existing motion-compensation methods for weight-bearing CBCT of the knee-joint and shows a thorough evaluation and comparison between the state-of-the-art MB and the novel, image-based approach using 2D/3D registration.

Our results show a substantial improvement of image quality for GC and NGI as well as for the MB approach compared to reconstructions without motion correction. The NGI method yielded higher UQI values and showed less streaking at the bone boundaries than the GC method. We believe that the NGI is indeed more robust to overlapping structures as indicated by Otake et al.¹⁵ This is of special importance in lateral views where we see increased overlap of left and right leg accompanied by an increased number of misregistrations in case of the GC method (see Fig. 6).

The goal of the proposed method was to achieve an image quality similar to that of the MB approach. As expected, the MB method was able to accurately restore the skin outline whereas the registration-based methods showed inaccuracies at the skin boundary that also led to slight streaking artifacts. In contrast, we see the smallest amount of streaking for the MB approach. The NGI method performed comparable to the MB method in reconstructing the bones’ outline. This is of special interest as a potential application is a 3D analysis of the joint space between the femur and tibia as outlined in Sec. 2.C.

Although the MB approach produces better visual results, we have noticed a lower UQI compared to the NGI method, especially for smaller flexion angles. Line profiles along a femur’s boundary revealed a deformation of the reconstructed bone outline with respect to the reference scan which can be seen as an intensity shift in Fig. 7. Note that the edge of the MB approach is generally higher than that of the reference which shows that the intensity shift is not due to a misalignment but due to a real distortion effect. A possible cause can be the assumption of a global, rigid transform per projection image which does not allow for nonrigid motion. If we incorrectly assume a rigid movement per projection, this can lead to a distortion in the reconstruction. In a future study, we plan to perform a statistical analysis of the directions and lengths of the residual distances in 2D. This may provide insight on the amount of nonrigidity present in the marker motion.

We deem MB methods unsuitable for the problem of reconstructing the knee under weight-bearing conditions for a number of reasons. First and foremost, markers are cumbersome and too time-intensive to attach by a physician in clinical routine. If not done carefully, markers may overlap in projections from some angles, leading to potential mismatching and lower estimation accuracy. Second, MB methods are restricted to a single rigid motion model. Rigid transformations of individual bones or even deformable models would require a considerably larger number of markers, exacerbating the problem of overlapping markers. On top of that, markers can only be attached to the skin, while the accurate relationship of bone and skin motion is unclear. Finally, markers degrade image quality due to metal artifacts. This work remedies the above mentioned problems by entirely image-based methods, thus possibly allowing a fully automatic system in the future. We currently rely on a semiautomatic segmentation and initialization of the supine bones. Methods that allow for a fully automatic segmentation of the bones and an automatic initial alignment could eliminate manual interaction and will be part of future work.

We have used the UQI for a qualitative evaluation of the reconstruction results. Note that the pipeline described in Sec. 2.C.2 requires a truly motion-free supine scan preferably of high quality. Based on the patient’s supine position and the good reconstruction quality of the supine scans (cf., Fig. 3), we could not identify patient motion in the supine scan. The image quality was superior to the standing scans, as the supine acquisition protocol used twice as many projection images. Another limitation of the evaluation method is that it also includes potential registration errors of the 3D/3D registration. To eliminate this subsequent registration we would require a ground truth motion of the bones, which is hardly possible during an in vivo study. Finally, the reported UQI values describe the mean values over the bone ROIs in Fig. 3. The ROIs include the bones and adjacent soft tissue, yet we do not claim that the UQI is an accurate measure for soft tissue deformation.

To evaluate the TPS extrapolation we computed the reprojection error of the markers (TRE) for the GC, NGI, and MB methods. As expected, the MB method performed best with a maximum TRE of 0.35 mm for the 35^∘ case. The NGI method yielded a maximum TRE of 0.92 mm for the same dataset, which is still acceptable. Note that the markers represent the boundary of the anatomically meaningful area and therefore have the largest distances to the bone surfaces on which the extrapolation is based. As is generally the case in extrapolation methods, the confidence of the TPS extrapolation decreases with increasing distance to the control points. Additionally, the MB cost-function aims to minimize exactly this error, whereas GC and NGI do not consider the markers in their optimization. Even though the proposed NGI method creates an accurate reconstruction of the bone outline, we still need to consider the effect of 2D/3D registration errors. As all our bone positions are estimated independently, errors in 2D/3D registrations may lead to deviations in relative bone position, e.g., between tibia and femur. Our analysis of relative bone motions in Sec. 3.E shows rather small rotational differences between the bones and only little variation in z-axis translations. Note that the estimated relative motion will always consist of a combination of the real ground truth motion and the residual error of the registration. Hence, for an exact measurement of relative bone motions, we would need access to the ground truth motion directly, which was not possible during our in vivo, weight-bearing acquisitions. Thus, it remains unclear if the increased deviations of translations in x- and y-axis correspond to registration errors or real variability of motion. A study using cadaver legs where tibia and femur are fixed to a device that applies a predefined motion pattern would allow an exact measurement of registration errors and is planned as future work.

As explained in Sec. 2.B.4, we reduced the bone segmentations to the bone outlines to limit the noise level in the DRRs. This makes the method similar to a mesh-to-image 2D/3D registration where the meshes are directly registered to the acquired projection images without the need of an expensive DRR generation step. An extensive overview of these methods is given in Ref. 39, where it is referred to as “feature-based” 2D/3D registration. A comparison of the two methods would be interesting for future work; yet, we expect that the current method is more robust to variations in the segmentation quality as it does not only consider segmented 3D positions but also the measured intensities. Moreover, most mesh-based registration methods require feature point detection in the projection images which will be difficult considering the high degree of overlapping structures in our acquisitions.

We will also investigate if we can perform the motion correction using a cost-function based on data consistency conditions (DCC) instead of 2D/3D registration. Methods based on image moments,⁴⁰ filtering in the Fourier domain,⁴¹ or by using the epipolar geometry^42,43 will be investigated. The motion is then estimated directly in the projection domain without the need for a motion-free scan and bone segmentations.

5. CONCLUSION

We presented a novel motion correction scheme to allow for weight-bearing CBCT imaging of the knee joint. The involuntary patient motion is estimated with respect to a motion-free reference scan in supine patient position. Left and right femur and tibia are segmented and registered to the acquired weight-bearing projections. Thus, six rigid motion parameters were estimated for each bone and each projection resulting in a total of 5952 parameters. To improve registration results, we also incorporated a regularizer that ensured smoothness of the motion-parameters over time. The motion was then used to estimate a TPS-based nonrigid deformation field for each projection which was directly incorporated into the backprojection step, yielding a motion-compensated reconstruction.

Our study included a thorough comparison between two versions of our proposed method and a state-of-the-art MB motion estimation method.⁴ All correction methods substantially improved image quality compared to reconstructions without motion correction. The GC similarity measure proved to be less robust to overlapping bone structures than the NGI similarity metric. Our quantitative evaluation over ROIs around the bones showed a mean UQI of 18.4 for no correction, 53.3 and 56.1 for the proposed method using GC and NGI, respectively, and 53.7 for the MB reference approach. Increased streaking was observed for GC, whereas the visual image quality for NGI was close to that of the MB approach. In contrast to the MB method, the proposed method does not require the attachment of markers which will improve the clinical workflow and patient comfort. Further, we found that the MB method causes small, nonrigid deformations at the bone outline which indicates that markers may not accurately reflect the internal motion at tibia and femur. Therefore, we believe that the proposed method is a promising alternative to MB motion management.

For future work, we plan further improvements of the 2D/3D registration algorithms, e.g., by incorporating an analytic gradient computation. Furthermore, we plan a thorough evaluation of the impact of residual registration errors on the relative positioning of bones.