Abstract
Escherichia coli dihydrofolate reductase (ecDHFR) is used to study fundamental principles of enzyme catalysis. It remains controversial whether fast protein motions are coupled to the hydride transfer catalyzed by ecDHFR. Previous studies with heavy ecDHFR proteins labeled with 13C, 15N, and nonexchangeable 2H reported enzyme mass-dependent hydride transfer kinetics for ecDHFR. Here, we report refined experimental and computational studies to establish that hydride transfer is independent of protein mass. Instead, we found the rate constant for substrate dissociation to be faster for heavy DHFR. Previously reported kinetic differences between light and heavy DHFRs likely arise from kinetic steps other than the chemical step. This study confirms that fast (femtosecond to picosecond) protein motions in ecDHFR are not coupled to hydride transfer and provides an integrative computational and experimental approach to resolve fast dynamics coupled to chemical steps in enzyme catalysis.
Dihydrofolate reductase (DHFR) catalyzes hydride transfer from the reduced nicotinamide adenine dinucleotide phosphate (NADPH) to 7,8-dihydrofolate (DHF) to produce 5,6,7,8-tetrahydrofolate (THF; Figure 1A). This reaction provides reduced folate for protein and nucleic acid synthesis. Escherichia coli DHFR (ecDHFR) is also useful to study fundamental principles of enzyme catalysis. A “network of coupled motions” throughout the protein has been suggested to promote the hydride transfer in ecDHFR.1,2 It remains controversial whether fast protein motions, on the time scale of femtoseconds (fs) to picoseconds (ps), are coupled to hydride transfer.3-7 Recently, ecDHFR has been characterized as the first example where rapid protein dynamics is not coupled to chemical barrier passage (see below).8
Figure 1.
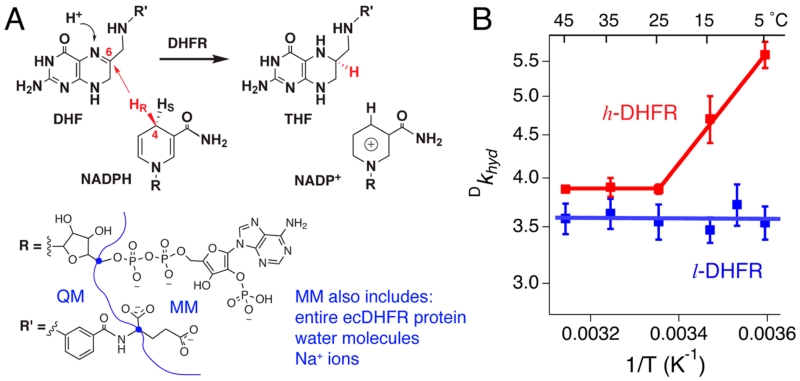
DHFR-catalyzed hydride transfer reaction and previous T-d KIE data. (A) Overall reaction catalyzed by DHFR. The blue dots in the structures indicate the boundary atoms that divide the substrates into QM and MM regions in our atomistic simulations. (B) Previously reported intrinsic deuterium isotope effects (Dkhyd) on the hydride transfer of l- and h-DHFRs (blue and red solid lines) at pH 9.5 The present report examines the difference between l- and h-DHFR deuterium KIEs at 5 °C.
Temperature dependence of kinetic isotope effects (T-d KIEs) is purported to probe the contribution of protein dynamics in enzymatic hydride transfer reactions.9 We previously reported the T-d KIEs of heavy ecDHFR (h-DHFR), in comparison with the native light ecDHFR (l-DHFR).5 In h-DHFR, the 13C, 15N, and nonexchangeable 2H (D)-labeled amino acids perturb enzyme bond vibrational dynamics on the femtosecond to picosecond time scale and these may also affect slower “coupled network” motions. Kinetic isotope effects (KIEs) of labeled NADPH were measured for both l- and h-DHFRs by competitive experiments at pH 9, and Northrop’s method was used to estimate “intrinsic” KIEs on the hydride transfer.10 The l-DHFR showed temperature-independent KIEs in the experimental temperature range (5–45 °C). For h-DHFR, the KIEs were temperature-independent at 25–45 °C, but they were temperature-dependent between 25 and 5 °C (Figure 1B, red line).5 In Marcus-like models,11,12 the results suggested different donor–acceptor distances (dDA) at the transition states (TSs) of l- and h-DHFRs at temperatures below 25 °C.9 In summary, the data suggested coupling of femtosecond to picosecond ecDHFR dynamics (thermally activated vibrations) to the TS of hydride transfer only in the heavy enzyme and only in the cold (5–25 °C).5 Here, we performed experiments and calculations to examine the proposed change in dynamics coupled to hydride transfer as a function of isotopic composition and temperature.
Other studies have reported small kinetic differences for the hydride transfer reactions of l- and h-DHFRs in the temperature range of 5–40 °C6 and attributed those small effects to C-segment dynamics of ecDHFR at pH 7.13 Those conclusions were drawn from differences in steady-state kcat and in the rate constants of fitting single-turnover kinetic data to a double-exponential equation.6,13 However, the extracted rate constants might not report on hydride transfer chemistry at all temperatures since substrate KIEs were not reported. Transition state theory is often used to rationalize such results, but the application of traditional TS theory has been questioned in understanding protein dynamics in enzymatic reactions.14,15
Here, we combine temperature-dependent transition path sampling (TPS)16,17 simulations with advanced kinetic experiments to resolve discrepancies for hydride transfer reactions of l- and h-DHFRs. Unlike umbrella sampling methods commonly used in quantum mechanics/molecular mechanics (QM/MM) and molecular dynamics (MD) simulations of enzymatic reactions,18,19 TPS is a dynamics-based method that reveals the reaction coordinate without any assumptions of geometry or energy characteristics for the TS.16,17 Thus, TPS generates reactive trajectories free of TS theory assumptions and reveals dynamic effects on the reaction coordinate.
In this study, we applied TPS simulations to l- and h-DHFRs, and the results indicated the same TS and barrier-crossing parameters for both enzymes, independent of temperature. We designed new kinetic experiments, and the results show hydride transfer rates and KIEs at pH 7 to be independent of ecDHFR protein mass, consistent with similar dynamic parameters identified by TPS simulations. On the contrary, dissociation of substrate from the Michaelis–Menten complex is faster for h-DHFR than l-DHFR. As both enzymes have the same hydride transfer rate, the steady-state kinetic parameters are altered. These new results resolve the relationship among T-d KIE, the hydride transfer TS, and femtosecond to picosecond protein dynamics of ecDHFR.
MATERIALS AND METHODS
Computational Details and Methods
Simulation Models
We used the CHARMM3520,21 computational package on a SGI Altix model ICE 8400 cluster to conduct QM/MM calculations and MD simulations of l- and h-DHFR·NADPH·DHF ternary complexes.8 The initial atomic coordinates were from the PDB entry 1RX2, and the crystallographic ligands (NADP+ and THF) were replaced with the substrates in silico. We employed the standard protonation states of all acidic and basic amino acids at physiological pH as determined by CHARMM. The atoms to be included in the QM region of the simulations were isolated as a separate “QM” residue and patched to the MM region by the two boundary atoms (Figure 1A). A 90 Å diameter sphere of water molecules was generated around the protein complex, with the edge of the water sphere at least 20 Å away from the edge of the initial protein complex. Our final simulation model contained 36 123 atoms: 69 QM ligand atoms (Figure 1A), 58 MM ligand atoms (the remaining 45 NADPH and 13 DHF atoms), 2489 protein atoms, 33 492 TIP3 water models (459 crystallographic water molecules, and 33 033 “solvent” water molecules from the generated water sphere), and 15 sodium ions for neutralizing the system. We implemented CHARMM27 all-atom force field with the topology and parameter files developed by Garcia-Viloca et al.22 to treat the QM residues in classical MD simulations. For QM/MM simulations, we used the Austin Model 1 (AM1) semiempirical approach to simulate the QM atoms, and the Generalized Hybrid Orbital method23 to treat the two boundary atoms in the ligands. All of our MD simulations used time steps of 1 fs for the integration of forces, and we applied the SHAKE algorithm24 on all covalent bonds with hydrogen atoms in the MM region.
For energy minimization, we first fixed all protein and ligand atoms and optimized the positions of water molecules and sodium ions for 25 steps of the Steepest Decent algorithm, followed by 100 steps of the Adopted Basis Newton–Raphson (ABNR) method. Next, we restrained only the protein backbone and ligand non-hydrogen atoms with a 100 kcal mol−1 Å−1 harmonic force and conducted 500 steps of ABNR minimization. For heating and equilibration, we used the Leapfrog Verlet algorithm and followed the protocol of Garcia-Viloca et al.22 First, we restrained the non-hydrogen atoms of protein and ligands with a 20 kcal mol−1 Å−1 harmonic force and slowly heated the system from 0 K to the target temperature (280 or 300 K) at a rate of 10 K ps−1. Next, we restrained only the non-hydrogen atoms of the nicotinamide ring of NADPH and the pteridine ring of DHF, with a harmonic force gradually decreasing from 10 to 1 kcal mol−1 Å−1, and equilibrated the system at the target temperature for 75 ps. Finally, the system was equilibrated for 400 ps of QM/MM simulations at the target temperature with no restraints. The potential energy, temperature, and structures of each system were stable during the final 300 ps equilibration.
TPS of DHFR-Catalyzed Hydride Transfer Reaction
We implemented the New Velocity Verlet (VV2 in CHARMM) algorithm with a Nosé–Hoover thermostat to generate canonical ensembles (i.e., constant temperature) of reactive trajectories for each system using a high perturbation TPS method.16,17 In order to determine if a generated trajectory is reactive, we used the donor-hydride distance (dDH) and acceptor-hydride distance (dAH) as the order parameter to distinguish between the reactant state (if dDH < 1.5 Å and dAH > 1.5 Å) and product state (if dDH > 1.5 Å and dAH < 1.5 Å). Starting from the equilibrated structure (which is in the reactant state), the first reactive trajectory was generated by restraining dAH to 1.25 Å with a 70 kcal mol−1 Å−1 harmonic force in a 250 fs QM/MM simulation. No restraints were used after generation of the first reactive trajectory.
Each of the following trajectories started from a randomly selected time slice from the previous reactive trajectory. Both the coordinates and momenta of all atoms in the selected time slice were perturbed by shooting moves before generating the new trajectory in order to achieve a stable acceptance ratio (the ratio between the number of reactive trajectories and the total number of all generated trajectories) of ca. 20% for each system.17 First, the coordinates were perturbed by a short QM/MM simulation (2–10 fs) with randomly assigned velocities drawn from a Boltzmann distribution at the same temperature. The resultant coordinates were only accepted based on a Metropolis acceptance criterion.17 If the resultant coordinates were rejected, then another time slice was randomly selected from the previous reactive trajectory to repeat the procedure until the perturbed coordinates were accepted. Next, the momenta of the selected time slice were perturbed by a zero-mean Gaussian distribution multiplied by a scaling factor (0.15) and then rescaled to ensure conservation of total energy and zero net angular and linear momentum of the entire system. Then, the resultant momenta were assigned to the perturbed coordinates to propagate QM/MM dynamics forward and backward in time for 250 fs, to generate a new 500 fs trajectory, with a Nosé–Hoover thermostat to maintain constant temperature. If the new trajectory was reactive (as analyzed by the order parameter), then it was accepted and used as the seed to generate the next 500 fs trajectory. Otherwise, the previous reactive trajectory was used again and the entire procedure was repeated until a new reactive trajectory was generated.
We generated 260 reactive trajectories with an acceptance radio of ca. 20% for each system. Covariance analysis of distances between randomly selected atoms suggests the reactive trajectories were sufficiently decorrelated after 10 consecutive generations. To remove any potential bias on the reaction dynamics due to the restraints applied on the first reactive trajectory, we discarded the first 35 reactive trajectories in each system. The remaining 225 reactive trajectories constituted the transition path ensemble (TPE) of each system. We calculated the all-atom root-mean-squared fluctuations (RMSFs) of each residue averaged over the entire TPE for each system and found the RMSFs to be similar for l- and h-DHFRs at both temperatures.
Committor Analysis
We selected 12 reactive trajectories (every ~20th generation) from the TPE of each of the four systems and conducted committor analysis to identify the TS and to calculate the barrier-crossing time for the hydride transfer reaction. For each system, the 12 selected trajectories were completely decorrelated with each other based on the covariance analysis, suggesting that they properly represented the widely distributed 225 reactive trajectories in the TPE. The committor is the probability for a structure to reach the product state vs reactant state with randomly assigned velocities drawn from a Boltzmann distribution. For each reactive trajectory, we initiated 50 trajectories of 250 fs QM/MM dynamics from each of the ~10 time slices in the vicinity of minimum dDA (Figure S1). The structure that shows 0.5 committor probability is the TS structure, and the time required for the committor to change from 0.1 to 0.9 is the barrier-crossing time.
Transition State Ensemble
The 12 identified TS structures constituted the TS ensemble for each of the four systems, which were analyzed for their geometric and energetic properties (Figures S1–S3 and Table 1). Critical geometric parameters of the TS, including the distances and angles between the donor (D), acceptor (A), and hydride (H), were found to be equal for all four systems (Figures S3 and Tables 1 and S1). We also analyzed the dynamic fluctuations of the same distances previously analyzed as part of a network of coupled motions in ecDHFR.1 Although the plots of these distances along the reaction progress (approximated by the antisymmetric combination of dDH – dHA) were similar to the previous analysis for l-DHFR at 300 K, they showed different features for the l-DHFR at 280 K as well as h-DHFR at 280 and 300 K. Since the TS of the hydride transfer is unperturbed, variations in the dynamic fluctuations of these distances are not coupled to the hydride transfer reaction on the subpicosecond time scale.
Table 1. Transition States, Barrier Crossing Times and Activation Free Energies for light and heavy DHFRsa.
|
dDA (Å) |
||||||
|---|---|---|---|---|---|---|
| DHFR | T (K) | from T-d KIEsb | from TPSa | dDH - dHA (Å)a | barrier-crossing time (fs)a | ΔG‡ (kcal/mol)c |
| light | 280 | 3.06 ± 0.08 | 2.82 ± 0.08 | 0.21 ± 0.07 | 6 ± 3 | 10 ± 2 |
| 300 | 2.72 ± 0.07 | 0.19 ± 0.07 | 8 ± 5 | 11 ± 2 | ||
| heavy | 280 | 3.36 ± 0.01 | 2.77 ± 0.08 | 0.11 ± 0.04 | 6 ± 3 | 10 ± 1 |
| 300 | 2.82 ± 0.06 | 0.21 ± 0.12 | 6 ± 2 | 11 ± 2 | ||
Parameters predicted from TPS simulations. Additional parameters are listed in Table S1 in Supporting Information. Experimentally measured activation free energies (ΔG‡) are also independent of enzyme mass.
Data from ref 5.
Parameters determined by pre-steady-state kinetic experiments.
Experimental Details and Methods
Chemical Materials
The l- and h-DHFRs, as well as [4R-2H]-NADPH (NADPD), were prepared and purified following published procedures.5 High purity THF was a generous gift from Prof. Amnon Kohen’s lab, University of Iowa. Nicotinamide [2,8-3H]-adenine dinucleotide ([2,8-3H-Ade]-NAD+) was purchased from American Radiolabeled Chemicals, Inc. The concentrations of protein and other compounds in solution were determined as previously described.5 Reagent concentrations refer to the final concentrations in the reaction mixture, unless otherwise specified. All kinetic experiments were conducted in 50 mM 2-(N-morpholino)ethanesulfonic acid (MES), 25 mM tris(hydroxymethyl)aminomethane (Tris), 25 mM ethanolamine, and 100 mM sodium chloride (MTEN buffer),25 with 5 mM dithiothreitol (DTT), unless otherwise specified.
Synthesis of 3H-Labeled NADPH
The radiolabeled cofactor NADPH was synthesized enzymatically from [2,8-3H-Ade]-NAD+, following published procedures.26,27 [2,8-3H-Ade]-NAD+ was phosphorylated by NAD+ kinase to produce [2,8-3H-Ade]-NADP+, which was then reduced to [2,8-3H-Ade]-NADPH by Thermoanaerobium brockii alcohol dehydrogenase (tbADH). In the first step, the reaction mixture contained 60 units of NAD+ kinase (from chicken liver), 2 μM commercial [2,8-3H]-NAD+ (27 Ci/mmol), 0.5 mM unlabeled NAD+, 4 mM adenosine triphosphate (ATP), 50 mM MgCl2, 19 units of pyruvate kinase (from rabbit muscle), and 40 mM phosphoenolpyruvate (to regenerate ATP), in 250 mM Tris buffer, pH 6.8, at 37 °C. The reaction mixture was incubated for 2 h at 37 °C to fully convert NAD+ into NADP+, and the enzymes were removed by ultrafilter centrifugation. Next, 262.5 mM isopropanol and 10 mM ZnCl2 were added into the reaction mixture, and the pH was adjusted to 8 at 37 °C. After purging the reaction mixture with argon gas on ice, 20 units of tbADH were added, and the reaction mixture was incubated for 25 min at 37 °C under argon to convert NADP+ into NADPH. Anaerobic conditions were crucial to produce [2,8-3H-Ade]-NADPH with high yield and purity, in accordance with a previous report.27 NADPH was purified on HPLC and lyophilized for storage at −80 °C, following published methods.26
Stopped-Flow Experiments
Transient kinetics of l- and h-DHFR were measured on an Applied Photophysics model SX20 stopped-flow instrument (dead time: 1 ms), following published procedures.5 Enzyme tryptophan residues are photoexcited at 290 nm, emitting fluorescence at 350 nm. Transient kinetic parameters were measured by monitoring the protein fluorescence through a 305 nm cutoff filter in the absence of NADPH. When NADPH is present, Förster resonance energy transfer (FRET) from tryptophan residues to bound NADPH emits fluorescence at 450 nm, and transient kinetic parameters were measured by monitoring FRET through a 400 nm cutoff filter.
Pre-Steady-State Kinetics at pH 7
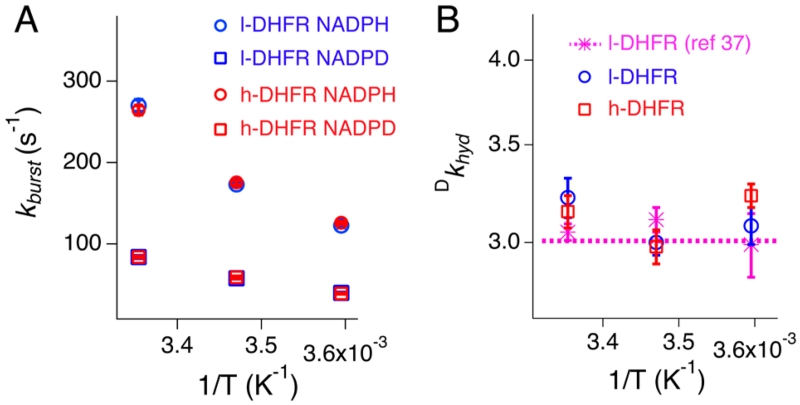
Pre-steady-state kinetics were measured by monitoring the FRET decay due to hydride transfer.5,28 DHFR (5 μM) was preincubated with 120 μM NADPH or NADPD for 3 min before rapid mixing with 100 μM DHF. The experiments were conducted at 5, 15, and 25 °C. The pH of MTEN buffer was adjusted to 7 at the target temperature prior to each experiment. The time traces of the FRET decay fit well to eq 1, where A and kburst are the amplitude and observed rate constant, respectively, of the initial burst phase, v is the steady-state rate of FRET decrease, and B is a constant. The kburst values at different temperatures were fit to the Eyring equation (eq 2) to estimate the free energy of activation (ΔG‡) for the kinetic step that dominates the burst phase kinetics. The observed rate constants and deuterium KIEs of the burst phase are shown in Figure 3 and Table S2. The empirical activation free energies (ΔG‡) are summarized in Table 1.
| (1) |
| (2) |
Figure 3.
Temperature and DHFR mass effects on the pre-steady-state rate constants (kburst; A) and deuterium KIEs (Dkhyd; B) measured by stopped-flow experiments at pH 7 (blue: l-DHFR; red: h-DHFR). The pre-steady-state Dkhyd values (B) are within the experimental errors of intrinsic KIEs measured by competitive experiments at pH 7 (data from ref 38). The kburst and Dkhyd values are also listed in Table S2.
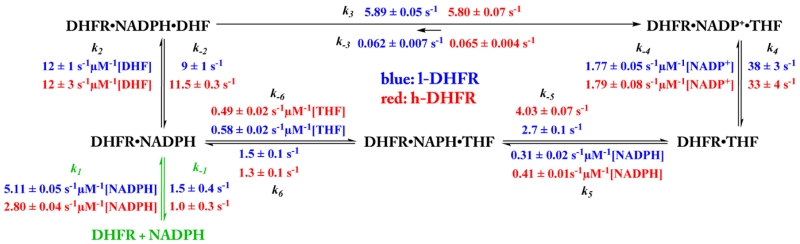
Kinetic Scheme at 5 °C, pH 9
Under saturating substrate conditions, the steady-state turnover of ecDHFR follows the kinetic pathway as described in Scheme 1.28 We measured all of the kinetic constants along this kinetic pathway at 5 °C, pH 9. The kinetic constants k1, k−1, k5, k−5, k6, and k−6 were measured using the relaxation method28 by rapidly mixing the ligand with the corresponding apoenzyme or binary complexes. The slow reverse reaction (i.e., the hydride transfer from THF to NADP+, details below) permits measurements of k4 and k−4 using the same method by mixing the DHFR·THF binary complex with NADP+ and monitoring the enzyme fluorescence at 350 nm. When THF is used (e.g., measurements of k4, k−4, k5, and k−5 in Scheme 1), the experiments were conducted under anaerobic conditions.
Scheme 1. Kinetic Mechanisms of l-DHFR (Blue) and h-DHFR (Red) at 5 °C, pH 9a.
aUnder saturating substrate concentrations, the cofactor NADPH predominantly binds to DHFR·THF complex during the catalytic turnover instead of the apoenzyme, except during the first turnover (k1 and k−1, green).
Pre-steady-state kinetics in the forward direction were studied by monitoring changes in FRET. DHFR (0.5 μM) was preincubated with 100 μM NADPH for 3 min before rapidly mixing with various concentrations of DHF (2–100 μM). Upon mixing with DHF (2–20 μM), the FRET signal fits to a double-exponential kinetic equation (Figure S4A). In the fast exponential phase, FRET increased with a rate constant () that showed linear dependence on DHF concentration (eq 3). In the slow exponential phase, FRET decayed with a rate constant () that showed hyperbolic dependence on DHF concentration (eq 4).29 The derivation of the observed rate constants followed the two-step reversible reaction sequence as described in ref 29. Both mathematical expressions of and involved rate constants governing the formation and depletion of the reaction intermediate DHFR·NADPH·DHF. Equations 3 and 4 assume that the hydride transfer step is irreversible (k−3 = 0), which is reasonable since k−3 was determined to be very small (details below, Table S3). Fitting the biphasic burst kinetics with Igor software (Figure S4B,C) provides the solutions for the hydride transfer rate and rate constants for DHF association and dissociation kinetics (k2, k−2, and k3 in Scheme 1).
| (3) |
| (4) |
All of the measured rate constants are shown in Scheme 1.
Reversibility of the Hydride Transfer and Overall Reaction at 5 °C, pH 9
The rates of l- and h-DHFR reactions in the forward and reverse directions were measured by monitoring the decrease and increase of 340 nm absorbance (accumulative Δε340nm = 11.8 mM−1 cm−1), respectively, under steady-state kinetics. The forward reaction rate was measured with 0.5 μM DHFR, 50-100 μM NADPH, and 50–100 μM DHF, and the reverse reaction rate was measured with 1 μM DHFR, 0.5–4 mM NADP+, and 50–200 μM THF, at 5 °C, pH 9, under anaerobic conditions. The measured steady-state rate constants are not affected by the ligand concentrations in the specified range. Rapidly mixing DHFR·NADPH with DHF also provided burst phase kinetics for DHF binding and hydride transfer, as described above. In contrast, rapid mixing of DHFR·THF with NADP+ did not show any burst phase in either the 340 nm absorbance or 450 nm FRET signals. The only burst signal was observed when monitoring protein fluorescence at 350 nm, which reports the binding kinetics of NADP+ as described above. The hydride transfer appears to be fully rate-limiting in the reverse direction of the overall reaction, and the measured steady-state rate constant is, therefore, the reverse hydride transfer rate (k−3 in Scheme 1). The equilibrium constant of the hydride transfer can be calculated from the forward and reverse rate constants of this step (Table S3). We also calculated the equilibrium constants for formation of NADPH and DHF from NADP+ and THF by measuring the total increase in 340 nm absorbance after the reaction. The rate and equilibrium constants of the hydride transfer and overall reactions are summarized in Table S3.
Forward Commitment Factor (Cf) Measurements
We measured the Cf for the hydride transfers of l- and h-DHFRs using the pulse–chase isotope-trapping method30 (also called intermediate-partitioning method31) at 5 °C, pH 9. DHFR was preincubated with [2,8-3H-Ade]-NADPH, in the absence and presence of 5 μM THF, to form the DHFR·[2,8-3H-Ade]-NADPH binary complex (10–30 μM) in a pulse solution. The experiments were conducted under anaerobic conditions when THF was present in the initial reaction mixture. The concentration of the radioactive DHFR·[2,8-3H-Ade]-NADPH binary complex (relative to the total amount of [2,8-3H-Ade]-NADPH; %EA0) was determined from the equilibrium constants measured by stopped-flow experiments (k1 and k−1 in the absence of THF or k5, k−5, k6, and k−6 in the presence of THF; Scheme 1). The pulse solution was rapidly diluted into the chase solution (final DHFR·[2,8-3H-Ade]-NADPH binary complex concentration was 0.67–2 μM) containing saturating concentrations of unlabeled NADPH (1 mM) and DHF (0.85 mM) and quenched at different time points by 1.7 mM methotrexate (a nanomolar inhibitor of DHFR). Independent control experiments were performed in the absence of enzymes, as well as in both the forward (with chase solution lacking NADPH) and reverse (with chase solution lacking DHF) directions of intermediate partitioning to correct for any errors due to trace amount of impurities. The 3H-labeled NADPH and NADP+ were separated on HPLC and analyzed on a liquid scintillation counter following published methods26 to determine the fraction of bound [2,8-3H-Ade]-NADPH converted to NADP+ (%P). This %P divided by %EA0 is the fraction of DHFR·[2,8-3H-Ade]-NADPH converted to products in the chase solutions (i.e., [P]/[EA0] = %P/%EA0). The fraction of [2,8-3H-Ade]-NADP+ formed from the initial DHFR·NADPH binary complex (F0) was obtained by extrapolation of the [P]/[EA0] values measured at different time points to t0. Under saturating concentrations of the substrate DHF, Cf is the partition between product formation and substrate release from the initial DHFR·[2,8-3H-Ade]-NADPH complex at t0. Thus, Cf can be calculated by Cf = F0/(1–F0) for initial reaction conditions. This pulse–chase isotope-trapping method allows the most direct experimental measurement of Cf as defined by eq 6 in the absence of THF or eq 7 in the presence of THF.
RESULTS AND DISCUSSION
Theoretical TS Is Independent of Temperature and ecDHFR Mass
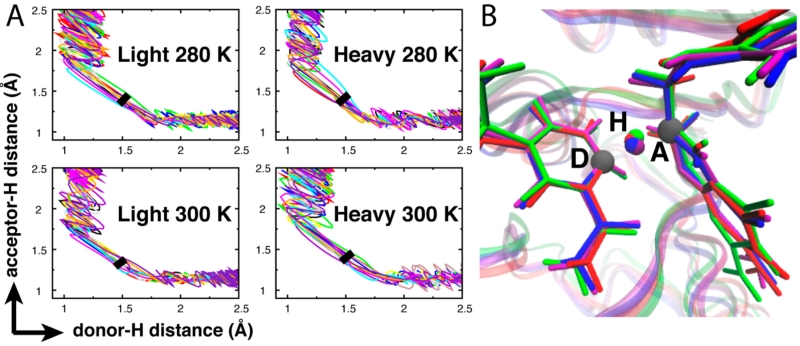
On the basis of Marcus-like models,11,12 previous experimental T-d KIE results indicated h-DHFR had an altered TS in the 5–25 °C range due to thermally activated vibrations of the protein coupled to the hydride transfer (Figure 1B).5 Present computational investigation disagrees with this proposal. We used the TPS algorithm with a Nosé–Hoover thermostat32,33 to conduct constant temperature simulations (Figures S1–S3) at temperatures above and below 25 °C. A canonical TPE containing 225 individual decorrelated reactive trajectories was generated from over 1000 highly perturbed dynamic trajectories for each of the hydride transfer reactions of l- and h-DHFRs at 280 K (7 °C) and 300 K (27 °C). The TPS method16,17 allowed analysis of geometric parameters as individual dynamics of reactive trajectories rather than the equilibrium average that is commonly accessed by other methods.1-4,7 The isotopic perturbation between l- and h-DHFRs showed variations in the dynamic fluctuations of some atomic distances, which were previously analyzed as part of the network of coupled motions.1,2 However, those variations did not produce significant differences in the reactive trajectories projected on the dDH, dAH, dDA distances or the D–H–A angle (Figures 2, S2, and S3). Previous studies proposed that the network of coupled motions on the millisecond time scale governs ecDHFR catalysis.1,2,34-36
Figure 2.
Temperature and ecDHFR protein isotope effects alter subpicosecond protein dynamics (Figure S2) but not the hydride transfer TS. (A) l- and h-DHFRs show the same reactive trajectories projected on the dDH and dHA distances. The thick black line in each plot marks the TS location determined by committor analysis (Figure S1). (B) Superimposition of four representative TS structures (purple: light 280 K; red: light 300 K; blue: heavy 280 K; green: heavy 300 K) indicates the same TS geometry for l- and h-DHFRs. The TS structures shown in this figure are extracted from the reactive trajectories shown in Figure S1.
We conducted committor analysis of representative reactive trajectories to identify and analyze TSs of the hydride transfer reactions (Figure S1). This TPS analysis found the same TS geometry for l- and h-DHFRs at 280 and 300 K (Figure 2). The magnitudes of dDA (Table 1) are similar for l- and h-DHFRs at both temperatures. These distances are shorter than those derived from previous T-d KIE data in the 5–25 °C range based on Marcus-like models (Table 1). Similar results have been reported for mutations of l-DHFR that altered the T-d KIEs, where QM/MM simulations found the wild-type and mutant l-DHFRs had equal dDA at the TS.3,4,37 Committor analysis also permits calculation of the barrier-crossing time for the hydride transfer reactions, which was the same for l- and h-DHFRs (Table 1). The computational data predict that ecDHFR is unlike other enzymes,8-13 where altered enzyme mass has been demonstrated to influence the probability of barrier crossing. In ecDHFR, any vibrational motions altered by protein mass or temperature do not affect the TS or barrier-crossing parameters.
Hydride Transfer KIEs at pH 7 Are Independent of Temperature and ecDHFR Mass
We conducted pre-steady-state experiments at pH 7 to estimate the hydride transfer kinetics of l- and h-DHFRs under physiologically relevant conditions. Pre-steady-state kinetics of l- and h-DHFRs were measured by stopped-flow fluorescence spectroscopy at 5, 15, and 25 °C, pH 7. Hydride transfer in the DHFR·NADPH·DHF complex causes the FRET signal to decay exponentially in the pre-steady-state burst phase (eq 1), prior to the steady-state kinetic phase.5 The burst phase rate constant (kburst) was independent of enzyme mass at all temperatures, with either NADPH or NADPD as the cofactor (Figure 3A and Table S2).
Fitting the kburst values of NADPH to the Eyring equation (eq 2) provided the empirical Gibbs free energy (Table 1). Deuterium KIEs on kburst, the ratio between kburst rates of NADPH and NADPD, were equal to the intrinsic KIEs38 reported for l-DHFR at pH 7 (Figure 3B; Dkhyd). Thus, kburst represents the hydride transfer rate (khyd) at pH 7. The pre-steady-state kinetic data indicate the hydride KIEs are independent of temperature and ecDHFR mass in the 5–25 °C range at pH 7. These results differ from the thermally activated dDA fluctuations suggested from previous T-d KIEs measured at pH 9.5 The enzyme mass-independent hydride transfer rates are consistent with similar dynamic parameters predicted by the TPS simulations, although sufficiently accurate hydride transfer rates cannot be calculated from the simulations.
Kinetic Mechanism and Commitment Factor
Differences in T-d KIEs between l- and h-DHFRs were observed for the steady-state competitive experiments at pH 9 (Figure 1B) but not for the pre-steady-state experiments at pH 7 (Figure 3B). The pH effects on T-d KIEs have been reported for l-DHFR before,39,40 and such effects were interpreted by pH-dependent kinetic commitments that affected the magnitudes of measured KIEs.38 In the competitive experiments of l- and h-DHFRs (pH 9), the largest KIE differences were observed at the lowest temperature (5 °C; Figure 1B). Those differences suggested larger kinetic commitment (Table 2, third column) and larger barrier-crossing probability for h-DHFR than l-DHFR under those experimental conditions.5
Table 2. Forward Commitment Factors (Cf) for the Hydride Transfers of l- and h-DHFRs Measured by Different Experiments at 5 °C, pH 9.
|
Cf directly measuredc |
||||
|---|---|---|---|---|
| DHFR | internal Cfa |
Cf derived from competitive KIEsb |
with 0 μM THF |
with 5 μM THF |
| light | 0.65 ± 0.07 | 1.5 ± 0.2 | 1.76 ± 0.07 | 1.44 ± 0.02 |
| heavy | 0.50 ± 0.01 | 6.6 ± 0.4 | 1.16 ± 0.05 | 0.93 ± 0.05 |
To investigate the proposed differences in the kinetic commitments of l- and h-DHFR, we measured the microscopic rate constants of both enzymes in a series of steady-state and pre-steady-state experiments (details described in the Materials and Methods section) at pH 9, 5 °C. Under saturating substrate conditions, the steady-state mechanism of ecDHFR is described in Scheme 1.28 Similar to the findings at pH 7, the hydride transfer rate was still independent of protein mass (k3 in Scheme 1). In contrast, small variations in ligand association/dissociation kinetics were observed for l- and h-DHFRs (e.g., k1, k−2, and k−5 in Scheme 1), which may cause small differences in kinetic commitments.
Since the hydride transfer is effectively irreversible (k−3 << k3 and k−3 << k4 in Scheme 1), the measured V/K KIE is related to the intrinsic KIE (e.g., Tkhyd) by forward kinetic commitment factor (Cf, eq 5)10
| (5) |
The kinetic mechanism of ecDHFR is complicated by slow release of THF, which does not dissociate from the enzyme until NADPH binds (Scheme 1). Consequently, in the competitive KIE experiments, the labeled NADPH binds to the apoenzyme only in the first turnover (k1 in Scheme 1), whereas it binds to the DHFR·THF binary complex in the subsequent turnovers (k5 in Scheme 1). The corresponding definitions of Cf are eqs 6 and 7, respectively10
| (6) |
| (7) |
These two definitions share the same internal Cf factor (k3/k−2), which reflects the internal barrier-crossing probability, i.e., the probability for the Michaelis–Menten complex to cross the hydride transfer barrier to form the products, relative to dissociation of substrates. The internal Cf is smaller for h-DHFR (0.50 ± 0.01) than l-DHFR (0.65 ± 0.07). The smaller Cf of h-DHFR is due to faster release of the substrate (k−2), whereas the hydride transfer rate (k3) remains the same with the l-DHFR.
Additional microscopic steps may be hidden from the stopped-flow measurements, rendering it impractical to calculate the full Cf based on eqs 6 and 7. However, additional microscopic steps will not alter the form of the equations, where the magnitude of Cf is dependent on THF concentration in eq 7.
Direct Measurements of Cf
Previous Cf calculated from competitive KIE experiments gave 6.6 ± 0.4 for h-DHFR (Table 2, third column), and this resulted in the T-d KIE for h-DHFR (Figure 1, red line).5 This Cf value was determined under steady-state conditions and involved additional kinetic parameters (eqs 6 and 7) external to the Michaelis–Menten complex (E·A·B in Scheme 1). The large difference for reported Cf values of l- and h-DHFRs (Table 2) led us to experimentally quantitate Cf for l- and h-DHFRs by pulse–chase isotopic-trapping experiments30,31 under the same conditions (5 °C, pH 9). The directly measured Cf is much smaller than the Cf derived for h-DHFR based on competitive KIE measurements (Table 2).
Equations 6 and 7 predict that Cf is dependent on the concentration of THF, a chemically unstable product. Previous competitive KIEs were measured under aerobic conditions when the NADP+ fractional conversion was 25–70%, and the rate of THF degradation was uncharacterized for those conditions. The effect of THF on Cf for l- and h-DHFRs was measured in the absence and presence of 5 μM THF in the initial reaction mixture. The presence of THF decreased the magnitudes of Cf (Table 2). As predicted, the Cf values measured under both conditions are larger than the internal Cf due to involvement of kinetics external to the Michaelis–Menten complex (eqs 6 and 7). Consistent with the internal Cf comparison, the full Cf values are also smaller for h-DHFR than l-DHFR. This finding suggests complex kinetics are involved in the extraction of KIEs based on Northrop’s method used earlier.5 This large difference between calculated and experimentally determined Cf values provides a cautionary note when interpreting Cf from competitive KIE results.
Comparison with Previously Published l- and h-DHFR Effects
Here, TPS simulations predict the same TSs and barrier-crossing times (ca. 6 fs) for hydride transfer in l- and h-DHFRs. Pre-steady-state kinetic results also show hydride transfer rates and KIEs to be independent of ecDHFR protein mass at pH 7. Microscopic rate constants at 5 °C, pH 9 revealed the same hydride transfer rate but faster substrate release for h-DHFR than l-DHFR. A change in this non-chemical step alters the barrier-crossing probability for h-DHFR without altering the nature of the transition state. Direct Cf measurements support these effects and show a dependence of Cf on the presence of THF. The current results contradict previously proposed differences between the hydride transfer steps of l- and h-DHFRs, but they are consistent with the variations in protein–ligand interactions observed for both enzymes.5
Previous T-d KIE experiments used Northrop’s method10 to determine intrinsic KIEs from the observed H/T and D/T KIEs on V/K (T(V/K)H and T(V/K)D, respectively) under steady-state conditions.5 Assumptions in this method (discussed in more detail in Supporting Information, eqs S1-S12) include the following: (1) the magnitudes of Cf for protium, deuterium, and tritium transfer reactions are related by the intrinsic KIEs of the respective isotopes and (2) the intrinsic KIEs are related by the semiclassical Swain–Schaad exponent (SSE, e.g., ln(kH/kT)/ln(kD/kT) = 3.34; eq S11 in Supporting Information).41,42 For ecDHFR, the dependence of Cf on THF concentrations (eq 7) renders the first assumption problematic. Differences were observed between the directly measured Cf and the Cf derived from competitive KIEs, indicating kinetic complications in the application of Northrop’s method. Chemical decomposition of THF may complicate the underlying kinetics for deriving intrinsic KIEs from the observed H/T and D/T KIEs. Another controversy is deviation of intrinsic KIEs from the semiclassical SSE relationship, as others have suggested.42-44
Other studies also reported altered hydride transfer kinetics by ecDHFR mass in the 5–40 °C range.6,13 These investigations relied on steady-state kcat measurements at pH 9 and single-turnover kinetics at pH 7. It is unclear if the extracted kinetic constants reflect hydride transfer. Thus, the reported kinetic differences are likely to arise from steps other than hydride transfer, as indicated by our current findings.
EcDHFR Differs from Other Heavy Enzymes
Our combined computational and experimental results support a hydride transfer rate and TS for ecDHFR independent of enzyme mass. Minor variations in subpicosecond dynamics of l-and h-DHFRs (Figure S2) did not change the TS or barrier-crossing time (ca. 6 fs) for the hydride transfer (Figures 2 and S3 and Table 1). The results are consistent with a catalytic mechanism sufficiently described by conformational and electrostatic fluctuations on slower time scales.36,45,46 The ecDHFR protein creates a geometric and electrostatic catalytic cage where the reaction coordinate is formed by favorable electrostatic apposition of the reactants.
Although ecDHFR does not couple subpicosecond protein dynamics to hydride transfer, other enzymes have shown both experimental and computational evidence for coupling of subpicosecond protein promoting vibrations to chemical barrier crossing.47-52 The simple construct and remarkable backbone flexibility of ecDHFR makes its dynamics–catalysis relationship most likely an exception, rather than the rule, of enzyme catalysis.
At this early stage of development, principles learned from heavy enzyme studies must be interpreted on a case-by-case basis. Enzymatic dynamic effects on catalysis depend on specific protein architecture and the nature of the chemical reaction. The use of ecDHFR to analyze the importance of rapid protein dynamics in enzymatic catalysis is inappropriate; there is no connection of rapid protein dynamics to TS barrier passage in light or heavy DHFR over the range of temperatures studied. The enzyme ecDHFR is likely to be an exception rather than a rule due to the architecture of the backbone. Integrated experimental and computational analysis of enzymes may lead to more comprehensive understanding of the enzyme structure–dynamics–catalysis relationship, providing new insights into the efficiency and specificity of enzymatic catalysts.
CONCLUSIONS
Experimental studies together with transition path sampling simulations indicate that the hydride transfer rate and TS of ecDHFR are independent of enzyme mass. This is an exception to all other enzymes studied by heavy enzyme methods. Previously reported kinetic differences between l- and h-DHFRs are likely to arise from kinetic steps other than hydride transfer, including altered microscopic association or dissociation kinetic rates. Our findings suggest that changes in apparent intrinsic KIEs calculated from the Northrop method may not always reflect chemical changes at the TS. Integration of computational transition path sampling with experimental isotope effects and reactant partition approaches are required to resolve the origin fast dynamics coupled to chemical steps in enzyme catalysis.
Supplementary Material
ACKNOWLEDGMENTS
We thank Amnon Kohen for providing high purify tetrahy–drofolate and Jean Masterson for technical assistance in developing the canonical transition path sampling method.
Funding
This work was supported by NIH program project GM068036.
ABBREVIATIONS
- DHFR
dihydrofolate reductase
- ecDHFR
Escherichia coli DHFR
- l-DHFR
light (wild-type) ecDHFR
- h-DHFR
heavy ecDHFR (uniformly labeled with 13C, 15N, and nonexchangeable 2H)
- NADPH
reduced nicotinamide adenine dinucleotide phosphate
- NADP+
oxidized nicotinamide adenine dinucleotide phosphate
- DHF
7,8-dihydrofolate
- THF
5,6,7,8-tetrahydrofolate
- Tris
tris(hydroxymethyl)aminomethane
- MES
2-(N-morpholino)ethanesulfonic acid
- MTEN buffer
50 mM MES, 25 mM Tris, 25 mM ethanolamine, and 100 mM sodium chloride
- KIE
kinetic isotope effect
- T-d KIE
temperature dependence of KIE
- FRET
Förster resonance energy transfer
- kburst
the rate constant of FRET decay in the burst phase when DHFR·NADPH is rapidly mixed with DHF on a stopped-flow instrument
- Dkburst
NADPH/NADPD KIE on kburst
- khyd
hydride transfer rate
- Dkhyd
intrinsic H/D KIE on khyd
- Tkhyd
intrinsic H/T KIE on khyd
- T(V/K)H
observed H/T (NADPH/NADPT) KIE on V/K
- T(V/K)D
observed D/T (NADPD/NADPT) KIE on V/K
- fs
femtosecond
- ps
picosecond
- QM
quantum mechanics
- MM
molecular mechanics
- MD
molecular dynamics
- TS
transition state
- TPS
transition path sampling
- TPE
transition path ensemble
- ABNR
Adopted Basis Newton–Raphson
- RMSF
root-mean-squared fluctuation
Footnotes
ASSOCIATED CONTENT
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biochem.5b01241.
Illustration of assumptions in using Northrop’s method to extract intrinsic KIEs; plots of dynamic fluctuations of geometric parameters during the hydride transfer reaction; additional analysis of the transition state; burst phase rate constants and KIEs; and kinetic and equilibrium constants of the reaction (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Agarwal PK, Billeter SR, Rajagopalan PT, Benkovic SJ, Hammes-Schiffer S. Network of coupled promoting motions in enzyme catalysis. Proc. Natl. Acad. Sci. U. S. A. 2002;99:2794–2799. doi: 10.1073/pnas.052005999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Wong KF, Selzer T, Benkovic SJ, Hammes-Schiffer S. Impact of distal mutations on the network of coupled motions correlated to hydride transfer in dihydrofolate reductase. Proc. Natl. Acad. Sci. U. S. A. 2005;102:6807–6812. doi: 10.1073/pnas.0408343102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Fan Y, Cembran A, Ma S, Gao J. Connecting protein conformational dynamics with catalytic function as illustrated in dihydrofolate reductase. Biochemistry. 2013;52:2036–2049. doi: 10.1021/bi301559q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Roston D, Kohen A, Doron D, Major DT. Simulations of remote mutants of dihydrofolate reductase reveal the nature of a network of residues coupled to hydride transfer. J. Comput. Chem. 2014;35:1411–1417. doi: 10.1002/jcc.23629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Wang Z, Singh P, Czekster CM, Kohen A, Schramm VL. Protein mass-modulated effects in the catalytic mechanism of dihydrofolate reductase: beyond promoting vibrations. J. Am. Chem. Soc. 2014;136:8333–8341. doi: 10.1021/ja501936d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Luk LY, Javier Ruiz-Pernia J, Dawson WM, Roca M, Loveridge EJ, Glowacki DR, Harvey JN, Mulholland AJ, Tuñón I, Moliner V, Allemann RK. Unraveling the role of protein dynamics in dihydrofolate reductase catalysis. Proc. Natl. Acad. Sci. U. S. A. 2013;110:16344–16349. doi: 10.1073/pnas.1312437110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Stojkovic V, Perissinotti LL, Willmer D, Benkovic SJ, Kohen A. Effects of the donor-acceptor distance and dynamics on hydride tunneling in the dihydrofolate reductase catalyzed reaction. J. Am. Chem. Soc. 2012;134:1738–1745. doi: 10.1021/ja209425w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Dametto M, Antoniou D, Schwartz SD. Barrier Crossing in Dihydrofolate Reductasedoes not involve a rate-promoting vibration. Mol. Phys. 2012;110:531–536. doi: 10.1080/00268976.2012.655337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Kohen A. Role of dynamics in enzyme catalysis: substantial versus semantic controversies. Acc. Chem. Res. 2015;48:466–473. doi: 10.1021/ar500322s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Northrop DB. Steady-state analysis of kinetic isotope effects in enzymatic reactions. Biochemistry. 1975;14:2644–2651. doi: 10.1021/bi00683a013. [DOI] [PubMed] [Google Scholar]
- (11).Borgis DC, Lee S, Hynes JT. A dynamical theory of nonadiabatic proton and hydrogen atom transfer reaction rates in solution. Chem. Phys. Lett. 1989;162:19–26. [Google Scholar]
- (12).Marcus RA. Enzymatic catalysis and transfers in solution. I. Theory and computations, a unified view. J. Chem. Phys. 2006;125:194504. doi: 10.1063/1.2372496. [DOI] [PubMed] [Google Scholar]
- (13).Luk LY, Ruiz-Pernia JJ, Adesina AS, Loveridge EJ, Tunon I, Moliner V, Allemann RK. Chemical Ligation and Isotope Labeling to Locate Dynamic Effects during Catalysis by Dihydrofolate Reductase. Angew. Chem., Int. Ed. 2015;54:9016–9020. doi: 10.1002/anie.201503968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Doron D, Kohen A, Nam K, Major DT. How Accurate Are Transition States from Simulations of Enzymatic Reactions? J. Chem. Theory Comput. 2014;10:1863–1871. doi: 10.1021/ct5000742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Pineda JR, Schwartz SD. Protein dynamics and catalysis: the problems of transition state theory and the subtlety of dynamic control. Philos. Trans. R. Soc., B. 2006;361:1433–1438. doi: 10.1098/rstb.2006.1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Bolhuis PG, Chandler D, Dellago C, Geissler PL. TRANSITION PATH SAMPLING: Throwing Ropes Over Rough Mountain Passes, in the Dark. Annu. Rev. Phys. Chem. 2002;53:291–318. doi: 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- (17).Dellago C, Bolhuis PG, Geissler PL. In: Transition Path Sampling, in Advances in Chemical Physics. Prigogine I, Rice SA, editors. John Wiley & Sons, Inc.; New York: 2002. pp. 1–78. [Google Scholar]
- (18).Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- (19).Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977;23:187–199. [Google Scholar]
- (20).Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- (21).Brooks BR, Brooks CL, III, Mackerell AD, Jr., Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Garcia-Viloca M, Truhlar DG, Gao J. Reactionpath energetics and kinetics of the hydride transfer reaction catalyzed by dihydrofolate reductase. Biochemistry. 2003;42:13558–13575. doi: 10.1021/bi034824f. [DOI] [PubMed] [Google Scholar]
- (23).Gao J, Amara P, Alhambra C, Field MJ. A Generalized Hybrid Orbital (GHO) Method for the Treatment of Boundary Atoms in Combined QM/MM Calculations. J. Phys. Chem. A. 1998;102:4714–4721. [Google Scholar]
- (24).Ryckaert J-P, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- (25).Ellis KJ, Morrison JF. Buffers of constant ionic strength for studying pH-dependent processes. Methods Enzymol. 1982;87:405–426. doi: 10.1016/s0076-6879(82)87025-0. [DOI] [PubMed] [Google Scholar]
- (26).Markham KA, Sikorski RS, Kohen A. Purification, analysis, and preservation of reduced nicotinamide adenine dinucleotide 2′-phosphate. Anal. Biochem. 2003;322:26–32. doi: 10.1016/j.ab.2003.07.010. [DOI] [PubMed] [Google Scholar]
- (27).Agrawal N, Kohen A. Microscale synthesis of 2-tritiated isopropanol and 4R-tritiated reduced nicotinamide adenine dinucleotide phosphate. Anal. Biochem. 2003;322:179–184. doi: 10.1016/j.ab.2003.08.012. [DOI] [PubMed] [Google Scholar]
- (28).Fierke CA, Johnson KA, Benkovic SJ. Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry. 1987;26:4085–4092. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- (29).Johnson KA. Transient-State Kinetic Analysis of Enzyme Reaction Pathways. enzymes. 1992;20:1–61. [Google Scholar]
- (30).Rose IA. The isotope trapping method: desorption rates of productive E.S complexes. Methods Enzymol. 1980;64:47–59. doi: 10.1016/s0076-6879(80)64004-x. [DOI] [PubMed] [Google Scholar]
- (31).Grissom CB, Cleland WW. Use of intermediate partitioning to calculate intrinsic isotope effects for the reaction catalyzed by malic enzyme. Biochemistry. 1985;24:944–948. doi: 10.1021/bi00325a020. [DOI] [PubMed] [Google Scholar]
- (32).Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984;81:511–519. [Google Scholar]
- (33).Hoover WG, Posch HA. Direct measurement of Lyapunov exponents. Phys. Lett. A. 1985;113:82–84. [Google Scholar]
- (34).Boehr DD, Schnell JR, McElheny D, Bae SH, Duggan BM, Benkovic SJ, Dyson HJ, Wright PE. A distal mutation perturbs dynamic amino Acid networks in dihydrofolate reductase. Biochemistry. 2013;52:4605–4619. doi: 10.1021/bi400563c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Reynolds KA, McLaughlin RN, Ranganathan R. Hot spots for allosteric regulation on protein surfaces. Cell. 2011;147:1564–1575. doi: 10.1016/j.cell.2011.10.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Arora K, Brooks CL., III Multiple intermediates, diverse conformations, and cooperative conformational changes underlie the catalytic hydride transfer reaction of dihydrofolate reductase. Top. Curr. Chem. 2013;337:165–187. doi: 10.1007/128_2012_408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Doron D, Stojkovic V, Gakhar L, Vardi-Kilshtain A, Kohen A, Major DT. Free energy simulations of active-site mutants of dihydrofolate reductase. J. Phys. Chem. B. 2015;119:906–916. doi: 10.1021/jp5059963. [DOI] [PubMed] [Google Scholar]
- (38).Liu CT, Francis K, Layfield JP, Huang X, Hammes-Schiffer S, Kohen A, Benkovic SJ. Escherichia coli dihydrofolate reductase catalyzed proton and hydride transfers: temporal order and the roles of Asp27 and Tyr100. Proc. Natl. Acad. Sci. U. S. A. 2014;111:18231–18236. doi: 10.1073/pnas.1415940111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Loveridge EJ, Allemann RK. Effect of pH on hydride transfer by Escherichia coli dihydrofolate reductase. ChemBioChem. 2011;12:1258–1262. doi: 10.1002/cbic.201000794. [DOI] [PubMed] [Google Scholar]
- (40).Sikorski RS, Wang L, Markham KA, Rajagopalan PT, Benkovic SJ, Kohen A. Tunneling and coupled motion in the Escherichia coli dihydrofolate reductase catalysis. J. Am. Chem. Soc. 2004;126:4778–4779. doi: 10.1021/ja031683w. [DOI] [PubMed] [Google Scholar]
- (41).Swain CG, Stivers EC, Reuwer JF, Schaad LJ. Use of Hydrogen Isotope Effects to Identify the Attacking Nucleophile in the Enolization of Ketones Catalyzed by Acetic Acid. J. Am. Chem. Soc. 1958;80:5885–5893. [Google Scholar]
- (42).Kohen A, Jensen JH. Boundary Conditions for the Swain–Schaad Relationship as a Criterion for Hydrogen Tunneling. J. Am. Chem. Soc. 2002;124:3858–3864. doi: 10.1021/ja016909e. [DOI] [PubMed] [Google Scholar]
- (43).Hirschi J, Singleton DA. The normal range for secondary Swain-Schaad exponents without tunneling or kinetic complexity. J. Am. Chem. Soc. 2005;127:3294–3295. doi: 10.1021/ja0430752. [DOI] [PubMed] [Google Scholar]
- (44).Shelton GR, Hrovat DA, Borden WT. Calculations of the effect of tunneling on the Swain-Schaad exponents (SSEs) for the 1,5-hydrogen shift in 5-methyl-1,3-cyclopentadiene. Can SSEs be used to diagnose the occurrence of tunneling? J. Am. Chem. Soc. 2007;129:16115–16118. doi: 10.1021/ja076132a. [DOI] [PubMed] [Google Scholar]
- (45).Hanoian P, Liu CT, Hammes-Schiffer S, Benkovic S. Perspectives on electrostatics and conformational motions in enzyme catalysis. Acc. Chem. Res. 2015;48:482–489. doi: 10.1021/ar500390e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Bhabha G, Biel JT, Fraser JS. Keep on moving: discovering and perturbing the conformational dynamics of enzymes. Acc. Chem. Res. 2015;48:423–430. doi: 10.1021/ar5003158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Masterson JE, Schwartz SD. Changes in Protein Architecture and Subpicosecond Protein Dynamics Impact the Reaction Catalyzed by Lactate Dehydrogenase. J. Phys. Chem. A. 2013;117:7107–7113. doi: 10.1021/jp400376h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Antoniou D, Ge X, Schramm VL, Schwartz SD. Mass Modulation of Protein Dynamics Associated with Barrier Crossing in Purine Nucleoside Phosphorylase. J. Phys. Chem. Lett. 2012;3:3538–3544. doi: 10.1021/jz301670s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Silva RG, Murkin AS, Schramm VL. Femtosecond dynamics coupled to chemical barrier crossing in a Born-Oppenheimer enzyme. Proc. Natl. Acad. Sci. U. S. A. 2011;108:18661–18665. doi: 10.1073/pnas.1114900108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Kipp DR, Silva RG, Schramm VL. Mass-dependent bond vibrational dynamics influence catalysis by HIV-1 protease. J. Am. Chem. Soc. 2011;133:19358–19361. doi: 10.1021/ja209391n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Toney MD, Castro JN, Addington TA. Heavy-enzyme kinetic isotope effects on proton transfer in alanine racemase. J. Am. Chem. Soc. 2013;135:2509–2511. doi: 10.1021/ja3101243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Pudney CR, Guerriero A, Baxter NJ, Johannissen LO, Waltho JP, Hay S, Scrutton NS. Fast protein motions are coupled to enzyme H-transfer reactions. J. Am. Chem. Soc. 2013;135:2512–2517. doi: 10.1021/ja311277k. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.