Oufti: An integrated software package for high-accuracy, high-throughput quantitative microscopy analysis

Summary

With the realization that bacteria display phenotypic variability among cells and exhibit complex subcellular organization critical for cellular function and behavior, microscopy has re-emerged as a primary tool in bacterial research during the last decade. However, the bottleneck in today’s single-cell studies is quantitative image analysis of cells and fluorescent signals. Here, we address current limitations through the development of Oufti, a stand-alone, open-source software package for automated measurements of microbial cells and fluorescence signals from microscopy images. Oufti provides computational solutions for tracking touching cells in confluent samples, handles various cell morphologies, offers algorithms for quantitative analysis of both diffraction and non-diffraction-limited fluorescence signals, and is scalable for high-throughput analysis of massive datasets, all with subpixel precision. All functionalities are integrated in a single package. The graphical user interface, which includes interactive modules for segmentation, image analysis, and post-processing analysis, makes the software broadly accessible to users irrespective of their computational skills.

Introduction

It is now well-established that even isogenic populations of bacterial cells display significant cell-to-cell variability that can be exploited by cells to survive stressful environments. In addition, bacterial cells feature sophisticated spatial, and often dynamic, subcellular organization that is essential for cellular function and behavior. As a result, microscopy techniques for single-cell analysis have become essential tools for the study of virtually all aspects of bacterial physiology, morphogenesis and behavior. However, extracting quantitative and statistically meaningful information remains a major rate-limiting step. To help address this issue, we previously released an open source MATLAB-based software package, known as MicrobeTracker, that identifies and tracks cells from phase contrast images (Sliusarenko et al., 2011). In addition to a cell contour, cell detection results in the creation of a ‘cell mesh.’ The cell mesh is a geometric representation of the cell that includes a centerline, cell pole coordinates, and evenly spaced polygon vertex pairs orthogonal to the long cell axis. These reliable properties enable straightforward extraction of cellular dimensions and spatial decomposition of fluorescent signals into cellular coordinates (Sliusarenko et al., 2011). MicrobeTracker has been used for a variety of studies, producing over 150 citations to date. However, some inherent constraints prevent MicrobeTracker from addressing current needs of its growing user base (> 1,500 registered users). For instance, it fails to detect cells in dense samples such as microcolonies, microfluidic chambers or any confluent cell samples where cells are touching each other. Furthermore, the application cannot handle large (> 2Gb) datasets. This is at odds with the growing need for high computational throughput due to increased sizes of camera chips, advances in microfluidics and other microscopy-related techniques that can generate thousands to millions of cells to analyze. Furthermore, MicrobeTracker can fail to accurately detect cell morphologies that significantly deviate from rod shapes, limiting the types of species that can be analyzed. MicrobeTracker also requires a MATLAB environment, and thus a MATLAB license, which can be prohibitively expensive.

Here, we describe a stand-alone open-source software package named Oufti that improves upon the design of MicrobeTracker to address the aforementioned limitations while retaining subpixel cell identification. The software can be downloaded from http://www.oufti.org/download/. The Oufti package also includes an algorithm for automated detection and characterization of fluorescent diffraction-limited objects in challenging samples where signals overlap. In addition, Oufti includes routines for subpixel detection of non-diffraction-limited objects, allowing quantitative characterization of nucleoids, filamentous structures, and subcellular objects with regular or irregular shapes. For user convenience, the software package provides plotting tools for data analysis, display of results, as well as various tools for visualization of the cell cycle and for subpixel image alignment and movie construction. Oufti has a user-friendly graphic user interface (GUI) and interactive modules so that knowledge in programming is not required for use. Oufti is available for Windows, Mac and Linux operating systems, has multi-thread computation, and is supported by a comprehensive website that includes documentation, examples, and interactive tutorials (please go to http://www.oufti.org to evaluate the Oufti website).

Results and Discussion

A description of the software package is available in the Experimental Procedures section; for more details, please see the Oufti website. Below we illustrate key features of the software package.

Cell identification in confluent cell samples

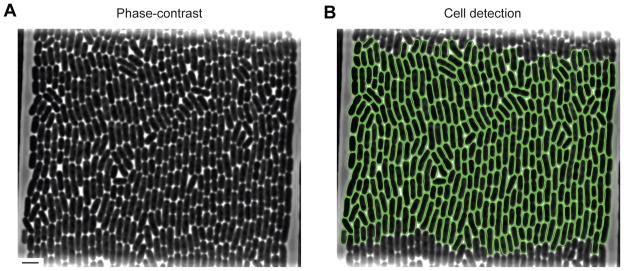
When grown on solid surfaces, bacterial cells form microcolonies where cells remain in tight contact with each other. Growth in microfluidic devices can also produce cells that remain in close contact, challenging segmentation algorithms. Oufti has the ability to identify cells and produce cell meshes even when cells form a confluent monolayer. A graphical user-interface facilitates determination of the best segmentation parameters that isolate individual cells. As an example of cell detection in a highly crowded sample, Fig. 1 shows Oufti contours of about 300 Escherichia coli cells in a tightly packed microfluidic chamber.

Fig. 1. Oufti detects individual cells in cell monolayers.

(A) Monolayer of wild-type E. coli strain BW25113 in a microfluidic chamber. Scale bar on the bottom left represents 5 μm. (B) Same as (A), but with 322 curated cell contours (green) defined with Oufti using the subpixel algorithm.

High-throughput analysis

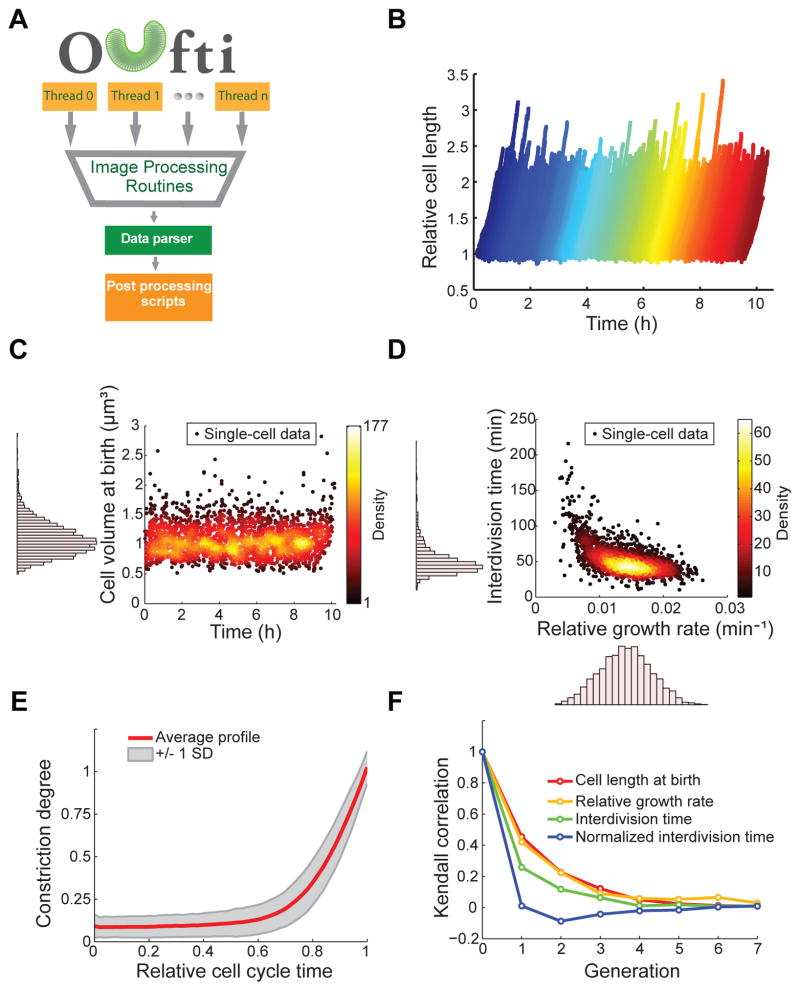
A key feature of Oufti is its high-throughput capability. Due to its efficient memory management and multi-threading capabilities, the software can reliably process massive image datasets, opening the door to high-throughput analysis of large strain libraries or microfluidic experiments. To illustrate its performance, we analyzed a multi-chamber microfluidic experiment where a monolayer of E. coli cells was imaged by phase contrast every 8 s for 10 h, generating a dataset of about 2×10⁶ cells. Fig. 2A illustrates Oufti’s high-throughput workflow, and Video 1 showcases its ability to track individual cells in a microfluidic chamber over thousands of images. By using Oufti, the users can obtain a dataset from which they can extract, at the single-cell level, a vast amount of data regarding growth, cellular dimensions, cell lineage, cell cycle, growth rate, cell constriction, etc. (see Fig. 2B–F for examples), providing a wealth of information with a high degree of statistical power.

Fig. 2. High throughput analysis of a microfluidic experiment with Oufti.

(A) Oufti work-flow includes parallel computation, exploiting multiple threads on the user’s computer. Following image processing (cell segmentation, cell detection, cell mesh creation, cell joining and/or splitting, etc.), a data parser for the text-formatted output organizes data to be analyzed with various post-processing functions. (B) Wild-type E. coli strain BW25113 was grown in microfluidic chambers in M9 supplemented medium at 30°C for about 10 h. Cells were detected and tracked over time using the subpixel algorithm. The plot shows the growth of each cell (normalized by length at birth) during the 10-h experiment. (C–F) Note that all plots were created with MATLAB scripts using the Oufti output results. These plots are presented as examples of post-analysis that can be done with Oufti-generated datasets. (C) Scatter plot of cell volume at birth versus time (n = 2,234 cells). The distribution of cell volumes at birth is shown as a histogram along the y-axis of the scatter plot. (D) Scatter plot of the interdivision time versus the relative growth rate (n = 2,234 cells). The distribution of both parameters is shown as a histogram along the corresponding axis. The relative growth rate was calculated by fitting L_be^Bt to cell length as a function of time, where L_b is cell length at birth, B is the growth rate and t is time. (E) The red line ± 1 SD (gray shading) shows the average cell constriction profile for the detected 2,234 cells, from no detectable constriction (constriction degree = 0) to cell division (constriction degree = 1). (F) Degree of correlation (Kendall rank sum correlation coefficient) from one generation to another for the cell length at birth, the relative growth rate, the interdivision time and the normalized interdivision time.

Precision, accuracy and computational efficiency of cell detection

Many studies require high-precision information in cell coordinates. This is crucial to obtain reliable measurements of cellular dimensions or to determine the spatio-temporal dynamics of fluorescently labeled molecules or structures. Oufti has two built-in cell detection methods, referred to as ‘pixel’ and ‘subpixel’ algorithms, that the user can select based on specific experimental needs. The pixel method entirely relies on pixel-based operations for cell identification, but has a local averaging function that creates smoothed (i.e., non-pixelated) cell contours and meshes. On the other hand, the subpixel algorithm employs a subpixel fitting routine. To evaluate how sensitive the pixel and subpixel algorithms are to noise (e.g., from the camera or small deviations in focus), we determined their accuracy (proximity to the true cell contour) and precision (reproducibility of cell contour localization).

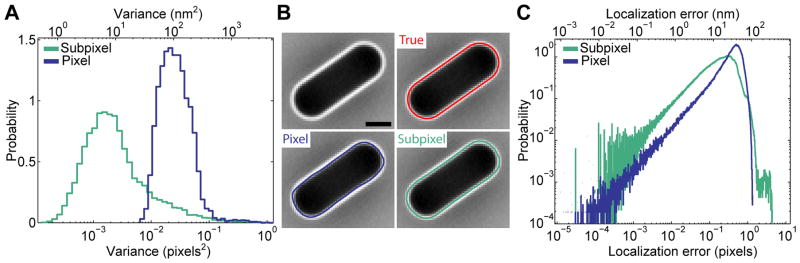
To calculate precision, we took 301 images of 116 growth-inhibited E. coli cells, obtained their contours for each frame and calculated the dispersion of localization for each cell edge (Fig. S1). Under our imaging conditions, we found that both pixel and subpixel algorithms are highly precise as the variance in cell edge position was very low (Fig. 3A). However, the precision of the subpixel method was superior, with a peak in variance of 0.0016 pixels² (6.6 nm²) compared to 0.02 pixels² (82 nm²) for the pixel method.

Fig. 3. Precision and accuracy of the pixel and subpixel cell detection methods.

(A) Variance of cell contour edge localization (14,660 edges from 116 cells, each sampled 301 times in a time-lapse experiment) from cell detection with the pixel and subpixel algorithms. Variance is measured in pixels² (bottom x axis) and nm² (top x axis). (B) Top left, simulated 2D phase-contrast image. The scale bar represents 1 μm. Top right, same but with the true edge location (red). Bottom left, same but with cell contour obtained with the pixel algorithm (blue). Bottom right, same but with cell contour obtained with subpixel algorithm (green). (C) Histogram of distance of cell contour edge localization to true cell edge coordinate (2,348,162 vertices from 22,500 cells). The localization error is measured in pixels (bottom x axis) and nm (top x axis).

To measure the accuracy of cell edge determination, we simulated phase-contrast images of E. coli and compared cell edge localization to the true boundary of the simulated cells (Fig. 3B). We found that the average localization error is about 0.4 pixels (26 nm) for pixel-based cell detection (Fig. 3C), which is close to the theoretical limit for any pixel-based method. Using the subpixel algorithm improves the accuracy, giving a mean localization error of 0.23 pixels (15 nm, Fig. 3C).

Oufti can readily analyze most image datasets on a standard laptop or desktop. For example, a conventional PC desktop (Windows 7 with Intel i7-3770 3.4 GhZ, 16 Gb, 4 threads) processes 1,200 Caulobacter crescentus cells from a large (2048×2048 pixels) sCMOS image in about 2.5 min with Oufti’s subpixel algorithm (Supporting information, Fig. S2), about 2.7 times faster than with MicrobeTracker. Using Oufti’s pixel algorithm brings the processing time for cell identification down to 6.6 s (with cell mesh) or 4.2 s (cell contour but no cell mesh), improving speed over MicrobeTracker by about 5 and 10 times, respectively. Oufti’s compatibility with high performance computing (HPC) further extends its potential for massive dataset size, where the only limitation comes from the number of CPU threads available on the host system.

Algorithm selection should be based on the sample and experiment. The subpixel algorithm is best used on confluent cell samples, poorly contrasted images, experiments for which the algorithm’s greater precision and accuracy would make a difference, or time-lapse experiments when cell lineages need to be tracked and cells need to be split because of division. In other situations, the user may want to use the pixel-based algorithm, which is comparatively much faster.

Identification of various cell morphologies

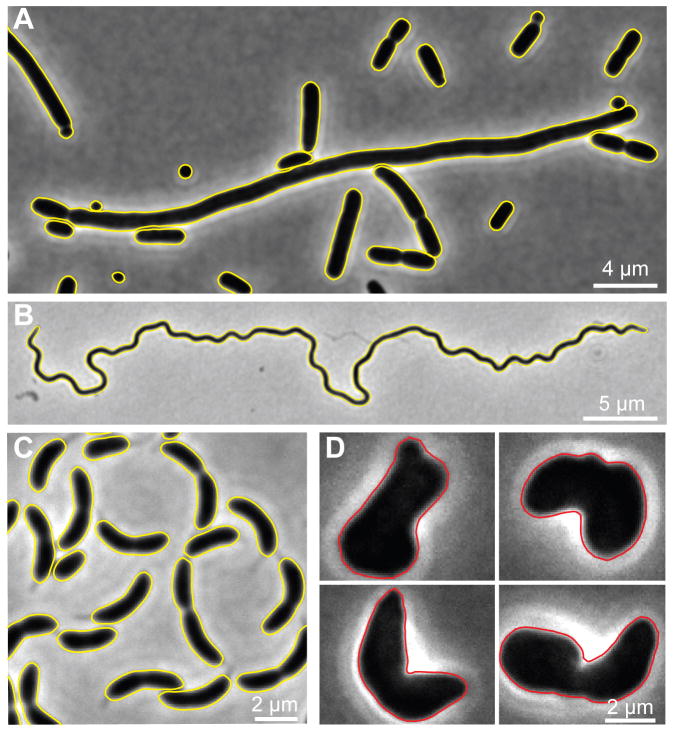
Oufti can handle various cell morphologies commonly found in the bacterial world, including —but not limited to—rods, curved rods, spheres, long filaments, and helices, even with the subpixel algorithm (Fig. 4A–C). It can also accommodate irregular shapes (Fig. 4D), although less robustly with the subpixel algorithm. The software can create cell meshes that allow determination of spatial information relative to cellular coordinates, regardless of cell morphology. A key step for obtaining cell meshes is segmentation (see Tutorial on Oufti website). Oufti has an interactive window where users can update segmentation parameters and visualize the results live. In addition, the user has the option of dragging, deleting, adding, splitting, joining and refining cell meshes.

Fig. 4. Oufti detects a variety of cell morphologies, even with the subpixel method.

Phase contrast images of (A) E. coli minC mutant, (B) Borrelia burgdorferi, (C) C. crescentus and (D) E. coli rodZ mutant cells. The cell contours computed with Oufti’s subpixel algorithm are depicted with yellow or red lines. Cell contours were obtained without curation except for the irregularly shaped rodZ mutant cells.

Detection of overlapping fluorescent foci

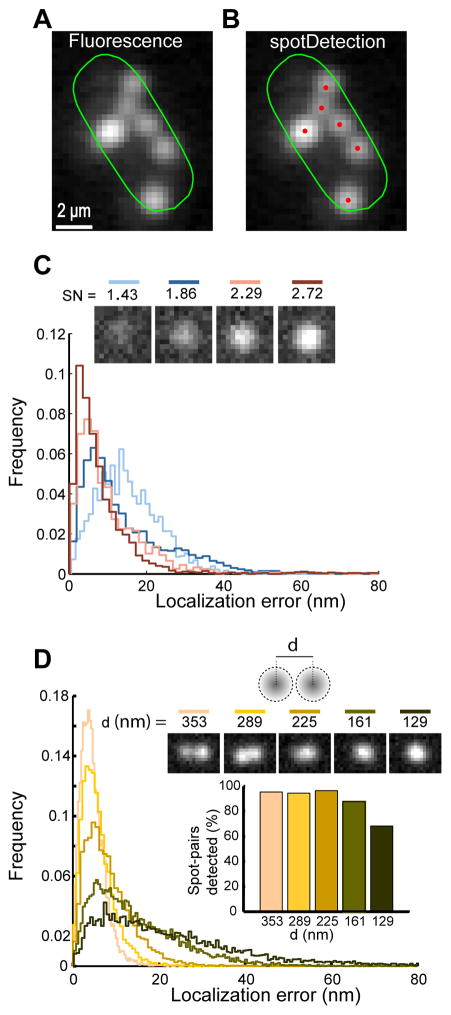
Beyond cell tracking and analysis, Oufti detects and quantifies fluorescence signals in cells, similar to MicrobeTracker (Sliusarenko et al., 2011). In addition, Oufti includes a module named spotDetection that identifies and characterizes cellular components (e.g., RNAs, chromosomal loci, plasmids and some protein clusters) that appear as diffraction-limited spots in epifluorescence images. Software tools are already available for spot analysis (Sliusarenko et al., 2011, Skinner et al., 2013, Herbert et al., 2014). However, they tend to perform well only when cells have a few foci that are well-resolved from one another. This requirement is not always satisfied. For example, in fluorescence in situ hybridization (FISH) microscopy images, small regulatory RNAs tend to form multiple foci that vary in intensity and often overlap with each other, as exemplified with the small RNA SgrS involved in phosphosugar stress response in E. coli (Fig. 5A). The spotDetection module enables precise spot identification and localization in such challenging samples (Fig. 5B). This module identifies potential fluorescent foci by filtering images in multiple spatial scales. Each potential spot is then fit by 1 to 4 Gaussian functions. Note that the multi-Gaussian analysis in spotDetection is optional as it adds significant computation time and a single-Gaussian analysis may be more appropriate when prior knowledge on the nature of the spots is available.

Fig. 5. Detection and quantitative characterization of fluorescently labeled SgrS RNAs using spotDetection.

(A) Probing E. coli SgrS small RNA using FISH microscopy reveals multiple fluorescent spots. The fluorescence image with Oufti cell contour is shown in log-scale to visualize the full spectrum of fluorescence spot intensities. (B) same as (A) but with spotDetection identification of fluorescent RNA foci (in red). (C) Localization error of spotDetection on diffraction-limited spots of varying signal-to-noise ratios (SN) from simulated images. Spots were detected using optimized parameters. Top inset shows example of single spots with corresponding SN values. Even when multiple Gaussian fitting was used, all spots were classified as single spots and fit with a single Gaussian. (D) Spot localization error for simulated spot pairs separated by a fixed distance d (top inset shows representative examples of spot pairs with their inter-spot distances). Graph inset shows the fraction of detected spot pairs as a function of inter-spot distance.

To measure the accuracy of spotDetection, we simulated diffraction-limited spots of varying intensities on a noise spectrum reconstructed from a CCD camera. The mean localization error for our simulated data was about 8 nm, 10 nm, 19 nm and 16 nm for signal-to-noise ratio values of 2.72, 2.29, 1.86 and 1.43, respectively (Fig. 5C). We also examined the performance of spotDetection in more challenging samples where simulated spot pairs overlapped (Fig. 5D). Even for overlapping spots that appeared as single spots by eye (spot inter-distance d below 225 nm), the localization error remained small (Fig. 5D).

Quantitative characterization of non-diffraction-limited objects

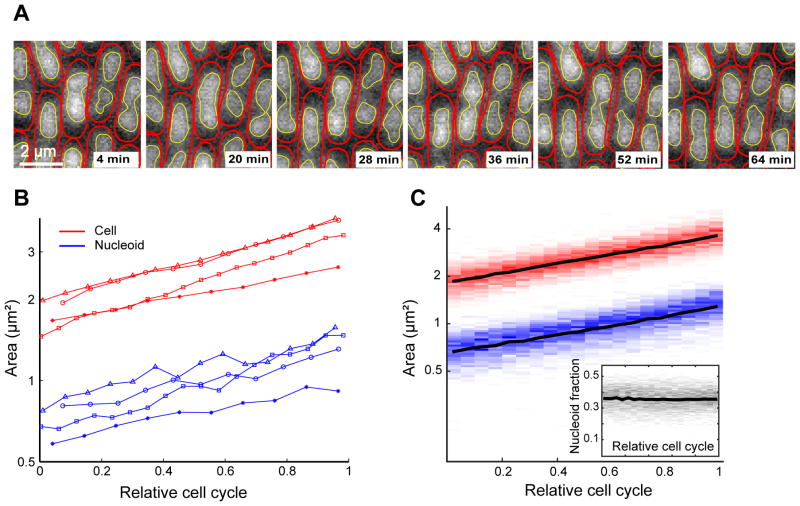
A number of cellular components (e.g., nucleoids, filamentous structures, subcellular objects with regular or irregular shapes, or proteins that form spatial gradients or patterns) produce signals that are not diffraction-limited and therefore cannot be characterized with a spot detection tool, which is designed for diffraction-limited signals. Therefore, we developed and implemented a subpixel method called objectDetection for characterizing the shape, cellular coordinates and intensity characteristics of signals that are beyond the diffraction limit. Fig. 6A and Video 2 illustrate the application of this utility to detect nucleoids and analyze their dynamics in growing and dividing E. coli cells. With this tool, we can extract quantitative information of detected objects. As an example, we quantified the area of nucleoids and cells over the course of the E. coli cell cycle (Fig. 6B shows 4 examples). Analysis of more than 700 cells shows that cells maintain a constant relationship between cell and nucleoid areas over the cell cycle (Fig. 6C).

Fig. 6. Detection and cell cycle quantification of nucleoid areas using objectDetection.

(A) Montage of fluorescence images from a microfluidic experiment showing E. coli cells with HU-mCherry-labeled nucleoids. The red and yellow contours show the cell and nucleoid contours, as determined by Oufti and its embedded objectDetection module, respectively. (B) Area of the cytoplasm (red) and nucleoid (blue) for four individual cells measured over the cell cycle. (C) Distribution of cell (red) and nucleoid (blue) areas for 740 cells are shown as intensity gradient. Black lines show the mean values. The inset plots the distribution of nucleoid-to-cell area ratio (gray) as intensity gradient and with mean (black line).

Post-processing features

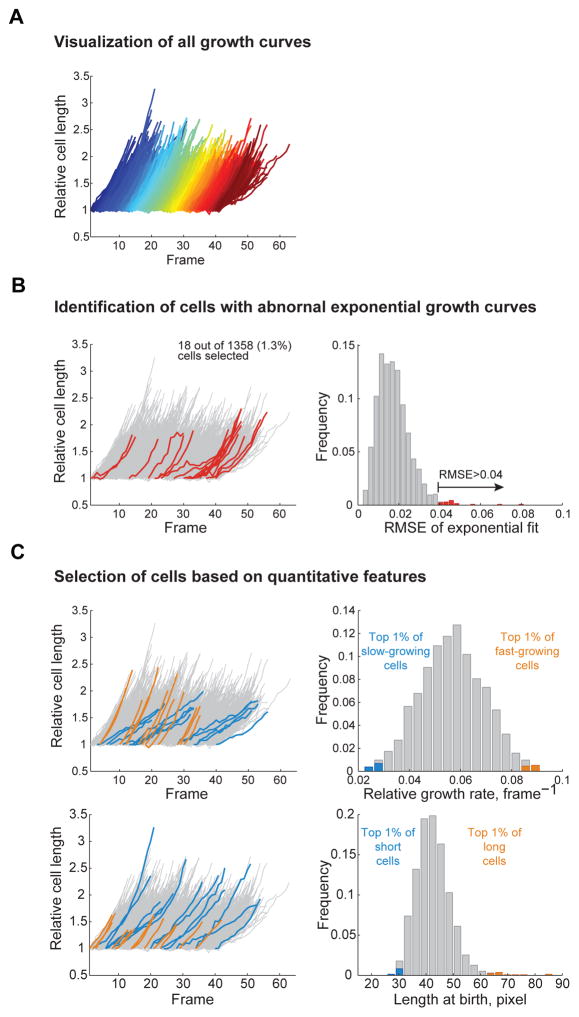
Oufti has additional useful modules enabling users to obtain plots and statistics without MATLAB. For example, for time-lapse experiments, Oufti offers cellListFilter, a tool that allows the user to visualize the growth curves of individual cells (Fig. 7A) or filter cells based on parameters such as cell length at birth, growth rate, cell cycle time, and root mean squared error of the growth curve’s exponential fit (shown on the Oufti website). This function can be used to curate datasets (to remove or manually correct poor cell contours) or to select a subset of cells with specific quantitative traits (Fig. 7B–C). The ‘movieConstruction’ module adjusts for shifts of images occurring during the time-lapse experiment by performing subpixel alignment of a region of interest over a set of time-lapse images defined by the user. The resulting aligned image series is then assembled and returned as a movie (Video 3). In the ‘cellCycleViewer’ module, the user can select a cell in any frame and immediately view the corresponding frame at birth and division (shown on the Oufti website). The ‘spotViewer’ module enables the user to verify spot identification and localization. In this application, the user can also manually select (or de-select) fluorescence foci for automatic two-dimensional (2D) Gaussian fitting (shown on the Oufti website).

Fig. 7. The cellListFilter module.

This module allows the user to quickly visualize the growth curves of all cells detected in a time-lapse experiment, as well as identify and select a subset of them for further refinement or analysis of the cell contours. (A) Typical output of the growth curve visualizing tool. (B) Cells with abnormal growth curves can be easily selected by choosing the growth curves that significantly deviate from exponential growth. A typical output is shown on the left panel where growth curves deviating from an exponential fit (root mean squared error RMSE >0.04) are highlighted in red on the left panel. The distribution of the RMSE values for all the growth curves fit is shown as a histogram on the right panel, with RMSE values > 0.04 highlighted in red. (C) The capability of selecting a subset of cells based on their growth rate or length at birth is illustrated with the blue and orange growth curves on the left panels, corresponding to the blue and orange bars on the histograms on the right panels. Cells and growth curves that are not included in the selection are represented with gray growth curves and bars.

User friendliness and accessibility

One of our goals was to make the software accessible to scientists with no formal computational experience. To this end, all modules have been integrated in a single, stand-alone package that is controlled by a user-friendly GUI; no MATLAB license is required. The Oufti application is interactive, and allows manual intervention throughout the analysis. The GUI also has a number of interactive modules embedded for real-time result monitoring.

All Oufti analyses are returned in MATLAB format, but can be exported as a *.csv file, which is compatible with Excel and other programming environments. For user convenience, Oufti is packaged with easy-to-use modules that can be used for data analysis once cell and signal detection is completed (see the Oufti website). In the software package, these tools are categorized in the “Tools” drop-down menu within the main GUI. Beyond tools for displaying cells/signals and for plotting their statistics, more advanced plots such as demographs (Hocking et al., 2012) and kymographs can be easily produced (see the Oufti website).

It is our hope that the robustness, versatility and wide user accessibility of the Oufti software package will open the door to new quantitative studies for researchers across the broad field of microbial sciences. Oufti applicability can extend beyond microbe-related studies, as its toolbox has functionality across a wide range of images.

Experimental Procedures

Cell detection

Oufti builds on MicrobeTracker’s methods (Sliusarenko et al., 2011). Cell detection occurs from either phase-contrast or fluorescence images by one of three user-selected segmentation methods that return binary images. For Laplacian of Gaussian cell detection (LoG), the image is convolved with a LoG kernel. Pixel locations where the magnitude of the LoG-filtered image is greater than the user-defined parameter logthresh are saved as cell edges. The second option is the valley detection implemented from MicrobeTracker (Sliusarenko et al., 2011). The final option is a cross-detection method; it combines LoG filtering with valley detection and is computed as

$$c=l(v+\gamma )>\alpha \gamma \beta ,$$ (1)

where l is the LoG filtered image, v is computed by the Valley detection method, γ is the mean of the 0.99 quantile of the gradient of the Gaussian filtered image, α is the standard deviation of LoG of an image, and β determines the thresholding strength over the cross of the two methods. Matlab’s bwtraceboundary function is used to convert binary segmented images into pixel-based cell contours.

For the ‘pixel’ algorithm, the cell contours are optionally smoothed with Fourier smoothing, and the user may also choose to create cell meshes (Sliusarenko et al., 2011). To reduce processing time, the algorithm is implemented as a multi-threaded process.

The subpixel algorithm, which is also a multi-threaded process, uses the aforementioned pixelated cell contours as initial guesses in an energy minimization procedure. The energy minimization function (Equation 2) deforms a sphero-cylinder to image objects determined from segmentation, as implemented from MicrobeTracker (Sliusarenko et al., 2011), with the modification that I₀, the threshold value measured from an image region of interest, is computed locally.

$$\overrightarrow{f}=-\underset{\begin{array}{c}\text{attraction}\text{to}\\ \text{high}\text{gradient}\end{array}}{\underbrace{a\nabla (\mid \nabla I\mid )}}+\underset{\begin{array}{c}\text{attraction}\text{to}\\ \text{threshold}\end{array}}{\underbrace{b\nabla (I-I_0)}}+\underset{\begin{array}{c}\text{attraction}\text{to}\\ \text{edge}\end{array}}{\underbrace{c\nabla (D)}}+\underset{\begin{array}{c}\text{attraction}\text{to}\\ \text{filled}\text{areas}\end{array}}{\underbrace{d{\overrightarrow{f}}_a}}-\underset{\begin{array}{c}\text{repulsion}\text{from}\\ \text{background}\end{array}}{\underbrace{e{\overrightarrow{f}}_r}},$$ (2)

where I is the image, D is the computed edge of an image, f⃗_a is the attraction force, f⃗_r is the repulsion force. The terms are monotonic and controlled by user-adjustable parameters a, b, c, d, and e. The local computation of I₀ induces a local force to attract the contour to the object edges, thus resulting in greater accuracy of cell contours. Using a local threshold value for attraction forces requires fewer iterations for the energy minimization process, thus allowing more robust identification of cells that are confluent or that have complex morphologies.

The energy minimization process is generally robust for tracking cells in time-lapse experiments. If the optimization fails due to a large image shift in space, the user may elect for Oufti to align the images by measuring image differences by Fourier correlation (Guizar-Sicairos et al., 2008) and applying the corresponding shift. In this case, the user simply needs to click on the ‘Align’ button prior to image analysis.

To improve computational efficiency and memory management, Oufti’s modules are implemented in several languages. C++ routines were written to replace built-in MATLAB functions to improve computational speed.

Data handling

Oufti returns numerical data that are hierarchically organized by frame and individual cells. For each cell, output includes cell dimensions, cell polarity, cell birth and division events, lineage information, fluorescence profiles, and optional data relevant to detected spots and objects.

Oufti includes a ‘high-throughput’ mode, which can be selected by the user in the GUI. A Perl routine was created to truncate large data files and accommodate high-throughput analysis of large datasets. In the high-throughput mode, data is saved on the fly, frame-by-frame, as a comma-delimited output file, with a ‘.out’ extension. Saving data in this format reduces the output file size compared to MATLAB’s output format, which becomes essential for large datasets. Oufti includes a module in the Tools tab, where users can import large ‘.out’ files into MATLAB format for visualization and post-processing purposes (see Oufti website for details).

Spot detection

By default, a Gaussian kernel is used to filter images by the a’trous wavelet method (Holschneider Matthias, 1990). The a’trous wavelet transformation of a function f(x) is computed between the difference of two consecutive approximations

$$W_j(k)=A_j(k)-A_{j-1}(k),$$ (3)

where at level j, the smoothed approximation A_j(k) at pixel x is given by the convolution

$$A_j(k)={\sum }_{l}h(l)A_{j-1}(k+2^{j-1}l),$$ (4)

where h(l) is a low-pass filter. The extension to 2D is done by convolution in the column and row direction with respect to x and y coordinates of the image. Objects determined from a filtered and thresholded image are used as initial guesses for spot localization via 2D Gaussian fitting

$$f(x,y)=b+h\ast e^{\left(-\left(\frac{{(x-x_0)}^2}{2{\sigma }^2}+\frac{{(y-y_0)}^2}{2{\sigma }^2}\right)\right)},$$ (5)

where b is the global background, h is the amplitude, x₀ and y₀ are the spot coordinates, and σ is the spread of the Gaussian. This procedure has the advantage of being able to readily distinguish between spots that are at or beyond the diffraction limit. Spots that are diffraction-limited are fit with a single Gaussian model and spots beyond the diffraction limit are fit with a mixture of 1–4 Gaussians. The Gaussian mixture with the best fit is returned. Fitting results are returned in image coordinates as well as projections onto the cell coordinate space.

Simulations to measure the accuracy of spotDetection

Diffraction-limited objects were simulated as

$$f(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\left({(x-{\mu }_x)}^2+{(y-{\mu }_y)}^2\right)/(2{\sigma }^2)},$$ (6)

where μ_x and μ_y are the x and y coordinates of the spot center, and σ is the standard deviation of the point spread function on our optical setup. f(x,y) was evaluated over all x and y less than or equal to 2 floor((20 σ)/2) + 1. Diffraction-limited objects were calculated as A f(x,y), where A was a normally distributed parameter (with mean of 10 and standard deviation of 1.5) that controls spot amplitude. These objects were then added to camera noise, which was simulated by Poisson distributed random numbers of mean 100. This Poisson distribution was found to be similar to dark images on our optical set-up. To achieve different signal-to-noise ratios (SN), spot amplitudes were multiplied by a constant factor 100, 200, 300, or 400 to create SN of 1.43, 1.86, 2.29, and 2.72, respectively. Spot amplitudes in the spot-pair simulations were drawn from a normal distribution of mean 4000 and sigma 600.

In addition to single-spot simulations, we performed simulations to create spot pairs at varying distances in order to test the ability of spotDetection to distinguish overlapping spots. Once spots were produced as described above, second spots were produced similarly and their coordinates were determined as [x, y] + [cos(θ), sin(θ)]*d, where θ was drawn from a uniform distribution, 𝒰(0, 2π), and d was a parameter that determines the radial distance between spot pairs.

Object detection

Images are pre-processed with a user-specified background subtraction algorithm: algorithm 1 for a subtraction of the average intracellular pixel value, algorithm 2 for a subtraction of the mean value of pixels that are not part of objects that are at least diffraction-limited in size, algorithm 3 for a combination of the first two methods, or algorithm 4 for a subtraction of the mean pixel value of the dim set returned from Otsu’s method (Otsu, 1979). Following background subtraction, raw fluorescence images are convolved with a second derivative and Gaussian filter (Laplacian of Gaussian, LoG)

$$\mathit{LoG}(x,y)=\frac{{dx}^2+{dy}^2-2{\sigma }^2}{{\sigma }^4}{e}^{\frac{-({dx}^2+{dy}^2)}{2{\sigma }^2}},$$ (7)

where x and y are pixel coordinates and σ is a user-specified parameter that controls the size of the convolution kernel. A cubic spline up-samples the convolution product by a user-defined factor. Up-sampled pixels that are zero-crossing components and cross zero with a magnitude beyond a user-defined magnitude parameter are returned as edge vertices. Edge vertices are assembled into polygons and returned as image feature contours.

Precision of cell edge localization

To evaluate the precision of the pixel and subpixel cell detection algorithms, we measured the fluctuations of cell mesh creation between frames obtained from a time-lapse microscopy experiment of non-growing E. coli K12 strain BW25113. Cells were grown at 37°C in M9 supplemented medium (containing 0.2% glucose, 0.1% casamino acid, 1 μg/ml thiamine) to mid-log exponential phase. Growth was arrested by the addition of 2 mM 2,4-dinitrophenol (DNP, final concentration). After 10 min at 37°C, cells were spotted on a 1% agarose pad made with the same medium and containing 2 mM DNP. They were then imaged by phase contrast microscopy on an Eclipse Ti-E microscope (Nikon) equipped with Perfect Focus System (Nikon), an ORCA-Flash4.0 CMOS camera (Hamamatsu Photonics), a phase-contrast objective Plan Apochromat 100x/1.45 NA (Nikon) and a SOLA light Engine® light source (Lumencor Beaverton) set at the specified intensity (25%, 50% or 75%). NIS-Element Ar software (Nikon) was used for image acquisition every 0.5 sec using an 80-ms exposure time. For cell detection with the pixel algorithm, the parameter fsmooth was set to 0 to prevent Oufti from performing Fourier smoothing of the cell meshes. After mesh creation with the pixel or subpixel algorithm, image shifts between frames were calculated locally to each cell by maximizing the image Fourier correlation (Guizar-Sicairos et al., 2008). The image shift from each frame for each cell was applied to the corresponding cell mesh so that all cell meshes were aligned to frame 1. A re-sampling template was then constructed for each cell from its cell mesh at its first frame. Each template consisted of lines orthogonal to each cell mesh edge and centered on that edge. The intersection of each cell mesh edge from each frame and the nearest template was calculated to create one-dimensional localization distributions for each cell mesh edge.

Accuracy of cell edge localization

To assess the accuracy of cell mesh creation, we simulated 22,500 2D phase-contrast images of rod-shaped cells with microlith (Mehta & Oldenbourg, 2014) with a phase-shift of pi/2, phase ring inner numerical aperture of 0.2, phase ring outer numerical aperture of 1.21, absorption of 2, wavelength of 546 nm. Virtual cells were simulated as rods with semi-circular end-caps, random orientation and a refractive index of 1.395 (Bryant et al., 1969). Simulated images were scaled from 0 to 100 and camera noise was modeled by adding random numbers from a Poisson distribution of mean 100. The accuracy of cell contours was determined by measuring the distance from each cell contour vertex to the simulated object boundary.

Microfluidic experiments

E. coli BW25113 cells were loaded and grown in microfluidic chambers (Campos et al., 2014, Ullman et al., 2013) in M9 supplemented medium (0.2% glucose, 0.1% casamino acid, 1 μg/ml thiamine) at 30°C for about 5 generations prior to imaging. Microscopy was performed on an Eclipse Ti-E microscope (Nikon) equipped with Perfect Focus System (Nikon), an Orca-R2 camera (Hamamatsu Photonics) and a phase-contrast objective Plan Apochromat 100x/1.45 NA (Carl Zeiss). Time-lapse images were acquired using NIS-Element Ar software (Nikon) and images were taken every 8 s with an exposure time of 100 ms in the phase-contrast channel.

Determination of cell division

For Fig. 2D, the cell division events were identified by measuring cell constriction. If the cell was constricted to a degree greater than the user-defined parameter splitThreshold, Oufti divided the cell and began tracking the two new daughter cells. For Fig. 2E, the constriction degree was computed from the cell contour and the inverted phase image. The intensity profile was integrated over the cell and smoothed with a kernel of size 3 pixels with geometric weighting ([0.25 0.5 0.25]). The minimum value (depth of constriction) was then compared to the maximal values on each side of the dip in the profile to obtain a degree of constriction from 0 (no constriction) to 1 (fully constricted). A constriction degree value was computed for each cell at each time point, generating a constriction profile for each cell. For cell-to-cell comparison and averaging purposes, the constriction profile of each cell was then resampled, using linear interpolation, to match the size of the smallest constriction profile, keeping equivalent weights for cells with different numbers of observations (because of different interdivision times).

Fluorescence in situ hybridization microscopy experiment

E. coli MG1655 was grown in M9 supplemented medium (containing 0.2% glycerol, 0.1% casamino acid, 1 μg/ml thiamine) at 37°C until mid-exponential growth phase. The expression of SgrS sRNA was then induced by adding 0.1% α-methylglucoside for 3 min at 37°C. RNA FISH was performed as previously described (Montero Llopis et al., 2010) with some modifications. Instead of using lysozyme, cells were permeabilized in 70% ethanol at room temperature for 10 min. The slides were then incubated at 37°C for 60 min in a 50% formamide solution (50% formamide, 2x DEPC-treated SSC). Hybridization was performed using a mixture of 6 LNA probes (2.5 nM each) at 42°C for 90 min in 50% formamide solution containing 10% dextran sulfate, 2 mM VRC, 40 U RNase inhibitor, 0.1% RNase-free BSA, 0.5 mg/ml E. coli tRNA, 35 μg/ml calf-thymus DNA. The slides were subsequently washed twice in 55% formamide and 2xSSC solution for 15 min at 37°C, followed by a 5-min wash with 1xSSC solution at 37°C. Images were acquired with a 100X/1.40 NA phase contrast objective (Carl Zeiss) on a Nikon Eclipse Ti-U controlled by MetaMorph (Molecular Devices) and equipped with a Hamamatsu Orca-II ER LCD camera. The sequences of the LNA probes were (with the LNA nucleotide underlined): 5′-AACCAGCACAACTTCGCTGT, TTGTGGGACGCTTAACCAAC, CAGTCCTTCAAGCATGGTTA, AATTGCGGTCATCCCACTGC, ATGCAGGCAAGTCAACTTTC, CACCAATACTCAGTCACACA. All probes were modified with a TYE563 fluorescent dye (Exiqon) at the 5′-end.