Classifying Individuals Based on a Densely Captured Sequence of Vital Signs: An Example using Repeated Blood Pressure Measurements during Hemodialysis Treatment

Abstract

Electronic Health Records (EHRs) present the opportunity to observe serial measurements on patients. While potentially informative, analyzing these data can be challenging. In this work we present a means to classify individuals based on a series of measurements collected by an EHR. Using patients undergoing hemodialysis, we categorized people based on their intradialytic blood pressure. Our primary criteria were that the classifications were time dependent and independent of other subjects. We fit a curve of intradialytic blood pressure using regression splines and then calculated first and second derivatives to come up with four mutually exclusive classifications at different time points. We show that these classifications relate to near term risk of cardiac events and are moderately stable over a succeeding two-week period. This work has general application for analyzing dense EHR data.

Graphical Abstract

Introduction

Compared to other data sources used in medical research, electronic health records (EHRs) contain a very heterogeneous range of data features and structures. This diversity provides many analytic opportunities as well as challenges. One of the unique aspects of some EHRs is the ability to capture dense longitudinal information on patients. These data may consist of, for example, respiratory measurements from an intensive care unit¹ or heart rate measurements from a surgical procedure². Such data present the opportunity to observe and analyze a patient’s changing vital signs over time.

In our current use case, we have blood pressure measurements taken during a hemodialysis (HD) session. Maintenance HD is an outpatient treatment that individuals with end stage kidney disease (ESRD) receive on a regular basis. A typical session occurs three times a week and lasts 3 – 4.5 hrs. During an HD session, regular blood pressure measurements are captured and stored in the electronic health record. With measurements in approximately 15–30 minute increments, a typical session will produce 6–12, so called “intradialytic,” blood pressure readings. In recent years there has been growing interest in how intradialytic blood pressure variability relates to risk of adverse events³.

A typical question that one may consider is: how do changes in intradialytic blood pressure relate to risk of a cardiovascular event? This raises the question of how best to analyze these data. If only one blood pressure measurement were available, one could simply regress the probability of cardiac event onto the blood pressure measurement in the form of a logistic regression. Extensions to this simple model have been proposed in the presence of multiple measurements^4–6. The challenge with these models is that they are difficult to implement and hard to interpret⁷. Instead, work in this area has focused on summarizing these measurements either as a mean, standard deviation, or maximum blood pressure differences during dialysis³. Such summary measures potentially lead to loss of information. Moreover, because the summary metrics are continuous, it makes identifying high risk patients challenging – though many summary measures will get broken into percentile categories.

Instead of summarizing individual blood pressure measures, we consider the task of classifying people based on their blood pressure pattern. By grouping people into mutually exclusive categories, the intention is to identify a high risk category upon which surveillance or treatment interventions could be targeted. Previous work has considered clustering individuals based on curves⁸. While these methods address the classification problem, one drawback is that the clusters are not intrinsic to an individual’s measurements but defined through the joint-distribution of all individuals in the sample. This means that given a different training sample, individuals may find themselves grouped into a different cluster. Moreover, with such cluster analyses it is not clear how best to classify a new individual.

In this paper, we suggest a novel approach for classifying people based on a sequence of measurements. Our goal is to create a simple classification system that can be performed both analytically as well as heuristically. We use regression splines to fit individual curves and then calculate derivatives of these curves to classify individuals based on their patterns at different time points. Our approach is able to classify individuals into mutually exclusive groups, independent of the classifications of others. We then show how these classifications relate to future risk of cardiovascular events. While our data are derived from patients undergoing HD, we emphasize that this approach is appropriate for any dense sequence of measurements.

Methods

Data Sources

We used two data sources for the current analysis: the United States Renal Data System (USRDS) and the EHR from DaVita Inc., a large dialysis organization. The USRDS is a national registry that includes almost all persons with treated ESRD⁹. Its backbone consists of medical claims submitted to Medicare, which is mandated by law to provide coverage to the majority of patients with treated ESRD, regardless of age. DaVita Inc. is the second largest provider of outpatient dialysis in the United States. Its EHR contains detailed information including hemodynamic parameters from each dialysis session. We used an anonymous crosswalk provided by the USRDS Coordinating Center to link the two datasets under a data use agreement between the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) and one of the authors (WCW).

Cohort

We selected all patients with ESRD for at least 90 days, who received maintenance HD at a DaVita facility for the 2-week period between Oct 5, 2008 and Oct 19, 2008. This was an arbitrarily chosen interval meant to represent typical HD. Since our focus was on typical sessions, we required all patients to be on thrice weekly HD and to have attended exactly 6 sessions during these two weeks. We further required that each session be at least 3 hours and no more than 4.5 hours in duration, and patients could not be on nocturnal HD. Additionally, to avoid temporal effects, all sessions for an individual had to start either in the morning (5am – 11am) or afternoon (11am – 5pm). Finally, to allow for ascertainment of medical claims information from the USRDS, patients had to have Medicare Parts A&B coverage by the initiation of the ascertainment window.

Variables

Intradialytic Blood Pressure

In the DaVita EHR, systolic blood pressure (SBP) is measured and recorded approximately every 15 – 30 minutes by an automated sphygmomanometer during each dialysis session. We removed SBP values that were <50 mm Hg, >250 mm Hg, or that were lower than the diastolic BP measurements. For each patient, we used SBP information from the six dialysis sessions during the two-week period specified above.

Additional Covariates

We abstracted data on patient age, sex, and race/ethnicity (white, black, Hispanic, other), time of session start (morning versus afternoon), average SBP at start of HD and at different time-points during HD (see below), and time since diagnosis of ESRD (i.e. dialysis “vintage”)

Outcomes

To assess the stability of the classifications, we abstracted SBP measurements during all dialysis sessions in the subsequent two weeks (Oct 20 – Nov 1, 2008). No restrictions were placed on the timing and number of sessions during this period. We also assessed whether the SBP categorizations were associated with a composite cardiovascular outcome. Using ICD-9 and death codes we ascertained events in the 90 days following the original two-week SBP categorization period: fatal or non-fatal myocardial infarction (MI) (410.**), stroke (433.**, 434.**, 436.**, 437.1*, 437.9*), or cardiac arrest (427.5).

Statistical Analysis

Classifying Serial Measurements

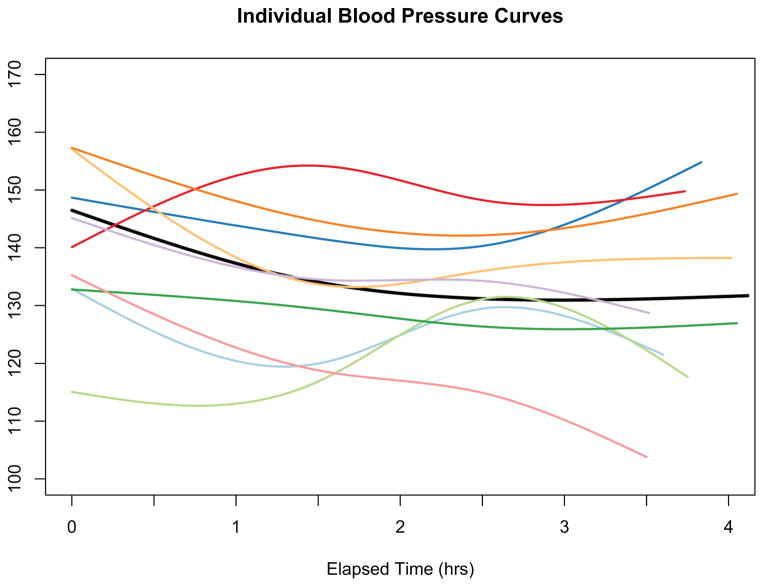
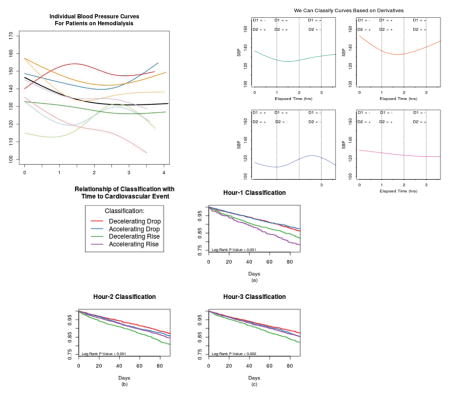
Our analytic challenge was to characterize a series of blood pressure measurements over a time period. As others have described, intradialytic SBP typically follows a non-linear pattern that drops sharply during the first hour of HD and levels off thereafter¹⁰. However as shown in Figure 1 this pattern is not consistent across all people. In devising a classification scheme we considered 2 goals:

Figure 1.

Individual systolic blood pressure curve for nine random individuals. The black represents the average curve for the entire sample. While the average curve shows the expected blood pressure pattern - drop during the first hour and then levelling off - there is noticeable variation across people.

1. We did not want a global classification, but wanted the classifications to take into account the temporality of the measurements.

2. We wanted our classifications scheme for an individual to be independent of the classifications of anyone else.

As a first step, for each individual over the two week period, we modeled the series of SBP measurements as non-linear curves. Multiple procedures exist for curve fitting including, polynomial regression, regression splines, smoothing splines, and locally weighted scatterplot smoothing (LOWESS). We chose to use natural cubic regression splines, but also explored other approaches, and emphasize that the methods suggested are applicable to any of these approaches. In brief, regression splines consist of piecewise polynomial functions that can change functional form at predefined cut points, called knots. Based on the placement of knots and the degree of the polynomial, one creates a basis, which in our case is a function of the elapsed time within a dialysis session. In order to address the goal of temporality, we sought to classify patients based on their SBP measurements at three time points: Hour 1 (early), Hour 2 (middle) and Hour 3 (late) of dialysis. Therefore, we placed our interior knots at 1.5 hours and 2.5 hours, in order to be equally spaced from the time points of interest, though other knot placements had minimal effect on the results. In addition to the interior knots, natural splines use boundary knots at both the beginning and end of the time sequence. One regresses the outcome (SBP) onto the basis of time, to get parameter estimates. Through the basis transformation and parameter estimates, one can generate predicted values of SBP at given time points, analogously to predicted values in linear regression.

Using the spline fit, we first estimated SBP at each of the three time-points (Hours 1, 2, and 3). Then we determined the slope and curvature by examining the signs of the first and second derivative, respectively. A curve’s first derivative reflects its slope, with positive values indicating an increasing slope and negative values a decreasing slope. The second derivative corresponds to the curvature, with a positive second derivative being convex and a negative one being concave. Physically, convexity and concavity refer to accelerating and decelerating changes respectively. While derivatives of splines can be calculated analytically, to illustrate the flexibility of the approach, we calculated the derivatives by taking first and second order differences. Specifically, after forming the spline basis and estimating the regression parameters, we fitted the model over a dense grid, which served to interpolate SBP measurements in approximately one-second increments. We then took the change in SBP (Δy) divided by the change in time (Δx), to calculate the first derivative and then repeated to calculate the second derivative. Finally, we took the sign of each derivative at the pre-specified time points. Thus at each time point, patients were categorized into one of four groups: Convex-Up, Concave-Up, Convex-Down, Concave-Down. Heuristically, we refer to these classifications as: Accelerating Rise, Decelerating Rise, Accelerating Drop, Decelerating Drop.

Statistical Analysis

To assess the robustness of choice of curve-fitting procedure, we used a subset of the data to fit each individual’s curve. We compared natural regression splines, smoothing splines, LOWESS and cubic polynomial regression, using leave-one-out cross-validation with absolute loss, to assess fit. Specifically, we randomly chose 1000 people and fit a curve using each of the procedures, leaving out one of the BP measurements. We then used this fit to predict the missing measurement. The absolute difference between the observed and predicted fit was calculated. This procedure was iterated across each of the BP measurements and the average of these differences was calculated.

Using the full data, we used natural cubic splines to fit the curves for each individual. After creating the classification, as described above, we assessed each classification’s relationship with outcomes. We fit Kaplan-Meier curves and Cox proportional hazards models for each of the three time points separately. We adjusted each model for the above covariates, and censored people at loss of Medicare Parts A&B coverage, kidney transplant, death due to non-cardiac causes, or at 90 days, whichever was first. Finally, for each individual in the cohort we abstracted the succeeding two weeks of blood pressure measurements, with out placing any of the “regular” restrictions as above. We then reclassified each person and assessed the stability of the classifications by calculating the agreement between the two time periods with the multicategory Kappa statistic¹¹.

All analyses were performed in R 3.1.2.¹²

Results

There were 18,538 patients undergoing maintenance hemodialysis who had exactly six dialysis sessions of 3 to 4.5 hours in duration during the specified two-week period. Of these patients, 5,416 (29%) were excluded based on their insurance payer status, and an additional 3,435 (26%) were excluded for not having a consistent HD start time, leading to a final cohort of 9,687 patients. Table 1 contains descriptive statistics of the study population. Over the two-week period, each patient contributed an average of 52 SBP readings (9 per session) with a maximum of 121 and minimum of 25.

Table 1.

Characteristics of Study Population

Sample	Accelerating Drop 2317 (24%)	Decelerating Drop 5224 (54%)	Accelerating Rise 1549 (16%)	Decelerating Rise 567 (6%)
Gender (female)	43%	38%	39%	36%
Race
White	32%	39%	33%	40%
Black	45%	38%	43%	35%
Hispanic	16%	16%	15%	17%
Other	8%	7%	9%	9%
Age (yrs)*	62 (52, 71)	64 (53, 73)	66 (54, 74)	66 (55, 75)
Time on Dialysis (yrs)*	3.8 (1.9, 6.4)	3.6 (1.7, 6.3)	3.4 (1.6, 5.9)	3.1 (1.4, 5.8)
Start Blood Pressure (mm/Hg)*	146 (132, 161)	149 (134, 164)	138 (124, 153)	140 (124, 155)
Time of Day (morning)	80%	79%	75%	73%
Hour 2 Classification
Accelerating Drop	24%	6%	59%	1%
Decelerating Drop	76%	38%	20%	0%
Accelerating Rise	0%	11%	17%	73%
Decelerating Rise	0%	46%	5%	27%
Hour 3 Classification
Accelerating Drop	8%	42%	22%	60%
Decelerating Drop	42%	9%	32%	0%
Accelerating Rise	0%	20%	3%	30%
Decelerating Rise	50%	29%	43%	10%

^*Median and Interquartile range

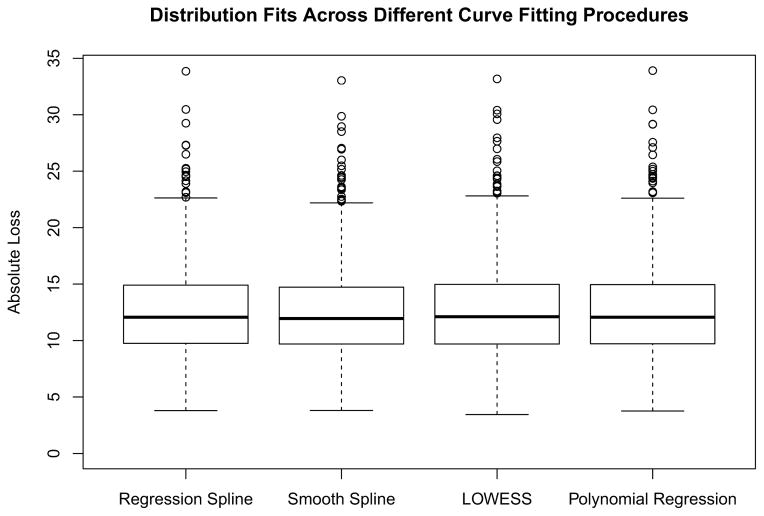
Using a random subset of 1000 people, we fit individual curves using four different curve fitting procedures. Figure 2 contains the fits with absolute loss based on leave-one-out cross-validation. There is virtually no difference in the overall fits among the four different algorithms, suggesting that each approximates an individual SBP curve equally well.

Figure 2.

Box plot comparing fits based on different curve fitting procedures. The predicted blood pressure versus the observed blood pressure under leave-one-out cross-validation is shown. There are minimal differences between the different methods.

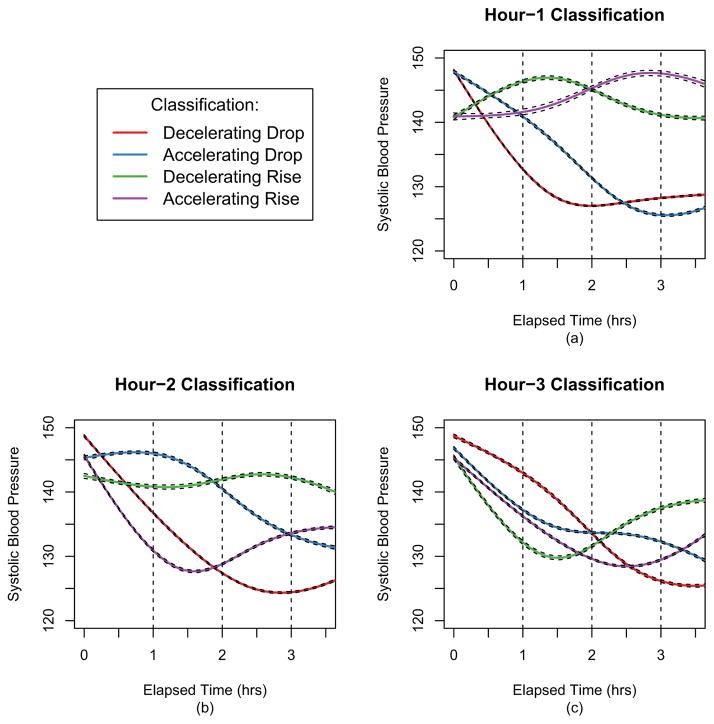
Among all patients, when classifying patients at 1 hour, 78% of patients had SBP that was dropping: 54% with Decelerating Drop and 24% with Accelerating Drop (Table 1). Patients categorized as Decelerating Drop generally had the lowest average SBP (132 mm/Hg) at 1 hour compared with patients in the other three categories (Figure 3a). When classifying patients at 2 hours, patients who are Decelerating Drop or Accelerating Rise at this time point have similarly lower mean SBP compared with patients who are Decelerating Rise or Accelerating Drop at this time point (Figure 3b). By 3 hours, differences in mean SBP among the patients are smaller (Figure 3c).

Figure 3.

The average systolic blood pressure curves for individuals at each of the classification points. At hour 1 (a) risers tend to start with lower SBP. At hour 2 (b) the greatest distinction is between the accelerating droppers & decelerating risers versus the decelerating droppers & accelerating risers. At hour 3 (c) there is more similarity across the different groupings.

Short-term Outcomes Related to SBP Pattern

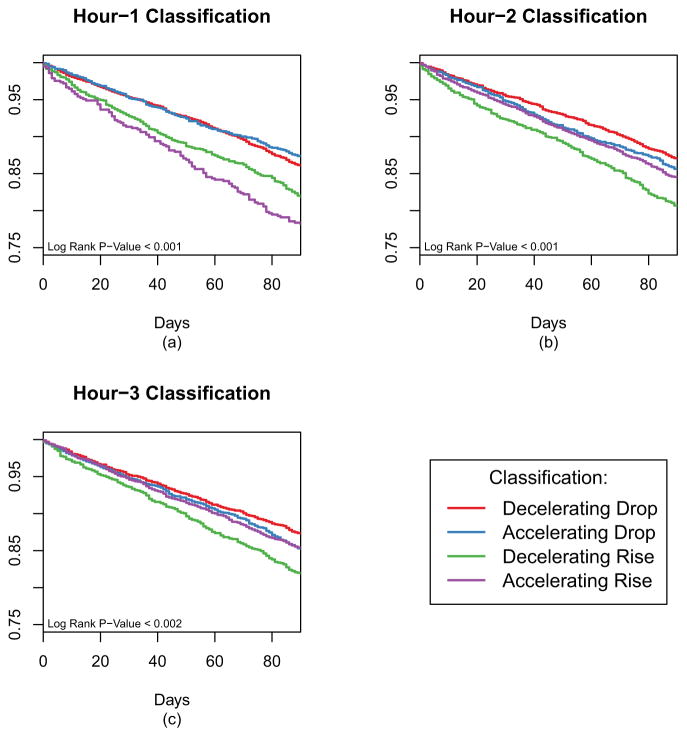
During the 90-day outcome ascertainment window, 1408 patients (14.5%) had a cardiovascular event, with the most common event being an MI. Using the 1 hour classification, patients with SBP rising (either Accelerating or Decelerating Rise) had worse outcomes than patients with dropping SBP (Figure 4a). However, classifying patients at 2 hours (Figure 4b), there is clear distinction based on the type of increase with patients categorized as Decelerating Rise having the worst prognosis and patients with Decelerating Drop at this time point having the best outcome. When classifying patients at 3 hours, outcomes were not significantly different among the four categories (Figure 4c). In adjusted models, the patterns remained generally the same as the Kaplan-Meier analysis, with the 1 and 2 hour classifications providing the best differentiation with regard to subsequent short-term cardiovascular risk (Table 2). In general, having a Decelerating Drop was associated with the best outcomes while having an Decelerating Rise was associated with the worst outcomes. We considered the joint effect of classifications at different time points by examining interactions between a classification at hour 1 and hour 2 (for example) but did not find any effect heterogeneity.

Figure 4.

Kaplan-Meier curves for time to a cardiac event (in 90 days) based on classifications. While each of the classification has significant differences, the greatest effects are seen at the hour 1 classification (a) and hour 2 classification (b).

Table 2.

Time to Cardiac Event – 90 Days of Follow-up

	1 hour	2 hour	3 hour
Accelerating Droppers	---	---	---
Decelerating Droppers	0.84 (0.72, 0.98)	0.93 (0.78, 1.10)	1.03 (0.87, 1.20)
Accelerating Risers	1.08 (0.88, 1.31)	1.20 (1.00, 1.43)	1.18 (0.98, 1.42)
Decelerating Risers	1.42 (1.14, 1.76)	1.12 (0.99, 1.28)	1.02 (0.87, 1.19)

- Adjusted for: Age, Sex, Race, Timing of Session, Starting SBP and at Each Time Point, Vintage

Stability of Classifications

To assess the stability of the classifications, we classified individuals based on their dialysis sessions from the following two weeks. We found that 71% patients categorized as Decelerating Drop at Hour 1 in the first two weeks remained in that category in the next two weeks. These percentages dropped to 60% and 38% at Hour 2 and Hour 3, respectively. Other SBP categories were less stable (Table 3). Overall, we found only modest agreement in SBP categorization in successive 2-week intervals at Hour 1 (Kappa = 0.30), Hour 2 (Kappa = 0.28) and Hour 3 (kappa = 0.18).

Table 3.

Stability of Classification in the Next 2 Weeks

1 hour – Classification
Original Classification	Acc Dropper	Dec Dropper	Dec Riser	Acc Riser
Acc Dropper	42%	44%	11%	3%
Dec Dropper	20%	71%	6%	3%
Dec Riser	19%	25%	44%	13%
Acc Riser	9%	37%	28%	25%
Overall Kappa 0.30

2 hour – Classification
Original Classification	Acc Dropper	Dec Dropper	Dec Riser	Acc Riser
Acc Dropper	40%	33%	15%	11%
Dec Dropper	15%	60%	6%	19%
Dec Riser	21%	21%	31%	27%
Acc Riser	7%	33%	11%	49%
Overall Kappa 0.28

3 hour – Classification
Original Classification	Acc Dropper	Dec Dropper	Dec Riser	Acc Riser
Acc Dropper	44%	20%	11%	25%
Dec Dropper	31%	38%	4%	28%
Dec Riser	29%	5%	30%	37%
Acc Riser	26%	16%	12%	45%
Overall Kappa 0.18

Discussion

In this paper we suggest a means of classifying individuals based on a series of longitudinal clinical measurements using the example of repeated blood pressure measurements routinely taken during HD sessions of patients with ESRD. This approach is based on characterizing the shape of a curve at different time points. By using a curve fitting procedure, such as splines, we calculated the signs of first and second derivatives. This results in one of four mutually exclusive classifications for each time point of interest.

Characterizing longitudinal measurements can be challenging. In the statistical literature, most work has focused on clustering of functional data. These approaches have a downside in that the defined clusters depend on the sample used to estimate them. Therefore there is nothing intrinsic about an individual’s classification making it challenging to classify a new individual. The clinical literature has approached this problem by summarizing measurements over the entire period of observation, such as a dialysis session or membership in a closed cohort³, typically as means or standard deviations. This approach can miss more subtle characteristics of the series of measurements.

Our analysis shows that intradialytic SBP patterns relate to short-term risk of experiencing a cardiovascular event. Although it has long been recognized that patients on HD with rising blood pressure during dialysis (i.e., intradialytic hypertension) have poorer prognosis than patients with a fall in blood pressure^13–15, we found that the relation is more complex and nuanced than that of simply rising or falling SBP. While at the 1 hour time point of HD, patients with falling SBP, regardless of accelerating or decelerating, have a lower risk of cardiac events than patients with increasing SBP at 1 hour, the same was not true at the 2-hour time point. Rather, patients with a decelerating drop in SBP at the 2-hour time point had the lowest risk of cardiovascular events, while patients having an accelerating drop or decelerating rise had an intermediate risk, and patients with an accelerating rise in SBP at the 2-hour time point had the highest risk of short-term cardiovascular events. By the 3-hour time point of HD, we saw no significant differences in risk of cardiovascular events among the four categories of SBP patterns. Our results suggest that assessing patterns of intradialytic SBP at different HD time points may provide important prognostic information to clinicians.

Our approach also has potential applications across a broad area of analyses within medical studies that capture a dense sequence of measures, whether in research studies or in health data routinely captured during the typical care of patients. For example, in the intensive care unit, respiratory rates can be used to assess risk of lung injury¹⁶; beat-to-beat heart rate variability from continuous electrocardiogram monitoring can help predict outcomes after stroke ^17,18; implant devices measuring blood pressure can assess risk of inflammation¹⁹. However, the use of EHRs also provides an opportunity to analyze integrated laboratory, comorbidity and hemodynamic information over time. Whether interventions based on real-time patterns of intradialytic SBP, perhaps in combination with other EHR data, will ultimately result in improved clinical outcomes remains to be tested in future studies.

Our work has several strengths and limitations. We took advantage of a large dataset to identify a relatively homogenous sample of patients undergoing regular hemodialysis. By requiring patients to have exactly 6 outpatient sessions we ensured that patients were not hospitalized (i.e. particularly ill) during the study period. We were able to illustrate that our method is robust to choice of curve fitting procedure. Furthermore we were able to assess the stability of the classification by looking at what classifications may be in the next two week period. Finally, our approach is very computationally easy since it is done on the individual level. This also means that it does not require any outside information. However, for this reason, this method will not apply well to all serial measurements in an EHR, but instead requires a minimal density of measurements to appropriately estimate the individual curves. For example this approach will likely not work as well with laboratory measurements that are taken more sporadically, requiring different analytic approaches²⁰. Additionally the proposed approach does not consider the magnitude of the derivatives. Our focus was on creating a simple classification system that could be observed in real time. However a method that explicitly considered the degree of change could result in a stronger, albeit more complicated predictor. The “functional data analysis” literature²¹ addresses this approach and future work could extend in this direction.

Overall we suggest an approach to classify individuals based on serially collected EHR data. This is an important and still open question that is worthy of further exploration from a joint statistical, informatics and clinical perspective.

Highlights.

• Electronic Health Records capture dense clinical information on patients

• Methods are needed to classify people based on clinical data

• We use splines to fit individual curves & classify people on curves’ derivatives

• We illustrate the approach on blood pressure measurements captured during hemodialysis

• The different classifications relate to risk of cardiovascular events