Determinants of rebound burst responses in rat cerebellar nuclear neurons to physiological stimuli

Key points

• Cerebellar Purkinje cells project GABAergic inhibitory input to neurons of the deep cerebellar nuclei (DCN) that generate a rebound increase in firing, but the specific patterns of input that might elicit a rebound response have not been established.

• We used recordings of Purkinje cell firing obtained during perioral whisker stimulation in vivo to create a physiological stimulus template to activate Purkinje cell afferents in vitro.

• DCN cell bursts were evoked by the stimulus pattern but not in relation to the perioral whisker stimulus, complex spikes or regular patterns within the Purkinje cell record.

• Reverse correlation revealed that bursts were triggered by an elevation‐pause pattern of Purkinje cell firing, with pause duration a key factor in burst generation.

• Our data identify for the first time a physiological pattern of Purkinje cell input that can be encoded by the generation of rebound bursts in DCN cells.

Abstract

The end result of signal processing in cerebellar cortex is encoded in the output of Purkinje cells that project inhibitory input to deep cerebellar nuclear (DCN) neurons. DCN cells can respond to a period of inhibition in vitro with a rebound burst of firing, yet the optimal physiological pattern of Purkinje cell input that might evoke a rebound burst is unknown. The current study used spike trains recorded from rat Purkinje cells in response to perioral stimuli in vivo to create a physiological pattern to stimulate Purkinje cell axons in vitro. The perioral stimulus‐evoked Purkinje cell firing pattern proved to be virtually ineffective in evoking a rebound burst despite the ability to reliably evoke rebounds using a traditional brief 100 Hz stimulus. Similarly, neither complex spike firing nor Purkinje cell patterns identified by CV2 analysis were reliably associated with rebound bursts. Reverse correlation revealed that the optimal Purkinje cell input to evoke a rebound burst was a sequential increase in mean firing rate of at least 30 Hz above baseline over 250 ms followed by a reduction of 40–60 Hz below baseline for up to 500 ms. The most important factor was the duration of a pause in Purkinje cell firing that allowed DCN cells to recover from a state of net inhibitory influence. These data indicate that physiological patterns of Purkinje cell firing can elicit rebound bursts in DCN cells in vitro, with pauses in Purkinje cell firing rate acting as a key stimulus for DCN cell rebound responses.

Key points

• Cerebellar Purkinje cells project GABAergic inhibitory input to neurons of the deep cerebellar nuclei (DCN) that generate a rebound increase in firing, but the specific patterns of input that might elicit a rebound response have not been established.

• We used recordings of Purkinje cell firing obtained during perioral whisker stimulation in vivo to create a physiological stimulus template to activate Purkinje cell afferents in vitro.

• DCN cell bursts were evoked by the stimulus pattern but not in relation to the perioral whisker stimulus, complex spikes or regular patterns within the Purkinje cell record.

• Reverse correlation revealed that bursts were triggered by an elevation‐pause pattern of Purkinje cell firing, with pause duration a key factor in burst generation.

• Our data identify for the first time a physiological pattern of Purkinje cell input that can be encoded by the generation of rebound bursts in DCN cells.

Abbreviations

aCSF

artificial cerebrospinal fluid

CV2

coefficient of variation 2

DCN

deep cerebellar nuclear

ISI

interspike interval

IPSP

inhibitory postsynaptic potential

Introduction

Ion channels localized to pre‐ and postsynaptic elements of neural networks regulate spike patterns to encode information. A limited number of cell types express ion channels that allow for a rebound response in the firing of a postsynaptic cell following inhibitory input. Cells that are capable of producing a rebound response are found in the deep cerebellar nuclei (DCN) that provide the only output from the majority of cerebellum. DCN cells in rats typically fire spontaneously at low frequency with Purkinje cells providing inhibitory input as the primary signal from cerebellar cortical circuitry. A rebound response allows DCN cells to respond to Purkinje cell inhibition with a graded increase in spike firing or a transient burst (De Zeeuw et al. 2011; Person & Raman, 2012 a; Heck et al. 2013; Steuber & Jaeger, 2013).

The ionic mechanisms that underlie rebound bursts in DCN cells have been extensively examined using in vitro slice preparations and modelling (Alvina et al. 2009; Zheng & Raman, 2009; Sangrey & Jaeger, 2010; Tadayonnejad et al. 2010; Feng et al. 2013; Schneider et al. 2013; Steuber & Jaeger, 2013). The typical means to evoke a rebound burst in vitro has been through current‐evoked membrane hyperpolarizations or by delivering a short duration, high frequency synaptic stimulus train (i.e. 100 Hz, 10 pulses) to Purkinje cell afferents. These stimuli reliably evoke a rebound response that can be further distinguished according to firing pattern into several rebound burst phenotypes (Uusisaari et al. 2007; Hurlock et al. 2009; Hoebeek et al. 2010; Pedroarena, 2010; Sangrey & Jaeger, 2010; Tadayonnejad et al. 2010; Steuber et al. 2011). However, the manner in which rebound bursts contribute to processing Purkinje cell input in vivo has not been clear. Direct patch clamp recordings of DCN cells in vivo confirmed the ability to evoke rebound responses upon delivering a traditional high frequency stimulus directly to Purkinje cells of the overlying cerebellar cortex (Hoebeek et al. 2010), or by optogenetic modulation of Purkinje cell firing (Witter et al. 2013; Heiney et al. 2014). The most promising stimulus is activation of inferior olivary nuclei and synchronous input by climbing fibre afferents (Hoebeek et al. 2010; Bengtsson et al. 2011; Steuber & Jaeger, 2013). Yet the features of a physiological pattern of Purkinje cell input that might be encoded through rebound burst generation in DCN cells have not been fully determined. Even our understanding of the nature of Purkinje cell firing, and thus the spike train that could be encoded by DCN cells, is in flux (De Schutter & Steuber, 2009; De Zeeuw et al. 2011; Person & Raman, 2012 b; Heck et al. 2013; Herzfeld et al. 2015). Purkinje cells recorded in awake unanaesthetized decerebrate cats exhibit a tonic discharge of essentially unvarying frequency in the absence of sensory input (Bengtsson et al. 2011). A coefficient of variation 2 (CV2) analysis of Purkinje cell firing in both awake and anaesthetized rats or mice identified regular spiking patterns of up to hundreds of milliseconds duration (Shin et al. 2007). Of equal potential value to encoding information are pauses in Purkinje cell firing rate (Shin & De Schutter, 2006; Steuber et al. 2007; De Schutter & Steuber, 2009; Yartsev et al. 2009; Cao et al. 2012; Heiney et al. 2014; Zhou et al. 2015). Finally, the synchronicity of either spike discharge or pauses in Purkinje cell firing have emerged as important factors controlling DCN cell output (De Schutter & Steuber, 2009; Person & Raman, 2012 b; Heck et al. 2013; Herzfeld et al. 2015).

Several questions thus remain as to whether physiological patterns of Purkinje cell firing can trigger rebound bursts in DCN cells, and if so, to which elements of the presynaptic signal might DCN cells respond with a rebound burst. To test this, we converted spike trains recorded from rat Purkinje cells in vivo in response to perioral whisker stimuli to deliver physiologically relevant stimulus trains to Purkinje cell inputs in vitro.

Methods

Ethical approval

Sprague‐Dawley rats were obtained weekly from Charles River (Sherbrooke, Canada) and maintained and killed according to the guidelines of the Canadian Council for Animal Care and Standard Operating Procedures established by the University of Calgary Animal Resource Centre, and conform to the principles of UK regulations, as described by Drummond (2009). Accordingly, animals were anaesthetized by inhalation of isoflurorane until unresponsive to tail pinch, and killed by decapitation.

Slice preparation

All chemicals were obtained from Sigma (St. Louis, MO, USA) unless otherwise noted. Male rats at postnatal days 12–18 (P12–18) were anaesthetized by gas inhalation of isofluorane until unresponsive to tail pinch and decapitated by guillotine. The cerebellum was dissected out in ice‐cold artificial cerebrospinal fluid (aCSF) composed of (in mm): 125 NaCl, 3.25 KCl, 1.5 CaCl₂, 1.5 MgCl₂, 25 NaHCO₃ and 25 d‐glucose preoxygenated by carbogen (95% O₂, 5% CO₂) gas. Transverse cerebellar slices (240 μm) were cut by Vibratome and placed in medium at 34°C for 60 min before storing in carbogen‐gased aCSF at room temperature (Molineux et al. 2008). Recordings were obtained from slices maintained at 32–34°C on the stage of a Zeiss Axioskop II microscope and cells were visualized through differential interference contrast optics and infrared light transmission.

Electrophysiology

Whole‐cell patch recordings were obtained using Multiclamp 700B amplifiers and pClamp software (Molecular Devices, Sunnyvale, CA, USA) with a DC 10 kHz bandpass filter. Current clamp recordings used an electrolyte of (in mm): 130 potassium gluconate, 0.1 EGTA, 10 Hepes, 7 NaCl, 0.3 MgCl₂, pH 7.3 via KOH, with 5 di‐Tris‐creatine phosphate, 2 Tris‐ATP and 0.5 Na‐GTP added from fresh frozen stock each day. Electrodes had a resistance of 6–8 MΩ and access resistance 8–15 MΩ, with cells rejected for any drift in access resistance of > 20%. A calculated junction potential of –10.7 mV was subtracted from current clamp recordings. All excitatory synaptic transmission was blocked during recordings using bath applied dl‐AP5 (25 μm), DNQX (10 μm, Tocris, Ellisville, MO, USA), and mGluR blockers MPEP (1 μm), CPCCOEt (10 μm) and JNJ1625958 (1.5 μm). Data analyses were performed using a combination of pCLAMP 10, Origin 8.0 (OriginLab, Northampton, MA, USA), and custom‐made Matlab scripts.

Recordings were confined to putative output cells identified by a large soma diameter (15–20 μm) that exhibited a set of three spike afterpotentials and spontaneous discharge of spikes at least 65 mV in amplitude (Uusisaari et al. 2007; Molineux et al. 2008; Uusisaari & De Schutter, 2011). To provide a similar baseline membrane voltage from which to compare the activity of different cells, resting membrane potential was adjusted by bias current injection to between –60 and –65 mV at the trough of spike afterhyperpolarizations (−61 ± 1.85 mV, n = 17). Under these conditions spontaneous spike frequency varied between 3.5 and 17.6 Hz for Transient burst and 3.8–10.2 Hz for Weak burst neurons, with no statistical difference in the mean firing rate between the population of Transient burst cells (8.9 ± 1.9 Hz, n = 8) and Weak burst cells (10.7 ± 3.1 Hz, n = 9; P = 0.5).

Stimuli

Recordings of Purkinje cell firing in vivo were generously provided by S. L. Shin and E. deSchutter (Okinawa, Japan) from anaesthetized rats during whisker stimulation presented at 2 s intervals (as per Shin et al. 2007). Purkinje cell spike trains were time‐stamped using custom Matlab scripts and converted to pulse trains (100 μs pulses) that were delivered as digital‐to‐analog signals through PClamp software to a stimulus isolation unit (Digitimer, Welwyn Garden City, UK) connected to a concentric bipolar stimulating electrode (Frederick Haer, Bowdoin, ME, USA). Stimulating electrodes were placed near the dorsal junction of the interpositus and lateral DCN in transverse tissue slices. To standardize the intensity of stimulation, we first established the maximal evoked inhibitory postsynaptic potential (IPSP) to a single stimulus and then reduced the stimulus to evoke an IPSP amplitude 60% of maximum. Stimulus intensity was also limited to a maximum of 30 V to avoid any electrolysis or tissue movement during presentation of full physiological spike trains. In all cases the stimulating and recording sites were directly monitored by video imaging and detection of either effect led to rejection of recorded data. A separate test of the reliability of burst output in response to the Purkinje cell input delivered the stimulus train six separate times to a Weak burst cell that maintained parameters within our acceptance criteria. These tests established that a given DCN cell discharged the first spike of 113 bursts with an extremely high probability (0.82 + 0.05) and within a 135 ± 42.4 ms time window over 100 s of stimulation, establishing a highly reliable response to a rat Purkinje cell spike train (data not shown).

Synaptic connectivity was judged acceptable if cells responded at 60% maximum intensity with a detectable IPSP, with single stimuli evoking an IPSP of −12.7 ± 1.54 mV (n = 17). Data were only accepted if spike amplitude and spontaneous activity continued as in control conditions and the evoked IPSP amplitude and rebound burst capability were retained following the physiological stimulus. If a subsequent physiological stimulus was to be delivered we first verified the integrity of the evoked IPSP, spike discharge and the ability to evoke a rebound response by delivering a 25 pulse 50 Hz test stimulus at least 1 min prior to the physiological stimulus. While long‐term plasticity of evoked IPSPs has been reported in the Purkinje–DCN synaptic relay (Aizenman et al. 2000), we found no significant long‐term change in IPSPs or the rebound response properties evoked by the stimulus patterns used here. The data presented in the current study were derived from a total of eight Transient burst and nine Weak burst neurons that met these criteria.

Data analysis

Custom Matlab scripts were used to extract segments of the recordings of DCN cell firing frequency before and following each stimulus to construct a stimulus‐triggered average in relation to perioral whisker stimuli. Baseline firing rate was defined as the mean frequency of spontaneous firing over 10 s of rest in each cell. While initial tests included potential bursts consisting of 1–2 interspike intervals (ISIs; reflecting 2–3 sequential spikes), we found a great deal of variability that might reflect an inability to distinguish bursts of this short a duration. We therefore restricted analysis to bursts consisting of at least two sequential ISIs (three spikes or more). DCN cell spike output was considered to reflect a rebound response if the instantaneous frequency exceeded 2× the standard deviation of the rate of spontaneous firing of that specific cell for at least two consecutive ISIs (≥ 3 spikes). We note that our use of a resting firing rate as the point of comparison to define rebound firing frequencies will, if anything, overestimate the number of rebound responses. The end of a burst was signified by the first spike of the first ISI that fell outside our burst criteria.

Instantaneous frequency plots were constructed by convolving each spike with a Gaussian kernel with a standard deviation inversely proportional to the firing frequency (Steuber et al. 2011). The Gaussian standard deviation ${\sigma }_k$ for each spike k was set to:

$${\sigma }_k=min\left(IS{I}_{\mathit{before}},IS{I}_{\mathit{after}}\right)\sqrt{2\pi }$$

where ISI_before and ISI_after are the ISIs directly before and after the spike. This limits the individual contribution of each spike to the maximum instantaneous rate preceding or following a spike (Steuber et al. 2011). We also used CV2 to measure the short term regularity of our Purkinje cell inputs in order to delineate regular patterns of Purkinje cell firing (see Shin et al. 2007) according to:

$$\mathrm{C}{\mathrm{V}}_2=\frac{2\left|IS{I}_{n+1}-IS{I}_n\right|}{\left(IS{I}_{n+1}+IS{I}_n\right)}$$

Statistics

Average values are reported as mean (SEM) and statistical comparisons were performed using pairwise and two‐tailed Student t tests in Origin software.

Results

Recordings were obtained from large diameter DCN neurons in the interpositus and lateral nuclei. The ability of cells to exhibit a rebound response was initially tested using a conventional 500 ms step hyperpolarizing current pulse, and identified as exhibiting a Transient or Weak burst phenotype (Molineux et al. 2006; Tadayonnejad et al. 2009). A difference in rebound burst frequency was apparent for current‐evoked hyperpolarizations restricted to membrane potential shifts to ∼–75 mV (the predicted E _Cl), with an increase in spike frequency in Transient burst neurons of 161.6 ± 28.54 Hz (n = 8) and in Weak burst neurons of 15.4 ± 5.53 Hz (n = 9) (Fig. 1 A). Stimulation of Purkinje cell axons at 60% maximum intensity evoked an inhibitory postsynaptic current with a peak amplitude of 60.7 ± 17.5 pA and peak latency of 6.2 ± 0.64 ms (n = 17) (Fig. 1 B). Repetitive stimulation at 50 or 100 Hz evoked an initial peak membrane hyperpolarization that often approached the predicted E _Cl, followed by a progressive decrease in IPSP amplitude (Fig. 1 B and C), as expected for Purkinje cell inputs to DCN cells (Telgkamp & Raman, 2002; Pedroarena & Schwarz, 2003). Before delivering the Purkinje cell stimulus pattern, the rebound phenotype of each DCN cell was identified using a pair of control tests consisting of a 500 ms hyperpolarizing current step or a train of 25 stimuli at 100 Hz (Fig. 1 A and C). Only cells that exhibited a statistically defined rebound burst in response to these control stimuli were included for study. The stimulus template of 100 s of Purkinje cell firing was then used to activate Purkinje cell afferents and record the DCN cell response.

Figure 1. Control recordings in large diameter DCN neurons .

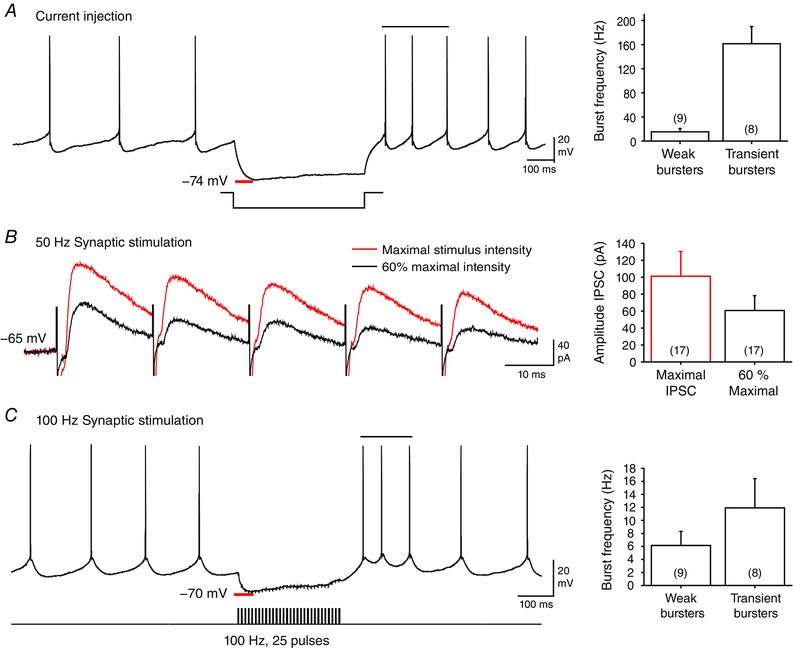
A, injecting a hyperpolarizing current step triggers a rebound firing increase in a Weak burst neuron, with statistically defined burst ISIs indicated by a horizontal bar. Bar plots show peak burst frequencies (above baseline firing rates) for Weak and Transient burst neurons following current pulses that approach E _Cl (−75 mV). B, a 50 Hz train of evoked inhibitory postsynaptic currents at maximal intensity (red trace) exhibits a characteristic depression over repeated stimuli. The intensity of Purkinje cell axon stimulation was adjusted to ∼60% of maximum and the stimulus train was superimposed (black trace). C, stimulating Purkinje cell synaptic inputs with a 100 Hz (25 pulse) train inhibits a representative Transient burst DCN neuron and elicits a rebound burst. Bar plots indicate the average peak frequency in Transient and Weak burst phenotypes. Statistically defined burst ISIs are indicated by a horizontal bar. Stimulus artefacts in B and C were digitally reduced.

Physiological stimulus characteristics

The Purkinje cell physiological spike train to deliver in vitro was originally collected in anaesthetized rats in vivo during presentation of 49 perioral whisker stimuli at approximately 2 s intervals over 100 s recording time (Shin et al. 2007). While the continuous record of 100 s of Purkinje cell firing was used to stimulate afferents in the slice, much of the analysis centred on perioral whisker stimuli by parsing the recording into 2 s segments in relation to the stimulus times. The mean instantaneous frequency of Purkinje cell firing was then calculated over a period of 500 ms pre‐stimulus to 1500 ms post‐stimulus time (Fig. 2 A). The baseline firing rate was 66.1 ± 28.62 Hz (n = 49) with perioral whisker stimuli invoking an increase in frequency of up to ∼110 Hz within 200 ms. The peak increase in firing was then followed by a decrease in frequency to an absolute value of ∼40 Hz (∼30 Hz below baseline) between ∼500 and 1300 ms following the stimulus (Fig. 2 B). The mean rate of firing over the last 500 ms of recording following each stimulus (67.3 ± 29.81 Hz, n = 49) was not significantly different from the pre‐stimulus baseline frequency (P = 0.81 Student's paired t test), indicating a recovery within 2 s of the stimulus applied to evoke these records.

Figure 2. Sensory‐evoked cell spike patterns recorded in vivo .

Records of Purkinje cell firing to perioral whisker‐evoked stimuli delivered every 2 s in recordings from an anaesthetized rat in vivo (Shin et al. 2007). In A and B, the 100 s recording is parsed into 2 s segments in relation to perioral whisker stimulus times, with 500 ms baseline of spontaneous firing preceding a stimulus and 1500 ms following (total of 49 stimuli per recording). Red lines at 500 ms indicate the timing of individual perioral whisker stimuli. A, raster plot of the timing of spike discharge in relation to each of the 49 separate perioral whisker stimuli, shown as individual rows. B, mean frequency of Purkinje cell firing as shown in A for all 49 sensory stimuli, with the grey shaded area reflecting the SEM. C, histogram of instantaneous event frequencies for the records shown in A. Red dashed line indicates the reported somatic spike frequency of 257 Hz at which axonal condition becomes less reliable (Monsivais et al. 2005).

While Purkinje cell axons have been reported to be capable of firing at rates of ∼438 Hz, we considered that the fidelity of transmission can become unreliable at the high frequencies inherent to complex spikes, with ∼50% failure at frequencies greater than ∼257 Hz (Monsivais et al. 2005). By plotting a histogram of interevent frequencies in the Purkinje cell stimulus file we found that 99.7% of the spike records fell below 257 Hz, with all events falling below 438 Hz (Fig. 2 C). This analysis confirmed that the majority of the spikes that comprised the Purkinje cell stimulus file were generated at rates within the following frequency of Purkinje cell axons. The record also contained 62 complex spikes, the potential significance of which was considered separately (see Fig. 9). We thus used the physiological train of Purkinje cell firing to stimulate a submaximal number of inhibitory afferents (60% maximal stimulus intensity) in a synchronized manner.

Figure 9. Purkinje cell complex spikes are not reliably associated with DCN cell burst responses .

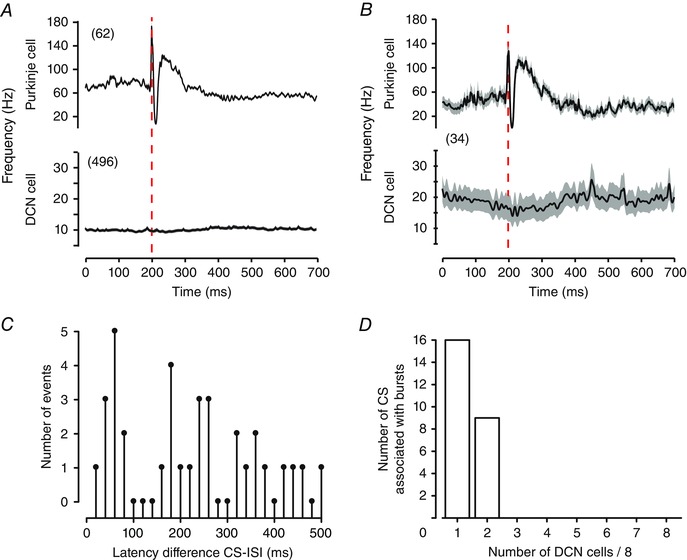
A, spike‐triggered averages of Purkinje cell complex spike responses in the stimulus input file and the associated mean DCN spike frequency response. Shown are the mean values of all complex spikes in the input stimulus file (n = 62) and the mean firing frequency response across all eight Transient burst DCN cells (n = 496). B, spike‐triggered averages of Purkinje cell complex spikes found through reverse correlation within a 500 ms window of a DCN cell burst ISI, and the corresponding average DCN cell response (n = 34). Traces represent mean values (black lines) with SEM indicated by the shaded areas. C, plots of the latency difference between DCN cell burst ISIs and complex spikes that occur within a 500 ms window preceding burst ISIs (10 ms bin width). D, plots of the ability of a specific complex spike within the Purkinje cell input file (n = 61) to be associated with burst ISIs when presented to eight Transient burst cells. Traces in B reflect mean values (black lines) with SEM indicated by the shaded areas.

Physiological stimulation

The Purkinje cell input pattern evoked a complex modulation of DCN cell membrane potential and firing rate depending on instantaneous input frequencies.

IPSPs

Examples of DCN cell responses to the Purkinje cell stimulus input pattern are shown in Figs 3 and 4 A. Most cells responded to the 100 s of stimulation with an initial rapid hyperpolarization towards E _Cl, and then a progressive depolarizing shift in the peak of the AHP trough (as an estimate of membrane potential) to a relatively stable baseline between −55 and −65 mV within ∼5 s of initiating the stimulus (Figs 3 A and 4 A). The extent to which the depolarizing shift in potential reflected a process of synaptic depression (Telgkamp & Raman, 2002; Pedroarena & Schwarz, 2003; Pedroarena, 2010), activation of depolarizing currents (i.e. I _H, I _NaP) (Sangrey & Jaeger, 2010; Engbers et al. 2011), a shift in driving force to E _Cl or the influence of conductance changes associated with tonic firing was not further examined here. The ability to detect individual IPSPs with normal amplitude near the end of the 100 s of stimulation indicated that IPSPs were not undergoing progressive failure or rundown. IPSP amplitude could also exhibit an apparent recovery from stimulus‐evoked decreases within tens of milliseconds. The amplitude of IPSPs during the physiological stimulus train was thus extremely variable and difficult to interpret based on visual inspection alone.

Figure 3. Physiological patterns of Purkinje cell spike firing evoke complex responses in DCN neurons .

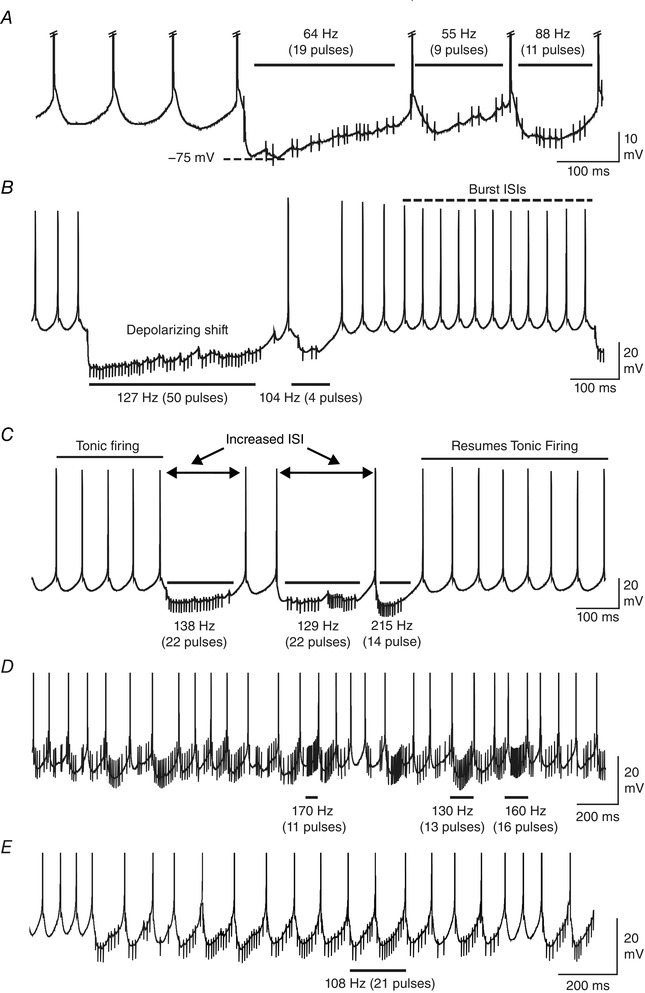
Shown are segments of DCN cell recordings with the mean value of presynaptic Purkinje cell stimuli and the number of pulses over the time periods denoted above horizontal bars. A, a Transient burst cell response reveals that IPSP amplitude and the net effect on membrane potential is highly dependent on subtle changes in the presynaptic stimulus ISI. B, a Transient burst cell showing that a cluster of stimuli at ∼127 Hz can elicit a response that satisfies the criteria of rebound burst ISIs (dashed line), but with a delayed onset from the end of the stimulus. A progressive decrease in IPSP amplitude and a depolarizing shift during Purkinje cell input are apparent. C and D, transient burst cells responding to higher frequencies of input exhibit an increase in the ISI (C) or near continuous firing (D) without rebound responses. E, the response of a different Transient burst cell, with the time of a perioral whisker stimulus shown by the horizontal bar. Spike amplitudes are truncated in A, D and E and stimulus artefacts are digitally reduced.

Figure 4. The DCN cell response to a physiological stimulus pattern of inhibitory synaptic input in vitro .

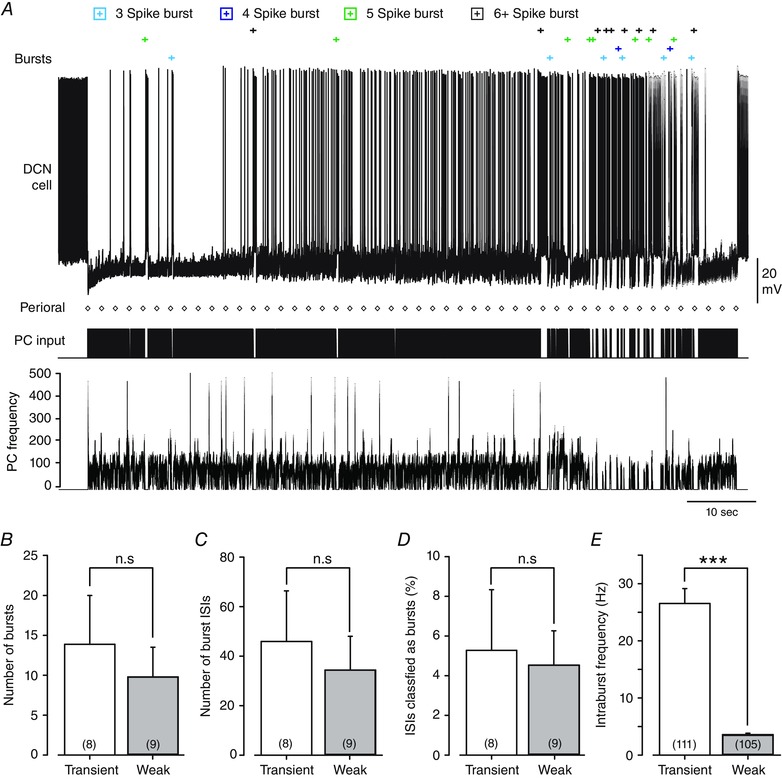
A, a representative Transient burst cell response to the Purkinje cell stimulus template over a full 100 s of stimulation. ISIs that are statistically defined as falling inside the burst criteria are marked at the top (Bursts), with the timing of the first spike of bursts identified according to the legend at the top. The timing of Purkinje cell input is shown below (PC input) together with instantaneous frequency. The timing of each perioral stimulus originally delivered in vivo is shown by diamonds (Perioral). B‐E, bar plots comparing burst discharge of Transient and Weak burst cells in response to the Purkinje cell input train shown in A over the 100 s of all recordings. No statistical differences were detected between Transient and Weak burst neurons in terms of the number of bursts detected (B) (P = 0.57), the number of burst ISIs (C) (P = 0.64) or the percentage of ISIs belonging to the burst category (D) (P = 0.83). E, transient burst cells exhibit a significantly higher mean intraburst frequency compared to Weak burst cells. Sample values shown in parentheses in B–D reflect total animals used, and those in E the total number of bursts in all recordings. Values are mean (SEM) by two‐sample t tests; ***P = 2.3 × 10⁻¹⁵; n.s., not significant.

Spike discharge

The response of DCN cells in terms of spike output was also difficult to interpret given the variable response observed upon even brief changes in the Purkinje cell input stimulus frequency. The Purkinje cell stimulus train hyperpolarized DCN cells to alter spike discharge by at least lengthening the ISI, but could also evoke spikes that fit the criteria of burst ISIs (Fig. 3 B and C). When a rebound burst was generated, the pattern of rebound firing often deviated from the Transient or Weak burst phenotypes evoked using a traditional current pulse or fixed frequency of inhibitory input. Thus, instead of a rapid transition to a burst response of high frequency following a stimulus (Tadayonnejad et al. 2010), many cells exhibited a gradual shortening of ISIs to an interval that fell within the burst criteria (Fig. 3 B), a pattern that has been recognized in the past (Pedroarena & Schwarz, 2003; Hoebeek et al. 2010; Pedroarena, 2010). In many cases a train of Purkinje cell input at even twice the frequency required of a traditional 100 Hz synaptic stimulus failed to elicit a rebound burst response (Fig. 3 C). Other DCN cells would respond to Purkinje cell stimuli by initially slowing in frequency but then essentially resume tonic firing (Fig. 3 D and E). Notably, this failure to evoke a rebound burst was evident even for segments of the physiological stimulus corresponding to the time of perioral whisker stimuli (Fig. 3 E).

Rebound responses

Rebound burst capability to a physiological stimulus was apparent for DCN cells exhibiting either a Transient or a Weak burst phenotype. The incidence of recording rebound burst ISIs is shown over the full 100 s of a Transient burst cell recording in Fig. 4 A. These data emphasize that the stimulus train could trigger relatively few burst ISIs in some cells despite the occurrence of 49 perioral whisker stimuli at ∼2 s intervals within the Purkinje cell train. There were also no statistical differences between Transient and Weak burst cells in terms of the number of bursts (P = 0.57), the number of burst ISIs (P = 0.64) or the percentage of ISIs classified as bursts (P = 0.83) (Fig. 4 B–D). The single significant difference detected was a higher intraburst frequency for Transient burst cells (Fig. 4 E). Interestingly, the greatest number of rebound burst ISIs was detected near the end of the stimulus train (Fig. 4 A). As indicated above, this did not appear to reflect an irreversible rundown of IPSPs, as brief pauses in the Purkinje cell stimulus would allow rapid recovery of IPSP amplitude. However, a distinctive property of the late phase of the Purkinje cell stimulus train was the presence of several pauses in firing over the same relative time frame as when DCN cell burst ISIs were detected (Fig. 4 A). This raised an interesting possibility that irregularity in the Purkinje cell train might exert greater influence over DCN cell rebound responses than the perioral stimuli.

To obtain a better estimate of the DCN cell response we extracted the average Purkinje cell response to the perioral whisker stimulus for direct comparison to the average DCN cell response. Mean spike frequency was calculated for all 49 perioral whisker stimuli across all DCN cells, providing records for 392 stimuli to eight Transient burst cells and 441 stimuli to nine Weak burst cells (Fig. 5 A–C). This analysis revealed that neither Transient nor Weak burst cells showed any substantial change in firing rate even after averaging across all stimuli (Fig. 5 C). We further compared the mean values of DCN cell firing over successive quarterly segments of the recordings (25 s each) and found no progressive change in stimulus‐evoked firing during the stimulation. The results obtained for Transient burst cells are shown in Fig. 5 D, but are qualitatively the same for Weak burst cells (data not shown). While a slight decrease in the mean DCN cell firing could be detected immediately following the stimulus in the fourth segment of recordings, this represented only a 2 Hz change in mean firing frequency (Fig. 5 D). Therefore, despite the fact that each cell responded faithfully to a fixed frequency 100 Hz stimulus with a rebound burst, the mean Purkinje cell firing rate increase to ∼110 Hz following perioral stimuli was essentially ineffective at triggering rebound bursts during the full physiological input train.

Figure 5. Purkinje cell input patterns associated with perioral whisker stimuli do not reliably evoke burst responses in DCN cells .

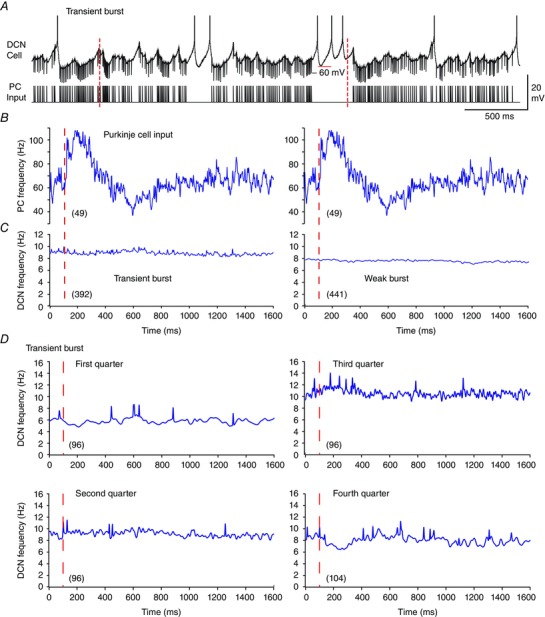
A, a representative and expanded segment of a recording from a Transient burst neuron with the structure of the Purkinje cell input train below. Dashed red lines indicate the timing of two perioral whisker stimuli originally delivered in vivo. B and C, the mean Purkinje cell firing rate (B) for 49 perioral whisker stimuli (red dashed lines) is positioned above the corresponding mean firing frequencies of Transient and Weak burst DCN cells (C). Data are averaged over all stimuli from eight Transient burst cells (left, 392 stimuli) and nine Weak burst cells (right, 441 stimuli), with records spanning from 100 ms preceding to 1500 ms following the stimuli. Note that DCN cell frequency is shown on an expanded scale compared to Purkinje cell input frequency and spikes are truncated in A. D, mean frequency plots of the DCN cell response in each successive quarter (25 s) of the 100 s Purkinje cell stimulus in the case of Transient burst neurons in relation to perioral stimuli as in B and C. The first three quarters each contain 12 perioral whisker stimuli, and the fourth quarter contains 13 stimuli, averaged across all cells in each burst phenotype. Total Purkinje cell stimulus numbers are shown in parentheses.

Reverse correlation

These data highlighted the need to reassess burst firing in DCN cells with respect to the actual pattern of Purkinje cell firing associated with the burst ISIs that were identified. For this we used reverse correlation between identified DCN cell bursts and Purkinje cell firing, irrespective of the actual Purkinje cell perioral whisker stimulus times. The time of the first spike of a defined DCN cell burst (t = 0) was used as the reference point to extract segments of Purkinje cell firing 1 s before and after the burst. The sample numbers for each average record varied between 56 and 66 depending on the number of bursts identified across eight Transient and nine Weak burst cells. The averaged records of firing frequency for all identified bursts (≥ 3 spikes) now identified a common pattern in the Purkinje cell firing rate in relation to DCN cell bursts. Specifically, Purkinje cell firing exhibited a sequential increase in frequency preceding a DCN cell burst, followed by a rapid decrease in firing rate at the onset of the first burst ISI and then a reduction or complete pause in firing before returning to baseline (Fig. 6 A and B). Associated with this ‘Elevation–Pause’ pattern in Purkinje cell firing was a corresponding initial decrease in DCN cell firing, and a subsequent rebound increase in firing during the pause in Purkinje cell firing rate. The magnitude of the rebound frequency increase was most prominent for Transient burst cells, with an elevation in firing of ∼60 Hz before declining to baseline within 500 ms. The Weak burst cell rebound response consisted of an elevation in firing to ∼35 Hz that also dissipated over ∼500 ms (Fig. 6 A and B). The one constant finding was that a rebound burst ISI in DCN cells was always associated with a rapid decrease or pause in Purkinje cell firing frequency.

Figure 6. Reverse correlation reveals the Purkinje cell firing pattern that evokes DCN cell burst ISIs .

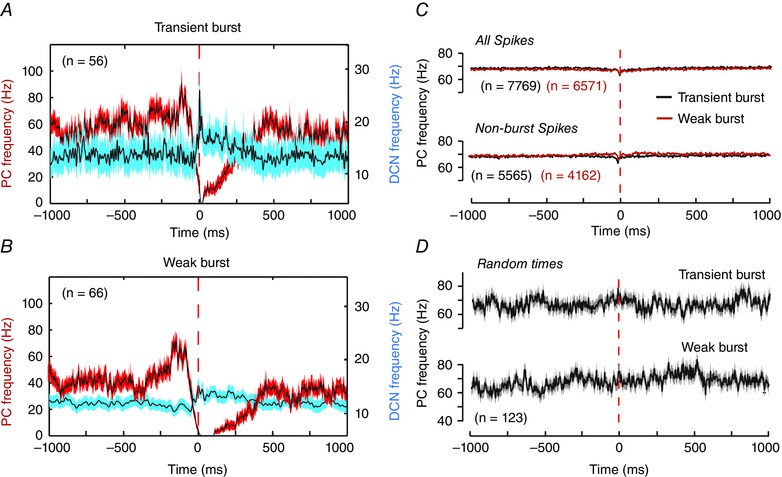
A and B, superimposed mean frequency plots of the Purkinje cell firing rate (red traces) and the associated DCN cell response (blue traces) for Transient burst (A) or Weak burst neurons (B). All data were extracted according to reverse correlation of Purkinje cell firing rates in relation to the timing of the first spike (0 ms) of all statistically defined DCN cell bursts of 3–8 ISIs irrespective of the time of perioral whisker stimuli. Frequencies are shown for data recorded 1 s before and after the timing of the first spike of a defined DCN cell burst. The data are averaged over all bursts collected from eight cells for Transient burst neurons (n = 56) and nine cells for Weak burst neurons (n = 66). C, superimposed records of the mean Purkinje cell firing rates in Transient and Weak burst cells identified when considering all Purkinje cell spikes irrespective of DCN cell burst ISIs (All spikes), or only the Purkinje cell spikes not associated with DCN cell bursts (Non‐burst spikes). D, mean Purkinje cell firing rates calculated in relation to random times of DCN cell responses not reflecting burst responses as controls for any potential non‐white noise statistical structure in the Purkinje cell input. All data are plotted on the same scale for comparison. Traces represent mean values (black lines) with SEM indicated by the shaded areas in A, B and D.

We extended these tests to consider the potential patterns of Purkinje cell firing that might be detected by reverse correlating all the spikes in a DCN record (burst and non‐burst ISIs) or just the non‐burst ISIs (Fig. 6 C). The results were striking in revealing that reverse correlations from DCN cell spikes in either category produced no recognizable pattern of Purkinje cell firing (Fig. 6 C), as compared to spikes corresponding to statistically defined burst ISIs (Fig. 6 A and B). An additional control test assigned random times within DCN cell records (equivalent to the number of multi‐spike bursts in each record) to reverse correlate the mean Purkinje cell firing rate before and after the selected times (Fig. 6 D). These tests confirmed the lack of any non‐white noise statistical structure within the Purkinje cell spike train that could account for the patterns for Purkinje cell firing identified through reverse correlation.

We next examined the characteristics of Purkinje cell firing that might be associated with different intensities of DCN cell rebound bursts (as estimated by the number of spikes in a burst). DCN cell bursts of 3–9 spikes were identified to reverse correlate and extract the mean frequencies of Purkinje cell firing. As the same essential results applied to both Transient and Weak burst cells, only the recordings for Transient burst cells are shown in Fig. 7 A. These comparisons revealed no clear pattern in either the duration or the peak frequency of Purkinje cell firing preceding bursts of varying duration. Thus, the duration of an increase in Purkinje cell firing ranged from 100 to 500 ms and the peak frequency from ∼90 to 110 Hz, but with no clear relationship to the number of ISIs in DCN cell bursts (Fig. 7 A). Rather, the most significant factor in Purkinje cell firing appeared to be the magnitude and duration of a decrease in firing rate just prior to and following the first burst ISI (Fig. 7 A). These initial assessments were confirmed by quantifying different aspects of the Purkinje cell Elevation–Pause pattern in relation to DCN cell bursts (Fig. 7 B and C). The degree of correlation between each of these measures was then assessed in relation to the number of successive DCN cell burst ISIs recorded across all records for eight Transient burst and nine Weak burst neurons (Table 1). As predicted by visual inspection of Purkinje cell firing rate, the duration of the pause in Purkinje cell firing showed a significant linear fit with the length of a DCN cell burst in both Transient burst (R ² = 0.541) and Weak burst cells (R ² = 0.411) (Fig. 7 C). By comparison, no significant relationship was apparent between the number of burst ISIs and the remaining parameters tested (Table 1). However, the current data are important in identifying a general Purkinje cell input stimulus that is sufficient to elicit a rebound response in DCN neurons. Specifically, the relevant pattern corresponds to an elevation in Purkinje cell firing rate to ∼30–60 Hz above baseline over at least 100 ms, followed by a rapid drop in frequency or pause in firing for at least ∼50 ms and up to ∼500 ms. The data are also valuable in confirming that the parameter most correlated to DCN cell spike bursts is a relative pause in Purkinje cell firing.

Figure 7. The intensity of a DCN cell rebound burst is strongly correlated to the duration of a pause in Purkinje cell firing .

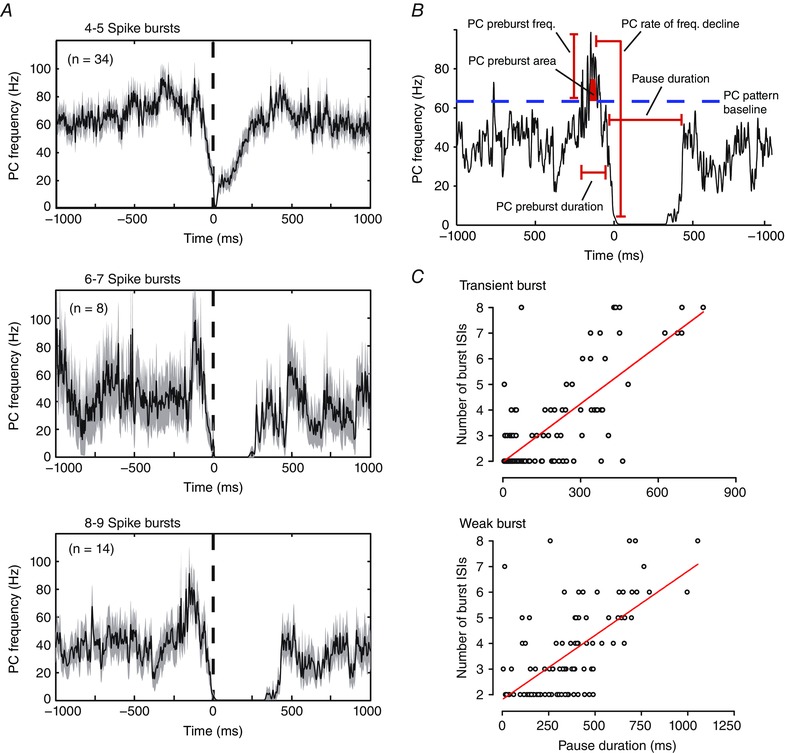
A, average frequency plots of the Purkinje cell firing rate extracted by reverse correlation in relation to the timing of the first spike (0 ms, dashed line) of all Transient DCN cell bursts consisting of the indicated number of ISIs. B, representative average Purkinje cell firing pattern identified through reverse correlation as evoking 8–9 spike bursts in Transient burst cells. Time 0 reflects the timing of the first spike of each statistically defined DCN cell burst ISI. The parameters of Purkinje cell firing measured are indicated, with Purkinje cell frequencies measured with respect to the mean firing rate over the entire 100 s stimulus input (dashed blue line). C, scatter plots of the duration of pauses in Purkinje cell firing (as defined in B) for Transient and Weak burst cells in relation to the number of ISIs in each DCN cell burst. Records include all bursts present across eight Transient burst neurons and nine Weak burst neurons. Traces in A reflect mean values (black lines) with SEM indicated by the shaded areas. Red lines in C reflect linear fits to the data. See also Table 1 for correlation metrics of all parameters indicated in B.

Table 1.

R² values for Purkinje cell reverse correlation metrics

	Rebound burst phenotype
Firing parameter	Transient	Weak
PC preburst frequency	0.006	0.008
PC decline	0.005	0.011
Duration PC preburst	0.109	0.010
PC pause duration	0.541	0.411
PC area preburst firing	0.085	0.069

Shown are the R ² values of the coefficient of determination for the number of DCN cell burst ISIs and mean Purkinje cell firing metrics identified through reverse correlation from the first ISI of DCN cell bursts (as in Fig. 7 B)

Regular Purkinje cell patterns detected through CV2 analysis

Of interest is that the physiological stimulus file implemented here was also used to identify patterns of firing within Purkinje cell spike trains in vivo through a CV2 analysis (Shin et al. 2007). A CV2 analysis is a method to perform a spike‐by‐spike comparison to define successive ISIs that are either of similar or shorter duration than the previous ISI, identifying patterns in firing rate. The CV2 analysis by Shin et al. of the perioral whisker input data showed that 72% of patterns contained only 2–3 spikes, 4% of patterns contained more than 10 spikes, with a maximum of 183 spikes (mean duration 45 ± 3.5 ms). The most common patterns exhibited spike frequencies of ∼65–200 Hz (mean 45.5 ± 4.1 Hz). By comparison, the reverse correlation analysis conducted here defined a Purkinje cell firing frequency increase preceding burst ISIs of up to 200 Hz but in the order of hundreds of milliseconds (Fig. 7 B). We thus compared the occurrence of CV2‐defined patterns of Purkinje cell firing to the frequency increase defined by reverse correlation. To focus our comparisons on the most effective Purkinje cell stimulus–DCN cell phenotype pair, we analysed the response of Transient burst cells, confirming that similar results applied to Weak burst cells (data not shown).

A CV2 analysis of the Purkinje cell stimulus file used here revealed a positively skewed distribution consisting of 6541 values with a mode of 0.02–0.04 (Fig. 8 A). Shin et al. (2007) defined CV2 values below a threshold value of 0.2 as corresponding to a pattern of Purkinje cell firing. In our Purkinje cell stimulus file, 3664 values fell below the 0.2 threshold (56% of total values), defining 643 patterns. An analysis of the duration of CV2‐defined patterns revealed a positively skewed distribution with 78% less than 50 ms in duration (Fig. 8 B). This relationship differed considerably from the duration of the Purkinje cell frequency increase identified by reverse correlation, which exhibited a normal distribution (R ² = 0.95, F _1,4 = 389.54, P < 0.05) with the highest number of events ∼700 ms duration and only 0.4% of events shorter than 50 ms (Fig. 8 B).

Figure 8. CV2 defined patterns in Purkinje cell firing are not reliably associated with DCN cell burst responses .

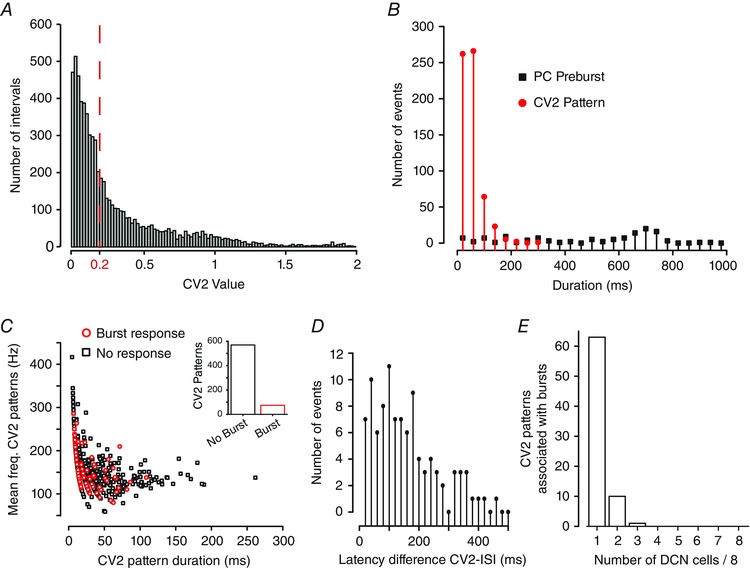
A, histogram plot of the CV2 scores for each ISI in the Purkinje cell stimulus input pattern (0.02 bin width). The red dashed line indicates the threshold CV2 below which ISIs are deemed to belong to a pattern (as in Shin et al. 2007), defining 643 patterns. B, plots of the number of defined CV2 patterns in the Purkinje cell stimulus input file of a given duration compared to the duration of Purkinje cell frequency increases preceding a defined burst ISI in Transient burst cells (see Fig. 7 A). Data are binned at 20 ms. C, scatter plot of Purkinje cell spike frequency versus duration of CV2 patterns sorted for those associated with a DCN burst response (red) or no burst response (black). Inset: the number of patterns that did or did not associate with DCN bursts. D, plot of the latency difference between DCN cell burst ISIs and CV2‐defined patterns in Purkinje cell firing that occur within a 500 ms window preceding burst ISIs (10 ms bin width). E, bar plots of the number of DCN cells in which a burst ISI was detected within 500 ms of a specific CV2‐defined pattern in the Purkinje cell stimulus input when presented to eight Transient burst cells.

To determine if CV2 patterns might be associated with DCN cell bursts, we used reverse correlation to identify any CV2 patterns that fell within the preceding 500 ms of the first ISI of DCN cell bursts. A window of 500 ms was chosen to include DCN cell bursts in which burst ISIs began with a delayed onset following high frequency Purkinje cell firing (i.e. Fig. 3 B). This analysis identified 74 CV2 patterns that occurred prior to a DCN cell burst and 569 CV2 patterns that did not (Fig. 8 C). As previously reported (Shin et al. 2007) a plot of spike frequency versus duration of CV2 patterns revealed a general tendency for patterns to exhibit higher frequency spike discharge as the pattern duration decreased (Fig. 8 C). Parsing these CV2 patterns into those that were or were not associated with DCN rebound bursts revealed no obvious difference in the plot of CV2 spike frequency versus duration (Fig. 8 C). Further analysis indicated that of the CV2 patterns that were associated with bursts, the average number of Purkinje cell spikes in the pattern was 4.3 ± 0.34 with a duration of 30.3 ± 2.61 ms (n = 74). The CV2‐defined patterns that were not associated with bursts contained 5.05 ± 0.18 spikes with an average duration of 35.9 ± 1.37 ms (n = 569). Therefore, the occurrence of a DCN cell burst was not associated specifically with either the mean number of Purkinje cell spikes/CV2 pattern (P = 0.15) or the mean CV2 pattern duration (P = 0.15).

To more carefully examine the temporal relationship between spike patterns and DCN cell burst ISIs we identified the absolute timing differences between each CV2‐defined pattern with respect to identified DCN cell burst ISIs. This analysis returned a positively skewed distribution in which 75 difference latencies occurred within 200 ms of the CV2‐defined pattern (75%), a timeframe at least consistent with a potential causal relationship (Fig. 8 D). Finally, we assessed whether specific CV2‐defined patterns were more effective at evoking bursts by comparing the ability for each CV2 pattern within the stimulus input file to evoke bursts across each of eight Transient burst cells. We found that the majority of CV2 patterns that were associated with a burst (63) were only correlated to a burst ISI in 1/8 cells, with 11 specific patterns associated with bursts in 2/8 cells (Fig. 8 E). However, none of the 63 CV2 patterns were associated with a burst ISI in more than 4/8 cells (50% probability). Therefore, the initial apparent association between CV2 patterns and the occurrence of a burst ISI does not apparently reflect a causal relationship, with any given CV2 pattern exhibiting a low probability of consistently evoking a burst when presented to eight different cells.

Climbing fibre discharge in Purkinje cells

Complex spike discharge in Purkinje cells consists of a rapid elevation in firing frequency and subsequent pause in discharge of simple spikes, a pattern that is at least qualitatively similar to the Elevation–Pause pattern identified through reverse correlation. The Purkinje cell stimulus file used here contained 62 complex spike firing times (see Shin et al. 2007). To explore the influence of complex spikes on DCN cell firing we examined the frequency of Purkinje and DCN cell firing over a period of 200 ms before until 500 ms after the first spike time of complex spikes. As similar results were obtained for both Transient and Weak burst cells we present the data for all eight Transient burst cells (n = 496 complex spikes) (Fig. 9 A).

The average Purkinje cell firing rate in relation to complex spike timings exhibited an increase in firing to ∼120 Hz over ∼100 ms that was followed by a decrease in firing of ∼20 Hz for up to 500 ms (Fig. 9 A). We interpret the elevation in spike frequency to correspond to the climbing fibre‐induced increase in Purkinje cell firing and the longer lasting decrease in firing to presumably reflect the pause in firing that follows a complex spike, a response reflecting both intrinsic ionic as well as network inhibitory mechanisms. Surprisingly, we found little effect of complex spikes on the average DCN cell response, with no apparent rebound during the initial decrease in Purkinje cell firing frequency or over the longer periods of modulations in Purkinje cell firing (Fig. 9 A). We then refined our criteria to detect through reverse correlation only complex spikes that occurred within a window of 500 ms preceding a DCN cell burst ISI. This process identified a total of 34 complex spikes across eight Transient burst cells (7% of all possible complex spikes). Averaging records over a period 200 ms before and 500 ms after the occurrence of a burst‐associated complex spike returned a similar pattern of Purkinje cell firing (Fig. 9 B). While there was some evidence for a subtle DCN cell response to the longer duration elements of Purkinje cell firing, there was still no rebound increase in firing during the initial complex spike‐associated pause in firing (Fig. 9 B).

We again compared the absolute timing differences between each complex spike with respect to identified DCN cell burst ISIs (Fig. 9 C). This analysis returned a weak positively skewed distribution with 17/33 difference latencies occurring within 200 ms of the complex spike time (51%). We thus examined the probability that a given complex spike was associated with DCN cell burst ISIs when delivered to all eight Transient burst cell recordings. We found that of 61 complex spikes in the record associated with burst ISIs, 16 (26%) were associated with a burst ISI in 1/8 cells and 9 (15%) were associated with a burst in 2/8 cells (Fig. 9 D). However, none of the 61 complex spikes was associated with a burst ISI in more than 2/8 cells. Therefore, we interpret these data to indicate that a given complex spike in a physiological spike train under these conditions had a low probability of evoking bursts when presented to eight different cells.

Discussion

The ionic basis of rebound burst discharge in DCN cells has been extensively studied through recordings in vitro but the ability for rebound bursts to contribute to sensory processing in vivo has been more difficult to assess. Tests for correlated firing or a reciprocal relationship in the firing patterns between Purkinje and DCN cells in vivo have had varied results. Paired recordings of Purkinje and DCN cells in decerebrate cats found that Purkinje cell simple spike discharge was poorly correlated to DCN cell activity and often not reciprocal in nature when it was detected (McDevitt et al. 1987; Person & Raman, 2012 b). In contrast, paired recordings of Purkinje and DCN cell activity in rats established that complex spike discharge can be correlated with periods of reduced firing in DCN cells (Blenkinsop & Lang, 2011; Witter et al. 2013). The ability to detect rebound increases in firing in DCN cells in vivo was also linked to inferior olivary stimulation and complex spike discharge (Hoebeek et al. 2010; Bengtsson et al. 2011). More recently, optogenetic stimulation that increased Purkinje cell firing was shown to be highly effective in producing an inhibition of DCN cell firing and rebound responses that varied according to the duration and strength of light stimulation (Witter et al. 2013; Heiney et al. 2014). It has thus been established that given synchronous input by a minimal population of Purkinje cells one can detect an associated inhibition of DCN cells and graded rebound responses. While the latest optogenetic studies have been especially powerful in establishing a relationship between Purkinje and DCN cell activities, the current state of optical probes still limit the stimulus options to step command excitation or inhibition of the targeted populations. The current work is important in identifying a combined ‘Elevation–Pause’ pattern of Purkinje cell firing from within a physiological stimulus train in relation to rebound firing in DCN cells. Moreover, the importance of the duration of a pause in Purkinje cell firing again emerges as a key determinant of eliciting a rebound burst response.

DCN cell responses to a physiological Purkinje cell spike train

The established means for evoking rebound bursts in vitro has been to deliver synaptic stimuli using constant frequency pulse trains (i.e. 100 Hz, 10 pulses) or current‐evoked membrane hyperpolarizations (Telgkamp & Raman, 2002; Aizenman et al. 2003; Uusisaari et al. 2007; Alvina et al. 2009; Pedroarena, 2010; Sangrey & Jaeger, 2010; Tadayonnejad et al. 2010). The current study instead used the spike train from a representative Purkinje cell recorded in vivo during perioral whisker stimulation to synchronously activate a relatively large number of Purkinje cell axons projecting into the DCN (∼60% of presumed maximum). The data showed virtually no response of DCN cells on average to Purkinje cell firing associated with the perioral whisker stimulus. The relative lack of a stimulus‐related rebound burst was striking given the degree of synchronous activation of Purkinje cell afferents and that the average increase in Purkinje cell firing frequency evoked by perioral whisker stimulation exceeded 100 Hz (50 Hz above baseline). This is important in reflecting a frequency increase higher than the 50 or 100 Hz inhibitory synaptic stimulus trains used in each cell to first verify that Purkinje cell input was capable of evoking a rebound burst. Yet a lack of rebound response to a train of Purkinje cell simple spikes has also been reported during in vivo recordings following peripheral stimulation (Bengtsson et al. 2011). Our results are also in line with proposals that the instantaneous rate of Purkinje cell firing may serve more as a rate code to establish a baseline level of inhibition that can be modified by pauses in Purkinje cell firing (De Schutter & Steuber, 2009; De Zeeuw et al. 2011). On the other hand, our lack of recording a whisker stimulus‐evoked rebound response might relate to factors inherent to in vitro recordings. An analysis conducted in the mouse reported that coding of whisker stimuli involved functional ensembles of Purkinje cells (Bosman et al. 2010) which our stimulation would not have correctly simulated here. The Purkinje cell recordings used here were also obtained in anaesthetized rats, a condition that can affect Purkinje cell firing (Ordek et al. 2013). The Purkinje cell firing patterns used in our study were obtained in animals of 300–500 g weight (Shin et al. 2007), indicating an age of ∼P60. The stage of DCN development for the P12–17 animals used for the current study may not yet include a response capability to sensory stimuli even though rebound bursts are readily evoked at this age. Taken together, it is possible that neurons recorded here are simply not ‘tuned’ to respond to the nature of sensory stimuli presented, or even that the perioral whisker stimulus does not reflect a significant signal for DCN cells. Finally, our in vitro recordings were conducted in the presence of blockers for ionotropic and metabotropic glutamate receptors that can be important in regulating DCN cell excitability (Zheng & Raman, 2011).

A recent study in mouse DCN revealed that synchronous Purkinje cell spike trains can entrain large diameter DCN cell output through a process of time‐locking (Person & Raman, 2012 a). Hoebeek et al. (2010) also defined a form of ‘timed‐spiking’ following single or repetitive stimuli to Purkinje cells reflecting an increased probability for discharge within ∼ 5–20 ms windows. Our attempts to detect a relationship between the instantaneous frequencies of Purkinje and DCN cell firing (i.e. input vs. output frequency) failed to extract a significant response under our conditions (data not shown). While the phase coding identified by Person and Raman may well factor into the response of DCN cells recorded here, it is difficult to estimate without control over the degree of synchronous input available through their use of dynamic clamp. The ability for DCN cells to implement phase coding can also vary according to cell type, with GABAergic nucleo‐olivary cells exhibiting no rebound response and IPSP kinetics too slow to reasonably employ an entrainment process (Najac & Raman, 2015). We recorded from large diameter rat Transient and Weak burst neurons, with at least Transient burst neurons representing either GABAergic or non‐GABAergic phenotypes (Molineux et al. 2006). It is thus difficult to compare the results obtained here directly with those of Person & Raman (2012 a). Our tests instead could be viewed as detecting aspects of Purkinje cell spike trains over a longer time frame than revealed through time‐locking.

Reverse correlation to identify Purkinje cell patterns related to burst ISIs

Reverse correlation revealed the Elevation–Pause pattern contained within a physiological Purkinje cell firing record that is sufficient to evoke burst ISIs in DCN cells. On average, the minimal Purkinje cell firing increase associated with a DCN cell burst ISI was ∼30–60 Hz above baseline for at least 100 ms followed by a substantial slowing or a complete pause in firing frequency over a period of up to 500 ms. It is not currently known if the Elevation–Pause pattern could represent a sensory‐relevant input embedded within the Purkinje cell spike train unrelated to the perioral whisker stimulus that we originally tested. The time frame of the Elevation–Pause pattern identified under our conditions is also longer than anticipated given previous work on temporal aspects of cerebellar processing (De Zeeuw et al. 2011). However, the range of frequency responses encoded in cerebellar circuitry may span a larger temporal window than previously considered (Person & Raman, 2012 b; Heck et al. 2013; Witter & De Zeeuw, 2015). It is doubtful that the overall duration of 750 ms identified here for an Elevation–Pause pattern will be required to elicit a burst of functional significance in vivo, where continual synaptic bombardment and background conductances are expected to shorten the timeframe of synaptic responses. It is also worth noting that our measurements were conducted from a relatively narrow window of resting membrane voltage given that we used bias current injection to establish a common baseline from which to compare results between cells. It is possible that network activity and associated shifts in resting membrane potential or tonic firing frequency could modulate the temporal aspects of an Elevation–Pause pattern capable of evoking rebound responses, as found in other systems (Person & Perkel, 2005).

The CV2‐defined patterns of firing in the Purkinje cell record could conceivably represent the first half of the Elevation–Pause pattern extracted through reverse correlation. However, CV2‐defined patterns of firing in the Purkinje cell record were very poorly correlated to DCN cell burst ISIs, at least as tested in vitro. If the CV2‐defined elevations in firing were accompanied by a subsequent pause or decrease in frequency that together could induce burst output in DCN cells, it has not been identified or tested here. A second Purkinje cell output that resembles an Elevation–Pause pattern is the complex spike. Surprisingly, we found no change in the average pattern of DCN cell activity in response to complex spike‐triggered input, or an association between DCN burst ISIs and the timing of complex spikes. Even a direct analysis of the effectiveness of individual complex spikes across multiple DCN cell recordings showed a very low probability of encountering a complex spike‐burst ISI association. These results are difficult to interpret given that complex spike discharge has been clearly associated with a decrease in DCN cell firing in vivo (De Schutter & Steuber, 2009; Hoebeek et al. 2010; Bengtsson et al. 2011; Blenkinsop & Lang, 2011; De Zeeuw et al. 2011; Witter et al. 2013). Our expectation is that the known convergence and synchronization of climbing fibre input from multiple Purkinje cells in different lobules will be a key factor in increasing their effectiveness at inducing a rebound response (De Schutter & Steuber, 2009; Bengtsson et al. 2011; De Zeeuw et al. 2011; Person & Raman, 2012 b; Witter et al. 2013; Herzfeld et al. 2015).

Minimal effective stimulus for rebound responses

The current study is important in indicating that an Elevation–Pause pattern of simple spike activity can be associated with a rebound burst ISI in DCN cells, at least in vitro. A constant component of the Elevation–Pause pattern was the rapid decrease in spike frequency over ∼100 ms that immediately preceded the onset of the initial ISI of a burst. There was also a clear correlation between the duration of the pause in Purkinje cell firing and the number of ISIs in a DCN cell burst. These data emphasize the importance of a temporary relief from Purkinje cell‐mediated inhibition to generating a rebound burst, as has been reported in in vivo analyses (Shin & De Schutter, 2006), dynamic clamp studies in vitro (Gauck & Jaeger, 2000) and modelling studies (Jaeger, 2007; Steuber et al. 2007; Steuber & Jaeger, 2013). A similar relationship to the occurrence of a rapid decrease or pause in presynaptic input and rebound firing was reported in thalamic neurons in response to inhibitory stimulus trains from the pallidal region (Person & Perkel, 2005). It has been proposed that Purkinje cells provide a varying baseline of inhibition reflecting a rate coding mechanism, such that a pause in Purkinje cell firing can provide a window of time for the DCN cell to activate a rebound response with specific latency, frequency, duration or precision (see De Schutter & Steuber, 2009). Both simple spike discharge and a pause in firing can also be synchronized between Purkinje cells separated by < 100 μm, with synchronization of ∼35% of simple spikes and ∼13% of pauses during sensory input (Shin & De Schutter, 2006). The potential role for pauses can vary, in that Cao et al. (2012) reported that pauses in Purkinje cell firing associated with repetitive input related to licking or respiration could be accounted for simply as a product of rate modulation. However, the effects of a pause in Purkinje cell firing on DCN cell output can be substantial, with dynamic clamp and optogenetic activation predicting that a 15–25 ms pause is sufficient to increase the DCN cell firing rate (Gauck & Jaeger, 2000; Heiney et al. 2014). While these values for pause duration are substantially shorter than the apparent minimum of ∼250 ms detected here we expect this value to be modified by the conditions inherent to the intact circuit in awake animals.

Additional information

Competing interests

The authors declare no competing interests in the publication of this work.

Author contributions

S.D., J.D.T.E., T.M.B. and R.W.T. contributed to the conception and design of the research; S.D., J.D.T.E. and T.M.B. performed the research; S.D., J.D.T.E. and R.W.T. analysed or interpreted the data; S.D., J.D.T.E. and R.W.T. wrote the manuscript. All authors approved the final version of the manuscript, and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved; all persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was carried out at the University of Calgary and was supported by a grant from the Canadian Institutes of Health Research (CIHR) (R.W.T.) and Studentships or Fellowships through the Queen Elizabeth II award (S.D.), Alberta Heritage Foundation for Medical Research (J.D.T.E.) or Alberta Innovates Health Solutions (T.M.B.), T. Chen Fong award (J.D.T.E.), Killam Foundation (J.D.T.E.), a CIHR‐CGS PhD studentship (J.D.T.E.) and a CIHR Postdoctoral Fellowship (T.M.B). R.W.T. is an AI‐HS Scientist.