Integrating mapping-, assembly- and haplotype-based approaches for calling variants in clinical sequencing applications

Abstract

High-throughput DNA sequencing technology has transformed genetic research and is starting to make an impact on clinical practice. However, analyzing high-throughput sequencing data remains challenging, particularly in clinical settings where accuracy and turnaround times are critical. We present a new approach to this problem, implemented in a software package called Platypus. Platypus achieves high sensitivity and specificity for SNPs, indels and complex polymorphisms by using local de novo assembly to generate candidate variants, followed by local realignment and probabilistic haplotype estimation. It is an order of magnitude faster than existing tools and generates calls from raw aligned read data without preprocessing. We demonstrate the performance of Platypus in clinically relevant experimental designs by comparing with SAMtools and GATK on whole-genome and exome-capture data, by identifying de novo variation in 15 parent-offspring trios with high sensitivity and specificity, and by estimating human leukocyte antigen genotypes directly from variant calls.

High-throughput DNA sequencing technologies now allow large quantities of high-quality sequence data to be generated at modest cost. However, despite substantial progress in algorithm development^1–6, the processing of these data into high-quality variant calls remains challenging⁷.

Quality requirements are particularly stringent for clinical applications. Here we identify four such requirements. First, algorithms should have high power to detect a wide range of variation, including single- and multiple-nucleotide variants (SNVs and MNVs) and structural variation including indels, sequence replacements and mobile element insertions. Although relatively rare, structural variation is enriched among variants with phenotypic effects⁸. In addition, the ability to quantify evidence for the absence of variation can also be essential in a clinical context. Second, pipelines must have low false discovery rates (FDRs), for instance, when identifying de novo mutations underlying mendelian disorders in parent-offspring trios, to minimize costly validation experiments. Third, pipelines should be able to cope with challenging loci, including highly repetitive sequence and reference errors, and be robust to high levels of local diversity to access clinically interesting regions such as the human leukocyte antigen (HLA) loci⁹. Fourth, pipelines should have low resource requirements and run on commodity hardware while achieving fast turnaround times.

With these requirements in mind, we developed a new method that integrates several approaches to this problem into a single, highly optimized implementation. The most common approach is to map reads to a reference genome^6,10–13 and either scan for systematic differences with the reference or identify haplotypes that are well supported by the data¹⁴. The strengths of this approach include high sensitivity^1,11; access to most of the human genome, including repetitive regions, by exploiting paired-end read information¹⁰; and relatively low resource requirements from processing reads in a streaming fashion¹². However, mapping approaches have several weaknesses. First, mapping-based callers often focus on a single variant type^1–4, leading to errors around indels and larger variants^2,15. Second, this approach can fail in highly divergent regions where systematic misalignments provide spurious support for SNVs and other variants¹⁶. Third, mapping-based callers tend to rely on the nucleotide-level accuracy of read alignments^3,4,15, and, although these can be improved by realigning around known indels¹, this process is costly, relies on a dictionary of known polymorphic indels and does not improve alignments around other variant types.

A complementary approach that avoids these limitations is reference-free sequence assembly^5,17–20. Assembly algorithms build a de Bruijn^5,20,21 or overlap^22,23 graph and search this data structure for evidence of polymorphisms. By not relying on a reference genome, this approach is variant agnostic, copes well with highly divergent regions, naturally works on the local haplotype level rather than on the level of individual variants and avoids the need for an initial mapping and alignment step. However, assembly algorithms typically have high computational requirements²¹, have lower sensitivity than mapping-based approaches⁵ and are limited by repetitive sequence, as contiguity information is lost when the reads are broken up into their consecutive k-mers during graph construction.

In addition to directly exploiting reads from the sample of interest, some algorithms borrow information across related samples^1–3,5. By separating the processes of identifying and genotyping variants, even a weakly supported variant in one sample can be confidently called if it is strongly supported by another sample or samples. This approach reduces the rate of false negative calls due to downward fluctuations in read coverage, a feature that is important in comparisons of tumors and metastases²⁴, population-based studies²⁵ and pedigrees including parent-offspring trios in de novo discovery designs.

Although each of these approaches has merit, no algorithm thus far combines all of them. Here we describe Platypus, an algorithm that combines a haplotype-based, multi-sample variant caller with local sequence assembly in a Bayesian statistical framework. We show that integrating the three approaches results in high sensitivity and specificity in several clinically relevant experimental designs, across a range of mutation types, including complex variation and indels of up to ~1 kb in size, in both low- and high-divergence regions of the genome. Besides variant calls, Platypus also provides reference calls and local linkage information between called variants, and we use these to estimate HLA genotypes directly from these data. The implementation has low resource requirements and provides one-step processing avoiding the need for intermediate files, enabling the rapid processing of large volumes of high-throughput sequencing data on standard hardware.

RESULTS

Local assembly and haplotype generation

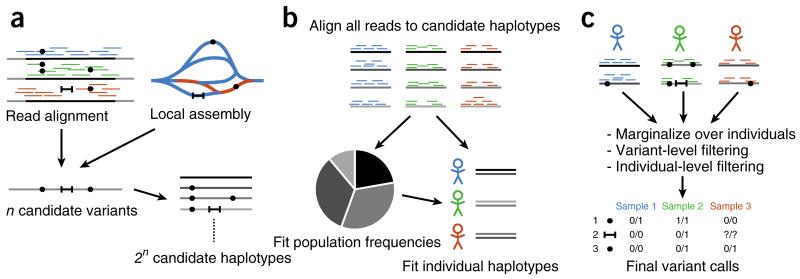
The algorithm begins by generating a set of candidate variants to consider in subsequent steps (Fig. 1a). Three sources of candidates may be considered: variants supported directly by read alignments, variants identified by assembly and variants from external sources, such as databases of known polymorphisms.

Figure 1.

Simplified flow diagram of the integrated calling algorithm. The three stages of the algorithm are pipelined without using intermediate files or separate processes. Mapped and sorted BAM files are used as input; merging, sample demultiplexing and read deduplication are all performed by Platypus. The resulting variant calls require no post-processing, except for a Bayesian filtering stage for de novo mutations. (a) Candidate variants are obtained from read alignments, local assembly and external sources (not shown), and candidate haplotypes are formed. (b) The support of each read for any candidate haplotype is computed by alignment, and population haplotype frequencies are fitted to a diploid segregation model. (c) Variants are called by first calling haplotypes, followed by marginalization over secondary variation. Filtering on the variant and sample levels results in a final call set. See the supplementary note for full details of the algorithm.

The assembler considers small (default of 1.5 kb) windows at a time, processing reads that map into the window, as well as their mates, irrespective of mapping status and location. A colored de Bruijn graph⁵ is generated from the read and reference sequences. Because the read orientation is known, as at least one read from each pair is mapped, we build the graph on the forward strand only. Next, an exhaustive depth-first traversal algorithm extracts all unique paths that begin and end on the reference sequence; each of these paths represents an alternative allele candidate. The algorithm, which always returns non-self-intersecting paths, is unaffected by repetitive elements causing complex loops and tangles or by the existence of multiple paths sharing subsets of the graph. This approach differs from that taken by most global assemblers, which typically identify relatively simple alternative paths (‘bubbles’) to achieve high specificity; by contrast, Platypus’s candidate generation stage is designed to achieve high sensitivity.

We then cluster candidate variants into well-separated windows that each contain a limited number of candidates. These candidates are then combined into an exhaustive list of haplotypes. If a window contains many candidates, we use an approximate likelihood computation to consider only the most promising haplotypes (up to 256 by default).

Estimation of haplotype frequencies

After the list of haplotypes is generated, their frequency is estimated under a diploid segregation model (Fig. 1b). First, the matrix of likelihoods of each of the reads given each of the candidate haplotypes is computed. This computation involves sequence alignment under an error model that includes position-dependent indel probabilities specific to the technology and single-base mismatch probabilities from read quality scores. An expectation-maximization (EM) algorithm estimates population haplotype frequencies from these likelihoods.

Calling and filtering

The estimated population haplotype frequencies are used as priors for calling haplotypes in each sample (Fig. 1c). We break up called haplotypes into their constituent variants and calculate variant- specific genotype calls and likelihoods by marginalizing over the other variants in the region. In this way, local linkage information encoded in reads helps to inform the genotype of linked variation within a window. We explicitly report some linkage information in the calls, which may be used in downstream phasing and imputation pipelines. We finally apply a set of filters to remove spurious calls due to data artifacts that are not modeled explicitly. These include filters for allele and strand bias, mapping quality, base quality, insert size, sequence context and posterior probability of the variant; we used default thresholds throughout.

A complete description of the algorithm is given in the Supplementary Note.

Application 1: calling variation from whole-genome data

To assess the performance of Platypus on whole-genome data, we analyzed publicly available data (75–86 × 100-bp paired-end Illumina HiSeq 2000 reads) from a well-studied parent-offspring trio (NA12878, NA12891 and NA12892; CEU cohort of samples from Utah of northern and western European ancestry). We used SNP chip and high-quality haploid fosmid data previously generated for NA12878 (ref. 26) to estimate sensitivity and FDRs. We compared Platypus to two widely used variant callers, the Genome Analysis Toolkit (GATK)¹ and SAMtools³. For GATK, we used the publicly available ‘best practices’ GATK call set made with the latest UnifiedGenotyper and a call set made with the HaplotypeCaller, using default arguments. The SAMtools call set was made using the published protocol (see the Supplementary Note for details).

Quality metrics indicated that Platypus achieved high specificity for both SNPs and indels (Table 1). The transition/transversion ratio (ti/tv) of 2.136 is comparable to previous estimates²⁵, indicating good specificity for SNPs. This was supported by a low non-reference call rate (0.024%) at sites called as homozygous reference by the Axiom SNP chip. Manual inspection and comparison with other call sets suggested that the large majority of these discrepancies were Axiom genotyping errors (Supplementary Table 1 and Supplementary Note). The ascertainment bias of SNP chips, including the fact that sites accessible to SNP chips tend to be easy to call from short-read data, implies that this figure likely underestimates the true FDR. Fosmid data allow us to place an upper bound on the FDR, using sites that are called as homozygous variant but where fosmid data support the reference sequence⁵. For Platypus, we found 8 such sites, resulting in an FDR upper bound of 0.4% (8/1,891). All discordant variants were in dbSNP137, and most (6/8) had a low genotype quality score (<45), with both measures indicating that these variants might represent genotyping errors of true heterozygous variants rather than false positive variant calls.

Table 1. Comparison of whole-genome and exome calls for three algorithms.

		Whole genome				Exome capture
	Platypus	GATK UG	GATK HC	SAMtools	Platypus	GATK UG	GATK HC	SAMtools
SNPs	3,450,678	3,249,953	3,295,960	3,657,268	14,721	15,185	14,075	15,501
ti/tv (all)	2.136	2.133	2.111	2.100	3.15	3.14	3.24	3.05
ti/tv (1000 Genomes)	2.152	2.138	2.122	2.113	3.19	3.18	3.26	3.17
Axiom GT concordance (%)	99.64	99.68	99.75	99.27	98.1	98.9	99.3	98.0
Axiom sensitivity (%)	94.10	94.81	95.48	96.80	90.01	90.42	86.40	89.14
Axiom reference call rate (%)	98.13	NA	NA	NA	92.33	NA	NA	NA
Axiom mono rate (%)	0.024	0.130	0.015	0.050	0.046	0.016	0.008	0.04
Fosmid sensitivity (%)	90.1	83.6	84.2	92.4	NA	NA	NA	NA
Fosmid FDR (%)	0.4	0.6	0.7	1.8	NA	NA	NA	NA
Indels	551,529	661,502	732,349	604,330	265	229	280	241
Frameshift fraction	0.496	0.500	0.488	0.460	0.502	0.507	0.520	0.489
Fosmid sensitivity (%)	53.0	57.2	72.5	53.6	NA	NA	NA	NA
Fosmid FDR (%)	4.6	8.0	7.7	10.5	NA	NA	NA	NA
Insertion/deletion	0.949	0.964	1.04	0.925	1.02	1.04	0.94	1.15
Complex	28,628	0	0	0	307	0	0	0
2-bp MNPs	24,331	0	0	0	98	0	0	0
Replacements	4,295	0	0	0	3	0	0	0
Runtime (real time, min)	24	700	2,176	127	11	45	268	23

ti/tv, transition-transversion ratio; 1000 Genomes, intersection with 1000 Genomes Project Phase 1 calls; GT concordance, concordance at called Axiom sites; mono rate, fraction of Axiom monomorphic sites that overlap with variant calls; FDR, false discovery rate; MNPs, multi-nucleotide polymorphisms defined as SNPs separated by at most 5 bp and the assembly k-mer size, if used; replacements, any variant not classified as a SNP, MNP or pure insertion or deletion; runtime, CPU minutes needed to process chromosome 20. Calls were made on data from the NA12878 trio, and calls for NA12878 were extracted. Exome calls were restricted to known coding regions. See the Supplementary Note for details Where meaningful, the best performing algorithm on any metric is indicated in bold.

On the basis of these data, we estimated Platypus’s sensitivity for SNP calls to be 94.1% and 90.1%, respectively, using Axiom data and fosmid sequences. These estimates are similar to those for the GATK UnifiedGenotyper (94.8% and 83.6%) and the GATK HaplotypeCaller (95.5 and 84.2%) and are somewhat lower than with SAMtools (96.8% and 92.4%). The majority of Axiom SNPs not called by Platypus were missed because of low read support (52%; 476/916 were supported by 2 or fewer reads), likely owing to variation in cell line subclones, or were called but flagged as uncertain (33%; 301/916). Platypus also identified regions where sequence data provided positive support for the absence of variation. Axiom data indicated that Platypus had over 98% sensitivity for calling reference sequence (reference calls were made at 254,066/258,914 of the Axiom homozygous reference sites).

Indels are more challenging to call accurately from short-read data than are SNPs because their genomic mutation rate is highly context dependent⁸ and correlates with sequencing error rates². In addition, indels are about tenfold less abundant than SNPs, so that a given false positive call rate translates into a tenfold higher FDR among indels than SNPs. From fosmid data, we estimated the FDR upper bound for indels at 4.6% (12/250), about half the FDR estimates for SAMtools and the GATK algorithms. Most of the discordant variants (7/12) had exact matches to dbSNP137, indicating that the true FDR might be lower. Manual inspection of the short-read and fosmid data showed that 5 of 12 discordant variants were called correctly but were reported across multiple call records, whereas the remainder are likely to be false positive calls in repetitive or tandem repetitive regions. We therefore estimated the FDR for indels at 2.8% (7/250).

Using fosmid data, we estimated Platypus’s sensitivity for indels at 53.0%. This low sensitivity is driven largely by indels in homopolymeric and tandem repetitive indel hotspots that are filtered out to address common sequence artifacts in these regions. Removing ~1% of highly repetitive genomic regions with high predicted indel rates (25.4 Mb; see ref. 8) increased sensitivity to 76.0% (GATK UnifiedGenotyper, 78.3%; GATK HaplotypeCaller, 81.0%; SAMtools, 75.5%).

Platypus also identified a large number of MNPs (defined as pairs of SNPs at most 5 bp apart) and complex replacement events, ranging in size from 2 to 66 bp. A substantial fraction of the base changes in these events matched previously seen SNPs (37.5%; 51,834/138,036). Some of these might correspond to two or more independent SNPs, but the majority are likely to have arisen from single mutational events affecting multiple nucleotides²⁷.

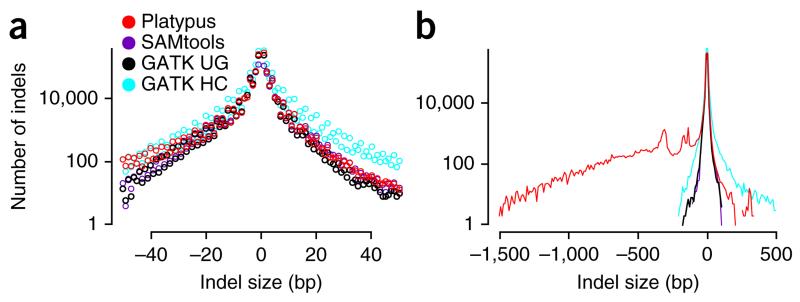
Local assembly allows Platypus to call variants considerably larger (up to ~1 kb) than those that can be identified within the alignment of a single read. Platypus was able to identify 27,608 deletions between 50 and 2,288 bp in length and 481 insertions between 50 and 504 bp in length. Most deletions had microhomology at both ends (≥2 bp for 83% of deletions; 22,860/27,608), implicating the microhomology-mediated end joining (MMEJ) pathway²⁸. For both insertions and deletions, we observed the known excess of variants of lengths of ~293–328 bp corresponding to recent integration events and MMEJ-mediated deletions of full-length Alu elements, as well as an excess of deletions of 132–138 bp in size corresponding to deletions of half of the polyA-flanked Alu dimer (Fig. 2). The strategy of mapping followed by local assembly requires reads contributing to a large insertion to be anchored by their mates, which limits the maximum length of insertions that can be called. We indeed found that the sensitivity for calling insertions was reduced relative to deletions. Nevertheless, Platypus was still able to identify eight full-length heterozygous Alu insertions, all of which had been previously validated²⁵.

Figure 2.

Size distribution of indel calls in the NA12878 trio. (a) Histogram of small indel calls (up to 50 bp) by size (negative size, deletion with respect to the reference sequence) for three calling algorithms. UG, UnifiedGenotyper; HC, HaplotypeCaller. (b) Smoothed histograms (10-bp bins) showing larger indels and peaks around ~300 bp corresponding to insertions and deletions of Alu transposable elements. Local assembly allows Platypus to detect insertions up to a few hundred basepairs in size and deletions of over 1 kb in size.

Application 2: calling SNPs and indels from whole-exome data

In clinical applications, whole-exome sequencing is often chosen over whole-genome protocols because of the lower cost and because most clinically interpretable variation occurs in coding sequence. Technically, exome capture data are sufficiently different from whole-genome data to warrant a separate assessment because of specific biases of the technology (variable capture efficiencies at polymorphic sites, strand biases at capture boundaries and large variations in coverage) and specific characteristics of the target (high GC content and existence of paralogous sequence due to pseudogenes).

We assessed the performance of Platypus using publicly available exome data from the NA12878 trio²⁵ (100-bp paired-end reads, average coverage of 210×), and we used SNP chip data to estimate the accuracy of variant calling and genotyping. The results mostly recapitulate those for whole-genome data. Platypus’s ability to call MNPs and complex variation is particularly useful in exome data, as reporting individual single-nucleotide changes can complicate the interpretation of amino acid changes.

The rate of discordant calls at sites genotyped as homozygous reference by the Axiom SNP chip was 0.046% (86/186,956; Table 1). A large fraction of discordant variants were called as complex variants of MNPs (40%; 35/86); in addition, the discordance rate increased threefold (to 0.132%) wherever two Axiom sites were within 2 bp of each other and decreased to 0.037% for isolated Axiom sites. This observation suggests that a large proportion of discordant calls represent false negative chip calls, likely because nearby variation results in probes failing to hybridize correctly. The same failure mode was observed in whole-genome calls (Supplementary Note). Other algorithms typically call MNPs as multiple SNPs and tend to filter out highly clustered variation, explaining the apparently better performance of these algorithms on this statistic; for example, when MNPs were excluded, Platypus’s genotype concordance increased to 98.9%.

Application 3: de novo mutations in parent-offspring trios

Several recent studies have successfully identified disease-causing de novo mutations using sequence data from parent-offspring trios, in both exomes^29–31 and whole genomes^32,33. Identifying 1 causal variant among approximately 70 de novo mutations³⁴ in a genome spanning 3 × 10⁹ bp requires false positive rates below 1 × 10⁻⁸. Existing studies achieve this by stringent filtering using supplementary data, including databases of known polymorphisms^29,31–34 or variants directly observed in other samples^29,31,34; sequence data from grandparents, siblings or monozygotic twins^7,32,33; functional annotations³³; known segmental duplications³³; or validation of candidate de novo mutations by Sanger sequencing^29,32,33. In addition, some studies omitted indels because of technical challenges^31,32,34, despite the relatively strong impact of indels on phenotype⁸.

Instead, we called de novo mutations of all types from trio sequence data alone and for filtering used a Bayesian model that quantifies the evidence for a de novo mutation compared to normal mendelian segregation. This approach allowed us to incorporate a low prior belief in a de novo mutation at any given site and to account for loss of parental heterozygote calls resulting from fluctuations in random coverage. Specifically, we use Bayes’ rule to compute the posterior probability of a de novo mutation event N given the read data d as

$$P\left(N\mid d\right)=\frac{P\left(d\mid N\right)p\left(N\right)}{p\left(d\right)}$$

where p(N) is the prior probability of a de novo mutation (set to 2 × 10⁻⁸ mutations per site per generation) and p(d) is the marginal likelihood of the data, computed as p(d|N)p(N) + p(d|M)p(M) + p(d|R)p(R). Here M and R denote the occurrence of a variant following normal mendelian segregation patterns and a non-variant locus, respectively, p(M) = 1 × 10⁻³ and p(R) = 1 − p(N) − p(M). We accept a putative de novo mutation if the posterior probability exceeds 0.5 (see the Supplementary Note for full details). This filter was applied to all variant callers.

To assess Platypus’s sensitivity, we again analyzed data from the NA12878 trio obtained from immortalized cell lines and made use of a study by Conrad et al. that identified 49 germline and 952 cell line de novo mutations using an exhaustive calling strategy followed by comprehensive validation³⁵. Before applying the Bayesian filter, Platypus identified all germline and 97% (924/952) of cell line mutations (Table 2); of the 28 mutations not called, 24 had very low read support, likely owing to non-clonality of the cell line sample, 2 overlapped deletion calls that were likely misinterpreted as SNPs in the Conrad data set³⁵, 1 locus was difficult to interpret and 1 represented a true false negative resulting from Platypus’s conservative default filters (Supplementary Table 2 and Supplementary Note). After applying the Bayesian filter, 94% (46/49) and 95% (909/952) of these sites had sufficient sequence coverage to overcome the prior probability of 2 × 10⁻⁸ mutations per base pair, corresponding to a prior expectation of ~70 de novo mutations per generation.

Table 2. Sensitivity for identifying known de novo mutations in the NA 12878 child.

		Conrad et al.35 overlap
		All calls		Bayesian filter
	DNMs	Germ line	Cell line	Germ line	Cell line
Platypus	2,635	100% (49/49)	97% (924/952)	94% (46/49)	95% (909/952)
GATK UG	2,301	78% (38/49)	89% (850/952)	78% (38/49)	89% (850/952)
GATK HC	2,697	98% (48/49)	95% (908/952)	98% (48/49)	95% (908/952)
SAMtools	4,146	100% (49/49)	99% (938/952)	98% (48/49)	98% (929/952)

DNMs, total number of de novo mutations identified.

To assess specificity, we analyzed high-depth sequence data (46–58× coverage, 100-bp paired-end Illumina HiSeq 2000 reads) for a parent-offspring trio that formed part of a larger clinical resequencing study (H.C. Martin, J.C. Taylor, C. Allan, M. Attar & C. Babbs et al., unpublished data). After Bayesian filtering, Platypus called 94 de novo mutations in the offspring: 88 SNVs, 1 MNV and 5 indels. Non-specific amplification and primer design issues resulted in uninterpretable data for 26 of these. Of the remaining 68 calls (including 5 indels), 63 were validated as true de novo mutations (60 SNVs and 3 indels; Supplementary Note), indicating a combined FDR of 7.4% for SNV and indel de novo mutation calls (5/68; 95% credible interval (CI) = 3–16%; Online Methods). It is possible that, among calls for which the validation experiment did not work, the FDR is higher, but it is hard to meaningfully estimate this rate. Two of the validated de novo mutations were clustered SNVs (genomic distance of 341 bp), suggesting that these two mutations were caused by a single mutational event³⁶. Of the five calls that did not validate, one was due to a missed parental variant due to read filtering on the basis of mapping quality. Mapping artifacts were also the likely cause of the four other false calls, as they were supported by reads of low mapping quality and lie in repetitive sequence such as LINE and SVA-C repeats.

Homoplasy among de novo variation

Platypus’s high specificity removes the need to filter by polymorphic status, enabling us to identify de novo mutations occurring at known polymorphic sites (homoplasies). Of the 92 de novo mutations called in the clinical resequencing study, 3 were previously identified as polymorphisms by the 1000 Genomes Project²⁵; 2 of these were validated as true de novo mutations, whereas validation of the third call was inconclusive. This high frequency of homoplasies is likely due to the combination of a large number of known polymorphisms and the existence of mutational hotspots, particularly at CpG dinucleotides. Calculation suggests that in every generation 3% of de novo mutations—or 2.1 out of an expected 70 mutations—occur on a polymorphic background. This explanation predicts that CpG-associated mutations are enriched among homoplastic de novo mutations (Supplementary Note).

To test this hypothesis, we made de novo mutation calls on a further 14 parent-child trios from the same clinical resequencing study. We intersected the resulting 1,007 de novo mutation calls (26–94 per sample, average of 67.1) with 1000 Genomes Project data, identifying 52 putative homoplasies (1–5 per sample, average of 3.5, all SNVs; Table 3). We found, as expected, a significant enrichment of CpG-associated mutations in comparison to non-homoplastic de novo mutations (26/52 versus 245/871; P = 0.001). The local haplotype around putative homoplastic de novo mutations either directly supported the call (34/52) or was inconclusive (9/52), whereas a false positive was indicated in 9 of 52 cases (Supplementary Table 3 and Supplementary Note).

Table 3. De novo variants called in 15 parent-offspring trios.

Sample	DNMs	SNPs or MNPs	Indels	1000 Genomesa
1	94	89	5	3
2	26	23	3	4
3	67	65	2	2
4	53	50	3	5
5	75	69	6	3
6	69	63	6	2
7	71	65	6	5
8	75	71	4	2
9	91	90	1	5
10	82	76	6	1
11	66	62	2	5
12	82	79	3	4
13	56	51	5	3
14	52	49	3	4
15	48	46	2	4
Average	67.1	63.2	3.8	3.5

^aVariants at polymorphic loci in 1000 Genomes Project Phase 1 release 3.

Application 4: genotyping HLA loci

Variation in the HLA genes is a major determinant of susceptibility to infectious and autoimmune diseases, making HLA genotyping of interest in medical genetics. The high sequence diversity and extensive paralogy of these genes present a challenge for HLA genotyping, which is typically performed by PCR amplification and probe hybridization³⁷. Genome-wide high-throughput sequencing data are also informative about the HLA genotype, but, although the use of global assembly has shown promise, mapping-based approaches are currently limited by the high density and complexity of variation in the region³⁸.

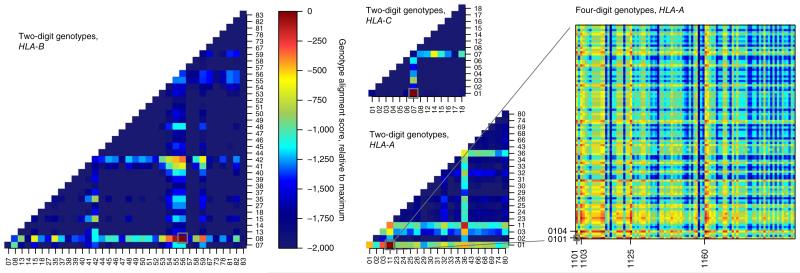
To assess Platypus’s ability to genotype HLA loci, we exploited its ability to provide explicit reference calls whenever it found positive evidence for the absence of variation, as well as local linkage information. By combining these data, we constructed small genotype contigs ranging in size from 15 to 192 bp across the classical HLA class I genes. We next aligned these contigs to the 2,186 known HLA-A, 2,796 HLA-B and 1,746 HLA-C haplotypes each identified by a hierarchical identifier (for example, HLA-B*56:01:01) and computed genotype likelihoods for all HLA genotypes from alignment scores. Finally, we extracted maximum-likelihood estimates for the three class I HLA loci (Supplementary Fig. 1).

This procedure resulted in unique and correct HLA-B and HLA-C genotypes at four-digit resolution in NA12878 (Fig. 3 and Supplementary Fig. 2). Three of the four alleles could be uniquely typed at six-digit resolution (Supplementary Table 4), better than was achieved by previous laboratory typing³⁹. The estimated genotype for HLA-A was unique and correct at the two-digit level, with the correct four-digit genotype (HLA-A*11:01/HLA-A*01:01) contained within the results. The remaining ambiguities are caused by a cluster of missing variants due to low-quality reads and to differences outside the exonic sequence that are not currently considered by the pipeline; for instance, the alleles HLA-A*01:01 and HLA-A*01:04N are identical except for a 1-bp–length difference due to a correctly called splicing variant 5′ to exon 4 causing a frameshift in the codon sequence (Supplementary Figs. 3 and 4 and Supplementary Note), which, however, was ignored in the genotyping pipeline.

Figure 3.

Genotypes of the HLA-A, HLA-B and HLA-C loci at two- and four-digit resolution. Combined genotype alignment scores relative to the maximum-scoring genotypes are shown as a heat map; gray boxes indicate correct genotypes. Correct and unique genotypes at four-digit resolution were estimated from Platypus reference and variant calls for HLA-B (HLA-B*56:01/HLA-B*08:01) and HLA-C (HLA-C*07:01/HLA-C*01:02) (heat maps for genotypes at two-digit resolution shown; see supplementary Fig. 2 for heat maps at four-digit resolution). For HLA-A, the correct genotype HLA-A*11:01/HLA-A*01:01 was among the highest scoring genotypes, but it could be resolved uniquely at two-digit resolution only (lower middle panel); ambiguities remained at four-digit resolution for both haplotypes (right; genotypes with identical scores are indicated).

DISCUSSION

We introduce a new approach to variant calling from high-throughput sequencing data that integrates ideas from mapping-, assembly- and population-based callers. By separating the calling process into a candidate generation stage, designed to optimize sensitivity, and a haplotype-based calling stage, designed for specificity, the algorithm performs well on both metrics. The resulting high specificity eliminates the need for aggressive filtering when calling de novo mutations in a parent-offspring design, simplifying such designs and widening their applicability. Using this pipeline, we find evidence for an average of ~2 homoplastic de novo mutations per generation.

To achieve the high sensitivity and specificity required for the detection of de novo mutations in a clinical context, it is necessary to control both the rate of false positive calls in the child and false negative calls in the parent. Sufficient sequence coverage in both parents and the child is necessary to achieve this. Using probabilistic rescaling of empirical coverage data, we find that Platypus achieves 95% sensitivity for de novo mutations with sequence data at an average coverage of 35×, with specificity comparable to the data presented in this report (Online Methods).

The algorithm has several features that are important in clinical designs. By using colored de Bruijn graphs to locally assemble candidate alleles, the algorithm is able to deal with both large variants up to 1 kb in size and highly diverse regions in the genome. In combination with the ability to make reference calls and to report local linkage information, this enables high-resolution genotyping of class I HLA genes from high-throughput sequencing data. The ability to make reference calls will be useful in other clinical contexts as well, including in screens for genetic predispositions for disease, where the ability to confidently exclude particular variants can be clinically relevant. Platypus performed well on both whole-genome and exome-capture data, and, particularly for exonic variants, its ability to call multi-nucleotide polymorphisms will help to correctly annotate the impact on protein-coding genes of these variants.

Platypus is a fast and efficient implementation of this algorithm, requiring neither a complex bioinformatics pipeline nor extensive computational resources. Platypus uses no intermediate files, minimizes access to BAM files and has low memory and CPU requirements, resulting in 5–90× faster processing times than with comparable algorithms (Table 1). Additional features including on-the-fly merging, demultiplexing and deduplication of BAM files further simplify processing and reduce I/O requirements.

Several extensions to the algorithm may be considered. For instance, the likelihood model does not include terms for the expected coverage or inferred fragment size; these would provide additional evidence that would further improve the algorithm’s ability to detect large (>1-kb) structural variation. Although the algorithm has been successfully used to detect somatic mutations in cancer tissue^40,41, it currently does not specifically handle such non-diploid samples, and tailored models will further improve performance for these applications. Nevertheless, the current implementation provides high-quality variant calls in a range of practical clinical settings, and we hope that it will contribute to an increased uptake of high-throughput sequencing technologies in the clinic.

URLs

In-Silico PCR, http://genome.ucsc.edu/cgi-bin/hgPcr; IMGT/HLA database, ftp://ftp.ebi.ac.uk/pub/databases/ipd/imgt/hla/; HLA Informatics Group, http://hla.alleles.org/; Sequencher, http://www.genecodes.com/. The call sets analyzed for this paper are available at http://www.well.ox.ac.uk/platypus-paper-data.

Software

Platypus is open source and freely available under a GPL license from http://www.well.ox.ac.uk/platypus.

ONLINE METHODS

Estimation of haplotype frequencies

After haplotypes are generated from candidate variants within a particular window, their frequencies are estimated on the basis of their likelihood p(r|h), where r and h denote read and haplotype, respectively. These likelihoods are calculated by aligning a read to the haplotype sequence with an underlying hidden Markov model (HMM). The likelihood of a read given a haplotype can be calculated using the Forward algorithm. The alignment algorithm includes models for base mismatches and indel errors. Mismatches are scored by adding up the Phred quality scores of mismatching bases. The indel error model is the same as the one used in Dindel².

After p(r|h) is calculated for all combinations of reads and haplotypes, an expectation-maximization algorithm is run to estimate the frequency of each haplotype h₁, …, h_a, under a diploid genotype model

$$L\left(R\mid {\left\{h_i,f_i\right\}}_{i=1\dots a}\right)=\underset{s}{\prod _{\text{samples}}}\underset{i,j}{\sum _{\text{hyplotypes}}}{f}_i{f}_j\underset{r\in R_s}{\prod _{\text{reads}}}\left(\frac{1}{2}p\left(r\mid h_i\right)+\frac{1}{2}p\left(r\mid h_j\right)\right)$$

Here f_i denotes the frequency of haplotype h_i in the population, a is the number of alleles considered, and R and R_s denote the sets of all reads and reads from sample s, respectively; the sum over haplotypes extends over all ordered pairs (i,j), i.e., genotypes.

Calling variants and calculating genotype likelihoods

The posterior support for any variant is computed by comparing the likelihood of the data given all haplotypes and the likelihood given only those haplotypes that do not include a particular variant, i.e., the likelihood in a nested model where the frequencies of haplotypes that do not include the variant are fixed to 0. For the latter model, the frequencies not fixed to 0 are scaled up to account for the estimated frequency of the excluded haplotypes

$$p\left(v\mid R\right)=\frac{p\left(v\right)L\left(R\mid {\left\{h_i,f_i\right\}}_{i=1\dots a}\right)}{p\left(v\right)L\left(R\mid {\left\{h_i,f_i\right\}}_{i=1\dots a}\right)+\left(1-p\left(v\right)\right)L\left(R\mid {\left\{h_i,\frac{f_i}{1-F_v}\right\}}_{i\in I_v}\right)}$$

where p(v) is the prior probability of observing variant v, I_v is the set of haplotype indices i for which h_i does not contain v and $F_v=\sum _{i\in I_v}{f}_i$. The likelihood of reads given haplotypes and their frequencies is computed as:

$$L\left(R\mid {\left\{h_i,f_i\right\}}_{i=1\dots a}\right)=\prod _{\text{samples}}\underset{i,j}{\sum _{\text{hyplotypes}}}{f}_i{f}_j\prod _{r\in R}\left(\frac{1}{2}p\left(r\mid {\mathit{h}}_i\right)+\frac{1}{2}p\left(r\mid h_j\right)\right)$$

Variants are called when their posterior support exceeds a threshold (by default, a Phred score of 5), using these frequencies as a prior.

Genotype likelihoods for a particular variant are calculated by marginalizing over the genotypes at other variant sites within the window being considered. The best likelihood is reported as a genotype call, and the posterior for this call is calculated in the usual way (as the prior times the likelihood of the call, divided by the sum of the prior times the likelihood over all genotypes considered) and reported as a ‘genotype quality Phred score’ (the Phred-scaled probability of the call being wrong, or 10 times negative 10-log of 1 minus the posterior probability of the call being correct) in the per-sample genotype quality field. Using the maximum-likelihood estimates of haplotype frequencies estimated from the data itself as priors when calling haplotypes and variants works well but tends to bias genotype calls, particularly for small pedigrees and single samples. To address this, we replace the estimated frequencies by a flat prior when calling genotypes if the number of samples is below 25. This bias also affects the reported genotype quality but does not affect the reported genotype likelihood.

Filtering variants

We applied the following default filters for all the calls used in this report:

• Allele bias: a variant is marked as allele bias if (i) the fraction of reads supporting the variant allele is less than the minimum of 0.5 and a user-specified threshold frequency (default of 20%; configurable via the –minVarFreq option) and (ii) the P value under a binomial model with a β prior is less than 0.001.

• Strand bias: a variant is flagged as strand biased if its supporting reads are skewed in terms of reads mapping to the forward and reverse strands, relative to the distribution seen in all reads. Specifically, the reads supporting the variant are tested against a β binomial distribution with parameters α and β, such that the smallest of these parameters is 20, and the parameters are such that the mean of the distribution equals the ratio observed in all reads. Variants are accepted if the P value exceeds 0.001.

• Bad reads: this filter triggers when, across reads supporting a variant, the median of the minimum base quality score close to the focal site (default of 7 bp on either side; configurable using –badReadsWindow) is too low (default of 15 or less; configurable using –badReadsThreshold). It also triggers when more than a fraction of reads are filtered out for the candidate generation stage; the default for this is 0.7 (configurable using –filteredReadsFrac).

• Mapping quality: we compute the root-mean-square mapping quality of all reads covering the variant site and filter out the variant if this value is less than 40 (configurable using –rmsmqThreshold).

• Quality over depth: we compute a value (the quality-over-depth score) that reflects the total evidence in favor of the variant per read supporting the variant. That is the Phred-scaled variant posterior as reported in the QUAL field of the VCF file divided by the number of reads that support the variant. Variants with a quality-over-depth value of less than 10 (configurable using –qdThreshold) are flagged as suspicious.

• Posterior quality (Q20): although variants are called and included in the output VCF, if they have a Phred-scaled posterior exceeding 5, all variants with posteriors below 20 are flagged as suspicious.

• Sequence context: to avoid calling variants in low-complexity regions that are prone to polymerase slippage and hence to spurious indel calls, we compute a sequence complexity statistic that measures the contribution of the 2 most frequent nucleotides among the 21 around a site; if this measure exceeds 95%, SNP calls are flagged as suspicious.

Validation of de novo mutation calls using Sanger sequencing

From the list of predicted de novo mutation calls obtained from 15 parent-offspring trios for which consent was obtained to use the sequencing data for research purposes, we designed PCR primers with Primer3 (refs. 42,43; version 2.3.5) using Tm 63, primer length 25–30 bp and product size ranging from 350–700 bp and avoiding common SNPs. We could not design primers for variants in difficult regions, such as those that completely lay within a medium-size repeat, for example, long interspersed nuclear elements (LINEs). For other difficult cases where variants were in repeats but flanking sequences showed overlap with unique sequences, we manually designed primers so that at least one primer (forward or reverse) overlapped with the unique sequences. All primer pairs were then checked manually using In-Silico PCR (see URLs) for targeted sequences.

We performed Sanger sequencing on PCR products amplified from trio DNA using BigDye Terminator mix version 3.1 (Applied Biosystems) and the ABI PRISM 3730 DNA sequencer. Sequence chromatogram traces were manually inspected to verify the de novo mutation pattern within the trio using Sequencher (Gene Codes). See Supplementary Figure 5 for Sanger sequencing traces of the validation experiments.

Estimating the 95% credible interval for the false discovery rate from validation data

Suppose that the true FDR among de novo mutations is p. The probability of observing k false positives among n validation experiments is

$$P\left(k\mid n,p\right)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)p^k{(1-p)}^{n-k}$$

Assuming a uniform prior on p, a conservative choice, the cumulative distribution function (CDF) of the posterior after observing k false positives can be written as

$$P\left(p<q\mid n,k\right)=\frac{{\int }_{p=0}^q\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)p^k{(1-p)}^{n-k}\mathrm{d}p}{{\int }_{p=0}^1\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)p^k{(1-p)}^{n-\mathit{k}}\mathrm{d}p}=\left(n+1\right)\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)B_q\left(k+1,n+1-k\right)$$

where B_q is the incomplete β function. For n = 68 and k = 5, the 95% credible interval of this distribution is 0.033–0.163.

Genotyping HLA loci

From the list of variant calls V = {V_i} and reference calls R = {R_i} of Platypus, a set H of haplotype pairs ($v_i^1,v_i^2$) and ($r_i^1\equiv r_i^2$) was generated. The $v_i^1$ and $v_i^2$ segments were obtained by first clustering variants (and intervening reference sequence) by the reported calling window. These clusters were then extended by 12 bp up- and downstream from the variant or variants and were trimmed to ensure no overlap with any other haplotype pairs (Supplementary Fig. 1).

For each HLA gene targeted for genotyping (HLA-A, HLA-B and HLA-C), we downloaded the known alleles from the IMGT/HLA database (see URLs; see also the HLA Informatics Group page). Let A = {a₁, a₂, …, a_N} be the set of known alleles available for a gene. We query the short segment set H against A using BLAST, generating BLAST scores that show the similarity of the short segments and the HLA alleles. Here we interpret the BLAST scores as proportional to the log probability of the variant (or reference) segment being v_i given haplotype a_j, apart from a constant additive term; in short

$$\log p\left(v_i\mid a_j\right)\propto \{\begin{array}{c}\max (S\left(v_i,a_j\right)\text{if}\phantom{)}L\left(\text{alignment}\right)=\mid v_i\mid \text{and percent identity}=100\%\hfill \\ 0\text{otherwise}\hfill \end{array}\phantom{\}}$$

Here we take the maximum across BLAST scores, as BLAST occasionally identifies multiple partial matches against a single allele a_j. Given the probabilities defined above, the (scaled) log likelihood of the genotype g = (a_i,a_j) is calculated as

$$\log L\left(g=\left(a_i,a_j\right)\mid D\right)\propto \sum \log p\left(V_k\mid g=\left(a_i,a_j\right)\right)+\sum \log p\left(R_k\mid g=\left(a_i,a_j\right)\right)$$

where

$$\log p\left(V_k\mid g=\left(a_i,a_j\right)\right)=\max \left(\log p\left(v_k^1\mid a_i\right)+\log p\left(v_k^2\mid a_j\right),\log p\left(v_k^1\mid {\mathit{a}}_j\right)+\log p\left(v_k^2\mid a_i\right)\right)$$

as the phasing of each local pair of haplotypes is unknown and

$$\log p\left(R_k\mid g=\left(a_i,a_j\right)\right)=\log p\left(r_k^1\mid a_i\right)+\log p\left(r_k^2\mid a_j\right)\left(\text{note that}{r}_k^1\equiv r_{\mathit{k}}^2\right)$$

The pairs of alleles that achieve the highest (scaled) maximum-likelihood value are chosen as the candidate genotypes for the HLA gene in question.

Variants from fosmid data

To obtain a set of validated variant calls, we used existing fosmid data and subjected these to stringent filtering (Supplementary Note). This filtering resulted in 4,004 SNV calls, 1,020 indel calls ranging in length from 1 to 701 bp, 5 MNVs and 52 complex variants.

Using this set of fosmid variants, we obtained for each call set a 2 × 3 coincidence matrix with rows marked as ‘present/absent in fosmid’ and columns marked with ‘0/0’, ‘0/1’ and ‘1/1’ according to the called genotype. Numbers in the coincidence matrix were obtained by considering the union of variants present in the call set of interest and those observed in the fosmid data. These data are presented in Supplementary Table 5.

Estimating coverage requirements for calling de novo mutations

We used the sensitivity and specificity estimates on the relatively high-coverage data in this report to assess coverage requirements for attaining 95% and 99% sensitivity for de novo mutations, on the basis of the premise that the false positive rate after applying the Bayesian filter is independent of coverage but sensitivity is dependent on it. We do this by modeling the outcome of the Bayesian model at true de novo mutation sites under a coverage distribution obtained by rescaling the empirical coverage distribution to a desired target average coverage. For details and results, see Supplementary Table 6 and the Supplementary Note.