Imaging and graphing of cortical vasculature using dynamically focused optical coherence microscopy angiography

Abstract.

Recently, optical coherence tomography (OCT) angiography has enabled label-free imaging of vasculature based on dynamic scattering in vessels. However, quantitative volumetric analysis of the vascular networks depicted in OCT angiography data has remained challenging. Multiple-scattering tails (artifacts specific to the imaging geometry) make automated assessment of vascular morphology problematic. We demonstrate that dynamically focused optical coherence microscopy (OCM) angiography with a high numerical aperture, chosen so the scattering length greatly exceeds the depth-of-field, significantly reduces the deleterious effect of multiple-scattering tails in synthesized angiograms. Capitalizing on the improved vascular image quality, we devised and tailored a self-correcting automated graphing approach that achieves a reconstruction of cortical microvasculature from OCM angiography data sets with accuracy approaching that attained by trained operators. The automated techniques described here will facilitate more widespread study of vascular network topology in health and disease.

1. Introduction

A recent enabling advance in optical coherence tomography (OCT) imaging has been the development of angiography methodologies to selectively image vasculature.^1–4 The motion of red blood cells (RBCs) and other scatterers within blood vessels can typically be observed as dynamic changes in OCT images. Building on this observation, angiography techniques based on amplitude and/or phase motion contrast have been developed as means of visualizing perfused vasculature in vivo.^1–3

Though three-dimensional (3-D) OCT angiography provides volumetric vascular information, morphometric analysis of vessels is often limited to two dimensions, typically using projections in the en face plane. By comparison, comprehensive quantitative volumetric analysis of brain vasculature has been demonstrated using two-photon laser scanning microscopy employing a plasma label,^5–7 yielding a topological graph of the vascular network. OCT angiography, in contrast to two-photon microscopy, offers label-free assessment of the functional (i.e., oxygen-delivering) microvascular network that is perfused with moving blood cells, and OCT is widely used clinically and in basic research. However, angiographic analysis methods have yet to fully capitalize on its volumetric imaging potential.

A significant obstacle to quantitative volumetric analysis of 3-D OCT angiography data is the degradation of lumen localization precision due to light originating from multiple-scattering events. This effect can be observed as dynamic scattering “tails” beneath large vessels, resulting mainly from RBC forward scattering followed or preceded by tissue backscattering.⁸ These tails may also be caused by changes in optical path length arising from the higher refractive index of RBCs crossing the beam path.⁹ Such tails appear to elongate imaged vessel lumens in the axial direction and cause overlap between superficial and deep vessels.

Optical coherence microscopy (OCM) combines the coherent detection methods of OCT with high transverse spatial resolution, typically by employing higher numerical aperture (NA) focusing.¹⁰ In this work, we show that high NA OCM angiography improves rejection of multiple-scattered photons, provided that the depth of field is much smaller than the scattering length, thus mitigating tail artifacts and facilitating 3-D analysis. We subsequently describe a self-correcting automated graphing protocol that can be used as a basis for robust quantitative analysis, such as computing 3-D blood vessel network topology, interconnectivity, and branching hierarchy from OCM angiography data.

2. Methods

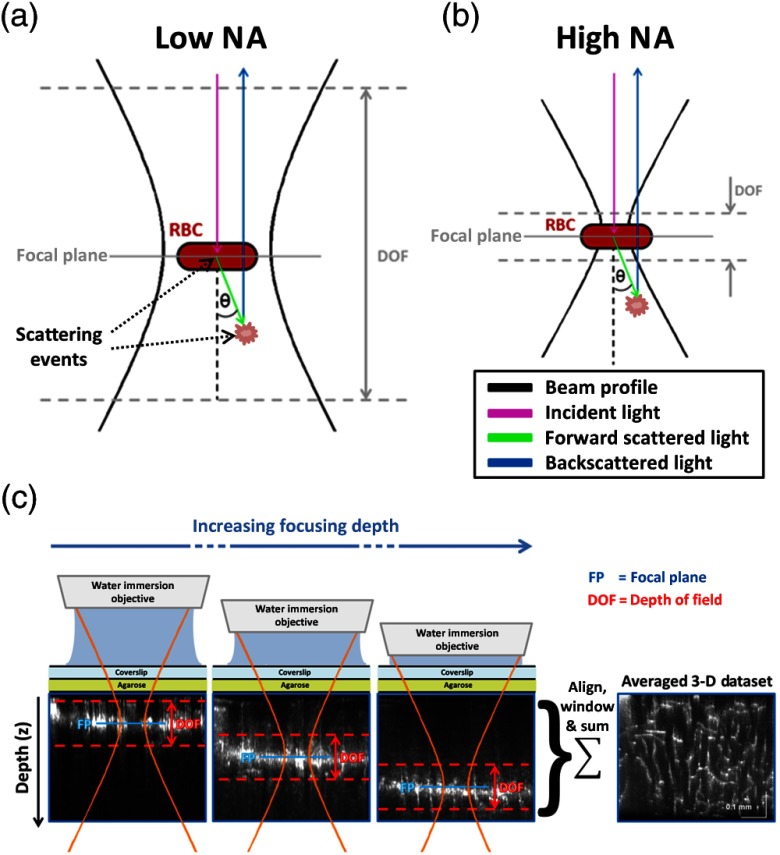
Angiograms were computed using an algorithm based on temporal filtering of the complex OCT signal.⁸ Sprague–Dawley rats (80 to 120 g, $N=2$) were anesthetized and ventilated with a mixture of air and ${\mathrm{O}}_2$, and imaged through a sealed cranial window using a 1310-nm spectral/Fourier domain OCM microscope. All experimental procedures were approved by the committee on research animal care. Figure 1 illustrates low NA [Fig. 1(a)] and high NA [Fig. 1(b)] imaging geometries. The full width at half maximum (FWHM) transverse resolutions were 7.2 and $1.8\mu \mathrm{m}$, respectively, with corresponding confocal parameters of 242.2 and $15.1\mu \mathrm{m}$. The confocal parameter for the high NA geometry was much smaller than typical scattering lengths in brain tissue ($\sim 285\mu \mathrm{m}$),¹¹ thus helping to reject light arising from multiple-scattering events [Fig. 1(b)]. Experimentally, for the high NA geometry, a water immersion objective was employed along with a dynamic focusing protocol, which we described in detail in a previous work.¹² This technique yields fine transverse resolution over an extended depth range, as depicted in Fig. 1(c). The axial resolution, mainly determined by the source coherence length and not the confocal parameter, was $3.6\mu \mathrm{m}$ for both low and high NA geometries.

Fig. 1.

(a) Low NA imaging geometry is sensitive to multiple-scattering events, while high NA imaging geometry (b) is not; (c) imaging using dynamic focusing at high NA to achieve high transverse resolution over an extended depth range.

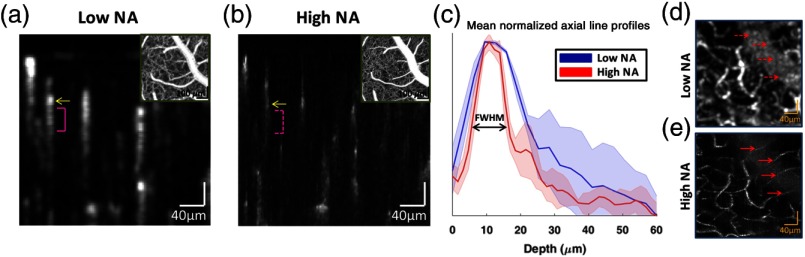
Figure 2 shows the impact of NA on localization of capillaries in OCT angiograms. Figure 2(a) shows a cross-sectional angiogram obtained with the low NA imaging geometry. Figure 2(b) shows a cross-sectional angiogram (synthesized from dynamically focused data sets) obtained with the high NA imaging geometry. Backscattering arising from an exemplary capillary lumen is marked by a yellow arrow in both angiograms. Multiple-scattering tails (pink brackets), with longer path lengths than the initial backscattering events, are more prominent in the low NA geometry [Fig. 2(a), solid] than in the high NA geometry [Fig. 2(b), dotted]. Figure 2(c) gives mean normalized axial line profiles for selected capillaries of similar size. The high NA geometry reduced the FWHM of the mean axial line profile by $\sim 1.9\times$, demonstrating better axial localization of vessels. Since the high NA geometry did not appreciably change the axial resolution, we attribute this improvement to better rejection of multiple-scattered light in the high NA geometry. Figure 2(d) shows a maximum intensity projection (MIP) of a region of interest under a large vessel, using low NA imaging geometry. Figure 2(e) shows an MIP of the same region with high NA, revealing vessel crossings that were obscured in the low NA MIP.

Fig. 2.

(a) Cross-sectional image obtained with low NA imaging geometry. The yellow arrow shows a capillary lumen, with the approximate extent of the corresponding multiple-scattering tail marked (pink bracket). (b) Cross-sectional image obtained with high NA imaging geometry and dynamic focusing. The yellow arrow shows the same capillary lumen, while the multiple-scattering tail (dotted pink bracket) is less prominent than in (a). Insets in (a) and (b) show en face MIPs. (c) Mean normalized axial line profiles of signal amplitude from selected capillaries of similar size, with standard deviations shown by the shaded regions. The estimated FWHM of the mean vessel axial line profile was $20.45\pm 4.64\mu \mathrm{m}$ using low NA, and $10.65\pm 1.78\mu \mathrm{m}$ using high NA and dynamic focusing. (d and e) En face MIP of a selected region of interest under a large vessel. The multiple-scattering and shadowing owing to the large vessel obscures deeper capillary crossings in the low NA case (d, dotted red arrows), whereas for the high NA case, these crossings can be clearly seen (e, solid red arrows).

The high NA OCM image data set, covering a $600$ micron cube, was subsequently used to form a 3-D representation, or graph, of the cortical vasculature. First, vascular structure within the image volume was enhanced using a multiscale technique.¹³ An empirically determined threshold was then applied to the enhanced data volume, yielding a binary mask representation of the vasculature. Morphological opening was implemented to mitigate the effect of noise on the mask. A skeletonization method^14,15 was then used to obtain a center-line map, or “skeleton,” which enabled the vasculature to be represented as a 3-D vectorized graph.¹⁶ Skeletonization methods are commonly confounded by noise or other artifacts that lead to errors in the skeleton topology, such as small spurious branches and vessel gaps that are not representative of the true underlying anatomy. Such errors are manifested as singly connected branches that are not consistent with the contiguous vascular graph. In prior work, such branches were resolved with the aid of manual input based on operator judgment in the form of interactive point-selection and curve-drawing,¹⁷ or labeling of training data sets to aid supervised machine-learning methods.¹⁸

In this work, errors in the vascular graph topology were resolved using an automated algorithm based on shortest-path computation. The algorithm could correct both erroneous gaps and spurious singly connected branches, but did not explicitly deal with incorrectly merged branches. First, the software identified all points on the skeleton for which a connecting branch was required, i.e., all skeleton voxels with only one neighboring voxel located within their $3\times 3\times 3$ neighborhood (excluding those adjacent to the boundary of the data volume). Each of these endpoints could be resolved by either (i) connecting it to the contiguous graph via a bridging strand; or (ii) removing the singly connected branch from the network. For each located endpoint, the software determined a list of candidate connection points consisting of nearby branch points (bifurcation points), as well as other singly connected branch endpoints. A candidate bridging strand was identified for each candidate connection point using a computation based on Dijkstra’s algorithm.¹⁹ Candidate bridging strands were validated using a simple ad hoc decision tree model, which imposed limits on the acceptable tortuosity and branching geometry. Validation of candidate bridging strands can also be performed using a classification model derived from the geometrical and/or intensity-based features of a manually approved training set.¹⁸ However, a MATLAB^® implementation of a bootstrap aggregated decision tree model (based upon a training set of approximately 1000 bridging strands) was found to be no more effective at validation than the simple ad hoc decision tree model. A path score was calculated for each valid candidate bridging strand, computed as $\sum _k{I}_e(k)/L^2$, where $L$ is the length of the strand and $I_e(k)$ is the enhanced image intensity at voxel $k$ traversed along the strand’s path. The candidate bridging strand with the highest path score was incorporated into the skeleton, thus rejoining the singly connected branch to the contiguous vascular graph. Singly connected branches with endpoints for which no viable bridging strands could be found were removed.

Four separate $256\times 256\times 400\text{\hspace{0.17em}\hspace{0.17em}voxel}$ cortical subgraphs (located within the capillary bed) were corrected using the automated procedure. Each graph was also corrected independently by three manual operators. The manual correction was performed using a custom-built MATLAB^® graphical user interface that allows the operator to manually select candidate connection points for correction via the aforementioned shortest-path algorithm.¹⁶

3. Results

A 3-D rendering of the segmented cortical vasculature (acquired using high NA imaging geometry and dynamic focusing) is shown in Fig. 3(a), representing both superficial (pial) vessels and the deeper capillary bed. Figure 3(b) shows an MIP of the capillary bed vessels from the enhanced image data. Figures 3(c) and 3(d) show MIPs of a section of the enhanced image data, overlaid with the manually and automatically corrected skeletons, respectively.

Fig. 3.

Correction of cortical vascular graphs acquired using the high NA imaging geometry and dynamic focusing. (a) 3-D representation of the segmented cortical vasculature showing pial vessels (arteries in red, veins in blue) and capillaries (gray). (b) MIP of capillary bed vessels from the enhanced OCM image data set. MIPs of image data from this data set were previously published by Srinivasan et al.¹² (c) MIP of image intensity from the highlighted section in panel b, overlaid with the original uncorrected skeleton (cyan) and branches drawn during manual correction (green). (d) MIP of image intensity, overlaid with the original uncorrected skeleton (cyan) and branches drawn during automated correction (red).

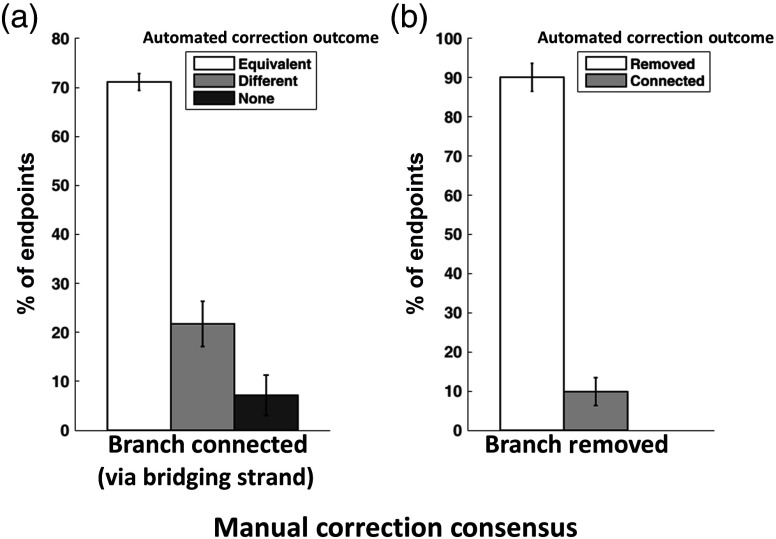
Consensus among manual corrections by multiple operators can provide a ground truth for the evaluation of automated skeleton correction methods.²⁰ Figure 4 summarizes the performance of the automated correction via comparison to that of the manual operators in terms of correction outcomes for endpoints, both in cases where all of the manual operators agreed upon equivalent bridging strands [Fig. 4(a)], and in cases where all manual operators elected to remove the endpoint branch [Fig. 4(b)]. Considering each of the three manual operators and the automated correction algorithm as independent observers, the accuracy of each observer with respect to the consensus established by the other three was also evaluated (data not shown). Though the automated method was not as effective in terms of correction accuracy, its performance was nonetheless comparable to that of the manual observers.

Fig. 4.

Performance of automated skeleton correction, measured against a consensus formed by three manual operators. (a) For cases where all three manual operators identified an equivalent bridging strand (i.e., connecting to the same branch), the automated method established an equivalent strand $71.1\pm 1.7\%$ of the time, a different bridging strand $21.8\pm 4.6\%$ of the time, or elected to remove the endpoint branch from the graph (when no viable candidate strands were found) $7.1\pm 4.1\%$ of the time. (b) For endpoints for which no manual operators identified a valid bridging strand (i.e., all elected to remove the endpoint branch), the automated correction was in agreement $90.1\pm 3.6\%$ of the time, whereas in $9.9\pm 3.6\%$ of cases, the automated algorithm found a viable bridging strand candidate and thus connected the endpoint to the contiguous skeleton.

Ultimately, the most effective use for a self-correcting graphing technique, such as the one described in this work, may be in a semiautomated approach. Such a hybrid approach would balance the enhanced speed of automatic algorithms with the superior ability of humans to perceive structure in the presence of noise or other confounds. Along these lines, we integrated automated correction with our graphical user interface such that the software presented the operator with a suggested bridging strand for each unconnected endpoint. We found that in $48.1\pm 4.8\%$ of cases, the operator accepted the suggested bridging strand as valid, pointing to the possibility for a significant reduction in manual effort through a semiautomated approach. Further reductions in manual effort could likely be achieved by presenting the operator with a choice of several bridging strands.

4. Discussion and Conclusion

In this work, we demonstrated that high NA OCM angiography, besides providing fine transverse resolution, also rejects multiple-scattered light arising from vessels. The improved angiogram quality achieved with high NA OCM imaging leads to better localization of vessel lumens, which is desirable for accurate volumetric segmentation and graphing. However, the higher NA and improved transverse resolution yield a reduced depth of field, which leads to longer imaging sessions with dynamic focusing and increased susceptibility to angiogram artifacts caused by sample motion, both of which represent limitations of the method.

The new automated graph correction approach described in this work emulates the features of manually guided skeleton correction.¹⁷ In cases where manual operators reached a consensus on the bridging strand, the automated algorithm agreed $71.1\pm 1.7\%$ of the time [Fig. 4(a)]. The automated algorithm agreed $90.1\pm 3.6\%$ of the time in cases where the manual operator consensus was to remove a branch [Fig. 4(b)]. This suggests an appreciable correspondence between manual and automated correction. Further advances in automated self-correction algorithms may enable graphing methods to be applied more widely than is currently possible with manual correction tools, with considerable benefit from the reduced human effort. Once corrected, vascular graphs can be used to compute quantitative measures of 3-D blood vessel network topology, interconnectivity, and branching hierarchy.^5,16 Therefore, the imaging and graphing approaches presented here could serve as comprehensive tools to analyze vasculature in health and disease.