Prospective motion correction with volumetric navigators (vNavs) reduces the bias and variance in brain morphometry induced by subject motion

Abstract

Recent work has demonstrated that subject motion produces systematic biases in the metrics computed by widely used morphometry software packages, even when the motion is too small to produce noticeable image artefacts. In the common situation where the control population exhibits different behaviours in the scanner when compared to the experimental population, these systematic measurement biases may produce significant confounds for between-group analyses, leading to erroneous conclusions about group differences. While previous work has shown that prospective motion correction can improve perceived image quality, here we demonstrate that, in healthy subjects performing a variety of directed motions, the use of the volumetric navigator (vNav) prospective motion correction system significantly reduces the motion-induced bias and variance in morphometry.

1 Introduction

The influence of motion on MRI neuroimaging studies, particularly high-resolution, 3D-encoded imaging where scan times can extend to several minutes, has long been recognized in both clinical and research environments (Maclaren et al., 2013, Zaitsev et al. (2015)). In both settings, images that are qualitatively considered to be motion-degraded are often discarded and rescanned. In some research studies, subjects are removed from analysis when their scans show unacceptable levels of motion degradation (e.g., (Qureshi et al., 2014, Harvard Center for Brain Science (2015))), while in other studies, efforts are made to match controls to experimental subjects with similar amounts of motion (Yendiki et al., 2014, Koldewyn et al. (2014)). All of these methods of dealing with motion must be used carefully to avoid introducing biases into group analyses. For example, removing subjects who move during their MRI scans, or selecting control subjects based on how much they move, may result in selection bias.

The importance of accounting for motion has been made clear by recent work showing that differences in motion between groups lead to not just a decrease in statistical power, but can introduce biases in a variety of neuroimaging experiments (Van Dijk et al., 2012, Power et al. (2012), Satterthwaite et al. (2012), Satterthwaite et al. (2013), Yan et al. (2013), Yendiki et al. (2014), Hess et al. (2014), Power et al. (2014), Reuter et al. (2015)). Connectivity analyses performed using functional (Van Dijk et al., 2012, Power et al. (2012), Satterthwaite et al. (2012), Satterthwaite et al. (2013), Yan et al. (2013), Power et al. (2014)) and diffusion-weighted data (Yendiki et al., 2014) both show significant sensitivity to subject motion. In the case of brain morphometry, (Reuter et al., 2015) demonstrated that the impact of motion is a continuous effect, with even small subject motions biasing the resulting measurements. As a result, only aggressive removal of motion-damaged data, beyond what is normally done in neuroimaging studies, could bring the effect of motion on grey matter volume and thickness estimates below a statistically significant level. This work concluded that even motion whose impact on image quality is effectively unnoticeable by visual inspection still biases the morphometric analysis.

The volumetric navigator (vNavs) system allows the scanner to track the subject’s head during the scan and prospectively correct for subject motion (Tisdall et al., 2012, Hess et al. (2011)). vNavs are inserted into the dead-time in MRI pulse sequences (normally once per TR), with each navigator acquiring a complete, but low-resolution head volume in roughly 300 ms. These navigator volumes are then rapidly registered, and the resulting estimates of subject motion are used to update imaging parameters “on the fly” during scanning, allowing the scanner to image in head-relative coordinates despite subject motion. These motion updates are inherently low-frequency, since they can only occur once per TR (e.g. every 2.53 seconds during our MEMPRAGE protocol), and subject motion between segments is not fully corrected. To address this, the system can automatically reacquire TRs that it determines to have been motion degraded based on it’s estimate of subject motion. Combining the prospective updates with retrospective reacquisition provides a substantial reduction in the impact of head motion on the output images.

In addition to vNavs, other prospective motion correction systems have also demonstrated qualitative improvements in image quality when subjects perform motions that would normally cause substantial artefacts (van der Kouwe et al., 2006, Zaitsev et al. (2006), Ooi et al. (2009), Brown et al. (2010), Kuperman et al. (2011), Hess et al. (2011), Tisdall et al. (2012), Maclaren et al. (2013), Zaitsev et al. (2015)). However, given the new awareness that even small amounts of motion may compromise morphometric data, we are interested in evaluating whether vNav-enabled scans can correct the motion-induced bias in morphometry, even when the motions performed are too small to cause obvious image artefacts.

We address this question using a superset of the data that was considered in (Reuter et al., 2015). The previous work considered only scans without prospective motion correction and derived statistical tests to evaluate the effects of motion on uncorrected studies. In the present work we add into our analysis scans where prospective motion correction with vNavs was used, and evaluate whether the corrected scans show a significantly smaller error due to motion than those without correction.

2 Materials and Methods

2.1 Scanning

Twelve healthy adult volunteers (5 male and 7 female; ages 21-43, mean age 26.9 years, standard deviation 7.2 years), having given informed consent, were scanned in a 3 T TIM Trio MRI System (Siemens Healthcare, Erlangen, Germany) using the 12-channel head matrix coil supplied by the vendor. For each subject, scans were performed during one visit and the scanning session was divided into two blocks of equal length. Between each of the two blocks, the subject was removed from the scanner and allowed to take as long a break as desired. During each scan block, subjects’ heads rested on a pillow, stabilized by foam blocks on both sides. Subjects were located in the bore such that the junction of the top of the nose and the brow was at isocenter.

Each visit included eight repetitions of a 3D multi-echo MPRAGE (MEMPRAGE) (Mugler and Brookeman, 1990, Mugler and Brookeman (1991), van der Kouwe et al. (2008)): two still scans (both without prospective motion correction), and then two scans in each of three motion conditions, giving a total of six motion scans. Scanning was performed using a research version of the vNavs-enabled MEMPRAGE pulse sequence, which is available as a research sequence for some Siemens scanner platforms. Subjects were asked to perform three qualitatively different motions: nodding (rotation around left-right axis), shaking (rotation around head-foot axis), and moving freely (each subject was directed to make up a short pattern to repeat, with the suggestion “draw a figure-8 with your nose.”). These motion types were chosen in order to cover a variety of motion directions. In studies of disease and aging there may be stereotyped patterns and frequencies of motion, but to the best of our knowledge these features of in-scanner behaviour have not yet been documented for any specific populations of interest. Our present study was not powered to differentiate effects of different motion types. Instead, our goal in having subjects perform a variety of motion types was to induce within-subject variability in the scans, under the assumption that each motion “type” would also lead to different amounts of motion.

For each type of motion, one repetition was performed with prospective motion correction disabled (but with vNavs measuring subject motion) while the other repetition had prospective motion correction enabled. Each block included scans with one of each motion type (still, nod, shake, and free), but whether the first or second repetition of each motion type had prospective correction enabled was randomized for each subject. Subjects were not informed as to whether or not motion-correction was being applied. Before each scan, an auto-align localizer (van der Kouwe et al., 2005, Benner et al. (2006)) was run to ensure each scan began in approximately equivalent alignment with the head. The order of the scans was randomized for each subject in order to reduce potential order-related biases in the results.

Before entering the scanner, subjects rehearsed the motions with the experimenter and were reminded that the motions should remain small (our experience from past studies being that MRI-naive subjects who are asked to move tend to perform very large motions). When inside the scanner, subjects were directed as to which motion to perform and the duration of each motion through written instructions projected on a screen at the head of the scanner bore and visible in a mirror attached to the coil. Subjects were told to begin moving when the screen switched to a move instruction and continue moving until presented with instructions to “remain still”. Subjects were instructed to remain still in whatever position they found themselves in when the screen switched back to “remain still” (their pre-scan verbal instructions included the phrase “freeze when the screen asks you to remain still”). Each subject was randomized to be either a “long” or “short” movement subject, with six subjects in each group. “Long” movement subjects were directed to move for a 15-second block during each minute of scanning, while “short” movement subjects were directed to move for a 5-second block during each minute of scanning. Subjects were not informed which group they were in. Similar to our use of multiple motion types, our goal in having long and short motion groups was not to study whether these two amounts of motion produced significantly different effects, but instead to help ensure larger between-subject variability than would occur if all subjects were asked to move for the same duration.

Scans were immediately stopped and repeated if a subject’s motion was estimated to have exceeded 8 degrees rotation or 20 mm translation in one TR. This limit is enforced by Siemens’ PACE motion-tracking system (Thesen et al., 2000), upon which the vNavs system is based.

All 3D MEMPRAGE scans were acquired with the same protocol: non-selective inversion and excitation, 2530 ms TR, 1220 ms TI, 256 mm × 256 mm × 176 mm FOV with 1 mm isotropic resolution, 4 echoes with a bandwidth of 650 Hz/pixel, and 2× GRAPPA acceleration in the outer-most phase-encode loop. The voxel-wise root-mean-squared combination of the four echoes was used for all subsequent analysis. vNavs (3D-encoded EPI volumes) were acquired once every MEMPRAGE TR as described in (Tisdall et al., 2012); the vNav protocol had a 256 mm × 256 mm × 256 mm FOV with 8 mm isotropic resolution, one excitation per slab and 3/4 partial Fourier in the slice direction, 11 ms TR, 5.3 ms TE, and a bandwidth of 4223 Hz/pixel. Total scan time for the scans without motion correction was 6:12, while the scans with motion correction included 18 extra TRs of reacquisition, and thus their total time was 7:00 (19 extra TRs need to be played for 18 reacquisitions to ensure each imaging TR is sandwiched between vNavs; for more details see (Tisdall et al. (2012))). The choice of 18 extra TRs was made based on the desire to keep a practical scan duration (in this case 7 minutes). In our study this number was kept constant for all subjects in the with-motion-correction conditions; in practice some versions of the vNavs system can automatically stop scans early if continued reacquisition is unnecessary. k-space was sampled in a linear order, and the motions were not timed with any particular focus to overlap with specific portions of k-space.

2.2 Morphometric analyses

Our goal in this study was to quantify how motion and vNavs prospective motion correction influence widely used morphometric analysis methods, and not focus on any particular analysis procedure. To this end, multiple morphometric analyses of the MEMPRAGE volumes were performed using FSL Siena 5.0.7, the voxel based morphometry VBM8 toolbox (Gaser, 2014) of the SPM8 package (Ashburner and Friston, 2005), and both the cross-sectional (Fischl, Sereno, and A. M. Dale, 1999, Fischl, Sereno, Tootell, et al. (1999)) and longitudinal (Reuter et al., 2010, Reuter et al. (2012)) analysis streams of FreeSurfer 5.3. The use of diverse tools, each producing their own metrics using independent algorithms, ensures that the observed effects of motion and motion correction were not an isolated artefact of a particular analysis procedure.

Percent brain volume change (PBVC) between two scans was estimated with FSL Siena. We computed seven PBVC measures for each subject by performing independent pairwise comparisons of the first still scan from the subject’s session with the second still scan and each of their six motion-corrupted scans. In FSL Siena standard-space masking was used as well as BET (−m option). Furthermore, the lower part of MNI152/Talairach space (–b −50) was ignored and the approximate center of the head passed to BET (–B “–c 135 100 90”)

Grey matter (GM) volumes were estimated using SPM/VBM. We computed eight GM volumes for each subject; one from each scan during their visit.

Automated segmentations of the cortical surfaces were generated from each scan using both the cross-sectional and longitudinal image-processing stream of FS. In the longitudinal processing stream, each scan was treated as a separate time point; surfaces were estimated first on a robust within-subject template generated from all of the subject’s scans, with a subsequent fine-tuning step to adjust the surfaces for each of the eight individual scans. This approach has been shown to reduce variability and prevents completely incorrect placement of surfaces in cases with severe motion. Thus, for each subject we produced 16 sets of surfaces — 8 scans, evaluated with both the cross-sectional and longitudinal FS streams. From each surface we computed the GM volume, producing 16 measures for each subject.

2.3 Calculation of subject motion metrics

During each MEMPRAGE TR, the vNavs system logs an estimate of the subject’s displacement relative to the first TR of the scan. While translations move all parts of the head equally, rotations displace different regions by different amounts. To summarize subject motion, we have opted to use the root-mean-square (RMS) of the displacement over all points inside a sphere with 64 mm radius, initially centered at isocenter (Jenkinson, 1999). This allows a summary of the displacement at each TR with a single number, in units of mm. These per-TR displacements were then averaged over the duration of the scan, and a single motion score computed for each scan, RMS displacement per minute (RMSpm), expressed in units of mm/min.

2.4 Visual inspection of data quality

All MEMPRAGE images were visually evaluated by an expert for motion-related artifacts (e.g., blurring and ringing) as well as general criteria that can affect image quality, including: head coverage, wrapping artifact, radiofrequency noise, signal inhomogeneity, and susceptibility distortions and drop-outs. An ordinal score was given to each criterion (none, mild, moderate, severe), and an overall qualitative score was given to each image (pass, warn, fail) using standardized methodology (Qureshi et al., 2014, Harvard Center for Brain Science (2015)).

2.5 Testing the effect of motion on morphometric analyses

We are interested in addressing several related concerns that can impact the design and analysis of morphometric studies:

• What is the effect size of motion on morphometry with- and without motion correction? Is there a significant difference between the two conditions? Is the effect small enough in either condition that we can just ignore it or does a motion measure need to be included in models analyzing morphometric measurements?

• How variable is the data with and without motion correction? Will motion-induced variance reduce studies’ ability to detect small effects, even if a motion measure is included in the model?

In the remainder of this section, we restate these general concerns as testable questions involving nested linear mixed effects models (Fitzmaurice et al., 2012, Bates (2010), Bates et al. (2014)).

Noting that our analysis pipeline with FSL Siena generated only relative change in brain volume (in our case, relative to the first still scan), we computed similar relative percentage change metrics for the other morphometry pipelines, giving us relative change in grey matter volume from SPM/VBM and relative changes in grey matter volume from the cross-sectional and longitudinal FreeSurfer streams. We call these our percentage change (PC) measures and address our questions with respect to the PC measures for all four morphometry pipelines.

Excluding our FSL Siena results, the remaining three data analysis pipelines (SPM/VBM, and FreeSurfer cross-sectional and longitudinal) all produced per-scan estimates of absolute grey-matter volume. Thus, we can also directly fit these measurements using linear mixed-effect models. We call these our grey matter volume (GMVol) measures, and address our questions with respect to the GMVol measures for the three morphometry pipelines where they are available.

In addition to the various measures we consider, we are also interested in whether the answers to the questions above are impacted by filtering the data. We consider three possible filtering cases: no filter, filtering based on visual QC (QC-filtered), and filtering based on RMSpm motion score (motion-filtered). In the QC-filtered case, we discard all data with a “fail” rating, as the remainder is data that would normally be included in morphometric studies (with “warn”-rated scans being evaluated more carefully to ensure automated segmentation appears correct). For the motion-filtered case, we discard all data with a motion score greater than 5 mm/min.

In total we therefore have 7 measures (4 PC and 3 GMVol) and 3 filters, giving a total of 21 conditions. The data and the Mathematica (Wolfram Research Inc., 2014) script for computing the results below are available as part of the online supplementary materials for this manuscript.

Our tests consist of comparing pairs of nested models, asking whether one model fits the measurements in a given condition significantly better than a different model. We fit our models’ free parameters to the data via maximum likelihood estimation, and compare them using likelihood ratio tests. The details of these operations are described in Appendix A.

2.5.1 Question 1

It has been previously shown that, on average, subject motion negatively biases the morphometry pipelines used in this study (Reuter et al., 2015). Based on this result, our first question is:

Q1. Does using prospective motion correction reduce the fixed effect of motion on morphometric measures?

To formulate our first question as a test of two hypotheses we define a base model, that accounts for motion but not for the use of motion-correction; all data both with- and without-motion-correction is fit jointly with one model.

For the PC data, the base model is

$${\text{PC}}_{i,j}=({\beta }_m+b_{m,i})\Delta m_{i,j}+{ϵ}_{i,j}$$ (1)

where i indexes subjects and j indexes repeated scans of a subject and

• PC_i,j is the measured percent change relative to the baseline scan (in our case, the first still scan),

• Δm_i,j is the difference between the measured RMSpm subject motion for the current scan and the baseline scan (in our case, the first still scan),

• β_m is the fixed effect of motion on PC measures,

• b_m,i is the random effect of motion on PC measures for the i^th subject, and

• ε_i,j is a random effect representing residual error.

Here, we make the assumption that all b_m,i are independently drawn from $N(0,{\sigma }_{b_m}^2)$ and all of the ε_i,j are independently drawn from $N(0,{\sigma }^2)$.

For the GMVol data, the base model is

$${\text{GMVol}}_{i,j}=({\beta }_m+b_{m,i})m_{i,j}+{\beta }_1+b_{1,i}+{ϵ}_{i,j}$$ (2)

where the parameters are

• β_m, the fixed effect describing the effect of motion on grey matter volume,

• β₁, the fixed effect describing grey matter volume when there is no motion,

• b_m,i, the random effect describing the effect of motion on grey matter volume for the i^th subject,

• b_1,i, the random effect describing grey matter volume when there is no motion for the i^th subject,

• m_i,j, the measured RMSpm subject motion for the i^th subject’s j^th scan, and

• ε_i,j, the random effect representing residual error.

We make the assumption that, for each i,

$$(b_{1,i},b_{m,i})~N\left(0,\left[\begin{array}{cc}\hfill {\sigma }_{b_1}^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{b_m}^2\hfill \end{array}\right]\right)$$ (3)

Some key points to note about these two models are:

• the PC model uses the relative motion between each scan and the first still scan, since the percentage change measurement being fit is also computed relative to the first still scan;

• the β_m and b_m,i parameters in both models describe the effect of motion, but they are not expected to have the same value since they describe different data sets in different units;

To complete the formal description of our question, we must also define an alternative model that we will test for signficantly superior fit relative to our base model. The alternative model for our first question splits the fixed effect of motion based on whether or not prospective motion-correction was used. For the PC data the moco fixed effect model is

$${\text{PC}}_{i,j}=[{\beta }_{\text{nomoco}}(1-{\text{moco}}_{i,j})+{\beta }_{\text{moco}}{\text{moco}}_{i,j}+b_{m,i}]\Delta m_{i,j}+{ϵ}_{i,j}$$ (4)

adding the parameters

• β_nomoco is the fixed effect of motion on PC measures when motion correction is not used,

• β_moco is the fixed effect of motion on PC measures when motion correction is used, and

• moco_i,j is 1 if motion correction was used and 0 otherwise.

For the GMVol data, the moco fixed effect model is

$${\text{GMVol}}_{i,j}=[{\beta }_{nomoco}(1-{\text{moco}}_{i,j})+{\beta }_{\text{moco}}{\text{moco}}_{i,j}+b_{m,i}]m_{i,j}+\beta +b_{1,i}+{ϵ}_{i,j}$$ (5)

where we now have the parameters

• β_nomoco, the fixed effect describing the effect of motion on grey matter volume when motion correction is not used, and

• β_moco, the fixed effect describing the effect of motion on grey matter volume when motion correction is used.

With these two models, we can now rewrite our first question in a form that can be answered with a likelihood ratio test:

Q1. Does the moco fixed effect model fit the data significantly better than the base model?

Question 1 addresses whether using vNavs for prospective motion correction has reduced the fixed effect of motion on morphometry by comparing β_nomoco to β_moco.

2.5.2 Question 2

Our next question relates to the variability in the data.

Q2. On top of any reduction in the fixed effect of motion on morphometry, does the use of prospective motion correction make the effect of motion more consistent between subjects?

This question is important in study design because even if the average effect of motion is smaller with prospective vNav motion correction, there might still be significant between-subject variability in the size of the effect. This between-subject variability might mask smaller sources of between-subject difference that would be of interest in a study (e.g., if the between-subject variability of the motion-effect is large, we will be less able to assert a between-subject difference is related to disease instead of motion when disease and motion both vary).

To state this question formally, we must introduce another model, that we will call the moco random effect model. Our new model splits the random effect due to motion into one effect for data acquired with motion correction and a second random effect for data acquired without motion correction. For the PC data, this model is

$${\text{PC}}_{i,j}=[({\beta }_{\text{nomoco}}+b_{\text{nomoco,i}})(1-{\text{moco}}_{i,j})+({\beta }_{moco}+b_{\text{moco,i}}){\text{moco}}_{i,j}]\Delta m_{i,j}+{ϵ}_{i,j}$$ (6)

where the new parameters are

• b_nomoco,i is the random effect of motion on PC measures for the i^th subject when motion correction is not used, and

• b_moco,i is the random effect of motion on PC measures for the i^th subject when motion correction is used.

We make the assumption that, for each i,

$$(b_{\text{nomoco,i}},b_{\text{moco,i}})~N\left(0,\left[\begin{array}{cc}\hfill {\sigma }_{b_{\text{nomoco}}}^2\hfill & \hfill {\sigma }_{b_{\text{nomoco}},b_{\text{moco}}}\hfill \\ \hfill {\sigma }_{b_{\text{nomoco}},b_{\text{moco}}}\hfill & \hfill {\sigma }_{b_{\text{moco}}}^2\hfill \end{array}\right]\right)$$ (7)

For the GMVol data, the moco random effect model is

$${\text{GMVol}}_{i,j}=[({\beta }_{\text{nomoco}}+b_{\text{nomoco,i}})(1-{\text{moco}}_{i,j})+({\beta }_{\text{moco}}+b_{\text{moco,i}}){\text{moco}}_{i,j}]m_{i,j}+{\beta }_1+b_{1,i}+{ϵ}_{i,j}$$ (8)

where the new parameters have the same definition as in the PC model above, and the covariance structure for the random effects are similarly

$$(b_1,b_{\text{nomoco},i},b_{\text{moco},i})~N\left(0,\left[\begin{array}{ccc}\hfill {\sigma }_1^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{b_{\text{nomoco}}}^2\hfill & \hfill {\sigma }_{b_{\text{nomoco}},b_{\text{moco}}}\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{b_{\text{nomoco}},b_{\text{moco}}}\hfill & \hfill {\sigma }_{b_{\text{moco}}}^2\hfill \end{array}\right]\right)$$ (9)

With these two models, we can now specify the formal version of our second question that we can address via a likelihood ratio test:

Q2. Does the moco random effect model fit the data significantly better than the moco fixed effect model?

Question 2 allows us to evaluate whether using vNavs for prospective motion correction has reduced the random effect of motion by comparing ${\sigma }_{b_{\text{nomoco}}}\text{to}{{\sigma }_b}_{\text{moco}}$. We note that we are comparing our moco random effect model to one where we have already split the fixed effects, instead of comparing against the base model. We do not compare against the base model because we could not differentiate the impact of motion correction on fixed or random effects — if our alternative model provided a significantly better fit we could be unable to tell why.

2.5.3 Question 3

Our next question address residual variability in the measurements.

Q3. On top of reductions in the per-subject effect of motion on morphometry, does using prospective motion correction reduce the per-scan variability of morphometry?

This question is related to the ability to resolve any effect in the analysis of the morphometry measurements. The lower the between-scan variability, the better able we are to find smaller effects that might otherwise be “below the noise floor”.

To state this question formally, we introduce the full model, splitting the residual into with- and without-motion-correction residuals. For the PC data, this model is

$${\text{PC}}_{i,j}=[({\beta }_{\text{nomoco}}+b_{\text{nomoc},i})(1-{\text{moco}}_{i,j})+({\beta }_{\text{moco}}+b_{\text{moco}},i){\text{moco}}_{i,j}]\Delta m_{i,j}+{ϵ}_{\text{nomoco},i,j}(1-{\text{moco}}_{i,j})+{ϵ}_{\text{moco},i,j}{\text{moco}}_{i,j}$$ (10)

where the new parameters are

• ε_nomoco,i,j is a random effect representing residual error when motion correction is not used, and

• ε_moco,i,j is a random effect representing residual error when motion correction is used.

We make the assumption that, for each $i\text{and}j,{ϵ}_{\text{nomoco,i,j}}~N(0,{\sigma }_{\text{nomoco}}^2)\text{and}{ϵ}_{\text{moco, i,j}}~N(0,{\sigma }_{\text{moco}}^2)$ are independent.

For the GMVol data, the full model is

$${\text{GMVol}}_{i,j}=[({\beta }_{\text{nomoco}}+b_{\text{nomoco},i})(1-{\text{moco}}_{i,j})+({\beta }_{\text{moco}}+b_{\text{moco}},i){\text{moco}}_{i,j}]m_{i,j}+{\beta }_1+b_{1,i}+{ϵ}_{\text{nomoco},i,j}(1-{\text{moco}}_{i,j})+{ϵ}_{\text{moco},i,j}{\text{moco}}_{i,j}$$ (11)

This allows us to formally state our question as:

Q3. Does the full model fit the data significantly better than the moco random effect model?

Question 3 allows us to see whether the residual error not explained by either the fixed or random effect of motion is reduced using vNavs for prospective motion correction by comparing σ_moco to σ_nomoco. As in the discussion of question 2, we have chosen to compare this order of parameter splitting in order to ensure that we are testing just the additional benefit of splitting the residual parameter, and not confounding it with the effects of splitting other parameters.

2.5.4 Question 4

Finally, we propose one additional question.

Q4. Are the fixed effects of motion on the morphometry measurements significantly different from zero?

In all of our conditions we find some non-zero fixed effect of motion on morphometry measurements. However, given the small sample size of our study, it is important to determine whether the fixed effects we observe are significant, or could just be due to fitting measurement noise. If the effects are significant in our small study, then we can expect that they would be signficant in a larger study acquiring data similarly (i.e., same sequence and protocol, same coil, same analysis software). If the effects are not significant, then we cannot conclude whether there is no fixed effect of motion, or whether the effect is small and a larger study is needed to measure it.

We can formalize this question by comparing our fit full model against full models with the same parameter values except with β_nomoco or β_moco set to 0. The formal version of our question is then:

Q4. Does the full model fit the data significantly better than the full model with one fixed effect parameter forced to 0?

3 Results and Discussion

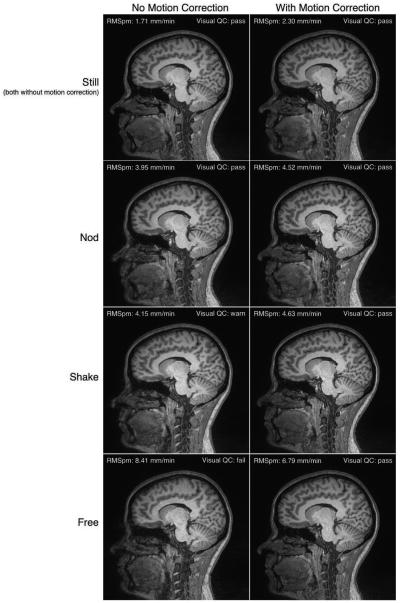
Figure 1 shows a representative slice from one subject’s volumes in all conditions. It also shows the motion and visual QC scores assigned to each image. This subject was chosen because the subject’s QC scores spanned all three levels (pass, warn, and fail), but the amount of motion is moderate, demonstrating a representative variation in the artefacts being discussed. In particular we note that none of these images show particularly “extreme” levels of motion artefact, indicating that the levels of motion we have explored in this work exemplify the scope of motion artefact that is likely to occur in many neuroimaging studies.

Figure 1.

Representative slice from one subject in all conditions. Each column represents whether motion correction was on or off; each row represents the type of motion the subject was asked to perform. Note that in both scans where the subjects was still (i.e., both the top-left and top-right images) there is no motion correction. Each image also displays the estimated RMSpm motion and the quality score assigned to the data by visual inspection.

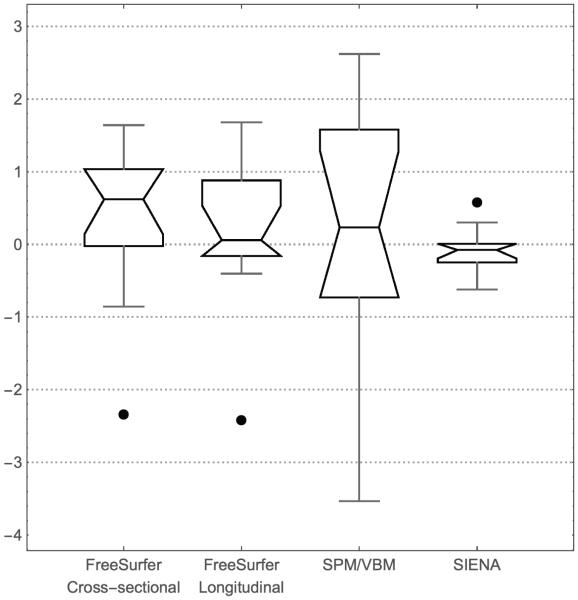
Figure 2 shows the distribution of percentage change in morphometric measures between still scans. We note that this measure of repeatability captures many possible sources of variation: inherent variability in the output of the software packages, variability in image inputs due to repositioning the subject in the scanner, and variability in subject motion between scans where they were asked to be still. More analyses of the impacts of these effects and others, can be found in (Han et al., 2006, Reuter et al., 2012, Maclaren et al., 2014).

Figure 2.

Distribution of percentage differences in relevant metric between first and second still scan, analyzed using each of the four pipelines. For FreeSurfer and SPM/VBM this is percentage change in grey matter volume, for SIENA this is brain volume. The whiskers in this plot represent the 3/2 inter-quartile range, and outliers beyond this are drawn as individual points.

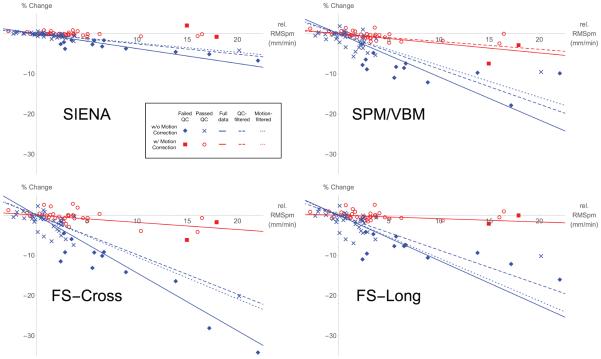
For each of the datasets (PC or GMVol), the results directly related to our four questions are summarized in two tables and one figure. Table 1 shows the p-values associated with the likelihood ratio test for each question, applied to the percentage change data in all 12 combinations of analysis package and measurement filtering. Figure 3 plots the RMSpm and percentage change of each scan relative to each subject’s first still scan. Overlaid on these plots are the maximum likelihood estimates of the fixed effect slopes from the full model (β_nomoco and β_moco in equation (10)) applied to the PC data. Note that in some conditions, the slopes are not significantly different from zero (e.g., Table 1 Question 4), and so are not plotted. Table 2 lists the maximum likelihood estimates of the parameters for the full model of the PC data in equation (10).

Table 1.

p-values of the likelihood ratio tests for each question, applied to the percentage change data. In each cell, the three p-values are given for the (left) full, (center) QC-filtered, and (right) motion-filtered data. Question 4 is split into two rows, one for each of the two fixed effects being tested against 0. Values greater than the p < 0.05 threshold are shown in bold.

	SIENA			SPM/VBM			FS Cross-sectional			FS Longitudinal
	full	QC	motion	full	QC	motion	full	QC	motion	full	QC	motion
Q1	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01
Q2	<0.01	<0.01	0.029	<0.01	<0.01	<0.01	<0.01	<0.01	0.056	<0.01	<0.01	0.030
Q3	0.426	0.446	0.379	<0.01	<0.01	0.088	<0.01	0.081	0.077	<0.01	<0.01	0.208
Q4 (βnomoco = 0)	<0.01	<0.01	<0.01	<0.01	<0.01	0.018	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01
Q4 (βmoco = 0)	0.214	0.140	0.325	<0.01	<0.01	0.163	0.020	0.062	0.269	<0.01	0.072	0.459

Figure 3.

Scatter plots of percentage change in relevant metric against measured subject motion relative to the first still scan for each subject. Each quadrant displays results from a different analysis pipeline. Each point represents one scan. For SIENA, the relevant metric is percentage change in brain volume. For SPM/VBM, cross-sectional FreeSurfer, and longitudinal FreeSurfer, the metric is percentage change in grey matter volume. Scans acquired without motion correction are represented in blue (“x” for scans that passed visual QC, diamonds for scans that failed), while scans acquired with motion correction are represented in red (circles for scans that passed visual QC, squares for scans that failed). For each of the three filtering conditions, the slope of the fixed effects of motion as fit with the full model (β_nomoco and β_moco in equation (10)) are plotted if they are significantly different from 0 (see Table 1 Question 4 for p-values). As with the scan points, with- and without-motion-correction slopes are plotted in red, and blue lines, respectively, with solid lines for the estimates from all data, dashed lines for the estimates from QC-filtered data, and dotted lines for the estimates using motion-filtered data.

Table 2.

Maximum likelihood estimates of the parameters for the full model for the PC data (equation (10)). In each cell, the three estimates are given for the (left) full, (center) QC-filtered, and (right) motion-filtered data.

	SIENA			SPM/VBM			FS Cross-sectional			FS Longitudinal
	full	QC	motion	full	QC	motion	full	QC	motion	full	QC	motion
βnomoco × 10	−3.71	−2.55	−2.32	−10.73	−8.78	−7.92	−14.37	−9.82	−10.4	−11.25	−8.64	−10.66
βmoco × 10	−0.13	−0.36	0.42	−2.39	−1.94	−1.51	−1.78	−1.5	1.87	−0.83	−0.85	−0.61
$\sqrt{{\sigma }_{b_{\text{nomoco}},b_{\text{moco}}}}\times 10$	0.47	0.72	1.44	2.28	2.18	0.53	1.83	3.29	5.77	2.04	2.19	2.05
σnomoco × 10	5.23	2.75	2.39	13.22	9.89	8.15	17.88	13.49	9.25	13.59	11.77	10.12
σmoco × 10	5.13	2.71	2.25	10.15	7.59	6.85	14.13	11.87	7.28	9.53	8.91	9.14

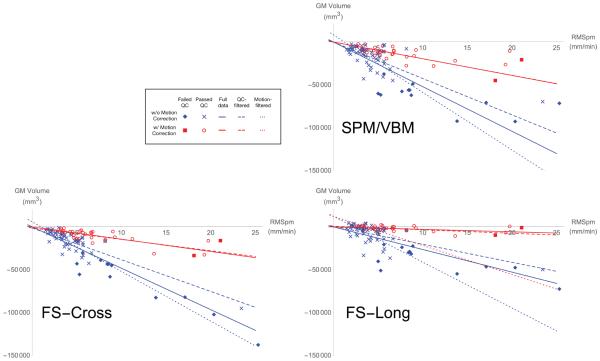
Paralleling the results for the PC data, Table 3 shows the p-values associated with the likelihood ratio test for each question, applied to the GMVol data in all 12 combinations of analysis package and measurement filtering. Figure 4 plots the RMSpm and estimated grey matter volume of each scan. Overlaid on these plots are the maximum likelihood estimates of the fixed effect slopes from the full model (β_nomoco and β_moco in equation (11)) applied to the GMVol data. As before, in conditions where the slopes are not significantly different from zero are not plotted (e.g., Table 3 Question 4). Table 4 lists the maximum likelihood estimates of the parameters for the full model of the GMVol data in equation (11).

Table 3.

p-values of the likelihood ratio tests for each question applied to the grey matter volume data. In each cell, the three p-values are given for the (left) full, (center) QC-filtered, and (right) motion-filtered data. Question 4 is split into two rows, one for each of the two fixed effects being tested against 0. Values greater than the p < 0.05 threshold are shown in bold.

	SPM/VBM			FS Cross-sectional			FS Longitudinal
	full	QC	motion	full	QC	motion	full	QC	motion
Q1	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01
Q2	<0.01	0.453	0.017	0.011	0.456	0.179	0.183	0.012	<0.01
Q3	<0.01	<0.01	<0.01	<0.01	0.047	<0.01	<0.01	<0.01	0.022
Q4 (βnomoco = 0)	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01	<0.01
Q4 (βmoco = 0)	<0.01	<0.01	0.107	<0.01	<0.01	0.096	<0.01	<0.01	<0.01

Figure 4.

Scatter plots of grey matter volume against measured subject motion. Each quadrant displays results from a different analysis pipeline. Each point represents one scan. For clarity of visualization, each scan’s position on the y-axis has been shifted to remove the effect of the estimated β₁ and b_1,i using the model in equation (11). This removes scaling differences between subjects and shifts the y-axis so that the extrapolated mean “zero-motion” grey matter volume for the full data is 0 mm³. Scans acquired without motion correction are represented in blue (“x” for scans that passed visual QC, diamonds for scans that failed), while scans acquired with motion correction are represented in red (circles for scans that passed visual QC, squares for scans that failed). For each of the three filtering conditions, the slope of the fixed effects of motion as fit with the full model (β_nomoco and β_moco in equation (11)) are plotted if they are significantly different from 0 (see Table 3 Question 4 for p-values). As with the scan points, with- and without-motion-correction slopes are plotted in red, and blue lines, respectively, with solid lines for the estimates from all data, dashed lines for the estimates from QC-filtered data, and dotted lines for the estimates using motion-filtered data.

Table 4.

Maximum likelihood estimates of the parameters for the full model for the GMVol data (equation (11)). In each cell, the three estimates are given for the (left) full, (center) QC-filtered, and (right) motion-filtered data.

	SPM/VBM			FS Cross-sectional			FS Longitudinal
	full	QC	motion	full	QC	motion	full	QC	motion
β1 × 10−5	6.82	6.82	6.9	4.92	4.9	4.97	4.96	4.96	5.08
βnomoco × 10−3	−5.21	−4.24	−6.72	−4.83	−3.7	−5.8	−2.64	−2.11	−5.35
βmoco × 10−3	−1.95	−1.93	−3.75	−1.44	−1.33	−3.51	−0.29	−0.41	−3.4
σb1 × 10−3	19.73	17.45	14.24	17.92	16.51	10.62	13.23	13.08	11.57
σbnomoco × 10−3	1.95	1.52	0.3	0	0	2.86	0	0	3.73
$\sqrt{{\sigma }_{b_{\text{nomoco}},b_{\text{moco}}}}\times {10}^{-3}$	0.84	0.77	0.07	0	0	1.04	0	0	1.37
σnomoco × 10−3	7.94	6.21	4.82	7.87	6.32	3.51	6.1	5.36	3.72
σmoco × 10−3	6.16	4.85	3.15	6.22	5.32	2.3	3.43	3.34	2.64

Overall, considering the results to all four of our questions in all of the conditions, we find that the use of vNavs for prospective motion correction significantly reduces the effects of motion on morphometry analyses. Critically, this reduction in motion-effects persists when data is aggressively filtered based on either visual inspection or a motion threshold taken directly from motion tracking during the scan. This means that prospective motion correction using vNavs provides a significant benefit to morphometry studies beyond the improvements that are made with traditional QC procedures.

Question 1 addresses the question of whether the motion-related bias previously noted in (Reuter et al., 2015) is reduced by using vNavs prospective motion corection. In every condition we considered, there was a highly significant reduction in motion-induced bias. This reduction is critical for studies where the factor of interest (e.g., age, disease) covaries highly with subject motion. In these cases, reducing the scale of the motion effect increases the ablity to detect the effects of interest. This difference in slope is apparent in Figures 4 and 5, where the motion-corrected (red) points clearly fall along a different line than the without-motion-correction (blue) points.

Figure 5.

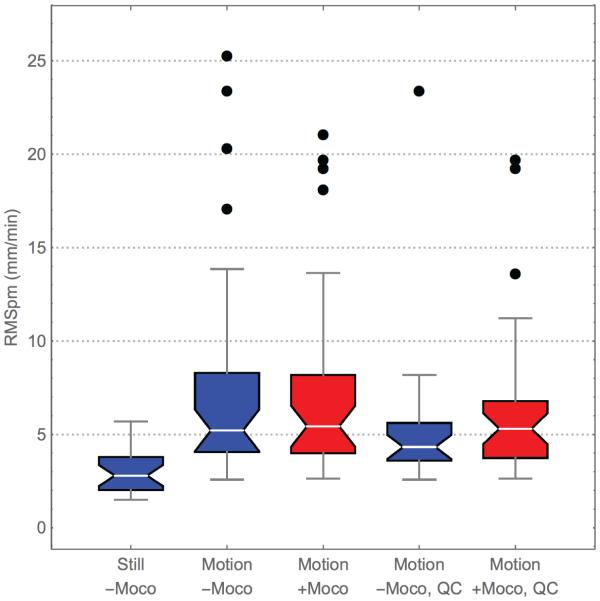
Distributions of subject motion in five categories: (from left to right) scans where the subject was asked to stay still and prospective motion correction was off; scans where the subject was asked to move and the prospective motion correction was off; scans where the subject was asked to move and the prospective motion correction was on; scans where the subject was asked to move, the prospective motion correction was off, and that passed visual QC; and scans where the subject was asked to move, the prospective motion correction was on, and that passed visual QC. For additional clarity, the plots are color-coded with blue for non-motion-corrected and red for motion-corrected. The whiskers in this plot represent the 3/2 inter-quartile range, and outliers beyond this are drawn as individual points.

Question 2 addresses whether the motion-related bias is made more consistent between subjects with prospective motion correction, while Question 3 addresses whether between-scan variability not explained as a linear effect of motion is also reduced by using prospective motion correction. Both of these questions relate to the variability in the data, so we will consider them together. Additionally, the results of these questions differed between the percentage change (PC) and grey matter volume (GMVol) data, so we will address each measurement type in turn.

In the PC data results for Question 2, we found (with the exception of one condition) a significant reduction in between-subject variability in the effect of motion on morphometry. However, in Question 3 we found mixed results, with less than half of the conditions showing a reduction in between-scan variability. Considering these two results together, we note that there is a reduction in variability with the use of prospective motion correction, although it is more often attributed to between-subject variability than between-scan variability.

In the GMVol data we find similar results, but with reversed pattern of significance, for Questions 2 and 3: Question 2 showed mixed results while Question 3 demonstrated a consistent significant reduction in between-scan variability. As with the PC data, we can combine these results to conclude that there is a general reduction in variability of GMVol measurements when prospective motion correction is used, although it is more attributed to a reduction in between-scan than between-subject variability.

Question 4 tests whether the fixed effects we’ve found in the full models are significant. We find that, in the without-motion-correction case, fixed effect of motion on the morphometry (β_nomoco) is significantly different from zero in all conditions. This result is consistent with the result of (Reuter et al., 2015), indicating that without prospective motion correction there is a significant bias regardless of what quality filtering is performed.

In contrast, the with-motion-correction fixed effect (β_moco) is only significantly different from zero in some conditions (more frequently in the GMVol data than in the PC data). We have illustrated this by plotting only the significant fixed effects in Figures 4 and 5. It is important to note that our failure to find a significant slope in some conditions does not imply that the fixed effect can be ignored if data from subsequent experiments is analyzed using a specific combination of pipeline and filter. It may be that the fixed effect is smaller in some conditions, but it may also be that the variability of the data is large enough to obscure small fixed effects. We can, however, conclude that, while prospective motion correction has significantly reduced the fixed effect of motion, it has not completely removed it, since some conditions still show a signficant fixed effect.

Taken together, our results show that using vNavs for prospective motion correction reduces both the fixed effect of motion on morphometry, and also the variability of the measurements, making data more consistent across motion-levels and across repeated measurements of the same subject. Both of these effects are important, as they diminish the impact of motion as a confounder in studies where motion may be correlated with the variable of interest.

Considering Figures 3 and 4, we note that the use of a single linear component to model the effect of motion on the morphometric measures may not fully capture the shape of the relationship in all cases. This is also reflected in Table 4, where we note that the estimated fixed effect of motion in all three pipelines increases as we filter the data. This implies that the effect of motion likely has higher-order components. It may also be the case that, since the vNavs system does not provide a perfect measure of subject motion, the RMSpm metric we used has a small upwards bias when the subject is still. This would tend to compress the lowest-motion scans in Figure 4 slightly right-ward, and in turn over-estimate the fixed effect of motion in low-motion scans while correctly estimating it in higher-motion scans. While a more complicated model could be created to describe all of these features of the data, and might provide benefit for the purposes of fully separating the effect of motion in a study where other effects were also present in the model, our results here make clear that our linear model provides an adequate approximation for the purposes of addressing our four questions.

Finally, Figure 5 shows the distribution of RMSpm subject motion in each of the experimental conditions. The motion distributions are similar in the with- and without-motion-correction conditions where subjects performed directed motions (second and third column of Figure 5), indicating that the amount of subject motion was consistent between the two conditions. However, after visual QC the distributions look quite different (fourth and fifth columns); the with-motion-correction data now includes scans with more motion than the without-motion-correction data. This shows that with vNavs prospective motion correction, the effective threshold for subject motion rendering a scan unusable according to visual inspection is higher. We would therefore expect that studies that suffer from motion may be able to retain more scans and thus have higher power to detect effects in conditions where subjects move. This increase in power from retaining more scans would be an additional increase, on top of that gained by reducing between-scan and between-subject variability through the use of prospective motion correction.

We have not addressed what features of the images are affected by subject motion and in turn cause our morphometry results to change. With the our current results, we cannot determine whether the images exhibit less apparent grey matter when subjects move, or if there are motion-related artefacts that violate assumptions of the morphometry algorithms we have considered. Further analysis of the segmentations and surfaces generated by the various pipelines, and potentially comparison with manually labelled data, is required to more thoroughly address this question.

4 Conclusion

Using repeated measurements of healthy subjects performing voluntary motion, we have shown that vNavs both reduce the effects of motion in morphometry analyses, and increase the number of scans that are available for analysis. In studies where motion leads to loss of scans and may potentially obscure the effects of variables of interest, our results indicate the use of prospective motion correction systems, such as vNavs, will reduce errors in inferences drawn from morphometry data. Expanding on the results of (Reuter et al., 2015), our results show that the improvements in data quality with vNavs prospective motion correction remain even after aggressive removal of motion-degraded data, either via visual inspection or filtering based on actual head motion measurements. Thus, prospective motion correction with vNavs can improve the accuracy of morphometric analyses beyond the improvement provided by QC methods.

While the results shown here are only representative of our specific protocol and acquisition hardware, significant improvements in image quality from the use of prospective motion correction systems has been documented repeatedly for many different systems and protocols (van der Kouwe et al., 2006, Zaitsev et al. (2006), Ooi et al. (2009), White et al. (2010), Brown et al. (2010), Hess et al. (2011), Tisdall et al. (2012)). We therefore expect that any of these similar systems might also offer an improvement in morphometric analyses. In practice, there are trade-offs between these different systems, with optical systems generally having greater applicabilty across a range of sequences but requiring more setup, and navigator-based methods being available for fewer sequences but requiring little extra effort for the user (surveys of the current state of motion correction methods for MRI can be found in (Maclaren et al., 2013, Zaitsev et al., (2015))). Thus, while the vNavs research sequences only operate on specific Siemens scanner platforms, due to the large amount of active research in motion measurement and correction, there is now likely to be some method of at least measuring, and likely also prospectively correcting, subject head motion on most scanner platforms.

Despite the availability of motion tracking and correction systems for a variety of platforms, it is important to note that we do not yet fully understand the mechanisms through which protocol, scanner hardware, and motion tracking system contribute to the scale and impact of motion on morphometry analyses. Therefore, it seems prudent for those performing studies on populations where motion correlates with parameters of interest to establish the sensitivity of their measurement and analysis pipeline to motion. It may be the case that certain combinations of protocols, scanners, or analysis pipelines are more or less sensitive to the effects of motion. In particular, high-channel count coils and accelerated parallel imaging methods are potential culprits for increased motion sensitivity, as are spectrally selective excitations such as water-selective and fat-saturation pulses that may be degraded due to subject motion in the static shim field. However, until more results are available from a greater variety of studies with different hardware and protocols, it is not possible to completely predict what components make a study more or less sensitive to motion. Following the experiment design we have presented here, other groups can evaluate the effect of motion on their specific study designs. Recognizing that large, multi-center studies often combine data from a variety of hardware and protocols, we have demonstrated that very small studies, using just a few volunteers, suffice to measure the effect of motion for each scanner configuration included in the study. This data may then be useful in distinguishing site-specific differences in motion sensitivity from actual differences in disease and treatment effect.

NIMG-15-2277R1 Highlights.

November 20, 2015

• We demonstrate that prospective motion correction with volumetric navigators (vNavs) significantly reduces the subject-motion-induced systematic biases in grey matter and brain volume estimates from several major software packages.

• We additionally show that prospective motion correction with volumetric navigators (vNavs) reduces variance in morphometry measures due to subject motion.

• Our analysis method can be applied to other MRI scanner equipment and pulse sequences, allowing other studies to evaluate the impact of motion on their morphometric measures of interest.

Appendix A. Fitting mixed effect models and evaluating likelihood ratio tests

In the conventional notation for linear mixed-effects model, we write

$$\mathit{y}=\mathbf{X}\beta +\mathbf{Z}b+ϵ$$ (12)

where ε is assumed to be drawn from the distribution N(0, I).

For fixed parameters θ, we have that y conditional on b, and b itself, are distributed

$$\begin{array}{cc}\hfill (y;b)& ~N(\mathbf{X}\beta +\mathbf{Z}\mathit{b},{\sigma }^2\mathbf{I})\hfill \\ \hfill \mathit{b}& ~N(0,{\Sigma }_{\theta })\hfill \end{array}$$ (13)

where n is the number of measurements. The notation Σ_θ is used to reenforce that Σ depends on the parameters θ that we are estimating. In our model we want to allow that the residuals o, might have different variances for different measurements. We can represent this by adding weights to our model; in our case the residuals in the with-motion-correction case are assumed to have variance σ², while the variances without-motion-correction case are assumed to be αΣ², where we need to estimate α as a parameter in our model. Thus, our weight matrix W_θ is a diagonal matrix that depends on the parameter set θ, having 1 along the diagonal where the measurements had motion correction, and α along the digonal where they do not have motion correction.

Finding the maximum likelihood estimate of θ for models with this structure is detailed in section 4.4.3 of (Bates, 2010), which gives the algorithm we have implemented in Mathematica.

Given an estimated parameter set $\widehat{\theta }$, our measurements are multinormal distributed

$$y~N(\mathbf{X}\beta ,{\sigma }^2\mathbf{I}+{\Sigma }_{\widehat{\theta }})$$ (14)

Using this distribution, we can compute the likelihood of $\widehat{\theta }$ given our data using the likelihood function for this distribution. If we have two estimated parameter sets, the null hypothesis ${\widehat{\theta }}_0$ and the alternative hypothesis ${\widehat{\theta }}_1$, the log-likelihood ratio test statistic can be written as

$$\text{LLR}\left(y\right)=2[{\ell }_{{\widehat{\theta }}_1}\left(y\right)-{\ell }_{{\widehat{\theta }}_0}\left(y\right)].$$ (15)

where ℓ_θ is the log-likelihood function associated with the multinormal distribution specified by parameter θ. We can produce a Monte Carlo estimate for the distribution of their likelihood ratio under the null hypothesis by drawing samples from the distribution associated with ${\widehat{\theta }}_0$, and computing the likelihood ratio, treating the random sample as the “measurement”. We can then compute the p-value for the likelihood ratio test, given our actual measurement, by comparing how many samples from the estimated distribution are more extreme than the likelihood ratio statistic evaluated at the actual measurement (North et al., 2002).