Skip to main content
PMC home page
Learning & Memory logoLink to Learning & Memory
. 2016 Mar;23(3):108–112. doi: 10.1101/lm.041277.115

Chunking improves symbolic sequence processing and relies on working memory gating mechanisms

Oleg Solopchuk 1, Andrea Alamia 1, Etienne Olivier 1, Alexandre Zénon 1,✉
PMCID: PMC4755266  PMID: 26884228

Abstract

Chunking, namely the grouping of sequence elements in clusters, is ubiquitous during sequence processing, but its impact on performance remains debated. Here, we found that participants who adopted a consistent chunking strategy during symbolic sequence learning showed a greater improvement of their performance and a larger decrease in cognitive workload over time. Stronger reliance on chunking was also associated with higher scores in a WM updating task, suggesting the contribution of WM gating mechanisms to sequence chunking. Altogether, these results indicate that chunking is a cost-saving strategy that enhances effectiveness of symbolic sequence learning.

One very influential breakthrough in the study of working memory (WM) was achieved by Miller when he proposed, more than half a century ago, that information clustering—or chunking—is used to circumvent the limited capacity of WM (Miller 1956). Since then, this process has been studied extensively, in particular in the context of sequence learning (Terrace 1991; Verwey 1996; Gobet and Simon 1998; Gobet et al. 2001; Sakai et al. 2003; Miyapuram et al. 2006; Bor and Seth 2012; Mathy and Feldman 2012; Wymbs et al. 2012). In addition to increasing WM capacity (Mathy and Feldman 2012; Li et al. 2013), efficient chunking strategy, by hypothetically decreasing WM load and freeing more cognitive resources (Lavie et al. 2004; Minamoto et al. 2015) should also benefit sequence processing. However, so far, the impact of chunking on sequence-learning performance strikingly lacks experimental support (Wymbs et al. 2012; Song and Cohen 2014), since most measures of chunking have failed to correlate with indexes of performance or learning rate.

Besides, the nature of the interactions between chunking and WM mechanisms during sequence learning remains debated. Computational models (O'Reilly and Frank 2006; Grossberg and Kazerounian 2011) have posited that chunking relies on WM gating, i.e., the process that controls the access of new information to WM (Gruber et al. 2006; O'Reilly and Frank 2006; Grossberg and Kazerounian 2011; Chatham et al. 2014). Indeed, chunking involves subprocesses thought to depend on WM gating: binding sensory inputs to specific serial position in WM (O'Reilly and Soto 2002; O'Reilly and Frank 2006) and filtering distractors from task relevant information during encoding and retrieval in WM (Gruber et al. 2006; D'Ardenne et al. 2012; Chatham et al. 2014), However, so far, the only experimental evidence supporting a possible interaction between chunking and WM gating processes arises from functional magnetic resonance imaging studies showing an overlap between the different brain structures involved in these two processes. Indeed, WM updating tasks—supposed to recruit WM gating processes—have been shown to activate the midbrain, caudate, and prefrontal cortex (Lewis et al. 2004; Murty et al. 2011; Badre 2012; D'Ardenne et al. 2012; Chatham et al. 2014), and, similarly, the neural correlates of chunking encompass both the prefrontal cortex (Bor et al. 2003; Clerget et al. 2012; Wymbs et al. 2012; Alamia et al. 2016 [in press]) and basal ganglia (Graybiel 1998; Jin and Costa 2010; Wymbs et al. 2012; Jin et al. 2014; Zenon and Olivier 2014).

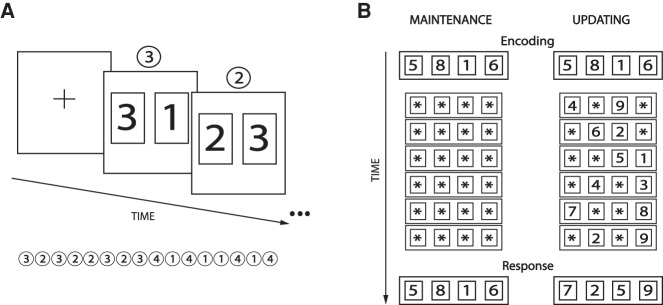
In order to address these issues experimentally, we correlated individual estimates of chunking strategy in a sequence-learning task with general task performance, cognitive workload (as indexed by pupil size), and performance in a WM updating task (Murty et al. 2011). Since motor sequence learning appears to depend less on attentional and central executive resources than nonmotor sequence learning (Hikosaka et al. 2002; Keele et al. 2003; Song et al. 2008), we opted in the present experiment for a symbolic sequence-learning task. Twenty-five right-handed individuals (10 males, mean age ± SD = 27.1 ± 4.1 yr) participated in the study after providing their informed consent. None of the participants had any physical or mental disorder that could influence their performance. The task (Alamia et al. 2016 [in press]) consisted in learning explicitly a sequence of 16 symbolic items (digits) by trial and error (Fig. 1A). In each display, the “target” (the digit belonging to the sequence) and a distractor were shown simultaneously on the computer screen and the participants had to identify and to designate the “target” by clicking on the corresponding—left or right—mouse button. The location—on the right- or the left-hand side of the screen—of target digits was pseudorandomized on every trial so that subjects could not anticipate the position of the next target, and therefore no motor sequence of responses could be learned. The sequence (3 2 3 2 2 3 2 3 4 1 4 1 1 4 1 4) was repeated six times per block and the task comprised of eight block repetitions. The WM task (Murty et al. 2011; Podell et al. 2012), administered prior to the sequence-learning task, consisted of a WM updating (16 trials) and a WM maintenance task (24 trials). Every trial started with the encoding phase, during which subjects had to remember a set of digits, and ended with the retrieval phase, during which they had to compare a currently remembered set of digits to the one displayed on the screen. Subjects pressed the left mouse button to indicate that the remembered set matched the probe set, and the right button otherwise. In the maintenance task, subjects were asked to remember, and retrieve after a 12-sec delay 4, 6, or 8 digits, while in the updating trials, they had to remember a series of four digits and to update constantly various items of this series before providing the response (Fig. 1B). The subject's performance was determined by computing the proportion of correct responses in each of these conditions. In nonmatching trials, a single digit was changed from the correct digit combination (Murty et al. 2011). The tasks were implemented using Psychtoolbox 3.0.9 (Brainard 1997) with Matlab 7.5 (The MathWorks). Stimuli were presented on a 19 inch CRT screen, running at 75 Hz, located at a distance of 58 cm. An Eyelink 1000+ eye tracker (SR Research Ltd.) was used to monitor eye movements, blinks, and pupil diameter at a sampling frequency of 500 Hz (see Zénon et al. 2014 for technical details).

Figure 1.

Figure 1.

Open in a new tab

(A) Sequence-learning task. After the display of a fixation cross (2.0 sec) at the beginning of each sequence, two rectangles appeared on the left and right parts of the screen, each containing either a target or distractor digit. The location (left or right) of all target digits was pseudorandomized on every trial so that subjects could not predict the position of the next target digit, and therefore the motor response to be provided. The participants indicated which rectangle they believed contained the digit belonging to the sequence by clicking on the corresponding mouse button (e.g., left mouse button if the sequence element is shown on the left). If a correct response was provided, the next pair of digits was immediately presented. If the participant selected the wrong digit, i.e., the distractor, a feedback sound was provided (0.3 sec), and the next pair of digits was displayed. If none of the digits was selected after 5.0 sec, the next pair appeared automatically. The sequence was repeated six times per block and the entire experiment was composed of eight blocks. (B) Working memory (WM) task. In the maintenance trials, subjects were given 4, 6, or 8 digits to remember during the encoding phase. Afterward, six displays alternated every 2 sec, in which all digits were replaced by asterisks indicating that the participants had to keep in memory the original set of digits, until the response display. In the updating trials, four digits were always presented during the encoding phase. Then six displays alternated every 2 sec, all containing four characters, either two asterisks and two new digits or one asterisk and three new digits (randomly interleaved). Subjects had to keep in memory the digit from the previous display where asterisks appeared, whereas the new digits had to replace the digits previously displayed at their corresponding positions. In both conditions, the trial ended with the display of a series of digits and the subjects had to evaluate whether it corresponded (left mouse button click) or not (right button) to the one they were holding in memory.

The final analysis was performed on 19 subjects as six subjects were discarded: five because they did not reach 80% accuracy in at least two out of the eight blocks of the sequence-learning task, and one subject because his average reaction times (RT) in all blocks were larger than the mean + 6 SD of the group. As a measure of sequence learning, we used RT computed as the time difference between digit display and button press. We took into account all button presses (correct and incorrect responses), but included only the blocks in which the subjects’ accuracy was higher than 80% (average index of the first block satisfying the criterion: 1.5 ± 0.7, mean ± SD) in which the subjects were still learning the sequence. We estimated the learning rate, i.e., the performance improvement across block repetitions, by fitting RT data with a power law (y = axb), and we considered b, the exponent of the power law, as an index of learning (Fig. 2A).

Figure 2.

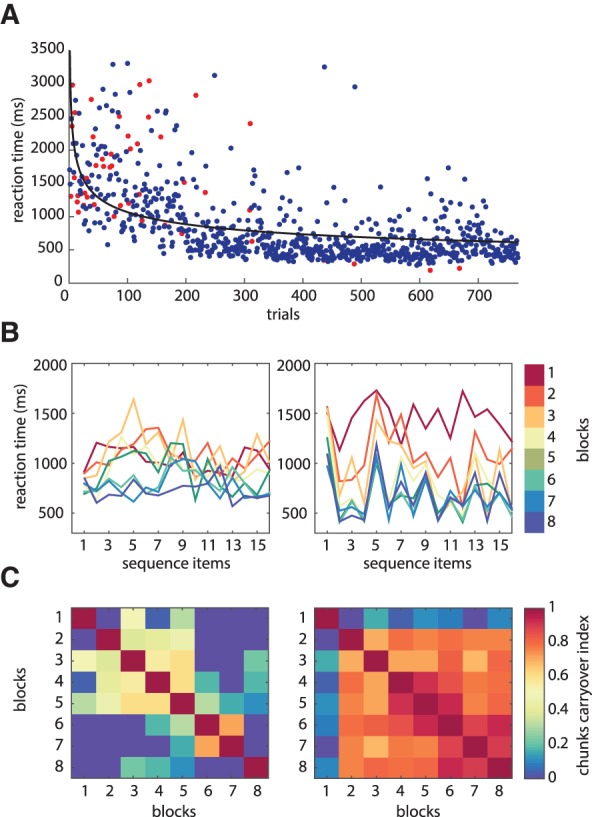
Figure 2.

Open in a new tab

(A) Reaction times from one example participant in the sequence-learning task. Trials in which an incorrect answer was given are marked in red. (B) Reaction times of two example subjects averaged for every block of the sequence-learning task. (C) Color matrix representing the coefficients of correlation between each pair of block-wise averaged reaction times of the two example subjects. The average of these coefficients provides the chunking carryover index (Ci), used as a measure of chunking in the present study. Stochastic RT patterns lead to low Ci (e.g., left part of the figure) whereas systematic RT patterns, regarded as signatures of chunking, lead to high Ci (right part of the figure).

To characterize the chunking strategy, we used the “chunk carryover” index (Ci) (Song and Cohen 2014) computed by averaging the RT for each sequence element within each block, then by computing pairwise Pearson correlations between item-wise averaged RT in all the valid blocks and finally by averaging all the obtained correlation coefficients (Fig. 2B,C). We also computed the mean chunk length for each subject (Bo and Seidler 2009). To do so, we identified the first element of each chunk by using the log-transformed RT for each sequence item computed for the last block (Block 8); then we performed a one-tail paired t-test to evaluate whether RT for each sequence item, n was significantly longer than for the neighboring positions (n + 1 and n − 1). We excluded the first two elements of the sequence as well as the last one from this analysis because the first and second items were considered to always belong to the first chunk, whereas the last sequence item always belonged to the last chunk (Bo and Seidler 2009). Afterward, we computed the mean chunk length by dividing total sequence length (16) by the number of chunks identified (including the first chunk of items 1 and 2).

All participants showed an overall high performance in the valid blocks (mean accuracy: 90%, SD: 0.08%), and exhibited a relatively consistent chunking strategy between subjects (ANOVA on average RT as a function of item position: F(15) = 4.1345, P = 6.9981 × 10−07; see Supplemental Fig. S1). Interestingly, we found that the extent to which each individual relied on chunking, estimated by means of the Ci index (mean ± SD: 0.53 ± 0.14; see Fig. 2), correlated negatively with their learning rate (rs = −0.6193, P = 0.0056, Spearman; see Supplemental Fig. S2A), indicating that consistent chunking benefits performance in terms of RT improvement. In contrast, we found that chunk length (mean ± SD: 5.34 ± 2.21) did not correlate with the sequence-learning rate (rs = −0.0745, P = 0.7618, Spearman).

Additionally, given that task-evoked increase of pupil diameter is regarded as a marker of cognitive workload (Hess and Polt 1964; Kahneman and Beatty 1966; Beatty 1982), we investigated whether large Ci were associated with stronger decreases in pupil size over time. Indeed, we found that Ci correlated negatively with the slopes of the change in phasic pupil response (see Fig. 3) across sequence repetitions (rs = −0.5070, P = 0.0284, Spearman), suggesting that chunking led to a decrease in cognitive workload across sequence repetitions.

Figure 3.

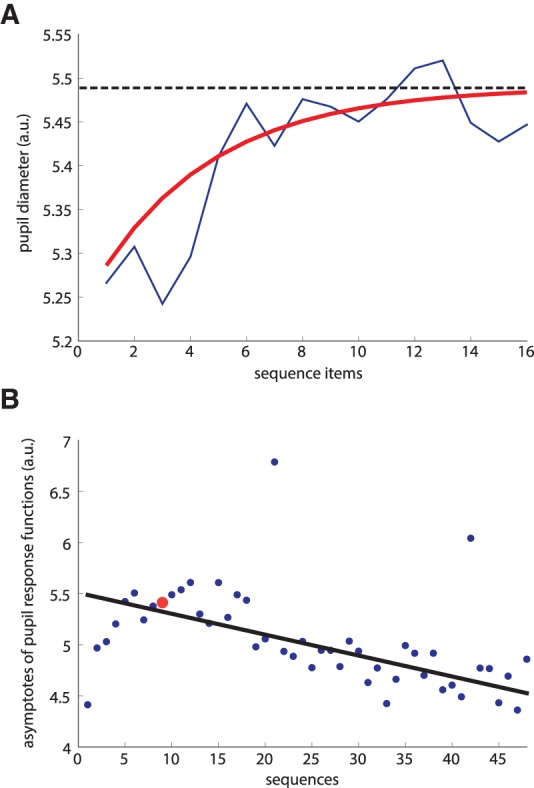
Figure 3.

Open in a new tab

Pupil diameter analysis. Prior to analyzing pupil diameter data, blink-related artifacts were filtered out and substituted by means of linear interpolation. Data were downsampled to 10 Hz and aligned on stimulus onset. We fitted the pupil diameter changes across each sequence using nonlinear least squares fitting with an exponential function: β1 − β2 × e−β3 × X, where X refers to the preprocessed pupillometric data and β1–3 are the parameters of the fit. We then computed the asymptote of these functions (Zénon et al. 2014), for each sequence, which corresponds to an estimate of the peak value of the pupil diameter during the sequence (A). We then computed the change in phasic pupil response across sequence repetitions (B), by means of a robust linear regression, which is less sensitive to outliers than ordinary least squares fitting method (function “robustfit”; Matlab, The MathWorks). A red point marks the asymptote of pupil response function illustrated in the panel above. Finally, we correlated the interindividual slope values with the corresponding chunking carryover indexes.

Regarding the WM tasks, subjects performed better in the WM maintenance (accuracy: 86% ± 11.7%, mean ± SD) than the WM updating task (74.6% ± 15.6%, mean ± SD). As expected, in WM maintenance, performance significantly decreased as a function of number of items (4, 6, or 8) in the series to be memorized (F(2,54) = 13.7, P < 0.0001, ANOVA), while performance in the WM updating task was not significantly different between trials in which two or three digits had to be updated (F(1,36) = 2.39, P = 0.19, ANOVA). Additionally, we did not find a significant correlation between performance in WM maintenance and updating tasks (rs = 0.268, P = 0.267, Spearman).

Moreover, we correlated the performance in the WM tasks and chunk parameters (Ci and chunk length). A significant positive correlation was found between the Ci and WM updating performance (rs = 0.6182, P = 0.0048, Spearman; see Supplemental Fig. S2B), indicating that better performance in the updating task was associated with more reliable chunking. In contrast, we did not find any significant correlation between Ci and WM maintenance performance (rs = 0.2563, P = 0.2896, Spearman).

Finally, the correlations between chunk length and WM measurements failed to reach significance (WM maintenance: rs = −0.18, P = 0.52, Spearman, WM updating: rs = −0.14, P = 0.62, Spearman), in apparent contradiction with previous results (Bo and Seidler 2009). This discrepancy could be explained by several differences between experimental conditions: (1) sequence modality (nonmotor versus motor sequence-learning task), (2) amount of training (48 versus at least 120 sequence repetitions), (3) task design (selection of sequence items displayed along with distractors versus self-paced sequence recall).

An important contribution of the present study is the finding that chunking improves performance in symbolic sequence processing by reducing cognitive workload and decreasing RTs over time. This finding is consequential because, although evidence for chunking has been reported repeatedly during sequence execution (Gobet et al. 2001; Sakai et al. 2003; Boyd et al. 2009; Perlman et al. 2010; Seidler et al. 2012; Lungu et al. 2014), previous attempts to determine its causal role in sequence processing have failed. For instance, a recent study investigating the neural correlates of chunking was unsuccessful in establishing a relationship between learning rate and chunking, as quantified by computing the network modularity (Wymbs et al. 2012). A potential problem with this approach is the assumption that an efficient chunking strategy progressively leads to chunks concatenation over time. However, a recent study investigating this question by measuring chunk formation, carryover and concatenation over an extended period of training, found no evidence in favor of chunk concatenation (Song and Cohen 2014), despite significant chunk formation. In addition, none of the chunking measures changed congruently with the improvement in RT occurring during training, a finding interpreted as evidence that chunking is not causally involved in sequence learning (Song and Cohen 2014). Along the same line, another recent study reported that Broca's area disruption by means of transcranial magnetic stimulation impedes learning of a motor sequence but without altering the chunking strategy, supporting also the lack of connection between chunking and learning performance (Clerget et al. 2012). The novelty of the present study lies in accounting for between-subject variability of chunking features, which allowed us to show that chunking is an effective strategy to improve symbolic sequence-learning performance, supposedly by alleviating cognitive workload.

Another goal of this study was to test how chunking relates to WM mechanisms, such as WM maintenance and gating, during symbolic sequence learning. While the overlap between the neural correlates of chunking and WM gating (Graybiel 1998; Bor et al. 2003; Gruber et al. 2006; Tremblay et al. 2010; Murty et al. 2011; D'Ardenne et al. 2012; Wymbs et al. 2012; Jin et al. 2014) was considered as indirect evidence of their possible interactions, in accordance with the computational models (O'Reilly and Frank 2006; Grossberg and Kazerounian 2011), we provide here, for the first time, behavioral evidence that chunking is linked to WM gating processes. This suggests that, in accordance with our prediction, chunking during sequence performance relies on the same mechanisms as in WM updating tasks, i.e., presumably the capacity to gate the access of information to WM while filtering irrelevant distractors (Gruber et al. 2006; O'Reilly and Frank 2006; D'Ardenne et al. 2012).

One possible important drawback of the present study is that the correlation between chunking strategy and WM updating could be due to the fact that participants subvocalized the sequence. We believe that this is unlikely given that the correlation between the measures of chunking and WM was specific to WM updating, while subvocalization should have impacted also WM maintenance performance, in accordance with the phonological loop hypothesis (Baddeley 2000). Furthermore, we did not observe a significant correlation between WM maintenance and updating, implying that the interindividual variability found in WM updating performance, and which correlated with chunking carryover, did not arise from sequence subvocalization. Therefore, even though the role of subvocalization strategies in sequence learning should be investigated further, we believe that the relationship between chunking and WM gating reported here cannot be simply explained by this confound.

Finally, the question arises as to whether chunking in symbolic and motor sequence learning might rely on different cognitive mechanisms, in accordance with the theoretical accounts of sequence learning that propose separate cognitive systems for symbolic and motor sequence processing (Seger 1997, 1998; Gheysen and Fias 2012). However, evidence for chunking has been reported in a large range of domains (e.g., low-level visual processing (Green and Bavelier 2003; Orbán et al. 2008), spatial memory (Sargent et al. 2010), etc.), arguing in favor of the existence of a domain-general mechanism, which would be common to both motor and nonmotor chunking processes. This hypothesis should be tested in further studies, for instance by means of carefully designed neuroimaging paradigms.

Supplementary Material

Supplemental Material
supp_23_3_108__index.html (909B, html)

Footnotes

[Supplemental material is available for this article.]

References

  1. Alamia A, Solopchuk O, D'Ausilio A, Bever VV, Fadiga L, Olivier E, Zénon A. 2016. Disruption of Broca's area alters higher-order chunking processing during perceptual sequence learning. J Cogn Neurosci in press. [DOI] [PubMed] [Google Scholar]
  2. Baddeley A. 2000. The episodic buffer: a new component of working memory? Trends Cogn Sci 4: 417–423. [DOI] [PubMed] [Google Scholar]
  3. Badre D. 2012. Opening the gate to working memory. Proc Natl Acad Sci 109: 19878–19879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beatty J. 1982. Task-evoked pupillary responses, processing load, and the structure of processing resources. Psychol Bull 91: 276–292. [PubMed] [Google Scholar]
  5. Bo J, Seidler RD. 2009. Visuospatial working memory capacity predicts the organization of acquired explicit motor sequences. J Neurophysiol 101: 3116–3125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bor D, Seth AK. 2012. Consciousness and the prefrontal parietal network: insights from attention, working memory, and chunking. Front Psychol 3: 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bor D, Duncan J, Wiseman RJ, Owen AM. 2003. Encoding strategies dissociate prefrontal activity from working memory demand. Neuron 37: 361–367. [DOI] [PubMed] [Google Scholar]
  8. Boyd LA, Edwards JD, Siengsukon CS, Vidoni ED, Wessel BD, Linsdell MA. 2009. Motor sequence chunking is impaired by basal ganglia stroke. Neurobiol Learn Mem 92: 35–44. [DOI] [PubMed] [Google Scholar]
  9. Brainard DH. 1997. The Psychophysics Toolbox. Spatial Vision 10: 433–436. [PubMed] [Google Scholar]
  10. Chatham CH, Frank MJ, Badre D. 2014. Corticostriatal output gating during selection from working memory. Neuron 81: 930–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Clerget E, Poncin W, Fadiga L, Olivier E. 2012. Role of Broca's area in implicit motor skill learning: evidence from continuous theta-burst magnetic stimulation. J Cogn Neurosci 24: 80–92. [DOI] [PubMed] [Google Scholar]
  12. D'Ardenne K, Eshel N, Luka J, Lenartowicz A, Nystrom LE, Cohen JD. 2012. Role of prefrontal cortex and the midbrain dopamine system in working memory updating. Proc Natl Acad Sci 109: 19900–19909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gheysen F, Fias W. 2012. Dissociable neural systems of sequence learning. Adv Cogn Psychol 8: 73–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gobet F, Simon HA. 1998. Expert chess memory: revisiting the chunking hypothesis. Memory 6: 225–255. [DOI] [PubMed] [Google Scholar]
  15. Gobet F, Lane PCR, Croker S, Cheng PC-H, Jones G, Oliver I, Pine JM. 2001. Chunking mechanisms in human learning. Trends Cogn Sci 5: 236–243. [DOI] [PubMed] [Google Scholar]
  16. Graybiel AM. 1998. The basal ganglia and chunking of action repertoires. Neurobiol Learn Mem 70: 119–136. [DOI] [PubMed] [Google Scholar]
  17. Green CS, Bavelier D. 2003. Action video game modifies visual selective attention. Nature 423: 534–537. [DOI] [PubMed] [Google Scholar]
  18. Grossberg S, Kazerounian S. 2011. Laminar cortical dynamics of conscious speech perception: neural model of phonemic restoration using subsequent context in noise. J Acoust Soc Am 130: 440–460. [DOI] [PubMed] [Google Scholar]
  19. Gruber AJ, Dayan P, Gutkin BS, Solla SA. 2006. Dopamine modulation in the basal ganglia locks the gate to working memory. J Comput Neurosci 20: 153–166. [DOI] [PubMed] [Google Scholar]
  20. Hess EH, Polt JM. 1964. Pupil size in relation to mental activity during simple problem-solving. Science 143: 1190–1192. [DOI] [PubMed] [Google Scholar]
  21. Hikosaka O, Nakamura K, Sakai K, Nakahara H. 2002. Central mechanisms of motor skill learning. Curr Opin Neurobiol 12: 217–222. [DOI] [PubMed] [Google Scholar]
  22. Jin X, Costa RM. 2010. Start/stop signals emerge in nigrostriatal circuits during sequence learning. Nature 466: 457–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jin X, Tecuapetla F, Costa RM. 2014. Basal ganglia subcircuits distinctively encode the parsing and concatenation of action sequences. Nat Neurosci 17: 423–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kahneman D, Beatty J. 1966. Pupil diameter and load on memory. Science 154: 1583–1585. [DOI] [PubMed] [Google Scholar]
  25. Keele SW, Ivry R, Mayr U, Hazeltine E, Heuer H. 2003. The cognitive and neural architecture of sequence representation. Psychol Rev 110: 316–339. [DOI] [PubMed] [Google Scholar]
  26. Lavie N, Hirst A, de Fockert JW, Viding E. 2004. Load theory of selective attention and cognitive control. J Exp Psychol Gen 133: 339–354. [DOI] [PubMed] [Google Scholar]
  27. Lewis SJ, Dove A, Robbins TW, Barker RA, Owen AM. 2004. Striatal contributions to working memory: a functional magnetic resonance imaging study in humans. Eur J Neurosci 19: 755–760. [DOI] [PubMed] [Google Scholar]
  28. Li G, Ning N, Ramanathan K, He W, Pan L, Shi L. 2013. Behind the magical numbers: hierarchical chunking and the human working memory capacity. Int J Neural Syst 23: 1350019. [DOI] [PubMed] [Google Scholar]
  29. Lungu O, Monchi O, Albouy G, Jubault T, Ballarin E, Burnod Y, Doyon J. 2014. Striatal and hippocampal involvement in motor sequence chunking depends on the learning strategy. PLoS One 9: e103885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Mathy F, Feldman J. 2012. What's magic about magic numbers? Chunking and data compression in short-term memory. Cognition 122: 346–362. [DOI] [PubMed] [Google Scholar]
  31. Miller GA. 1956. The magical number seven. Psychol Rev 63: 81–97. [PubMed] [Google Scholar]
  32. Minamoto T, Shipstead Z, Osaka N, Engle RW. 2015. Low cognitive load strengthens distractor interference while high load attenuates when cognitive load and distractor possess similar visual characteristics. Atten Percept Psychophys 77: 1659–1673. [DOI] [PubMed] [Google Scholar]
  33. Miyapuram KP, Bapi RS, Pammi CVS, Ahmed A, Doya K. 2006. Hierarchical chunking during learning of visuomotor sequences. 2006 IEEE Int Jt Conf Neural Netw Proc. [Google Scholar]
  34. Murty VP, Sambataro F, Radulescu E, Altamura M, Iudicello J, Zoltick B, Weinberger DR, Goldberg TE, Mattay VS. 2011. Selective updating of working memory content modulates meso-cortico-striatal activity. Neuroimage 57: 1264–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Orbán G, Fiser J, Aslin RN, Lengyel M. 2008. Bayesian learning of visual chunks by human observers. Proc Natl Acad Sci 105: 2745–2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. O'Reilly RC, Frank MJ. 2006. Making working memory work: a computational model of learning in the prefrontal cortex and basal ganglia. Neural Comput 18: 283–328. [DOI] [PubMed] [Google Scholar]
  37. O'Reilly RC, Soto R. 2002. A model of the phonological loop: generalization and binding. In Proceedings of Advances in Neural Information Processing Systems 14, pp. 83–90, MIT Press, Cambridge, MA. [Google Scholar]
  38. Perlman A, Pothos EM, Edwards DJ, Tzelgov J. 2010. Task-relevant chunking in sequence learning. J Exp Psychol Hum Percept Perform 36: 649–661. [DOI] [PubMed] [Google Scholar]
  39. Podell JE, Sambataro F, Murty VP, Emery MR, Tong Y, Das S, Goldberg TE, Weinberger DR, Mattay VS. 2012. Neurophysiological correlates of age-related changes in working memory updating. Neuroimage 62: 2151–2160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sakai K, Kitaguchi K, Hikosaka O. 2003. Chunking during human visuomotor sequence learning. Exp Brain Res 152: 229–242. [DOI] [PubMed] [Google Scholar]
  41. Sargent J, Dopkins S, Philbeck J, Chichka D. 2010. Chunking in spatial memory. J Exp Psychol Learn Mem Cogn 36: 576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Seger CA. 1997. Two forms of sequential implicit learning. Conscious Cogn 6: 108–131. [DOI] [PubMed] [Google Scholar]
  43. Seger CA. 1998. Independent judgment-linked and motor-linked forms of artificial grammar learning. Conscious Cogn 7: 259–284. [DOI] [PubMed] [Google Scholar]
  44. Seidler RD, Bo J, Anguera JA. 2012. Neurocognitive contributions to motor skill learning: the role of working memory. J Mot Behav 44: 445–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Song S, Cohen L. 2014. Impact of conscious intent on chunking during motor learning. Learn Mem 21: 449–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Song S, Howard JH Jr, Howard DV. 2008. Perceptual sequence learning in a serial reaction time task. Exp brain Res 189: 145–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Terrace HS. 1991. Chunking during serial-learning by a pigeon 0.1. Basic evidence. J Exp Psychol Behav Process 17: 81–93. [DOI] [PubMed] [Google Scholar]
  48. Tremblay PL, Bedard MA, Langlois D, Blanchet PJ, Lemay M, Parent M. 2010. Movement chunking during sequence learning is a dopamine-dependant process: a study conducted in Parkinson's disease. Exp Brain Res 205: 375–385. [DOI] [PubMed] [Google Scholar]
  49. Verwey WB. 1996. Buffer loading and chunking in sequential key-pressing. J Exp Psychol Hum Percept Perform 22: 544–562. [Google Scholar]
  50. Wymbs NF, Bassett DS, Mucha PJ, Porter MA, Grafton ST. 2012. Differential recruitment of the sensorimotor putamen and frontoparietal cortex during motor chunking in humans. Neuron 74: 936–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zenon A, Olivier E. 2014. Contribution of the basal ganglia to spoken language: is speech production like the other motor skills? Behav Brain Sci 37: 576. [DOI] [PubMed] [Google Scholar]
  52. Zénon A, Sidibé M, Olivier E. 2014. Pupil size variations correlate with physical effort perception. Front Behav Neurosci 8: 286. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
supp_23_3_108__index.html (909B, html)
supp_23.3.108_Supplemental_Fig1.eps (776.3KB, eps)
supp_23.3.108_Supplemental_Fig2.eps (815.5KB, eps)
supp_23.3.108_Supplemental_Materials.docx (61.7KB, docx)

Articles from Learning & Memory are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES