Combining Fourier and Lagged k-Nearest Neighbor Imputation for Biomedical Time Series Data

Abstract

Most clinical and biomedical data contain missing values. A patient’s record may be split across multiple institutions, devices may fail, and sensors may not be worn at all times. While these missing values are often ignored, this can lead to bias and error when the data are mined. Further, the data are not simply missing at random. Instead the measurement of a variable such as blood glucose may depend on its prior values as well as that of other variables. These dependencies exist across time as well, but current methods have yet to incorporate these temporal relationships as well as multiple types of missingness. To address this, we propose an imputation method (FLk-NN) that incorporates time lagged correlations both within and across variables by combining two imputation methods, based on an extension to k-NN and the Fourier transform. This enables imputation of missing values even when all data at a time point is missing and when there are different types of missingness both within and across variables. In comparison to other approaches on three biological datasets (simulated and actual Type 1 diabetes datasets, and multi-modality neurological ICU monitoring) the proposed method has the highest imputation accuracy. This was true for up to half the data being missing and when consecutive missing values are a significant fraction of the overall time series length.

Graphical Abstracts

1. Introduction

Missing values occur in almost all real world data, and are especially common in biomedical data [1] due to equipment errors, varied sampling granularity, or fragmentation of the data. Data collected from a hospital, such as from ICU data streams or an electronic health record (EHR), can have missing values due to patients moving between hospitals and units (or having gaps in medical care), monitors being disconnected to perform a surgical procedure, and sensors being displaced and among other reasons. In the neurological ICU data we analyze, a catheter measuring temperature in the bladder was displaced, intracranial monitors are disconnected to perform an angiogram, and dropped packets led to some values not being stored on the server. Data collected in an outpatient setting, such as from individuals with Type 1 diabetes wearing a continuous glucose monitor, may have even more potential for missingness. In the real world a patient may choose to not wear a sensor for social reasons, devices may not be suitable for all activities, and they may fail more frequently. In the diabetes-related dataset we analyze in this paper, not all sensors could be worn during aquatic activities, for example, and in one case a device failed while a participant was rock climbing.

While analyses of these various data can uncover factors leading to recovery from stroke or causing unhealthy changes in blood glucose, there are practical issues around missing data that must be addressed first. Causal inference is key to effectively predicting future events or preventing them by intervening and has been a growing area of work in biomedical informatics [2]. When data are not missing completely at random, though, the independence assumptions of these methods will fail and spurious inferences may be made. Ignoring missing values can lead to computational problems such as bias (if an expensive test is only ordered when a doctor suspects it will be positive), difficulties in model learning (when different subsets of variables are present for different patients), and reduced power (if many cases with missing values are not used).

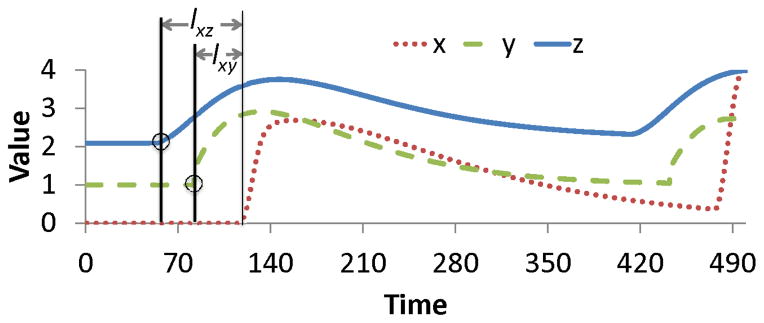
Many approaches have been developed for imputing values, but they have failed to address a few key issues: correlations between variables across time, multiple types of missingness within a variable (making it both MAR – missing at random, and NMAR – not missing at random), and timepoints where all data are missing. Take Figure 1, showing three variables where x is correlated with both y and z at two different lags (l_xy and l_xz respectively). If x is missing at time t, then existing methods would impute this value using the values of y and z at time t. Instead, imputation should be based on the values of y and z at t − l_xy and t − l_xz respectively.

Figure 1.

The value of x is missing at time t. Variables y and z are correlated with x at lags l_xy and l_xz respectively.

Second, there may be multiple types of missingness in a variable, yet most current methods (e.g. [3, 4]) assume that each variable can only have one type of missingness. In reality, the values of variables and their presence or absence are often correlated. For example, the presence of measurements for blood glucose may depend on the past values of glucose but will also depend on insulin levels and food intake.

Finally, single devices are often used to measure multiple signals (e.g. cellphone accelerometer and GPS, laboratory test panel), making it likely that multiple values will be missing at a single instance. This poses challenges for many methods, which require some non-missing data to impute values for a particular instance.

In this paper we propose FLk-NN, which combines the Fourier transform and lagged k-NN to impute missing data from continuous-valued time series, where there may be lagged correlations between variables, data may be both MAR and NMAR, and entire time points may be missing. We compare the approach to others on multiple datasets from the biological domain (one simulated, and then actual clinical data and data from body-worn sensors), demonstrating that our proposed work has the highest imputation accuracy for all ratios of missing data on both datasets, even with up to 50% of the dataset missing and while being able to impute values for all missing points.

2. Related work

We briefly describe existing methods for handling missing data and refer the reader to [5, 6] for a full review.

First, there are multiple types of missing data that each require different imputation strategies. When data are missing completely at random (MCAR), the probability of a variable’s data being missing, P(V), is independent of both the variable itself and the other observed variables, O. That is:

$$P(V\mid V,O)=P(V).$$ (1)

For example, data from a continuous glucose monitor is only captured if the monitor is within the range of the receiver. If a patient walks to another part of a building and leaves the receiver in his or her office, then data will not be recorded. When data are MCAR, it is possible to ignore the missing values.

Missing at random (MAR) is when the probability of data for V being missing is dependent on variables other than V. Thus imputation can be based on the observed values of other variables. Mathematically,

$$P(V\mid V,O)=P(V\mid O).$$ (2)

For instance, the likelihood of a particular test being done (and its value being recorded) may depend in part on a patient’s health insurance. In the case of our ICU data, data missing due to a monitor being disconnected to perform a surgical procedure may be MAR.

Finally, data that are not missing at random (NMAR) are those that are neither MCAR nor MAR. Thus the probability of a variable being missing may depend on the missing variable itself. For instance, a person who measures his or her glucose with a fingerstick monitor may measure more frequently if the values seem unusually high or low (suggesting either a calibration error or a dangerous change in glucose) or less frequently if values are stable and within their target range. Thus, blood glucose would be NMAR as its presence depends on itself rather than on other measured variables. With MAR and MCAR data, one can focus on correlations between missing and observed data, while NMAR needs specification of the missingness model.

2.1. Ignoring Missing Values

The simplest approach to missing data is simply to ignore it. With complete case analysis (also called listwise deletion), the most commonly used approach in clinical trials according to [7], only patients without missing data points are included in the analysis. In an extreme case, if all patients who experience no improvement in their condition drop out of a trial, then this approach would overestimate the efficacy of the intervention. That is, when the missing outcome data are not MCAR, the analysis may be biased [8]. Note that this approach would also ignore patients who missed an intermediate followup visit, as only those with complete data are included. All variables may not be used in all analyses, so another approach is pairwise deletion, which removes instances if the currently used variables are missing [3]. This will still lead to bias when the data are not MCAR, for the same reasons as above, and still reduces statistical power [5]. As a result, recent guidelines for patient-centered outcomes research have highlighted the importance of not ignoring missing data in addition to working to prevent its occurrence, making accurate imputation a priority [9].

2.2. Single Imputation (SI)

There are two primary categories of imputation methods. The first, single imputation, generates a single value to replace each missing value. Historically, an efficient way of doing this is to simply replace each missing value with the mean or mode for the variable [10, 11]. For biomedical data, mean imputation (MEI) would mean replacing every patient’s heart rate data with the mean value for heart rate in the dataset. This can lead to bias and also an underestimate of standard errors [12, 13].

One of the key problems with MEI is that it treats every missing instance identically, yet based on the similarity of an instance to other existing data, we can better estimate the value of missing variables. For example, if data from a continuous glucose monitor is missing, but we have blood glucose (BG) at the same time, then instances with a similar BG will provide better estimates than just the mean value. This is what k-Nearest Neighbor (k-NN) based methods do by identifying the k most similar instances using the observed values of other variables. Then the values are combined into a single estimate using approaches such as the weighted average [14] or a kernel function [15]. When a single nearest neighbor is used (k = 1), this is called hot deck. These k-NN based methods may be appropriate when data are MAR, meaning that the missing value is correlated with other observed variables. However, since it does not incorporate the missing variable itself, it cannnot handle NMAR data.

Further, while k-NN is generally more accurate than MEI, experiments on real high-dimensional phenomic data did not find that a single method was best for all datasets when comparing variations of k-NN to methods such as Multivariate Imputation by Chained Equations (MICE) and miss-Forest [16]. One drawback of k-NN is that, because it relies on the values of other variables, it cannot impute a value when all variables are missing in an instance, and may be less accurate as more variables are absent. This is a major limitation when measurements come from one device or when they are always either all present or absent.

Other approaches such as model-based methods [17] and expectation maximization (EM) [18] may have higher accuracy, but are computationally expensive and problem specific. In clustering based single imputation (SI) methods [19, 20], data are first clustered using the non-missing values and then missing values are imputed using the instances of the cluster that contain the missing value instance. A hybrid clustering and model based method was proposed by Nishanth et al. [21] where they combine k-means with artificial neural network (ANN) and found that the method is more accurate than individual model based techniques (e.g. ANN) on financial data. However, the performance decreases when there are fewer complete instances and a higher missing rate. As with k-NN based methods, these assume that data are MAR. When they are NMAR, this will bias the parameter estimates. This has also been shown experimentally [22].

2.3. Multiple Imputation (MI)

The second key category of imputation methods are where multiple values are generated for each missing instance and then inferences from the multiple resulting datasets are combined [23].¹ Since there is often uncertainty about the value of a missing result, imputing multiple possible values can capture both this uncertainty and the likely distribution of possible values.

Two methods for the imputation phase are the multi-variate normal (MVN) model, which assumes that the variables are continuous and normally distributed and ICE or MICE, which uses a chained equation to fill the missing values [26, 27]. MICE has several advantages over MVN such as enabling imputation with both continuous and categorical variables, and when variables have different types of missingness (though not when multiple types of missingness occur within a single variable).

Results of the imputation can be combined by averaging [28, 29], bagging [29], and boosting [30]. Schomaker and Heumann [29] experimented on simulated data and showed that model averaging can give more accurate estimates of the standard error.

Current methods make two primary assumptions that are not always appropriate for biomedical data. First, when data are MAR, variables are assumed to be correlated with no time lag. However, many biological processes (such as the metabolism of carbohydrates) have a temporal component, so carbohydrates from a meal will not be instantaneously reflected in blood glucose. Second, each variable is often assumed to have only a single type of missingness, but in reality, the missing values will likely depend on the variable itself and other variables. Thus blood glucose may depend on both glucose itself as well as meals. Finally, we often encounter situations where all values are missing, due to either a failure of a single sensor or all sensors being disconnected, but methods such as k-NN cannot impute if there is no data for an instance. A brief comparison of our approach and others is shown in Table 1, where methods are compared in terms of ability to impute completely missing time instances, inclusion of time lags for correlations, and ability to handle variables that are both MAR and NMAR.

Table 1.

Comparison of methods, with ours being FLk-NN.

Name	Impute empty instances	Lagged relationships	NMAR	Multi missingness in a variable
MEI	Yes	No	No	No
k-NN	No	No	No	No
Model-based	Yes	No	No	No
EM	Yes	No	No	No
Probabilistic EM	No	No	No	No
MICE	Yes	No	No	No
Fourier	Yes	No	Yes	No
FLk-NN	Yes	Yes	Yes	Yes

3. Method

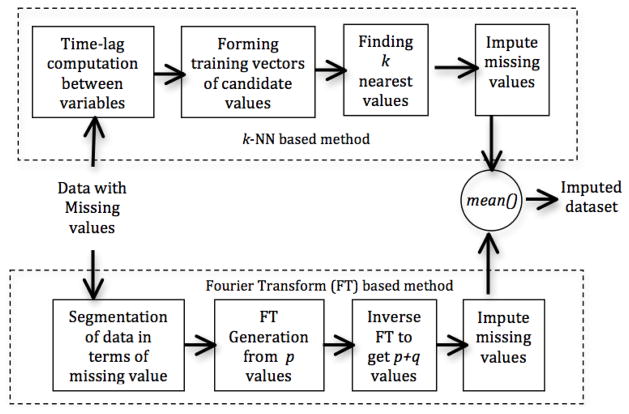
We now introduce a new method for imputing missing values in time series data with lagged correlations and multiple types of missingness within a variable. Our proposed method, FLk-NN, is a combination of two imputation methods: i) an extension of k-NN imputation with lagged correlations and ii) the Fourier transform. The system block diagram is shown in Figure 2. The Matlab code is available at https://github.com/kleinberg-lab/FLK-NN.

Figure 2.

Block diagram for Fourier and Lagged k-NN combined system (FLk-NN). Here, k is the number of nearest neighbors, p is the number of observed values from beginning to prior data point of a missing value, q is the number of missing values after those observed p values.

First, we develop an extension to k-NN with time lagged correlations using cross-correlation. Since correlations may persist for a period of time and time measurements may be uncertain, we introduce lagged k-NN (Lk-NN), which has two parameters: k, the number of nearest neighbors, and p the number of time lags. Thus we take the p lags with the strongest correlation for each pair of variables and then later the k nearest neighbors across all lags (weighted by the strength of the correlation), averaging the results. While this incorporates time dependent correlations, it cannot account for dependencies of a variable on itself and cannot be used when all data at the lagged timepoints are missing. Thus we also develop an imputation approach based on the Fourier transform, which uses only the data for each variable to impute its missing values, enabling us to handle these completely missing instances. By combining Lk-NN, which handles MAR and the Fourier transform, which handles NMAR, we can impute values when both types of missingness occur.

Then, when results from both methods are available, they are averaged for each value (otherwise the one present value is used). Combining Lk-NN with the Fourier-based method overcomes the limitation of nearest neighbors methods requiring some data present at each instance and improves accuracy by handling both MAR and NMAR missing data.

3.1. Lk-NN Method

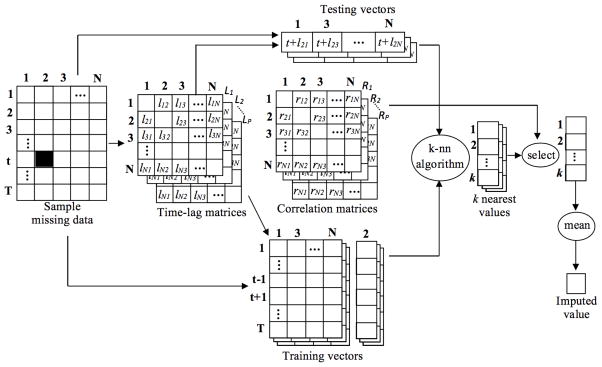
Normally, k-NN finds similar instances by, say comparing the values of variables at time 1 to those at time 10. However, correlations may occur across time. For example, insulin does not affect blood glucose immediately and weight and exercise are correlated at multiple timescales. This is shown in Figure 1, where there is a lag between a change in the value of y and x’s response. To handle this, we develop a new approach for constructing the test and training vectors using lagged correlations, where the time lags can differ between pairs of variables. This is illustrated in Figure 3.

Figure 3.

An example of Lk-NN for a single missing value (indicated by the black cell), where N is the number of variables, T is the number of time-instances, L_i is the i^th time lag matrix, l_xy is the time lag from x to y variable, p is the number of lag and correlation matrices, and k is the number of nearest neighbors.

3.1.1. Calculating Time Lags

To form the test and training vectors, we first identify which variables are correlated and at which time lags. We use the cross-correlation, which is a similarity measure of two time-series as a function of a time delay applied to one of them [31]. The cross-correlation, r_xy, between variables, x and y, for time delay d is:

$$r_{xy}(d)=\frac{c_{xy}(d)}{\sqrt{c_{xx}(0)c_{yy}(0)}},$$ (3)

$$c_{xy}(d)=\{\begin{array}{ll}\frac{1}{T-d}{\sum }_{t=1}^{T-d}(x_t-\overline{x})(y_{t+d}-\overline{y}),\hfill & \text{if}d\ge 0\hfill \\ \frac{1}{T+d}{\sum }_{t=1-d}^T(x_t-\overline{x})(y_{t+d}-\overline{y}),\hfill & \text{otherwise}\hfill \end{array}$$ (4)

where T is the length of the series, χ̄ and ȳ are the mean of x and y respectively, d varies from −(D − 1) to (D − 1), and D is the maximum time delay. Since some values for x and y may be missing, we use only the instances where both are present in this calculation.

Matrices are constructed for each of the p lags, with the correlations ordered from 1 … p by decreasing strength. Thus, for each pair of variables L₁ contains the lag, d, with the strongest correlation (max |r_xy|) and L_p the lag with the weakest. Each L is an N × N matrix, where elements represent the time lags for each correlation between the N variables. An element l_xy can be positive (values of variable y have a delayed response in time unit l_xy to values of x) or negative (values of variable x have a delayed response of time unit l_xy for values of y) and l_xy = −l_yx. The diagonal elements of the matrix are not computed since those elements give the auto-correlation of the signal and are not used in this algorithm. For all l_xy, the corresponding correlation values, |r_xy|, are stored in the matrices R₁ … R_p, which are used in the neighbor selection step.

3.1.2. Forming Vectors

Formation of vectors with Lk-NN is more complex than for k-NN since we must account for multiple lags that differ across variable pairs. Instead we create a set of test and training vectors for each of the p lags. Below we describe how to create the vectors for a single lag.

Say a variable, x, is missing at time t and x has a time lagged relationship with variables y and z, with lags l_xy and l_xz respectively. The test vector is then formed using the values of y and z at t+l_xy and t + l_xz. Training vectors are formed in similar way and the values of x, which are the candidate values for imputation, are stored separately. Training vectors are generated from the existing values of x and the time instances resulting after adding the lags must be within 1 to T (length of data). This makes the boundary of time instances of training vectors for a missing value:

$$[max(1,1-min(l_{x1}\dots l_{xN})),min(T,T-max(l_{x1}\dots l_{xN}))]$$ (5)

where l_x1, …, l_xN are the time lags of correlations between x and all N variables for the current lag matrix.

3.1.3. Finding Neighbors and Imputing Missing Values

Once the lags are found and vectors formed, the next step is finding the nearest neighbors for each missing instance. Since the strength of the correlation between variables and across the p lags may differ substantially, we incorporate a weight into our distance measure. Note that each neighbor may be based on different variables if some are missing. This ensures that neighbors based on highly correlated variables with their associated lags are given more weight rather than weakly correlated variables or only the nearest values in time.

Most current methods use the Euclidean distance as a proximity measure, but this does not incorporate the differing correlations. Instead we propose a weighted modification of the Euclidean distance that is similar to the Mahalanobis distance but can handle missing values in both test and training vectors.

The distance between instances x and y is:

$$d(x,y)=\frac{\sqrt{{\sum }_{i=1}^N(x_i\wedge y_i)\times {(x_i-y_i)}^2\times w_i}}{{\sum }_{i=1}^N(x_i\wedge y_i)}$$ (6)

where N is the number of variables, and w_i is the weight, which is the normalized correlation coefficients between missing variables and i^th variable. Here Σ w_j = 1 for j being non-missing pairs of variables of x and y. The logical and of x and y ensures that only instances where values for both are present are included. This is the average weighted Euclidean distance between two vectors computed for non-missing pairs of values, where highly correlated variables have larger impact on the distance compared with less correlated variables. The result is p sets of k nearest neighbors (one set of neighbors for each L matrix). We then average the values for the k neighbors with the lowest weighted distance (out of the set of p × k neighbors).

Algorithm 1.

Fourier transform based imputation

Input:
	Data matrix, Y = {V1, V2, …, VN}, is a set of variables, where each Vi = {v1, v2, …, vT}, and vj is the jth data point;
Output:
	Data matrix, Y with imputed values
1:	for each V in Y do
2:	ts = min(j), where vj is missing, 1 ≤ j ≤ T;
3:	while ts ≠ ∅ do
4:	te = min(j), where vj is non-missing, ts ≤ j ≤ T;
5:	F = DFT(v1, v2, …, v(ts−1));
6:	u = IDFT(F, te);
7:	vj = uj, where ts ≤ j ≤ te;
8:	ts = min(j), where vj is missing and 1 ≤ j ≤ T;
9:	end while
10:	end for
11:	return Y

3.2. Fourier Method

While Lk-NN accounts for correlations between variables, we also need to incorporate patterns within a variable to handle data that are NMAR. To do this, we develop an imputation method based on the Fourier transform that uses past values of each variable to impute each missing value.

First, a data segment is formed with the data from the beginning of the signal up to the last non-missing data point. Where values v₁ through v_p−1 are present (or imputed), and v_p … v_q are missing, the Fourier descriptors are obtained with:

$$F_k=\sum _{j=1}^{p-1}{v}_j\times {\mathrm{e}}^{-(2i\pi /p-1)(j-1)(k-1)}$$ (7)

where F_k is the k^th Fourier descriptor with 1 ≤ k ≤ (p − 1), and $i=\sqrt{-1}$.

Then, the imputed value for time m, where p ≤ m ≤ q, can be calculated from the Fourier descriptors with:

$$v_m=\frac{1}{p-1}\sum _{k=1}^{p-1}{F}_k\times {\mathrm{e}}^{(2i\pi /p-1)(j-1)(m-1)(k-1)}$$ (8)

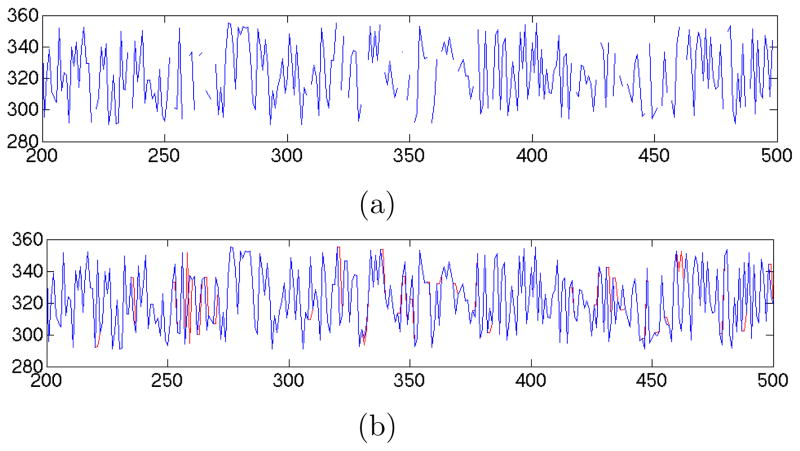
where the notation is same as equation (7). Algorithm 1 shows the process where DFT(v) (the discrete Fourier transform) generates Fourier descriptors for a variable, v, and IDFT(F, t) (inverse DFT) regenerates a signal of length t from the Fourier descriptors, F. An example of the result on a set of simulated data is shown in Figure 4 where most of the imputed data points are near the actual value.

Figure 4.

An example of Fourier based imputation for one variable, (a) with simulated missing data points, (b) the actual data (in blue) with the imputed data (in red).

The proposed method aims to estimate the most accurate value for each missing value based on the observed data. Thus if the given data do not capture the high frequency components (i.e. sampling frequency is less than 2*Nyquist frequency), the FFT will not be as accurate on these components and will approximate a value using the lower frequency components of the data.

3.3. Combining the methods for FLk-NN

For each missing data point, we impute one value using each of the described methods and then must combine these. Since model averaging gives a more stable and unbiased result compared with other approaches such as bagging and weighted mean [29], we average the value estimated by the two methods, and call the resulting combined approach FLk-NN.

3.4. Time complexity

The computational complexity of Lk-NN is a combination of two processes: cross-correlation and k-NN. For two time series of the same length, T, and maximum delay, D, the complexity is O(DT) for cross-correlation, making the complexity $O(\left(\begin{array}{c}N\\ 2\end{array}\right)DT)$ for N variables. The complexity of k-NN for x missing values is O(xTN). Therefore, the total time complexity of Lk-NN is $O(\left(\begin{array}{c}N\\ 2\end{array}\right)DT+\mathit{xTN})$. Note that the efficiency of this method can be improved by a look-up table of distance between instances. In our Fourier method, we used the fast Fourier transform (FFT) algorithm, which has the complexity O(T log T). Thus the complexity of imputing x missing values with the Fourier method is O(xT log T). Hence, the complexity of FLk-NN is $O(\left(\begin{array}{c}N\\ 2\end{array}\right)DT+\mathit{xTN}+\mathit{xT}logT)$.

4. Experimental Results

4.1. Data

We compared the proposed approach to others on three biomedical datasets, one simulated dataset (enabling complete control over the amount of data that is missing) and two real datasets, one collected from an ICU and another collected during daily life (free-living conditions).²

Simulated diabetes (DSIM) dataset

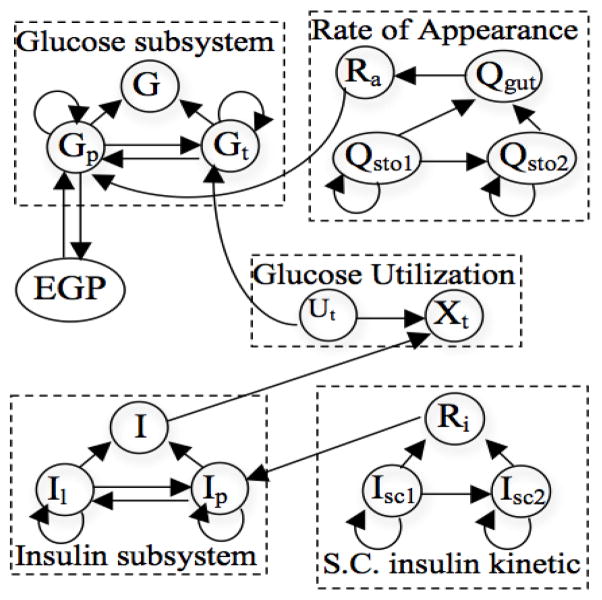
We used the glucose-insulin simulation model developed by Dalla-Man et al. [32] to construct a simulated dataset, DSIM. The model describes the physiological events occurring after a meal and was created by fitting the major metabolic fluxes estimated (endogenous glucose production, meal rate of appearance, glucose utilization, and insulin secretion) in a model-independent way on a wide population [32]. This model has been validated with human subjects [32] and approved by the FDA for use in pre-clinical trials [33], and is thus more realistic than examples such as random networks. The model contains a set of submodules that affect one another with varying delays. We generated one day of data for each of 10 patients by randomly selecting patient parameters (e.g. body weight, meal amount and timing, and insulin dose) within realistic ranges (e.g. body weight within 50kg–120kg). Data was recorded at every minute, yielding 1440 time points for the 16 variables listed in Table 2. We added Gaussian noise to make the data more similar to real-world cases. The relationships embedded in the model are shown in Figure 5.

Table 2.

Variables in DSIM dataset.

Symbol	Name
G	Glucose concentration
Gp	Glucose mass in plasma
Gt	Glucose mass in tissue
I	Insulin concentration
Ip	Insulin mass in plasma
It	Insulin mass in tissue
Ut	Glucose Utilization
Xt	Insulin in the interstitial fluid
EGP	Endogenous glucose production
Ra	Glucose rate of appearence
Qsto1	Solid glucose in stomach
Qsto2	Liquid glucose in stomach
Qgut	glucose mass in the intestine
Ri	Rate of appearence of insulin in plasma
Isc1	Nonmonomeric insulin in subcutaneous space
Isc2	Monomeric insulin in subcutaneous space

Figure 5.

Simulated glucose data variables and relationships.

NICU dataset

In the second experiment we used physiologic data collected from a set of subarachnoid hemorrhage (SAH) patients admitted to the Neurological intensive care unit (NICU) at Columbia University [34]. Data on cardiac and respiratory variables, and brain perfusion, oxygenation, and metabolism were continuously collected from 48 patients. However, the set of variables collected (a max of 22) differed for each patient as did the number of timepoints, as it covered the duration of ICU stay. Data duration ranged from 2.5 to 24.7 days, with a mean of 12.33 days. The majority of data were recorded at 5 second intervals, which were then minute-averaged so that all recordings were synchronized to the same time points. This resulted in an average of 17,771 time points for each patient, with a standard deviation of 10,216. As the amount of missing data differed widely due to factors such as interventions, device malfunctions and loss of connectivity between the device and network, we selected a subset of 9 patients with fewer missing values and used 3 days of data. It was necessary to ensure a sufficient amount of data present at the start, as we later removed varying amounts of data to test the methods and compare imputed to actual values. Table 3 gives the baseline amount of missing data for each subject. For the simulated missing data, the missing ratios indicate the total fraction of missing values (original + simulated).

Table 3.

Baseline level of missing data in NICU dataset averaged across all variables.

Patient	# of variables	original missing
P1	11	0.1%
P2	14	9.37%
P3	16	3.28%
P4	14	8.16%
P5	16	4.62%
P6	18	8.68%
P7	13	9.96%
P8	16	6.57%
P9	18	4.54%

DMITRI dataset

Our third dataset is the Diabetes Management Integrated Technology Research Initiative (DMITRI), developed by Heintzman [35]. Data were collected from 17 individuals with Type 1 Diabetes (7 females) aged 19 to 61 years over at least 72 hours. The participants wore a number of sensors including a continuous glucose monitor (CGM), heart rate monitor, insulin pump, two activity monitors and a sleep monitor. Recording frequencies for the devices varied, but all were synced to the 5-minute intervals of the CGM. As in the NICU dataset, the data had varying amounts of missing values, ranging from around 16 to 30% per participant. This is due to factors such as loss of connectivity (between CGM and receiver), removal of devices (such as during bathing) and potential device malfunctions. Further not all sensors are used at all times (e.g. the sleep sensor is only worn during sleep). We excluded data from 3 of the 17 participants due to the large amount of missing data. This yielded an average of 1146 timepoints. Table 4 gives the baseline amount of missing data for each subject along with the number of variables.

Table 4.

Baseline level of missing data in DMITRI dataset averaged across all variables.

Participant	# of variables	original missing
P1	11	29.68%
P2	9	25.81%
P3	9	25.66%
P4	11	15.67%
P5	10	25.19%
P6	9	25.79%
P7	11	21.61%
P8	10	28.38%
P9	8	15.89%
P10	11	20.98%
P11	10	21.97%
P12	10	27.53%
P13	11	26.67%
P14	10	22.2%

4.2. Procedure

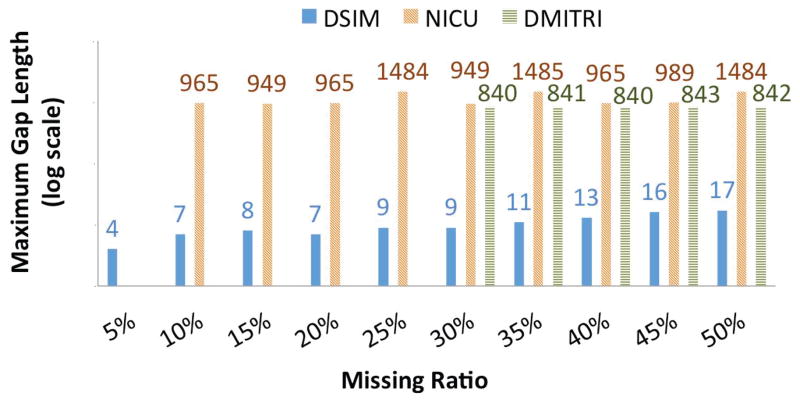
We created synthetic missing data by deleting randomly selected values. If the selected data point was already missing (which can occur in the NICU and DMITRI datasets), we select another and repeat this until the target missing ratio is reached. The ratios are 5% to 50%, 10% to 50%, and 30% to 50% in increments of 5% for DSIM, NICU, and DMITRI respectively. The maximum length of consecutively missing values (gaps) for both the datasets are shown in Figure 6. The maximum gap length is 17 for DSIM, 1485 for NICU, and 843 for DMITRI.

Figure 6.

Maximum gap length of DSIM and NICU datasets. Note that the NICU data begins at 10% and DMITRI data at 30% due to the existing missing values.

We compared our system with several methods representing different types of imputation.

MEI [11]: Missing values are imputed by computing the mean of non-missing values of a variable.

Hot deck and k-NN [14]: Euclidean distance is used to find the k neighbors and the weighted average of these is used to impute. For k-NN, we used k = 5, which gave the best for this algorithm in preliminary tests and for Hot Deck k is always 1.

BPCA [18]. This probabilistic method applies Bayesian principal component analysis prior to the conventional E-M process. We used the authors’ BPCAfill.m code³ with two parameters set to their default values, k = number of variable −1 and maxepoch = 200.

EM [36]: This iterated linear regression analysis replaces the conditional maximum likelihood estimation of regression parameters in the traditional E-M algorithm with a regularized estimation method. We used the RegEM package⁴ with the default values for the parameters (e.g. maximum number of iteration: 30, regression method used: multiple ridge regression).

Inpaint [37]: This statistical model based approach extrapolates non-missing elements using an iterative process. We used the authors’ code⁵ with the default value for number of iterations, which is 100.

MICE [26]: As a multiple imputation method we used MICE, which employs chained equation to impute. We used the mice R package⁶ with all parameters set to their defaults.

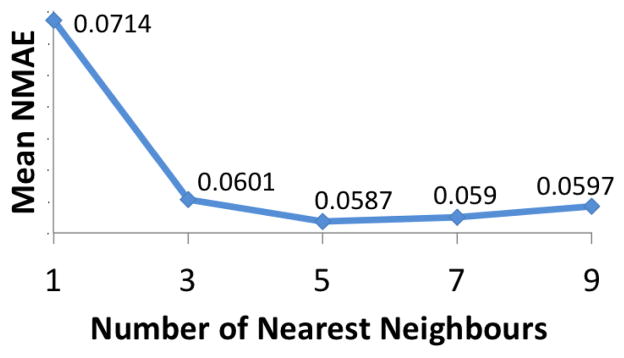
FLk-NN: We used D = 60 (i.e. 1 hour), as this is a likely time window for most of the biological effects, and p = 3 to enable multiple lags without drastically increasing computational complexity. Using two randomly selected datasets from DSIM, we experimented with 1 to 9 neighbors (in increments of 2) and found that the commonly used value of 5 gave the highest accuracy(Figure 7). Thus we used k = 5.

Figure 7.

Mean NMAE of our method for different number of nearest neighbors (k) on two DSIM datasets.

We used the authors’ code for each algorithm when available and implemented MEI, hot deck, and k-NN ourselves.

We evaluate the performance of each approach based on distance between imputed and actual values, using the normalized mean absolute error (NMAE):

$$\mathit{NMAE}=\frac{1}{n}\sum _{i=1}^n\frac{\mid d_i^{ac}-d_i^{\mathit{imp}}\mid }{V_{\mathit{max}}-V_{\mathit{min}}}$$ (9)

where n is the number of missing data points, $d_i^{ac}$ and $d_i^{\mathit{imp}}$ are the i^th actual and imputed values respectively, and V_min and V_max are the min and the max value of variable of $d_i^{ac}$ computed by ignoring the missing values. NMAE is computed for each subject individually (10 for DSIM, 9 for NICU), and then averaged.

4.3. Results

DSIM

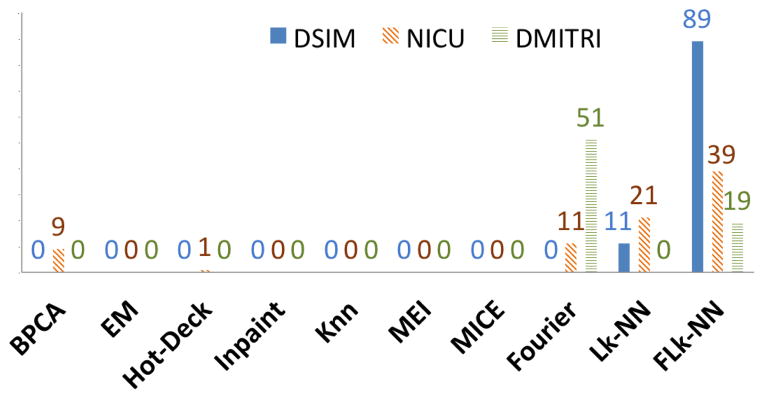
Table 5 shows the mean of the NMAE for each method highlighting the lowest error. For all missing ratios our combined method, FLk-NN, gives the lowest average NMAE. Further, Lk-NN has lowest NMAE for the 5% missing ratio and is ranked second for all other ratios. Figure 8 shows the number of times each method gives the highest accuracy out of the 100 total datasets, with FLk-NN yielding the highest accuracy in 89 cases and Lk-NN the highest in the other 11 cases. Thus, including lagged correlations in k-NN improves accuracy when data have temporal correlations and the missing ratio is high.

Table 5.

Mean of NMAE for DSIM dataset.

Method	5%	10%	15%	20%	25%	30%	35%	40%	45%	50%
BPCA	0.046	0.047	0.049	0.051	0.052	0.053	0.055	0.057	0.059	0.061
EM	0.057	0.054	0.053	0.053	0.053	0.053	0.055	0.056	0.058	0.060
Hot deck	0.053	0.055	0.057	0.059	0.063	0.069	0.081	0.095	0.108	0.116
Inpaint	73.4	79.8	82.0	81.7	88.4	89.9	98.8	100.9	105.3	109.1
k-NN	0.044	0.046	0.047	0.049	0.051	0.056	0.064	0.076	0.088	0.098
MEI	0.179	0.178	0.178	0.178	0.178	0.178	0.178	0.178	0.178	0.178
MICE	0.063	0.065	0.065	0.065	0.068	0.069	0.072	0.074	0.076	0.081
Fourier	0.048	0.049	0.050	0.049	0.051	0.051	0.053	0.053	0.056	0.058
Lk-NN	0.041	0.042	0.043	0.044	0.046	0.046	0.047	0.048	0.051	0.056
FLk-NN	0.041	0.041	0.042	0.043	0.044	0.044	0.045	0.046	0.048	0.051

Figure 8.

Number of times each method gives the highest imputation accuracy.

Among the existing methods, k-NN and BPCA had better results for lower missing ratios but their accuracy decreases significantly as the missing ratio increases. On the other hand, EM was less accurate for lower missing ratios but the accuracy did not decrease as significantly as the missing ratio increased and it gave better accuracy than k-NN and BPCA for higher ratios.

Note that the accuracy of the combined approach, FLk-NN, is higher than the individual approaches, Fourier and Lk-NN, for every missing ratio since the combined approach includes relationships within and across variables, and the DSIM data has auto-correlations with lagged correlations, as shown in Figure 5. For example, in Figure 5, liquid glucose in the stomach (Q_sto2) depends on Q_sto1 and itself.

Figure 6 shows the maximum number of consecutive occurrences of missing values (i.e. gap of values within observed values) where DSIM has a maximum gap length of 17. Large gaps have an impact on Fourier but less influence on Lk-NN, which uses lagged correlations with other variables and leads to better results when the methods are combined.

Our Lk-NN can impute if some of the variables are missing in test vector but is unable to impute if all the lagged values are missing (e.g. a subject wearing sensors went out of network coverage for a longer period of time) whereas the Fourier method can impute in this situation. On the other hand, Fourier cannot impute missing values that occur before the first observed value (e.g. due to starting delay of a device) while Lk-NN can handle this. Across the DSIM datasets an average of 1.27% of missing values could not be imputed by Lk-NN, while FLk-NN imputed all missing values.

A two tailed un-paired t-test (for unequal variance) found that for all missing ratios, the NMAE of FLk-NN is significantly different from that of other methods (p < 0.0003) except Lk-NN. FLk-NN and Lk-NN are significantly different for 20% to 50% (p < 0.0003), but not for 5% to 15% using the threshold p < 0.05.

NICU

For this dataset, we compute NMAE for the simulated missing data points only. Table 6 shows the mean NMAEs of NICU. The best mean values for each missing ratio are highlighted in bold. Our proposed methods out-performed all other methods, where Lk-NN has lowest mean NMAE for the 10% missing ratio and FLk-NN was best for all other missing ratios. Figure 8 shows the number of times each method gives the highest imputation accuracy for this dataset. FLk-NN has highest proportion (39 out of 81), with Lk-NN being second (21 of 81), and Fourier third (11 of 81).

Table 6.

Mean of NMAE for NICU dataset.

Method	10%	15%	20%	25%	30%	35%	40%	45%	50%
BPCA	0.082	0.124	0.146	0.177	0.197	0.203	0.190	0.190	0.199
EM	0.046	0.049	0.049	0.051	0.053	0.055	0.057	0.060	0.062
Hot deck	0.026	0.031	0.039	0.049	0.064	0.078	0.091	0.101	0.110
Inpaint	1.410	1.491	1.569	1.642	1.731	1.798	1.852	1.950	2.017
k-NN	0.024	0.027	0.031	0.036	0.045	0.055	0.066	0.076	0.084
MEI	0.089	0.092	0.091	0.091	0.091	0.091	0.091	0.091	0.091
MICE	0.057	0.062	0.064	0.066	0.069	0.073	0.076	0.080	0.084
Fourier	0.025	0.025	0.027	0.028	0.030	0.030	0.032	0.035	0.040
Lk-NN	0.019	0.022	0.024	0.027	0.029	0.032	0.035	0.039	0.044
FLk-NN	0.020	0.021	0.022	0.024	0.026	0.027	0.030	0.033	0.038

Compared with the DSIM dataset, the accuracy of many other methods such as BPCA deteriorated significantly due to the increased amount of non randomly-generated missing values whereas our method’s accuracy improved. k-NN and EM had the best accuracy of the existing methods but their accuracy drops significantly as the amount of missing data increases, while FLk-NN showed a more gradual decrease in accuracy as the ratio increased.

For the NICU dataset, Lk-NN could not impute an average of 1.71% of missing values, and for k-NN the amount is 1.99%, while FLk-NN imputed all missing values. The p-value of the difference between our approach and the others using an unpaired t-test was significant for all methods from 15% to 50% missing ratios (p < 0.0005). For the 10% missing ratio, all other methods are significantly different (p < 0.0007) except Lk-NN.

DMITRI

Once again we computed the NMAE for the simulated missing values, as reported in Table 7 where the lowest error is highlighted in bold. For this dataset our three proposed methods had the lowest error rates, with the Fourier method performing the best. The Fourier method has highest proportion of imputation accuracy (51 out of 70) with FLk-NN being the second best (19 out of 70) as shown in Figure 8.

Table 7.

Mean of NMAE for DMITRI dataset.

Method	30%	35%	40%	45%	50%
BPCA	0.072	.072	0.077	0.081	0.084
EM	0.07	0.07	0.071	0.072	0.075
Hot deck	0.079	0.085	0.095	0.104	0.108
Inpaint	55.74	48.99	48.81	56.18	59.45
k-NN	0.067	0.071	0.077	0.082	0.089
MEI	0.106	0.107	0.106	0.106	0.107
MICE	0.103	0.103	0.105	0.108	0.111
Fourier	0.041	0.044	0.047	0.049	0.055
Lk-NN	0.061	0.067	0.067	0.068	0.071
FLk-NN	0.045	0.048	0.050	0.051	0.055

The p-value of the difference between Fourier and the others using an unpaired t-test was significant for all the methods from 30% to 45% missing ratios (p < 0.0085). For the 50% missing ratio, all other methods are significantly different (p < 2.4e⁻¹⁴) except FLk-NN.

4.4. Choosing an appropriate imputation method

While our combined method outperformed all other methods on the first two datasets, the Fourier transform by itself was best for the DMITRI data. If one knew that the DMITRI data were primarily NMAR, then they could know in advance that the Fourier-based method would be best. However in many cases it is difficult to know what type of missingness will be encountered and there has not yet been a way of testing whether data are MAR (though this assumption is made by k-NN methods) [38]. To determine what approach will be most accurate for a particular dataset, though, one can simulate missing values from a subset of the observed data points and compare the approaches.

To demonstrate this, we simulated 5% missing values on top of the existing missing values of our two real-world datasets (DMITRI and NICU) and then computed the NMAE of each imputation method for the simulated missing values only. The results are shown in Table 8 with the lowest error highlighted in bold. We found that FLk-NN should be used for NICU and Fourier for the DMITRI dataset.

Table 8.

Mean of NMAE for additional 5% simulated data on NICU and DMITRI dataset

	NICU	DMITRI
BPCA	0.047	0.072
EM	0.048	0.07
Hot deck	0.029	0.073
Inpaint	1.42	42.95
k-NN	0.026	0.064
MEI	0.092	0.106
MICE	0.06	0.101
Fourier	0.0258	0.04
Lk-NN	0.019	0.063
FLk-NN	0.018	0.045

A similar approach can be used to evaluate the tradeoff between imputation accuracy and computation time. On the DSIM dataset, the average execution time per missing value was 0.00005s for Fourier and 0.253 for Lk-NN and the combined method. Thus depending on the amount of data to be imputed and the accuracy of each, the faster method could be preferable. One could test both Fourier and the combined FLk-NN method on a subset of data with synthetically created missing values to determine the accuracy of each method. For example, if one decides that increase of NMAE from 0.018 to 0.026 (shown in table 8) is acceptable for the NICU dataset, the Fourier based method can be used for faster imputation.

4.5. Imputation with missing rows

One of the key benefits of our proposed approach is that the combined method enables imputation when an entire row is missing, meaning that all variables at a particular time are missing. This is a realistic challenge with biomedical data where measurements may come from a single device or there’s a loss in connectivity preventing recording.

To evaluate this, we created another simulated missing dataset using the DSIM data. Here for each subject, 10% of rows were deleted. All imputation methods were applied and evaluated using the same approach as described earlier. Note that BPCA, hot deck, and k-NN cannot impute at all in this case. For Lk-NN, though the time instances are fully missing for a missing value, the test vector may not be empty because of the use of time lags, where the lagged values may be present. However, this did not occur and Lk-NN was able to impute all missing values.

The NMAE for the remaining methods across the 10 datasets is shown in Table 9, which shows that our proposed method, FLk-NN, has the highest accuracy and lowest standard deviation. Lk-NN and Fourier were second and third respectively. A t-test shows that the NMAE of FLk-NN is significantly different from that of other methods (p < 0.0051) other than Lk-NN. Note that the accuracy of EM and MEI is the same here since EM first initializes missing values using MEI and then optimizes those values, but in this situation it did not optimize.

Table 9.

Mean of NMAE for DSIM where 10% of rows are missing, meaning all variables are absent for the missing instances. BPCA, Hot Deck, and k-NN cannot handle such cases and are not reported here.

EM	Inpaint	MEI	MICE	Fourier	Lk-NN	FLk-NN
0.182	28.39	0.182	0.206	0.049	0.045	0.043

5. Conclusion

Missing values are common in big data, where often many variables have correlations across time. Further, these data are rarely missing completely at random, especially when multiple signals are collected from a single device that may face errors or malfunction. Here we propose a novel imputation method that incorporates varying time lags between correlated variables and auto-correlations within the variables. The main contributions of this paper are two-fold: i) it incorporates time lagged correlations between the variables during imputation and ii) it can handle multiple types of missingness occurring in a single variable, whereas existing methods cannot handle these cases. Moreover, the proposed system is able to impute with high accuracy in the case of empty instances while some of the state-of-the-art methods cannot impute values at all. The system obtained the best accuracy in terms of NMAE for both simulated and real world biological datasets and outperformed other bench-mark methods. Experimental results show that the system can impute plausible data even if 50% of a dataset is missing with many consecutively missing values and in the presence of fully empty instances in the data.

Highlights.

• We develop a new imputation method for missing data that are both MAR and NMAR

• This method enables imputation when all data at a time instance are missing

• Incorporates time lagged correlations improves accuracy

• Method significantly reduced imputation error on simulated and real biomedical data