Summary
Individualized treatment rules recommend treatments on the basis of individual patient characteristics. A high-quality treatment rule can produce better patient outcomes, lower costs and less treatment burden. If a treatment rule learned from data is to be used to inform clinical practice or provide scientific insight, it is crucial that it be interpretable; clinicians may be unwilling to implement models they do not understand, and black-box models may not be useful for guiding future research. The canonical example of an interpretable prediction model is a decision tree. We propose a method for estimating an optimal individualized treatment rule within the class of rules that are representable as decision trees. The class of rules we consider is interpretable but expressive. A novel feature of this problem is that the learning task is unsupervised, as the optimal treatment for each patient is unknown and must be estimated. The proposed method applies to both categorical and continuous treatments and produces favourable marginal mean outcomes in simulation experiments. We illustrate it using data from a study of major depressive disorder.
Some key words: Continuous treatment, Exploratory analysis, Personalized medicine, Treatment regime, Tree-based method
1. Introduction
Individualized treatment rules are increasingly being used by clinical and intervention scientists to account for patient response heterogeneity (e.g., Ludwig & Weinstein, 2005; Hayes et al., 2007; Allegra et al., 2009; Cummings et al., 2010). These treatment rules belong to the new era of personalized medicine (Piquette-Miller & Grant, 2007; Hamburg & Collins, 2010). There is a vast literature on estimation of treatment rules that maximize the mean of a desirable clinical outcome using data from randomized or observational studies. Regression-based methods model the response as a function of patient characteristics and treatment, and select treatments that maximize the predicted mean outcome (Brinkley et al., 2010; Qian &Murphy, 2011). However, because such methods indirectly infer the optimal treatment rule through a regression model, an interpretable, parsimonious treatment rule can be obtained only via a simple regression model which is subject to misspecification; on the other hand, a complex regression model may mitigate the risk of misspecification but at the cost of producing an unintelligible treatment rule (Zhang et al., 2012b). Policy-search or direct-maximization methods offer an alternative to regression-based methods that attempt to search for the best treatment rule in a large class of potential rules (Zhang et al., 2012a, 2012b; Zhao et al., 2012; Zhang et al., 2013), thereby separating the class of decision rules from an underlying regression model. However, without an interpretable representation of the model behind these approaches, clinical investigators may be hesitant to use the estimated treatment rule to inform clinical practice or future research.
Since Breiman et al. (1984) introduced the classification and regression tree algorithm, tree-based methods have enjoyed a great deal of popularity in statistical and machine learning research, largely due to the interpretability and communicability of decision trees. Indeed, trees have been advocated as a tool for representing more complex prediction models to laymen (Craven & Shavlik, 1996). The classification and regression tree algorithm recursively partitions the covariate space into rectangular sets and then fits a simple model within each partition to the response (Breiman et al., 1984; Hastie et al., 2009, ch. 9.2); thus, the classification and regression tree algorithm provides a flexible nonparametric procedure to explore the underlying model structure (Ripley, 1996; Sutton, 2005).
Tree-based methods have been used in personalized medicine primarily for the purpose of identifying subgroups of subjects with outlying, large or small, treatment effects or strong adverse side-effects relative to subjects in some reference population of interest. Such methods include interaction trees (Su et al., 2008, 2009), virtual twins (Foster et al., 2011), and subgroup identification based on differential effect search (Lipkovich et al., 2011). Existing subgroup identification methods aim primarily to find interactions between treatment and covariates. Zhang et al. (2012a) recast treatment selection with binary treatments as a classification problem and used the classification and regression tree algorithm as an illustrative example.
We present a general purpose approach to estimating optimal personalized treatment rules representable as decision trees. The proposed method can be used with high-dimensional covariates, discrete or continuous treatments, and data from observational or randomized studies. In the case of continuous treatments, standard methods for estimating the mean outcome under a specified treatment rule, such as inverse probability weighting, cannot be applied because a required absolute continuity condition does not hold. We derive a novel kernel smoother for estimating the mean outcome in the case of continuous treatments by approximating a deterministic treatment rule with a stochastic one. The proposed estimator relies on a bandwidth parameter, and we derive a plug-in estimator of the optimal bandwidth. The proposed algorithms are available as part of the R package MIDAs (R Development Core Team, 2015) and are provided in the Supplementary Material.
2. Minimum impurity decision assignments decision trees
2·1. Optimal individualized treatment rules
We observe , comprising n independent identically distributed triples (X, A, Y) where X ∈ ℝp denotes the baseline subject characteristics, A ∈ 𝒜 represents the treatment received, and can be discrete or continuous, and Y ∈ ℝ is an outcome coded so that higher values are more desirable. An individualized treatment rule is a map π : ℝp → 𝒜 such that a patient presenting with X = x is assigned treatment π(x). Let Y*(a) denote the potential outcome under treatment a ∈ 𝒜 (Rubin, 1978), and define Y*(π) = Y*{π(X)} to be the potential outcome under π. The performance measure of π is the marginal mean outcome E{Y*(π)}, and the optimal rule, πopt, satisfies E{Y*(πopt)} ≥ E{Y*(π)} for all π. Let p(a | X) denote the conditional density of A given X, with respect to an appropriate dominating measure. We make the following assumptions.
Assumption 1 (Positivity)
There exists ε > 0 such that p(a | X) ≥ ε with probability 1 for all a ∈ 𝒜.
Assumption 2 (Strong ignorability)
The potential outcomes {Y*(a) : a ∈ 𝒜} are conditionally independent of A given X.
Assumption 3 (Consistency)
We have Y = Y*(A).
These assumptions are standard and will allow us to connect the potential outcomes with the observed data. Let Eπ denote the expectation with respect to (X, A, Y) under the restriction that A = π(X), i.e., that all patients are assigned treatments according to π; then, under Assumptions 1–3, it can be shown (Zhang et al., 2012b) that the marginal mean outcome under π is equal to Eπ (Y). We use this representation to construct an estimator of πopt that applies to either observational or randomized study data.
Unlike traditional decision tree problems, the target of estimation, πopt(x), is not directly observed for the associated patient characteristics X = x. For example, in a classification problem a correct label Y = y is observed for each observed X = x; similarly, in a regression problem an outcome Y = y is observed for each X = x. In the treatment selection problem, information about πopt(x) is available only indirectly through the outcome Y = y. Thus, any purity measure used to construct splits in a decision tree must make use of this indirect information. We develop purity measures for discrete and continuous treatments and then use these purity measures in a recursive algorithm to estimate an optimal tree-based individualized treatment rule.
2·2. Purity measures for treatment allocation
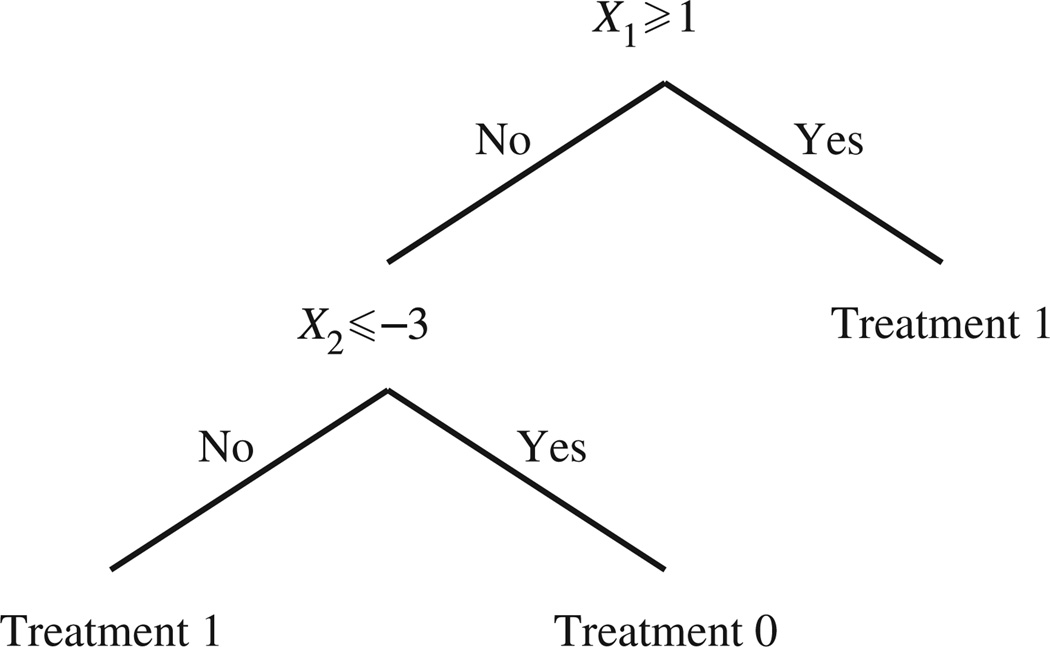
We first consider the binary treatment setting, where 𝒜 = {0, 1}; generalizations are given below. In the binary treatment case, any decision rule π partitions the domain of X, ℝp, into two regions: ℛ0 = {x ∈ ℝp : π(x) = 0} and ℛ1 = ℝp \ ℛ0 = {x ∈ ℝp : π(x) = 1}. Let and be the partition of ℝp induced by the optimal decision rule πopt. Then identification of πopt is equivalent to identifying and . For a set of triples 𝒪 = {(j, τ, b)} where j ∈ {1, …, p}, τ ∈ ℝ and b ∈ {−1, 1}, we say that r is the rectangle defined by 𝒪 if x ∈ r if and only if b(xj − τ) ≥ 0. The rectangle defined by ∅ is taken to be ℝp. We define a rectangular region as any finite combination of intersections and unions of rectangles. Both rectangles and their complements are rectangular regions. For simplicity of notation, we assume that X is a continuous random vector; this avoids having to distinguish between closed and open rectangles. A tree-based approach estimates the sets and using rectangular regions in ℝp. Figure 1 shows an example of a decision rule composed of rectangles r1 = {(1, 1, 1)} and r2 = {(2,−3,−1)} with rectangular regions and . The tree in Fig. 1 assigns treatment 0 to subjects presenting covariates X = x which satisfy x1 < 1 and x2 ≤ −3 and assigns treatment 1 otherwise. While this tree resembles a classification tree, with labels 0 and 1, it is fundamentally different in that the decision rule does not attempt to describe the rule by which the observed treatments were assigned but rather the rule by which treatments should be assigned to future patients.
Fig. 1.
A decision rule composed of rectangles r1 = {(1, 1, 1)} and r2 = {(2,−3,−1)} with rectangular regions and .
To form a tree-based estimator of πopt, we need a measure of node purity that will facilitate a recursive splitting procedure. In determining how to create two child nodes from a parent node determined by, say, the rectangular region ℛ during the process of recursive partitioning, the general goal is to make the data corresponding to each of the child nodes more pure than the data in the parent node (Sutton, 2005). Intuitively, the first split in the tree is found by determining the rectangle r such that r and rc best approximate and , respectively. Recursively, for a given terminal node ℛ, we seek the rectangle r such that splitting ℛ to form two new terminal nodes ℛ ∩ r and ℛ ∩ rc will most dramatically improve our current estimates of and . A node purity measure provides a criterion to formalize the foregoing search procedure. We first describe a measure of node purity when there are a finite number of treatments, and then extend this measure to the continuous treatment case.
2·3. Purity measures for discrete treatments
In the discrete treatment case, the set of treatments is finite and coded so that 𝒜 = {0, 1, …, K}. For a ∈ 𝒜 and x ∈ ℝp, let p(a | x) denote pr(A = a | X = x). We assume that the function p(a | x) is known and that p(a | X) is bounded away from 0 and 1 with probability 1 for each a ∈ 𝒜. If these probabilities are not known, as is the case with observational data, they may be estimated from the data, for example by using a multinomial logistic regression. Recall that the performance measure of a rule π is the expected outcome when patients are assigned treatments according to π. Under the foregoing assumptions, we can apply a change of measure to express the performance of π in terms of the observed data. For any function g : ℝp → ℝ and policy π, define the random variable Lg(π) = Lg(π, X, A, Y) = {Y − g(X)}1π(X)=A/p{π(X) | X} and let Cg(π) = E{Lg(π)}; then it can be shown that Eπ (Y) = C0(π), where 0 denotes the function g(x) ≡ 0 (Zhang et al., 2012a, 2012b; Zhao et al., 2012). However, for any fixed function g, πopt = arg maxπ Cg(π), because
so that the arg max over π depends only on C0(π). One choice for g is g(x) = E{Y | X = x, A = π̃(x)} for some reference rule π̃ ; it turns out that this choice minimizes the variance of Lg(π) when π = π̃. Hereafter, we write E{Y | X, π(X)} as shorthand for E{Y | X = x, A = π(x)}|x=X. The following result is proved in the Supplementary Material.
Lemma 1
Assume that p(a | X) ∈ [ε, 1 − ε] with probability 1 for some ε > 0 and all a ∈ 𝒜. Then, for any g : ℝp → ℝ and any rule π, var{Lg(π)} ≥ var{LE{Y | X, A=π(X)}(π)}.
Because our goal is to estimate πopt, it is natural to use a crude estimator of πopt as a reference rule. The reference rule is used to reduce variance and does not affect consistency. Thus, in practice, a simple, convenient estimator of πopt can be used as the reference rule. Hereafter, we write C(π) for CE{Y | X, πopt(X)}(π). Let m̂ (x) denote an estimator of E{Y | X = x, A = πopt(x)}; we obtain an estimator of m̂ by first constructing an estimator of E(Y | X = x, A = a), say Q̂(x, a), by regressing Y on X and A using a flexible model, and then defining m̂ (x) = maxa Q̂ (x, a). In our simulations, we estimated E(Y | X = x, A = a) using random forests (Breiman, 2001), although other methods are possible. For an arbitrary rule π, the plug-in estimator of C(π) is Ĉ (π) = En[{Y − m̂(X)}1π(X)=A/p{π(X) | X}], where En denotes the empirical expectation operator. We use Ĉ (π) as the basis for our purity measure. For any rectangle r, let πr,a,a′ denote the rule that assigns treatment a to all subjects in r and treatment a′ to all subjects in rc. For any rectangular region ℛ and rectangle r, define the purity of the partitioning of ℛ into ℛ ∩ r and ℛ ∩ rc as
| (1) |
The above purity measure estimates the performance of the best decision rule that assigns a single treatment to all subjects in ℛ ∩ r and a second treatment to all subjects in ℛ ∩ rc.
2·4. Purity measures for continuous treatments
In the continuous treatment setting we assume that 𝒜 = (0, 1). For a ∈ 𝒜, let p(a | x) denote the density of A given X = x. We assume that p(a | x) is known and that ε ≤ p(a | X) holds for all a ∈ 𝒜 with probability 1 for some fixed ε > 0. If this density is not known, it can be estimated, for example using mean-variance models (Carroll & Ruppert, 1988). The estimation of personalized treatment rules with continuous treatments has not been well studied. A major difficulty with regression-based methods is that one must first model Q(x, a) = E(Y | X = x, A = a) and then invert it to find πopt(x) = arg supa∈(0,1) Q(x, a). Correctly specifying a functional form for Q(x, a) that is interpretable yet sufficiently expressive and easily inverted within a continuous range of treatments is nontrivial when x is moderate- or high-dimensional. Our tree-based approach uses an estimator of m(x) = E{Y | X = x, A = πopt(x)} to reduce variance in the purity measure, but this need not be interpretable, nor does it require easy invertibility, so a flexible model for m(x) can be used. Furthermore, correct specification of the model for m(x) is not needed for consistency, because the optimal decision rule πopt is invariant with respect to g(x) in Cg(π).
In order to define a purity measure, we require an estimator of the quality of an arbitrary rule π : ℝp → 𝒜. The change of measure applied in the discrete treatment case is not meaningful for continuous treatments because E[Y 1A=π(X)/p{π(X) | X}] ≡ 0. Instead, we propose a smoothed version of the discrete purity measure (1) that replaces the nonsmooth indicator function with a kernel smoother νπ,h(a | x) = h−1κ([f (a) − f {π(x)}]/h) f′(a), where κ is a symmetric density function, h is the kernel bandwidth, and f is a one-to-one function mapping the treatment space (0, 1) to ℝ, with derivative f′. For example, one simple approximation to π is νπ,h(a | x) = (2h)−1 f′(a)1| f(a)−f{π(x)}|≤h. Thus, we approximate a rule π with a class of distributions over (0, 1) indexed by ℝp, so that νπ,h(a | x) has mass around π(x). Indeed, νπ,h(a | x) defines a distribution over treatments for each value of x ∈ ℝp and is therefore called a stochastic rule (Sutton &Barto, 1998). Using a stochastic rule to approximate a nonstochastic or deterministic rule effectively smooths over treatments. The precision of the approximation νπ,h(a | x) to π(x) depends on how peaked the function f′(a)κ([f(a) − f{π(x)}]/h)/h is at π(x). However, we will show below that making the function too peaked will lead to unstable results due to inflated variance.
For any fixed function g : ℝp → ℝ, define Lg(νπ,h) = Lg(νπ,h, X, A, Y) = {Y − g(X)} × νπ,h(A | X)/p(A | X) and Cg(νπ,h) = E{Lg(νπ,h)}. Then C0(νπ,h) is the importance sampling representation of the expected outcome if all patients are assigned treatment according to the stochastic rule νπ,h. The plug-in estimator of Cg(νπ,h) is Ĉg(νπ,h) = En[{Y − g(X)}νπ,h(A | X)/p(A | X)]. The following lemma characterizes how the bias and variance of Ĉg(νπ,h) depend on the bandwidth h.
Lemma 2
Assume that p(a | X) ≥ ε with probability 1 for some ε > 0 and all a ∈ 𝒜, and that κ(u) is symmetric about 0 and satisfies . Then, for any g : ℝp → ℝ and any rule π,
and var{Ĉg(νπ,h)} = O{1/(nh)}.
The mean squared error of Ĉg(νπ,h) is approximately
which is a function of the sample size, the bandwidth and the kernel function. This expression shows that a requirement for the mean squared error to decrease to zero as n increases is that h → 0 and nh → ∞. Under additional assumptions, we derive a plug-in estimator of the optimal bandwidth.
The expectation E{νπ,h(A | X)/p(A | X) | X} is unity; hence, for an arbitrary function g, it follows from the same argument as in the discrete case that arg maxπ Cg(νπ,h) = arg maxπ C0(νπ,h). Similarly, for a fixed reference rule π̃ and kernel κ, the choice of g(x) = E{Y | X = x, A = π̃(x)} minimizes the variance of Lg(νπ,h) at π = π̃. Thus, as in the discrete case, we use a crude estimator of πopt as our reference rule. To derive a plug-in bandwidth estimator, we assume that
| (2) |
where h, ℓ and ψ are arbitrary functions from ℝp into ℝ, ∈ ℝp, and ε is an independent additive error with mean zero and variance . The form of the working model in (2) is a generalization of that used by Rich et al. (2014) for adaptively modelling warfarin dose response. Here g(x) = h(x) + πopt(x)ℓ(x) + πopt(x)2ψ(x)/2 and E{Y − g(X) | X, A = π(X)}2 = ε2. Under the assumed model we have (∂2/∂a2)E{Y − g(X) | X, A = a}|a=πopt(X) = ψ(X), which is independent of the optimal rule πopt. Furthermore, we choose f(u) = u − 1/2 so that f′(u) ≡ 1. We assume a uniform treatment randomization so that p(u | x) ≡ 1. Ignoring higher-order error terms, the bandwidth that minimizes the mean squared error is
from which we obtain the plug-in estimator
| (3) |
where σ̂ε and ψ̂ are obtained by regressing Y on X and A using (2) with working models for h(x), ℓ(x) and ψ(x). In our simulations we used E(Y | X, A) = XTρ + XTβ(a − XTγ)2, which corresponds to h(X) = XTρ + (XTβ)(XTγ)2, ℓ(X) = 2XTβXTγ and ψ(X) = 2XTβ; the parameters indexing this model were estimated using nonlinear least squares with a ridge penalty added for stability.
Write C(νπ,h) for CE{Y | X,A=πopt(X)}(νπ,h). With m̂(x) denoting an estimator of E{Y | X = x, A = πopt(X)}, the plug-in estimator of C(νπ,h) is
we use this estimator as the basis for our purity measure. In our simulated experiments we take h = ĥ, which we recommend using in practice, although other choices are possible. Write νa′h(a | x) as shorthand for κ[{ f(a) − f(a′)}/h] f′ (a)/h. For any rectangular region ℛ and rectangle r, define the purity of partitioning ℛ into ℛ ∩ r and ℛ ∩ rc with respect to κ as
This estimates the performance of the best stochastic decision which is concentrated about a single value for subjects in ℛ ∩ r and around a second value for subjects in ℛ ∩ rc. In practice, the supremum is taken over observed values a in the training data.
2·5. Recursive splitting
Having defined the purity measures, we can now describe how to select the split at each stage in the recursive splitting. Generally, it is preferable to choose the split that leads to the greatest increase in node purity, defined in terms of 𝒫(ℛ, r) for discrete treatments and 𝒫κ (ℛ, r) for continuous treatments. We use the discrete case as an illustrative example, and apply the same strategy to the continuous case by simply replacing 𝒫(ℛ, r) with 𝒫κ(ℛ, r).
To grow the tree at a parent node associated with rectangular region ℛ, say, we split on the rectangle r that maximizes the total purity of its two child nodes 𝒫(ℛ, r). We then repeat the splitting process on each of the new nodes. Of course it is not possible to split the tree indefinitely, and so stopping measures based on tree complexity and node size are employed. For any rectangular region ℛ, define 𝒫(ℛ) = 𝒫(ℛ, ∅). Let μ ∈ ℕ denote a minimum node size, sometimes called a bucket size. We employ the following splitting rules.
Rule 1
If nEn1X∈ℛ < 2μ, do not split.
Rule 2
If nEn1X∈ℛ ≥2μ, compute r̂ = arg maxr {𝒫(ℛ, r) : min(nEn1X∈ℛ∩r, nEn1X∈ℛ∩rc)≥ μ}. If 𝒫(ℛ, r̂) ≥ 𝒫(ℛ) + λ, then split ℛ into ℛ ∩ r̂ and ℛ ∩ r̂c; otherwise do not split.
Here λ > 0 is a small positive constant representing a threshold for practical significance. Typically, μ and λ are dictated by problem-specific considerations and are not treated as tuning parameters. If the current data are representative of the whole subject population, i.e., if the data can be viewed as a random sample from the population from which future patients will be drawn, the splitting strategy outlined above ensures that the treatment recommended in a terminal node is the one maximizing the expected outcomes for subjects in the node. See the Supplementary Material for a more detailed description of the tree-growing algorithm.
2·6. Pruning
Each split in the tree-growing algorithm increases, or at least cannot decrease, the purity measure. Therefore, unless either λ or μ is large, the above splitting strategy will produce a large tree and potentially overfit the data. A standard strategy employed when building decision trees is to first construct a large tree and then prune the tree back by merging sibling nodes together, choosing which nodes to merge by using some global measure of performance; this is generally regarded as a superior strategy to building a smaller tree by stopping the splitting early (Breiman et al., 1984). We adopt the following simple pruning strategy, which is applied to each pair of siblings until no further merging is possible.
Strategy 1
For siblings ℛ ⋃r and ℛ ⋃rc with common parent ℛ, if 𝒫(ℛ, r) < 𝒫(ℛ) + η then merge; otherwise do not merge.
Here η > 0 is a tuning parameter which we choose by using a ten-fold crossvalidation estimator of the marginal mean outcome. In particular, let π̂η denote the estimated treatment rule using complexity parameter η, and let ĈCV(π̂η) be the crossvalidation estimator of Eπ̂η(Y). Define η̂ = arg maxη ĈCV(π̂η). Then the final decision rule is π̂η̂.
3. Experiments
3·1. Preliminaries
In this section we conduct a series of simulation experiments to examine the finite-sample performance of the minimum impurity decision assignments estimator. Here, performance is measured in terms of average marginal mean outcome obtained; that is, for an estimator π̂ of πopt, we compute E{Eπ̂(Y)}, where the outer expectation is taken with respect to the data used to estimate π̂. The average marginal mean outcome obtained was estimated using Monte Carlo methods with a large test set of size 10 000 for the inner expectation and 1000 training sets for the outer expectation. For discrete treatments we use a random forest (Breiman, 2001) to estimate m(x) = maxa Q(x, a) using the default settings of the R package randomForest; for continuous treatments we set m(x) to be identically zero.
To form a baseline for comparison, we also consider two regression-based estimators (Zhao et al., 2011; Schulte et al., 2014). Regression-based estimators first estimate Q(x, a) = E(Y | X = x, A = a) using a regression model, obtaining Q̂ (x, a), say, and then estimate the optimal decision rule as π̂ (X) = arg supa∈𝒜 Q̂ (x, a). In the discrete case we consider two estimators of Q(x, a): a parametric estimator that assumes a linear working model of the form QLM(x, a) = xTβ +Σ𝒜\{0} xTψa, which we estimate using least squares, and a nonparametric estimator that uses support vector regression with radial basis functions, which we denote by QSVR(x, a). The estimator QSVR uses as features x and all pairwise interactions between x and a; the method is tuned using five-fold crossvalidation with mean squared prediction error as the criterion. Diagnostic plots for the linear model using a draw of the data of size n = 250 in the p = 25 case are displayed in the Supplementary Material; these plots do not exhibit any major signs for concern, so an analyst might consider a linear decision rule to be adequate. In the continuous treatment case, regression-based estimators were constructed by first discretizing treatment into quartiles and then using the foregoing discrete treatment models.
3·2. Discrete treatments
We consider generative models in which treatments are binary and randomized to take the values±1with equal probability, the covariates X are uniformly distributed on the p-dimensional unit cube [0, 1]p for p = 10, 25 and 50, and Y = u(X) + Ac(X) + Z where Z is an independent standard normal variate and u and c are functions from [0, 1]p to ℝ. The three generative models that we consider all use , where kp and τp are chosen so that var{u(X)} = 5 and E{u(X)} = 10 − E{|c(X)|}. Thus, for all generative models the mean outcome under the optimal regime is E{m(X)} + E{|c(X)|} = 10. The forms of c we consider are:
| (4) |
| (5) |
| (6) |
Hence var{Ac(X)} = var{u(X)} = 5 in all settings. The optimal regime for (4) is to assign treatment a = 1 to all patients with x1 ≤ 0·6 and x2 ≤ 0·2, and assign treatment a = −1 otherwise. Thus, under the optimal treatment rule 48% of patients would receive treatment a = 1. Similarly, the optimal regime for (5) is to assign treatment a = 1 to all patients with x1 ≤ 0·3 and x2 ≥ 0·2, and assign treatment a = −1 otherwise. However, in contrast to (4), under the optimal treatment rule for (5) only 24% percent of patients would receive treatment a = 1. The optional regime for (6) assigns treatment a = 1 to all subjects with x1 + x2 > 1 and a = −1 otherwise. Thus, the optimal treatment regime for (6) assigns treatment a = 1 to 50% of the subjects. The optimal regimes for both (4) and (5) are representable as decision trees, whereas that for (6) is not. The performance of minimum impurity decision assignments on (4) and (5) demonstrates the method’s ability to correctly identify underlying tree structure when it is actually present, whereas the performance on (6) measures the impact of a simple model misspecification.
The average performance of minimum impurity decision assignments and of the two regression-based methods is summarized in Table 1; we have also included the performance obtained under πopt and a rule that guesses randomly. The reported values are based on 1000 Monte Carlo replications and a training set of size n = 250; simulations with larger sample sizes gave qualitatively similar results and are therefore omitted. The minimum impurity decision assignments estimator performs well across all settings, yielding the best performance for models (4) and (5), and it is competitive, despite being misspecified, in model (6). Most striking is that the performance of minimum impurity decision assignments remains stable as the number of noise variables increases; this could be due in part to the automatic variable-selection property of decision trees. In contrast, the performance of the regression-based methods deteriorates as p increases.
Table 1.
Marginal mean outcomes obtained from minimum impurity decision assignments, two regression-based methods, and random guessing. Data are generated from binary treatment examples with a sample size of n =250; reported values are based on 1000 Monte Carlo replications, using a test set of size 10 000
| Model | p | MIDAs | QLin | SVR | Random |
|---|---|---|---|---|---|
| (4) | 10 | 9·86 | 9·31 | 9·39 | 7·76 |
| (4) | 25 | 9·87 | 9·20 | 9·17 | 7·76 |
| (4) | 50 | 9·88 | 9·03 | 8·80 | 7·76 |
| (5) | 10 | 9·77 | 9·55 | 9·53 | 7·76 |
| (5) | 25 | 9·76 | 9·44 | 9·36 | 7·76 |
| (5) | 50 | 9·77 | 9·21 | 8·94 | 7·76 |
| (6) | 10 | 9·15 | 9·74 | 9·60 | 7·76 |
| (6) | 25 | 9·14 | 9·51 | 9·35 | 7·76 |
| (6) | 50 | 9·15 | 9·32 | 8·99 | 7·76 |
MIDAs, minimum impurity decision assignments; QLin, Q-learning with a linear model; SVR, Q-learning with support vector regression; Random, random guessing.
3·3. Continuous treatments
In the continuous treatment case, we consider generative models in which treatments are uniformly distributed on (0, 1), the covariates X are uniformly distributed on the p-dimensional unit cube [0, 1]p, and Y = u(X) + c(X, A) + Z, where Z is an independent standard normal variate and u(x) and c(x, a) are, respectively, functions from [0, 1]p and [0, 1]p × (0, 1) to ℝ. The three generative models that we consider use the same form for u(x) as in the discrete case, with constants τp and κp chosen so that var{u(X)} = 5 and E{u(X)} = 10 − E{supac(X, a)}. Let φ and Φ denote the density and cumulative distribution of a standard normal random variable, respectively. The three forms of c(x, a) we consider are:
| (7) |
| (8) |
| (9) |
Here (w)+ = max(0, w), and in each case the positive proportionality constant is chosen so that var{c(X, A)} = 5. The optimal regime for (7) treatment a = 0·25 when x1 ≥ 0·7, a = 0·5 when x1 < 0·7 and x2 > 0·5, and a = 0·75 otherwise. The optimal regime for (8) assigns treatment a = 0·20 if x1 > 0·5 and x3 > 0·5, a = 0·40 if x1 > 0·5 and x3 ≤ 0·5, a = 0·60 if x1 ≤ 0·5 and x2 > 0·25, and a = 0·80 otherwise. Thus, both (7) and (8) have an inherent tree structure. In contrast, the optimal regime for (9) is πopt(X) = (x1 + x2)/2 and so the tree-based decision rule is misspecified. We used the uniform kernel and the plug-in estimator (3) to choose the bandwidth for the minimum impurity decision assignment.
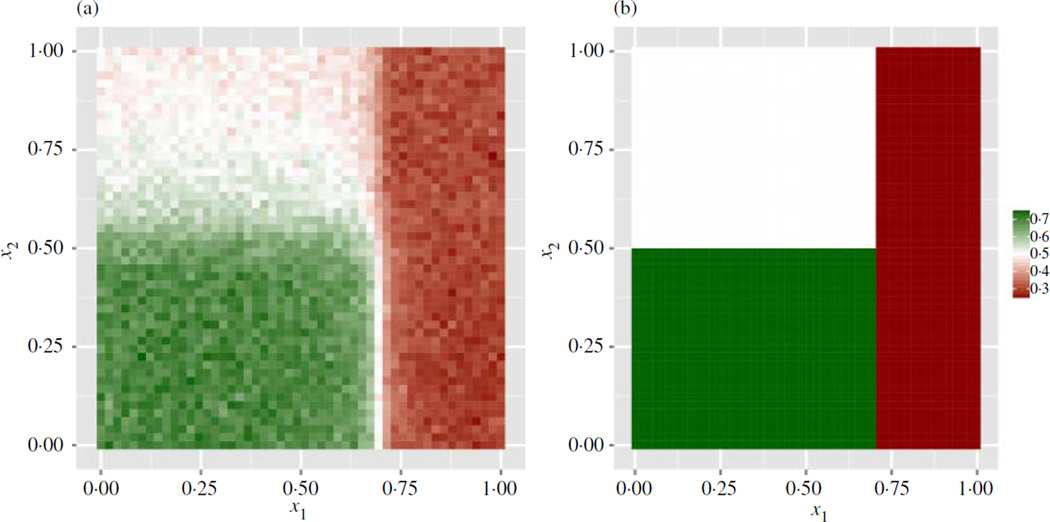
The average performances of minimum impurity decision assignment and the two regression-based methods are reported in Table 2. Minimum impurity decision assignment has the highest average performance of the methods compared. In addition, the estimator appears somewhat robust with respect to the addition of noise variables, as in the discrete treatment case. To give a sense of the rule estimated by minimum impurity decision assignment, Fig. 2 shows the average learned decision rules for (7) over 150 Monte Carlo replications as a function of the predictors x1 and x2 when p = 25 and n = 250. Corresponding figures for models (4)–(6), (8) and (9) are presented in the Supplementary Material, and show that the minimum impurity decision assignments estimator is roughly unbiased for the true underlying structure. The plug-in bandwidth estimator performed well despite violation of the assumptions used in its derivation. Additional simulations, omitted for brevity, indicated that the bandwidth σ̂ε/n1/5 performed equally well.
Table 2.
Marginal mean outcomes obtained from minimum impurity decision assignments, two regression-based methods, and random guessing. Data are generated from continuous treatment examples with a sample size of n =250; reported values are based on 1000 Monte Carlo replications, using a test set of size 10 000
Fig. 2.
Heatmaps of true and estimated optimal treatment rules: (a) average treatment assignment as a function of x1 and x2 over 25 learned decision rules for (7), with p = 25 and n = 250; (b) optimal treatment assignment as a function of x1 and x2 for (7); optimal treatment assignment for (7) depends exclusively on x1 and x2.
4. Nefazodone study
In this section we apply the minimum impurity decision assignments method to data from a randomized trial comparing the drug nefazodone with cognitive behavioural therapy as treatments for chronic depression (Keller et al., 2000). Patients were randomized to receive, with equal probability, nefazodone, cognitive behavioural therapy, or both nefazodone and cognitive behavioural therapy. Cognitive behavioural therapy requires as often as twice-weekly visits to a clinic, and thus imposes significant time and monetary burdens on patients relative to treatment with nefazodone alone. An important question is whether cognitive behavioural therapy is necessary for all patients in the population of interest, either alone or as an augmentation to nefazodone, or if there is a subgroup of patients for which cognitive behavioural therapy is unnecessary. We perform a complete case analysis.
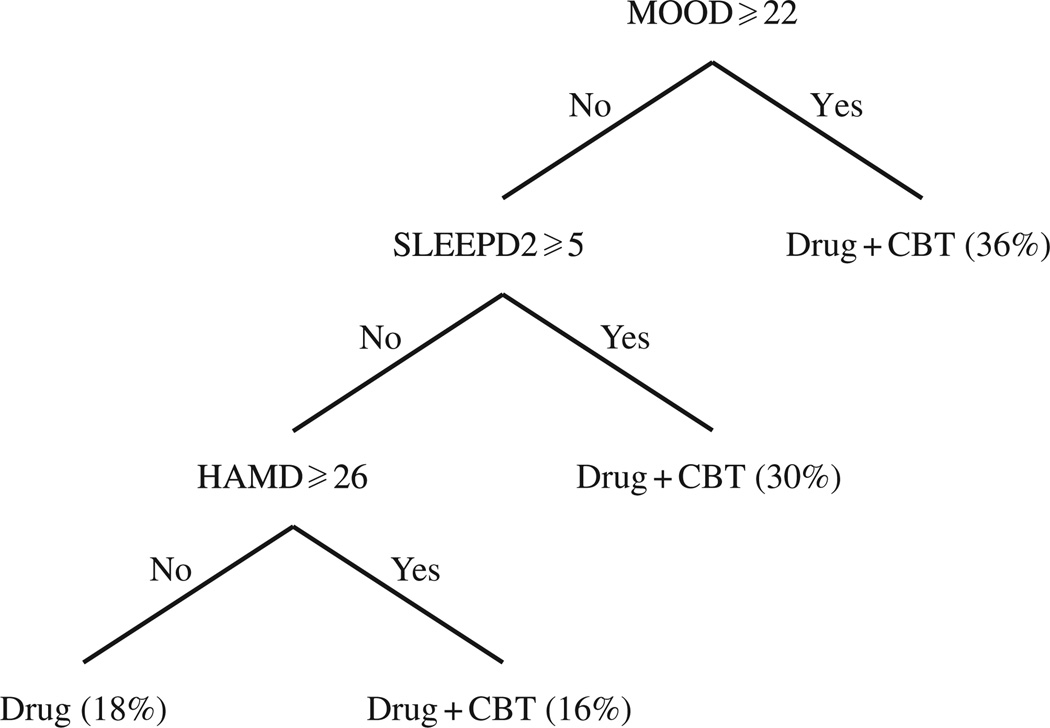
The data we use in this analysis comprise 215 subjects randomized to nefazodone, 212 randomized to cognitive behavioural therapy, and 220 randomized to both. The primary outcome of the study was a score measured on the Hamilton Rating Scale for Depression, which we use as our response. To match our development, which assumes that higher values are better, we subtract each score on the rating scale from 50. We consider 22 potential covariates for tailoring treatment; these are listed in the Supplementary Material. Figure 3 shows the decision rule estimated by minimum impurity decision assignment. The estimated decision rule assigns nefazodone and cognitive behavioural therapy to patients with a high mood disturbance, high sleep disturbance, or high baseline depression score. So the estimated decision rule recommends intensive treatment, i.e., nefazodone together with cognitive behavioural therapy, to patients presenting with more severe symptoms.
Fig. 3.
Learned decision rule for nafazodone study: patients with high mood disturbance (MOOD), poor sleep (SLEEPD2), or more severe depression symptoms (HAMD) are assigned nefazodone and cognitive behavioural therapy (Drug + CBT); others are assigned nefazodone only.
The marginal mean outcome of the learned decision rule, estimated using ten-fold crossvalidation, is 38·8, which turns out to be the marginal mean outcome of assigning all subjects to the more intensive nefazodone and cognitive behavioural therapy. A linear decision rule fit using ridge regression tuned with generalized crossvalidation assigns all subjects to combined nefazodone and cognitive behavioural therapy. Thus, the difference between the learned decision rule using minimum impurity decision assignments and assigning all patients to nefazodone and cognitive behavioural therapy is not significant. Hence, for reasons of cost and patient burden, one should prefer the rule learned by minimum impurity decision assignments, which assigns the drug alone to 18% of patients. Assigning all patients to nefazodone has an estimated marginal mean outcome of only 33·9, suggesting that the minimum impurity decision assignments estimator has effectively identified individuals in the population who are unlikely to benefit from augmenting nefazodone with cognitive behavioural therapy.
5. Discussion
Decision trees are a cornerstone of exploratory analysis and the canonical example of an interpretable predictive model. Trees are particularly suitable for treatment allocation rules because they are easily interpreted and vetted by intervention scientists. Furthermore, unlike other flexible decision rules (e.g., Zhao et al., 2009, 2012; Zhang et al., 2013), they do not require additional computation to determine a recommended treatment for a newly presenting patient; thus, they are easily deployed and disseminated.
An important extension of this work is the development of tree-based treatment rules for multi-stage treatment problems. There is growing interest in evidence-based sequential treatment rules for the treatment of chronic illness. It is increasingly appreciated that nonlinear models are required for sequential decision rules (Laber et al., 2014). One approach is to use flexible models based on machine learning techniques, but for the reasons mentioned above, this may lead to models which are not interpretable or easily disseminated. We believe that the direct search framework (Zhang et al., 2013) is an avenue by which our work can be extended to the multi-stage setting.
Supplementary Material
Acknowledgement
Eric Laber acknowledges support from the U.S. National Institutes of Health.
Footnotes
Supplementary material available at Biometrika online includes: a list of potential predictors for the case study in § 4; proofs of the technical results in § 2; a detailed description of the tree-growing algorithm, referenced in § 2; and computer code implementing the minimum impurity decision assignments algorithm.
Contributor Information
E. B. Laber, Email: laber@stat.ncsu.edu, Department of Statistics, North Carolina State University, 2311 Stinson Drive, Raleigh, North Carolina 27695, U.S.A..
Y. Q. Zhao, Email: yqzhao@biostat.wisc.edu, Department of Biostatistics and Medical Informatics, University of Wisconsin-Madison, Madison, Wisconsin 53792, U.S.A..
References
- Allegra CJ, Jessup JM, Somerfield MR, Hamilton SR, Hammond EH, Hayes DF, McAllister PK, Morton RF, Schilsky RL. American society of clinical oncology provisional clinical opinion: Testing for KRAS gene mutations in patients with metastatic colorectal carcinoma to predict response to anti-epidermal growth factor receptor monoclonal antibody therapy. J. Clin. Oncol. 2009;27:2091–2096. doi: 10.1200/JCO.2009.21.9170. [DOI] [PubMed] [Google Scholar]
- Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]
- Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Monterey, California: Wadsworth and Brooks; 1984. [Google Scholar]
- Brinkley J, Tsiatis A, Anstrom KJ. A generalized estimator of the attributable benefit of an optimal treatment regime. Biometrics. 2010;66:512–522. doi: 10.1111/j.1541-0420.2009.01282.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll RJ, Ruppert D. Transformation and Weighting in Regression. New York: Chapman and Hall; 1988. [Google Scholar]
- Craven MW, Shavlik JW. Adv. Neural Info. Proces. Syst. 9 (NIPS 1996) San Francisco: Morgan Kaufmann Publishers; 1996. Extracting tree-structured representations of trained networks; pp. 24–30. [Google Scholar]
- Cummings J, Emre M, Aarsland D, Tekin S, Dronamraju N, Lane R. Effects of rivastigmine in Alzheimer’s disease patients with and without hallucinations. J. Alzheimer’s Dis. 2010;20:301–311. doi: 10.3233/JAD-2010-1362. [DOI] [PubMed] [Google Scholar]
- Foster JC, Taylor JM, Ruberg SJ. Subgroup identification from randomized clinical trial data. Statist. Med. 2011;30:2867–2880. doi: 10.1002/sim.4322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamburg MA, Collins FS. The path to personalized medicine. New Engl. J. Med. 2010;363:301–304. doi: 10.1056/NEJMp1006304. [DOI] [PubMed] [Google Scholar]
- Hastie TJ, Tibshirani RJ, Friedman J. The Elements of Statistical Learning. 2nd ed. New York: Springer; 2009. [Google Scholar]
- Hayes DF, Thor AD, Dressler LG, Weaver D, Edgerton S, Cowan D, Broadwater G, Goldstein LJ, Martino S, Ingle JN, et al. HER2 and response to paclitaxel in node-positive breast cancer. New Engl. J. Med. 2007;357:1496–1506. doi: 10.1056/NEJMoa071167. [DOI] [PubMed] [Google Scholar]
- Keller MB, McCullough JP, Klein DN, Arnow B, Dunner DL, Gelenberg AJ, Markowitz JC, Nemeroff CB, Russell JM, Thase ME, et al. A comparison of nefazodone, the cognitive behavioral-analysis system of psychotherapy, and their combination for the treatment of chronic depression. New Engl. J. Med. 2000;342:1462–1470. doi: 10.1056/NEJM200005183422001. [DOI] [PubMed] [Google Scholar]
- Laber EB, Linn KA, Stefanski LA. Interactive model building for Q-learning. Biometrika. 2014;101:831–847. doi: 10.1093/biomet/asu043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipkovich I, Dmitrienko A, Denne J, Enas G. Subgroup identification based on differential effect search: A recursive partitioning method for establishing response to treatment in patient subpopulations. Statist. Med. 2011;30:2601–2621. doi: 10.1002/sim.4289. [DOI] [PubMed] [Google Scholar]
- Ludwig JA, Weinstein JN. Biomarkers in cancer staging, prognosis and treatment selection. Nature Rev. Cancer. 2005;5:845–856. doi: 10.1038/nrc1739. [DOI] [PubMed] [Google Scholar]
- Piquette-Miller M, Grant D. The art and science of personalized medicine. Clin. Pharmacol. Therap. 2007;81:311–315. doi: 10.1038/sj.clpt.6100130. [DOI] [PubMed] [Google Scholar]
- Qian M, Murphy SA. Performance guarantees for individualized treatment rules. Ann. Statist. 2011;39:1180–1210. doi: 10.1214/10-AOS864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2015. ISBN 3-900051-07-0. http://www.R-project.org. [Google Scholar]
- Rich B, Moodie EEM, Stephens DA, Platt RW. Simulating sequential multiple assignment randomized trials to generate optimal personalized warfarin dosing strategies. Clin. Trials. 2014;11:435–444. doi: 10.1177/1740774513517063. [DOI] [PubMed] [Google Scholar]
- Ripley BD. Pattern Recognition and Neural Networks. Cambridge: Cambridge University Press; 1996. [Google Scholar]
- Rubin D. Bayesian inference for causal effects: The role of randomization. Ann. Statist. 1978;6:34–58. [Google Scholar]
- Schulte PJ, Tsiatis AA, Laber EB, Davidian M. Q- and A-learning methods for estimating optimal dynamic treatment regimes. Statist. Sci. 2014;29:640–661. doi: 10.1214/13-STS450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su X, Zhou T, Yan X, Fan J, Yang S. Interaction trees with censored survival data. Int. J. Biostatist. 2008;4:1–26. doi: 10.2202/1557-4679.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su X, Tsai C-L, Wang H, Nickerson DM, Li B. Subgroup analysis via recursive partitioning. J. Mach. Learn. Res. 2009;10:141–158. [Google Scholar]
- Sutton CD. Classification and regression trees, bagging, and boosting. In: Rao CR, Wegman EJ, Solka JL, editors. Handbook of Statistics. Vol. 24. Amsterdam: Elsevier; 2005. pp. 303–329. [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Cambridge: Cambridge University Press; 1998. [Google Scholar]
- Zhang B, Tsiatis AA, Davidian M, Zhang M, Laber E. Estimating optimal treatment regimes from a classification perspective. Stat. 2012a;1:103–114. doi: 10.1002/sta.411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Tsiatis AA, Laber EB, Davidian M. A robust method for estimating optimal treatment regimes. Biometrics. 2012b;68:1010–1018. doi: 10.1111/j.1541-0420.2012.01763.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Tsiatis AA, Laber EB, Davidian M. Robust estimation of optimal dynamic treatment regimes for sequential treatment decisions. Biometrika. 2013;100:681–694. doi: 10.1093/biomet/ast014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Kosorok MR, Zeng D. Reinforcement learning design for cancer clinical trials. Statist. Med. 2009;28:3294–3315. doi: 10.1002/sim.3720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Zeng D, Socinski MA, Kosorok MR. Reinforcement learning strategies for clinical trials in nonsmall cell lung cancer. Biometrics. 2011;67:1422–1433. doi: 10.1111/j.1541-0420.2011.01572.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Zeng D, Rush AJ, Kosorok MR. Estimating individualized treatment rules using outcome weighted learning. J. Am. Statist. Assoc. 2012;107:1106–1118. doi: 10.1080/01621459.2012.695674. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.