Complex adaptive behavior and dexterous action

Abstract

Dexterous action, as conceptualized by Bernstein in his influential ecological analysis of human behavior, is revealed in the ability to flexibly generate behaviors that are adaptively tailored to the demands of the context in which they are embedded. Conceived as complex adaptive behavior, dexterity depends upon the qualities of robustness and degeneracy, and is supported by the functional complexity of the agent-environment system. Using Bernstein’s and Gibson’s ecological analyses of behavior situated in natural environments as conceptual touchstones, we consider the hypothesis that complex adaptive behavior capitalizes upon general principles of self-organization. Here, we outline a perspective in which the complex interactivity of nervous-system, body, and environment is revealed as an essential resource for adaptive behavior. From this perspective, we consider the implications for interpreting the functionality and dysfunctionality of human behavior. This paper demonstrates that, optimal variability, the topic of this special issue, is a logical consequence of interpreting the functionality of human behavior as complex adaptive behavior.

Complex Adaptive Behavior

The adaptive functioning of biological systems has been taken to depend upon the presence of particular general qualities. Qualities of robustness, degeneracy, and complexity have been observed in systems ranging from cells to societies and have been taken to underlie these systems adapted functionality (Edelman & Gally, 2001; Levin, 2003; Whitacre, 2010).

Robustness, degeneracy, and complexity are interrelated qualities. Robustness identifies a special case of the term stability. A system is taken to be robust to the extent that its functioning can be reliably preserved across changes in context (i.e. variation in both internal and external conditions). To berobust, a system must have the potential for redundant means of realizing a given function. In the case of designed systems, functional redundancy is typically realized through the duplication of elements with each possessing fixed functional roles. If one part fails, its role can be taken up by an identical part that is identically situated. For complex biological systems, including human behavior, the topic of this paper, robustness is often realized by multifunctional (degenerate) parts with each part possessing the capacity to assume context sensitive roles. In such systems, a given system function can be realized by different parts and the same part can realize distinct functions. Complex biological systems have been taken to be degenerate at all levels of system functioning (Kelso, 2012). Analysis of the structure of interconnectivity in simulated biological networks reveals that the occurrence of robustness and degeneracy as network properties depends upon the functional form of interconnectivity (i.e. compositional complexity) in the network (Edelman & Gally, 2001; Tononi, Sporns, & Edelman, 1999; Whitacre & Bender, 2010). In this research, optimally complex systems supporting degeneracy are found to possess components that optimally balance competing tendencies to be both functionally integrated (i.e. the tendency to be coordinated with other parts) and functionally segregated (i.e. the tendency to possess a coherence of function that is unaffected by other parts).

In this paper we consider the case for conceiving the situated functionality of human actions as complex adaptive behavior. Here, complex adaptive behavior is introduced as a term to capture the adaptive (in the evolutionary sense of the word) capacity for behavior to be variably and reliably adapted (in the sense of behavioral flexibility) to the context within which it is embedded. Thus, complex adaptive behavior is introduced as a theoretically and empirically grounded perspective on the functionality of human behavior. It identifies a basis for attempting to understand the capacity for intentional agents to robustly attain intended ends (i.e. goals) by degenerate means. The characterization of complex adaptive behavior presented here provides a starting point for attempts to interpret the “functionality” of human actions and for understanding both pathological and non-pathological behavior.

Qualities of robustness, degeneracy, and complexity as they relate to everyday human actions are revealed in ecological analyses of perceiving and acting in natural contexts (Bernstein, 1967; 1996; Gibson, 1979). Moreover, an appreciation of these qualities can be seen to have motivated the application of systems approaches, dynamical systems theory, and complexity science to the study of human behavior. In what follows, we attempt to trace this path, with the aim of gaining an appreciation of and elementary theory of complex adaptive behavior.

The challenge of dexterity

Bernstein’s (1967; 1984; 1996) ecological analysis of human activity reveals a capacity to act that is adapted to both the requirements of the intended behavior and to the ever changing demands of the context in which that act is situated. Appreciation of Bernstein’s analysis reveals a capacity that easily ranks among the most sophisticated of human achievements, a capacity that Bernstein identified with the term dexterity. Dexterity, by contrast to the commonly used descriptor of human activity “movement”, is an ecological concept. It incorporates in its definition the context sensitivity inherent to the organization of intentional actions. It refers to the capacity to preserve task-specific relations between the actor and environment across variations in environmental context (Turvey, 2007; Reed & Bril, 1996). In consequence, dexterity is not a property of movement per se. Rather, dexterity is found in the ability of an actor to flexibly generate motor solutions that are adapted to the emerging demands of any situation.

The demand for a theory of dexterity is rooted in an appreciation of the non-trivial context sensitivity inherent to the organization of even the simplest of motor acts. Bernstein (1967) recognized that the innervation of movement by the nervous system must invariably be reconciled with the ever changing anatomical, physiological, and mechanical context in which that movement occurs. Across subtle changes in bodily postures and in mechanical context, the same muscle, when similarly innervated, can produce distinct motor outcomes. Conversely, different muscles in different contexts can produce the same motor outcomes (Turvey, Fitch & Tuller, 1982; Higgins, 1985). In situ, a single muscle can be found to assume different functions at different times within a single movement. Dependent upon context, a muscle can be seen to perform as a motor, brake, strut, tuner, meter, and spring (Dickinson et al., 2000). Moreover, muscles conventionally taken to be part of the same anatomical group can assume distinct context specific mechanical functions (Ahn & Full, 2002). Such findings reveal context specific functioning of muscles in the service of an intended action. More generally they speak to the multifunctional degenerate nature of the neuro-biomechanical components comprising the human action system.

Bernstein (1996, p. 215) characterized dexterity as the “ability to create a perfect key for any emerging lock”. Motivating this metaphor is recognition of the intractable context conditioned variability of situated behavior, and a logical consequence of context conditioned variability, that absolute repetition of a movement pattern is not possible in a natural environment. For Bernstein (1984) skilled actions are necessarily morphological (i.e. dynamically evolving) objects. Repeated practice of a behavior, rather than constituting the repeating of a remembered stereotyped solution, is taken to constitute a process of repeatedly solving a constantly evolving motor problem with techniques that are changed and perfected from repetition to repetition over variations in context. To anticipate our discussion of the dynamical systems perspective, for Bernstein (1996), emergent solutions to motor problems possess intrinsic dynamics properties. These dynamics increase the chance of a solution being repeated. From context conditioned variability it follows that the variability of performance observed in the analysis of motor behavior reflects both the fact that internal and external conditions never exactly repeat themselves and the fact that the dexterous actor is forever attempting to adapt to the exigencies of those conditions (Nonaka & Bril, 2014; Stergiou & Decker, 2011).

In attempting to characterize the requisite organization supporting dexterity, Bernstein (1996) identified four hierarchically structured levels, the basement level of tone, the level of muscular-articular links (or synergies), the level of space, and the level of action. For Bernstein (1996) a dexterous act is flexibly comprised of, at minimum, two functionally defined levels of organization; a leading level that embodies features of switch ability, resourcefulness, and maneuverability of behavior, and a background level that embodies features of harmony, obedience and precision of work in behavior. These leading and background levels constitute distinct functional roles to be taken on by the levels of tone, synergies, space, and action. The distinction between leading and background levels is employed by Bernstein in an attempt to capture the essential functional qualities of dexterity. The distinction between leading and background levels we take here to be synonymous with the adaptability/flexibility of behavior on the one hand, and with the robustness/stability of behavior on the other. Following Bernstein, and consistent with attempts to understand the evolved functionality of biological systems through the concepts of robustness, degeneracy, and complexity, we take these dual characteristics of dexterous activity to be requisite qualities of any account of complex adaptive behavior.

The challenge of distilling functional simplicity from compositional complexity

Part and parcel of the challenge of accounting for the functional organization that might support dexterity of action is the degrees of freedom problem (Bernstein, 1967). Broadly construed, the degrees of freedom problem concerns how the many component parts of the action system (e.g. cells, motor units, muscles, joints) can become harnessed so as to produce harmoniously coordinated behavior. Restated, with respect to the challenge of dexterity, how can context-adapted (i.e. functional) simplicity be distilled from compositional complexity (Turvey, 1988). For Bernstein, it is the level of muscular-articular links (or synergies) that plays a key role in imposing degrees of constraint to organize the many degrees of freedom of the motor apparatus. The challenge faced by this level of functional organization is to bring the muscles of the body into task and context appropriate relations (Gelfand et al., 1971; Fitch, Tuller, & Turvey, 1982).

The possibility of coherent relations being formed between muscles in the performance of motor behaviors has been investigated through the application of multidimensional factorization methods to the analysis of the patterns of activation across multiple muscles (Cappellini et al. 2006; d’Avella et al. 2006; d’Avella et al. 2003;Ting & Macpherson 2005; Torres-Oviedo, Macpherson, & Ting, 2006; Tresch, Cheung, & d'Avella, 2006). Consistent with Bernstein’s hypothesis, these studies reveal invariant patterns of interrelation between subsets of muscles (i.e. synergies). The observed recruitment of subsets of muscles into synergies appears to follow functional principles with observed patterns often reflecting sensible biomechanical decompositions of the overall muscle complex (Berniker et al., 2009; Hof, 2007). The observation of the same synergies being employed in multiple tasks has led to the claim that varied behaviors might be explained in terms of task-specific compositions of finite sets of muscle synergies (d’Avella, Saltiel, & Bizzi, 2003; Ivanenko, Poppele, & Lacquaniti, 2004). Of note, the observed synergies vary in the degree to which they are reliably observed across tasks (i.e. the degree to which their form is context independent). Although some “task invariant” synergies are observed across tasks, other “task specific” synergies are also observed (d’Avella & Bizzi, 2005). Such differences are informative of the functional character of particular muscles and their intrinsic tendencies to assume particular functional roles (Turvey, 2007). Recent evidence suggests that motor expertise is associated with a greater degree of sharing (i.e. degeneracy) of motor synergies across related tasks (Sawers & Ting, 2014).

Evidence of task-specific assemblages of degrees of freedom can also be drawn from perturbation studies (Cole & Abbs, 1987; Kelso et al., 1984; Marsden, Merton, & Morton, 1983). Perturbing one degree of freedom during a functional movement is found to result in fast compensatory adjustments among many other degrees of freedom. The observed adjustments are functionally differentiated with some parts of the responses being far removed in both space and time from the point of perturbation (Bernstein, 1967; Turvey, 1990; Turvey, 2007). To anticipate later discussion, such remote adjustments bear conceptual similarity to evidence of long range correlations in the organization of human behavior.

Consistent with the expectation of muscles becoming assembled into task and context appropriate relations, patterns of neuro-muscular torques for practiced behaviors are tuned to the biomechanical context in which they are situated with muscle action working to compliment the field of forces provided by the environment as well as the motion dependent torques of the limbs (Fowler & Turvey, 1978; Zernicke & Schneider, 1993). Analysis of motor performance that separately quantifies task-invariant fluctuations (i.e. those fluctuations in motor organization that do not affect task performance) and task-varying fluctuations (i.e. those fluctuations that are detrimental to task performance) reveals behavior to be organized in way that minimizes task-varying fluctuations and leaves relatively unconstrained task-invariant fluctuations (Cusumano & Cesari, 2006; Latash, Scholz, & Schöner, 2002; Müller & Sternad, 2009; Scholz, Schöner, Latash, 2000). These analyses reveal a system organized such that 1) variation in degrees of freedom that affect task performance are constrained, 2) variation in degrees of freedom that do not affect task performance are unconstrained, and 3) co-variation between task relevant degrees of freedom that do not impact task performance is permitted. The last of these qualities speaks to a system that is not only task constrained, but one that is also degenerate in that it retains the capacity to flexibly organize and reorganize its component parts in a variety of ways so as to preserve task performance. The functional utility of the implied degeneracy is supported by observations that greater degrees of task-invariant fluctuations benefit dual-tasking performance (Zhang et al. 2008) and reactions to unexpected perturbations (Gorniak, Fledman, & Latash, 2009; Mattos et al. 2011). Moreover, older adults performing postural control and gait tasks, show lessened task-invariant fluctuations and exaggerated task-varying fluctuations when compared to younger adults (Decker et al., 2012; Hsu et al., 2014).

In sum, dexterous behavior is both robust, in the sense that intended ends are reliably achieved across changing circumstance, and degenerate, in the sense of those ends are achieved by varied context appropriate means. The challenge to be met is that of accounting for a system 1) whose many degrees of freedom are constrained to act as a context conditioned functional unit, and 2) whose functionality is preserved across contexts through adaptive co-adjustments of its composing degrees of freedom.

The challenge of coupling activity to situation

If dexterity of action is revealed in the capacity to generate context appropriate actions, then an account of dexterity requires a theory of information that can couple the potential for adapted action to the demands of a situation. For Gibson (1966; 1979), the evolved function of perceptual systems is the detection of information that functionally couples actor to situation. In his systematic ecological analysis of the visual perceptual system (Gibson, 1950; 1966; 1979), Gibson uncovered information contained within the nested dynamic structure of the optic array that held the potential to functionally couple an actor to the opportunities for useful or meaningful action offered by the surrounding environment.

Investigations of Gibson’s ecological theory have since uncovered information in the form of invariant structure and invariant patterns of change in the optic array that 1) specifies the possibilities for action (i.e. affordances) offered by the surrounding environment (Chemero, 2000; Fajen, 2007; Gibson et al., 1987; Kinsella-Shaw, Shaw, & Turvey, 1992; Mark, 1987; Warren, 1984; Warren & Whang, 1987) and 2) adaptively and dynamically couples actor to situation on a moment by moment basis (Lee, 1976; 2009; Rushton, Harris, & Wann, 1999; Warren, 1988; Warren, 2006).

Gibson’s theory of ecological information is a systems theory. The informational variables functionally coupling actor to situation are defined at the level of the actor-environment system. The case of catching a fly ball provides an elegant simple example of this approach (Chapman, 1968; McBeath, Shaffer, & Kaiser, 1995; Zaal & Michaels, 2003). In the simplest variant of the task modelled by Chapman (1968), catching a fly ball is shown to require that the actor couple movement to the optical variable d² tan(θ) / dt², where θ is the elevation angle subtended by the ball and the horizon. To catch the ball the actor can simply modulate running speed until d² tan(θ) / dt² is equal to zero. In other words, if you run so as to cancel out the optical acceleration of the ball, you will intercept it. Paralleling the context specific functional assemblages of muscles evidenced in the organization of the human action system, the information coupling actor to environment in catching fly balls represents a context specific solution. Analysis of the task of rhythmically bouncing a ball on a racquet provides another example of a context specific solution with emergent functional properties (Wei & Sternad, 2008). Performers of this task discover a simple adaptive solution. If the racquet’s trajectory is visually coupled to the trajectory of the ball such that it is decelerating around the moment before contacting the ball, then the ball-racquet system is found to act to passively damp out small perturbations introduced to the system. Thus a system is formed that possesses the emergent property of an intrinsic self-stabilizing dynamics. Notably, these “smart” solutions are predicated upon the specific constraints of the task and have emergent functional properties (Runeson, 1977).

The cases of fly ball catching and ball bouncing provide simple examples of a task-dynamic modelling strategy. The task-dynamic approach has been applied broadly in attempts to understand the emergence of form and functionality in varied human behaviors (Saltzman & Kelso, 1987; Schöner, 1990; Eiler et al., 2013; Warren, 2006), as well as in attempts to implement such situated functionality in artificial systems (Beer, 2014). This strategy takes as its starting point the ecological assumption that the form and functionality of adaptive behavior does not in here in the organization of the actor or the environment. Rather, adaptive functionality is taken to reside in co-acting constraints supplied by the actor, the environment, and the task. This confluence of constraints is assumed to scaffold an emergent task dynamics (Kugler & Turvey, 1987; Warren, 2006).

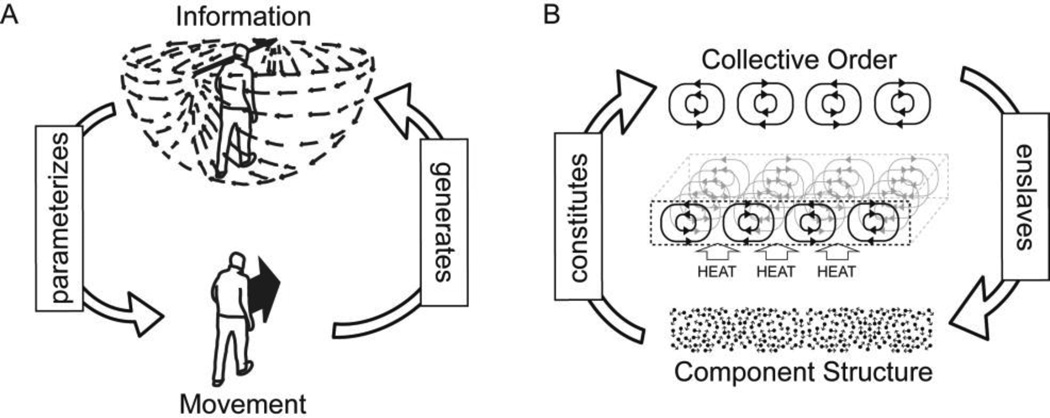
In task-dynamic models perception and action are functionally codependent (Kugler & Turvey, 1987; Shaw & Turvey, 1981; Turvey, 1977; Turvey, 2004). This codependence is simply exampled in the perception-action dynamics of visually guided locomotion (figure 1A). In visually guided locomotion, the coordinated actions of the limbs generate movement. Movement, in turn, generates motion specific information in the form of invariant styles of transformation of the optic array (Gibson, 1979; Koenderink, 1986) and, in turn, motion specific information is used to parameterize dynamics of coordinated action (Fajen, 2007; Finley, Statton, & Bastian, 2014). While the interactivity evidenced in this minimal example appears simple, the theoretical implications are non-trivial. The interdependence of perception and action within task dynamic models introduces degrees of constraint that support the adaptive coupling of activity to situation. The form of causation implied by task dynamic models takes the form of a perceiving-acting cycle in which the micro level of motor coordination and the macro scale of emergent ecological information are co-constraining (Kugler & Turvey, 1987).

Figure 1.

Macro-micro interdependencies evidenced in A) the perception-action dynamics of visually guided locomotion, and B) the self-organized patterns of fluid motion observed when a layer of viscous fluid is heated from below.

Interdependencies of perception and action are especially evident in the case of the haptic perceptual subsystem of dynamic touch. Dynamic touch (a.k.a. active touch, kinesthesis, muscle based perception) identifies a subsystem of the haptic perceptual system in which information about the body’s relation to itself (proprioception) and the body’s relation to the environment (exproprioception) is conveyed in patterns of tissue deformation detected by mechanoreceptors embedded in those tissues (Carello & Turvey, 2004; Solomon, 1988). Patterns of deformation over the tissues of the body (i.e. muscles, tendon, and fascia) have recently been taken to define a tension array comparable in function to the optic array (Turvey & Fonseca, 2014). This capacity, for the tissues of the body to form a tension array that provides a medium for informationally coupling actor to situation, is predicated upon the degrees of constraint arising from the compositional complexity of the action system. These include the morphology of the body conceived as a nested tensegrity structure (Turvey & Fonseca, 2014), the dynamics constraining the relationship between muscle forces and bodily motion (Carello & Turvey, 2004; Harrison et al., 2011), the invariant structure (i.e. spatiotemporal symmetry) of muscle activation patterns characterizing coordinated movements (Turvey et al., 2009), and the task-specific (functional) organization characterizing flexibly assembled action (Harrison, Kuznetsov, & Breheim, 2013).

Paralleling the nested structure of the optic array (Gibson, 1979; Heft, 1996), the tension array is spatially and temporally nested, supporting nested levels of functional coupling of actor to situation. At each scale invariant structure and invariant patterns of change in the tension array are dependent upon scale specific constraints. At the micro scale of segment-segment relations, information about the layout of the body and changes in the layout of the body are constrained by the invariants of the physical dynamics that relate forces to movements (Harrison et al., 2011; Pagano & Turvey, 1995; Silva & Turvey, 2012). At the mesoscale of coordinated action, information about the coordinated act is constrained by the spatiotemporal symmetries (invariant structure) of the coordination (Harrison, Kuznetsov, & Breheim, 2013; Turvey et al., 2009; Turvey et al., 2012). Lastly, at the macro scale of agent embedded in extended environment, information about the layout of environmental surfaces surrounding the actor is constrained by the invariant structure of mechanical encounters between actor and environment (Harrison & Turvey, 2010). At each scale, information-about is conveyed in in variances defined with respect to time extended transformations and the detection of information-about requires exploratory actions that subsume such transformations (Harrison et al., 2011). At each of these nested scales of functional embedding, the emergence of functional information coupling activity to situation is supported by scale specific constraints.

Gibson’s analysis suggests that dexterity of perception must necessarily accompany dexterity of action. If dexterity of action is the ability to refine motor solutions adapted to situations, then dexterity of perception is its dual and captures the ability to differentiate information (c.f. Gibson & Gibson, 1955) that supports the creative exploitation of resources for activity offered by the environment (Higgins, 1991; Reed, 1982; 1996).

Self-organization

Bernstein’s and Gibson’s ecological analyses implicate an organization of adaptive behavior that takes the form of context conditioned special purpose assemblages (Turvey et al., 1978; Shaw & Turvey, 1981). Given this theoretical starting point, the challenge for a theory of adaptive behavior is to understand how such functional assemblages might be formed. In his ecological theory, Gibson (1979), sought an accounting that would allow adaptive behavior to be “regular without being regulated” (p. 225). This has since been interpreted to mean that adaptive behavior might be understood to be self-organized in as far as it capitalizes upon the emergent regularities of the entire actor-environment system (Warren, 2006; Richardson et al., in press).

Taken as a fundamental mechanism of pattern formation, self-organization occurs when a system, with many mutually interacting degrees of freedom that is open to exchanges of energy, matter, and information with its surroundings spontaneously organizes its internal structure and its dynamics (Haken, 1983; Iberall, 1972; Prigogine & Nicolis, 1971). For Haken (1980; 1983a; 1983b; 1984), principles of self-organization can be found to apply generally across physical, chemical, and biological systems. It is from this perspective of Haken’s theory of Synergetics that we initially begin to consider the possibility that complex adaptive behavior might be underwritten by general principles of self-organization. The simplest and most general form of self-organization is the non-equilibrium phase transition. The non-equilibrium phase transition is paradigmatically exampled in Bénard convection instability (Bénard, 1901). Bénard convection instability concerns the phenomenon of complex patterns of fluid motion (e.g. a honeycomb pattern of tessellated convection rolls) spontaneously emerging when a shallow layer of viscous fluid contained in a dish is heated from below and cooled from above (figure 1B). For Haken (1983a), the emergence of order in the non-equilibrium phase transition requires the existence of both a potential and a set of relevant constraints. In the case of Bénard convection, the potential is the temperature gradient formed across the upper and lower surfaces of the fluid and the set of relevant constraints includes the balance of physical forces that determine fluid motion. Given a temperature gradient in this system, the fluid in the lower layers expands and becomes lighter and an elevating (i.e. Archimedes principle) force is generated in that region of the fluid. When the temperature gradient is relatively small, the tendency for vertical movement of the fluid is suppressed by the counteracting forces of fluid viscosity (i.e. friction in the fluid) and gravity. If the temperature gradient is increased, a critical point can be reached when the balance of forces is tipped and a macroscopic motion starts in the fluid. Heated parts of the lower layers of the fluid move up and they are replaced by cooler parts of the fluid from the surface which, in turn, begin to be heated, thus establishing a cycle. According to Haken’s (1983a) slaving principle the movement of the fluid at this critical point establishes, or more precisely selects, a macroscopic collective dynamic (i.e. the convection rolls) to which the states of the microscopic components in the system (i.e. molecules) become enslaved. The relatively faster time scale dynamics of the components become drawn into ordered relation by the larger amplitude, relatively slower timescale dynamics, of the collective dynamics.

The emergence of ordered fluid motion in any form in the Bénard convection instability is underwritten by principles of energy dissipation. For low temperature gradients, the fluid is motionless and energy is dissipated by conduction. Past the critical temperature gradient, fluid moves across the gradient and energy is dissipated by convection. The emergence of ordered behavior depends upon the particular balance of constraints in the system. These principally include the balance of temperature gradient, viscosity, gravity, and depth of the fluid layer. The relation of these constraints is mathematically captured by the Rayleigh number, such that as the Rayleigh number increases, a number of patterns is consecutively observed, including horizontal rolls, vertical rolls, and turbulence¹. The specific form, size, shape, and, arrangement of convection rolls that emerges in this system depends upon the constraints captured by the Rayleigh number, together with environmental constraints such as the size and shape of the dish in which the experiment is performed (Koschmieder, 1993).

Self-organization in dissipative (i.e. far from thermal equilibrium) systems has motivated a dynamical systems approach to understanding the emergent form of coordinated human and animal behavior (Beek & Beek, 1988; Haken et al., 1985; Kelso, 1995; Kugler et al., 1980; Kugler & Turvey, 1987; Schöner, Haken, & Kelso, 1986; Schöner & Dineva, 2007; Turvey, 1990, Richardson et al, in press; Van Der Berg, 2000; Warren, 2006). With respect to the challenge of distilling functional simplicity from compositional complexity, this approach suggests two principles: 1) the emergent form of adaptive behavior is conditioned by the confluence of physical, informational, and task constraints; and 2) the emergent functionality of behavior is embodied in the system dynamics arising from the interactions between system components (i.e. the systems compositional complexity).

Constraints as context conditioners

From a dynamical systems perspective, the emergent form of adaptive behavior is hypothesized to depend upon the confluence of constraints provided by organism, environment, and task (Beer, 2014; Newell, 1998; Schöner, Dose, & Engels, 1995, Warren, 2006). The dynamical systems approach to motor behavior is paradigmatically exampled in Thelen’s (Thelen, Fisher, & Ridley-Johnson, 1984; Thelen and Smith, 1994) accounting of an initially puzzling phenomenon in the field of infant development. In an infant’s first year, coordinated stepping behavior is seen to appear, disappear, and then reappear again. Thelen elegantly demonstrated that developmental changes in the balance of two fundamental constraints, specifically, the strength the infants legs (the magnitude of the available onboard potential) relative to the weight of the legs (a task relevant constraint), could account for the phenomenon. The idea that basic system constraints shape the emergent form and function of behavior is similarly evidenced in the instilled functionality of simple robotic walking and running devices (Collins et al., 2005; Full, Farley, & Winters, 2000; Kuo, 2007). These devices embody the biomechanical constraints present in relations between bones, muscles, and connective tissues in the human body. Such constraints allow limbs to move some ways but not others. Paralleling the emergent functionality of ball bouncing, the coordinated stable gait patterns observed in these simple devices remain stable in the face of small perturbations, and they do so without requiring active control (Blickhan et al., 2007; McGeer, 1990). Generalizations of the principles of constraint in such devices have been used to produce unified perspectives on the emergent form of legged locomotion for animals differing numbers of legs, body masses, locomoting speeds, and movement over terrains of varied compliances (Full, Farley, & Winters, 2000; Golubitsky et al., 1999).

These results, taken together with insights from task dynamic models of behavior (Beer, 2014; Warren, 2006), suggest that, in a given embedded context, a particular mesh of physical and informational constraints is promoted and can be harnessed so as to reduce degrees of freedom to favor behavior that is context appropriate (van Orden, Kloos, & Wallot, 2009).

Interactivity of nervous-system, body, and environment

Much recent work has been devoted toward an understanding the compositional complexity of the actor-environment system and the role of such complexity in supporting adaptive behavior. Recent analyses have considered the in situ functionality of brain (Bassett & Gassiniga, 2011; Kelso, 2012), spinal cord (Loeb, 2001), and the myofascial-skeletal complex constituting the body (Turvey & Fonseca, 2014). Such analyses motivate perspectives on the challenges of dexterity and the challenges of distilling simplicity from complexity from which adaptive behavior is hypothesized to be consequent of, as opposed to in spite of, the compositional complexity of the agent-environment system. They suggest that the functional organization that supports dexterity of behavior is consequent of, as opposed to in spite of, interdependencies that span nervous-system, body, and environment (Cheil & Beer, 1999).

Specific examples of non-trivial interdependencies can be found across all levels of organization of the agent-environment system. For example, across the levels of nervous-system and body, the emergent stable form of coordinated limb oscillations has been shown to depend upon the co-acting constraints of the neural and physical dynamics (Hatsopoulos, 1996; Hatsopoulos & Warren, 1996). Similarly, the neural dynamics carried over the circuitry of neural “pattern generators” have been repeatedly shown to only find appropriate functional expression in situ within their embedded neurochemical (Selverston, 1988) and biomechanical context (Beer, Chiel, & Gallagher, 1999) and situated with respect to the body by way of proprioceptive feedback from the periphery (Pearson, 1987; Rossignol et al., 2007). Across the levels of body and environment, it can again be shown that movement only finds adaptive expression with respect to the field of forces offered by, and generated in interaction with, the environment. This point is clearly evidenced in the coordinated swimming motions of lampreys whose coordinated undulations are specifically tailored to, and therefore dependent upon, the field of forces generated by the emergent hydrodynamics of the surrounding fluids (Williams et al., 1995). In each case, appreciation of the role of system component is seemingly only expressible in context.

Interactivity and emergent behavioral form

The potential for interdependencies among interconnected system components to underwrite the emergent functional form of coordinated behavior was identified by von Holst (1934; 1973) in his investigations of animal locomotion. In his experiments on the multi-limb coordination of centipedes, von Holst observed that selective amputation of legs, leaving the centipede with only four or six limbs, spontaneously transformed the travelling wave pattern of inter-limb coordination, typical to the intact animal, into the inter-limb coordination patterns typical of hexapods and quadrupeds. Thus, by changing the number of limbs, von Holst observed the emergence of coordination patterns suited to the new capabilities of the animal. The spontaneous emergence of stable quadrupedal coordination patterns is also observed when two people, walking one behind the other, are mechanically coupled to each other, chest-to-back, through a large foam block (Harrison & Richardson, 2009). Coupled solely through the foam block, stable quadrupedal pace, trot, and diagonal-walk patterns spontaneously and unintentionally form with the pace pattern being the gait pattern most typically observed. When the potential for visual coupling between the two people is permitted, such that the person walking at the back can see the rhythmically oscillating shoulder movements of the person in front of them, the emergent form of coordination is affected and a trot pattern replaces the pace pattern as the most typically observed pattern. In each of these experiments, absolute (i.e. phase and frequency locked) coordination patterns are observed with the emergent stable form of coordination dependent upon the details of the physical, informational, and neural couplings between the participating effectors.

In sharp contrast to his observations of absolute coordination in centipede locomotion, von Holst’s experimental studies of coordination between dorsal and pectoral fins in lipfish revealed instances of relative coordination in which the two fins were found to visit all possible relative phase relations. von Holst observed that this state of relative coordination did not represent an absence of coordination, rather, the two fins were found to exhibit an attraction to some phase relations more than others, demonstrating intermittent periods of absolute coordination at particular phase modes, interspersed with periods of phase wandering.

For von Holst, the form and stability of the patterns he observed across his many experiments could be explained by the balance of two underlying general processes captured by the concepts of maintenance tendency and magnet effect. The maintenance tendency concerns the intrinsic dynamics of a system component, or, in the case of oscillating fins or legs, the tendency for a particular effector to act at its own preferred frequency. In contrast, the magnet effect concerns the tendency of system components to become entrained to the dynamics of other system components, or, in the case of oscillating fins or legs, the tendency of a particular effector to force its own preferred frequency upon other effectors. By recourse to a particular interaction of these two tendencies, von Holst was able to interpret the many patterns of coordination observed across his studies of animal locomotion. When competition between the two effectors was low (i.e. the maintenance tendencies of the involved effectors were similar) and cooperation between the effectors was high (i.e. the magnet effect was strong), absolute (phase locked) coordination resulted. When competition was high relative to cooperation (i.e. the maintenance tendencies of effectors differ markedly and the magnet effect was weak), relative coordination resulted.

Interactivity and self-organized stability and flexibility

Motivated by Haken’s (1983a) provocative claim that principles of self-organization apply generally across physical, chemical, and biological systems and by von Holst’s observations of general principles underlying coordinated rhythmic behaviors, Haken, Kelso, & Bunz (1985) tested the hypothesis that the qualities of stability and flexibility observed in coordinated behaviors are self-organized. More specifically they set out to demonstrate that the stability and flexibility of simple coordinated actions can be shown to be emergent properties of a self-organized collective dynamics arising from the component level dynamics of non-linearly coupled biological oscillators. Considering the minimally sufficiently complex case, Haken et al., (1985) modelled the component level dynamics of a system of two non-linearly coupled self-sustaining oscillators (figure 2A). They also modeled the collective level dynamics of this system and demonstrated a formal relationship between the two levels of description, showing that the equations of motion for the collective dynamics could be derived from the underlying component level dynamics. The significance of non-linear coupling at the component level is that it gives rise to multi-functionality at the collective level (figure 2B), that is, it allows for the possibility of multiple modes of collective behavior co-existing in the systems collective dynamics (Kelso, 2012). Following the observations of von Holst, the collective dynamics in this model depend upon parameters that determine the balance of tendencies for competition and cooperation between the coupled oscillators. These tendencies are interpretable as general constraints on the system dynamics, comparable to the physical principles constraining pattern formation in Bénard convection.

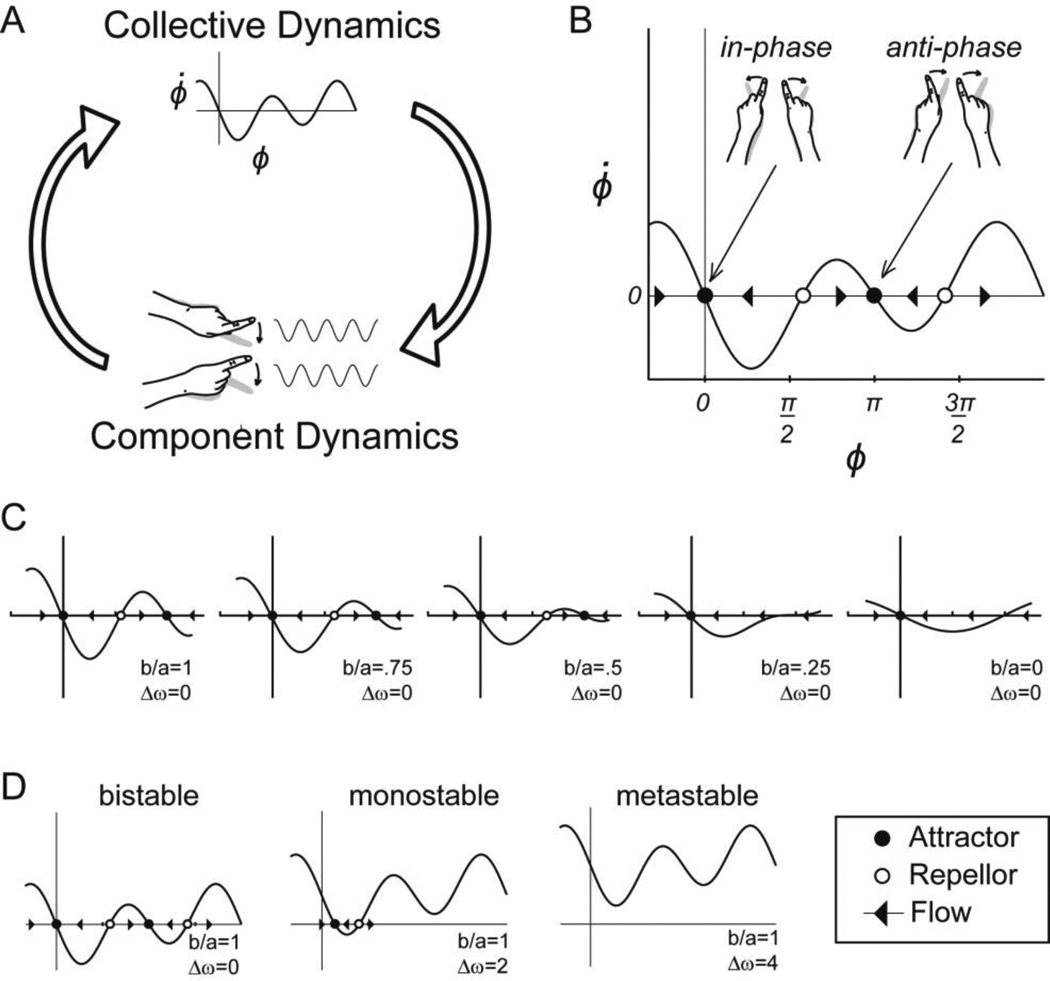
Figure 2.

The dynamics of rhythmically coordinated finger movements. A) The coordinated action of muscles acting to rhythmically oscillate the left and right index fingers is found to give rise to the collective dynamics of equation 1. B) The collective variable relative phase (ϕ) captures the coordinated state of the components. For example, in-phase coordination (ϕ=0) identifies a collective state in which identical muscles of the left and right hand are used synchronously. The dynamics (i.e. change over time) of ϕ reveals stable fixed points (●) to which the collective state of the system is attracted, and unstable fixed points (○) from which the collective state of the system is repelled. The direction of change is shown with arrows depicting the direction of flow. C) Changes in strength of coupling between left and right fingers modelled with the parameter b/a in equation 1 give result in the loss of a fixed point attractor as b/a in varied from 1 to 0. D) Dynamical regimes observed as a function of difference in the natural frequencies of component oscillators captured by the parameter (Δω).

The state of the collective dynamics in this model is captured by the relative phase (ϕ) of the two coupled oscillators. This collective variable indexes, in a single variable, how the parts of the system are related. For example, a relative phase of 0° indicates that the oscillators are coordinated in-phase, whereas a relative phase of 180° indicates that the two oscillators are in coordinated in an anti-phase pattern. The collective variable dynamics (i.e. change over time in ϕ) is given by:

$$\dot{\varphi }=\mathrm{\Delta }\omega -a\text{ sin}(\varphi )-2a\text{ sin}(\varphi )-\surd \overline{Q}{\zeta }_t.$$ [1]

The dot notation here denotes differentiation with respect to time. The term Δω indexes differences in the natural frequencies of the two component oscillators. It quantifies the tendency of non-linearly coupled oscillators with differing natural frequencies (ω) to oscillate at their individual preferred frequencies. The parameters a and b in the model are related to the collective frequency of coordinated movement such that an increase in collective frequency is represented as a decrease in the ratio b/a. More precisely, b/a represent the tendency of the two oscillators to cooperate and to be drawn toward each other’s natural frequencies such that an increase in b/a represents an increase in the degree of which the components are drawn into a stable collective pattern. The last term on the right side of the equation represents system noise. ζ_t is a Gaussian white noise process that dictates a stochastic force of strength Q acting on the collective variable dynamics (Schöner et al. 1986). Taken together with the two sine functions, the parameters Δω and b/a, determine the stable states of the collective dynamics. For Δω = 0 and b/a = 0, a single stable state at 0° (or in-phase coordination) is present in the collective dynamics. In this case, for any starting value of ϕ, the collective variable dynamics (ϕ̇) is such, that the collective state of the system will invariably be drawn to a stable pattern of in-phase coordination. Thus, the collective dynamics captures the emergent stability of the collective behavior. To use the language of dynamical systems theory, a point attractor is present in the collective variable dynamics at 0°. For Δω = 0 and b/a = 1, a significant change is present in the collective variable dynamics, two stable states are present, one at 0° (in-phase coordination) and one at 180° (anti-phase coordination). In this situation the system is multi-stable. For an initial relative phase close to 0° the system will be attracted to the in-phase attractor. For an initial relative phase close to 180°, the system will be attracted to the anti-phase attractor (figure 2B).

In the literature this model has become known as the HKB model. Since its development, the scientific impact of the HKB model has been wide-reaching. In large part, this is due to the discovered potential in this model to support a number of explicit, testable, and non-obvious predictions based upon specific features of the collective dynamics (Kelso, 1995; Kelso, 2012; Mitra, Amazeen,& Turvey, 1998). For example, if Δω = 0 and b/a is varied from a value of 1 to 0, by slowly increasing the collective frequency, a critical point is reached at b/a = 0.25 where the anti-phase attractor disappears from the collective dynamics (figure 2C). Given this scenario in a system initially arranged to be in anti-phase coordination, we can predict that, as the collective frequency is increased, a critical point will be reached at which the collective organization of the system will spontaneously transition from anti-phase to in-phase. We can also predict hysteresis in this system, such that if b/a is subsequently varied from a value of 0 to 1, we would not expect the system to transition back to anti-phase. Other predictions from the model include the existence of critical slowing down and critical fluctuations. Close the critical point of the anti-phase attractor disappearing, the collective dynamics are only weakly drawn to towards the anti-phase attractor. At this point, if the system is perturbed away from an anti-phase coordination pattern, the movement of the system back to anti-phase should occur slowly (i.e. critical slowing down). Additionally, at this point the relative contribution of system noise to the collective variable dynamics is enhanced (i.e. critical fluctuations) and greater variability in the collective variable is predicted. Each of these predictions has been empirically observed in the coordination dynamics of the left and right index fingers (Kelso, 1984; Haken et al., 1985), in coordination between arms and legs (Kelso & Jeka, 1992), in coordination between an arm and a oscillating visual stimulus (Byblow et al., 1995; Wimmers el al., 1992), and even in the visually coupled coordination of legs belonging to two different people (Schmidt et al., 1990). The variation of functional and material composition across these systems is significant; it speaks to the fundamental role of general principles of constraint in determining the emergent form and functionality of behavior. It also speaks to the point that the distinction between component level dynamics and collective level dynamics is defined functionally (Kelso, 1995). Expanding on this point, these functionally defined levels of organization have been taken to be nested within a larger system of multi-scale dynamics, with the component level dynamics emerging from the interactions of components from below and the collective level dynamics participating as components for levels above (Kelso & Engstrøm, 2006).

Moving beyond the confines of a minimal model of two non-linearly biological coupled oscillators, the hallmarks of self-organization predicted by the general theory of non-equilibrium phase transitions, such as hysteresis, spontaneous transitions, critical fluctuations, and critical slowing down, have been observed broadly across a variety of complex systems, ranging from the Bénard convection instability we used to example this variety of self-organization (Wesfreid et al., 1978) to gait transitions (Diedrich & Warren, 1995), postural control (Bardy et al., 2002), visual perception (Attneave, 1971; Hock, Kelso, & Schöner, 1993; Tuller et al., 1994), and even the emergence of cognitive insights (Stephen, Dixon, & Isenhower, 2009). Across these systems we consequently find evidence in support of the claim that complex adaptive behavior is underwritten by general principles of self-organization.

With respect to the challenge of distilling functional simplicity from compositional complexity, Haken’s slaving principle implies that not only does the constrained cooperation of a system of self-organized components act to bring about stable collective dynamics, but that the collective dynamics simultaneously acts as an emergent higher level regulator (as Gibson anticipated), taking control of the system as a whole and determining the behavior of the components (c.f. Chemero & Turvey, 2007; Rosen, 2000). The implied circular (i.e. self-entailing) causality, implicit both in Haken’s slaving principle and in the perception-action cycle discussed previously, presents an organizational form that naturally supports qualities of robustness and degeneracy. With respect to the challenge of dexterity, the slaving principle is consequently of deep potential significance. It holds promise of a mechanism through which the context conditioned functioning and recruitment of components might be interpreted. Moreover, following Turvey (2007), if one considers a system composed of context sensitive components, each with its own set of potentialities to take on particular functional roles, the slaving principle may provide a central principle for understanding complex adaptive behavior conceived as a cooperativity of enslaved roles.

Thus far, our discussion of the emergent collective dynamics of two non-linearly coupled biological oscillators has revealed 1) a mechanism for self-organized stable collective behavior and 2) a mechanism for switching between modes of coordination driven by the dynamics of the non-equilibrium phase transition. With respect to the challenge of dexterity, switching of this kind represents only a minimal form of behavioral flexibility/adaptability engendered in the coexisting potentialities for the system to be organized in either in-phase or anti-phase coordination. The potential for mechanisms supporting behavioral flexibility that do not depend upon the dynamics of the non-equilibrium phase transition is clearly appreciable when one considers the fact that the organization of behavioral systems is soft-molded (Kugler & Turvey, 1987). That is, behavioral systems are constituted in large part by informational linkages (Kelso, 1994), and the stabilities of the emergent collective variable dynamics in behavioral systems are predicated upon such linkages (Fink et al., 2000; Kelso et al., 2001; Mechsner et al., 2001). The role of informational linkages in supporting behavioral flexibility is evidenced in investigations of the role of participant intentions on the dynamics of bimanual coordination. Participants, given the intention to do so, can, to a limited degree, stabilize coordination patterns that would otherwise be unstable (Kelso, 1984). They can also intentionally switch between the coexisting stable modes of a multi-stable collective dynamics (Scholtz & Kelso, 1990; De Luca et al., 2010).

The concept of metastability provides a potential mechanism for self-organized behavioral flexibility. Meta-stability emerges from particular parameterizations of the dynamics of systems of coupled oscillators. For the minimal case of two non-linearly coupled oscillators captured by equation 1, when Δω = 0, either a mono-stable dynamics (i.e. a stable in-phase attractor) or a multi-stable dynamics (i.e. stable in-phase and anti-phase attractors) is observed depending upon the particular value of b/a(figure 2D). For the case of Δω ≠ 0, the possibility of an addition third dynamical regime emerges, in which for particular values of Δω and b/a, no stable states exist, but a tendency remains for the collective variable dynamics to dwell in the regions where the stable states used to be (figure 2D). Such regions are termed “ghost attractors”. This is the mode of behavior recognized by von Holst as relative coordination. In this meta-stable regime, the small degree of attraction that exists towards ghost attractors produces transient periods of dwelling in the vicinity of the weakly stable states (phase trapping) and periods of uncoordinated behavior (phase wandering) in which all potential relative phase relations can be visited. In the meta-stable mode, increased flexibility is reflected in the potential for the system to explore all possible collective states, the ease with which the system can move between multiple weakly stable states, and the possibility that small changes in parameters can switch the system from one weakly stable state to another. These qualities have led to the description of meta-stable dynamics as “creative” dynamics and the hypothesis that self-organized metastable dynamics are necessary for complex adaptive behavior (Kello & Van Orden, 2009; Kelso, 2012).

At the level of behavior, meta-stable dynamics have been observed in weakly coupled systems such as in the case of unintentional motor coordination between people (Lopresti-Goodman et al., 2008; Richardson et al., 2007). They have also been observed in patterns of inter-segmental coordination during quiet upright stance (James, 2013; Wang & Newell, 2012). In this latter case, the heterogeneity of coordinated components appears to facilitate degeneracy that is observed as flexible switching between redundant modes of coordinating posture. Meta-stable dynamics have also been observed in models of the neuro-dynamics of perception (van Leeuwen, Steyvers, & Nooter, 1997) and have been investigated as a potential principled basis of the rapid switching and reorganization of neural dynamics in the cortex (Bressler & Kelso, 2001). Paralleling the dynamics of coordinated actions, the dynamics of coordinated neural activity in the cortex has been taken to depend upon a balance of integrative and segregative processes (Kelso, 2012; Tononi, Edelman, & Sporns, 1998). Following our earlier discussion of muscle roles, segregation can be thought to concern the tendency of particular ensembles of neurons to take on particular functional roles, and integration can be thought to concern the tendency for those ensembles to become enslaved into a task and context conditioned neural dynamics. In situ, the roles taken on by cortical ensembles might be identifiable as sensory or motor, or they might be taken as related to intentions, plans, memories, or emotions. Of import to our present concerns, in coordination these ensembles appear to play a significant role in embodying the constraints of task, organism, and environment, thus supporting the adaptive coupling of activity to situation.

Interactivity and self-organized exquisite context sensitivity

With respect to the challenge of dexterity, the significance of the concept of meta-stability is carried in the possibility it examples of coordinated behavior self-organized to a state of exquisite context sensitivity. In a meta-stable system even a small change in the context of constraints can act to reorganize collective behavior, potentially adaptively conditioning it to the dynamically evolving demands of the situation. The flexibility of the meta-stable state is achieved at the cost of lost behavioral stability. This apparent trade-off between stability and flexibility as we move from mono-stability, to multi-stability, to meta-stability, begs the question, how can dexterous activity be both robust, such that an intended behavior can be reliably repeated and, at the same time, degenerate such that the potential for flexibly switching between degenerate context appropriate means of realizing that behavior is retained? One possibility, consistent with the hypothesis of a meta-stable dynamics of the central nervous system (Kelso, 2012) and with Bernstein’s distinction between functionally defined leading and background levels, is that the elementary form of robustness engendered by the dynamical stability of a collective level dynamics, is constituted by meta-stable components. In other words, it is constituted by context sensitive components, whose functioning and participation in collectively regulated behavior depends on how they are situated.

Investigations of the behavior of complex systems reveals that even simple systems of interconnected component scan give rise to the emergence of complex behavior (Bak, Tang, & Wiesenfeld, 1987; Prigogine & Stengers, 1984). The hypothesis that a system of many interconnected components could be self-organized to a state of exquisite context sensitivity finds direct support in the theory of self-organized criticality (Bak, 1996). The theory of self-organized criticality considers the behavior of a large class of non-equilibrium systems that are composed of many degrees of freedom, whose interaction is governed through simple coupling rules. The many degrees of freedom in these systems exhibit threshold nonlinearities (i.e. switching is between discrete states), and the coupling rules in these systems are spatially and temporally localized, such that any degree of freedom is only directly influenced by its nearest neighbors (Pruessner, 2012). Of interest here is the observation that even in the case of the simple form of interconnectivity engendered in this class of complex systems, qualities that we have identified to be relevant to complex adaptive behavior can be seen to emerge.

The phenomenon of self-organized critical behavior is evidenced in the simple physical system of an iron magnet heated to the point of a ferromagnetic-paramagnetic phase transition. A material is ferromagnetic when is exhibits magnetization in the absence of an external magnetic field, and it is paramagnetic when the material does not retain any magnetization in the absence of an externally induced magnetic field. As shown by Pierre Curie, at low temperatures an iron magnet is ferromagnetic. As an iron magnet is progressively heated, the magnetization of the material is found to steadily decrease up to a critical temperature of 1043 K, above which the material retains no magnetization and the system transitions to a paramagnetic state. If the material is cooled, magnetization returns for temperatures below the critical temperature. The behavior of this system has been interpreted in theoretical physics with respect to the interactions of atomic components (Maris & Kadanoff, 1978). At the atomic level, the iron magnet can be reasonably approximated as a regular lattice of iron atoms. In each iron atom electrons orbit the nucleus creating a small local magnetic field and an associated alignment of that local magnetic field termed spin. Magnetization of the material is a function of the alignment of spins of its composing atoms. Magnetization consequently provides a collective variable, indexing the ordered patterning of spins in the material. Given the small magnetic field of each atom, the spin of each atom is only affected by the spin of its nearby neighbors, such that a tendency exists for spins of close by atoms to be aligned similarly. In contrast, thermal agitation of the atoms in the material due to heating disrupts the alignment of spins and creates a tendency in the system for spins to be aligned randomly. Thus, as with our previous examples, a balance of integrative and segregative tendencies between interacting components is seen to constrain the emergent form of collective behavior. At low temperatures all spins are aligned and a strong magnetic field results. An ordered state is observed that is invariant in both space and time (i.e. spins are aligned and remain so over time). At higher temperatures thermal agitation of the atoms in the material disrupts the alignment of spins, and creates a tendency in the system for spins to be aligned randomly, and for magnetization to be weak. At above critical temperatures spins change randomly over time. In this state, spins are correlated weakly in both space and time, and collective behavior vanishes.

Of principle concern in the theory of self-organized criticality is the behavior that is observed when the iron magnet is heated to a critical point, at the boundary between ordered and disordered behavior. In this critical state, spatially and temporally extended stable patterns of spin alignment emerge, and the fluctuations of spin alignments across the system take on a theoretically interesting form (see Biney et al., 1992; Christensen & Moloney, 2005; Sornette, 2004, for expanded reviews). At the critical point, large correlated structures of coordinated spin alignments, up to the size of the whole system, can transiently form, and the spatial distributions of aligned spins (i.e. cluster sizes) shows self-similar (i.e. power law) scaling. With regard to the issue of exquisite context sensitivity, at the critical point this system exhibits its highest susceptibility to perturbation, such that a change of a single spin has the potential to reorder the spin alignments of the entire system. Susceptibility of this kind creates long-range dependencies across the entire system (Bak & Chen, 1991) and examples a self-organized system able to respond to a change in one degree of freedom by a change in many other degrees of freedom.

The theory of self-organized criticality predicts that complex systems are self-organized to critical states (Bak, 1996; Bak et al., 1987). Rather than a critical state requiring fine tuning of an external parameters (such as temperature), it is assumed that the parameter dynamics of the system are self-organized so as to bring the system to the required critical point (Sornette, 1994). Critical states are consequently seen as attractors of a non-typical kind (Blanchard, Cessac, & Krüger, 2000; Mehta & Barker, 1994; Paczuski, Maslov & Bak, 1994). Non-typical in the sense that the critical state is at once highly unstable and, at the same time, the most robust attractor for the dynamics of a complex system (Chialvo, 2008).

Systems said to be self-organized to a critical state include avalanches in piles of rice (Frette et al., 1996), earthquakes (Bak & Tang, 1989), ant foraging (Halley & Burd, 2004), the coordinated collective behavior of schools of fish (Bonabeau & Dagorn, 1995), and flocks of birds (Cavagna et al., 2010). In each case system behavior appears to be driven to a critical state. In the case of a flock of birds, the flock, considered as a unitary system, is organized to a state at which it is adaptively poised to maximally respond to environmental perturbations (Cavagna et al., 2010). Recently it has also been suggested that perceptual systems, faced with the challenge of responding adaptively to information carried in patterns of intensity changes spanning several orders of magnitude, are self-organized to a critical state of multi-scale sensitivity (Chialvo, 2006; Kinouchi & Copelli, 2006). In this work it was shown that neural network connectivity, when self-organized to a critical state, becomes endowed with the functionality of being able to respond robustly to both small and large intensity changes in a particular ambient energy array. This is shown to be achieved without loss of sensitivity or saturation. Expanding upon this idea, the hypothesis that the neural networks are self-organized to a state of criticality and meta-stability that allows them to quickly and adaptively couple activity to situation has received much recent attention (Alstrøm & Stassinopoulos, 1995; Chialvo, 2010; Linkenkaer-Hansen et al., 2001; Usher, Stemmler, & Olami, 1995). Recent investigations of the multi-scale dynamics of coordination between regions in the human brain reveal a scale invariant topology of cortical interconnectivity, supporting a functional network dynamics poised on the boundary of stability/instability (Bassett & Bullmore, 2006; Bassett et al., 2006). The critical network dynamics observed in this research have been interpreted to be supporting a task invariant intrinsic network dynamics and a task specific parameterization of those intrinsic dynamics (Cole et al., 2014). Additionally, these critical network dynamics have been shown to support the emergence of task-specific long-range cortical interconnectivity (Bassett et al., 2006).

The possibility of emergent scale-invariant functionality is of general significance to the challenge of coupling activity to situation and deserves elaboration. Complex adaptive behavior unfolds over multiple nested spatial and temporal scales. Behavior observed at any particularly chosen scale (usually what we can fit into the laboratory) is nested within the dynamics of activity that unfold at longer time scales and nests within it dynamics of activity that unfold at shorter time scales (Gottlieb, 1999; Vrobel, 2011). Behavior at any scale is only functional to the extent that it is adaptively situated with respect to levels above and acts to situate the levels below. The organization and resulting dynamics of behavior are in consequence fundamentally fractal in nature (Turvey, 2007; Turvey & Fonseca, 2014). Complex adaptive systems self-organized to exhibit scale invariant functionality have been taken to possess adaptive evolutional advantages (West, 2006). In the case of complex adaptive behavior, scale independent organizational principles can be widely observed. Perceptual systems appear to be organized to detect invariant relations rather than magnitudes (Fechner, 1860; MacKay, 1963; Gibson, 1979) and coordinated actions reveal scale invariant principles of constraint (Bernstein, 1967; Viviani & Terzuolo, 1980). Even principles of memory that support the coupling of activity to situation over time scales ranging from minutes to days and years, appear to apply invariantly across multiple temporal scales (Brown, Neath, & Chater, 2007).

Interactivity and self-organized robustness and degeneracy

Of interest in the theory of self-organized criticality, and to our present consideration of complex adaptive behavior, is the claim that scaling laws, when discovered in the collective variable dynamics of a complex system, provide a signature of self-organization to an adaptive critical state (Bak, 1996; Davidsen & Schuster, 2000; Stanley, 1971). More specifically, such systems have been taken to be self-organized non-equilibrium systems in which energy is pumped in relatively slowly and is dissipated as fractals in space and time (Chialvo, 2008). In the case of our developed example of an iron magnet heated to a critical temperature, the complex behavior of the micro level components is reflected in long-range correlated structure (i.e. self-similar scaling in time) of the collective variable dynamics of the system, measured as changes over time in the net magnetization of the material (Christensen & Moloney, 2005).

The presence of serial correlations in a time series reveals dependencies in time. Such dependencies can take the form of short-range correlations where the current state is found to depend upon the previous state, or just a few prior states (Box & Jenkins, 1976) or the form of long-range correlations. Long-range correlated time series exhibit serial dependencies in time, spanning multiple time scales. For example, in a persistent time series, a positive trend in the past is likely to be followed by a positive trend in the future, and a negative trend in the past is likely to be followed by a negative trend in the future. Furthermore, a positive trend at one scale of analysis is likely to be both nested within similar trends expressed at larger scales and nested within it similar trends at smaller scales. Thus, long-range correlated time series exhibit statistical self-similarity. Long-range correlation refers specifically to the slow decay over time of an autocorrelation function. The decay function tends to follow a power law and theoretically never reaches zero. The consequent implication of long-range correlations observed in behavioral time series is rich temporal embeddedness, such that each behavioral event is found to be nested with respect to all proceeding and all future events. In the literature this phenomenon is referred to variously as 1/f noise, 1/f scaling, long-term memory, and fractal process (Eke et al., 2000; Goldberger, 1990; Van Orden, Holden, & Turvey, 2005; West, 2006). In these terms, memory refers to the observation that systems exhibiting long-range correlations give the appearance of keeping a memory of the system’s history. 1/f is in reference to the power spectrum of such time series, with 1/f referring to the condition where each frequency has a power proportional to its period of oscillation. Fractal refers to the statistical self-similarity that characterizes such series.

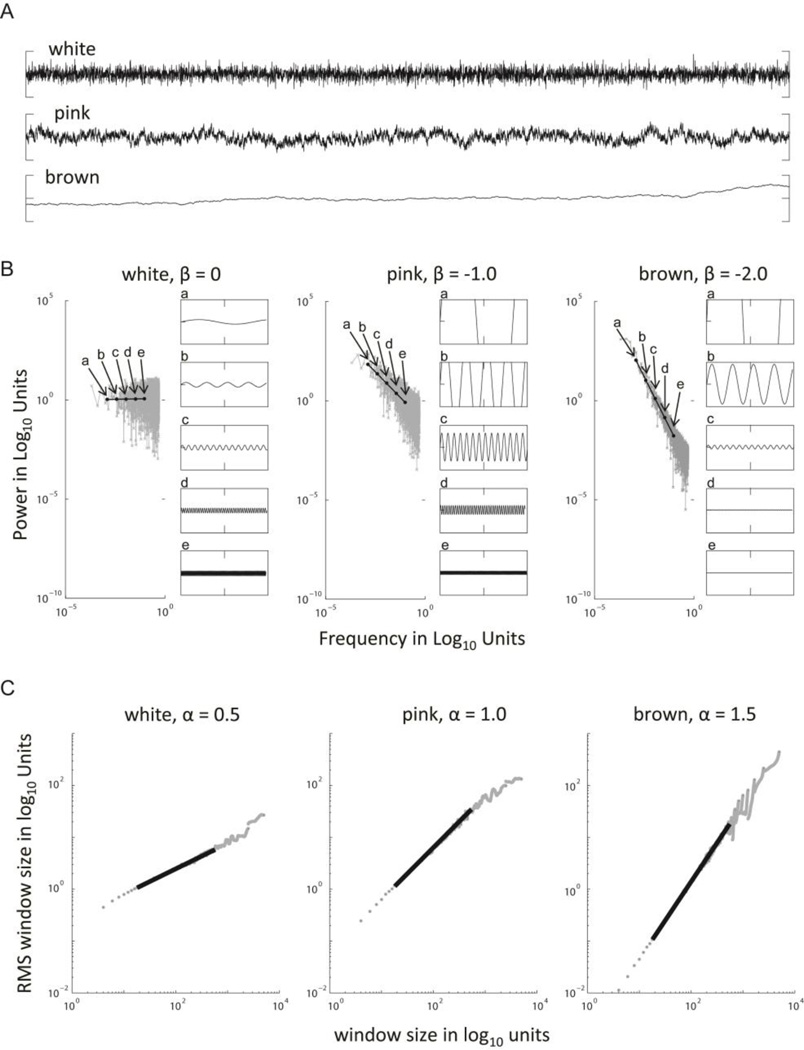
Long-range correlations in a behavioral time series can be assessed by a range of methods. These include rescaled range analysis (Hurst, 1951), power spectral analysis (Eke et al., 2000, Delignières et al., 2005), and detrended fluctuation analysis (Peng et al., 1993). In the case of power spectral analysis, the strength or persistence of long-range correlations is indexed by the negative slope of the log-log power spectrum (figure 3B), giving rise to the notation 1/f^β, where β indexes the slope. β=1 identifies a special case, commonly termed 1/f noise, 1/f scaling, or pink noise. Pink here simply refers to the fact that visible light with the same spectral slope has a pinkish hue.

Figure 3.

A) Time series varying with respect to the strength or persistence of long range correlations. B) Power spectral analysis of the white, pink, and brown noise time series. Long-range correlations indexed by the slope (β) of a regression line filled to the log-log power spectrum. The variation of fluctuations across scales for white, pink, and brown noise is depicted with sine waves. C) Detrended fluctuation analysis of white, pink, and brown noise time series. Long-range correlations indexed by the slope (α) of a regression line filled to the data.

For our present purposes we will refer to the strength or persistence of long range correlations with respect to the scaling exponent α derived from detrended fluctuation analysis (DFA). DFA exploits the diffusion properties of the long-range correlated time series. In DFA, the log of the amplitude of fluctuations observed at a scale defined by the size of an observation window (F(n)) is plotted against the log of the size of the observation window (n). The linear slope of a regression line fitted to this data yields a value for the scaling exponent α (figure 3C). With respect to α, an absence of long-range correlations or fractal scaling in a time series, is identified with α = 0.5. This phenomenon is also referred to as white noise, white reflecting to the observation that in white light, equal power is observed at all periods. Pink or 1/f noise is indexed by α = 1.0. In the literature, values anywhere in the range of 0.75 <α< 1.25 are commonly interpreted as reflecting pink noise. Pink, in contrast to white noise, reflects the presence of persistence in the time series (i.e. increasing trends tend to be followed by increasing trends). Brown noise (named with reference to Brownian motion) is indexed by α = 1.5. Brown or 1/f² noise reflects the presence of strong persistence in the time series. Anti-persistence, although it is not of direct relevance for the purposes of our discussions, is observed for the case of 0 <α< 0.5, (see Torre & Balasubramaniam, 2011, for an accessible and contained review of the various measures of the strength long range correlations and their interrelation).

The functional significance of 1/f scaling, as revealed though the theory of Self-Organized Criticality, is the exquisite context sensitivity afforded to a system poised at a near critical state. Of present concern, is the potential significance of 1/f scaling in informing our understanding of complex adaptive behavior. To this end we shall now revisit the HKB model of the emergent collective dynamics two non-linearly coupled biological oscillators. In our discussion of the HKB model we encountered the challenge of understanding how self-organized behavior in this system could be, at one and the same time, dynamically stable and adaptively flexible. In the HKB model the flexibility to switch between dynamically stable states is predicated upon the dynamics of a phase transition. Nearing the point of a phase transition, fluctuations play a functional role, acting to push the system out of its presently weakly stable states, and acts to transition the system to a more stable state (Collins, Park, & Turvey, 1998;Schöner, Haken, & Kelso, 1986). Consistent with this simple role, fluctuations in the HKB equation are modelled as a Gaussian white noise process. Contrary to this particular prediction of the model, recent experimental investigations of rhythmic bimanual coordination tasks have observed long-range correlations, that is 1/f scaling or pink noise (as opposed to white noise), in the collective variable dynamics (i.e. relative phase) of inter-limb coordination (Torre, Delignières, & Lemoine, 2007; Torre &Balasubramaniam, 2011). Of specific note in this research, is the finding that the presence of long-range correlations was not dependent upon whether the behavior was performed at frequencies close to, or far from, the point of spontaneous phase transition. DFA of relative phase, yielded α exponents of 0.83 and 0.78 for movements performed as comfort frequencies for in-phase and anti-phase coordination patterns respectively and α exponents of 0.78 and 0.82 for movements performed at close to the critical transition point for in-phase and anti-phase coordination patterns respectively (Torre &Balasubramaniam, 2011). Given the assumption that the presence of long-range correlations is indicative of a system poised on the critical boundary between stability and flexibility, these results clearly evidence the possibility of behavior simultaneously self-organized to a state of both dynamic stability and criticality. In this example, we have what would seem to be minimal instantiation of a system that is both robust, in the sense of dynamic stability, and degenerate, in the sense of possessing critically poised degrees of freedom with the implied capacity to be flexibly reorganized.

While the results of these studies seem to suggest that self-organized dynamic stability and self-organized criticality are independent dimensions of complex adaptive behavior, other studies provide evidence of their adaptive interaction. Again considering the dynamics of bimanual coordination, Torre (2010) found that the movement frequency at which participants spontaneously switched from anti-phase to in-phase depended upon the strength of the long-range correlations in the relative phase dynamics. Stronger long-range correlations were associated with transitions at lower frequencies. Curiously, the amplitude of baseline fluctuations for each participant was not predictive of the frequency of transition. Investigations of the stride to stride fluctuations of locomotion also speak to the issue of the interdependence of self-organized dynamic stability and self-organized criticality. Hausdorff et al. (1996) observed that although α for walking at a comfortable pace and α for walking speeds close to self-organized transitions were each in the range of pink noise (slow walking, α = 0.98; walking at comfort pace, α = 0.90; fast walking, α = 0.97), walking at speeds that were closer to transition points produced stronger long-range correlations. Expanding on this observation, analysis of the long-range correlations on stride to stride variability across a range of speeds, for both walking and running, reveals consistently observed pink noise but with a steady increase in the strength of long-range correlations as the system moves progressively closer to the point of a self-organized phase transition (Jordan & Newell, 2008).

From these intriguing results it is clear that a deeper understanding of coordinated behaviors as they approach the point of a spontaneous phase transition will be revealing of the functional organization supporting complex adaptive behavior. This approach is methodologically consistent with the technique of classifying dynamical systems by way of their scaling exponents at the point at which a phase transition begins (Hilborn, 1994). In general, it seems to be a reasonable assumption that both of these self-organized processes contribute to the context conditioned breaking down, and subsequent building up, of informational constraints supporting the robustness of complex adaptive behavior.

Long-range correlations have been widely considered as a universal hallmark of complex self-organizing dynamical systems (Bak & Chen, 1991). In addition to the examples of coordinated motor behavior considered in this section, long-range correlations (specifically 1/f scaling) have been discovered in time series of eye movements (Aks, Zelinsky, &, Sprott, 2002), movements coordinated in time to environmental stimuli (Delignières & Torre, 2009), reaction times in cognitive tasks (Gilden, 2001; Van Orden et al., 2003), brain activity (e.g. Bédard, Kröger and Destexhe, 2006; Novikov et al., 1997), mood changes over the course of a day (Isenhower et al., 2012), and even self-esteem ratings over the course of a year (Delignières, Fortes, & Ninot, 2004). The evident ubiquity of long-range correlations in human behavior has led to general claims regarding their significance for adaptive human behavior, including the suggestions that they reflect the intrinsic timing characteristics of human movement (Riley & Turvey, 2002), they index a state of optimal movement variability (Stergiou & Decker, 2011; Stergiou, Harbourne, &Cavanaugh, 2006; Stergiou, Yu, & Kyvelidou, 2013), and they index an optimal coordination of degrees of freedom across actor and task environment (Van Orden, Kloos, & Wallot, 2009).

In the theory of optimal movement variability the functional significance of long-range correlations is interpreted with respect to the changes in the persistent structure of motor behavior that accompany changes in strength of long-range correlations (Stergiou & Decker, 2011; Stergiou, Harbourne, &Cavanaugh, 2006; Stergiou, Yu, & Kyvelidou, 2013). In this theory, at one extreme, an absence of long-range correlations (i.e. white noise) indicates unconstrained variability and flexibility unhindered to the point of behavioral instability. At the other extreme (i.e. brown noise), overly persistent structure is taken to be indicative of inflexibly constrained degrees of freedom and of behavioral rigidity, reducing the capacity for behavior to be flexibly conditioned to the demands of the situation. The 1/f scaling, pink noise, is taken to be adaptive middle ground diagnostic of an optimal state of motor performance. Taken together with the theory of self-organized criticality, the theory of optimal movement variability predicts that optimal or skilled action should be self-organized to a critical state at the border of stability and flexibility indexed by 1/f scaling. Consistent with this expectation, long-range correlations in motor performance (Wijnants et al., 2009; Nourrit-Lucas et al., 2014) and in the exploratory movements of the eye and the body supporting perception (Stephen & Anastas, 2011; Stephen, Arzamarski, & Michaels, 2010) are found to increase in the direction of 1/f scaling as an actor becomes more skilled at a task. At a longer time scale of the developmental trajectory, long-range correlations are similarly found to increase in the direction of 1/f scaling as a child develops toward adulthood (Hausdorff et al., 1999; Kiefer et al., 2014). At the opposite end of the developmental spectrum, deviations away from 1/f scaling have been observed with increasing age (Hausdorff et al., 1997).

In light of some of the insights developed presently in regards to an account of complex adaptive behavior, we propose here that the theory of optimal movement variability could be generalized into a theory of complex adaptive behavior. From this theoretical perspective, complexity measures indexing the compositional complexity of behavior should be expected not only to be diagnostic of a balance between behavioral stability and flexibility, they should also be expected to be revealing of behavioral robustness and degeneracy. Robustness, to recap, identifies a special case of the term stability, conveyed in the ability of a system to maintain its functioning reliably across changes in context. Defined as such, robustness abstracts the concept of stability to a functional level of analysis. To recap, degeneracy identifies the capacity of a system to adaptively realize intended ends through flexible recruitment of multifunctional parts. Degeneracy consequently identifies a special case of the term flexibility. Recent evidence obtained from simulations of degenerate neural networks appears to be consistent with this generalization. It observes a direct link between the strength of long-range correlations produced by a given network and the degree of degeneracy in the network’s organization (Delignières, & Marmelat, 2013). Also consistent with this generalization, is recent experimental evidence suggesting that participants coordinating their footfalls, while walking to a visually flashing metronome, are able to do so more flexibly, that is, by more varied means, if the metronome contains long-range correlations in its variability (Rhea et al., 2014). Flexibility in this study was revealed as a greater variety of forms of coupling between actor and environmental stimuli (c.f. Torre & Wagenmakers, 2009).

Complex adaptive behavior as special purpose assemblages

Given the theoretical significance we have placed upon the concept of long-range correlations, we are motivated to consider an important basic question, what conclusions can be drawn from a particular observation of long-range correlations in a particular context? For example, does the observation of 1/f scaling in a participant’s ability to rhythmically coordinate two fingers speak to a general facility for robustness of behavior pervading multiple dimension of that participant’s behavior? Support for this possibility can be drawn from cases of the seemingly invariant manifestation of long-range correlations across multiple simultaneous measures of behavior. For example, in the case of gait variability, 1/f scaling is reliably observed across a range of measured gait parameters (Jordan, Challis, & Newell, 2007). Contrary to the results of this particular study, it has been more common to find that long-range correlations in human behavior are task and individual specific (Chen, Ding, & Kelso, 2001; Coey et al., 2013; Delignières & Torre, 2009; Holden et al., 2011; Kello et al., 2007; Torre et al., 2011; Washburn, Coey, & Richardson, 2013). Comparing long-range correlations observed for performances of rhythmic tapping and rhythmic circle drawing tasks over repeated trials, Torre et al. (2011) observed that, although individuals tended to produce characteristic long-range correlations independent of task or trial (i.e. an individualized tendency for stronger or weaker long-range correlations), long-range correlations across tasks were not correlated. Long-range correlations in gait have been shown to be equally task specific. In a study comparing the long-range correlations in across a range of gait parameters (i.e. step frequency, step length, and step speed), under conditions of both unconstrained walking (i.e. walking at a relaxed comfortable pace) and constrained walking (i.e. walking in time to an auditory metronome), Terrier et al. (2005) observed a significant decrease in long-range correlations in the constrained condition, but only for the step speed parameter. Decker, Cignetti, & Stergiou (2013) similarly observed gait parameter specific changes in long-range correlations. In this study, changes in dual tasking context were found to affect the long-range correlations of step speed, but changes were not found to affect step time nor step length.

Given the evident sensitivity of experimentally observed values of long-range correlations to changes in the context of constraints, what does a particular scaling exponent quantify? One approach, consistent with Gibson’s and Bernstein’s ecological analyses of situated behavior, has been to consider long-range correlations as quantifications of the dynamics of self-organized, context conditioned, special purpose assemblages. This approach is developed by van Orden and colleagues (2010; van Orden, Kloos, & Wallot, 2009) in the hypothesis that long-range correlations reflect a specific balance of tendencies of order and disorder that results from the interaction of voluntary (controlled) and involuntary (uncontrolled) degrees of freedom. Of note, this approach is broadly consistent with the theories of Synergetics and Self-Organized Criticality in as far as it assumes a fundamental role for the general principle of a balanced competing processes supporting self-organization. From this perspective uncontrolled (involuntary) degrees of freedom inject unsystematic change into human performance. These unsystematic changes act as sources of unsystematic perturbation, and consequent disorder, to the organization of behavior, and as such they are assumed to “whiten” behavior (i.e. moving the scaling exponent toward α=0.5). Controlled (voluntary) degrees of freedom provide a source of order and are represented in the softly assembled informational linkages that couple actor to situation. In contrast, controlled (voluntary) degrees of freedom are assumed to act to increase the scaling exponent. Of particular interest in this account is the possibility that originally uncontrolled (involuntary) degrees of freedom can become controlled (voluntary) degrees of freedom by becoming embodied in task specific informational linkages. It follows that more dexterous individuals could, to a greater degree than less dexterous individuals, be able to incorporate changes in context as controlled degrees of freedom rather than uncontrolled degrees of freedom. This particular prediction finds empirical support in recent comparisons of skilled craftsmen performing the dexterous task of fabricating beads from stone with repeated precise strikes of a hammer (Nonaka & Bril, 2014). The movements of both high quality and low quality craftsmen (high and low differentiating the quality of product they produced in their workshops) were found to produce statistically indistinguishable 1/f scaling when working with stone as a base material. When faced with the novel challenge of crafting glass (an unfamiliar and more fragile material) rather than stone, a “whitening” of behavior was observed for the low quality (less dexterous) craftsmen and a “pinkening” was observed for the high quality (more dexterous) craftsmen. Thus, the change in the context of constraints had differential consequences for the less and more dexterous craftsmen. For the less dexterous craftsmen the impact seems to have been the introduction of additional uncontrolled degrees of freedom. By contrast, for the more dexterous craftsmen the impact seems to have been the creation of additional controlled degrees of freedom, suggesting that the changes in the context of constraints were incorporated into their actions. Interpreted with respect to the balance of controlled and uncontrolled degrees of freedom, this “pinkening” implicates an ability to flexibly adapt to changing conditions, and as such it appears to evidence a robustness of behavior in dexterous actors. Interpreted with respect to a balance of stability and flexibility predicted by the theory of optimal movement variability, “pinkening” implicates a reorganization of behavior to a state of greater flexibility and context sensitivity, and as such it appears to evidence enhanced degeneracy. Taken together these two complementary characterizations reveal the key functional qualities of complex adaptive behavior in dexterous acts.

Multi-scale interactivity and dexterity

The theories of Self-Organized Criticality and Synergetics (exampled by the HKB model) differ in an important regard. Emergent collective behavior in the case of self-organized criticality stems from interactions unfolding on a strictly local scale, whereas, as evidenced in the collective dynamics of coupled oscillators, the emergent collective behavior in Synergetics stems from cross-scale interdependency. Given that long-range correlations can evidently be generated by systems devoid of cross-scale interactions, it suggests that measures of long-range correlations may be insensitive to an important dimension of complex interactivity underlying complex adaptive behavior.

The macro-micro circular causality implicit in the HKB model, and in task dynamic models notwithstanding, cross-scale interactivity has been directly evidenced in a range of coordinated motor behaviors (Goodman & Kelso, 1983; Tilsen, 2009; Wijnants et al., 2012). In the otherwise seemingly context independent motor behavior of discretely extending an index finger, Goodman and Kelso (1983) demonstrated coherent phase coupling of finger movements to background physiological tremor (i.e. to what would normally be considered to be biological noise). Specifically, finger movement onset was found to be adaptively constrained to occur at the moment of maximal momentum in the direction of the intended discrete movement. More recently, Wijnants et al. (2012) investigated the performance of a rhythmic precision aiming task at three distinct time scales of the behaviors dynamics. In this task participants rhythmically moved one hand back and forth between two targets on a table in front of them. At the faster time scale, the harmonicity (i.e. energetic efficiency) of each component motion moving the hand back and forth between the two targets was considered. At an intermediate temporal scale of task analysis, measures of movement speed and accuracy were considered, and at the slowest scale the cycle-to-cycle motor variability (i.e. long-range correlations) was considered. Under the task instructions to move as fast and as accurately as possible between the two targets, reliable correlations between each of the measures were observed. Strategic differences in how the task was performed were found to reliably permeate across all levels of analysis, revealing a task specific coupling spanning all nested scales of performance.

The introduction of cross-scale interactivity into self-organized criticality models transforms the dynamics of the system into a multiplicative form (Olemskoi & Kharchenko, 2012). In complex systems, multiplicative interactions take the form of cross-scale non-linear couplings, acting to transport energy and information across nested levels of scale-dependent dynamics (Ihlen & Vereijken, 2010). To account for multiplicative interactions of complex systems, multiplicative cascade dynamic models have been developed. Cascade dynamic models have been applied in a variety of complex systems (Stanley & Meakin, 1988; Mandelbrot, 2001) including most recently to investigations of human behavior (Harrison et al., 2014; Ihlen, Skjæret, & Vereijken, 2013; Ihlen & Vereijken, 2010; Scafetta, Griffin, & West, 2003; Stephen & Dixon, 2011; Stephen & Mirman, 2010). In these models it is assumed that the presence of multiplicative interactions give rise to heterogeneities in the fractal dynamics of complex systems (Ihlen & Vereijken, 2010; Kelty-Stephen et al., 2013). An index of the degree of variation in a given systems fractal dynamics is consequently taken to reveal the degree to which multiplicative interactions are constraining that systems dynamics. Measures of multifractality, indexing the variation of fractal scaling exponents that themselves relate fluctuations to scale, are used to quantify the strength of interactions across scales. Multifractality is indexed by computing and quantifying a multi-fractal spectrum (Chhabra & Jensen, 1989; Kelty-Stephen et al., 2013; Ihlen & Vereijken, 2013). The width and shape of the multifractal spectrum is taken to directly relate to the width and shape of the distribution of random multipliers that capture the multiplicative interactions across temporal scales.

The relevance of multifractal measures to our present concerns is in the potential they offer for capturing additional dimensions of the complex interdependencies supporting the emergent functionality of complex adaptive behavior. Returning to the case of the more and less dexterous bead craftsmen, Nonaka & Bril (2014) observed greater multifractal spectrum widths in the more dexterous craftsmen, suggesting a greater degree of compositional complexity revealed as greater cross-scale interactivity. Moreover, the introduction of the challenging task of crafting glass had no effect on multifractal spectrum width for the more dexterous group, suggesting the complex interdependences of the dexterous craftsmen were robust to changes in the context of constraints. In contrast, for the less dexterous craftsmen a marked decrease in multifractal spectrum width resulted from the challenge of the crafting an unfamiliar material. The functional consequence of this decrease in cross-scale interactivity can be interpreted to suggest a decrease in the context conditioned cross scale interactions supporting the adaptive coupling of craftsman to situation. Given such an interpretation the decrease in multifractal spectrum width could be interpreted to imply a less robust behavioral organization of the less dexterous craftsman.

Complex interactivity, emergent functionality, and pathology

Paralleling the balance of integrative and segregate tendencies taken to support the adapted functionality of biological systems (Edelman & Gally, 2001; Tononi, Sporns, & Edelman, 1999; Whitacre & Bender, 2010), the functionality of complex adaptive behavior is observed presently to depend upon general principles of self-organization underwritten by balances of competing constraints. The emergent functionality of complex adaptive behavior is taken here to be predicated upon the compositional complexity of the agent-environment system. More specifically, the complex interactivity of nervous system, body, and environment, is taken to underlie the emergence of 1) context conditioned behavioral forms (i.e. dexterity of action) and 2) adaptive couplings of activity and situation (i.e. dexterity of perception). In sum, a general perspective on the functionality of human behavior is suggested in which it is assumed that adaptive behavior capitalizes upon compositional complexity. From this perspective measures derived from complexity science designed to quantify compositional complexity are assumed to be strong candidate measures for quantifying the adapted functionality of human behavior. In the case of measures of long-range correlations (e.g. DFA), the observation of 1/f scaling can be interpreted with respect to adaptive functionality of human behavior in a number of ways. With respect to the challenge of dexterity, long-range correlations are revealing of behavior self-organized to a state of exquisite context sensitivity, allowing for the adaptive coupling of activity to situation. The absence of a characteristic scale implied by long-range correlations speaks to a multi-scale sensitivity of perceptual systems and of activity coupled to situation across spatially and temporally nested scales of behavior. With respect to the robustness of behavior, long-range correlations are revealing of an agent-environment system organized to critical state in which desired ends can be flexibly achieved by degenerate means. Long-range correlations are consequently taken to be revealing of the compositional complexity of the agent that supports multiple means of realizing desired ends and of a complimentary compositional complexity of the environment that supports the invitation for degenerate means for realizing the intended behavior. In the case of measures of multifractality, the observation of multiplicative interactions can be interpreted with respect to the coupling of activity to situation across nested spatiotemporal scales, such that a change in one detail can be responded to with self-organized changes spanning multiple spatiotemporal scales of behavior. Multifractality also potentially speaks to increases in behavioral robustness supported by cross-scale compositional complexity evidenced in the capacity to incorporate new task constraints as controlled rather than uncontrolled degrees of freedom. Taken together interpretations of fractal and multifractal analyses present a compelling starting point for understanding dimensions of dexterity and for building a basic account of complex adaptive behavior (figure 4).

Figure 4.

The results of fractal and multifractal analyses are consistent with the hypothesis that more dexterous behavior is associated with fractally nested scales of activity supported by non-linear couplings of components both within and across scales.

This perspective of behavioral functionality conceived as complex adaptive behavior has received considerable attention as a paradigm for interpreting deficits in behavioral functionality consequent of aging and pathology (Goldberger et al., 2002; Harbourne, & Stergiou, 2009; Kyriasis, 2003; Lipsitz & Goldberger, 1992; Stergiou, Harbourne, & Cavanaugh, 2006; Vaillancourt, & Newell, 2002; van Orden, Kloos, & Wallot, 2009). Consistent with the presently considered thesis of complexity as a resource for adaptive behavior, the functional consequences of aging and pathology have been taken to be associated with a loss of compositional complexity and have been interpreted in terms of deficits in the ability of the dysfunctional systems to support states of optimal complexity. This approach is situated theoretically amid general calls for a systems approach to interpreting pathology from within both systems biology (Ahn et al., 2006) and complexity science (West, 2006).

From the perspective of complex adaptive behavior, loss of behavioral functionality is taken to be quantifiable by measures of compositional complexity derived from complexity science. In the case of long-range correlations, a large body of evidence supports a connection between this measure and deficits in behavioral functionality. Shifts away from 1/f scaling in measures of behavior have been associated with general indexes of behavioral functionality such as increased rates of falling over from slips or trips in older adults (Bigelow & Berme, 2011; Herman et al., 2005; Norris et al., 2005) as well as with specific sensorimotor pathologies, such as Huntington’s disease (Hausdorff et al., 1997), Parkinson’s disease (Hausdorff, 2009), autism (Lai et al., 2010), and dyslexia (Wijnants et al., 2012). Moreover, the degree of departure of long-range correlations from 1/f scaling has been found to predict the severity of disorder (Hausdorff et al., 1997; Pan et al., 2007). These results can be positioned with respect to evidence of a more general link between 1/f scaling and health. Deviations from 1/f scaling have been associated with decreased recovery rates following traumatic brain injuries (Burr, Kirkness, & Mitchell, 2008), pathological states in heart functioning states such as atrial fibrillation and congestive heart failure (Goldberger, 1996; Goldberger et al., 2002; Havlin et al., 1999), and Alzheimer’s disease (Abásolo, Hornero, Gómez, García, & López, 2006). In the case of measures of multifractality, a general link between multifractal spectrum width and healthy functioning is similarly evidenced. Wider spectrum widths have been associated with healthy heartbeat dynamics contrasted with pathological signals of congestive heart failure patients (Ivanov et al., 2001). With respect to the functionality of behavior, reduced spectrum widths have also been observed in individuals affected by Parkinson’s disease relative to healthy controls (Morales & Kolaczyz, 2001).

The wider implications of the link between complexity and functionality have just begun to be explored. A compelling example of the successful application of ideas from complexity science is evidenced in the improved gas exchange and respiratory mechanics of “fractal” mechanical ventilators (Boker et al., 2002; Lefevre et al., 1996; Mutch et al., 2000a; 2000b; 2000c). In this research it has been shown that ventilators designed to mechanically assist breathing in a way that incorporates the long-range correlations of breathing, successfully mimics the dynamics of respiration, exhibits enhanced functionality in delivering oxygen to the tissues of the lung, and improves support to failing organs. Research in our laboratory has begun to explore the direct application of the perspective of behavioral functionality conceived as complex adaptive behavior. Paralleling the research on fractal ventilators, we have found that through the use of fractal auditory stimuli, the fractal dynamics of gait in older adults can be made to mimic the fractal dynamics of young healthy individuals (Kaipust et al., 2013; Hunt, McGrath, & Stergiou, 2014). Whether such fractal stimuli will act to confer the various dimensions of adaptive functionality suggested by the theory of complex adaptive behavior remains to be seen.