Genome-wide gene–gene interaction analysis for next-generation sequencing

Abstract

The critical barrier in interaction analysis for next-generation sequencing (NGS) data is that the traditional pairwise interaction analysis that is suitable for common variants is difficult to apply to rare variants because of their prohibitive computational time, large number of tests and low power. The great challenges for successful detection of interactions with NGS data are (1) the demands in the paradigm of changes in interaction analysis; (2) severe multiple testing; and (3) heavy computations. To meet these challenges, we shift the paradigm of interaction analysis between two SNPs to interaction analysis between two genomic regions. In other words, we take a gene as a unit of analysis and use functional data analysis techniques as dimensional reduction tools to develop a novel statistic to collectively test interaction between all possible pairs of SNPs within two genome regions. By intensive simulations, we demonstrate that the functional logistic regression for interaction analysis has the correct type 1 error rates and higher power to detect interaction than the currently used methods. The proposed method was applied to a coronary artery disease dataset from the Wellcome Trust Case Control Consortium (WTCCC) study and the Framingham Heart Study (FHS) dataset, and the early-onset myocardial infarction (EOMI) exome sequence datasets with European origin from the NHLBI's Exome Sequencing Project. We discovered that 6 of 27 pairs of significantly interacted genes in the FHS were replicated in the independent WTCCC study and 24 pairs of significantly interacted genes after applying Bonferroni correction in the EOMI study.

Introduction

Complex diseases are caused by multiple genes and their interactions.¹ Interaction analysis provides a complementary strategy to the genome-wide association studies (GWAS).^{2, 3} Many statistical methods including logistic regression and linkage disequilibrium (LD)-based methods have been developed to detect interaction.^{2, 4, 5, 6, 7, 8} However, these methods were originally designed to detect interaction for common variants and are difficult to apply to rare variants because of their high type 1 error rates and low power to detect interaction between rare variants.

The rapidly developed next-generation sequencing (NGS) technologies detect ten million genomic variants including both common and rare variants.^{9, 10, 11} The critical barrier in interaction analysis for rare variants is the curse of dimensionality of the data and the low frequencies of rare variants in the data. The high dimension of the data for interaction analysis poses two great challenges. The first challenge is to reduce prohibitive amount of computational time. An all-pairs scan of the SNPs genome wide may take many years to complete.⁵ The second challenge for genome-wide interaction analysis with NGS data arises from the multiple statistical tests.

The current paradigm of pairwise interaction analysis is lack of power to detect interaction between rare variants in a population due to the low frequencies of the rare variants. Interactions may be present in only a few samples, or even no sampled individuals at all will display the interaction effects. Large discrepancies in the number of observations between different combinations of rare variants will cause serious problems in identifying interactions in the population.

The development of novel concepts and statistics for testing interaction between rare variants and between rare and common variants, which can reduce the dimensionality of the data, the number of tests and the time of computations, and improving the power to detect interaction are urgently needed. To meet this challenge, we first change a basic unit of interaction analysis from a pair of SNPs to a pair of genes (or genomic regions). We take a gene as a basic unit of the interaction analysis and collectively test interaction between all possible pairs of SNPs within two genes. This new paradigm of interaction analysis has two remarkable features. First, it uses all information in the gene to collectively test interaction between multiple SNPs within the gene. Second, it will largely reduce the number of tests and will alleviate multiple testing problems.

After we change the unit of interaction analysis, we then use functional data analysis techniques to further reduce the dimensionality of the data. We use genetic variant profiles, which will recognize information contained in the physical location of the SNP as a major data form.¹² The densely typed genetic variants in a genomic region for each individual are so close that these genetic variant profiles can be treated as observed data taken from curves.¹³ The genetic variant profiles are called functional. Since standard multivariate statistical analyses often fail with functional data,^{14, 15} we formulate a test for interaction between two genes as a functional logistic regression model. Functional logistic regression is a natural extension of the standard logistic regression for traditional interaction analysis.

The functional logistic regression for interaction analysis can properly combine all pairwise interaction tests to obtain an overall test for interaction between all variants in two genes (or genomic regions). The functional logistic regression uses data reduction techniques to compress the signal into a few functional principal components. Since rare variants are infrequent and irregularly spaced, each individual has relatively little information available. The functional logistic regression can effectively pool the data across all individuals to maximize the available information.

To evaluate its performance for interaction analysis, we use large-scale simulations to calculate the type I error rates of the functional logistic regression for testing interaction between two genes and to compare its power with pairwise interaction analysis, logistic regression on principal components and collapsing method. To further evaluate its performance, the functional logistic regression for interaction analysis is applied to three datasets: (1) the early-onset myocardial infarction (EOMI) exome sequence datasets with European origin (EA) from the NHLBI's Exome Sequencing Project (ESP), (2) coronary artery disease (CAD) dataset from the Wellcome Trust Case Control Consortium (WTCCC) study and (3) the Framingham Heart Study (FHS) dataset. We find that the functional logistic regression for interaction analysis substantially outperforms the current pairwise interaction analysis method and collapsing method in both power analysis and real data applications.

MATERIALS AND METHODS

Functional logistic regression model for gene–gene interaction analysis

We first define the genotypic function. Consider two genomic regions [a₁, b₁] and [a₂, b₂]. Let x_i(t) and x_i(s) be genotypic functions of the i-th individual defined in the regions [a₁, b₁] and [a₂, b₂], respectively. Let t and s be a genomic position in the first and second genomic regions, respectively. Define a genotype profile x_i(t) of the i-th individual as an indicator variable for genotype at a SNP.

Next, we extend the traditional logistic regression model to the functional logistic regression for modeling main and interaction effects (Supplementary Note 1):

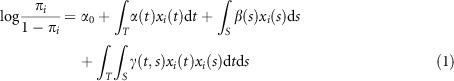where α(t) and β(t) are the putative genetic additive effects of two SNPs located at the genomic positions i and s, respectively, γ(t,s) is the putative interaction effect between two SNPs located at the genomic positions t and s.

We expand genotype functions in terms of eigenfunctions (Supplementary Note 1):

Substituting equation (2) into equation (1), we obtain

where 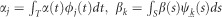and 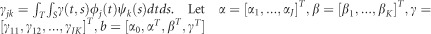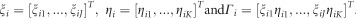. Then, we have

where .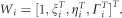

The traditional odds ratio concept defined for locus can also be extended to the genomic region. The odds ratio associated with the first genome region and the second genome region are, respectively, defined as 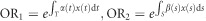. The odds ratio associated with susceptibility in both first and second genomic regions is then computed as 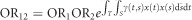. Define a multiplicative interaction measure between two genomic regions as 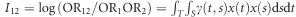. If we assume that each genomic region has only one SNP, then we have OR₁=e^α, OR₂=e^β, OR₁₂=OR₁OR₂e^γ and I₁₂=γ, which are consistent with the standard results for traditional analysis of interaction between two SNPs.

Test statistics

Assume that the total number of individuals in cases and controls is n. Let y_i,i=1, 2, … n denote the disease status of the i-th individual. A value of 1 (y_i=1) is used to indicate ‘disease' and a value of 0 (y_i=0) to indicate ‘normal'. From equation (4), it follows that

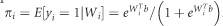. The likelihood function is given by

The maximum likelihood method will be used to estimate parameters b.¹⁶ Let 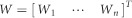. The variance–covariance matrix of the estimate b̂ is given by

where D=diag (π₁, …, π_n).

Now we study to test interaction between two genomic regions (or genes). Formally, we investigate the problem of testing the following hypothesis:

γ(t, s)=0, ∀t∈[a₁, b₁], s∈[a₂, b₂], which is equivalent to testing the hypothesis in equation (4):

Let Λ be the matrix corresponding to the parameter γ of the variance matrix Var (b̂) in equation (6). Define the test statistic for testing the interaction between two genomic regions [a₁, b₁] and [a₂, b₂] as

Then, under the null hypothesis H₀: γ=0, T₁ is asymptotically distributed as a central χ²_(JK) distribution.

Results

Null distribution of test statistics

In the previous section, we showed that the test statistics T₁ is asymptotically distributed as a central χ²_(JK) distribution. To examine the validity of this statement, we performed a series of simulation studies to compare their empirical levels with the nominal ones. We first consider the common variants. We used the MS software¹⁷ to generate a population of 2 000 000 chromosomes with 500 SNPs in a genomic region, including 150 (30%) common with MAF≥0.05, 50 (10%) low frequency with 0.01<MAF<0.05 and 300 (60%) rare with MAF≤0.01 SNPs, under a neutrality model. We randomly selected 10% of the variants as risk variants. Two haplotypes were randomly sampled from the population and assigned to an individual. The number of sampled individuals identified as controls ranges from 1000 to 3000. We consider two scenarios to sample cases: (1) β_G=0, β_H=0 and β_GH=0; and (2) β_G=log2, β_H=log2 and β_GH=0. We assume baseline penetrance 0.001, where 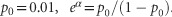. In evaluation of type 1 error rates of functional logistic regression, we selected top of the functional principal components in the expansion of genotypic functions, which account for 80% of the genetic variation in the genomic regions being tested. In addition to functional logistic regression, we also examined the null distribution of the collapsing method,¹⁸ pairwise logistic regression and PCA logistic regression in which the number of principal components was selected such that they account for 80% of genetic variations in the genomic regions being tested.

Table 1 and Supplementary Tables S1 and S2 summarize the type I error rates of the functional logistic regression for testing the interaction between two genes with common, rare and all variants, respectively, at the nominal levels α=0.05, α=0.01 and α=0.001. Supplementary Tables S3–S5,S6–S8 and S9–S11 summarized the type I error rates of the collapsing method, pairwise logistic regression and PCA logistic regression for testing the interaction between two genes with common variants, rare variants and all variants, respectively. These tables showed that the type I error rates of the functional logistic regression and PCA logistic regression for testing interaction between two genomic regions in any cases were not appreciably different from the nominal levels. However, we observed that the type 1 error rates of the collapsing method for interaction analysis were inflated and the type 1 error rates of the pairwise logistic regression for testing interaction were deflated.

Table 1. Type 1 error rates of functional logistic regression for testing interaction between two genes with common variants.

Sample size	βG=βH=0			βG=2, βH=0			βG=βH=2
	0.05	0.01	0.001	0.05	0.01	0.001	0.05	0.01	0.001
1000	0.0480	0.0103	0.0010	0.0569	0.0098	0.0010	0.0524	0.0109	0.0011
1500	0.0513	0.0105	0.0010	0.0510	0.0098	0.0009	0.0492	0.0107	0.0010
2000	0.0497	0.0102	0.0010	0.0493	0.0105	0.0010	0.0532	0.0101	0.0011
2500	0.0518	0.0099	0.0010	0.0516	0.0096	0.0010	0.0532	0.0101	0.0011
3000	0.0519	0.0103	0.0010	0.0504	0.0102	0.0010	0.0501	0.0105	0.0011

Power evaluation

To evaluate the performance of the functional logistic regression for testing the interaction between two genomic regions for a qualitative trait, we used simulated data to estimate their power to detect a true interaction. We also used MS software to simulate 1 000 000 individuals with 120 variants in the first gene and 80 variants in the second gene. An individual's disease status was determined based on the individual's genotype, disease interaction models and the penetrance for each locus. We consider three disease interaction models: dominant × dominant, recessive × recessive and additive × additive models as shown in Supplementary Table 12. We assumed α=−4.60, β_G=log2 and β_H=log2. We also assumed that the parameters in the disease interaction models across all pairs of risk variant sites are equal and the risk variants were assumed to influence disease susceptibility jointly. However, we only consider pairwise interactions between two risk SNPs that were located in different genomic regions. Each individual was assigned to the group of cases or controls depending on their disease status. The process for sampling individuals from the population of 2 000 000 haplotypes was repeated until the desired samples were reached for each disease model. We assumed that 2000 cases and 2000 controls were sampled.

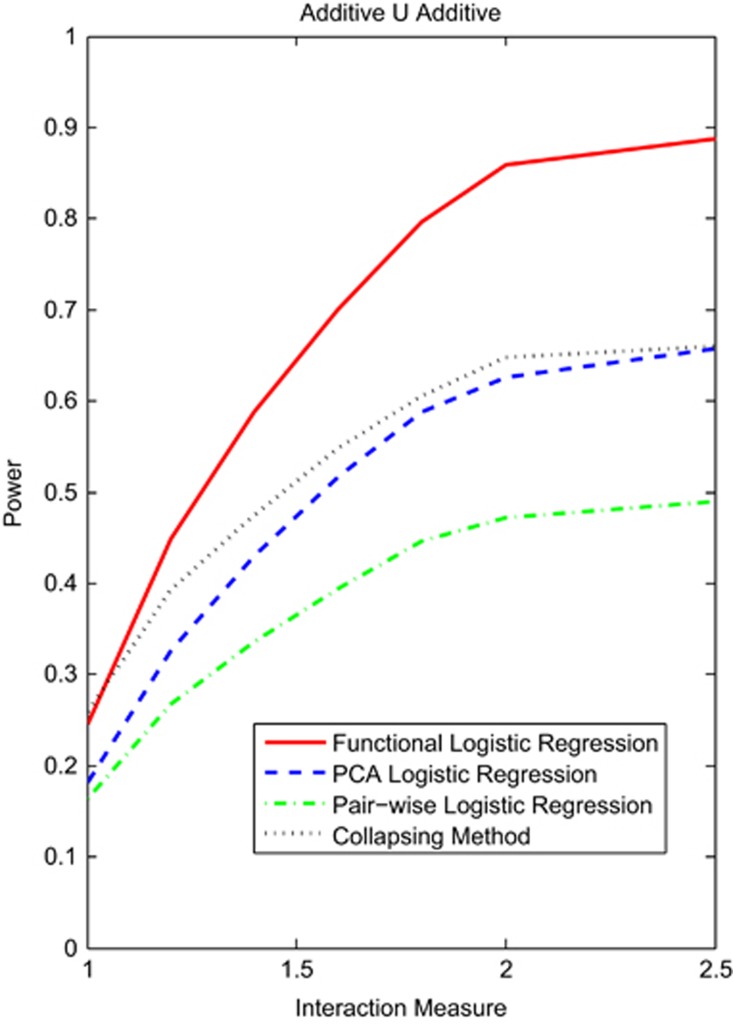
We first study the power of statistics for testing interaction between two genomic regions with rare variants. Figure 1 and Supplementary Figures S1 and S2 plotted the power curves of four statistics: the functional logistic regression, the PCA logistic regression, collapsing method and the pairwise logistic regression, where permutations were used to adjust for multiple testing for testing interaction between two genomic regions as a function of an interaction measure at the significance level α=0.05 under the additive ∪ additive, dominant ∪ dominant and recessive ∪ recessive interaction models, respectively. We assumed 2000 cases and 2000 controls, and 10% of risk variants. We observed that the functional logistic regression had the highest power and that the pairwise regression where we tested the interaction between all possible pairs of SNPs in two genomic regions (genes) had the lowest power among four statistics under all scenarios. The power of functional logistic regression was substantially higher than that of the pairwise logistic regression tests. Difference in power between the functional logistic regression and the other three test statistics dramatically increased with the interaction measure.

Figure 1.

Power curves of four statistics: the functional logistic regression, the PCA logistic regression, collapsing method and the pairwise logistic regression, where permutations were used to adjust for multiple testing for testing interaction between two genomic regions that consist of rare variants as a function of an interaction measure at the significance level α=0.05 under the additive ∪ additive model, assuming 2000 cases and 2000 controls, and 10% of risk variants.

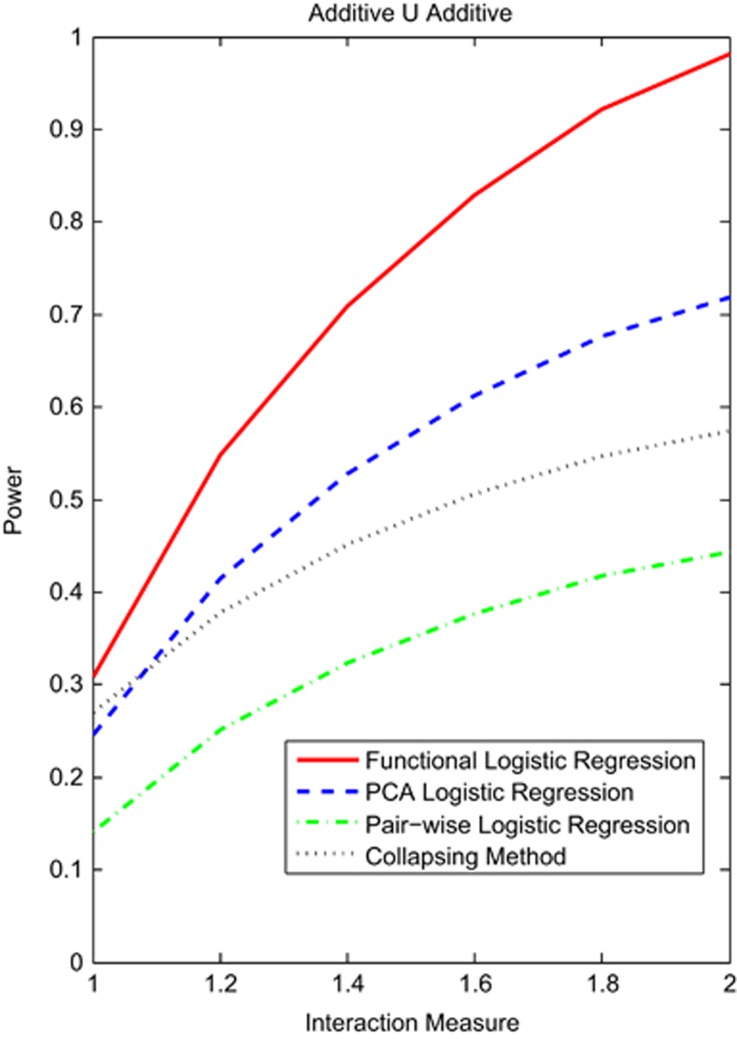
Next, we evaluate the power of tests for common variants. Figure 2 and Supplementary Figures S3 and S4 showed the power curves of four statistics for testing the interaction between two genomic regions with common variants under the additive ∪ additive, dominant ∪ dominant and recessive ∪ recessive interaction models, respectively. The sample sizes and proportion of risk variants were assumed as before. The power of all tests for interactions between the genomic regions with common variants were higher than that with rare variants under the same conditions, but the power patterns of the four tests for the common variants were similar to that for rare variants except for the PCA logistic regression under the additive ∪ additive and dominant ∪ dominant. We observed that the power of the functional logistic regression was the highest, followed by the PCA logistic regression and collapsing method. The power of the pairwise logistic regression tests was the lowest.

Figure 2.

Power curves of four statistics: the functional logistic regression, the PCA logistic regression, collapsing method and the pairwise logistic regression, where permutations were used to adjust for multiple testing for testing interaction between two genomic regions that consist of common variants as a function of an interaction measure at the significance level α=0.05 under the additive ∪ additive model, assuming 2000 cases and 2000 controls, and 10% of risk variants.

To further evaluate the power of the tests, we plotted the Supplementary Figures S5–S7 showing the power curves of four statistics for testing the interaction between two genomic regions with all variants (common, low-frequency and rare variants) under the additive ∪ additive, dominant ∪ dominant and recessive ∪ recessive interaction models, respectively. The power of the functional logistic regression is still highest among the four statistics.

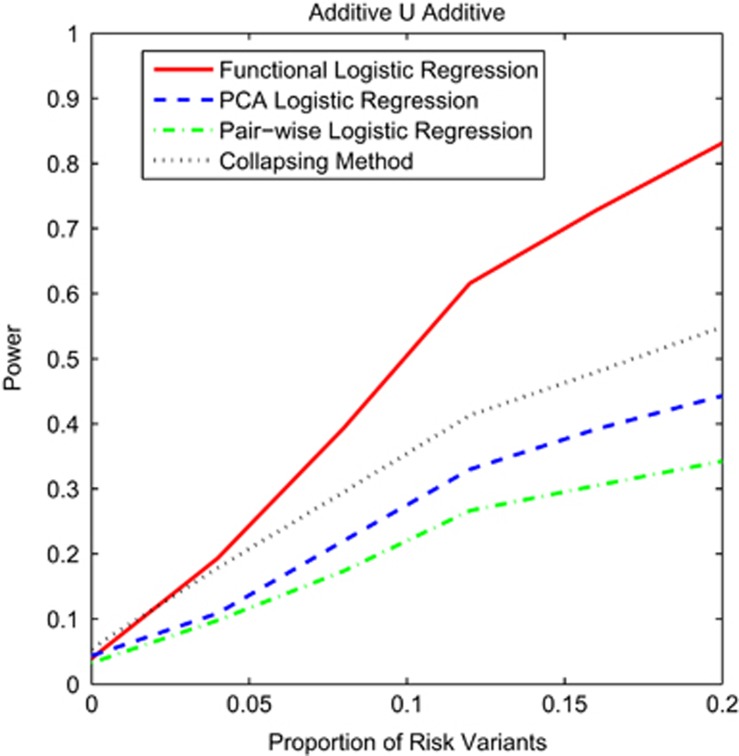
The number of variants has a large impact on the power of the tests for interaction. Figure 3 and Supplementary Figures S8 and S9 showed the power curves of the four statistics for testing interaction between two genomic regions with rare variants as a function of the proportion of risk alleles under the additive ∪ additive, dominant ∪ dominant and recessive ∪ recessive interaction models, respectively. We assumed 2000 cases and 2000 controls, and the interaction measure of 2 for the additive ∪ additive, dominant ∪ dominant interaction models, 3000 cases and 3000 controls, and interaction measure of 3 for the recessive ∪ recessive interaction model. We observed that the power of the functional logistic regression for testing the interaction was the highest among the four statistics, followed by the collapsing method, PCA logistic regression and the pairwise logistic regression. Since the collapsing method had large type 1 error rates, when the proportion of risk variants was close to zero (0.02), the power of collapsing method under the additive ∪ additive interaction model was higher than that of the functional logistic regression.

Figure 3.

Power curves of four statistics: the functional logistic regression, the PCA logistic regression, collapsing method and the pairwise logistic regression, where permutations were used to adjust for multiple testing for testing interaction between two genomic regions that consist of rare variants as a function of proportion of risk variants at the significance level α=0.05 under the additive ∪ additive model, assuming 2000 cases and 2000 controls, and the interaction measure of 2.5.

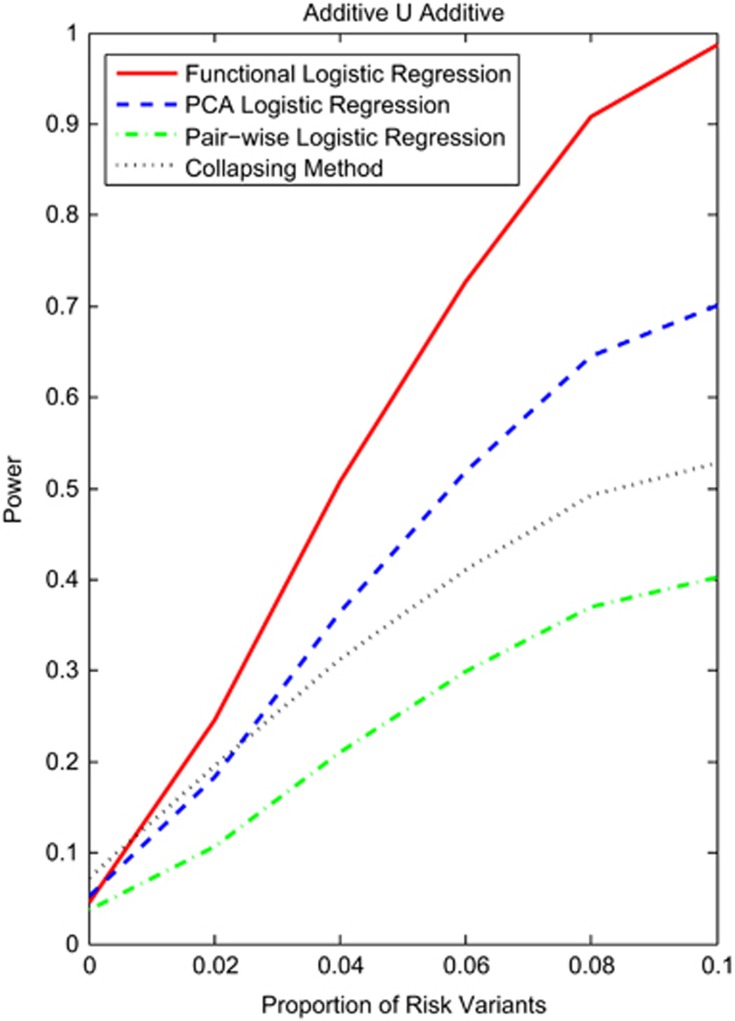
To examine the power pattern for common variants, we plotted Figure 4 and Supplementary Figures S10 and S11 that showed the power curves of the four statistics for testing interaction between two genomic regions with common variants as a function of the proportion of risk alleles under the additive ∪ additive, dominant ∪ dominant and recessive ∪ recessive interaction models, respectively. We observed that the power of the functional logistic regression for testing interaction between genes with common variants was the highest for all proportion of risk variants, followed by the PCA logistic regression, collapsing method and pairwise logistic regression.

Figure 4.

Power curves of four statistics: the functional logistic regression, the PCA logistic regression, collapsing method and the pairwise logistic regression, where permutations were used to adjust for multiple testing for testing interaction between two genomic regions that consist of common variants as a function of proportion of risk variants at the significance level α=0.05 under the additive ∪ additive model, assuming 2000 cases and 2000 controls, and the interaction measure of 2.5.

Application to real data examples

To further evaluate their performance, the four statistics for testing interaction were first applied to the FHS for cardiovascular disease (CVD) and then to the WTCCC for CAD study. We included all SNPs (the SNPs in introns and exons) in 5 kb frank of the gene in the analysis. We used gene annotation database hg19/NGRCh37 build, which match our datasets to define the gene/snp annotation. The FHS included 2827 individuals (633 individuals with CVD and 2194 controls) in the interaction analysis.¹⁹ The WTCCC CAD study included 1929 cases and 2938 controls.²⁰ A total of 8108 genes that were common in FHS and WTCCC CAD datasets were included in the interaction analysis. A P-value for declaring significant interaction after applying the Bonferroni correction for multiple tests was 1.52 × 10⁻⁹. The results for the FHS were summarized in Table 2. In total, 27 pairs of genes consisting of 54 distinct genes showed significant evidence of interaction with P-values <1.22 × 10⁻⁹, which were calculated by the functional logistic regression method. Supplementary Table S2 also listed P-values for testing interactions between genes by PCA logistic regression, collapsing method (grouping all variants with MAF≤0.1) and the minimum of P-values for testing all possible pairs of SNPs between two genes and P-values of pairwise logistic regression by permutation using standard logistic regression. If none of the variants with MAF≤0.1 exists, the statistics based on the collapsing method cannot be calculated, therefore we put NA in Table 2. We investigated whether these interacted genes in the FHS can be replicated in the WTCCC datasets. Since, we will carry out 27 tests, the P-value for declaring replication after the Bonferroni correction for multiple tests was 0.0019. We observed that 6 of the 27 pairs of significantly interacted genes in the FHS were replicated in the independent WTCCC study (Table 3). In Table 3, we also listed an additional six pairs of genes. Although they did not reach significant levels, the P-values were quite small in the two independent studies.

Table 2. P-values of 27 pairs of significantly interacted genes identified by FLR.

Gene 1	Chr	P-value	Gene 2	Chr	P-value	P-value
		Gene 1			Gene 2	FLR	PCALR	Collapsing	Pairwise (minimum)	Pairwise (permutation)
NR2F2	15	8.4E−01	CEP192	18	9.8E−01	6.9E−24	6.8E−07	NA	3.98E−02	5.05E−02
SSPN	12	1.0E−01	Nbla00526	12	5.9E−01	1.0E−20	3.2E−06	NA	1.61E−02	7.01E−02
GRIK2	6	3.8E−01	ATG5	6	2.6E−01	1.5E−20	4.3E−06	NA	2.75E−04	6.41E−02
ZEB2	2	2.9E−01	SETMAR	3	4.8E−02	1.4E−18	4.3E−06	7.9E-02	1.32E−02	5.75E−02
DMGDH	5	6.6E−01	FHL5	6	1.3E−01	2.0E−17	3.3E−06	NA	7.76E−02	9.97E−02
PTPN22	1	8.1E−01	SMARCAL1	2	7.0E−01	2.5E−17	5.1E−03	NA	8.26E−04	1.27E−02
CASC4	15	6.6E−01	ARIH1	15	3.0E−01	2.1E−16	4.3E−07	NA	3.11E−02	6.87E−02
RHOBTB3	5	3.2E−01	BAI3	6	3.6E−01	4.8E−16	8.5E−06	NA	8.98E−03	9.60E−02
PADI3	1	4.8E−01	CHIA	1	7.1E−01	8.4E−16	1.6E−02	1.7E-01	1.97E−05	6.00E−05
PCDHAC2	5	5.8E−01	CYP39A1	6	9.2E−01	1.4E−15	5.6E−06	1.7E-01	4.49E−02	6.34E−02
DPP4	2	2.9E−01	CHMP2B	3	2.1E−02	3.5E−15	6.2E−03	4.4E-01	7.46E−04	1.44E−03
KIF24	9	3.5E−03	SLC16A12	10	3.4E−02	1.0E−14	1.2E−02	NA	6.04E−04	1.38E−02
GANC	15	1.7E−01	CIB2	15	7.7E−01	1.2E−14	2.7E−03	NA	3.73E−03	5.34E−03
IFFO2	1	6.0E−01	AKT3	1	7.1E−01	4.1E−14	1.8E−06	NA	4.26E−03	7.03E−02
TTC23L	5	6.5E−01	RICTOR	5	2.2E−01	7.6E−14	7.4E−06	NA	4.47E−03	2.79E−02
SCRN1	7	7.3E−01	FRMD3	9	4.6E−01	1.0E−13	2.6E−07	NA	8.79E−03	7.43E−02
STX8	17	4.4E−01	C2CD2	21	5.5E−01	1.3E−13	8.3E−04	NA	1.66E−03	1.78E−02
IGSF11	3	6.9E−01	BST1	4	7.6E−01	9.0E−13	8.8E−07	NA	2.11E−03	4.81E−02
CSNK1A1P	15	8.7E−01	NCOA3	20	2.5E−01	1.0E−12	3.6E−03	NA	1.13E−05	3.60E−04
NT5C1B	2	4.1E−01	POU1F1	3	3.4E−03	1.3E−12	8.4E−06	1.3E-01	2.06E−02	2.33E−02
LPIN1	2	5.9E−01	KAT2B	3	2.4E−01	1.4E−12	9.0E−06	NA	1.09E−02	1.00E−01
TPO	2	7.5E−01	PRKCE	2	1.9E−03	2.6E−12	2.3E−06	NA	1.26E−03	8.84E−02
NUP188	9	7.4E−01	APBB1IP	10	6.0E−01	6.8E−12	6.3E−06	NA	1.54E−02	9.99E−02
LRRC40	1	3.4E−01	ST6GALNACV	1	1.0E+00	7.0E−12	1.3E−01	NA	1.40E−05	9.79E−05
FANK1	10	2.3E−01	UBE4A	11	3.9E−01	2.4E−11	1.3E−06	NA	6.77E−02	7.74E−02
XRCC2	7	1.6E−01	TTF1	9	4.9E−01	6.0E−10	1.0E−05	NA	2.05E−01	9.24E−02
SGCG	13	4.2E−01	TUBGCP3	13	9.8E−01	1.2E−09	9.5E−02	NA	1.35E−03	7.24E−03

Table 3. A list of genes showing significant interaction in FH and WTCCC studies.

				P-value
				FHS		WTCCC
Gene 1	Chr	Gene 2	Chr	FLR	Pairwise (minimum)	FLR	Pairwise (minimum)
PTPN22	1	SMARCAL1	2	2.46E−17	8.26E−04	9.69E−04	2.25E−03
PADI3	1	CHIA	1	8.40E−16	1.97E−05	1.58E−08	5.18E−02
DPP4	2	CHMP2B	3	3.51E−15	7.46E−04	9.13E−09	2.05E−02
GANC	15	CIB2	15	1.20E−14	3.73E−03	2.53E−06	7.18E−02
CSNK1A1P	15	NCOA3	20	1.00E−12	1.13E−05	3.21E−08	1.02E−03
LRRC40	1	ST6GALNACV	1	7.04E−12	1.40E−05	4.04E−08	1.58E−02
TTBK2	15	TSHZ2	20	5.94E−09	1.39E−03	1.09E−08	8.44E−04
LIPJ	10	PCBP2	12	8.22E−09	9.04E−04	1.68E−08	2.10E−02
WIRE	17	KCNJ15	21	1.79E−08	2.25E−04	2.21E−07	5.23E−03
CTBP2	10	KCNJ1	11	2.27E−08	2.09E−03	1.08E−07	6.29E−03
PNLIPRP1	10	C11orf64	11	1.09E−07	3.28E−04	6.21E−07	2.42E−02
IL22RA1	1	CAPN8	1	1.15E−07	1.37E−04	1.70E−08	1.18E−02

We observed several remarkable features from these results. First, we often observed the pairwise interaction between common and common variants (74%), rare and common variants (13%), rare and rare variants (4%) and low-frequency and common variants (9%), but less observed was the significant pairwise interaction between low frequency and low-frequency variants, and low-frequency and rare variants with P-values for testing interaction <1.0 × 10⁻⁴ in Tables 2 and 3, where variants with MAF<0.01 were defined as rare variants, variants with 0.05≥MAF≥0.01 defined as low-frequency variants and variants with MAF≥0.05 were defined as common variants. Second, pairs of SNPs between two genes jointly had significant interaction effects, but individually each pair of SNPs made mild contributions to the interaction effects as shown in Supplementary Table S13. Third, the FLR often had a much smaller P-value to detect interaction than PCA logistic regression, collapsing method and the minimum of P-values of pairwise logistic regression tests. Fourth, Tables 2 and 3 showed that genes may not show even mild marginal association, but they did demonstrate significant evidence of interaction.

It is interesting to note that many genes in Table 3 were reported that they were either associated with diseases or their protein products form protein–protein interaction networks.^{21, 22, 23, 24, 25, 26, 27, 28}

To investigate interaction between genes with NGS data, the four statistics were applied to the EOMI exome sequence data from the NHLBI's ESP (that can be downloaded from dbGaP), where a total of 1126 individuals (786 cases and 376 controls) with EA were exome sequenced. A total of 12 675 genes were included in the analysis. A P-value for declaring significant interaction after applying the Bonferroni correction for multiple tests was 622 × 10⁻¹⁰. In total, 24 pairs of genes showed significant evidence of interaction with P-values <1.23 × 10⁻¹¹, which were calculated by the functional logistic regression (Table 4). In Table 4, we also listed P-values for testing interactions between genes by PCA logistic regression, collapsing method and the minimum of P-values for testing all possible pairs of SNPs between two genes using standard logistic regression. For the majority of the pairs of genes, the collapsing method could not be applied and hence the P-values for these pairs of genes were not listed in Table 4. In contrary with the FHS and WTCCC studies, we often observed the pairwise interaction between rare and rare variants (69%), rare and common variants (19%), but less observed was significant pairwise interaction between common and common variants (12%). The variation of all pairs of SNPs between genes TMEM52 and TET3 could not been observed in either cases or controls. Therefore, in Table 4 NA to indicate that that the logistic regression for all pairs of SNPs could not been carried out. Again, Table 4 demonstrated that the P-values by the functional logistic regression were much smaller than that by the PCA logistic regression, collapsing methods and by the traditional pairwise logistic regression test. Similar to the CVD in the FHS and WTCCC studies, we also observed that pairs of SNPs between two genes jointly had significant interaction effects, but individually each pair of SNPs made mild contributions to the interaction effects as shown in the Supplementary Table S14 where P-values of 8 out of 25 pairs of SNPs were <0.0373. However, deep analysis revealed that the traditional logistic regression for interaction analysis was designed for common variants and should be extended to meet the challenge arising from rare variants (Supplementary Note 2). In other words, if the risk alleles at the two loci do not jointly appear in the cases, but are jointly presented in the controls then the interaction measure will become negative infinite I_GH=−∞. Again, if the risk alleles at the two loci are jointly present in cases, but never appeared in controls then interaction measure will be assigned positive infinite I_GH=∞. They are strongly interacted with each other to cause disease. Supplementary Table S15 listed the interaction measure of 13 pairs of rare variants that were not present in Supplementary Table S14 by the extended logistic regression analysis. In the functional logistic regression analysis, these rare variants were compressed into a few functional principal components and hence their interaction information were preserved in the interaction analysis between two genes and the P-value for testing interaction between TMX4 and C20orf7 were very small (P-value <1.09 × 10⁻¹⁸).

Table 4. P-values of 24 pairs of significantly interacted genes identified by FLR in EOMI dataset.

Gene 1			Gene 2			Interaction
						P-value
Gene symbol	Chr	P-value	Gene symbol	Chr	P-value	FPCA	PCA	Collapsing	Pairwise
SLC25A11	17	6.10E−01	C17orf76	17	6.65E−01	9.29E−37	4.84E−03	NA	2.14E−03
OR1M1	19	7.47E−01	LILRA5	19	2.25E−01	5.62E−28	1.15E−04	NA	3.96E−03
NUFIP2	17	7.78E−01	BECN1	17	5.34E−01	8.50E−27	3.05E−03	NA	1.90E−02
ZBTB7A	19	9.25E−01	ZSCAN1	19	7.89E−01	1.24E−26	1.03E−02	NA	1.14E−02
ENTPD5	14	7.85E−02	C14orf180	14	6.96E−01	2.32E−26	1.90E−03	NA	7.21E−03
TMX4	20	5.50E−01	C20orf7	20	8.93E−01	1.09E−18	1.96E−05	NA	6.25E−05
ZNF770	15	8.06E−01	SPATA5L1	15	3.06E−01	1.03E−17	1.85E−05	NA	4.79E−03
UBE2J2	1	1.35E−01	CCDC108	2	NA	1.56E−17	1.29E−05	6.85E−01	8.59E−04
FAM100A	16	4.36E−02	GDPD3	16	9.19E−01	2.05E−17	5.35E−06	NA	8.24E−05
TMEM52	1	7.02E−02	TET3	2	NA	2.44E−17	1.52E−13	4.51E−01	NA
SLC35E2	1	8.39E−01	TRAK2	2	NA	4.11E−17	4.63E−07	9.41E−01	1.80E−05
UBE2J2	1	1.35E−01	GRHL1	2	NA	1.01E−16	8.58E−06	NA	8.59E−04
OR4Q3	14	8.87E−01	SERPINA9	14	7.05E−01	1.20E−16	4.37E−06	NA	9.93E−04
UBE2Q2	15	8.02E−01	ABHD2	15	1.31E−01	1.66E−16	2.22E−03	NA	1.23E−02
C1orf174	1	6.75E−01	FAM128B	2	4.51E−01	1.21E−15	1.53E−05	2.26E−01	7.54E−04
SLC35E2	1	8.39E−01	STRADB	2	6.25E−01	6.51E−15	2.68E−06	5.18E−01	1.80E−05
ZNF317	19	5.28E−01	TMEM145	19	6.01E−01	1.24E−14	2.68E−06	NA	1.05E−02
TNFRSF14	1	1.96E−01	UXS1	2	4.32E−02	1.58E−14	1.05E−05	7.26E−01	4.45E−03
HES7	17	4.48E−01	KPNA2	17	6.13E−01	2.55E−14	1.90E−05	NA	5.20E−04
CD209	19	2.24E−01	NFIX	19	3.56E−01	2.73E−14	1.61E−05	NA	3.63E−04
FAM57A	17	2.85E−01	CBX1	17	3.79E−01	3.68E−14	1.18E−06	NA	1.11E−06
CYP1A1	15	1.30E−01	C15orf58	15	6.58E−01	6.43E−14	3.11E−06	NA	2.90E−07
TM4SF5	17	8.95E−01	G6PC3	17	2.78E−01	1.23E−11	5.89E−06	NA	6.04E−06

From the literature, we know that genes ZBTB7A, ZNF770, HES7 and STRADB formed protein–protein interaction networks with other proteins.^{26, 30, 35, 36, 37} ZSCAN1, UBE2J2, GDPD3, TET3, SERPINA9, ABHD2 and CYP1A1 were involved in the interaction with other proteins and associated with Alzheimer's disease, neurodegeneration, type 2 diabetes, ischemic stroke and CAD.^{29, 31, 32, 33, 34, 38, 39}

Discussion

The widely used methods for interaction analysis are based on pairwise interaction analysis. The pairwise interaction analysis was originally designed for testing the interaction between common variants and is difficult to apply to genome-wide interaction analysis for NGS data due to its lack of power to detect interaction between rare variants and rare and common variants, prohibitive computational time, and thus extremely large number of tests being conducted. To address these central themes in interaction analysis with NGS data, we shift the paradigm of interaction analysis from the pairwise test to the collective group test where we take a genome region (or gene) as a basic unit of interaction analysis and collectively test interaction between all possible pairs of SNPs within two genome regions (or genes). The purpose of this paper is to address several issues in the gene-based new paradigm of interaction analysis.

The first issue is how to use all genetic information in the genome region. To overcome limitations of pairwise interaction analysis, we proposed the functional logistic regression for collectively testing interactions between two genomic regions. The functional logistic regression first expands the genotype profiles in a genomic region (gene) in terms of orthonormal eigenfunctions. Genetic information across all variants in the genomic region including all single variant variation and their LD is compressed into a few functional principal component scores. We use genetic information compressed into functional principal component scores to globally test interaction between two genomic regions (genes).

The second issue is how to reduce the number of tests and save computational time in genome-wide interaction analysis. To reduce the dimensionality of the data, the number of tests, the time of computations and improving the power to detect interaction, we take a genomic region (or a gene) as a unit of interaction analysis and use functional data analysis to compress high-dimensional genetic data. Using large simulations and real data analysis, we showed that the proposed functional logistic regression for interaction analysis substantially improve the power and dramatically save the amount of computational time.

The third issue is how to unify the tests that can be used to test the interaction between rare and rare, rare and common, and common and common variants. The traditional pairwise logistic regression is designed for testing interaction between common variants and unable to deal with these extremely low-frequency variants. There is an increasing need to develop statistics that can be used to test interaction among the entire allelic spectrum of variants. From large-scale simulations and real data analysis, we showed that the functional logistic regression for testing interaction had the correct type 1 error rate and higher power than pairwise tests in all scenarios.

Owing to the lack of power of the widely used pairwise tests for interaction and the computational intensity, the number of genome-wide gene–gene interaction analysis has been limited. Many geneticists question the universe presence of significant gene–gene interaction. Very few genome-wide interaction analyses with NGS data and very few results of significant interaction have been replicated. To our knowledge, we are among the first to conduct genome-wide interaction analysis with exome sequencing data. From genome-wide interaction analysis of CVD and the EOMI, we have several important observations.

First, in interaction analysis with NGS data, we often observed large proportions of interactions between rare and rare variants, and rare and common variants, but observed less significant pairwise interaction between common and common variants. Second, we demonstrated that the interactions between genes can be replicated in the two independent GWAS although less interaction between SNPs can be replicated in the two studies. Third, we observed that the P-values by the functional logistic regression were much smaller than that by other existing tests in all real data analyses. Forth, there is a difference in pairwise testing two SNPs for interaction, and testing two genes. The extra power comes from the point that multiple SNPs within a gene may contribute to the disease risk.

Transition of analysis from low-dimensional data to extremely high-dimensional data demands on changes in the concept of interaction and exploration of dimensional data reduction techniques. The paradigm shift from pairwise interaction analysis to gene–gene interaction analysis with a gene as a unit of analysis and functional data analysis will provide a powerful tool for interaction analysis with NGS data. However, the results in this paper are considered preliminary. The number of eigenfunctions in the expansion of the genetic variant function will influence the performance of the functional logistic regression for interaction analysis. Although the propose approach can largely reduce the dimension of data for interaction analysis, genome-wide gene–gene interaction analysis still needs intensive computations. We are facing great challenges in genome-wide interaction analysis with NGS data. The main purpose of this paper is to stimulate research in developing novel concepts, methods and algorithms for genome-wide interaction analysis with NGS data.

The authors declare no conflict of interest.